
Interactive Chan-Vese Approach with Random Walk for Medical
Images Segmentation
Mohammadreza Hosseini
1
, Arcot Sowmya
1
and Tomasz Bednarz
2
1
School of Computer Science and Engineering, UNSW, Kensington, Sydney, Australia
2
Science and Engineering Faculty, QUT, George St, Brisbane, Australia
Keywords: Interactive, Chan-Vese, Random Walk, Energy Function.
Abstract: In this paper, we present a novel interactive variational approach to image segmentation within a Chan-Vese
framework. We propose a parameterized energy function that can be modified based on user input, and also
incorporate in it a probabilistic term that defines reachability of a pixel from a user-selected `internal’ object
pixel. The proposed approach shows promising improvement over automatic segmentation methods when
applied to medical images.
1 INTRODUCTION
Segmentation involves separating an image into
regions with some similarities. Segmentation by
evolving a contour to detect an object boundary has
been discussed before (Chan and Vese, 2001), (Kass
et al., 1988). Object detection is achieved by
minimizing the energy associated with the current
contour, usually modeled as the sum of an internal
and external energy. Level set methods are another
approach to detect object boundaries in an image
(Malladi et al., 1995). The central idea is to
represent an evolving contour using a signed
distance function, where its zero level is correlated
to the actual contour. Then, according to the motion
equation of the contour, a similar flow for the
implicit surface can be estimated. The optimal
surface zero level set is then used to determine the
object boundary. The surface flow when applied to
the zero level will reflect the propagation of the
contour. External energies relying on the image
gradient alone can miss object borders that are not
necessarily defined by their gradient. The Chan-
Vese level set method uses a stopping term instead,
that relies on the similarity of intensities in the
object against the background (Chan and Vese,
2001). The basic assumption in the Chan-Vese
method is that two regions of approximately
piecewise-constant intensity form the image. In
images where this assumption is violated because of
the presence of different objects with different
intensities, Chan-Vese fails to segment the objects
from the background. This is the main reason that
experienced observer inputs continue to be
important for image data segmentation, especially
medical images (Ben-Zadok et al., 2009). In this
paper, an interactive Chan-Vese method with user
inputs, provided as a series of selected pixels inside
the object of interest, will be explored. The
segmentation effects of adding another energy term
that models the probability of getting from a pixel to
one of selected pixels inside the object, will also be
studied.
The outline of this paper is as follows. In the
next section, a brief overview of the interactive
segmentation approaches is provided. A brief
overview of active contours is provided in section
2.1, followed by a full description of the Chan-Vese
method in section 2.2. In section 3 we introduce a
novel energy minimization model and discuss its
relationship to the Chan-Vese segmentation
approach. In section 3.1 a reachability term that
increases segmentation accuracy is added to the
proposed energy function. In section 4, we validate
our model by performing experiments on real
medical images, showing the advantages of the
proposed method, and we end the paper with a brief
concluding section.
2 BACKGROUND
To overcome the limitations of automatic
segmentation methods, researchers have proposed
Hosseini, M., Sowmya, A. and Bednarz, T.
Interactive Chan-Vese Approach with Random Walk for Medical Images Segmentation.
DOI: 10.5220/0005685400630070
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 2: BIOIMAGING, pages 63-70
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
63

new human collaborative techniques that guide the
segmentation towards the object of interest (Zhao et
al., 2013). This collaboration mostly occurs by
means of the user providing an object shape prior,
selecting some seeds inside the object of interest, or
providing boundaries around the object of interest.
The forms of collaboration differ mainly by the type
of human interaction. Prior information about object
shape or intensity distribution can be used in the
energy function and the posterior distribution
computed from the prior. Energy minimization
usually leads to selecting a segmentation that has
higher posterior. These approaches are usually
referred to as Bayesian methods for image
segmentation (Cremers et al., 2007; (Cremers et al.,
2007).
In images where objects and background may
exhibit very similar intensity characteristics, higher-
level prior knowledge about the shape of an
expected object can be merged in the Bayesian
formulation of the image segmentation problem
(Tsai et al., 2003). The use of graph-edge weights
that contain information about a level-set function of
a template, in addition to the usual boundary and
region terms, is another Bayesian approach for
image segmentation using prior shape (Chang et al.,
2008). This allows the edges of the graph to convey
information about the image as well as the prior
shape knowledge.
Boykov and Jolly (2001) and Boykov and
Kolmogorov (2000) proposed a very effective graph
cut approach for interactive image segmentation. An
initial trimap =
{
,
,
}
partitions the image
into three sets:
is the set of foreground pixels
selected by the user,
the set of background pixels
also selected by the user, and
the set of unmarked
pixels. It is assumed that the intensity distributions
of the foreground and background are either known
prior, or assembled directly from labeled pixels in
the respective trimap. For every pixel, an energy
function that evaluates the fit of the pixel to the data
model is computed. This energy function encourages
coherence in regions of similar intensities. The
graph cut algorithm adjusts the current segmentation
efficiently without recomputing the whole solution
from scratch when new seeds are incorporated into
the system. GrabCut (Kolmogorov and Blake, 2004)
is the first modification of the basic graph cut
segmentation model. In this approach the user
defines a bounding box around the object to be
segmented. The intensity distributions of the target
object and the background are estimated using a
Gaussian mixture model. This is used to construct a
Markov random field over the pixel labels, with an
energy function having internal energy that prefers
connected regions to have the same label. Using a
graph cut approach to minimize the function, the
pixel labels are estimated. This estimate is expected
to be more accurate than the original, and the two-
step procedure is repeated until convergence. The
absence of strong boundaries and the presence of a
number of objects with similar intensity profile in
some medical images cause this method to fail.
Incorporation of shape priors using a level-set
template within this framework may minimize these
problems (Freedman and Zhang, 2005).
Another type of interactive segmentation method
works by selecting seeds inside the object of interest,
with no prior information about the foreground and
background assumed (Ben-Zadok et al., 2009).
Based on user selected seeds, a new energy term is
incorporated in the energy function. This energy
term prefers that selected seeds are part of the final
object segmentation. Another approach to interactive
segmentation is through belief propagation (Zhu et
al., 2010), which starts with the user selecting seeds
inside the object of interest. The method iteratively
estimates the belief of one labeled pixel about other
pixels having the same label. Belief integration is
then used to compute the pixel label.
Random walk performs multi-label, interactive
image segmentation (Grady, 2006; Kumar et al.,
2013). Given a small number of pixels with user-
defined labels, the algorithm starts by determining
the probability that a random walker starting at each
unlabeled pixel will reach one of the pre-labeled
pixels. By assigning each unlabeled pixel to the label
that has the greatest probability, high-quality image
segmentation is obtained.
To improve the efficiency of this approach the
use of image priors to find disconnected pieces of an
object was proposed (Ruiz et al., 2015); (Grady
2005), while removing the necessity of user
interaction.
Interactive segmentation in all of the above-
discussed methods is implemented by aggregating
user input in an energy function. It is reasonable to
ask how the methods will perform if instead of
extracting a single feature based on user input,
multiple features were extracted and integrated with
the energy function. As will be discussed in this
paper, creating more features from user input and
defining energy functions based on these new
features, improves the accuracy of the interactive
method. This improvement is especially significant
in decreasing the number of pixels that are
incorrectly classified as an object.
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
64

2.1 Active Contour
The active contour model or “snakes” is a
framework for extracting objects from possibly
noisy 2D images (Kass et al., 1988). This framework
attempts to minimize the energy associated with the
current contour as a sum of an internal and external
energy such that:
i. The external energy is minimal when the snake
is at the object boundary position
ii. The internal energy is minimal when the
contour has a shape that is ‘similar’ or ‘close’
to the shape of the sought object.
In order to guarantee the stability of contour
evolution, mechanisms are used to avoid overlap of
control points, which also enables the splitting and
remerging of contours during evolution (Osher et al.
1988). Two general issues with snakes, including
poor convergence of concave boundaries and low
performance of poor initialization, can be solved
using a gradient vector flow (GVF) snake model (Xu
et al. 1988). This new active contour external energy
is computed as spatial diffusion of the gradient of an
edge map extracted from the image. For overcoming
the high computational time of GVF, other
approaches such as speedup GVF that require less
time to estimate the diffusion process is also
proposed.
2.2 Chan-Vese Approach
The Chan-Vese method (Chan and Vese 2001)
provides a model for detecting objects in an image
using the active contour and Mumford Shah’s
model, when boundaries are not defined by
gradients.
Let : Ω⟶ℝ where Ω⊂ ℝ
be an image. Let =
(,) specify the coordinates of the pixels in the
image . It is assumed that the image is composed of
two objects (background and foreground). The goal
is to evolve a curve C, such that C is at the boundary
of the object in the image. Defining
,
as the
average intensities of pixels inside and outside of the
curve respectively, the Chan-Vese method defines
the energy function
(
,
,
)
as follows:
(
,
,
)
=
(
(
,
)
)
|
(
,
)
|
(1)
+
(
,
)
+
|
(
,
)
−
|
(
,
)
+
|
(
,
)
−
|
(
1
−
(
,
)
)
where ≥0,≥0,
,
>0 are fixed parameters,
H is a Heaviside function and ⊂Ω is represented
by the zero level set of function : Ω→R such that
=
{
(
,
)
∈
Ω
:
ϕ
(
x
,
y
)
=
0
}
(
)
=
{
(
,
)
∈
Ω
:
ϕ
(
x
,
y
)
>
0
}
(
)
=
{
(
,
)
∈
Ω
:
ϕ
(
x
,
y
)
<
0
}
(2)
3 INTERACTIVE CHAN-VESE
METHOD
Assume that user inputs
{
=
(
,
)|
=1…
}
are available. These points are selected by the user
and are inside the object of interest, which we will
refer to as seeds. The assumption is that the
intensities of the selected seeds are a good
representation of the pixel intensities inside the
object. We define
=
min
{
(
)
|
=
1
,
…
,
}
=
max
{
(
)
|
=
1
,
…
,
}
(3)
which are the maximum and minimum of seed
intensities. We design two new energy terms where
one is penalized if the segmentation includes objects
with intensities lower than or higher that , and
the other one is penalized if the segmentation does
not contain objects with intensities in the range
[,]. The two functions L1 and L2 are defined as
follows:
(
)
=
2
−
−
−
1
(
)
=
(
)
(4)
where
,
are positive even integers. To
incorporate user feedback in the formulation of the
energy term in the original Chan-Vese model, we
introduce L1 and L2 into the original formulation as
follows:
(
)
=
(
,
)
|
∇
(
,
)
|
+
(
,
)
+
(
,
)
(
,
)
+
(
(
,
)
)
(
1
−
(
,
)
)
(5)
Clearly,
(
)
will be minimized if pixels with
intensities in the range
[
,
]
are within the
segmented region, and pixels with intensities outside
the range are outside the segmented region. The
results of applying this new energy function within
the Chan-Vese framework on various biomedical
images are displayed in Fig 1. It is obvious that for
Interactive Chan-Vese Approach with Random Walk for Medical Images Segmentation
65

some segmentation problems, the method performs
well, but in other cases, where there are many
objects in the same intensity range as the object of
interest, the segmentation may not be aligned with
user expectation. To overcome these limitations, an
additional energy term is introduced into the
definition of the energy function. This new term will
be referred to as reachability and is discussed next.
3.1 Reachability
To improve the generalizability of the proposed
method, a reachability concept is utilized to guide
the flow of the level set function. Reachability
ℜ
(
,
)
is defined as the probability of getting from
a pixel
(
,
)
to one of user-selected seed pixels by
moving randomly inside the image. It is assumed
that each pixel is connected to its four neighbours
and every edge connecting a pixel to its neighbour
has a weight. An edge with larger weight has a
higher chance of being picked for the next
movement from the current pixel. It can be argued
that by adding a reachability component to the
energy function developed in the last section, the
user can more specifically select an object from an
image. In the new energy function, seeds are not
only used to select the intensity range, but also to
remove other objects, which are not reachable from
the seed pixels. Reachability is inspired by random
walk based segmentation (Grady 2006). It is
assumed that the image is represented as an
undirected weighted graph =(,) where V is
the set of image pixels and E is the set of pairs of
four neighbour pixels in the image. These graph
weights are defined in such way that similar pixels
have weights with higher values. In our approach
similar pixels are those whose intensities are in the
range of
[
,
]
. Based on this assumption, a new
weight function is developed that assigns higher
weights to edges with both vertices in the required
range. For every
,
∈ where
,
∈ , the
edge weight is defined as
,
=
(
,
)
(6)
Where
,
=
(
)
−
(
)
+
−
(
)
(7)
and
(
)
is the image intensity at . In (7), edges
with end pixel intensities very close to the centre of
the range have the lower value of
,
and as a
result have a higher weight compared to other edges.
To calculate reachability ℜ, the set of image
pixels is partitioned into three different sets: “labeled
set”
, which are the seeds, “labeled background”
, which are pixels that definitely are not part of the
object since their intensities are not in the range
[,], and “Unlabeled set”
, which are the
remaining pixels. It turns out that ℜ
(
,
)
is the
harmonic solution to a combinatorial Dirichlet
problem with the seed labels as the boundary
condition (Grady 2006). The harmonic function that
satisfies the boundary condition also minimizes the
Dirichlet integral (x). By defining the
combinatorial Laplacian matrix as
=
=
−
0
ℎ
(8)
and assuming that the nodes in L are ordered such
that seed nodes are first, background nodes are
second and unseeded nodes are third,
[
]
can be
decomposed as
[
]
=
1
2
[
,
,
]
(9)
where
(,),
(
,
)
and
(,) correspond to
the reachability of the seeded, background and
unseeded nodes respectively. Differentiating
[
]
with respect to
and finding the critical points
yields
=
−
(10)
where
is the reachability of unseeded pixels.
Since the reachability of the seeded pixels is one and
background pixels have zero chance of reaching the
seeded pixels, ℜ
(
,
)
can be expressed as:
ℜ
(
,
)
=
1
,
(
,
)
∈
0
,
(
,
)
∈
(
,
)
,
(
,
)
∈
(11)
The proposed energy function is a modification of
equation (5) and now can be defined as follows:
=
(
)
−
Γ
(
ℜ
(
(
,
)
)
)
(
,
)
(12)
where
is the same as discussed in (5) ,
>0
is a fixed parameter and Γ
(
)
, referred to as the
gamma function, is selected in such a way that it has
lower value for high reachability, and higher value
for lower reachability. In the new energy function,
every pixel is not only tested for its similarity with
the intensity range of the object, but it is also
evaluated for its reachability to one of the seeds. If
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
66

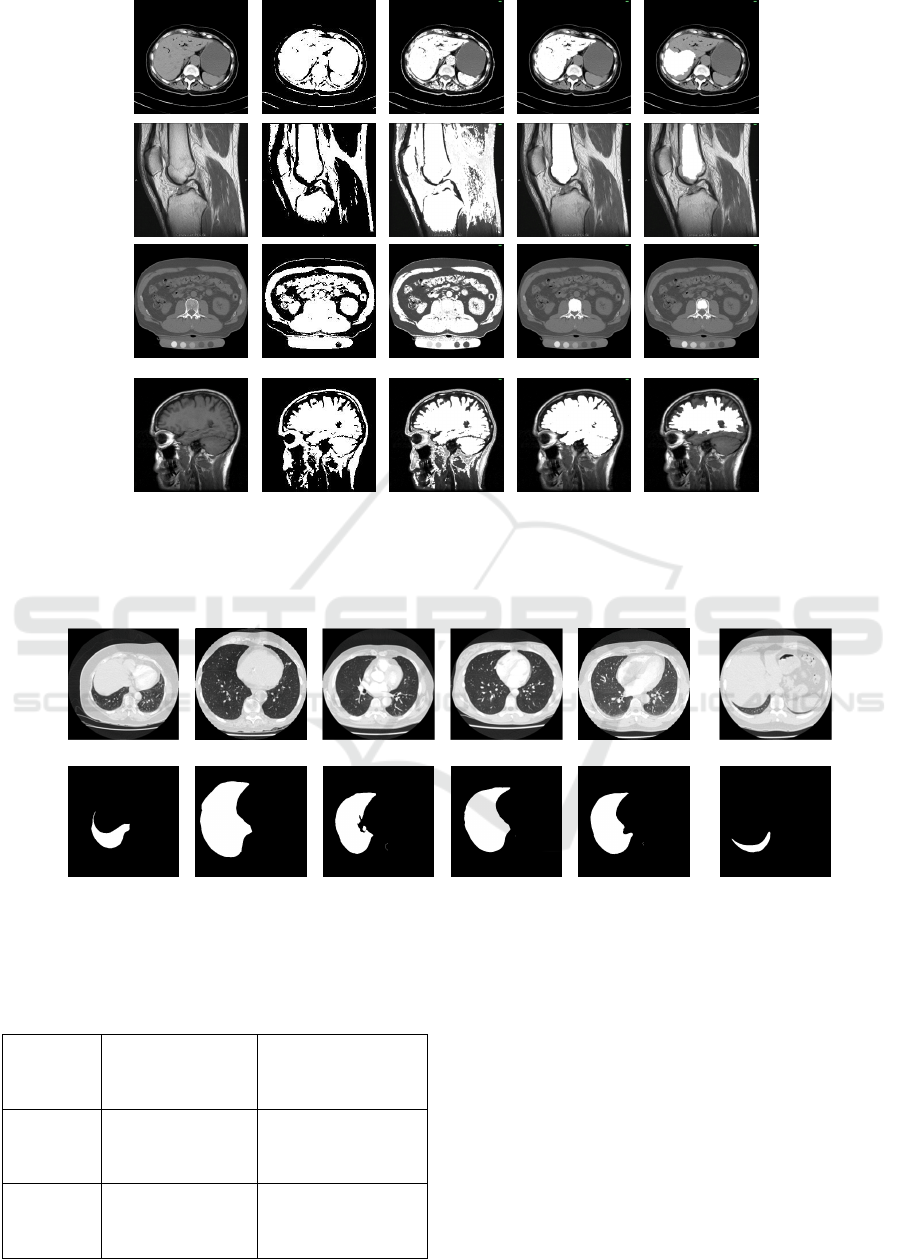
Figure 1: Applying the interactive Chan-Vese method on gray scale images. The first row shows the original images,
second row shows the results of the interactive segmentation method in (5) and the third row the original Chan-Vese
method. The first column is an image of a biofilm. The interactive approach can successfully detect the biofilm boundary.
In the second column, the method can identify the boundary of the tumour. This is because the tumour has intensity range
entirely different from other parts of the image. In the last two columns, the objects of interest are the stomach and Femur
respectively; as there are other objects with the same intensity as the object of interest, some other pixels are also returned
as the object, which is not the expected result.
the intensity of a pixel matches with the intensity
range but it is not reachable, it will eventually be
removed from the final segmentation.
4 EXPERIMENTAL RESULTS
The performance of the proposed algorithm, which
we shall refer to as “Interactive Segmentation with
Random walk”, is tested experimentally. In Fig 2, the
results of applying the interactive approach on a
series of medical images are shown. It is obvious that
the combination of intensity range and reachability in
the definition of the energy function provides
significant improvement, compared to each applied
separately. To evaluate the accuracy of the proposed
interactive method, extensive experiments were
conducted on a series of lung images from 50
different patients.
For every patient, 5 slices of the 3D lung scans
were selected and the boundaries were extracted by
an experienced radiologist to produce the ground
truth (Fig 3). The definitions used to compare the
segmentation results to ground truth appear in Table
1. Based on these definitions, the true positive
percentage is defined as :
=
+
∗
100
(13)
and the false positive percentage as:
=
+
∗
100
(14)
The average and standard deviation of true
positives and false positives computed over all
patient images are shown in Figs 4 and 5, and
establish that Interactive segmentation with random
walk has nearly the same average true positive value
as Chan-Vese, while providing a much better average
false positive value.
The proposed algorithm was further evaluated on
the test dataset using two other well-known
interactive segmentation methods, namely random
walker and (Grady 2006) and GrabCut (Kolmogorov
and Blake 2004). As Figs 6 and 7 reveal, GrabCut
has higher performance in detecting true pixels inside
the object, but is worst among the three in removing
unrelated pixels.
The bounding box around an object of interest
can describe more comprehensively the object
intensity variations compared to a few seeded pixels
selected by the user. This could explain the higher
true positive percentage of GrabCut in comparison to
the other two methods. At the same time, the
interactive segmentation with random walk approach
performs better compared to random walker alone.
Interactive Chan-Vese Approach with Random Walk for Medical Images Segmentation
67
a b c d E
Figure 2: Results of applying different methods for extracting region of interest from an image a) Original images b)
Automatic Chan-Vese method, no control over the region of interest c) Proposed method without reachability (
=0) d)
Proposed method with reachability (
> 0) e) Segmentation using only reachability in definition of energy function.
Figure 3: Lung image data set taken from 50 different patients. The first row is the original image and the second row is the
right lung detected by an experienced radiologist.
Table 1: Metrics used for comparing the segmentation
results.
Detected as
foreground
Detected as
background
Foreground
Pixel
True Positive (TP) False negative (FN)
Background
Pixel
False positive (FP) True negative (TN)
The high FPP of GrabCut in comparison to the other
two methods is because there is a chance that
unrelated pixels inside the object of interest might
also contribute to the object Gaussian mixture
model, resulting in a higher FPP. As shown in these
figures, the interactive segmentation with random
walk approach has low average FPP, which means
that it is able to remove unrelated pixels from the
final segmentation. At the same time, it performs
better than random walk in retaining related pixels in
the final segmentation.
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
68

In Figs 8 and 9, Dice Similarity Coefficient (DSC)
and the ratio of true positive rate over false positive
rate for all four different methods shows the
promising results for the proposed Interactive
segmentation with random walk method.
5 CONCLUSION
In this paper we propose a new method for detecting
objects of interest based an interactive Chan-Vese
method. The algorithm starts with the user selecting
some points inside an object. The intensities of
selected points are used to guide the flow of a level
set method. To further refine the results, a
reachability term is used in the definition of the level
set energy function. The results show the superiority
of our approach compared to the normal Chan-Vese
approach as well as random walk segmentation
alone in detecting true object pixels. It also
outperforms GrabCut in identifying background
pixels.
Figure 4: The average and standard deviation of true
positives over all images.
Figure 5: Average and standard deviation of false positives
over all images.
In this work, we assume that the user selects
pixels uniformly from a variety of intensities that
may exist in the object of interest. The effect of non-
uniform pixel selection inside the object of interest is
worth further investigation.
Figure 6: Average and standard deviation of TPP.
Figure 7: Average and standard deviation of FPP.
Figure 8: Dice Similarity Coefficient (DSC).
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
Interactive Chan-Vese
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
Interactive Chan-Vese
75%
80%
85%
90%
95%
100%
105%
Random
Walker
Interactive GrabCut
-0,1%
0,0%
0,1%
0,2%
0,3%
0,4%
0,5%
0,6%
0,7%
Random
Walker
Interactive GrabCut
Interactive Chan-Vese Approach with Random Walk for Medical Images Segmentation
69
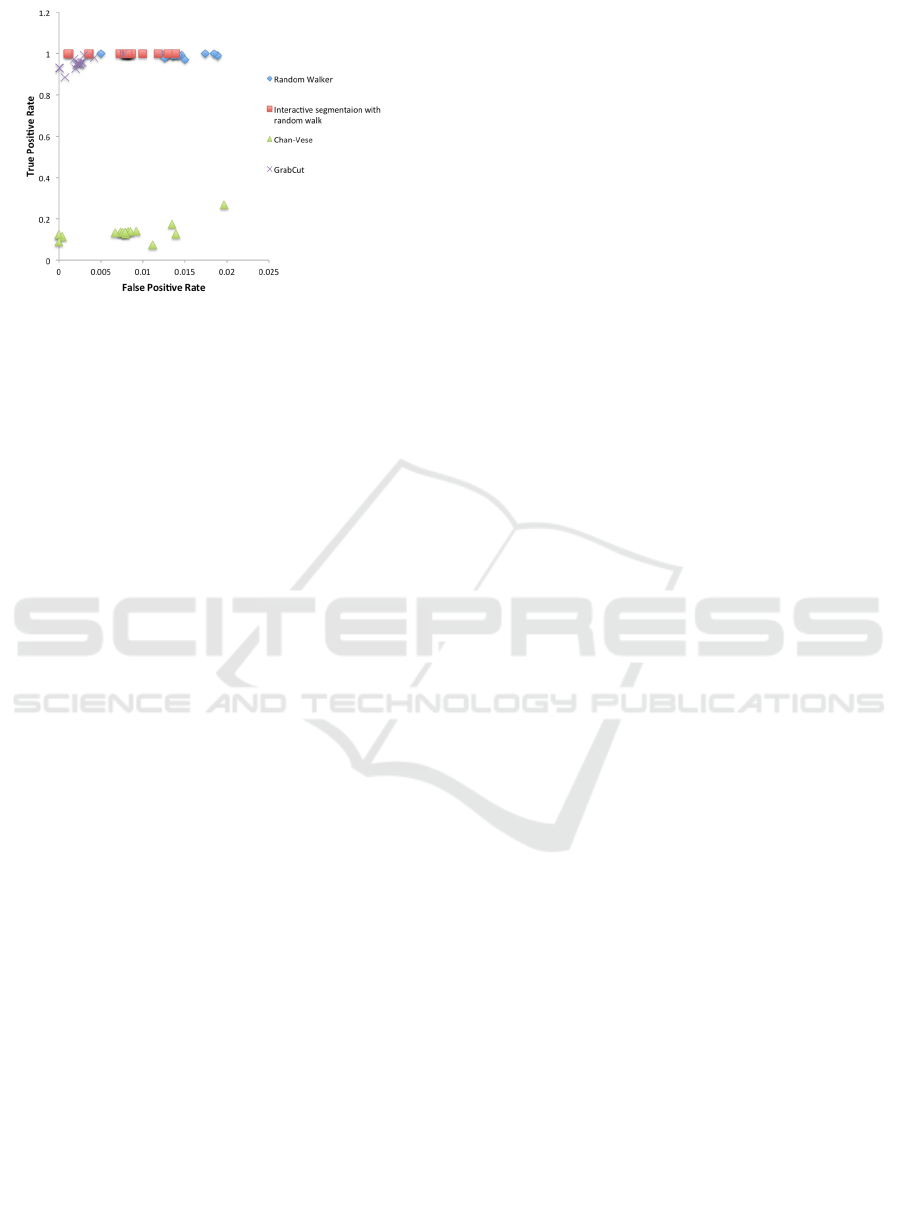
Figure 9: True positive rate vs. False positive rate.
REFERENCES
Ben-Zadok, N., Riklin-Raviv, T., Kiryati, N., 2009.
Interactive level set segmentation for image-guided
therapy. In IEEE Int. Symp. on Biomedical
Imaging, pages 1079-1082.
Cremers, D., Fluck, O., Rousson, M., Aharon, S., 2007. A
probabilistic level set formulation for interactive organ
segmentation. In Medical Imaging 2007: Image
Processing, 6512 (1): 120-129.
Cremers, D., Fluck, O., Rousson, M., Aharon, S., 2007. A
probabilistic level set formulation for interactive organ
segmentation. In Medical Imaging 2007: Image
Processing, 6512 (1): 120-129. Chan, T., Vese, L.,
2001. Active contours without edges. In IEEE Trans.
Imag. Proc., vol. 10, pp. 266-277.
Grady, L., 2006. Random walks for image segmentation.
In IEEE Trans. Pattern Analysis andMachine
Intelligence.
Jha, S.K, Bannerjeeb, P., Banika, S., 2013. Random
Walks based Image Segmentation Using Color Space
Graphs, In Procedia Technology,Vol. 10, pp. 271–278.
Boykov, Y., Jolly, P., 2001. Interactive Graph Cuts for
Optimal Boundary &, Region Segmentation of Objects
in N-D Images. In Proc. Int',l Conf. Computer
Vision, vol. I, pp. 105-112.
Rother, C., Kolmogorov, V., and Blake, A. 2004.
Grabcut—interactive foreground extraction using
iterated graph cuts. In ACM Transactions on Graphics
(SIGGRAPH).
Freedman, D., Zhang, T., 2005. Interactive Graph Cut
Based Segmentation with Shape Priors. In Proc. IEEE
Conf. Computer Vision and Pattern Recognition.
Malladi, R., Sethian, J.A, Vemuri, B.C, 1995. Shape
modeling with front propagation: A level set approach.
In IEEE Trans. Pattern Anal. Machine Intell., vol.
17, pp.158 -175.
Kass, M., Witkin, A.,Terzopoulos, D., 1988. Snakes:
Active contour models. In Int. J. Comput. Vis., vol.
1, pp.321 -331 1988.
Cremers, D., Rousson, M., Deriche R., 2007. A review of
statistical approaches to level set segmentation:
Integrating color, texture, motion, and shape. In Int. J.
Comput. Vis., vol. 72, no. 2, pp.195-215.
Tsai, A., Yezzi, A., Wells, W., Tempany, C., Tucker, D.,
Fan, A., Grimson, E., Willsky, A., 2003. A shape
based approach to curve evolution for segmentation of
medical imagery. In IEEE Trans. Medical Imaging,
22(2).
Chang, H., Yang, Q., Parvin, B., 2008. A Bayesian
Approach for Image Segmentation with Shape Priors.
In IEEE Conference on Computer Vision and Pattern
Recognition.
Boykov, Y., Kolmogorov, V., 2000. Interactive organ
segmentation using graph cuts. In Int. Conf. on
Medical Image Computing and Computer-Assisted
Intervention, pages 276-286.
Zhu, Y., Cheng, S., Goel, A., 2010. Interactive
segmentation of medical images using belief
propagation with level sets. In Proc. 2010 IEEEInt.
Conf. Image Process., pp.4113-4116.
Ruiz, E., Kjer, H.M, Vera, S., Ceresa, M., Paulsen, P.,
González-Ballester, M.A., 2015. Random Walks with
Shape Prior for Cochlea Segmentation. In Proceedings
of CARS 2015.
Grady, L., 2005. Multilabel random walker segmentation
using prior models. In IEEE Conference of Computer
Vision and Pattern Recognition, San Diego, CA, June
2005, vol. 1, pp. 763–770.
Osher, S., Sethian, J.A., 1988. Fronts propagation with
curvature-dependent speed: Algorithms based on
Hamilton, Jacobi Formulation. In Jounrnal of
Computaional Physics. 12-49.
Xu, C., Prince, J.L., 1988. Snakes,shapes and gradient
vector flow. In IEEE image processing. 359-369.
Olszewska, J., De Vleeschouwer, C., Macq, B., 2007.
Speedup gradient vector flow b-spline active contours
for robust and real-time tracking. In ICASSP, 905-908.
Zhao, F., Xie, X. 2013. An overview of Interactive
Medical Image Segmentation. In British Machine
Vision Association and Society for Pattern
Recognition. 1-22.
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
70
