
Fence Patrolling with Two-speed Robots
Jurek Czyzowicz
1
, Konstantinos Georgiou
2
, Evangelos Kranakis
3
, Fraser MacQuarrie
3
and Dominik Pajak
4
1
Departemant d’Informatique, Universite du Quebec en Outaouais, Gatineau, Qu
´
ebec, Canada
2
Department of Mathematics, Ryerson University, Toronto, Ontario, Canada
3
School of Computer Science, Carleton University, Ottawa, Ontario, Canada
4
Department of Computer Science FFPT, Wroclaw University of Technology, Wroclaw, Poland
Keywords:
Idleness, Mobile Robots, Patrolling, Speed, Walking, Scheduling.
Abstract:
A fence is to be patrolled collectively by n robots. At any moment a robot may move in one of the two possible
states: walking or patrolling. Each state is associated with a maximal moving speed which cannot be exceeded.
We want to schedule the perpetual movements of the robots so as to minimize the idleness, defined as the
smallest time interval within which every point is always visited by some robot. First, we give a centralized
algorithm constructing schedules with optimal idleness, and subsequently we show an interesting application
to a transportation problem concerning Scheduling with Regular Delivery. Our main contribution is the study
of distributed, dynamical schedules for patrolling robots with only primitive capabilities. Surprisingly, we are
able to design a dynamic schedule for very weak collections of two robots (silent, oblivious, passively mobile),
achieving the optimal idleness. Part of our contribution is a very technical analysis of the dynamics of special
families of dynamical systems of n robots that we call regular. For such systems we also propose a highly
non-trivial O(n
2
) algorithm to decide whether or not robots converge to a stable configuration thus verifying
if the dynamic schedule is optimal.
1 INTRODUCTION
Fence patrolling is the act of perpetual monitoring of
a domain, modelled as a unit segment, by a set of mo-
bile robots. As the robots cannot continuously moni-
tor all points of the domain, a standard efficiency mea-
sure of patrolling is the notion of idleness - the size of
the minimal time interval for which all points of the
domain are always visited (independently of the start
of this interval). Patrolling algorithms attempt to pro-
duce the schedules, (i.e. the trajectories of the robots
in time) minimizing idleness.
In previous research, the robots were supposed
to have either the same or different maximal speeds
of their patrolling movements. In this paper we as-
sume that the patrolling activity requires more elabo-
rate work than just walking within the domain, e.g.,
when foraging or harvesting which take longer than
walking, and in computing applications, web page in-
dexing, forensic search, code inspection, packet sniff-
ing which require a more involved inspection. Conse-
quently, we assume the maximal patrolling speeds to
be strictly smaller than the maximal walking speeds.
We suppose that each robot is capable of pa-
trolling in only one direction (arbitrarily chosen) of
the segment while walking is permitted in both direc-
tions. It is worth noting that the fence problem for
robots patrolling in both directions appears to be quite
difficult. Indeed, optimal idleness algorithms were
found only for fence patrolling of up to three robots,
(cf.(Czyzowicz et al., 2011; Dumitrescu et al., 2014;
Kawamura and Kobayashi, 2012)). Such one-way pa-
trolling assumption is natural for humans, e.g. in text
inspection (cf. the difficulty of the backward spelling
game). Several mechanical devices operate actively
in one direction only, e.g. combine and forage har-
vesters, snow-plowers. Also traveling up the hill,
swimming against river flow, carrying heavy loads -
all these activities require slower operating speeds.
We solve optimally the patrolling problem in the
centralized scenario. We also show how to apply our
algorithm to natural optimization problem in trans-
portation concerning Scheduling with Regular Deliv-
ery. Next, and more surprisingly, using a very weak
Czyzowicz, J., Georgiou, K., Kranakis, E., MacQuarrie, F. and Pajak, D.
Fence Patrolling with Two-speed Robots.
DOI: 10.5220/0005687102290241
In Proceedings of 5th the Inter national Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 229-241
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
229

collection of mobile robots with only primitive capa-
bilities, we are able to design a distributed strategy
converging to the same optimal solution thus achiev-
ing the same idleness as the optimal centralized al-
gorithm. Our robots are anonymous, oblivious, silent
(no communication permitted) and they cannot pro-
cess any information, as well as they are not aware of
their numbers or their speeds. They are subject to pas-
sive mobility, i.e. their movement is dynamically con-
trolled by their contacts with the environment. The
robots are only capable of walking or patrolling with
maximal speed and their perception mechanism per-
mits only to recognize a collision with the environ-
ment (i.e. the endpoints of the segment or another
robot). This is the first study of the patrolling problem
in a decentralized setting thus leading to the design of
a distributed, self-stabilizing algorithm (cf (Dijkstra,
1982)[EWD386, pp 34-35], which discusses a solu-
tion to a cyclic relaxation problem).
1.1 Related Work
Patrolling is the act of surveillance, consisting of
walking perpetually around an area in order to pro-
tect or supervise it, and has been studied intensively
in robotics (Almeida et al., 2004; Chevaleyre, 2004;
Elmaliach et al., 2009; Elmaliach et al., 2008; Hazon
and Kaminka, 2008; Machado et al., 2002; Yanovski
et al., 2003) where it is often viewed as a version
of terrain coverage, a central task in robotics. It is
useful in ecological monitoring, detecting intrusion,
monitoring and locating objects or humans (that may
need to be rescued from a disaster), detecting net-
work failures or even discovering web pages which
need to be indexed by search engines (Machado et al.,
2002). Boundary and area patrolling have been stud-
ied in (Agmon et al., 2008; Elmaliach et al., 2009;
Elmaliach et al., 2008; Pasqualetti et al., 2010; Hare
et al., 2015) with approaches placing more emphasis
on experimental results.
Idleness is the accepted measure of algorithmic ef-
ficiency of patrolling and is related to the frequency
with which the points of the environment are visited
(Almeida et al., 2004; Alpern et al., 2011; Cheva-
leyre, 2004; Elmaliach et al., 2009; Elmaliach et al.,
2008; Machado et al., 2002)) (this last criterion was
first introduced in (Machado et al., 2002)). Diverse
approaches to patrolling based on idleness criteria are
discussed in (Almeida et al., 2004). Patrolling as a
game between patrollers and intruder is studied in
(Alpern et al., 2009; Alpern et al., 2011; Amigoni
et al., 2010). Elsewhere patrolling is studied based on
swarm or ant-based algorithms (Elor and Bruckstein,
2010; Marino et al., 2009; Yanovski et al., 2003).
Robots are memoryless (or having small memory),
decentralized (Marino et al., 2009) with no explicit
communication permitted either with other robots or
the central station, and may have local sensing capa-
bilities (Elor and Bruckstein, 2010). Ant-like algo-
rithms usually mark the visited nodes of the graph
and (Yanovski et al., 2003) presents an evolutionary
process. This paper shows that a team of memoryless
robots, by leaving marks at the nodes while walking
through them, after relatively short time stabilizes to
the patrolling scheme in which the frequency of the
traversed edges is uniform to a factor of two (i.e., the
number of traversals of the most often visited edge
is at most twice the number of traversal of the least
visited one).
Theoretical graph-based approaches to patrolling
can be found in (Chevaleyre, 2004). In (Pasqualetti
et al., 2010), polynomial-time patrolling solutions
for lines and trees are proposed. For the case of
cyclic graphs, (Pasqualetti et al., 2010) proves the NP-
hardness of the problem and a constant-factor approx-
imation is proposed.
Optimal patrolling with same-speed robots in
mixed domains, where regions to be traversed are
fragmented by components that do not need to be
monitored, is studied in (Collins et al., 2013). Pa-
trolling with robots that do not necessarily have iden-
tical speeds offers several surprises both in terms of
the difficulty of the problem as well as in terms of
the algorithmic results obtained. Such a study has
been initiated in (Czyzowicz et al., 2011) and inves-
tigated further in (Dumitrescu et al., 2014; Kawa-
mura and Kobayashi, 2012). The partition strategy,
where each robot patrols and walks along a separate
area, has been proven to work for two robots in (Czy-
zowicz et al., 2011), and for three in (Kawamura and
Kobayashi, 2012).
Standard capabilities of mobile robots usually in-
clude communication, computation, and environment
perception. For many reasons (e.g. production cost,
limited or specific applications) one may wish to deal
with robots of reduced ability, especially if they are
needed in large numbers. In such cases, feasibility
issues, rather than computation efficiency are sought
(Angluin et al., 2006; Angluin et al., 2007; Beauquier
et al., 2010; Cieliebak et al., 2012). (Angluin et al.,
2006) introduced population protocols (see also (An-
gluin et al., 2007; Beauquier et al., 2010)), where
robots are subject to passive mobility, also used in our
paper. Passive mobility aims to model volatile envi-
ronments like water flow, wind or unstable mobility
of agents’ carriers. Further, (Beauquier et al., 2010)
considered different speed of such agents. (cf. also
(Czyzowicz et al., 2013)).
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
230

1.2 Our Model, Problem Definition &
Notation
Consider a set R of n mobile robots r
1
,... ,r
n
each
associated with some patrolling speed p
i
and some
walking speed w
i
, where p
i
< w
j
for i, j = 1,...,n.
Robots perpetually move along the unit segment [0,1]
in both directions. At any moment, a robot r
i
may
be in a walking state in which it moves at its walking
speed w
i
or in the patrolling state and moving at its
patrolling speed p
i
. Each robot may walk in both di-
rections but its patrolling is always done in the same
direction of the interval [0,1]. Hence we can say that
each robot is associated with its patrolling direction
(positive or negative direction of the interval) which
does not change throughout its entire movement.
The Fence Patrolling Problem: Let S denote a pa-
trolling schedule, i.e. an algorithm associated with
each of the robots dictating on what speed and in
what direction every robot moves at each moment of
time. Given a schedule produced by algorithm A, the
idle time I
A
(P,t) of a point P at time t is defined as
the amount of time needed to the next visit of P af-
ter time t by any robot of R: I
A
(P,t) = min{t
v
> t :
∃i(0 ≤ i ≤ n such that r
i
(t
v
) = P)}−t, where we de-
note by r
j
(t) the point of the segment visited by r
j
at
time t, for t ∈ [0,∞). We are interested in an algo-
rithm minimizing the maximal idle time taken over
all points P and all time moments t. However, as
it may be impossible to design an algorithm which
achieves the best possible idle time right from the start
of the schedule (e.g. robots may be in an unsuitable
position to achieve this) we will be allowing any fi-
nite delay for checking idle times of segment points.
More exactly, the idleness of algorithm A is defined as
I
A
= inf
T ≥0
sup
0≤p≤1
I
A
(P,T ). An optimal patrolling
algorithm is a schedule which optimizes the idleness
among all possible patrolling algorithms under con-
sideration.
It will be useful to observe that our goal may
be viewed as the following equivalent maximization
task. Suppose that the robots operate in an infinite
line. What is the maximal length segment [0, L] and
the perpetual movement of the robots of R, such that
in each unit time interval [t,t + 1] each point of [0, L]
is visited at least once by a robot in patrolling state.
We call such a length L the patrolling range of R.
The Distributed Model: In this model, robots have
only very primitive capabilities allowing them to ex-
ecute separate schedules which change according to
their perception of the environment. They are oblivi-
ous and silent (cannot communicate) and they cannot
process any information. Besides two-speed mobil-
ity they can perceive the environment by recognizing
obstacles (i.e., endpoints) or other robots that they do
not even need to recognize. They are not aware of
their patrolling or walking speeds nor of the length
of the segment. In the schedules produced by our
distributed algorithms the robots function according
to the bouncing-rule: if a robot collides with another
robot or a segment endpoint, then it changes direction
as well as moving-state. A patrolling schedule of n
robots is in a stable configuration (x
∗
1
,. .. ,x
∗
n
) if robot
i moves within the interval [x
∗
i−1
,x
∗
i
] (we set x
∗
0
= 0
and x
∗
n
= 1), bouncing always at its endpoints.
Scheduling with Regular Delivery: Our tech-
niques allow us to solve the following transportation
problem. Suppose that at point 1 of the unit segment
there is an infinite quantity of a commodity that is
transported to point 0 by robots R. Each robot may
carry one item of the commodity using a speed not ex-
ceeding p
i
or it may travel with no load with a speed
not exceeding w
i
. At any time a robot r
i
may drop the
item it is carrying at the point currently occupied by
r
i
or it may pick up an item present at its current posi-
tion. In particular, when two robots meet at a point an
item being carried by one of them may be transferred
to the other one. At all times no robot may carry more
than one commodity item. What is the smallest value
I, such that during any time interval (kI, (k + 1)I] a
new item is delivered to point 0.
1.3 Our Contributions & Organization
of the Paper
We attempt to solve the Fence Patrolling Problem us-
ing centralized or distributed algorithms. As a warm-
up, we give in Section 2 an optimal centralized al-
gorithm for the problem, whose solution serves as a
benchmark for subsequent sections. We conclude in
Section 2.2 with an interesting application to an opti-
mization transportation problem. Our main technical
contributions appear in Section 3 where we study the
Fence Patrolling Problem in a distributed setting and
where robots have only primitive capabilities. First,
in Section 3.1 we optimally solve Fence Patrolling
with 2 primitive robots. In the same section, we also
develop the main ideas we built upon for patrolling
with an arbitrary number of robots. Then, in Sec-
tion 3.2 we introduce a generic distributed solution
for patrolling with primitive robots. Our solution in-
duces a complex dynamical system, whose analysis is
the main focus of the remaining of the sections. Sec-
tion 3.3 proposes a technical and highly non-trivial
analysis of the dynamics of primitive robots, and con-
Fence Patrolling with Two-speed Robots
231

cludes with an efficient and analytic algorithm for
deciding whether the system of robots converges to
an optimal solution. Finally, Section 3.4 studies re-
stricted, yet natural families of primitive robot col-
lections that have the potential of inducing dynamic
systems that converge to stable and optimal solutions.
With non-trivial and technical arguments, we con-
clude by showing that special families of three and
four primitive robots do solve the Fence Patrolling
problem optimally.
2 OPTIMALLY SOLVING FENCE
PATROLLING BY
CENTRALIZED ALGORITHMS
In this section we give the general, centralized al-
gorithm generating optimal patrolling schedules for
the Fence Patrolling Problem and for any number of
robots.
2.1 Schedule Obtained by a Centralized
Algorithm
Consider the schedule defined by Algorithm 1. The
Algorithm 1: Centralized Schedule.
Input: Set of robots R with associated walking and
patrolling speeds
Output: Schedule of R
1: Let σ
j
=
∑
j
i=1
1
1/p
i
+1/w
i
for j = 1,. .. ,n
2: for j = 1,...,n do
3: Place robot r
j
at initial position x
j
= σ
j
/σ
n
4: repeat forever
5: In patrolling state, move (left) at speed p
j
until reaching point x
j−1
6: In walking state, move (right) at speed w
j
until reaching point x
j
idea of the algorithm is to divide the unit interval into
subsegments, and to make each robot operate only in
the subsegment associated with it. Robot r
i
is associ-
ated with a subsegment of size proportional to
p
i
w
i
p
i
+w
i
.
Each robot zigzags between the endpoints of its sub-
segment patrolling in one direction and walking in the
opposite direction.
Theorem 2.1. Algorithm 1 produces an optimal pa-
trolling schedule.
Before we provide the proof of Theorem 2.1 we
show Lemmata 2.2 and 2.3.
Lemma 2.2. The idleness I
1
of Algorithm 1 satisfies
I
1
= 1/
∑
n
i=1
1
1/p
i
+1/w
i
.
Proof. As σ
j
, j = 0, .. ., n, is an increasing se-
quence, each robot r
j
operates within the subsegment
[x
j−1
,x
j
], for j = 1,. .. ,n, having interior disjoint with
all other subsegments. Consider any index j and any
point x ∈ [x
j−1
,x
j
]. Denote by t
∗
a time when r
j
is in
the patrolling state and r
j
(t
∗
) = x. Before r
j
visits x
in patrolling state the next time, it has to traverse from
x to x
j−1
patrolling followed by walking the subseg-
ment [x
j−1
,x
j
] and patrolling from x
j
to x. The time
needed for this equals
x −x
j−1
p
j
+
x
j
−x
j−1
w
j
+
x
j
−x
p
j
=(x
j
−x
j−1
)
1
p
j
+
1
w
j
=
1
∑
n
i=1
1
1/p
i
+1/w
i
Lemma 2.3. Let D > 1 be the distance patrolled by
robot r
i
during some time interval. Then in the same
time interval r
i
must walk distance at least D −1.
Proof. Suppose, by symmetry, that r
i
can patrol only
in the right-to-left (i.e. negative) direction of the in-
terval. The difference between the initial and the final
position of the robot equals to R −L, where L denotes
the sum of the lengths of its left-to-right moves and
R denotes the sum of the lengths of its right-to-left
moves. Observe that R −L ≤1. As the total patrolling
distance is at most R and the total walking distance is
at least L we have the claim of the lemma.
We are now ready to prove Theorem 2.1.
Proof of Theorem 2.1. Consider any algorithm A
and its idleness I
A
. It is sufficient to show, that for any
ε > 0 there exists a time interval T = [t
∗
,t
∗
+ I
1
−ε]
during which some point of the segment is not pa-
trolled by any robot. Let κ be an integer such that
κ >
∑
n
i=1
1/w
i
1/p
i
+1/w
i
ε
∑
n
i=1
1
1/p
i
+1/w
i
. Consider any time interval K of
size = κI
A
. We prove that K must contain interval T
with the property from the claim made above.
Let d
i
denote the distance traversed by r
i
while
patrolling during interval K. As each point of the seg-
ment must be patrolled at least κ times during time
interval K we have
∑
n
i=1
d
i
≥ κ. By Lemma 2.3 we
have
d
i
p
i
+
d
i
−1
w
i
≤ κI
A
, hence d
i
≤
κI
A
+1/w
i
1/p
i
+1/w
i
. There-
fore κ ≤
∑
n
i=1
d
i
≤κI
A
∑
n
i=1
1
1/p
i
+1/w
i
+
∑
n
i=1
1/w
i
1/p
i
+1/w
i
and
I
A
≥
1
∑
n
i=1
1
1/p
i
+1/w
i
−
∑
n
i=1
1/w
i
1/p
i
+1/w
i
κ
∑
n
i=1
1
1/p
i
+1/w
i
≥
1
∑
n
i=1
1
1/p
i
+1/w
i
−ε
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
232

This proves Theorem 2.1.
Due to Lemma 2.2, it follows that almost all points
of the segment have the same idle time (with the ex-
ception of the endpoints of subsegments which may
be alternately visited by two robots). From Algo-
rithm 1, it follows that each robot r
i
operates solely
inside a subsegment of size
1
1/p
i
+1/w
i
/
∑
n
i=1
1
1/p
i
+1/w
i
,
for i = 1, .. ., n. By scaling down the consideration to
the idle time of 1 we easily obtain:
Corollary 2.4. The patrolling range of robot r
i
hav-
ing patrolling speed p
i
and walking speed w
i
equals
1
1/p
i
+1/w
i
. The patrolling range of a set of robots
equals the sum of their patrolling ranges.
2.2 Application to Transportation:
Scheduling with Regular Delivery
In this section we show an interesting application of
our previous findings in Scheduling with Regular De-
livery (see Section 1.2 for the definition). The fol-
lowing Proposition shows that the idleness of Algo-
rithm 1 is the optimal value for the problem concern-
ing Scheduling with Regular Delivery.
Proposition 2.5. The solution (i.e., the optimal time
interval) of the problem concerning Scheduling with
Regular Delivery for the set of robots R equals I
1
- the
idleness of Algorithm 1.
Proof. Each robot of Algorithm 1 revisits the left end-
point of its subinterval (and also its right endpoint)
regularly at time intervals of I
1
. It is then possible
to synchronize robot movements so that each robot
gets to its subsegment left endpoint (or right endpoint)
exactly at the same when arrives there the left (resp.
right) neighbouring robot. Suppose that robot r
n
picks
up an item at each visit to point 1 of the segment, and
that, each time a robot reaches the left endpoint of
its subinterval, it transfers the carried item to its left
neighbour. Then each robot r
i
either walks left-to-
right unload with speed w
i
or transports one item trav-
eling right-to-left. Consequently, r
1
delivers one new
item to point 0 at regular time intervals I
1
. The opti-
mality follows by the argument similar to that used in
the proof of Theorem 2.1.
3 FENCE PATROLLING WITH
PRIMITIVE ROBOTS / THE
DISTRIBUTED CASE
In this section we consider the case when the collec-
tion of patrolling robots acts in a distributed way (see
Section 1.2 for the model). We are interested in an
algorithm having the same idleness as the one of the
optimal centralized algorithm even if our robots are
very weak. For notational reference we will assume
that there exist two motionless robots r
0
and r
n+1
(i.e.
w
0
= p
0
= w
n+1
= p
n+1
= 0), positioned at the left
and right endpoint, respectively. This way every robot
r
i
, for i = 1, .. ., n, bounces at its left or right neighbor.
We have the following lemma.
Lemma 3.1. For any collection R of robots there
exists a centralized algorithm producing an optimal
schedule in stable configuration, in which the robots
behave according to the bouncing rule.
Proof. Consider the partition of the unit interval as in
line 1 of Algorithm 1. By Corollary 2.4 each robot
executing Algorithm 1, within the same time inter-
val, independently covers a segment subinterval pro-
portional to its patrolling range. It is then possible
to reschedule the robots’ starting times so that each
robot arrives at the left endpoint of its subinterval ex-
actly at the same time as when its left neighbor ar-
rives at the right endpoint of its interval, resulting in a
meeting.
We will attempt to design a distributed algorithm
producing robots trajectories converging to a schedule
of a stable configuration of robots. The task seems of
special interest, given that robots are assumed to be
oblivious and silent.
3.1 Distributed Optimal Schedule for
Two Robots
The purpose of this section is to demonstrate that two
primitive robots can optimally solve the Fence Pa-
trolling Problem.
Let I
opt
be the optimal idleness of the offline
schedule for two robots. We design an algorithm, for
which for any ε > 0 there exists a time t
∗
, such that
in every time interval [t,t + I
opt
+ ε], with t ≥t
∗
, each
point of the segment is visited by some robot. Ob-
viously, using such weak robots, it is impossible to
design an algorithm which achieves optimal idle time
only after some finite time of their operation. This
would need robots capable of recognizing the param-
eters of the environment (e.g. patrolling and walk-
ing speeds of robots, distance traveled, time between
collisions, etc.). Since robots react only when collid-
ing with each other, or when they reach one endpoint
(as if they do not know when collisions will occur or
where the endpoints are) we slightly abuse standard
terminology and we call our algorithm online.
We show that Algorithm 2 is the optimal one, i.e.
its idleness equals the idleness of the optimal offline
Fence Patrolling with Two-speed Robots
233
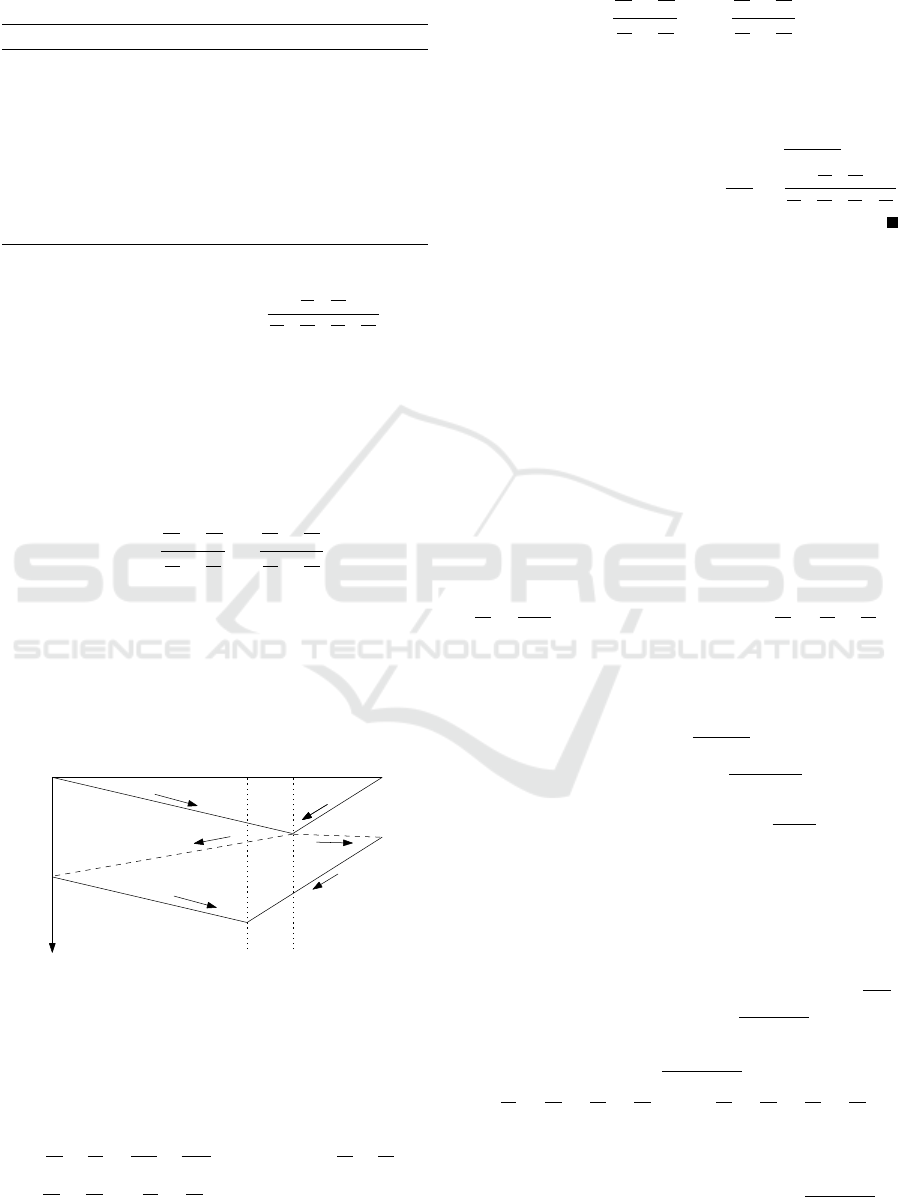
Algorithm 1. The first critical observation is that col-
lision points converge to a stable configuration.
Algorithm 2: Online Schedule for Two Robots.
Input: Two robots r
1
,r
2
placed at the two segment
endpoints
Output: Schedule of R
1: Both robots start in patrolling state moving to-
wards each other.
2: Each robot switches state and direction when col-
liding either with the other robot or with an end-
point.
Lemma 3.2. The sequence of collision points of Al-
gorithm 2 converges to the point
1
p
2
+
1
w
2
1
p
1
+
1
w
1
+
1
p
2
+
1
w
2
.
Proof. Suppose that the two robots following the
schedule produced by Algorithm 2 meet at a point x,
0 < x < 1. Suppose also that before the meeting both
robots were in the patrolling state and moving towards
each other. We show first that the next meeting occurs
at a point x
0
such that
x
0
= −
1
w
1
+
1
w
2
1
p
1
+
1
p
2
x +
1
p
2
+
1
w
2
1
p
1
+
1
p
2
(1)
Indeed, as p
1
< w
2
and p
2
< w
1
no robot can
be caught from behind by another one, while walk-
ing along the segment. Consequently, both robots
reach the segment endpoints and they restart pa-
trolling while moving towards each other, eventu-
ally colliding at x
0
. As both robots spend the same
0
1
p
1
w
1
w
2
p
2
t
xx
0
Figure 1: Two robots r
1
,r
2
start by patrolling in opposite di-
rections. They first collide at a point x and they both change
to walking. After bouncing (not necessarily at the same
time) at the endpoints of the interval [0,1] they change to
patrolling and meet anew at point x
0
. The vertical line indi-
cates time.
time while traveling from x to x
0
(cf. Figure 1) we
have
x
w
1
+
x
0
p
1
=
1−x
w
2
+
1−x
0
p
2
. Therefore x
0
1
p
1
+
1
p
2
=
−x
1
w
1
+
1
w
2
+
1
p
2
+
1
w
2
. We see from Identity (1)
that x
0
= −Ax + B where
A :=
1
w
1
+
1
w
2
1
p
1
+
1
p
2
,B :=
1
p
2
+
1
w
2
1
p
1
+
1
p
2
. (2)
If x
1
is the initial collision point then we see that
the kth collision point satisfies the recurrence x
k
=
−Ax
k−1
+ B. This yields a geometric series from
which it follows that x
k
= (−A)
k
x
0
+B
1−(−A)
k
1+A
. Since
A < 1 as k → ∞ we get x
k
→
B
1+A
=
1
p
2
+
1
w
2
1
p
1
+
1
w
1
+
1
p
2
+
1
w
2
which completes the proof.
Our intention is to generalize the lemma above for
dynamic systems with arbitrarily many robots. Till
then, we show that Algorithm 2 produces the optimal
schedule.
Theorem 3.3. The idleness of the schedule of Algo-
rithm 2 equals I
1
- the idleness of the optimal schedule
produced by the centralized algorithm.
Proof. It is sufficient to show that for any ε > 0 there
exists a point in time t
∗
such that for any t > t
∗
and
any time interval T = [t,t + I
1
+ ε] each point of the
segment is patrolled by some robot. Observe that
from the start to the first meeting point x
0
robot r
1
patrols the interval [0,x
0
], while during the same time
interval r
2
patrols the interval [x
0
,1]. Hence we have
x
0
p
1
=
1−x
0
p
2
. Solving for x
0
we get x
0
=
1
p
2
/
1
p
1
+
1
p
2
.
Observe that the distance D = |x
k
−x
k−1
| between
the (k −1)-th and k-th meeting points (defined in the
proof of Lemma 3.2)
D =
(−A)
k
x
0
+ B
1−(−A)
k
1+A
−
(−A)
k−1
x
0
+ B
1−(−A)
k−1
1+A
=
((−A)
k
−(−A)
k−1
)(x
0
−
B
1 + A
)
= |(−A)
k
(B −x
0
(A + 1))|
= A
k
(B −x
0
(A + 1))
(since A > 0 & (B −x
0
(A + 1)) > 0)
is converging to 0, since |A| < 1. As x
k
and x
k−1
are
on the different sides of the convergence point
B
1+A
,
within every time interval I
1
+
D
min(p
1
,p
2
)
the entire
segment is jointly patrolled by both robots. Let K
be such that K ≥ log
A
ε·min(p
1
,p
2
)
B−x
0
(A+1)
and let t
∗
> (K +
1)(
1
p
1
+
1
w
1
+
1
p
2
+
1
w
2
). As (
1
p
1
+
1
w
1
+
1
p
2
+
1
w
2
) is
the time between two consecutive bounces between
robots r
1
,r
2
, after time t
∗
the robots bounced at least
k times. Hence (as 0 < A < 1) for t > t
∗
the idle time
I(p,t) of every point p is I(p,t) ≤ I
1
+
D
min(p
1
,p
2
)
=
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
234

I
1
+
A
k
(B−x
0
(A+1))
min(p
1
,p
2
)
≤I
1
+ε, which proves the theorem.
Observe that Algorithm 2 works even if the robots
do not necessarily start their respective schedules at
the same time. Indeed, because p
i
< w
j
, i, j = 1,2,
when the second robot wakes up and starts patrolling
it cannot meet the robot which started first while this
robot is in the walking state. Therefore the robots
meet when they are both in the patrolling state and
the subsequent meetings converge to the same point
as before.
Note that, when robots start walking rather than
patrolling, their subsequent meeting points do not
converge.
1
On the other hand if one robot starts in
the walking state while the other one in the patrolling
state the convergence is possible in at most one of
the two symmetric cases, depending which among the
two values 1/p
1
+ 1/w
2
or 1/w
1
+ 1/p
2
is larger. In
particular, when 1/p
1
+ 1/w
2
= 1/w
1
+ 1/p
2
(e.g. in
the case of identical robots) the meeting points alter-
nate between two symmetric positions on the segment
and the idleness is clearly suboptimal (cf. Fig. 2).
0
1x
(0)
= x
(2)
x
(1)
p
1
w
1
w
2
p
2
Figure 2: Two robots r
1
,r
2
perpetually alternate between
x(0) and x(1) (r
1
starts by patrolling and r
2
by walking).
Here w
1
= 5, p
1
= 3
1
7
,w
2
= 10, p
2
= 4.
3.2 Distributed Schedule for n Primitive
Robots
In this section we propose a distributed solution for
an arbitrary number of primitive robots that induces
an interesting dynamic system, which we analyze in
subsequence sections.
As observed for the case of two robots, the conver-
gence was attested if the two robots were colliding al-
ways in the patrolling state. For more than two robots
this condition can no longer be guaranteed as all but
two robots collide with both neighbors. We begin our
1
This follows from the proof of Theorem 3.3, as in this
case, the critical value of quantity A =
1/p
1
+1/p
2
1/w
1
+1/w
2
> 1 (the
roles of patrolling and walking speeds are swapped in the
equation for x
0
).
analysis by proposing Algorithm 3, an intuitive dis-
tributed schedule that assumes the bouncing rule, i.e.
that robots can respond to bounces by flipping their
moving state (e.g. from walking to patrolling) and
their moving direction. Moreover, as in our setting
robots will start walking simultaneously at the same
segment endpoint we naturally assume that p
i
6= p
j
(and that w
i
6= w
j
), otherwise identical robots would
always stay together and only one of them would con-
tribute to the patrolling algorithm. As all robots pa-
Algorithm 3: Distributed Schedule for Many Robots.
Input: A collection R of robots with distinct pa-
trolling and walking speeds
Output: Schedule of R
1: All robots start from the rightmost endpoint of the
interval, in patrolling state moving right-to-left.
2: Each robot switches state and direction while col-
liding with the other robot or with an endpoint.
trol in the same direction and they change states only
when meeting we can conclude with the following:
Observation 3.4. Algorithm 3 produces a dynamic
schedule with Regular Delivery, for a given set of
robots.
Notice that our algorithm defines a complex dy-
namical system of memoryless robots moving back
and forth in an interval. The analysis of the system
dynamics is very complicated, given that robot col-
lisions might occur either between robots moving in
opposite directions, or in the same directions (i.e. a
collision may happen from behind). In what follows
we analyze the dynamics under the assumption that
we have one type of collisions, which as we shall see
in the next subsections naturally arise by restricting
the configuration of the robot speeds to what we later
call monotone speeds.
We call the dynamical system that arises from Al-
gorithm 3 regular if collisions occur only between
robots that move in opposing directions, and there-
fore collisions happen only between a robot that is
in patrolling state moving right-to-left and a robot in
walking state moving left-to-right. We are interested
in answering whether regular dynamical systems con-
verge in a stable configuration, and whether this con-
figuration has optimal idle time. Below we propose
a highly efficient algorithm for verifying whether a
regular dynamical system has this property (for any
number of robots). Then we answer this question in
the positive for up to 4 robots, under the assumption
that speeds satisfy a natural condition.
Fence Patrolling with Two-speed Robots
235

3.3 Dynamics for Regular Systems of
Primitive Robots
Dynamic systems of primitive robots induced by Dis-
tributed Algorithm 3 are highly complex and difficult
to analyze. The purpose of this section is to provide a
deep and technical analysis of the dynamics of regu-
lar systems. We conclude the section by proposing a
highly non-trivial algorithm for deciding convergence
of primitive robots in a stable configuration (where
robots eventually move in disjoint subintervals).
Notice that in every dynamical system, and at ev-
ery point in the time horizon, robots will appear on
the interval in the same order. We rename the robots
so that robot i+1 is always to the right of robot i, after
they develop according to Algorithm 3. Below we de-
note by x
i
t
the point in the interval where robots r
i
,r
i+1
bounce for the t-th time. The purpose of the next
lemma is to predict points x
i
t
. The reader may view
it as the analogue of (part of the proof of) Lemma 3.2
that dealt with only two robots.
Lemma 3.5. In a regular system we have
1
p
i+1
+
1
w
i
x
i
t+1
−
1
p
i
+
1
w
i
x
i−1
t+1
=
1
p
i+1
+
1
w
i+1
x
i+1
t
−
1
p
i
+
1
w
i+1
x
i
t
Proof. First we claim that x
i−1
t
< x
i
t
, i = 1,. .. ,n,
and that robots r
i−1
,r
i
bounce at x
i−1
t
before r
i
,r
i+1
bounce at x
i
t
. Indeed, let τ(x
i
t
) denote the time of this
bounce. Note that robot r
1
(while patrolling) bounces
first at the origin and on its way back (now walk-
ing) bounces with robot r
2
(which is patrolling). Af-
ter robot r
2
bounces with robot r
1
, it begins walking
and eventually bounces with robot r
3
which moves
in opposite direction and is patrolling, etc. This rea-
soning shows that x
i−1
1
< x
i
1
, i = 1,. ..,n as well as
that r
i−1
,r
i
bounce for the first time before r
i
,r
i+1
do.
Since the system is regular, each robot alternates its
bounces between both neighbors r
i−1
, r
i+1
which is
sufficient to conclude the claim.
Next observe that between time τ(x
i
t
) and τ(x
i
t+1
)
robot r
i−1
first patrols right-to-left the interval
[x
i−1
t+1
,x
i
t
] then it walks left-to-right the interval
[x
i−1
t+1
,x
i
t+1
]. During the same time interval r
i
first
walks left-to-right the interval [x
i
t
,x
i+1
t
] then it patrols
right-to-left the interval [x
i
t+1
,x
i+1
t
] (see Figure 3).
Comparing both times we get
x
i
t
−x
i−1
t+1
p
i
+
x
i
t+1
−x
i−1
t+1
w
i
=
x
i+1
t
−x
i
t
w
i+1
+
x
i+1
t
−x
i
t+1
p
i+1
. Regrouping terms implies the
lemma.
t
p
i
w
i
p
i+1
w
i+1
w
i+1
p
i+1
p
i
w
i
x
i−1
t+1
x
i
t
x
i
t+1
x
i+1
t
Figure 3: Two time consecutive bounces between robots
r
i
,r
i+1
.
We can rewrite the recurrence in Lemma 3.5 in a
more concise matrix form. Define the following ma-
trices.
A = diag
1
p
i+1
+
1
w
i
i=1,...,n−1
−L-diag
1
p
i
+
1
w
i
i=2,...,n−1
(3)
B = diag
1
p
i
+
1
w
i+1
i=1,...,n−1
(4)
−U-diag
1
p
i
+
1
w
i
i=2,...,n−1
(5)
c
T
=
0,. .. ,
1
p
n
+
1
w
n
,
where by L-diag and U-diag we mean the low and
upper diagonal matrices of dimension (n −1) ×(n −
1) and entries as indicated placed below and above
the main diagonal, respectively.
Theorem 3.6. Consider a regular dynamical system
of n robots (produced by Algorithm 3) and let A, B,c
be the matrices defined in Equations (4). If the moduli
(norms) of all eigenvalues of the matrix A
−1
B are less
than 1, then the schedule of Algorithm 3 converges to
a schedule in stable configuration which is also opti-
mal (w.r.t. to centralized algorithms). In particular,
for every ε > 0, after Θ (log1/ε) bounces (iterations)
of any pair of neighboring robots the idle time I
3
(p,t)
is such that I
3
(p,t) ≤ (1 + ε)
1
∑
n
i=1
1
1/p
i
+1/w
i
.
Proof. Let X
t
∈ R
n−1
be the vector
x
1
t
,. .. ,x
n−1
t
T
.
Then the recurrence of Lemma 3.5 can be rewritten in
matrix form as AX
t+1
+BX
t
= c. From this, we derive
that
X
t
=
(−1)
t
A
−1
B
t
+
I + A
−1
B
−1
I −(−1)
−1
A
−1
B
t
A
−1
c.
Next consider the eigenvalue decomposition A
−1
B =
QΛQ
T
, where Q is an orthogonal matrix. Then
A
−1
B
t
= QΛ
t
Q
T
, and since lim
t→∞
Λ
t
= 0 as all
eigenvalues have norm less than 1, we conclude
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
236

that lim
t→∞
X
t
exists, i.e. the sequence converges to
X
∗
=
I + A
−1
B
−1
A
−1
c = (A + B)
−1
c and the con-
vergence is linear. From the definition of the recur-
rence, it follows that the schedule of Algorithm 3 con-
verges to the schedule S which is in stable configura-
tion X
∗
.
By Corollary 2.4 which, in view of Lemma 3.1,
applies also to stable configurations the patrolling
range of the collection of robots equals
∑
n
i=1
1
1/p
i
+1/w
i
and by the rate of convergence, after Θ (log1/ε)
bounces of neighboring robots, the idle time is already
no more than than (1 + ε)
1
∑
n
i=1
1
1/p
i
+1/w
i
.
Note that already Theorem 3.6 suggests a nu-
merical method for checking whether the dynamical
system arising from Algorithm 3 converges or not;
given patrolling and walking speeds p
i
,w
i
, first com-
pute matrix A
−1
, and then calculate all eigenvalues of
A
−1
B and verify that their norm is less than 1. Ma-
trix inversing can be done explicitly and efficiently,
say by Gauss-Jordan elimination or by LU decompo-
sition. Finding however the eigenvalues of the non-
Hermitian matrix A
−1
B is at least as difficult as find-
ing the roots of high degree polynomials. In light
of Abel’s impossibility theorem, one has to rely on
numerical methods to verify that the moduli of the
eigenvalues of A
−1
B are indeed less than 1. In fact,
a number of sophisticated numerical methods have
been proposed to efficiently find eigenvalues of spe-
cial families of matrices.
We depart from this approach, and in contrast to
numerical methods, we propose an explicit, symbolic
and efficient algorithm for verifying the precondi-
tion of Theorem 3.6 without explicitly computing the
eigenvalues of A
−1
B. Our strategy is to first give an
explicit expression of A
−1
, which in turn will allow
us to calculate the characteristic polynomial of A
−1
B.
Finally, we invoke a powerful theorem that charac-
terizes the range of polynomial roots (without finding
them), and that can be exploited algorithmically.
We begin by calculating the characteristic polyno-
mial of A
−1
B. Note that for a group R of n robots, the
characteristic polynomial of A
−1
B is of degree n −1.
Also, any r ×r leading principal minor A
−1
B can be
computed from the r ×r leading principal minors of
A,B, which only depend on robots 1,. .. ,r +1. In fact
the r ×r leading principal minor A
−1
B is exactly the
critical matrix whose eigenvalues determine the con-
vergence of Algorithm 3 for input robots 1,...,r + 1.
So, we are motivated in denoting by D
r
(λ) the char-
acteristic polynomial of the r ×r leading principal mi-
nor A
−1
B (i.e. D
n−1
(λ) = |A
−1
B −λI|). We choose
to abbreviate D
r
(λ) by D
r
. The next lemma provides
two alternative recursive relations for D
r
(each will
be convenient in different arguments) that allow us to
compute D
n−1
, and will be also used later to establish
convergence for special cases of robots.
Lemma 3.7. Consider matrices A, B as defined
in (4), and introduce the abbreviations a
i
:=
1
p
i+1
+
1
w
i
,b
i
:=
1
w
i+1
+
1
p
i
,c
i
:= −
1
p
i+1
−
1
w
i+1
, and α
i
:=
b
i
a
i
−
c
2
i−1
a
i−1
a
i
,β
i
:=
c
2
i−1
a
i−1
a
i
. Then for the characteristic polyno-
mials D
r
, the following equivalent recurrences hold
true for all r ≥ 2
D
r
= (α
r
−λ) ·D
r−1
+
r−2
∑
t=1
α
t+1
·
r
∏
j=t+2
β
j
!
·D
t
+
b
1
a
1
r
∏
j=2
β
j
, (6)
D
r
=
b
r
a
r
−λ
D
r−1
+
c
2
r−1
a
r−1
a
r
λD
r−2
(7)
and with initial conditions D
1
=
b
1
a
1
−λ, D
0
= 1.
Proof. The inverse of A is a lower triangular matrix
and can be easily verified to be defined as
A
−1
i j
:= (−1)
i+ j
∏
i−1
t= j
c
t
∏
i
r= j
a
r
, if j ≤ i
and is 0 otherwise. Therefore, for the (so-called
Hessenberg matrix, as it has zero entries above the
first subdiagonal) matrix A
−1
B we have that
A
−1
B
i j
= (−1)
i+ j
b
j
a
i
i−1
∏
t= j
c
t
a
t
−
c
j−1
a
i
i
∏
t= j
c
t−1
a
t−1
!
if i ≥ j −1, and 0 otherwise, with the understanding
that c
0
= 0. The following interesting relation holds
for the entries of A
−1
B, that is useful in finding the
characteristic polynomial of the matrix.
A
−1
B
i, j
= −
c
i−1
a
i
A
−1
B
i−1, j
, ∀i > j. (8)
Next we introduce D
0
r
to denote a small variation of
D
r
. D
0
r
is the determinant of the same principal minor
of A
−1
B −λI (up to entry (r,r)) with the only dif-
ference that the entry (r,r) is replaced by
A
−1
B
r,r
,
instead of
A
−1
B −λI
r,r
.
With this notation, we can evaluate
A
−1
B −λI
by expanding the determinant with respect to the en-
tries (n −1,n −1) and (n −2, n −1). Using Equa-
tion (8), we observe that
D
r
=
b
r
a
r
−
c
2
r−1
a
r−1
a
r
−λ
!
D
r−1
+
c
2
r−1
a
r−1
a
r
D
0
r−1
, (9)
D
0
r
=
b
r
a
r
−
c
2
r−1
a
r−1
a
r
!
D
r−1
+
c
2
r−1
a
r−1
a
r
D
0
r−1
, (10)
Fence Patrolling with Two-speed Robots
237

where the recurrence ends at D
1
=
b
1
a
1
−λ and D
0
1
=
b
1
a
1
. Repeated substitution of (10) to (9) and some di-
rect calculations imply recurrence (6). Recurrence (7)
is obtained from (6) by subtracting two consecutive
terms of the sequence D
r
.
Notice that Lemma 3.7, and in particular Equa-
tion (7), allows us to calculate the characteristic poly-
nomial D
n−1
of A
−1
B by performing no more than
Θ(n
2
) arithmetic operations (additions, multiplica-
tions and divisions) between speeds p
i
,w
i
. Next we
give an efficient algorithm for deciding whether the
moduli of the roots of an arbitrary polynomial f : R 7→
R are all less than 1. Our intention is to run Algo-
rithm 4 with input D
n−1
, i.e. the characteristic poly-
nomial of A
−1
B.
Algorithm 4: Decide Convergence.
Input: A polynomial f : R 7→ R of degree t of the
form
∑
t
i=0
γ
i
λ
i
1: Set γ
(0)
i
= γ
i
, for i = 0, .. .,t.
2: For j = 0,...,t −1 and for k = 0, .. ., j + 1 com-
pute γ
( j+1)
k
= γ
( j)
0
γ
( j)
k
−γ
( j)
n−j
γ
( j)
n−j−k
.
3: Compute δ
j+1
:= γ
( j+1)
0
=
γ
( j)
0
2
−
γ
( j)
n−j
2
for
j = 0, .. .,t −1.
Output: YES if and only if δ
1
< 0 and δ
j
> 0 for
j = 2, .. .,t.
Theorem 3.8. A set of n robots R for which the out-
put of Algorithm 3 gives a regular dynamical system
converges to a stable configuration if and only if Al-
gorithm 4 outputs YES on input D
n−1
. As a result,
convergence can be decided in Θ(n
2
) arithmetic op-
erations.
Proof. By Theorem 3.6, the regular dynamical sys-
tem converges to a stable configuration if and only
if all eigenvalues of A
−1
B (as defined in (4)) have
moduli less than 1. The characteristic polynomial of
A
−1
B can be computed in Θ(n
2
) many operations, as
a corollary of Lemma 3.7. Clearly, Algorithm 3.8
requires no more than Θ(n
2
) arithmetic operations.
Therefore,we can decide convergence in Θ(n
2
) arith-
metic operations as long as we can show that Algo-
rithm 4 correctly decides whether the input polyno-
mial f has all its roots (real or complex) strictly inside
the unit circle.
Correctness of Algorithm 4 is an immediate corol-
lary of Theorem 42,1, p. 150 in (Marden, 1949): “Set
∆
r
=
∏
t
j=1
δ
j
, ,r = 1,. .. ,t and suppose that k many
of the products ∆
r
are negative, and the remaining
t −k of them are positive. Then f has exactly k roots
strictly inside the unit circle, exactly t −k roots strictly
outside the unit circle (and hence no roots on the unit
circle).”
3.4 Monotone Robot Collections, and
Convergence
In this section we demonstrate some special families
of primitive robots that can solve Fence Patrolling op-
timally. The analysis even of the restricted families of
three or four robots remains surprisingly technical and
non-trivial.
Our technical results of Section 3.3 on regular dy-
namical systems raise the question whether such sys-
tems exist. A natural family of robots is when ei-
ther the sum or the product of patrolling and walking
speeds is constant for all robots or when some con-
stant “power” of a robot may be used for improving
its patrolling ability at the expense of its walking abil-
ity. In such a collection of robots, all patrolling speeds
are dominated by the walking speeds, and the non-
increasing order of patrolling speeds is the inverse or-
der of that of the walking speeds. We make the defi-
nition formal.
Definition 3.9. The collection R of n robots is called
monotone if for i, j = 1, .. ., n: 1) p
i
< w
i
, 2) p
i
6= p
j
,
and 3) p
i
< p
j
=⇒ w
i
> w
j
.
A natural example of a monotone collection of
robots is one where each robot i independently de-
cides how to distribute it’s energy e, which is the same
for all robots, to walking and patrolling speeds w
i
, p
i
respectively, such that w
i
+ p
i
= e. As it is observed
before, a collection of robots that develop according
to Algorithm 3 preserve the order they appear on the
line. Without loss of generality we may assume that
their indices are consecutive along the segment, i.e.
that w
n
> w
n−1
> ··· > w
1
> p
1
> p
2
> ··· > p
n
.
Lemma 3.10. For a monotone collection of robots R,
the dynamical system that arises from Algorithm 3 is
regular (i.e. collisions occur while robots approach
each other, the left one being in the walking state and
the right one in the patrolling state.)
Proof. Initially all robots walk right-to-left until the
fastest walking robot collides with the left endpoint
and starts walking left-to-right. Any “head on” colli-
sion results in the right robot switching to patrolling
left-to-right and the left robot switching to patrolling
right-to-left. So it is sufficient to prove that colli-
sions from behind never take place. Suppose to the
contrary, that there exists such a collision between
a pair of consecutive robots on the segment, r
i
,r
i+1
,
for i = 1, .. ., n −1. Obviously r
i
,r
i+1
cannot collide
when r
i
moves left and r
i+1
moves right. If both
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
238

robots move right-to-left then, by assumption, they
must be walking, and since w
i
< w
i+1
, r
i
cannot catch
r
i+1
. Similarly, if both robots move left-to-right, by
assumption, they are patrolling and since p
i
> p
i+1
,
r
i+1
cannot catch r
i
.
As an immediate observation, we also obtain that
b
i
a
i
< 1 &
(c
i−1
)
2
a
i−1
a
i
< 1 (11)
for all i = 1,...,n−1 and i = 2,...,n−1 respectively,
and for all regular collections of n robots, where
a
i
,b
i
,c
i
are as in Lemma 3.7. In fact, the characteristic
polynomial D
n−1
has leading coefficient (−1)
n
, while
it is also immediate from (7) that the constant coeffi-
cient is
∏
n−1
i=1
b
i
a
i
< 1. This automatically shows that
the condition δ
1
< 0, of Algorithm 4, holds true for
monotone collections of robots. In fact, we conjec-
ture that monotone collections of robots always con-
verge to a stable configuration, i.e. that δ
j
> 0 for
j = 2,...,n−1, but a general proof is eluding us. Still
the proof of convergence for up to n ≤3 robots is easy
to establish. The proof of the next proposition relies
on (11).
Proposition 3.11. For a monotone collection of n ≤3
robots the schedule produced by Algorithm 3 has the
optimal idleness.
Proof. We show that the conditions of Theorem 3.6
are satisfied. The case of 1 robot is straightforward.
For n = 2 robots, the characteristic polynomial is
D
1
=
b
1
a
1
−x, which by (11) has one real root with
absolute value less than 1.
Now we turn our attention to n = 3, and by (7)
the characteristic polynomial D
2
(λ) has the form
P
W
(λ) := (U − λ)(V − λ) + W λ = λ
2
− (U + V −
W )λ +UV , where U,V,W are non negative constants
which by (11) are strictly less than 1.
We show that the moduli of the roots of P
W
(λ)
are less than 1. First we observe that P
0
(λ) has this
property.
Case 1: If P
W
(λ) has real roots, then these are ρ
(W )
1,2
=
U+V −W±
√
(U+V −W )
2
−4UV
2
, with the understanding
that ρ
(W )
1
,ρ
(W )
2
correspond to the square root having
positive and negative sign respectively. Then we ob-
serve that ρ
(W )
1
< ρ
(0)
1
< 1, while also ρ
(W )
1
> −W /2 >
−1/2 (by ignoring the positive terms). Hence
−1/2 < ρ
(W )
1
< 1. Similarly, we see that ρ
(W )
2
<
(U +V )/2 < 1 (by ignoring the negative terms). And
finally note that U + V −
p
(U +V −W )
2
−4UV >
−W, since (U + V + W )
2
> (U + V −W )
2
−4UV .
Therefore, ρ
(W )
2
> (−2W )/2 = −1, concluding that
−1 < ρ
(W )
2
< 1, as well.
Case 2: If P
W
(λ) has complex roots, say σ
1
,σ
2
, then
it must be the case that kσ
1
k
2
= kσ
2
k
2
= σ
1
σ
2
=
UV < 1.
We now prove convergence of monotone collections
of n = 4 robots by using a refinement of monotonicity.
Definition 3.12. The collection R of n robots is called
strongly monotone if it is monotone and for all r we
have
1
p
r
+
1
w
r+1
1
p
r
+
1
w
r−1
>
1
p
r
+
1
w
r
2
.
Due to the definitions of a
i
,b
i
and that of α
i
in Lemma 3.7, asking that a collection of robots is
strongly monotone is equivalent to asking that α
r
> 0
for every r (see (6)). This allows us to show that char-
acteristic polynomials associated with such robots
have no negative real roots. We can now prove that
the characteristic polynomial of every strongly mono-
tone collection of robots has real roots less than 1 in
absolute value.
Theorem 3.13. For every monotone (not necessarily
strongly) collection of n robots, D
r
(λ) preserves sign
for all λ ≥ 1. If in addition robots are strongly mono-
tone, then D
r
(λ) preserves sign (and is actually posi-
tive) for all λ < 0. As a result all real roots of D
r
lie
strictly between 0 and 1.
Proof. The less technical proof concerns the strongly
monotone collections of robots. For this consider the
cone C of polynomials of the form
∑
r
t=0
(−1)
t
ρ
t
λ
t
,
where ρ
t
> 0 , i.e. polynomials whose odd-degree
monomial coefficients are negative, and whose even-
degree monomial coefficient are positive. Clearly, any
polynomial p(λ) ∈ C is positive for every λ < 0 (and
is actually decreasing).
We claim that for all r ≥0, D
r
∈C . To that end, we
first observe that the statement is true for r = 0,1. For
any r ≥ 2, we invoke (6). Since all α
i
,β
j
are positive
reals, we can show that D
r
∈ C as long as we can
verify that (α
r
−λ) ·D
r−1
∈ C (the rest of summands
in (6) are conical combinations of polynomials in C ).
It is straightforward now to check that −λD
r−1
∈ C ,
hence (α
r
−λ) ·D
r−1
= α
r
D
r−1
+ (−λD
r−1
) ∈ C , as
wanted.
Now we focus on a monotone (not necessarily
strongly) collection of robots. We prove by induction
on r that for all λ ≥ 1, D
r
is a polynomial which is
positive and increasing, if r is even
negative and decreasing, if r is odd
Indeed, the statement is true for r = 1, 2. Next we
turn our attention to r ≥ 3. We have in mind to in-
voke (7). Now fix any λ
0
≥ 1. Note that
b
r
a
r
−λ
0
< 0.
Next observe that if r is even, then D
r−1
(λ
0
) < 0 and
D
r−2
(λ
0
) > 0, so that D
r
(λ
0
) > 0. Similarly, if r is
Fence Patrolling with Two-speed Robots
239

odd, then D
r−1
(λ
0
) > 0 and D
r−2
(λ
0
) < 0, so that
D
r
(λ
0
) < 0, exactly as wanted.
Next we show the promised monotonicity. Let’s
denote by D
0
r
(λ) the first derivative of D
r
(λ) with re-
spect to λ. Then we see that
D
0
r
(λ) =
−λD
r−1
(λ) +
b
r
a
r
−λ
D
0
r−1
(λ)
+
c
2
r−1
a
r−1
a
r
D
r−2
(λ) +
c
2
r−1
a
r−1
a
r
λD
0
r−2
(λ)
If r is even then we argue that D
0
r
(λ) > 0 for all
λ ≥ 1. Indeed, we have that
−λD
r−1
(λ) = −·+ ·− = +
b
r
a
r
−λ
D
0
r−1
(λ) = −·− = +
c
2
r−1
a
r−1
a
r
D
r−2
(λ) = + ·+ = +
c
2
r−1
a
r−1
a
r
λD
0
r−2
(λ) = + ·+ ·+ = +
Since all summands of D
0
r
(λ) are positive, D
r
(λ) is
increasing.
Similarly, if r is odd, we show that D
0
r
(λ) < 0 for
all λ ≥ 1. Indeed, we have that
−λD
r−1
(λ) = −·+ ·+ = −
b
r
a
r
−λ
D
0
r−1
(λ) = −·+ = −
c
2
r−1
a
r−1
a
r
D
r−2
(λ) = + ·− = −
c
2
r−1
a
r−1
a
r
λD
0
r−2
(λ) = + ·+ ·− = −
Since all summands of D
0
r
(λ) are negative, D
r
(λ) is
decreasing.
In order to show that a group of strongly monotone
robots converges to a stable configuration, it remains
to prove all complex roots of D
r
have norm < 1; this
is the main idea behind the proof of Proposition 3.14.
Proposition 3.14. For a strongly monotone collection
of n = 4 robots the schedule produced by Algorithm 3
has the optimal idleness.
Proof of Proposition 3.14. Again, we show that the
conditions of Theorem 3.6 are satisfied. When
n = 4, and using (7), we can write the char-
acteristic polynomial we need to study, that has
the form D
3
(λ) = (A
3
− λ)(A
2
− λ)(A
1
− λ) +
λ(B
2
(A
3
−λ) + B
3
(A
1
−λ)), where by A
i
we abbre-
viate b
i
/a
i
and by B
i
we abbreviate c
2
i−1
/a
i−1
a
i
. Next
we argue that all roots of D
3
have norm less than 1.
By assuming strong monotonicity, Theorem 3.13 says
that all real roots have norm between 0 and 1. Hence,
we only need to check any complex roots. All we
need to use below is that 0 ≤ A
i
,B
i
< 1, and this fol-
lows by assuming simple (speed) monotonicity.
Since D
3
is of degree 3, it always has a real root,
call it r, and at most two complex roots (that are con-
jugate to each other), say with norm kρk. Since the
constant term of D
3
is A
1
A
2
A
3
, it follows that kρk =
A
1
A
2
A
3
r
. Next we prove that r ≥min{A
1
,A
2
,A
3
}, con-
cluding what we need. Indeed, consider the polyno-
mial
1
B
2
+ B
3
D
3
(λ)
=
1
B
2
+B
3
(A
3
−λ)(A
2
−λ)(A
1
−λ)
+λ
B
2
B
2
+B
3
(A
3
−λ) +
B
3
B
2
+B
3
(A
1
−λ)
which clearly has the same roots as D
3
(λ). Now,
the root r above is a value for λ that satisfies
the following equality
1
B
2
+B
3
(A
3
−λ)(A
2
−λ)(A
1
−
λ) = −λ
B
2
B
2
+B
3
(A
3
−λ) +
B
3
B
2
+B
3
(A
1
−λ)
. The
left-hand-side polynomial, which is of degree 3, has
real roots A
1
,A
2
,A
3
, and most importantly it is de-
creasing for all x ≤ min{A
1
,A
2
,A
3
} and for all λ ≥
max{A
1
,A
2
,A
3
}. The right-hand-side polynomial is
of degree 2, and has two real roots. One of them
is 0, and the other, call it r, is a convex combina-
tion of A
1
,A
3
, hence we have min{A
1
,A
3
} ≤ r ≤
max{A
1
,A
3
}. Moreover, the degree 2 polynomial
is negative for 0 < λ < r and positive for λ > r,
and is increasing for all λ ≥ r. Since r is in the
line segment between min{A
1
,A
3
},max{A
1
,A
3
}, it
must be the case that the graphs of the two polyno-
mials intersect for some λ between min{A
1
,A
2
,A
3
}
and max{A
1
,A
2
,A
3
}.Therefore, r ≥ min{A
1
,A
2
,A
3
}
as wanted.
4 CONCLUSION
Patrolling a given domain with a swarm of two-speed
robots is a challenging problem with interesting trade-
offs. Its difficulty, even for patrolling a segment, is
due to the fact that there are many patrolling strate-
gies to be taken into account. We gave an optimal
offline algorithm for any robot collection and opti-
mal dynamic schedules for two robots. We also gave
an efficient algorithm deciding self-stabilization of a
distributed schedule for the case of regular dynamical
systems. We proved that the distributed algorithm is
self-stabilizing for up to four robots whose speeds sat-
isfy a certain monotonicity property. However, con-
vergence of our distributed algorithm for more than
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
240

four robots (whose speeds satisfy a certain mono-
tonicity property) remains open. The case of differ-
ent domains is interesting and can be surprisingly de-
manding.
ACKNOWLEDGEMENTS
For the first and third author, this research was sup-
ported in part by NSERC grants.
REFERENCES
Agmon, N., Kraus, S., and Kaminka, G. A. (2008). Multi-
robot perimeter patrol in adversarial settings. In ICRA,
pages 2339–2345.
Almeida, A., Ramalho, G., Santana, H., Tedesco, P. A.,
Menezes, T., Corruble, V., and Chevaleyre, Y. (2004).
Recent advances on multi-agent patrolling. In SBIA,
pages 474–483.
Alpern, S., Morton, A., and Papadaki, K. (2009). Optimiz-
ing randomized patrols. Operational Research Group,
London School of Economics and Political Science.
Alpern, S., Morton, A., and Papadaki, K. (2011). Patrolling
games. Operations research, 59(5):1246–1257.
Amigoni, F., Basilico, N., Gatti, N., Saporiti, A., and
Troiani, S. (2010). Moving game theoretical pa-
trolling strategies from theory to practice: An usarsim
simulation. In ICRA, pages 426–431.
Angluin, D., Aspnes, J., Diamadi, Z., Fischer, M., and Per-
alta, R. (2006). Computation in networks of passively
mobile finite-state sensors. Distributed Computing,
18(4):235–253.
Angluin, D., Aspnes, J., Eisenstat, D., and Ruppert, E.
(2007). The computational power of population pro-
tocols. Distributed Computing, 20(4):279–304.
Beauquier, J., Burman, J., Clement, J., and Kutten, S.
(2010). On utilizing speed in networks of mobile
agents. In Proceeding of the 29th ACM SIGACT-
SIGOPS Symposium on Principles of distributed com-
puting, pages 305–314. ACM.
Chevaleyre, Y. (2004). Theoretical analysis of the multi-
agent patrolling problem. In IAT, pages 302–308.
Cieliebak, M., Flocchini, P., Prencipe, G., and Santoro,
N. (2012). Distributed computing by mobile robots:
Gathering. SIAM J. Comput., 41(4):829–879.
Collins, A., Czyzowicz, J., Gasieniec, L., Kosowski,
A., Kranakis, E., Krizanc, D., Martin, R., and
Morales Ponce, O. (2013). Optimal patrolling of frag-
mented boundaries. In SPAA.
Czyzowicz, J., Gasieniec, L., Kosowski, A., and Kranakis,
E. (2011). Boundary patrolling by mobile agents
with distinct maximal speeds. Algorithms–ESA 2011,
pages 701–712.
Czyzowicz, J., Kranakis, E., and Pacheco, E. (2013). Lo-
calization for a system of colliding robots. In ICALP
(2), pages 508–519.
Dijkstra, E. W. (1982). Selected writings on computing: a
personal perspective. Springer-Verlag New York, Inc.
Dumitrescu, A., Ghosh, A., and Csaba, D. T. (2014).
On fence patrolling by mobile agents. CoRR,
abs/1401.6070.
Elmaliach, Y., Agmon, N., and Kaminka, G. A. (2009).
Multi-robot area patrol under frequency constraints.
Ann. Math. Artif. Intell., 57(3-4):293–320.
Elmaliach, Y., Shiloni, A., and Kaminka, G. A. (2008). A
realistic model of frequency-based multi-robot poly-
line patrolling. In AAMAS (1), pages 63–70.
Elor, Y. and Bruckstein, A. M. (2010). Autonomous multi-
agent cycle based patrolling. In ANTS, pages 119–
130.
Hare, J., Gupta, S., and Wilson, J. (2015). Decentralized
smart sensor scheduling for multiple target tracking
for border surveillance. In ICRA, pages 3265–3270.
IEEE.
Hazon, N. and Kaminka, G. A. (2008). On redun-
dancy, efficiency, and robustness in coverage for mul-
tiple robots. Robotics and Autonomous Systems,
56(12):1102–1114.
Kawamura, A. and Kobayashi, Y. (2012). Fence patrolling
by mobile agents with distinct speeds. In ISAAC,
pages 598–608.
Machado, A., Ramalho, G., Zucker, J.-D., and Drogoul, A.
(2002). Multi-agent patrolling: An empirical analysis
of alternative architectures. In MABS, pages 155–170.
Marden, M. (1949). The Geometry of the Zeros of a Polyno-
mial in a Complex Variable, volume 3 of Math. Surv.
AMS.
Marino, A., Parker, L. E., Antonelli, G., and Caccavale, F.
(2009). Behavioral control for multi-robot perimeter
patrol: A finite state automata approach. In ICRA,
pages 831–836.
Pasqualetti, F., Franchi, A., and Bullo, F. (2010). On op-
timal cooperative patrolling. In CDC, pages 7153–
7158.
Yanovski, V., Wagner, I. A., and Bruckstein, A. M. (2003).
A distributed ant algorithm for efficiently patrolling a
network. Algorithmica, 37(3):165–186.
Fence Patrolling with Two-speed Robots
241
