Proposed Resource Allocation Schemes for Rainy Free Space Optical

Network

Abdallah S. Ghazy

, Hossam A. I. Selmy

and Hossam M. H. Shalaby

Egypt-Japan University of Science and Technology (E-JUST), Alexandria, Egypt

Cairo University, Cairo, Egypt

Keywords:

Free Space Optical, Rainy Weather Inﬂuence, Dynamic Networks, Relayed Networks, Resource Allocation

Scheme, Lexicographic and Lex-Max-Min Optimization Theories.

Abstract:

Free space optical (FSO) connections present promising solution for the limited access issue of the last mile

networks. However, several factors contribute to signiﬁcant FSO link performance degradation. One of Most

serious conditions is the inﬂuence of the rain, that frequently appear, thus making the implementation of

strongly connected FSO networks a demanding issue. Dynamic FSO networks is attractive ones over the

robust static ones, i.e, partial and full relayed networks, for this demanding issue. In this paper two new

resource allocation Schemes are proposed for cooperative-dynamic FSO networks, as attractive solution for

both atmospheric variation and high cost of robust static network problems. Each Scheme is formulated

as integer linear multi-objective optimization problem (ILP-MOP), where reliability-fairness, capacity and

bit-error rate functions are targeted. And each scheme is composed of lexicographic, lex-max-min and lex-

min-max criteria. Each ILP-MOP is solved using exhaustive search method to obtain the guaranteed optimal

solution(s). The simulation results is used to reveal that two schemes are more reliable-fairness and cost

efﬁcient than the robust static topology, specially at sever weather conditions. Also, the results show the two

schemes have different behavior, where one prioritize the reliability-fairness over capacity utilization and the

another does the opposite.

1 INTRODUCTION

Free space optics (FSO) is line of site (LOS) wire-

less optical communication used as a promising and

feasible solution for last mile connectivity problem

where remote network nodes have to be connected

to central backbone node. With the signiﬁcant devel-

opment in the optical technology in the last decade,

more FSO links are deployed in a given service area

to meet the user’s huge demands on internet services

and applications(Kim et al., 2001). Generally, FSO is

used instead of optical ﬁbers when short implemen-

tation time, ﬂexible installation and low implementa-

tion cost are required (Refai et al., 2006). FSO link

could be used to connect different nodes like mobile

base station, telephone ofﬁce or private networks to

central backbone node as indicated in Fig. 1.

Even though the attractive features of FSO, it suf-

fers from the free space channel impairments in in-

frared (IR) band spectrum, i.e., weather conditions,

background radiations and air turbulence (Kim et al.,

2001), (Bloom et al., 2003), (recommendation ITU-

R P.1814, 2007). The weather conditions include

fog, rain and snow that could absorb and scatter the

transmitted optical signal (Vavoulas et al., 2012). In

addition, eye safety regulation restricts the power of

the transmitted light beam to certain threshold which

consequently limits the communication range of FSO

links (Bloom et al., 2003). Hence, suitable network

topologies have to be investigated to mitigate the

weather impairments and provide the required qual-

ity of service (QoS) for different nodes.

The conventional FSO network implements static

direct links (D-L) between ﬁber backbone node and

FSO link

Backbon

FSO node

Figure 1: Last-mile FSO connection, the end users could

use wire or wireless connections to FSO node.

Ghazy, A., Selmy, H. and Shalaby, H.

Proposed Resource Allocation Schemes for Rainy Free Space Optical Network.

DOI: 10.5220/0005688400740081

In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 76-83

ISBN: 978-989-758-174-8

FSO nodes as indicated in Fig. 2(A). Although,

this static topology has simple and low cost imple-

mentation, it has the worst communication perfor-

mance against sever weather conditions. To overcome

this degradation, serial-relayed topology is addressed

(Vavoulas et al., 2012). In this topology, one or more

relays are inserted between far nodes and backbone

node. The relay has two optical transceivers and is

located at equal distances from other nodes (optimal

placement)(Kashani et al., 2013), as indicated in Fig.

2(B) for partial relayed links network (P-L). By in-

creasing number of intermediate relays between re-

mote nodes and backbone node, the best FSO link

performance could be achieved. Obviously, this en-

hancement in the network performance comes at a

signiﬁcant increase in the network cost. The topol-

ogy where each node is supported with one relay is

called fully relayed links network (F-L) as indicated

in Fig. 2(C).

(A) (B)

(C)

FSO Link

Relay Node

Node with one Transceiver

Fiber Backbone

Figure 2: Different recent static topologies at last-mile, (A)

Direct Link model (D-L), (B) Partial Relayed Link Model

(P-L), (C) Full Relayed Link Model (F-L).

Better performance could be achieved at reason-

able lower cost by implementing dynamic (recon-

ﬁgurable) FSO network topologies (Milner et al.,

2002). These dynamic topologies are classiﬁed ac-

cording to network resources sharing into coopera-

tive and non-cooperative topologies. In dynamic non-

cooperative FSO network topologies no resources are

shared among different users (Milner et al., 2002).

Users with bad links switch their trafﬁc to users with

relatively better links and the transmission rate of

each user is kept the same. This is achieved by in-

creasing transmission rates of good links to be sum

of switched transmission rates. Clearly, increasing

transmission rate of optical link is not feasible and

has practical limitations (Bloom et al., 2003).

To overcome these limitations, dynamic cooper-

ative topologies are introduced. In these topolo-

gies, users with bad optical links switch their trans-

missions to users with better links and share their

links capacities. Clearly, transmission rate of a

good optical link is divided between node’s trafﬁc

and switched transmissions in order to keep qual-

ity of service for switched ones. In other words,

the networks’ users cooperate and share their re-

sources (optical bandwidths) to keep connectivities

between backbone node and far users which in turn

increases FSO network’s reliability (decrease num-

ber of dropped nodes) during rainy weather condi-

tions. Moreover, at given weather conditions, the

network resources could be fairly allocated (achieves

near the same transmission rate to backbone node)

among different users by implementing proper re-

source allocation scheme. Although, the number of

optical transceivers available at each node plays an

important role in the network performance, it is still

much lower than that required in static topologies to

achieve the same performance.

In this paper, two fair and cooperative resource

allocation schemes are proposed to enhance the per-

formance of dynamic cooperative FSO networks

against atmospheric variation which is caused by rain

droplets. The reset of this paper is organized as the

following. Section 2 presents FSO link model. Sec-

tion 3 illustrates reconﬁgurable cooperative FSO net-

work parameters. Section 4 introduces the proposed

resource allocation schemes. Section 5 shows the nu-

merical evaluations for proposed resource allocation

schemes. Lastly, section 6 concludes the ﬁnal net-

work evaluations and the remarkable notes.

2 FSO LINK MODEL

Three main factors affect the FSO link performance

namely, link losses, turbulence (scintillation) and

noises. The link losses include both atmospheric and

geometric losses. These losses cause signal scat-

tering, absorbing and spreading(Gagliardi and Karp,

1995). The atmospheric loss includes fog, rain, snow

(recommendation ITU-R P.1814, 2007). Naturally,

these weather phenomena fog. rain, and snow rarely

occur concurrently, and this allows in studying rainy

inﬂuence separately (Vavoulas et al., 2012). At sever

rainy weather conditions, the scintillation has rela-

tively small impact and could be neglected (Vavoulas

et al., 2012), (Khalighi and Uysal, 2014). Therefore,

the total FSO link loss in this case is given by

Proposed Resource Allocation Schemes for Rainy Free Space Optical Network

γ = γ

rain

+ γ

geo

. dB (1)

Where γ presents the total link loss. Also γ

rain

and

geo

are rain and geometric losses, respectively.

The rain loss is calculated using Jaban’s empirical

model, as (recommendation ITU-R P.1814, 2007).

rain

= 1.58 × D

0.63

× L . dB (2)

Or by using France’s empirical model, as (recommen-

dation ITU-R P.1814, 2007).

rain

= 1.076 × D

0.67

× L . dB (3)

Where D is the rain fall rate in mm/h and L is the

distance in km.

Even in clear weather conditions, the geometric loss

is presented due to the spreading of the beam when

propagating through the medium of free space. This

loss is calculated by (Bloom et al., 2003):

geo

= 10 × log



+ L × Θ



. dB (4)

Where d

is the receiver diameter, d

is the transmit-

ter diameter, both in mm, Θ is divergence angle in

mm.rad/km.

The system noise include both external noise (am-

bient or background noise) and internal noise (dark

current and thermal noises). When the background

radiation level is relatively high, for example in out-

door FSO links, the receiver thermal noise is ignored

and the system noise is modeled using Poisson’s

model (shot-noise limited receiver). Also, the se-

lected modulation formate plays important role in the

FSO link performance (Gagliardi and Karp, 1995).

The prime intensity modulation/direct detection tech-

niques, namely, none return-zero on-off keying (NR-

OOK) are considered in this paper. Hence, at given

transmitted q

photons/slot and channel loss, γ, q

(γ × q

) is the average number of received signal pho-

tons per slot and q

is the average number of received

ambient photons per slot. The bit-error-rate of OOK,

, when model the photo detector as shot-noise lim-

ited receiver is given by (Gagliardi and Karp, 1995).

∑

q=0

+ q

)

exp[−(q

+ q

)]

∞

∑

q=mt

)

exp[q

]

(5)

And

log



1 +



. (6)

Where, m

is the threshold of bit detection.

In the considered network, the homogeneous

weather is assumed over all the network regions. In

other words, all FSO links are affected by the same

speciﬁc atmospheric losses (dB/km) and the same

background radiation level impacts all FSO receivers.

Figure 3: Reconﬁgurable-Cooperative network, (A) Net-

work topology . (B) Reconﬁguration of the links versus the

atmospheric variation using the proposed schemes, where

in (B.1) at clear weather and in (B.2) at rainy weather con-

ditions.

3 RECONFIGURABLE

COOPERATIVE FSO

NETWORK PARAMETERS

Currently, the signiﬁcant innovation in pointing, ac-

quisition and tracking system (PAT) makes the dy-

namic FSO network more feasible than before (Dat

et al., 2010). In reconﬁgurable topologies, the number

of FSO transceivers could be signiﬁcantly reduced by

replacing actual FSO relay nodes by transceivers on

other working nodes (virtual FSO relay nodes) (Mil-

ner et al., 2002).

Generally, the cooperative FSO network consists of

N nodes (v

,..., v

) with arbitrary geographical dis-

tribution in addition to the backbone node v

. The

number of optical transceivers at k

node is denoted

by Z

where {k} ∈ {1,... ,N}. The backbone node is

assumed to be equipped with N optical transceivers.

In the considered FSO network, the inner n

nodes

near to the backbone node are assumed to have two

transceivers while the far n

= N −n

nodes have only

one transceiver, i.e. Z

∈ {1,2}. An example of re-

conﬁgurable cooperative FSO network with one cen-

tral node and nine remote nodes is indicated in Fig.

3(A). In this network N = 9, each node of the inner

four nodes has two transceivers (n

=4) and each node

of the outer ﬁve nodes has one transceiver (n

=5), to-

tal additional transceivers is w =

∑

k=1

− 1) = 4.

At clear weather conditions, all nine nodes are di-

rect connected to the central node as indicated in

Fig. 3(B.1). At high density fall rate of rain, each

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

node could switch to its neighbor node to maintain its

connectivity to the central node as indicated in Fig.

3(B.2).

The losses of all FSO links (rain and geomet-

ric attenuations) are summarized in γ matrix, γ =

(γ

,. .., γ

;. .., γ

i j

,. .. ; γ

,. .., γ

), where γ

i j

the loss coefﬁcient of link between transmitter of i

node and receiver of j

node. Clearly, 0 ≤ γ

i j

≤ 1,

= 0 and γ

i j

= γ

for any {i, j} ∈ {0, 1,. .., N}.

At a given weather state, the cooperative FSO net-

work could be connected with different feasible con-

ﬁgurations that satisfy the required QoS parame-

ters, i.e. grantee minimum bit rates at bit error

rates less than certain threshold. The number of

these conﬁgurations is Λ. For l

conﬁguration, l ∈

{

1,2, ... ,Λ

}

, the connection status between network

nodes are summarized in connections matrix G

l00

,. .., g

l0N

;. .., g

li j

,. .. ; g

lN0

,. .., g

lNN

), where g

li j

is the connection status between i

and j

nodes in

conﬁguration l and g

li j

∈ {0, 1}. The connection be-

tween nodes i and j is established in conﬁguration l if

li j

= 1. Also, bidirectional links are assumed so that

li j

= g

l ji

and g

lii

= 0.

Moreover, all FSO links are assumed to have the

same average transmitted power, i.e., the power of op-

tical link between nodes i and j in conﬁguration l

is constant, P

li j

= P. However, to increase link ca-

pacity and guarantee an error rate less than a spec-

iﬁed maximum BER

li j

< BER

max

, the link between

nodes i and j in conﬁguration l adapts its transmission

rate, T

li j

, to be one of m + 1 discrete values, where

li j

∈ {0,x

.. .,x

} and x

< x

< ... < x

The transmission rate of node k in conﬁguration

l is denoted by T

, where T

∑

j=0

lk j

. The

bit rate of node k (its own trafﬁc) through connec-

tion to node j in conﬁguration l is denoted by R

lk j

The overall bit rate of node k in conﬁguration l is

∑

j=0

lk j

. Obviously, R

≤ T

and {R

}

∈ {0, x

,. .., x

}. The end-to-end bit error rate

of node k in conﬁguration l, BER

, is bounded by

BER

≤ BER

max

The bit rates and bit error rates associated with all

nodes in the feasible conﬁgurations could be summa-

rized in (Λ × N) matrices R and E, respectively. For a

given conﬁguration l, the bit rates for all nodes are

represented in vector (1 × N) r

, r

∈ R. Also, the

bit error rates in that conﬁguration are summarized in

vector (1 × N) e

, e

∈ E. The network capacity asso-

ciated with conﬁguration l is C

∑

k=1

, and all

capacities associated with all feasible conﬁguration

are summarized in vector (Λ× 1) C, C

∈ C. Also, the

maximum network capacity that could be achieved by

any conﬁguration is that obtained from direct links

conﬁguration l

∗

and is deﬁned by C

max

∑

k=1

∗

Network Parameters:

v : Nodes vector (1 × (N + 1))

γ : Loss coefﬁcient Matrix ((N + 1) × (N + 1))

G : Connections matrix ((N +1) × (N + 1))

: Bit rate of k

node

r : Bit rate vector (1× N)

R : Bit rate matrix (Λ × N)

BER

: Bit error rate of k

node

e : Bit error rate vector (1 × N)

E : Bit error rate matrix (Λ × N)

BER

max

: Bit error rate threshold

: Capacity of the Network for l

conﬁguration

C : Capacity vector (Λ × 1)

max

: Maximum Capacity

: Capacity utilization for l

conﬁguration

: Transmission rate of k

node

: Number of transceivers of k

node

w : additional number of transceivers in the network

i j

: Power of i, j link

i.e. C

≤ C

max

The size of the feasible space, Λ, is upper bounded

by the following inequation:

Λ <

N+1

∑

ii=1



N + 1



j j=Z

∑

j j=0



N + 1

j j



)

kk=Z

∑

kk=0



N + 1



)

(7)

Clearly, the size of feasible space is deﬁned by num-

ber of FSO nodes, number of nodes equipped by one

transceiver, and number of nodes equipped by two

transceivers.

4 PROPOSED FAIR

COOPERATIVE RESOURCE

ALLOCATION SCHEME

Dynamic cooperative FSO networks deploy resource

allocation schemes in order to increase capacity, reli-

ability and fairness as well as to decrease the bit error

rate under rainy weather conditions. Increasing net-

work capacity is achieved by maintaining the largest

number of direct links to central node. Also, increas-

ing network’s reliability implies decreasing number

of dropped users, while enhancing fairness means

near the same bit rates are assigned to different sup-

ported users. Obviously, at clear weather conditions,

all nodes are direct connected to the central node to

get highest bit rates (maximum network capacity) at

bit error rates less than a predeﬁned threshold as in-

dicated in Fig. 3(B.1). On contrary, at bad weather

conditions, direct links of far nodes are dropped and

switched to other nodes according to the resource al-

location scheme in order to keep to connectivities to

the central node. Resource allocation in dynamic co-

operative FSO network could be optimized for sev-

eral performance metrics. Given number of optical

Proposed Resource Allocation Schemes for Rainy Free Space Optical Network

transceivers in each node (one or two transceivers in

our case), loss coefﬁcient matrix of FSO links γ and

transmitted power for FSO link; many feasible conﬁg-

urations could enable k

node (k ∈

{

1,..., N

}

) to have

bit rate R

∈ {0, x

,..., x

} at bit error rate less than

the threshold BER

≤ BER

max

. Among these feasible

conﬁgurations, one or more could achieve highest net-

work’s reliability, fairness, capacity and/or lowest bit

error rate.

In this section, two resource allocation schemes are

proposed to enhance the performance of dynamic co-

operative FSO networks. However, these schemes

are proposed for FSO networks that use two opti-

cal transceivers for inner nodes and one transceiver

for outer nodes as indicated in Fig.1 (A) as current

case study. The schemes use concept of lex-max-min

fairness which is widely used in computer and wire-

less networks to overcome the congestion and limited

reliability of the network (Ogryczak and Sliwinski,

2007). lex-max-min fairness is a criteria for achieving

near equal resource sharing between N nodes at a rel-

atively high network capacity, i.e avoiding inefﬁcient

fairness (allocate the lowest bit rate, x

, for all nodes

to achieve the maximum fairness). lex-max-min fair-

ness is the generalization of ordinary max-min fair-

ness as it searches sequentially for next maximals in

case two or more solutions have the same maximal at

one level in space of feasible solutions (Ogryczak and

Sliwinski, 2007), (Ogryczak and

Sliwi

nski, 2006).

The ﬁrst proposed scheme is called lex-max-min con-

strained fairness (LMMCF) which aims to enhance

network’s capacity while keeping the fairness be-

tween different nodes. The second proposed scheme

is called lex-max-min fairness (LMMF) that aims to

enhance both reliability and fairness of the network

regardless the capacity. The LMMCF scheme targets

three objective functions; maximizing network capac-

ity then maximizing bit rate fairness and then mini-

mizing bit-error rate. However, the LMMF scheme

targets two objective functions; maximizing bit rate

fairness then minimizing bit-error rate.

Clearly, the optimized objective functions are con-

ﬂicted, so each scheme is presented by multiple objec-

tive optimization problem (MOP). There are several

methods to treat MOPs such as lexicographic (hier-

archical), weighted summation, product and bounded

objective-functions (Marler and Arora, 2004). Lexi-

cographic is a criteria to optimize the conﬂicted ob-

jectives hierarchically and it has the ability to achieve

the schemes goals (Isermann, 1982), (Marler and

Arora, 2004). Lexicographic presents LMMCF prob-

lem in three optimization levels and LMMF in two

levels based on the priorities between the objectives.

4.1 LEX-MAX-MIN Constrained

Fairness Scheme

This scheme aims to increase network capacity then

proceed to improve both network reliability and fair-

ness. The network capacity is the summation of all

nodes’ bit rates. Also, the improvement in both reli-

ability and fairness raised by maximizing bit rates of

far nodes. Speciﬁcally, at the ﬁrst optimization level,

LMMCF scheme selects from the feasible Λ conﬁgu-

rations the ones that maximize network capacity. Af-

ter that in the second optimization level, the scheme

searches the previously selected conﬁgurations for

the ones that maximize the minimum bit rate for all

nodes. If there are more than one conﬁguration that

have the same max-minimum bit rate, the LMMCF

scheme proceeds to select from them the conﬁgura-

tions that have next max-minimum bit rate (sequen-

tial max-min optimization) (Ogryczak and Sliwinski,

2007). However, if there are more than one conﬁgura-

tion with the same sequential max-minimum values,

the LMMCF selects from them in a third optimization

level the conﬁguration that has sequential minimum

of maximum bit error rate values (sequential min-max

optimization) (Ogryczak and

Sliwi

nski, 2006).

Lexicographic represents the problem in three lev-

els of optimization based on the priorities between the

objectives as:

Max

(

k=N

∑

k=1

: C

∈ C

)

Lex-Max-Min

{

= (R

,..., R

) : r

∈ R

}

Lex-Min-Max

{

= (BER

,..., BER

) : e

∈ E

}

Subject to :

BER

≤ BER

max

, R

∈ {0,x

,..., x

li j

= P, Z

∈ {1,2}, k ∈

{

1,..., N

}

l ∈

{

1,..., Λ

}

{

i, j

}

∈

{

0,1, ...,N

}

, j 6= i.

(8)

Several constraints are imposed in the stated

multi-objective optimization problem. The bit error

rate of each node must less than a predeﬁned thresh-

old. Also, only speciﬁc discrete values for the bit rates

are allowed. Moreover, the same average transmitted

power is used for all nodes. Clearly, in this optimiza-

tion problem, the improvement in the bit rate fairness

between different users is restricted by the network

capacity.

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

4.2 LEX-MAX-MIN Fairness Scheme

Toward more increasing in the network reliability and

fairness, the capacity could not be considered and se-

lect among the feasible conﬁguration ones that maxi-

mize the reliable and fair conﬁguration(s), then pro-

ceeding to minimize the bit error rates (maximize

QoS). Lexicographic represents the problem in two

levels of optimization based on the priorities between

the objectives as in:

Lex-Max-Min

{

= (R

,..., R

) : r

∈ R

}

Lex-Min-Max

{

= (BER

,..., BER

) : e

∈ E

}

Subject to :

BER

≤ BER

max

, R

∈ {0,x

,..., x

li j

= P, Z

∈ {1,2}, k ∈

{

1,..., N

}

l ∈

{

1,..., Λ

}

{

i, j

}

∈

{

0,1, ...,N

}

, j 6= i.

(9)

This MOP is solved at the same previous con-

straints. Both equations (9) and (8) are classiﬁed as

integer linear programming (ILP) optimization prob-

lems (discrete linear MOP). Each equation could be

solved using exhaustive search (ES) method to obtain

the optimal solution(s). ES method generates all pos-

sibles network forms (Λ) then evaluates the objective-

functions and lastly compares between feasible solu-

tion to select the optimal one(s) (global max and min

values) (Paar and Pelzl, 2009). However, the schemes

could be solved by ES method in open time like off-

line schemes (precomputed optimal values) to over-

come the time computing complexity of ES method.

Clearly, two schemes provide different service lev-

els and the SLA (Service Level Agreement) between

the nodes (end users) and backbone (optical service

provider) determines the appropriate resource alloca-

tion technique.

According to the proposed schemes, it is suitable

to add an index to measure the fairness between the

N nodes. Jains index, F, is the most common and

appropriate one (Jain et al., 1998).

F =



∑

k=N

k=1



N ×



∑

k=N

k=1



, 0 ≤ F ≤ 1 . (10)

5 SIMULATION AND

NUMERICAL RESULTS

In this section LMMCF and LMMF resource alloca-

tion schemes are evaluated and compared to tradi-

Table 1: Simulation Parameters.

Link parameters Values

Signal wavelength (λ) 1550nm

Divergence angle (Θ) 2 mm.rad/m

Diameter of Transmitter (d

) 4 cm

Diameter of Receiver (d

) 20 cm

average transmitted signal counts/slot (q

= q

/γ) 250,000

average background counts/slot (q

) 50

Average transmitted Power (P) -15 dBm

Average background noise power -52 dBm

Discrete bit-rates ({x

,..., x

}) in Gbps 1, 3/4, 1/3, 1/2, 1/3, 1/4

Modulation formate NR-OOK

BER threshold (BER

max

) 10

−4

Area of FSO Network 3 × 3 km

Area of FSO-node Cell 1 × 1 km

tional robust static ones to indicate the superior per-

formance of the proposed schemes. The evaluations

consider four performance parameters which are re-

liability, capacity, fairness and bit-error rate. Four

topologies which are considered in the evaluations are

direct link (D-L) (Fig. 2(A)), partial relayed (P-L)

(Fig. 2(B)), full relayed (F-L) (Fig. 2(C)) and recon-

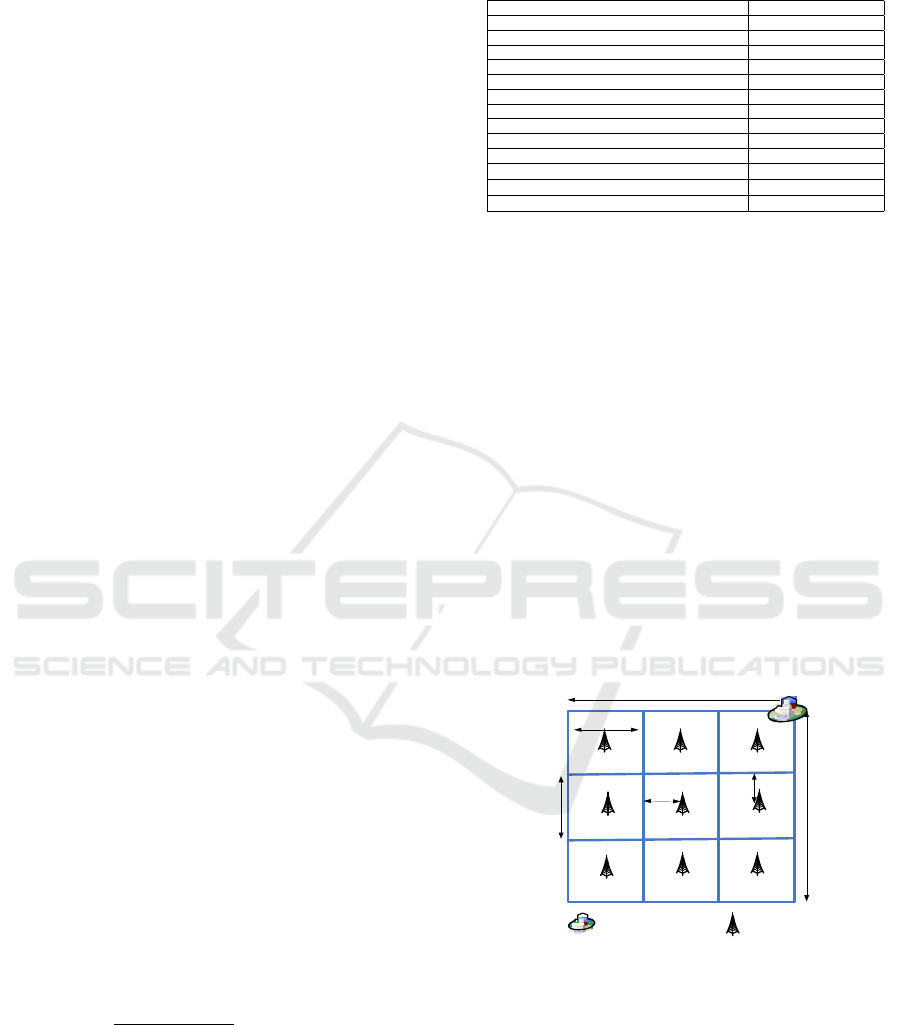
ﬁgurable cooperative (Fig. 3(A)) models. The num-

ber of the transceivers for these networks are 18, 24,

36, and 22 respectively. As shown in Fig. 4, the as-

sumed service area of the considered FSO networks

is 3 ∗ 3 km and nine FSO nodes are assumed to be lo-

cated uniformly in this area. Moreover, same homo-

geneous weather is assumed through out the service

area. All FSO links operate with predeﬁned six bit

rates, m = 6, at constant average optical power. Ta-

ble.1 shows the assigned values of the simulated FSO

network parameters which are selected to be in the

practical range, also we use Japan’s rain loss model.

Backbone node

3 km

1 km

0.5 km

(1)

(2)

(5)(6)

(7)(8)

(9)

(

)

(3)

(0)

FSO node

Figure 4: Dimensions of simulated FSO networks.

Figure 5 indicates the reliability of the topologies

versus rain fall rates. Clearly, at D ≤ 3mm/h the 9

nodes for all topologies work properly using their di-

rect FSO links. On contrary, at D ≥ 180mm/h all

nodes for all topologies are dropped i.e. can’t achieve

minimum bit rate, 0.25Gbps, at bit error rate less than

threshold 1e− 4. Between these two rain fall rate lev-

els, different network topologies have different per-

formances. At D=20mm/h the dropped nodes in the

D-L, P-L, and LMMCF/LMMF are 6, 3 and 2 nodes

Proposed Resource Allocation Schemes for Rainy Free Space Optical Network

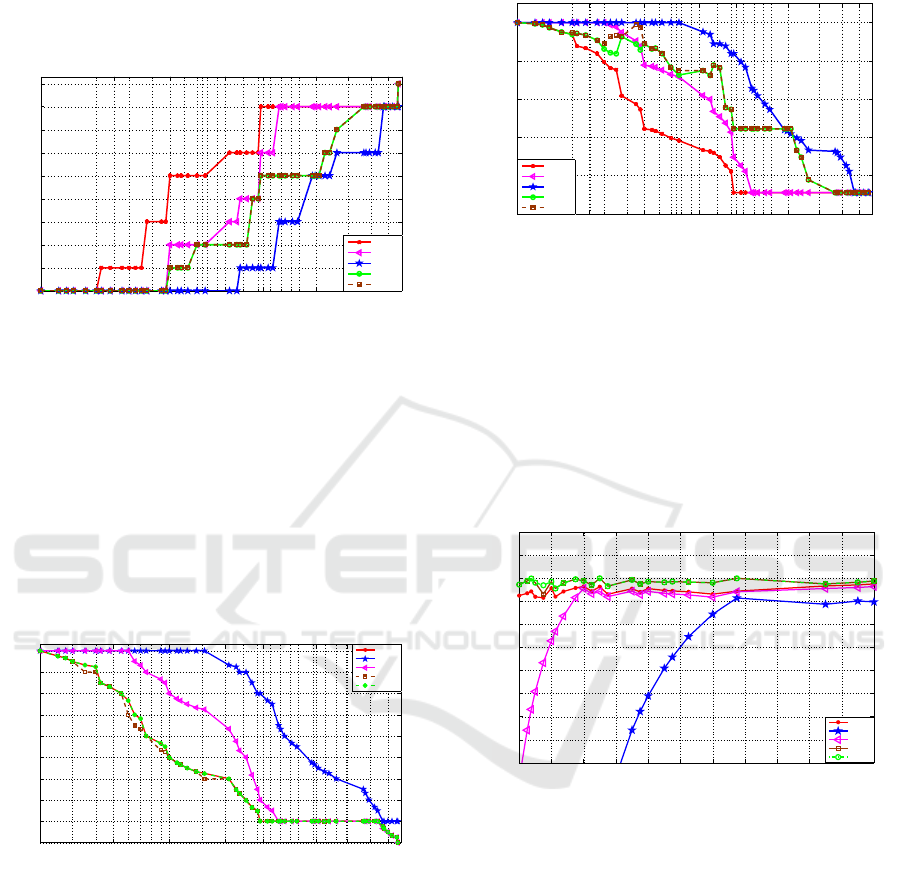
respectively. Although, LMMCF and LMMF have

identical performance curves, but in general the re-

liability of LMMF is better than the LMMCF due to

its ﬂexibility in link reconﬁguration (no capacity con-

straint).

2 32 62 92 122 15218010 205

Rain fall rate (D) in mm/h

Dropped nodes

D−L

P−L

F−L

LMMCF

LMMF

Figure 5: Reliability versus the rain fall rate (D) for ﬁve

networks; D-L, F-L, P-L, LMMCF and LMMF.

Figure 6 shows the capacity of the networks where

the capacity is 9Gbps for all topologies at D ≤

3mm/h, and zero at D ≥ 180mm/h. And the perfor-

mance of three topologies D-L, LMMCF and LMMF

are almost the same, however the D-L and LMMCF

topologies are better than the LMMF at certain D val-

ues as expected. Numerically, at D = 7mm/h the

capacity of D-L and LMMCF are 6Gbps while in

LMMF it is 5.5Gbps, this is due to the maximization

capacity in LMMCF scheme.

10 92 1803210 20 622 5 122 152

Rain fall rate(D) in mm/h

Capacity in Gbps

D−L

F−L

P−L

LMMF

LMMCF

Figure 6: Capacity (C) versus the rain fall rate (D) for ﬁve

networks; D-L, F-L, P-L, LMMCF and LMMF.

Figure 7 explains the fairness between the nodes

in the capacity of the backbone node. The maximum

fairness is 1 at D ≤ 3mm/h for all topologies. The

proposed approaches improve the fairness and out-

perform P-L, specially at channel degradation. At

D = 10mm/h the fairness is 0.9 for both LMMCF and

LMMF, 0.8 for P-L and 0.45 for D-L as shown. Note

that, the fairness performance in LMMF case is better

than that in LMMCF case as indicated from the MOPs

formulations and numerical results. LMMF is better

than LMMFC in fairness performance curve, speciﬁ-

cally, at D = 9mm/h the fairness is 1 and 0.9 for both

LMMF and LMMCF respectively.

2 32 62 92 122 15218010 205

0.2

0.4

0.6

0.8

Rain fall rate (D) in mm/h

Jain Fairness (F)

D−L

P−L

F−L

LMMCF

LMMF

Figure 7: Fairness (F) versus the rain fall rate (D) for ﬁve

networks; D-L, F-L, P-L, LMMCF and LMMF.

Figure 8 indicates to the bit-error rate of the net-

works, and both LMMF and LMMFC have the same

performance around 10

−5

bit error rate and dos not

exceed 10

−4

. However the F-L and P-L outper-

form the two other topologies, because the proposed

schemes prioritize the reliability-fairness over the bit-

error rate. We show the result for D ≤ 25mm/h, be-

cause the networks at D ≥ 25mm/h have little number

of survived nodes.

2 4 6 8 10 12 14 16 18 20 22 24

−20

−18

−16

−14

−12

−10

−8

−6

−4

−2

Avergae Bit Error rate

Rain rate (D) In mm/h

D−L

F−L

P−L

LMMF

LMMCF

Figure 8: Average error rate (BER) versus the rain fall rate

(D) for ﬁve networks; D-L, F-L, P-L, LMMCF and LMMF.

6 CONCLUSION

Two new resource allocation schemes, namely,

LMMCF and LMMF have been proposed to increase

both reliability and fairness of cooperative reconﬁg-

urable FSO networks at last-mile during sever rainy

weather conditions. The proposed schemes outper-

form both D-L and P-L traditional schemes. Further-

more, this enhancement comes at much lower imple-

mentation cost as the number of installed transceivers

for P-L and LMMCF/LMMF are 24 and 22 respec-

tively. In addition, LMMCF and LMMF have dif-

ferent optimization criteria, where LMMF gives the

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

priority for fairness and reliability over the capacity,

while LMMCF does the opposite. The exhaustive

search method has been used to solve the two ILP-

MOPs. In order to overcome the solution complex-

ity for LMMCF/LMMF the optimal solution(s) could

be computed off line, then it could be registered as

lookup table in FSO tracking controller, which recon-

ﬁgures the topology to optimal conﬁguration versus

the rain fall rate in real time environment.

REFERENCES

Bloom, S., Korevaar, E., Schuster, J., and Willebrand,

H. (2003). Understanding the performance of free-

space optics [invited]. Journal of optical Networking,

2(6):178–200.

Dat, P. T., Bekkali, A., Kazaura, K., Wakamori, K.,

and Matsumoto, M. (2010). A universal platform

for ubiquitous wireless communications using radio

over fso system. Journal of Lightwave Technology,

28(16):2258–2267.

Gagliardi, R. M. and Karp, S. (1995). Optical Communica-

tions. Wiley, New York, 2ed edition.

Isermann, H. (1982). Linear lexicographic optimization.

Operations-Research-Spektrum, 4(4):223–228.

Jain, R., Chiu, D., and Hawe, W. (1998). A quantitative

measure of fairness and discrimination for resource al-

location in shared computer systems. arXiv preprint

cs/9809099.

Kashani, M. A., Safari, M., and Uysal, M. (2013). Opti-

mal relay placement and diversity analysis of relay-

assisted free-space optical communication systems.

Journal of Optical Communications and Networking,

5(1):37–47.

Khalighi, M. A. and Uysal, M. (2014). Survey on free space

optical communication: A communication theory per-

spective. Communications Surveys & Tutorials, IEEE,

16(4):2231–2258.

Kim, I. I., McArthur, B., and Korevaar, E. J. (2001). Com-

parison of laser beam propagation at 785 nm and 1550

nm in fog and haze for optical wireless communica-

tions. In Information Technologies 2000, pages 26–

37. International Society for Optics and Photonics.

Marler, R. T. and Arora, J. S. (2004). Survey of

multi-objective optimization methods for engineer-

ing. Structural and multidisciplinary optimization,

26(6):369–395.

Milner, S. D., Ho, T.-H., Smolyaninov, I. I., Trisno, S., and

Davis, C. C. (2002). Free-space optical wireless links

with topology control. In International Symposium

on Optical Science and Technology, pages 175–180.

International Society for Optics and Photonics.

Ogryczak, W. and

Sliwi

nski, T. (2006). On direct meth-

ods for lexicographic min-max optimization. In Com-

putational Science and Its Applications-ICCSA 2006,

pages 802–811. Springer.

Ogryczak, W. and Sliwinski, T. (2007). Lexicographic max-

min optimization for efﬁcient and fair bandwidth allo-

cation. In International network optimization confer-

ence (INOC).

Paar, C. and Pelzl, J. (2009). Understanding cryptography:

a textbook for students and practitioners. Springer

Science & Business Media.

recommendation ITU-R P.1814, I. (2007). Prediction meth-

ods required for the design of terrestrial free-space op-

tical links.

Refai, H. H., Sluss, J. J., Refai, H. H., and Atiquzzaman,

M. (2006). Comparative study of the performance of

analog ﬁber optic links versus free-space optical links.

Optical Engineering, 45(2):025003–025003.

Vavoulas, A., Sandalidis, H. G., and Varoutas, D. (2012).

Weather effects on fso network connectivity. Jour-

nal of Optical Communications and Networking,

4(10):734–740.

Proposed Resource Allocation Schemes for Rainy Free Space Optical Network