Truncated, Impossible, and Improbable Differential Analysis of ASCON

Cihangir Tezcan

Department of Mathematics, Middle East Technical University, Ankara, Turkey

Institute of Informatics, Department of Cyber Security, CYDES Laboratory, Middle East Technical University,

Ankara, Turkey

Institute of Applied Mathematics, Department of Cryptography, Middle East Technical University, Ankara, Turkey

Keywords:

ASCON, Truncated Differential, Impossible Differential, Improbable Differential, Undisturbed Bits.

Abstract:

ASCON is an authenticated encryption algorithm which is recently qualiﬁed for the second-round of the Com-

petition for Authenticated Encryption: Security, Applicability, and Robustness. So far, successful differential,

differential-linear, and cube-like attacks on the reduced-round ASCON are provided. In this work, we pro-

vide the inverse of ASCON’s linear layer in terms of rotations which can be used for constructing impossible

differentials. We show that ASCON’s S-box contains 35 undisturbed bits and we use them to construct 4 and 5-

round truncated, impossible, and improbable differential distinguishers. Our results include practical 4-round

truncated, impossible, and improbable differential attacks on ASCON. Our best attacks using these techniques

break 5 out of 12 rounds. These are the ﬁrst successful truncated, impossible, and improbable differential

attacks on the reduced-round ASCON.

1 INTRODUCTION

The Competition for Authenticated Encryption: Se-

curity, Applicability, and Robustness (CAESAR) is

an ongoing cryptographic competition where authen-

ticated encryption schemes are challenging. The ﬁrst

round of the competition had 56 ciphers and recently

on 07.07.2015 it was announced that 29 of them qual-

iﬁed for the second round. It is expected that the third

round candidates will be announced around June 2016

and a ﬁnal portfolio will be announced at the end

of 2017. However, these dates are tentative because

cryptanalysis effort required to analyze candidates is

unpredictable.

ASCON (Dobraunig et al., 2014) is one of the au-

thenticated encryption schemes that made it to the

second round of the CAESAR competition. Un-

til now, this cipher is successfully analyzed against

differential, differential-linear, and cube-like attacks.

Currently the best key recovery attack on this scheme

breaks 6 out of 12 rounds and the best forgery attack is

on 4 rounds. Although the designers analyze ASCON

for impossible differential attacks, they only achieve

a 5-round impossible differential for the permutation.

It can be used to distinguish the ASCON permutation

from a random permutation but it cannot be used di-

rectly in a key recovery or forgery attack.

In this work, we ﬁrst analyze ASCON’s S-box and

provide its undisturbed bits which can be used to con-

struct longer truncated, impossible, or improbable dif-

ferentials. Then we analyze ASCON’s linear layer.

We prove that its invertible and provide its inverse

in terms of XOR of rotations of binary words. Then

we analyze the security of ASCON against truncated,

impossible, and improbable differential cryptanalysis

and provide the ﬁrst attacks which use these tech-

niques. We provide truncated differential key recov-

ery attacks on 4 and 5 rounds, impossible differential

attacks on 4 rounds, and improbable differential at-

tacks on 5 rounds of ASCON. Moreover, we provide

5 round truncated, impossible, and improbable dif-

ferential distinguishers which requires much less data

when compared to the impossible differential distin-

guisher of the designers.

This paper is organized as follows: In Sect. 2, we

describe ASCON and summarize the previous crypt-

analysis results on this cipher. In Sect. 3, we analyze

ASCON’s S-box and provide its undisturbed bits. In

Sect. 4, we prove that the linear layer of ASCON is

invertible and provide its inverse in terms of rotations.

In Sect. 5, we provide the ﬁrst truncated, impossible,

and improbable differential key recovery attacks on

ASCON. We conclude our paper in Sect. 6.

Tezcan, C.

Truncated, Impossible, and Improbable Differential Analysis of ASCON.

DOI: 10.5220/0005689903250332

In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), pages 325-332

ISBN: 978-989-758-167-0

325

2 ASCON

2.1 Design

ASCON is an authenticated encryption scheme that

is submitted to ongoing CAESAR competition and it

qualiﬁed for the second-round. It is a substitution-

permutation network and it is based on a sponge-like

construction with a state size of 320 bits. ASCON’s

mode of operation is based on MonkeyDuplex (Dae-

men, 2012).

The initial design of ASCON, which is referred to

as v1.0, supported two key lengths, 96 and 128 bits.

However, the designers removed the 96-bit key sup-

port when tweaking for the second-round of the com-

petition. Since 80-bit security is not suggested today,

removing the 96-bit key variant is probably a good

call since it may not be secure in the close future. The

tweaked ASCON is referred to as v1.1 and we focus on

this latest version in this paper. The tweaked version

provides two recommended parameter sets referred to

as ASCON-128 and ASCON-128a.

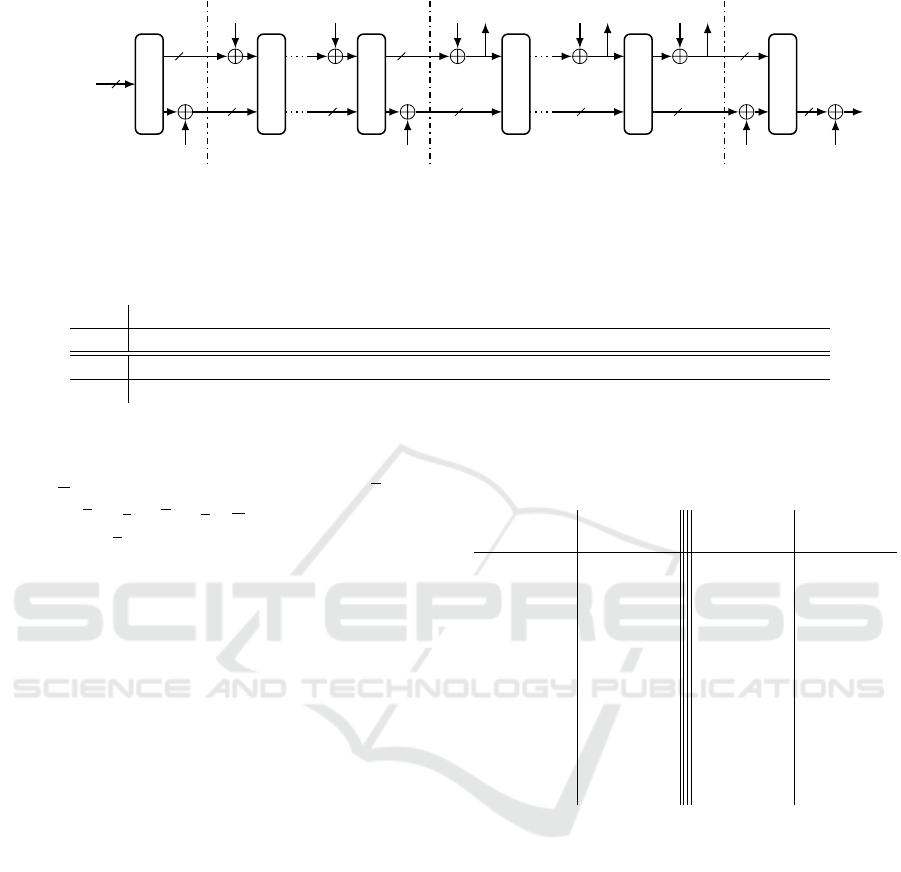
The encryption consists of four steps: Initializa-

tion, processing associated data, processing the plain-

text, and ﬁnalization. The 320-bit state is represented

with ﬁve 64-bit words x

,.. .,x

. The scheme uses

two permutations p

and p

which applies the round

transformation p iteratively a and b times. These

steps are illustrated in Figure 1.

For ASCON-128, we have a = 12 and b = 6. For

ASCON-128a we have a = 12 and b = 8. Both ver-

sions use 128-bit key, nonce and tag. However, data

block size is 64 for ASCON-128 and 128 for ASCON-

128a.

The round transformation of ASCON ﬁrst adds a

constant to x

, applies a nonlinear substitution layer

and then applies a linear layer. The substitution layer

applies a 5-bit S-box 64 times in parallel. This S-box

is afﬁne equivalent to the Keccak (Bertoni et al., 2011)

χ mapping and is provided in Table 1. The linear layer

is actually XOR of right rotations of the 64-bit words

,.. ., x

. The linear layer can be described as fol-

lows:

) = x

⊕ (x

≫ 19) ⊕ (x

≫ 28)

) = x

⊕ (x

≫ 61) ⊕ (x

≫ 39)

) = x

⊕ (x

≫ 1)⊕ (x

≫ 6)

) = x

⊕ (x

≫ 10) ⊕ (x

≫ 17)

) = x

⊕ (x

≫ 7)⊕ (x

≫ 41)

2.2 Security

We can divide the attacks into two categories, forgery

and key recovery. Forgery attacks focus on the ﬁ-

nalization and key recovery attacks focus on the ini-

tialization phases of ASCON. When analysing AS-

CON, we can target either the initialization in a nonce-

respecting scenario, or the processing of the plaintext

in a nonce-misuse scenario.

In case of an attack on the ﬁnalization of AS-

CON, suitable characteristics may contain differences

in stateword x

at the input of the permutation. The

rest of the statewords have to be free of differences.

For the output of the ﬁnalization, the only require-

ment is that there is some ﬁxed difference pattern in

and x

. Knowledge about the expected differences

in x

, x

, and x

at the output of the permutation is not

required. When we focus on the initialization, differ-

ences are allowed in the nonce x

, x

and the output is

observed only for x

(i.e. output difference should be

at x

The ﬁrst analysis of ASCON is done by the de-

signers in the CAESAR competition submission doc-

ument (Dobraunig et al., 2014). They provided

collision-producing differentials and 5-round impos-

sible differential for the permutation. In (Dobraunig

et al., 2015), these observations are further improved

to obtain 6-round cube-like, 5-round differential-

linear key recovery attacks and 4-round differential

forgery attack. They also provided linear and differ-

ential bounds and 12-round zero-sum distinguishers

for the permutation that requires 2

130

time complex-

ity.

Moreover, Todo provided integral distinguishers

for various numbers of rounds for the ASCON permu-

tation (Todo, 2015).

Finally, Jovanovic et al. proved that ASCON’s

sponge mode is secure even for higher rates (Jo-

vanovic et al., 2014).

3 ANALYSIS OF ASCON’s S-BOX

ASCON designers provide differential and linear

properties of ASCON’s S-box in (Dobraunig et al.,

2014). The maximum differential probability of the

S-box is 2

−2

and its differential branch number is 3.

The maximum linear probability of the S-box is 2

−2

and its linear branch number is 3. The algebraic de-

gree of the S-box is 2. A different 5 × 5 S-box with

smaller maximum differential probability and linear

probability could easily be chosen by the designers.

However, this S-box was intentionally chosen because

it requires very small area in hardware and performs

very fast in software and hardware.

Deﬁnition 3.1. (Tezcan, 2014) For a speciﬁc input

difference of an S-box, if some bits of the output dif-

ference remain invariant, then we call such bits undis-

turbed.

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

326

IVkK kN

320

∗

t−1

K k0

∗

Initialization Associated Data Plaintext Finalization

Figure 1: The encryption of ASCON. Figure is taken from the cipher’s ofﬁcial website http://ascon.iaik.tugraz.at/.

Table 1: ASCON’s 5-bit s-box.

x 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

S(x) 4 11 31 20 26 21 9 2 27 5 8 18 29 3 6 28

x 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

S(x) 30 19 7 14 0 13 17 24 16 12 1 25 22 10 15 23

Deﬁnition 3.2. (Evertse, 1987) An n × m S-Box S is

said to have a linear structure if there exists a nonzero

vector α ∈ F

together with a nonzero vector b ∈ F

such that b · S(x) ⊕ b · S(x ⊕ α) takes the same value

c ∈ F

for all x ∈ F

We further analyzed this S-box for other crypto-

graphic properties and observed that it has 91 lin-

ear structures. 35 of them corresponds to coordi-

nate functions, thus by (Makarim and Tezcan, 2014)

they are undisturbed bits in the forward direction and

they are provided in Table 2. Moreover, ASCON

has 2 undisturbed bits for the inverse S-box, namely

00010 →???1? and 01000 →?1???. Although the in-

verse S-box is not used in the encryption or decryp-

tion process, its undisturbed bits can be used when

constructing impossible differentials via the miss-in-

the-middle technique.

Deﬁnition 3.3. (Tezcan and

Ozbudak, 2014) Let S be

a function from F

to F

. For all x,y ∈ F

that satisfy

S(x) ⊕S(y) = µ, if we also have S(x ⊕ λ)⊕S(y ⊕ λ) =

µ, then we say that S has a differential factor λ for the

output difference µ. (i.e. µ remains invariant for λ).

Recently, a new S-box property called differential

factor is introduced in (Tezcan and

Ozbudak, 2014)

which shows that some key bits may not be captured

in a differential attack or its variants. This observation

may be used to reduce the time complexity of the key

guess step of differential attacks. On the other hand,

it increases the time complexity of exhaustive search

for the remaining key bits phase. Differential factors

are used in (Tezcan and

Ozbudak, 2014) to reduce the

time complexity of differential-linear attacks on SER-

PENT (Biham et al., 1998). Although ASCON’s S-box

does not have the best cryptographic properties, sur-

prisingly it does not contain any differential factors.

Table 2: Undisturbed Bits of ASCON’s S-box.

Input Output Input Output

Difference Difference Difference Difference

00001 ?1??? 10000 ?10??

00010 1???1 10001 10??1

00011 ???0? 10011 0???0

00100 ??110 10100 0?1??

00101 1???? 10101 ????1

00110 ????1 10110 1????

00111 0??1? 10111 ????0

01000 ??11? 11000 ??1??

01011 ???1? 11100 ??0??

01100 ??00? 11110 ?1???

01110 ?0??? 11111 ?0???

01111 ?1?0?

4 ANALYSIS OF ASCON’s LINEAR

LAYER

The inverse of ASCON’s linear layer is not provided in

(Dobraunig et al., 2014) because ASCON is a sponge

construction and the inverse of this layer is not re-

quired in the decryption process. However, in order

to obtain impossible differential distinguishers using

the miss-in-the-middle technique, we need the inverse

permutation to check differentials in the reverse order.

We will also use them as ﬁltering conditions when

we are choosing plaintext-ciphertext pairs in our trun-

cated and improbable differential attacks.

The linear layer consists of XOR of right rotations

of the 64-bit words x

,.. ., x

. Thus, the ﬁrst thing to

check whether such an operation is invertible or not.

Truncated, Impossible, and Improbable Differential Analysis of ASCON

327

The following theorem shows when XOR of rotations

of binary words are invertible.

Theorem 4.1. (Rivest, 2011) If n is a power of 2,

v is an n-bit word, and r

, r

, ..., r

are distinct

ﬁxed integers modulo n, then the function R(v) =

R(v;r

,.. ., r

) = (v ≪ r

) ⊕ (v ≪ r

) ⊕ .. .(v ≪

) is invertible if and only if k is odd, where (v ≪ r)

denotes the n-bit word v rotated left by r positions,

and where ’⊕’ denotes the bit-wise ’exclusive-or’ of

n-bit words.

Theorem 4.1 shows that the linear layer of ASCON

is invertible since k = 3 for all of the ﬁve transfor-

mations Σ

,.. ., Σ

. If we consider n-element vectors

over the ﬁnite ﬁeld F

, one can obtain R(v) by multi-

plying v by an n × n circulant matrix over F

having

k ones per row and per column. Thus, inverse of R(v)

can be obtained by ﬁnding the inverse of this circulant

matrix via reducing it to row-reduced echelon form by

means of row operations. This way we obtained the

inverse of the linear layer and the right rotations re-

quired to perform the inverse linear layer is provided

in Table 3.

5 TRUNCATED, IMPOSSIBLE,

AND IMPROBABLE

DIFFERENTIAL ANALYSIS

Statistical attacks on block ciphers make use of a

property of the cipher so that an event occurs with

different probabilities depending on whether the cor-

rect key is used or not. We represent these probabil-

ities with p

for the correct key and p for the wrong

ones. For instance, differential cryptanalysis (Biham

and Shamir, 1991) considers characteristics or differ-

entials which show that a particular output difference

should be obtained with a relatively high probability

when a particular input difference is used. Hence,

when the correct key is used, the predicted differences

occur more frequently (i.e. p

> p). In a classical dif-

ferential characteristic the differences are fully spec-

iﬁed and in a truncated differential (Knudsen, 1994)

only parts of the differences are speciﬁed.

On the other hand, impossible differential crypt-

analysis (Biham et al., 2005) uses an impossible dif-

ferential which shows that a particular difference can-

not occur for the correct key (i.e. probability of this

event is exactly zero). Therefore, if these differences

are satisﬁed under a trial key, then it cannot be the

correct one (i.e. p

= 0). Thus, the correct key can

be obtained by eliminating all or most of the wrong

keys.

Table 3: Linear layer of ASCON consists of XOR of rota-

tions of binary words. Since the inverses of these operations

are not required in the decryption process, they are not pro-

vided by the designers in the submission document. We

provide the inverse of the linear layer which can be used for

constructing impossible differentials. All of the rotations

are to the right.

Permutation Rotations Size

0 19 28 3

−1

0 3 6 9 11 12 14 15 17

18 19 21 22 24 25 27 30 33

36 38 39 41 42 44 45 47 50

53 57 60 63

0 61 39 3

−1

0 1 2 3 4 8 11 13 14

16 19 21 23 24 25 27 28 29

30 35 39 43 44 45 47 48 51

53 54 55 57 60 61

0 1 6 3

−1

0 2 4 6 7 10 11 13 14

15 17 18 20 23 26 27 28 32

34 35 36 37 40 42 46 47 52

58 59 60 61 62 63

0 10 17 3

−1

1 2 4 6 7 9 12 17 18

21 22 23 24 26 27 28 29 31

32 33 35 36 37 40 42 44 47

48 49 53 58 61 63

0 7 41 3

−1

0 1 2 3 4 5 9 10 11

13 16 20 21 22 24 25 28 29

30 31 35 36 40 41 44 45 46

47 48 50 53 55 60 61 63

Moreover, it is shown in (Tezcan, 2010) that it is

also possible to obtain differentials so that the pre-

dicted differences occur less frequently for the correct

key (i.e. p

< p). This new cryptanalytic technique is

called the improbable differential attack and the im-

possible differential attack can be seen as a special

case of it where p

= 0.

5.1 Truncated Differential Analysis

5.1.1 4-Round Truncated Differential

Distinguisher

Undisturbed bits of ASCON’s S-box allows us to ob-

tain long truncated differentials. We ﬁrst focus on

probability 1 truncated differentials in order to con-

vert them to impossible differentials via the miss-in-

the-middle technique. The longest truncated differ-

ential we could ﬁnd in the encryption direction with

probability 1 is on 3.5-rounds of ASCON and it is pro-

vided in Table 4. By adding the permutation layer to

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

328

the end, this differential can be used to distinguish 4

rounds of the permutation with only 2 chosen nonces.

Table 4: Truncated differential ∆

with probability 1 that

covers 3.5 rounds of p in binary notation. Undisturbed bits

are shown in bold. Substitution and permutation layers are

denoted by S and P, respectively.

3.5-Round Truncated Differential

1000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

1000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

?000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

?00000000000000000000000000000000000000?000000000000000000000?00

??0000?000000000000000000000000000000000000000000000000000000000

?000000000?000000?0000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

??0000?000?000000?000000000000000000000?000000000000000000000?00

?000000000?000000?000000000000000000000?000000000000000000000?00

??0?00?000?00000??0??0000?00??0000?0?0??00000?000000000000?00?00

??0?00??00?000?00?000000000000000000?00??0000?000?000000?0?00??0

????00??00???000???0000?000000000000000??0000?000000000000000??0

??0000??00??00?0???0?00?000?000000?0000?000000000?000000?0000?00

?000?00?00?00000??000000?0000000000000??0?0000?0000?000000?00?00

?????0??00???0?0?????00???0???0000?0?0????000??00?0?0000?0?00??0

?????0??00???0?0???0?00??00?000000?0?0????000??00?0?0000?0?00??0

?????0??00???0?0?????00???0???0000?0?0????000??00?0?0000?0?00??0

??0??0??00??00?0?????00???0???0000?0?0????000??00?0?0000?0?00??0

????????0?????????????????????????????????????????0???0????????0

?????0????????????????????????0?0???????????0??0????0?0?????0???

???????????????????????????????00??????????0????0????00?????0???

?????0??????????????????????????0??????????0???0????0?0?????0???

?????????0??0????????????????????????0????????????0???0?????????

??????????????????????????????????????????????????????0?????????

5.1.2 4-Round Truncated Differential Attack

We cannot use our 3.5-round truncated differential ∆

in a key recovery attack because we can only provide

input differences at the words x

and x

. We observe

that if we provide the input difference 3

to a single

S-box, then the output difference is 1

with probabil-

ity 2

−3

. Then with probability 1, we have 54

S-

box with 0

output difference at the end of substitu-

tion layer of round 4. After the permutation layer we

focus on the word x

because this is the only word

that we can work on in an attack to the initialization

phase. Thus, output differences that have the differ-

ence 0 corresponding to the most signiﬁcant bit of

the 54

after the application of the inverse permu-

tation provided in Table 3 are the right pairs for our

attack. Since half of the output differences make that

bit have 0 difference, this ﬁltering condition has prob-

ability 1/2. Details of this differential are provided in

Table 5. Since this is a probability 1 differential dis-

tinguisher, complementing the output differences pro-

vides a 4-round impossible differential distinguisher.

For a wrong key, this differential holds with prob-

ability p = 1/2. However, it holds with probability

= 1 for the correct key. If we think ASCON as a

block cipher where the plaintext is XORed with the

key, then we can capture 2 bits of the key correspond-

ing to the active S-box with 2

data complexity and

negligible time and memory complexity. Due to the

symmetry of the cipher, remaining key bits can be

captured by applying the same attack with shifting the

input difference. However, key is not XORed with the

plaintext in ASCON and the S-box input difference 3

gives the output difference 1

when the correspond-

ing two key bits are 1. Hence, this attack can be used

with the symmetry of the cipher to check if the two

key bits corresponding to the active S-boxes are 1.

Approximately 16 of them would be 1 and thus the

attack should work for them. And the remaining 48 of

them can be found via exhaustive search which would

require 3

4-round ASCON encryptions.

Table 5: 4-Round truncated differential attack. Substitution

and permutation layers are denoted by S and P, respectively.

4-Round Truncated Differential Attack

0000000000000000000000000000000000000000000000000000000000000000

1000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

−3

0000000000000000000000000000000000000000000000000000000000000000

1000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

1000000100000000000000000000000000000000010000000000000000000000

?000000?000000000000000000000000000000000?0000000000000000000000

1000000100000000000000000000000000000000010000000000000000000000

?000000?000000000000000000000000000000000?0000000000000000000000

?0000?0?00000000000?000000?0?000000?00000?000000000000000000?000

0000100000000000100000000000000000000011000000100000000000000100

??0000???0000?000000000000000000000000000??0000?0000000000000000

?000000?00?000000?000000?0000000000000000?000000000?000000?00000

?000000?000000?000?0000000000000000000000?000000?000000000000000

??00?????0?00??0????0000?0?0?000000?00??0??000???00?000000?0??00

??0010???0?00??01??00000?0000000000000110??0001??00?000000?00100

??001????0?00??01???0000?0?0?000000?00110??0001??00?000000?0?100

?000??0?00?000?0????0000?0?0?000000?00??0?0000?0?00?000000?0??00

?????????0???????????0????????00????????0????????00??0?0???0??0?

?????????0??0???????0??????0?000??0??0????????????0???0????0????

???101???????????????01???0000?0000000011???110???0????00???0010

??00?????0??0????????1??????????01???0?00???0?0??10??0010?????01

??0???0?00???0??????0?0????0?00?0?0?0???0??00??0?00?0?0?0?????00

??????????????????????????????????????????????????0?????????????

?????????0????????????????????????????????????????0?????????????

5.1.3 5-Round Truncated Differential Attack

We can perform a 5-round attack on ASCON by giving

input difference to 35 S-boxes and check if all of

the output differences are 1

. Thus, we need to guess

2 · 35 = 70 bits of the key. To the bottom of these dif-

ferences, we add a 4-round truncated differential that

holds with probability 2

−3

which is provided in Table

Truncated, Impossible, and Improbable Differential Analysis of ASCON

329

6. For a wrong key, this differential holds with prob-

ability p = 1/2. However, it holds with probability

= 1/2 + 1/8 for the correct key.

Table 6: 5-Round truncated differential attack. Substitution

and permutation layers are denoted by S and P, respectively.

5-Round Truncated Differential Attack

0000000000000000000000000000000000000000000000000000000000000000

1111110001110100100011101100111100011000110011111010010100001101

0000000000000000000000000000000000000000000000000000000000000000

−105

0000000000000000000000000000000000000000000000000000000000000000

1111110001110100100011101100111100011000110011111010010100001101

0000000000000000000000000000000000000000000000000000000000000000

1000000000000000000000000000000000000000000000000000000000000000

−3

0000000000000000000000000000000000000000000000000000000000000000

1000000000000000000100000000100000000000000000000000000000000000

1000000000000000000000000000000000000001000000000000000000000100

0000000000000000000000000000000000000000000000000000000000000000

?000000000000000000?00000000?0000000000?000000000000000000000?00

?00000000000000000010000000010000000000?000000000000000000000?00

1000000000000000000000000000000000000001000000000000000000000100

?000000000000000000?00000000?00000000001000000000000000000000100

?000000000000000000?00000000?0000000000?000000000000000000000?00

?00?000000000000?00?00000?00?000000000??0000000?00000000?0?00?00

?0010000000000?010000000010000000000?00?000000000000000000?00?00

0101001000000000000000000000000000000000100001000000000000000010

?000000100?000100?0?00000000??000000?0?000000?000100000010000000

?000??0?00000000?00?000000?0?000000?00??0?0000?0000000000000??00

??0?????00?000?0??0?00000??0??00000??0????000???01000000?0?0???0

??0?????00?000?0??0?00000??0??00000??0????000???0?000000?0?0???0

?10???1?00?000?0??0?00000??0??00000??0??1?000??00?000000?0?0??10

?10???1?00?000?0??0?00000??0??00000??0??1?000???0?000000?0?0??10

?00???0?00?000?0??0?00000??0??00000??0??0?000???01000000?0?0??00

????????0???0?????0??0?????0??0??????0?????0?????0000???????????

????????00??0?????0????????0??0???0?????????????0?000?0????????0

????????????1????????0??0????????0?????????0????0????00????????1

?0??????1???0?????1????1??????0?0????0??0???0?????1???0?????????

????????00??????????0??????0??00??0?????0????????00????????0??0?

??????????????????????????????0?????????????????????????????????

−1

??????????????????????????????0?????????????????????????????????

Table 7: Impossible differential of (Dobraunig et al., 2014)

that covers 5 rounds of p in hexadecimal notation. It holds

with probability p = 2

−320

for a random permutation.

Input difference Output Difference

0000000000000000 0000000000100000

0000000000000000 0000000000000000

0000000000000000 9 0000000000000000

0000000000000000 0000000000000000

8000000000000000 0000000000000000

If ASCON were a block cipher where the plain-

text is XORed with the key, then we could perform

a key recovery attack where knowledge of 2

110

data

would be enough to distinguish 70 bits of the key

from the wrong ones and around 2

101

5-round AS-

CON encryptions would be required. However, key is

not XORed with the plaintext in ASCON and the S-

box input difference 3

gives the output difference 1

when the corresponding two key bits are 1. So the

attack works when the key bits corresponding to the

35 active S-boxes are all 1. So the attack works for

a weak key space of size 2

128−2·35

= 2

. The weak

key space becomes around 2

when we use the sym-

metry of the cipher but it is still very small compared

to 2

128

. Therefore, if the attacked key is in the weak

key space, then we capture its 70 bits with negligible

time complexity and recover the remaining bits with

exhaustive search that requires 2

5-round ASCON

encryptions. However, if the key is not in this weak

key space, then the attack only becomes slightly faster

than the exhaustive search, namely 2

128

−2

5-round

ASCON encryptions.

Note that the whole differential provided in Table

6 can be seen as a 5-round truncated differential dis-

tinguisher with probability 2

−107

. Hence, we can use

it with 2

109

data to distinguish the 5-round ASCON

from a random permutation. Complementing the out-

put differences provides a 5-round improbable differ-

ential distinguisher that works similar to this 5-round

truncated differential.

5.2 Impossible Differentials

ASCON’s security against impossible differential at-

tacks is discussed in (Dobraunig et al., 2014) by the

designers and they obtained a 5-round impossible dif-

ferential via computer search. This differential can be

used to distinguish the permutation p and it is pro-

vided in Table 7. However, for a random permuta-

Table 8: An impossible differential that covers 5 rounds of p

in binary notation. Substitution and permutation layers are

denoted by S and P, respectively. The miss-in-the-middle

is obtained by combining the 3.5-round ∆

in the forward

direction with the 1.5-round differential in the backward di-

rection that is provided below.

5-Round Impossible Differential

3.5-round truncated differential ∆

??????????????????????????????????????????????????????0?????????

Impossible

????????????????????????????????????????????????????????????????

1110000101100010110011111011111101010100101000110100011010100101

????????????????????????????????????????????????????????????????

0??0?0??0?00?0000??00????0????0???0???00?0?0?00???000?0000?00?0?

0110101101001000011001111011110111011100101010011100010000100101

0??0?0??0?00?0000??00????0????0???0???00?0?0?00???000?0000?00?0?

0000000000000000000000000000000000000000000000000000000000000000

0110101101001000011001111011110111011100101010011100010000100101

0000000000000000000000000000000000000000000000000000000000000000

1000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

330

Table 10: Summary of attacks on ASCON.

Type Rounds Time Method Source

Key Recovery 6/12 2

Cube-like (Dobraunig et al., 2015)

Key Recovery 5/12 2

Cube-like (Dobraunig et al., 2015)

Key Recovery 5/12 2

Differential-Linear (Dobraunig et al., 2015)

Key Recovery 5/12 2

or 2

127.99

Truncated/Improbable Sect. 5.1.3

Key Recovery 4/12 2

Differential-Linear (Dobraunig et al., 2015)

Key Recovery 4/12 3

Truncated/Impossible Sect. 5.1.2

Forgery 4/12 2

101

Differential (Dobraunig et al., 2015)

Forgery 3/12 2

Differential (Dobraunig et al., 2015)

Table 9: Summary of impossible, improbable, and truncated

differential distinguishers on ASCON.

Rounds Data Method Source

5/12 2

109

Improbable Diff. Sect. 5.1.3

5/12 2

109

Truncated Diff. Sect. 5.1.3

5/12 2

256

Impossible Diff. Sect. 5.2

5/12 2

320

Impossible Diff. (Dobraunig et al., 2014)

4/12 2

Impossible Diff. Sect. 5.1.1

4/12 2

Truncated Diff. Sect. 5.1.1

tion this impossible differential holds with probability

p = 2

−320

. Thus, one needs to use the whole code-

book to use it as a distinguisher. Moreover, since

the output differences are fully speciﬁed, it cannot be

used in a key recovery or forgery attack.

We consider truncated differentials in the decryp-

tion direction to obtain impossible differentials by

combining them with our 3.5-round truncated differ-

ential ∆

. We cannot ﬁnd such long truncated differ-

entials in the decryption direction because a single bit

difference to the permutation provides differences at

more than 30 bits because of the inverse linear trans-

formations. Moreover, the inverse of ASCON’s S-box

has only two undisturbed bits. The longest truncated

differentials we could ﬁnd covers 1.5 rounds in the

decryption direction. Thus, we can use them to ob-

tain 5-round impossible differentials using the miss-

in-the-middle technique. An example of such an im-

possible differential is provided in Table 8. The dif-

ferences are fully speciﬁed in this impossible differ-

ential, too. However, note that since the contradiction

is obtained at a single bit, half of the differences given

only to x

or x

at P5 still make it miss in the middle

due to the undisturbed bits. Since we can give 2

dif-

ferent differences to the x

or x

, we have p = 2

−256

for this bundle of impossible differentials instead of

p = 2

−320

6 CONCLUSIONS

ASCON’s S-box contains many undisturbed bits and

in this study we used them to construct truncated, im-

possible, and improbable differentials. We provide

the results of our distinguishers in Table 9. Our best

attacks break 5 out of 12 rounds of ASCON and they

are provided in Table 10. These attacks can be pre-

vented by replacing ASCON’s S-box with a crypto-

graphically more secure one. However, ASCON’s S-

box is deliberately chosen this way mainly because of

its bit-sliced implementation with few, well pipelined

instructions.

Our attacks show that further analysis may pro-

vide truncated, impossible or improbable differential

distinguishers or attacks on 6 or more rounds of AS-

CON. However, the full scheme looks resistant to

these type of attacks. Thus, we conclude that the se-

curity/performance trade-off due to the choice of the

S-box is well justiﬁed and the full cipher is secure

against truncated, impossible, and improbable differ-

ential attacks. However, our analysis and differentials

can be used to obtain better attacks when combined

with other cryptanalysis techniques.

ACKNOWLEDGEMENTS

This work was supported by The Scientiﬁc and Tech-

nological Research Council of Turkey (T

ITAK)

under the grant 115E447 titled ”Quasi-Differential

Factors and Time Complexity of Block Cipher At-

tacks”.

REFERENCES

Bertoni, G., Daemen, J., Peeters, M., and Assche, G. V.

(2011). The Keccak SHA-3 submission. Submission

to NIST (Round 3).

Truncated, Impossible, and Improbable Differential Analysis of ASCON

331

Biham, E., Anderson, R. J., and Knudsen, L. R. (1998).

Serpent: A new block cipher proposal. In Vaude-

nay, S., editor, Fast Software Encryption, 5th Interna-

tional Workshop, FSE ’98, Paris, France, March 23-

25, 1998, Proceedings, volume 1372 of Lecture Notes

in Computer Science, pages 222–238. Springer.

Biham, E., Biryukov, A., and Shamir, A. (2005). Cryptanal-

ysis of Skipjack reduced to 31 rounds using impossi-

ble differentials. J. Cryptology, 18(4):291–311.

Biham, E. and Shamir, A. (1991). Differential cryptanalysis

of DES-like cryptosystems. J. Cryptology, 4(1):3–72.

Daemen, J. (2012). Permutation-based encryption, authen-

tication and authenticated encryption. DIAC - Direc-

tions in Authenticated Ciphers.

Dobraunig, C., Eichlseder, M., Mendel, F., and Schl

affer,

M. (2014). ASCON v1, submission to the CAESAR

competition.

Dobraunig, C., Eichlseder, M., Mendel, F., and Schl

affer,

M. (2015). Cryptanalysis of Ascon. In Nyberg, K., ed-

itor, Topics in Cryptology - CT-RSA 2015, The Cryp-

tographer’s Track at the RSA Conference 2015, San

Francisco, CA, USA, April 20-24, 2015. Proceedings,

volume 9048 of Lecture Notes in Computer Science,

pages 371–387. Springer.

Eisenbarth, T. and

Ozt

urk, E., editors (2015). Lightweight

Cryptography for Security and Privacy - Third Inter-

national Workshop, LightSec 2014, Istanbul, Turkey,

September 1-2, 2014, Revised Selected Papers, vol-

ume 8898 of Lecture Notes in Computer Science.

Springer.

Evertse, J.-H. (1987). Linear Structures in Blockciphers. In

Chaum, D. and Price, W. L., editors, EUROCRYPT,

volume 304 of Lecture Notes in Computer Science,

pages 249–266. Springer.

Jovanovic, P., Luykx, A., and Mennink, B. (2014). Beyond

2 c/2 security in sponge-based authenticated encryp-

tion modes. In Sarkar, P. and Iwata, T., editors, Ad-

vances in Cryptology - ASIACRYPT 2014 - 20th Inter-

national Conference on the Theory and Application of

Cryptology and Information Security, Kaoshiung, Tai-

wan, R.O.C., December 7-11, 2014. Proceedings, Part

I, volume 8873 of Lecture Notes in Computer Science,

pages 85–104. Springer.

Knudsen, L. R. (1994). Truncated and higher order differ-

entials. In Preneel, B., editor, Fast Software Encryp-

tion: Second International Workshop. Leuven, Bel-

gium, 14-16 December 1994, Proceedings, volume

1008 of Lecture Notes in Computer Science, pages

196–211. Springer.

Makarim, R. H. and Tezcan, C. (2014). Relating undis-

turbed bits to other properties of substitution boxes.

In (Eisenbarth and

Ozt

urk, 2015), pages 109–125.

Rivest, R. L. (2011). The invertibility of the XOR of

rotations of a binary word. Int. J. Comput. Math.,

88(2):281–284.

Tezcan, C. (2010). The improbable differential attack:

Cryptanalysis of reduced round CLEFIA. In Gong, G.

and Gupta, K. C., editors, Progress in Cryptology - IN-

DOCRYPT 2010 - 11th International Conference on

Cryptology in India, Hyderabad, India, December 12-

15, 2010. Proceedings, volume 6498 of Lecture Notes

in Computer Science, pages 197–209. Springer.

Tezcan, C. (2014). Improbable differential attacks on

Present using undisturbed bits. J. Computational Ap-

plied Mathematics, 259:503–511.

Tezcan, C. and

Ozbudak, F. (2014). Differential factors:

Improved attacks on SERPENT. In (Eisenbarth and

Ozt

urk, 2015), pages 69–84.

Todo, Y. (2015). Structural evaluation by generalized inte-

gral property. In Oswald, E. and Fischlin, M., editors,

Advances in Cryptology - EUROCRYPT 2015 - 34th

Annual International Conference on the Theory and

Applications of Cryptographic Techniques, Soﬁa, Bul-

garia, April 26-30, 2015, Proceedings, Part I, volume

9056 of Lecture Notes in Computer Science, pages

287–314. Springer.

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

332