Aircraft Unsteady Aerodynamic Hybrid Modeling based on

State-space Representation and Neural Network

Ouyang Guang, Lin Jun and Zhang Ping

Science and Technology on Aircraft Control Laboratory, Beihang University, XueYuan Road 37, Beijing, China

Keywords: Unsteady Aerodynamics, State-space Representation, Back-propagation Neural Network, Parameter

Identification, Model Optimization.

Abstract: This paper proposes a hybrid model which combines state-space representation and back-propagation neural

network to describe the aircraft unsteady aerodynamic characteristics. Firstly, the state-space model is

analysed and evaluated using wind-tunnel experimental data. Subsequently, back-propagation neural

network is introduced and combined with state-space representation to form a hybrid model. In this hybrid

model, the separation point model in state-space representation is reserved to describe the time delay of the

unsteady aerodynamic responses, while the conventional polynomial model is replaced by back-propagation

neural network to improve accuracy and universality. Finally, lift coefficient and pitch moment coefficient

data from the wind-tunnel experiments are used to estimate the hybrid model. With high similarity to the

wind-tunnel data, the hybrid model presented in this paper is proved to be accurate and effective for aircraft

unsteady aerodynamic modeling.

1 INTRODUCTION

The increasing agility requirements of modern

aircrafts have invoked the development of the

unsteady aerodynamic models. When flights are

limited within a certain envelope of angle of attack,

the traditional linear aerodynamic model is effective

enough due to the incoherence between aerodynamic

characteristics and the movement process. However,

as the high angles of attack region becomes more

accessible for modern aircrafts, the problem of

adequate mathematical modeling of aerodynamic

characteristics at separated and vortex breakdown

flow conditions arises (Goman et al., 1994).

Considering the significant role that unsteady

aerodynamic forces and moments play in aircraft

stability and maneuver control, efficient and

universal unsteady aerodynamic modeling methods

are in urgent demand.

According to (Greenwel et al., 2004), a wide

range of nonlinear unsteady aerodynamic modeling

techniques have been developed in recent years. For

instance, in (Goman et al., 1994), the authors put

forward the state-space representation of

aerodynamic characteristics of an aircraft at high

angles of attack. Thereafter, state-space model and

modified state-space model are also adopted by

(Zakaria et a., 2015) and (Williams et al., 2015) to

model two-dimensional airfoils and lift hysteresis

separately. Analogously, (Kumar et al., 2012) adopts

steady-state stall model for nonlinear modeling. In

(Chen et al., 2004), Volterra series model is used in

nonlinear unsteady aerodynamics investigation.

Development of neural network has recently led

to significant progress in the unsteady aerodynamic

modeling field (Wang et al., 2010). With high

modeling accuracy and expandability to multiple

variables, neural networks have become a hot topic

in unsteady aerodynamic modeling field. Several

studies have been conducted recently in unsteady

aerodynamic neural network modeling. The

researchers in (Kumar et al., 2011) use neural

Gauss–Newton method to study longitudinal

aerodynamic modeling. Support vector machines

model is adopted for unsteady aerodynamic

modeling in (Wang et al., 2015). Feed-forward and

recurrent architectures neural networks are studied

and compared in (Ignatyev et al., 2015).

Although unsteady aerodynamic modeling has

been studied for many years, there is still no

universal solution for different aircrafts due to

limited understanding of the flow mechanism. At the

time of this writing, there is still no standard

232

Guang, O., Jun, L. and Ping, Z.

Aircraft Unsteady Aerodynamic Hybrid Modeling Based on State-Space Representation and Neural Network.

DOI: 10.5220/0005691702320239

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 232-239

ISBN: 978-989-758-173-1

unsteady aerodynamic model. However, some

attempts are still proved to be of great value. For

example, the state-space model can represent time

delay characteristics, which reasonably describes

actual physical mechanism of wing flow separation

and reattachment. Relatively, neural network model

can serve as universal approximators for unknown

aircraft systems and be easily extended to multi-axis

motions modeling. Therefore, an intuitive and

meaningful attempt is to combine these two models

and get an unsteady aerodynamic hybrid model with

all these advantages.

This paper is organized as follows: In Section 2,

aircraft unsteady aerodynamic mechanism is

discussed. Subsequently, state-space model is

introduced and evaluated using the wind-tunnel

experimental data. Section 3 describes the back-

propagation neural network and the hybrid unsteady

aerodynamic model. Nested parameter optimization

algorithm for the hybrid model is also given in this

section. In Section 4, the hybrid model is finally

validated with lift coefficient and pitch moment

coefficient data which come from the wind-tunnel

experiments.

2 STATE-SPACE PRESENTATION

2.1 Unsteady Aerodynamic Mechanism

As a key factor of unsteady aerodynamic modeling,

mechanism research has a significant impact on

model validation. According to (Sun et al., 2015),

unsteady flow separation vortices at the trailing edge

are the causes of the unsteady aerodynamic

characteristics. During maneuvers, the wing flow

separates and reattaches. As adjustment process of

the surface vortex has dynamic time delay

characteristic, the aerodynamic forces and moments

show obvious unsteady phenomena. For example,

pneumatic hysteresis loop can be seen from the

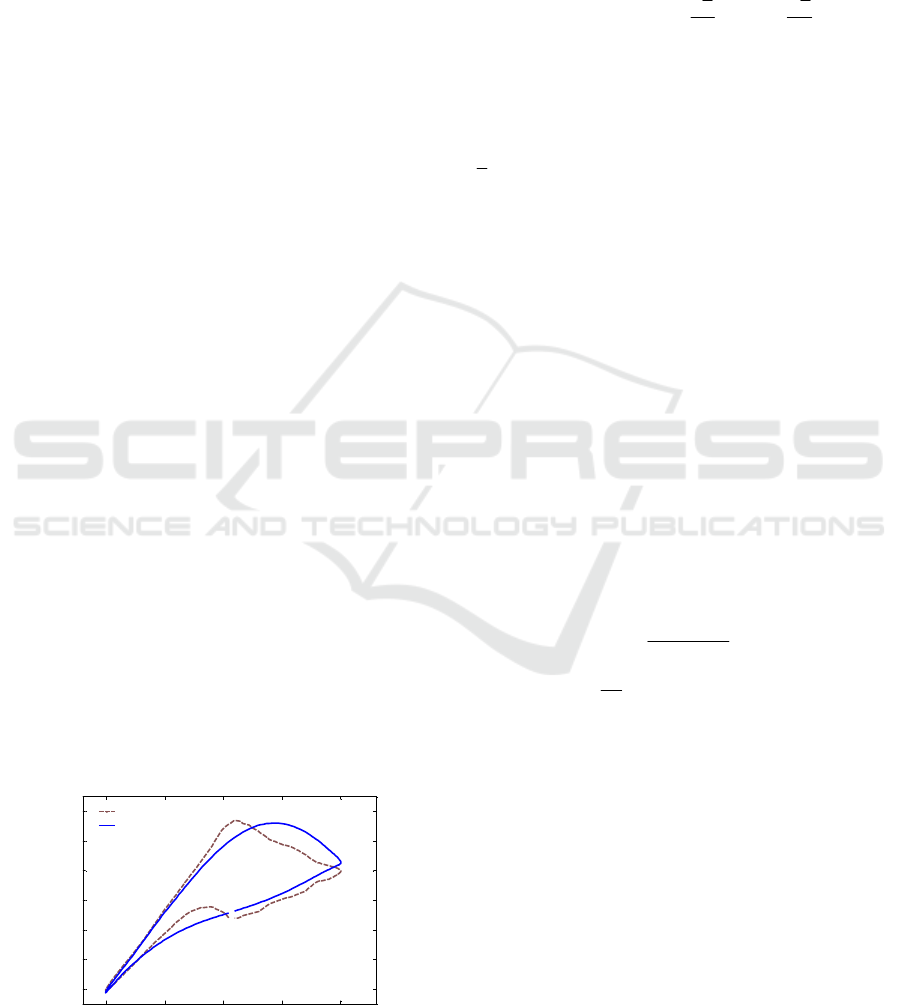
Figure 1: Linear aerodynamic model.

wind-tunnel data of the longitudinal forced pitch

oscillations in Fig. 1.

Linear model is a conventional aerodynamic

model. In many practical cases, the aerodynamic

forces and moments are approximated by linear

terms in their Taylor series expansions. In the case

of lift coefficient, the function is defined as follows:

() () ()

LLs Lq L

qc c

CC C C

αα α

=+ +



(1)

Where

is the total lift coefficient,

denotes the static lift coefficient.

, q

are angle of

attack and pitch angle rate separately.



are

corresponding dynamic factors.

presents air speed,

is the wing mean geometric chord. Linear model

assumes that aerodynamic forces and moments

depend only on the instantaneous values of the flight

states. Due to lacking the considerations of unsteady

aerodynamic effects, the outputs of linear model

often contain notable error at high angles of attack

comparing to the wind-tunnel data (Fig. 1).

2.2 State-space Model

The state-space model takes time delay of flow

separation and reattachment into account. An

internal variable which describes the flow state is

introduced by (Goman et al., 1994) to express time

delay of unsteady aerodynamics at high angles of

attack. This internal state variable is called the

longitudinal position of the separation point

. The

movement of the separation point for unsteady flow

conditions is defined as follows:

(*)

102

()

σα α

τατα

−

+= −



(2)

Function

()x

is the static variation which

depends on the instantaneous angle of attack

is defined as the angle of attack when separation

point reaches the middle of airfoil chord,

is slope

factor.

The unsteady fluid mechanics processes are

divided into two groups. The first group is the quasi-

steady effects such as circulation and boundary-layer

convection lags, which tend to delay flow separation

or burst onset by an amount roughly proportional to

the pitch rate. This combined effect is expressed as

an argument shift

()x

ατα

−



. Where the parameter

defines the total time delay associated with the

above effects. The second group of flow phenomena

0 20 40 60 80

0.5

1.5

2.5

Lift coefficient

Angle of attack/deg

Linear Model

Wind-Tunnel Data

Aircraft Unsteady Aerodynamic Hybrid Modeling Based on State-Space Representation and Neural Network

233

define the transient aerodynamic effects, in which

any disturbance of the separated flow is followed by

an adjustment or relaxation back to the steady-state.

The adjustment process is governed by a first-order

ordinary differential equation (Formula 2) with

relaxation time constant

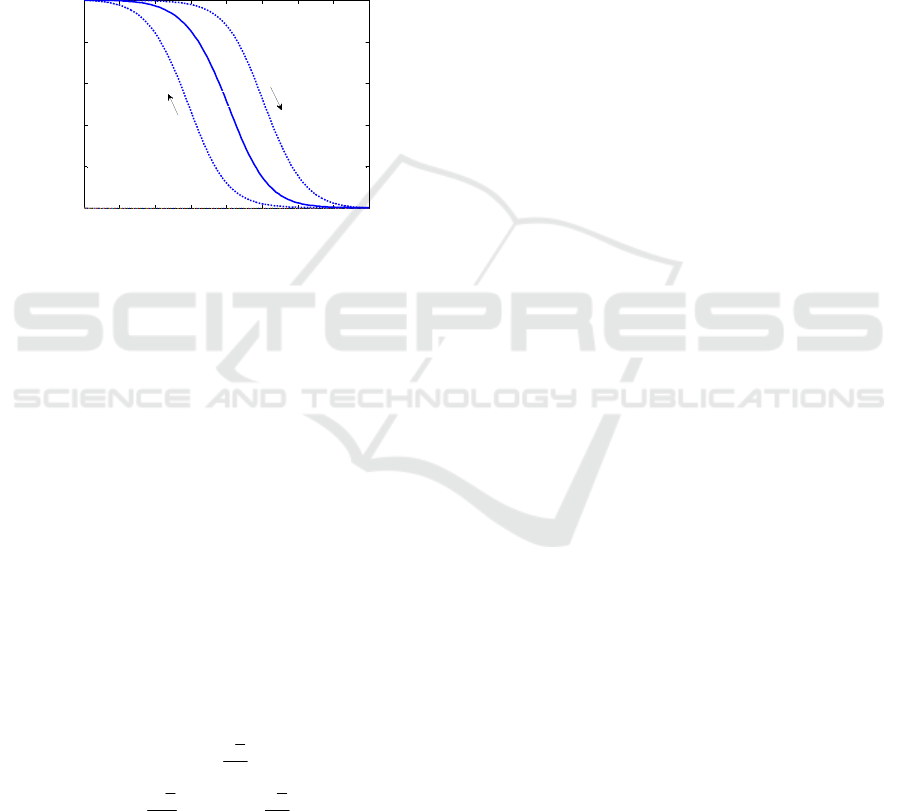
The solid line and dashed lines show the

variations of the separation point position for steady

and unsteady conditions separately in Fig. 2. The

difference between solid line and dashed lines

causes the pneumatic hysteresis of unsteady

aerodynamics.

Figure 2: Instantaneous separation point variations.

In state-space model, aerodynamic forces and

moments depend on not only the instantaneous

values of the flight states, but also the instantaneous

separation point position that can differ considerably

from its stationary value. Since the pitch oscillations

are considered with



, the effects of



are no

longer included in the subsequent longitudinal

unsteady aerodynamic coefficient expressions. The

corresponding unsteady lift coefficient state-space

representation is：

() (,,)

LLs Ld

CC C qx

αα

(3)

The static coefficient

is conventionally

approximated with the first three items in its Taylor

series expansion, while the dynamic coefficient

is approximated with the first five items in its Taylor

series expansion.

00 0

() ()

() () ()

() ()

Ls Ls Ls

Ld L Lq

CC Cx Cx

CCxCx Cx

qc qc

Cx C x

αα

=+ +

=+ + +

(4)

All the corresponding factors in both the static

coefficient and the dynamic coefficient can be

expressed with second-order polynomial functions,

and

in the lower formula.

001020

01 2

()

Lsa Ls Ls Ls

LLLL

Cx k kxkx

αα α

αααα

=+ +

(5)

Where

012

Ls Ls Ls

kkk

ααα

and

012

LLL

kkk

ααα

are

unknown parameters in the polynomial aerodynamic

model. Totally, 26 parameters should be determined

for the lift coefficient state-space representation,

including four parameters

,,,

σα τ τ

in the

separation point model (Formula 2) and all the

relevant factors in the polynomial model (Formula

5).

2.3 State-space Model Evaluation

Suitable simulations of the maneuvers in the wind

tunnels are important for understanding the physics

of complex flow phenomena (Hosder et al., 2007).

These maneuvers should allow the physical

simulation of aircraft dynamic behavior, which is

subject to the dynamic similarity of the aircraft

model, and identification of the aircraft aerodynamic

model structure and its parameters (Pattinson et al.,

2013). For the case of symmetrical motion of the

wing in the longitudinal plane, pitch-only oscillation

has been successfully used to characterize unsteady

aerodynamics at high angles of attack (Pattinson et

al., 2012). In this paper, Forced large-amplitude

pitch oscillations are executed in the wind tunnel.

The corresponding experimental data of

aerodynamic forces and moments are collected and

used to estimate the aerodynamic models.

Harmonic motions in pitch oscillations with a

fixed center of gravity are implemented:

sin(2 )

2cos(2)

Aft

qfA ft

αα π

αππ

=−

==−



(6)

Oscillations were carried out with amplitude

40A

and different pitching frequencies

. The

initial angle of attack

is set to

, so the angle

of attack

varies from

. Lift coefficient

and pitch moment coefficient data at

0.4

Hz=

0.6

Hz=

and

0.8

Hz=

are used to testify the

validity of the state-space model. After a proper

parameter optimization for lift and pitch moment

state-space models with Nelder-Mead method and

particle swarm optimization method, the

comparisons between optimized state-space model

and corresponding wind-tunnel data are partly

shown in the following figures:

0 10 20 30 40 50 60 70 80

0.2

0.4

0.6

0.8

Angle of attack/deg

Instantaneous separation point x

(

)

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

234

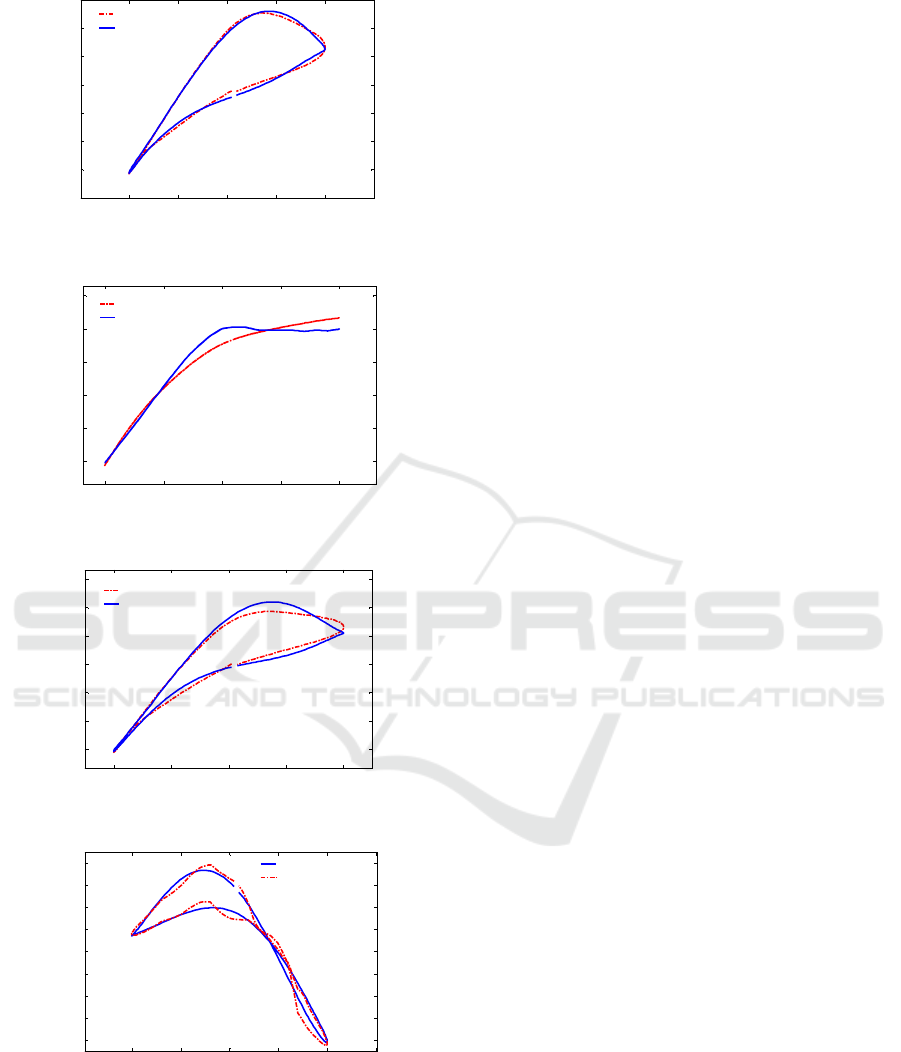
Figure 3: Lift coefficient response at f=0.6Hz.

Figure 4: Static lift coefficient response.

Figure 5: Lift coefficient response at f=0.4Hz.

Figure 6: Pitch moment coefficient response at f=0.6Hz.

The figures above reveal that state-space model

can approximate the wind-tunnel experimental data

to a certain extent. Fig. 5 and Fig. 6 show that

though state-space model can effectively reflect time

delay characteristics of unsteady aerodynamics at

high angles of attack, the model responses are not

always in good agreement with the wind-tunnel data.

The polynomial model is not accurate enough to

describe the nonlinear static aerodynamic coefficient,

like the static lift coefficient in Fig. 4.

Goman’s nonlinear differential equation concept

provides the most promising combination of relative

simplicity, retention of physical significance in its

parameters, and ability to model a wide range of

common flow features (Greenwel et al., 2004).

However, modifications should be added to state-

space model to capture more accurate and reliable

unsteady aerodynamic responses.

3 HYBRID MODEL

Neural networks (NN) have recently been shown to

be an effective tool for modeling nonlinear unsteady

aerodynamics regardless of the aircraft

configurations. In previous studies, a simple time

delay is generally added to the flight states

instantaneous values as the input signals in unsteady

aerodynamic NN model. Though sometimes these

NN models can achieve good accuracy due to the

excellent approximating performance, actual

physical mechanism of unsteady aerodynamics is

not clearly reflected and the NN models are usually

oversized with redundant neurons. As a meaningful

attempt in this paper, a hybrid model which

combines state-space representation and back-

propagation neural network is presented to integrate

respective advantages in these two models.

3.1 Back-propagation Neural Network

Back-propagation neural networks (BPNN) are the

most widely applied neural network models. The

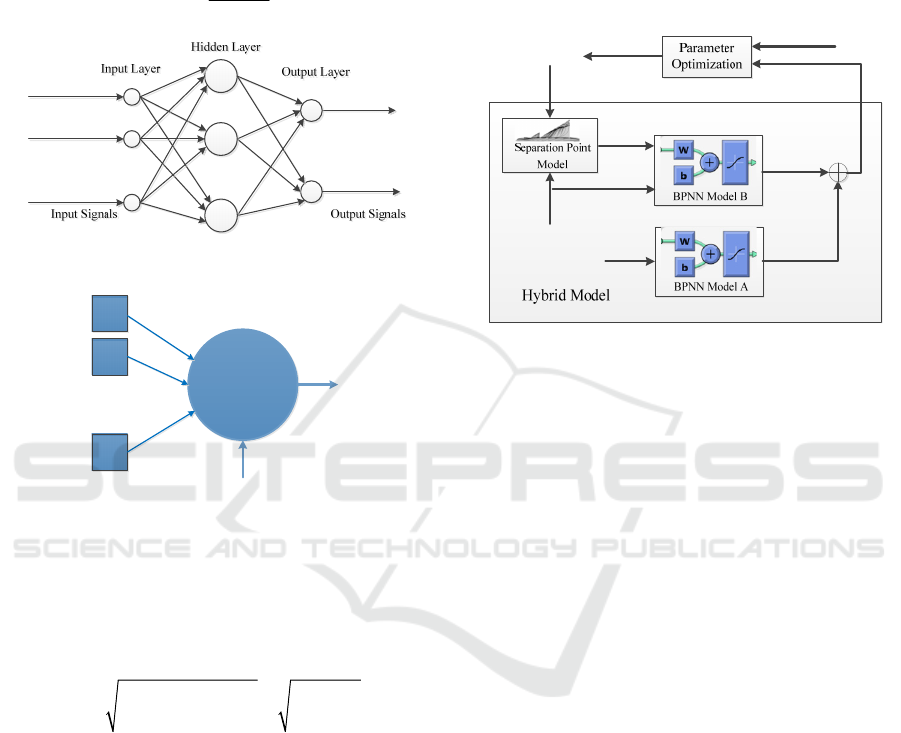
structure of generalized three-layer neural network

consists of the input layer, the hidden layer and the

output layer (Fig. 7). The node in the neural network

is called the neuron. Each neuron receives signals

from the neurons in the previous layer, and

calculates its output through a specific transfer

function.

Fig. 8 shows the typical neuron transfer model.

For nodes in the hidden layer, input signals are

(1,2,...,)

jn=

. These signals are summed with

weight values

corresponding to the signal

connections. Bias value

is added to the weighted

sum of the input signals to generate a summed value

net

. The final output

of the node is mapped

through a commonly used hyperbolic tangent

-20 0 20 40 60 80 100

-0.5

0.5

1.5

2.5

Angle of attack/deg

Lift coefficient

State-Space Model

Wind-Tunnel Data

0 20 40 60 80

0.5

1.5

2.5

Angle of attack/deg

Static lift coefficient

State-Space Model

Wind-Tunnel Data

0 20 40 60 80

0.5

1.5

2.5

Angle of Attack/deg

Lift coefficient

State-Space Model

Wind-Tunnel Data

0 20 40 60 80 100

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

0.1

0.15

Angle of attack/deg

Pitch moment coefficient

Wind-Tunnel Data

State-Space Model

Aircraft Unsteady Aerodynamic Hybrid Modeling Based on State-Space Representation and Neural Network

235

sigmoid transfer function as the nonlinear activation

function. The nodes in the output layer share the

same scheme as the nodes in the hidden layer.

2et

() 1

net x w s

gfnet

−

== −

∑

(7)

Figure 7: Generalized neural network structure.

∑

Figure 8: Typical neuron transfer model.

To minimize the mean-squared error

between

BPNN model response

and the actual response

, the error value

is propagated backwards

through the network for weight values and bias

values updates.

min ( ) / /

Bj Rj j

EyyNeN

=− =

∑∑

(8)

Gradient descent method is used in the back-

propagation neural network for parameter learning.

When the mean-squared error decreases and reaches

a given threshold range, parameter optimization

stops and the BPNN model is regarded as an

acceptable approximator to the actual model.

3.2 Hybrid Model Structure

To obtain a more accurate and reliable unsteady

aerodynamic model and reflect actual flow

separation characteristics, the unsteady aerodynamic

hybrid model is proposed in this paper. As the

differential equation of the separation point can be

used to simulate time delay of unsteady aerodynamic

responses, the separation point model is reserved in

the hybrid model. As far as model accuracy and

output response approximation are concerned, back-

propagation neural network is introduced to replace

the conventional polynomial model. The structure of

unsteady aerodynamic hybrid model is shown in the

following figure.

()t

()

,,,

σα τ τ

()

() ()tt

αα



()

Figure 9: Unsteady aerodynamic hybrid model structure.

Fig. 9 shows that in lift coefficient unsteady

hybrid model, the static lift coefficient and the

dynamic lift coefficient are identified separately. As

the static coefficient only depends on the angle of

attack, a simple BPNN model A is adopted to

describe the nonlinear steady mapping between

these two variables. For the dynamic lift coefficient,

the separation point model is firstly used to generate

the separation point

from

and



. Subsequently,

BPNN model B is introduced with

αα



and

input signals to simulate the unsteady lift component.

The dynamic lift coefficient

is added to the

static lift coefficient

to form the total lift

coefficient response

. Finally,

is compared to

the wind-tunnel lift coefficient data to optimize the

relevant parameters in the hybrid model.

3.3 Hybrid Model Optimization

Two sets of unknown parameters exist in the

unsteady aerodynamic hybrid model. Four

parameters

,,,

σα τ τ

in the separation point model

decide the separation point dynamic characteristics,

while all the relevant weight values and bias values

in BPNN model reveal the nonlinear mapping

function of the unsteady aerodynamic forces and

moments. All of the above unknown parameters

should be identified and optimized to realize the best

model response.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

236

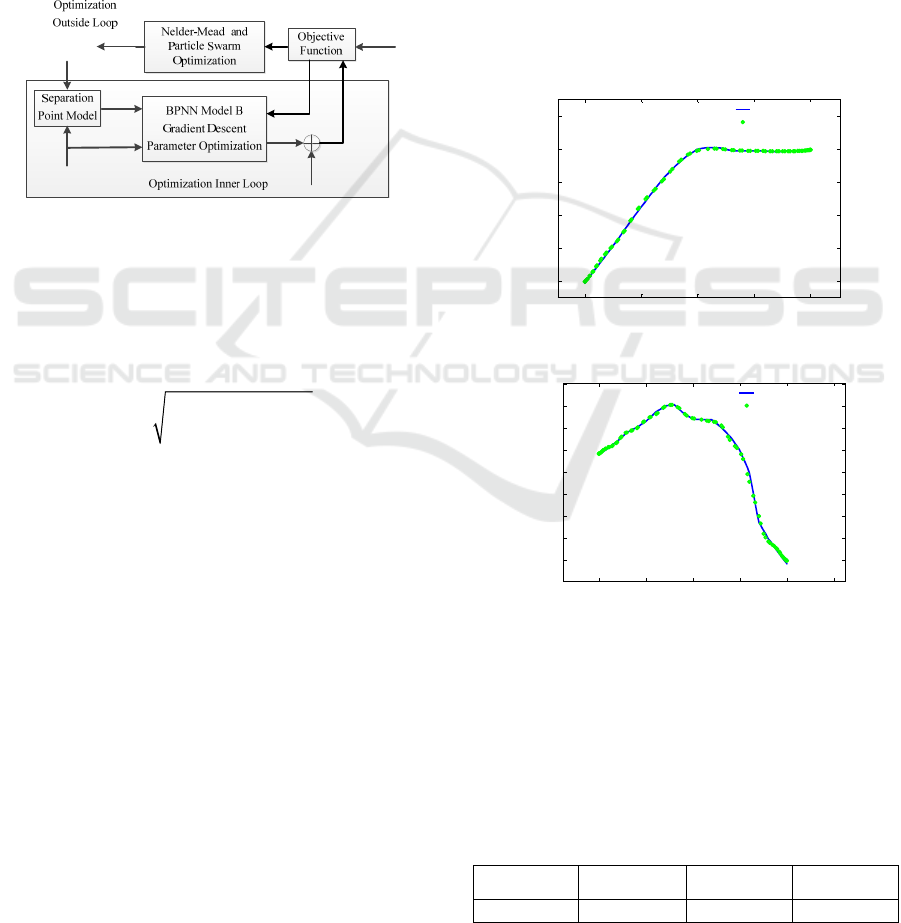
For the unknown values in BPNN model A, a

direct gradient descent method is taken to optimize

the corresponding parameters. When it comes to the

dynamic aerodynamic component identification, a

nested parameter optimization algorithm is used.

The four parameters

,,,

σα τ τ

are optimized as the

outside loop of the nested optimization structure, the

corresponding optimization algorithms are Nelder-

Mead method and particle swarm optimization

method. The relevant weight values and bias values

in BPNN model B are identified with gradient

descent method as the inner loop. The nested

parameter optimization structure is as follows:

()

,,,

σα τ τ

()

() ()tt

αα



()

Figure 10: Nested parameter optimization structure.

In the case of dynamic lift coefficient

identification, the optimal objective function is

defined as the mean-squared error between the

hybrid model response and the wind-tunnel data, as

shown in the following formula.

min ( ) /

Lj Lj

CC N

=−

∑

(9)

As far as the number of the hidden layer neurons

is concerned, an oversized network could overfit and

overlearn for a special data set. Conversely, an

undersized network with too few hidden layer

neurons could significantly reduce the results

accuracy (Boëly et al., 2010). For the parameter

identification of the hybrid model, a large enough

integer value is chosen as the number of the hidden

layer neurons to ensure the model response accuracy.

After the parameters

,,,

σα τ τ

are determined with

the oversized BPNN model B, a model

simplification process is executed to reduce the

redundant neurons. Useless and redundant neurons

are deleted one-by-one and the parameters in BPNN

model B are readjusted until the mean-squared error

exceeds the pre-determined threshold. Finally, a

simplified hybrid model is achieved without

lowering model accuracy criterion.

4 SIMULATION RESULTS

The considered unsteady aerodynamic hybrid model

is tested using the wind-tunnel experimental data. As

it is mentioned in Section 2, the lift coefficient and

pitch moment coefficient data come from the forced

large-amplitude pitch oscillations at

0.4

Hz=

0.6

Hz=

and

0.8

Hz=

. Two thirds of the

experimental data are used to train the neural

networks in the hybrid model, and one third of the

experimental data are used to evaluate the hybrid

model performance.

For the hidden layer in BPNN model A, 6

neurons are enough to create a more accurate static

aerodynamic model comparing to state-space model.

The responses of the static BPNN models are

illustrated in Fig. 11 and Fig. 12.

Figure 11: Static lift coefficient response.

Figure 12: Static pitch moment coefficient response.

As for the identifications of the dynamic

aerodynamic component, 30 hidden layer neurons

are set as the initial size of BPNN model B. The

four parameters

,,,

σα τ τ

are firstly identified

using the nested optimization algorithm mentioned

in Section 3.

Table 1: Identification results in separation point model.

/deg

0.11 41.2 0.042 0.047

0 20 40 60 80

0.5

1.5

2.5

Angle of attack/deg

Static lift coefficient

Wind-Tunnel Data

BPNN Model

0 20 40 60 80 100

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

0.1

0.15

Angle of attack/deg

Static pitch moment coefficient

Wind-Tunnel Data

BPNN Model

Aircraft Unsteady Aerodynamic Hybrid Modeling Based on State-Space Representation and Neural Network

237

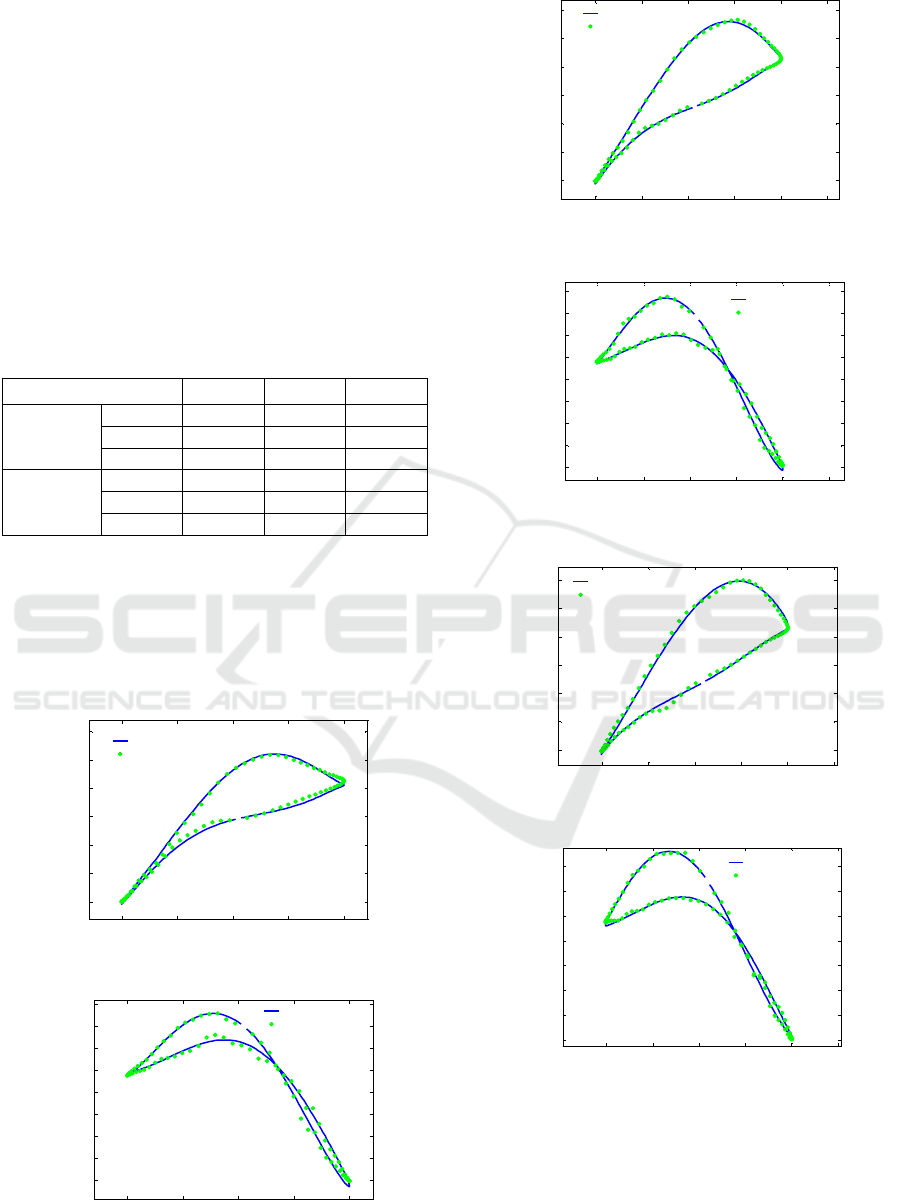
Subsequently, model simplification process is

carried out to reduce the redundant neurons. The

simplification results indicate that 6 hidden layer

neurons are accurate enough to represent the

nonlinear mapping relation in BPNN model B for

lift coefficient modeling. As for the pitch moment

coefficient, 7 hidden layer neurons are necessary to

guarantee model accuracy. The optimized unsteady

aerodynamic hybrid models are compared with the

conventional state-space models. The mean-squared

errors

are listed in Table 2. SS-M is short for

state-space model, CH-M denotes the complicated

hybrid model with 30 hidden layer neurons, SH-M

represents the simplified hybrid model.

Table 2: Mean-squared error comparisons.

/10J

−

f=4Hz f=6Hz f=8Hz

Lift

coefficient

SS-M 7.87 4.58 8.66

CH-M 3.05 1.34 2.47

SH-M 3.32 1.61 3.46

Pitch

moment

coefficient

SS-M 4.79 4.12 11.1

CH-M 0.42 0.35 0.40

SH-M 1.05 0.56 0.57

Comparing to conventional state-space model,

the hybrid model can achieve obvious accuracy

improvement in approximating the unsteady

aerodynamic response. The response results of the

simplified hybrid models achieve good agreements

with different wind-tunnel experimental data, which

are illustrated in the following figures.

Figure 13: Lift coefficient response at f=0.4Hz.

Figure 14: Pitch moment coefficient response at f=0.4Hz.

Figure 15: Lift coefficient response at f=0.6Hz.

Figure 16: Pitch moment coefficient response at f=0.6Hz.

Figure 17: Lift coefficient response at f=0.8Hz.

Figure 18: Pitch moment coefficient response at f=0.8Hz.

5 CONCLUSIONS

A hybrid model which combines state-space

representation and back-propagation neural network

0 20 40 60 80

0.5

1.5

2.5

Angle of attack/deg

Lift coefficient

Wind-Tunnel Data

Hybrid Model

0 20 40 60 80

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

0.1

0.15

Angle of attack/deg

Pitch moment coefficient

Wind-Tunnel Data

Hybrid Model

0 20 40 60 80 100

0.5

1.5

2.5

Angle of attack/deg

Lift coefficient

Wind-Tunnel Data

Hybrid Model

0 20 40 60 80 100

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

0.1

0.15

Angle of attack

Pitch moment coefficient

Wind-Tunnel Data

Hybrid Model

0 20 40 60 80 100

0.5

1.5

2.5

Angle of attack/deg

Lift coefficient

Wind-Tunnel Data

Hybrid Model

0 20 40 60 80 100

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

0.1

Angle of attack/deg

Pitch moment coefficient

Wind-Tunnel Model

Hybrid Model

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

238

is proposed in this paper to describe the aircraft

unsteady aerodynamic characteristics. According to

the simulation results, the conventional state-space

model has limited approximation quality in

modeling unsteady aerodynamics. For the purpose of

improving model accuracy and universality, back-

propagation neural network is introduced and

replaces the polynomial model in state-space

representation. The unsteady aerodynamic hybrid

model is identified and optimized with nested

optimization algorithm using the wind-tunnel data in

forced large-amplitude pitch oscillation experiments.

With satisfactory similarity to the wind-tunnel data,

the hybrid model presented in this paper is validated

to be effective in both reflecting unsteady time delay

characteristics and representing complex nonlinear

mapping relation for unsteady aerodynamics at high

angles of attack.

ACKNOWLEDGEMENTS

This work was made possible thanks to the support

of Science and Technology on Aircraft Control

Laboratory.

REFERENCES

Boëly, N., Botez, R. M., 2010. New approach for the

identification and validation of a nonlinear F/A-18

model by use of neural networks. IEEE Transactions

on Neural Networks, 21(11):1759–1765.

Chen, G., Xu, M., and Chen, S. L., 2004. Reduced-order

model based on volterra series in nonlinear unsteady

aerodynamics. Journal of Astronautics, 25(5): 492–

295.

Goman, M., Khrabrov, A., 1994. State-space

representation of aerodynamic characteristics of an

aircraft at high angles of attack. Journal of

Aircraft, 31(5):1109-1115.

Greenwell, D. I., 2004. A Review of Unsteady

Aerodynamic Modeling for Flight Dynamics of

Manoeuvrable Aircraft. In AIAA Atmospheric Flight

Mechanics Conference and Exhibit, Paper 2004-5276.

Hosder, S., Simpson, R. L., 2007. Experimental

investigation of unsteady flow separation on a

maneuvering axisymmetric body. Journal of aircraft,

44(4): 1286–1295.

Ignatyev, D. I., Khrabrov, A. N., 2015. Neural network

modeling of unsteady aerodynamic characteristics at

high angles of attack. Aerospace Science and

Technology, 41: 106–115.

Kumar, R., Ghosh, A. K., 2011. Nonlinear Longitudinal

Aerodynamic Modeling Using Neural Gauss-Newton

Method. Journal of Aircraft, 48(5): 1809–1813.

Kumar, R., Mishra, A., Ghosh, A. K., 2012. Nonlinear

Modeling of Cascade Fin Aerodynamics Using

Kirchhoff's Steady-State Stall Model. Journal of

Aircraft, 49(1): 315–319.

Pattinson, J., Lowenberg, M. H., Goman, M. G., 2012.

Multi-Degree-of-Freedom Wind-Tunnel Maneuver

Rig for Dynamic Simulation and Aerodynamic Model

Identification. Journal of Aircraft, 50(2): 551–566.

Pattinson, J., Lowenberg, M. H., Goman, M. G. 2013.

Investigation of Poststall Pitch Oscillations of an

Aircraft Wind-Tunnel Model. Journal of

Aircraft, 50(6): 1843–1855.

Sun, W., Gao, Z., Du, Y., Xu, F., 2015. Mechanism of

unconventional aerodynamic characteristics of an

elliptic airfoil. Chinese Journal of Aeronautics, 28(3):

687–694.

Wang, B. B., Zhang, W. W., Ye, Z. Y., 2010. Unsteady

Nonlinear Aerodynamics Identification Based on

Neural Network Model. Acta Aeronautica Et Sinica,

31(7): 1379–1388.

Wang, Q., Qian, W., He, K., 2015. Unsteady aerodynamic

modeling at high angles of attack using support vector

machines. Chinese Journal of Aeronautics, 28(3):

659–668.

Williams, D. R., Reißner, F., Greenblatt, D., Müller-Vahl,

H., Strangfeld, C., 2015. Modeling Lift Hysteresis

with a Modified Goman-Khrabrov Model on Pitching

Airfoils. In 45th AIAA Fluid Dynamics Conference,

Paper 2015-2631.

Zakaria, M. Y., Taha, H. E., Hajj, M. R., Hussein, A. A.,

2015. Experimental-Based Unified Unsteady

Nonlinear Aerodynamic Modeling For Two-

Dimensional Airfoils. In 33rd AIAA Applied

Aerodynamics Conference

, Paper 2015-3167.

Aircraft Unsteady Aerodynamic Hybrid Modeling Based on State-Space Representation and Neural Network

239