Nonlinear Model for Complex Neurons in Biological Visual Visions
Sasan Mahmoodi and Nasim Saba
Electronic and Computer Science, University of Southampton, Building 1, University Road, SO17 1BJ,
Southampton, Hampshire, U.K.
Keywords: Complex Neurons, Biological Visual Systems, Nonlinear Systems, Nonlinear Cells.
Abstract: Complex cells in biological visual vision are well known to be nonlinear. In this paper, it is demonstrated that
these nonlinear complex cells can be modelled under some certain conditions by a biologically inspired model
which is nonlinear in nature. Our model consists of cascaded neural layers accounting for anatomical evidence
in biological early visual visions. In the model proposed in this paper, the axons associated with the complex
cells are considered to operate nonlinearly. We also consider the second order interaction receptive maps as
directional derivatives of the complex cell's kernel along the direction of orientation tuning. Our numerical
results are similar to the biologically recorded data reported in the literature.
1 INTRODUCTION
The concept of visual receptive fields is introduced in
(Hartline 1938) as a region in visual field in which if
visual stimuli are presented, the corresponding cell
responds. The sub-regions associated with ON and
OFF responses are then discovered in (Kuffler, 1953).
Hubel and Wiesel introduce the orientation tuning of
neurons in the primary visual cortex (Hubel and
Wiesel, 2005). The receptive mapping techniques
based on white noise stimuli are then exploited in
(DeAngelis et al., 1995; DeAngelis and Anzai, 2004).
Motion perception based on energy models is also
investigated in (Adelson and Bergen, 1985) by using
oriented filters in the space-time domain. In fact,
biological experiments quantitatively indicate that the
linear visual receptive fields are Gaussian-related
kernels. In a mathematical setting, scale-space theory
presents a general framework for early visual systems
by postulating a set of axioms which an early visual
system is expected to possess. Such a framework then
leads to Gaussian-related kernels characterizing any
linear visual system including early biological visual
systems when they behave linearly (see e.g. Weickert
et al., 1999; Lindeberg, 2011; Lindeberg, 2013; ter
Haar Romeny et al., 2001; ter Haar Romeny, 2003;
Koenderink, 1988; Florack, 1997). On the other hand,
a model based on the anatomical and physiological
properties of biological visual systems is proposed in
(Mahmoodi, 2015) to derive Gaussian-related kernels
in spatial as well as spatio-temporal domains. The
model presented in (Mahmoodi, 2015) is not linear in
nature. Therefore the conditions under which this
system become linear is discussed in (Mahmoodi,
2015). Under such conditions, linear Gaussian related
filters are derived (Mahmoodi, 2015). In such a
model, the functionalities of Lateral Geniculate
Nucleus (LGN) cells and simple cells such as linear
isotropic separable, non-isotropic separable and non-
separable (velocity-adapted) cells, with Gaussian
related receptive fields can be explained (Mahmoodi,
2015). In this paper, the nonlinearity of this model is
also considered and it is demonstrated that under
certain conditions, the behaviour of nonlinear
complex cells may be attributed to this non linearity
of the model. Here our contribution is to explain the
nonlinear nature of complex cells by using the
nonlinear model of early visual system proposed in
(Mahmoodi, 2015). We also demonstrate that the
second order interactions of receptive maps for
complex cells may be explained as directional
derivatives of the neuron's kernel along the direction
of orientation tuning. The structure of the rest of the
paper is as follows. In section 2, our nonlinear model
is explained. Section 3 presents the numerical
analyses and results and finally conclusions are drawn
in section 4.
2 MODEL
The nonlinear model proposed in (Mahmoodi, 2015)
162
Mahmoodi, S. and Saba, N.
Nonlinear Model for Complex Neurons in Biological Visual Visions.
DOI: 10.5220/0005692601620167
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 162-167
ISBN: 978-989-758-170-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

behaves linearly under some certain conditions. The
linear mode of this nonlinear model is therefore fully
investigated in (Mahmoodi, 2015). Linear Gaussian-
related kernels associated with linear Lateral
Geniculate Nucleus (LGN) cells and simple cells in
strait cortex are derived for when the model behaves
linearly. Complex cells on the other hand are
nonlinear. Here we exploit the nonlinearity of the
model presented in (Mahmoodi, 2015) to explain the
nonlinear behaviour of the complex cells. According
to the model presented in (Mahmoodi, 2015), neurons
in early biological visual system are connected in
layers which are cascaded from retina to striate
cortex.
A layer of neurons is shown in Figure (1-top).
These neurons are cascaded in a way that the axons
of the neurons in the previous layer are connected to
the dendrites of the neurons in the current layer. A 2D
illustration of these cascaded layers are depicted in
figure (1-bottom).
Each horizontal line in this figure, represents a
neural layer and vertical layers represent axons to
connect a layer (a horizontal line) to the next one
(another horizontal line above the previous line). It
is believed that most complex cells have a linear-
nonlinear (L-N) structure. The linear part of these
cells is simply a linear Gaussian-related kernel
(DeAngelis and Anzai, 2004). The first step is
therefore to find a formula to explain the input-output
relationship of the nonlinear part of these complex
cells. Axons transmitting neural spikes from a neuron
to another one are modelled as transmission lines. If
neuron A sends n spikes through its axon to neuron
B. The potential received in the dendrites of neuron B
is calculated as (see Mahmoodi, 2015 for more
details):



N
n
N
n
nn
h
nho
aTT
t
tzv
aTtzvtzw
11
)exp(
2
),(
)exp(),(),(

(1)
where
n
T
= the time the nth spike is released from
neuron A
t = the time that a spike reaches to neuron B from
neuron A,
N = the total numbers of spikes,
z = the length of axon,


















t
zCR
C
tG
CRt
tzv
zz
z
z
zz
h
4
expexp
1
2
1
),(
2

z
G
,
z
C
, and
z
R
= conductance, capacitance, and
resistance of the axon (transmission line) per unit
length,
and finally
2
2
4t
zCR
C
G
a
zz
z
z

.
Figure 1: (top) the configuration of neurons in a layer with
respect to spatial coordinates x and y (bottom) the 2D
representation of the configuration of neurons in the
cascaded layers of neurons.
n
T
can be written as the summation of all time
intervals between consecutive spikes, i.e.:



n
m
mn
TnTT
1
(2)
where
T is the average time interval between
consecutive spikes. Let us consider the case where a
series of spikes are transmitted through axon from
neuron A to neuron B in a time period much less than
the time required for spikes to travel from neuron A
to neuron B, i.e.
tT
n
)( max
n
. By replacing (2) in
(1) and assuming that
tT
n
)( max
n
and therefore
ignoring the second term in (1), one can write:
x-axis
x
-axis
Flow
of
Visual
Signal
y axis
Nonlinear Model for Complex Neurons in Biological Visual Visions
163




N
n
ho
Tantzvtzw
1
)exp(),(),(
(3)
Equation (3) can be rewritten as:
1
1
)exp(),(),(



e
e
Tatzvtzw
N
ho
(4)
It is also reasonable to assume the average time
interval between consecutive spikes is too small, i.e.
1Ta
. Equation (4) therefore is approximated as:
1
1
),(),(



e
e
tzvtzw
N
ho
(5)
According to classical rectification model for neural
firing rate (Carandini and Fester, 2000), the input
potential of neuron A is proportional to firing rate and
therefore N. Equation (5) determines the input-output
relationship of a cell behaving nonlinearly. For small
values of potentials, N is very small and therefore
0),( tzw
o
According to classical rectification model
(Carandini and Fester, 2000), N increases linearly
with respect to input potential
in
V
, i.e.
in
kVN

Therefore for large positive potentials, the input-
output relationship of such a nonlinear cell will look
like a half rectified power function as reported in
(DeAngelis and Anzai, 2004) and shown in figure (2-
bottom).
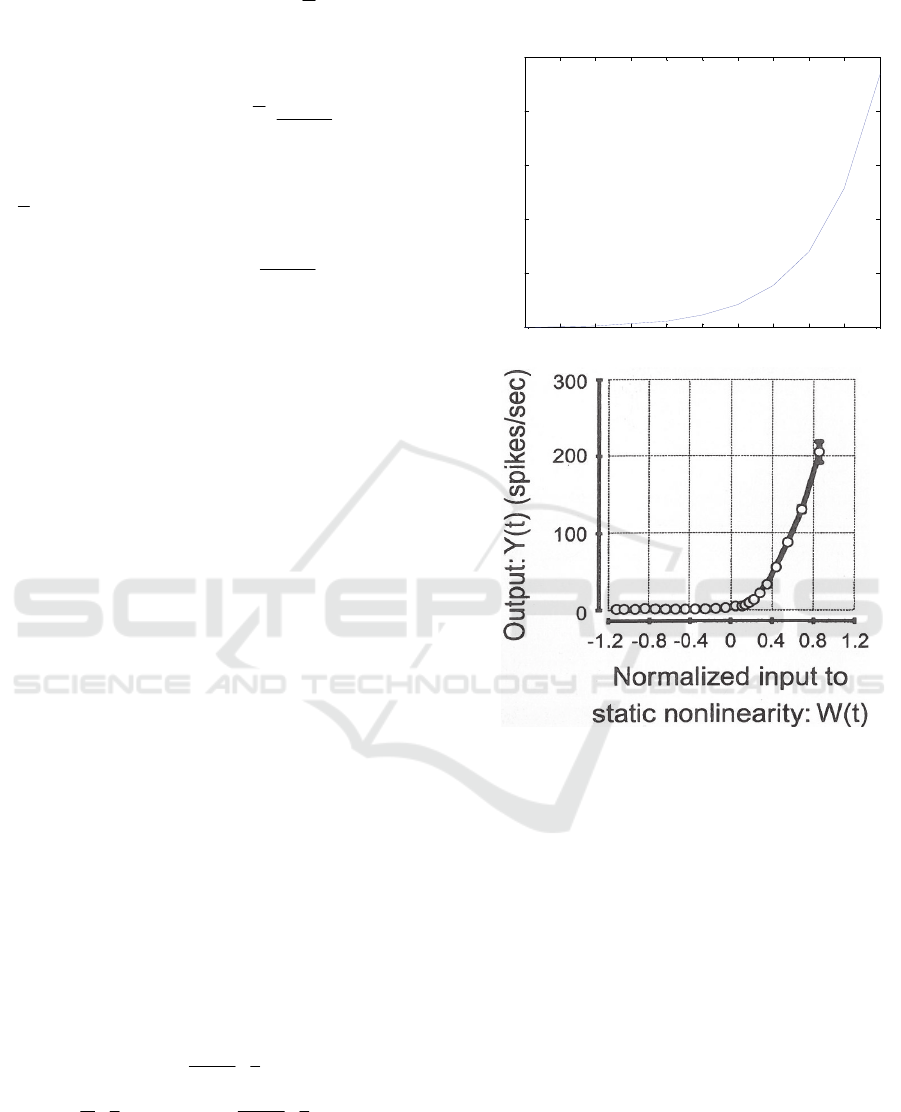
3 NUMERICAL RESULTS
Figure (2-top) shows the input-output relationship for
a nonlinear cell according to equation (5) and as an
example for k=5, i.e. for
in
VN 5
. The similarity
between figure (2-top) and figure (2-bottom) as
reported in (DeAngelis and Anzai, 2004) is
interesting and important.
The linear part of a complex cell is simply the sum
of three cells with linear isotopic kernels such as the
one shown in figure (1-bottom).The outputs of these
three cells are summed by another cell whose axon
behave nonlinearly governed by equation (5), i.e.:
),()
2
)(2
(),(
2
2
),(
2
)(2
),(),,(
1
1
tzv
t
yxh
t
yxh
t
yxhtyx
nn
n




































(6)
where
),( yxh
n
is the isotropic kernel for layer n and
)(t
is the impulse response of the cells' axons
behaving linearly (Mahmoodi, 2015). The outputs of
these three cells are summed by another cell
according to equation (6).
Figure 2: (top) The input-output relationship calculated
based on equation (5) and for k=5, (bottom) Biologically
recorded input-output relationship according to (DeAngelis
and Anzai 2004).
The impulse response of the axon behaving
nonlinearly for this cell is represented by
),( tzv
. The
spatio-temporal profile of a complex cell consisting
of three simple cells with linear isotropic kernels for
a single stimuli (nonlinear case) is shown in figure (3-
top). This is similar to the biological recorded data
shown in figure (3-bottom) in (DeAngelis and Anzai,
2004).
The response of this nonlinear complex cell for
the case where two simultaneous and spatially
separated stimuli (second order interactions) are
presented in the visual field, is shown in figure (4-
top).On the other hand, there are some other complex
cells described by equation (7):






),(),(),(),(),,( tzvyxhyxhyxhtyx
x
n
x
n
x
n






(7)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
50
100
150
200
250
Input Potential
Output Potential
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
164

Figure 3: (top) The spatio-temproal profile of a nonlinear
complex cell for a single stimulus. (bottom) The
biologically recorded spatio-temporal profile according to
(DeAngelis and Anzai, 2004).
The neural configuration of equation (7) is
depicted in figure (1-top). In this configuration, the
nonlinear-behaving axon of the cell summing the
outputs of the three cells is represented by
),( tzv
in
equation (7). In this paper, we hypothesize that the
receptive map in the case of the second order
interactions is equivalent to directional derivatives
along the direction of the orientation tuning of the
kernel
),,( tyx 
in equation (6) or (7). For a complex
cell whose kernel is represented by equation (7), this
second order interactions is described by:
)(sin
)2sin()(cos
2
2
2
2
2
2
2
2
2






y
yx
xn











(8)
where
)sin()cos(  jin



is along the
direction of orientation tuning of the cell. The
directional derivative of equation (8) for
o
45 
is
calculated in figure (4-top).
Figure 4: (top) A nonlinear receptive field map calculated
by using equations (7) and (8) (bottom) the biologically
recorded second order interactions of a receptive map for a
complex cell as reported in (DeAngelis and Anzai, 2004).
The similarity between the map calculated in
figure (4) and the biologically recorded data in figure
(4-bottom) as reported in (DeAngelis and Anzai,
2004) is interesting.
A fourth order directional derivative in space x
and time t for a complex cell represented by equation
(6) is calculated in figure (5-top). The biologically
recorded result shown as the second order interaction
of a spatio-temporal profile of a complex cell shown
in figure (5-bottom) as reported in (DeAngelis and
Anzai, 2004) is similar to our result depicted in figure
(5-top).
Nonlinear Model for Complex Neurons in Biological Visual Visions
165

Figure 5: (top) Fourth order directional derivative of a
spatio-temporal (x-t) receptive map, (bottom) second order
interactions for x-t receptive map of a complex cell as
reported in (DeAngelis and Anzai, 2004).
As can be seen from figure (5-top), there are five
lobes (three positive and two negative lobes) among
which the middle lobe is the strongest. This is similar
to the biologically recorded data shown in figure (5-
bottom) as reported in (DeAngelis and Anzai, 2004).
This second order interaction map is reminiscent of
the space-time inseparable linear maps predicting the
direction selectivity of complex cells. It is noted that
the fourth order directional derivatives should be
calculated along the tilt of space-time response
pattern.
4 CONCLUSIONS
A nonlinear model based on the model presented in
(Mahmoodi, 2015) to explain the nonlinear behaviour
of complex cells is proposed here. According to our
model, the nonlinearity of the complex cells may be
routed from the fact that the axons of neurons behave
nonlinearly under certain conditions. These
conditions are explained here. In this paper, some
approximations to this nonlinear model of neurons are
made to demonstrate that the complex cells behave
like half rectified power functions corresponding to
biologically recorded data. It is then shown here that
the space-time calculated receptive map in our model
for the complex cells when a single stimulus is
presented to the neuron, is similar to the biological
receptive field of the complex cells. We then
hypothesize that the second order interactions of
complex cells recorded in biology may be equivalent
to the directional derivatives of the visual receptive
map of the complex cells. Our results demonstrate
that the directional derivatives of the space or space-
time visual receptive maps of complex cells show
similar response patterns to the biologically recorded
second order interactions confirming our hypothesis.
REFERENCES
Adelson E, Bergen J 1985. Spaio-temporal Energy Models
for the Perception of Motion. Journal of Optical Society
of America A, Vol. 2, pp. 284-299.
Carandini M, Ferster D 2000. Membrane Potential and
Firing Rate in Cat Primary Visual Cortex. Journal of
Neuroscience, Vol. 20, No. 1, pp. 470-484.
DeAngelis GC, Anzai A 2004. A Modern View of the
Classical Receptive Field: Linear and non-Linear
Spatio-temporal Processing by V1 Neurons. In L.M.
Chalupa, and J.S. Werner (eds.), The Visual
Neurosciences, Vol 1, MIT Press, Cambridge, pp.
704-719.
DeAngelis DC, Ohzawa I, Freeman RD 1995. Receptive-
field Dynamics in the Central Visual Pathways. Trends
in Neurosciences, Vol. 18, pp:451-457.
Florack, L 1997. Image Structure. Series in Mathematical
Imaging and Vision, Springer, Dordrecht.
Koenderink JJ 1988. Scale-Time, Biological Cybernetic,
Vol. 58, pp. 159-162.
Hartline HK 1938. The Response of Single Optic Nerve
Fibres of the Vertebrate Eye to Illumination of the
Retina. American Journal of Physiology, Vol. 121, pp.
400-415.
Hubel DH, Wiesel TN 2005. Brain and Visual Perception:
the Story of a 25-year collaboration. Oxford University
Press, Oxford.
Kuffler SW 1953. Discharge Patterns and Functional
Organization of Mammalian Retina. Journal of
Neurophysiology, Vol. 16, No. 1, pp. 37-68.
Lindeberg T 2011. Generalized Gaussian Scale-Space
Axiomatic Comprising Linear Scale-Space, Affine
Scale-Space and Spatio-Temporal Scale-Space.
Journal of Mathematical Imaging and Vision, Vol. 40,
pp: 36-81.
Lindeberg T 2013. A Computational Theory of Visual
Receptive Fields. Biological Cybernetics, Vol. 107, pp:
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
166

589-635.
Mahmoodi, S., 2015. Linear Neural Circuitry Model for
Visual Receptive Fields. Journal of Mathematical
Imaging and Vision.
ter Haar Romeny B 2003. Front-End Vision and Multi-
Scale Image Analysis. Springer Dordrecht.
ter Haar Romeny B, Florack L, Nielsen M 2001. Scale-time
Kernels and Models, In: Scale-Space and Morphology,
Proceedings of Scale-Space’01, Vancouver, Canada,
LNCS, Springer, Berlin.
Weickert J, Ishikawa S, Imiya A (1999) Linear Scale Space
has First been proposed in Japan, Journal of
Mathematical Imaging and Vision, Vol. 10, pp. 237-
252.
Nonlinear Model for Complex Neurons in Biological Visual Visions
167