
Denoising 3D Computed Tomography Images using New Modified
Coherence Enhancing Diffusion Model
Feriel Romdhane, Faouzi Benzarti and Hamid Amiri
SITI Laboratory, National Engineering School of Tunis, El Manar University, Tunis, Tunisia
Keywords: 3D-CT Images, 3D-Denoising Method, Diffusion Tensor, CED Model.
Abstract: The denoising step for Computed Tomography (CT) images is an important challenge in the medical image
processing. These images are degraded by low resolution and noise. In this paper, we propose a new method
for 3D CT denoising based on Coherence Enhancing Diffusion model. Quantitative measures such as
PSNR, SSIM and RMSE are computed to a phantom CT image in order to improve the efficiently of our
proposed model, compared to a number of denoising algorithms. Furthermore, experimental results on a real
3D CT data show that this approach is effective and promising in removing noise and preserving details.
1 INTRODUCTION
Computed Tomography (CT scan) is a diagnostic
medical test which consists in measuring the X-ray
absorption by the tissue in order to reconstruct 2D
images or 3D anatomical structures. The quality of
CT images depends on the amount of the X-ray
radiation, so the low-dose lead to increase the noise
in image, and the large radiation increase the risk of
cancer. That’s why the noise filtering while reducing
radiation dose is a challenge task of almost studies in
denoising CT images. Several removal noise
methods for 3D CT data have been proposed in
literature. Among these methods, the anisotropic
diffusion was widely used for denoising medical
data (Romdhane et al., 2014); (Mendrik et al., 2009);
(Perona and Malik, 1990); (Kroon et al., 2010);
(Weickert, 1998); (Weickert, 1999). It’s based on
the use of Partial Differential Equations (PDE)
making a strong diffusion in homogeneous zones
and low diffusion across boundaries. It allows
eliminating the noise while preserving the image
discontinuities. Weickert (Weickert, 1999) used a
nonlinear PDE based on a diffusion tensor in order
to describe local variation present in images by
applying the smoothing process according to the
directional information. He proposed a Coherence
Enhancing Diffusion (CED) model, it is able
enhancing the structural elements and for medical
applications it's applied successfully and leads to
facilitate the analysis. Many regularisation used in
the anisotropic diffusion such as (Frangakis and
Hegerl, 2001), (Meijering et al., 2002),
(Tschumperlé, 2006), (Pop et al., 2007), (Mendrik et
al., 2009) and (Magnier et al., 2013).
This paper shows a modified 3D Coherence
Enhancing Diffusion model applied for denoising
3D CT data. The paper is organized as follows:
section 2 introduces the anisotropic diffusion tensor,
section 3 describes the proposed model, section 4
presents results in terms of denoising quality and
section 5 concludes the work.
2 ANISOTROPIC DIFFUSION
TENSOR
Perona and Malik (Perona and Malik, 1990) were
proposed the first nonlinear anisotropic diffusion
model developed for image enhancement. The
nonlinear PDE equation is given by:
).( IcdivI
t
(1)
Where I is 3D image, div denotes the divergence
operator,
is the gradient operator, t is the
diffusion time and
(.)c
is the diffusivity function
that weights the gradient to control the diffusion
process. Among the diffusivity function, Perona and
Malik used the following equation:
2
exp
k
I
Ic
(2)
Romdhane, F., Benzarti, F. and Amiri, H.
Denoising 3D Computed Tomography Images using New Modified Coherence Enhancing Diffusion Model.
DOI: 10.5220/0005692701010105
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 103-107
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
103

Weickert (Weickert, 1999) used a tensor in the
nonlinear partial differential equation (PDE) of
Perona and Malik, taking into account the
orientation of the gradient and the flow towards the
orientation of interesting features among the
diffusion.
) ( IDdivI
t
(3)
Where D(.) is the diffusion tensor constructed from
the eigenvectors
21
, vv and
3
v ( ],,[
1312111
vvvv )
and the eigenvalues
21
,
and
3
of the structure
tensor
J
defined as follow:
)(
T
IIKJ
(4)
Where:
I is the gradient of the smoothed image
at scale σ and
K
is a Gaussian kernel with standard
deviation ρ. The tensor D(.) is given by:
3..1
),(
n
njnin
vvjiDwith
cfe
fbd
eda
D
(5)
Weickert proposed two models to construct the
tensor: the first one is using the Coherence
Enhancing Diffusion (CED) function and the other is
the Edge Enhancing Diffusion (EED). In this paper
we focus only in the CED model which preserves
small structures and enhances tubular structures. The
3D extension was developed on (Weickert, 1999)
where author proposed the following diffusion
functions:
elsee
orif
k
c
,)1(
0 0 1
2
)2ln(
32
3
2
1
(6)
Where
2
32
))/((
k
,
is a small parameter
)1,0(
which keeps the tensor D uniformly
positive definite and
c
is the CED contrast
parameter. These definitions replay an only smooth
in one orientation of space
3
v using the ratio
between the second and the third eigenvalues of the
structure tensor.
3 NEW PROPOSED CED MODEL
Several regularizations were proposed for CED
model in 3D-domain. The most interesting
regularization was the one which force the diffusion
process along both the second and third eigenvectors
(Pop et al., 2007). Our proposed model is inspired
from the model of Sorin Pop (Pop et al., 2007) while
using the notion of dimensionality of structures
defined by Van Kempen (Van Kempen et al., 1999).
Plane-like and line-like structures are two
available linear structures in the 3D-case, that’s why
Bakker (Bakker et al., 2001) defined two measures
to estimate the semblance of seismic fault:
32
32
21
21
,
lineplane
CC
(7)
Considering the similarity between faults in seismic
imagery and edges in 3D imagery, the authors in
(Pop et al., 2007) proposed the edge indicator using
the measures defined previously as follow:
)1(
planelineedge
CCC
(8)
And their CED proposed model is called CED-D
defined by the following equation:
elsee
Kif
Ch
K
C
edger
,)1(
0
)()(
3
1332
1
(9)
Where
)(sh
r
is a sigmoid function which plays the
role of a fuzzy corner and edge detector through the
value of two parameters the threshold
1,0
and
the slope γ, defined by:
1)1(tanh
1)(tanh
)(
s
sh
r
(10)
As shown in equation (9), the eigenvalue
2
takes
values between
1
and
3
, with regularization by the
sigmoid function
r
h .
Using the confidence measure described in (8),
we propose the new model as follow:
elsee
Kif
else
K
C
Kif
K
C
edge
,)1(
0
, tanh
0
3
2
1
(11)
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
104
Where k is the measure of coherence defined as:
2
32
2
31
2
21
)()()(
K
(12)
Our model allows guaranteeing the diffusion along
the second and the third direction with respect to the
nature of the linear structures according to the
confidence measure
edge
C
. Moreover, the hyperbolic
tangent function is used to represent a transition
phenomenon between two states (i.e. in our 3D case
the line and plane-like structures), so it supports the
role of the edge indicator. The absolute value
guarantees that the tensor remains always with
positive eigenvalues. The coherence measure K acts
as a diffusion barrier; for K
≫
C, the diffusion is
along the two directions
3
v and
2
v and when K
tends to 0 the diffusion seems to be isotropic and
doesn’t exceed
value. The next section present
experiment results for denoising synthetic and real
CT images compared to other CED models.
4 RESULTS
4.1 Synthetic Data
In this section, we first simulate we first test a 3D
Shepp-Logan Phantom image with volume size
(
102128128 ) to improve the performance of the
proposed denoising algorithm compared to other
denoising model such as: the original CED proposed
by Weickert (Weickert, 1999), the total variation
model (TV), bilateral model and CED-τD (Pop et al.,
2007). As quantitative measures, we use the Peak
Signal-to-Noise Ratio (PSNR), the root mean square
error (RMSE) and the Structural Similarity Index
(SSIM) (Wang et al., 2004). The phantom dataset is
corrupted with 3% and 5% additive Gaussian white
noise (Figure 2-b and Figure 3-b successively). The
parameters for our model and for the two others are
fixed to:
1
, 01.0
,
2
, 15.0t and
01.0C .
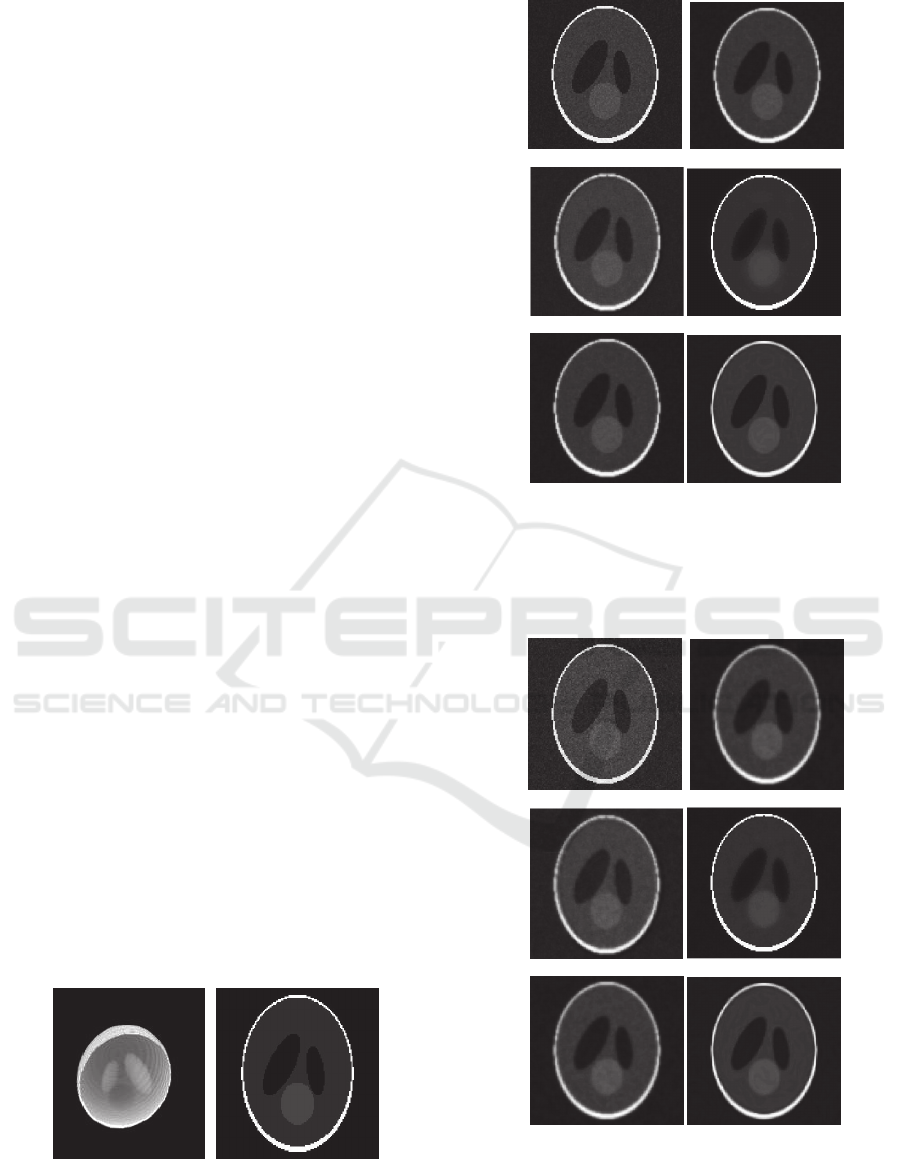
-a- -b-
Figure 1: -a- 3D view of 3D Shepp-Logan Phantom, -b-
Transversal Slice of 3D Shepp-Logan Phantom.
-a- -b-
-c- -d-
-e- -f-
Figure 2: Performance of the diffusion methods of 4
iterations: -a- 3% Gaussian white noisy image, -b-
CED_Weickert model , -c- Total Variation model (TV), -
d- Bilateral model, -e- CED_D model, -f- CED_proposed
model.
-a- -b-
-c- -d-
-e- -f-
Figure 3: Performance of the diffusion methods for 4
iterations: -a- 5% Gaussian white noisy image, -b-
CED_Weickert model, -c- Total Variation model (TV), -d-
Bilateral model, -e- CED_D model, -f- CED_proposed
model.
Denoising 3D Computed Tomography Images using New Modified Coherence Enhancing Diffusion Model
105
As shown in the figures (Fig. 2 and Fig. 3), our
model reduces noise significantly more than the
others, moreover it preserves well the edges and
enhances the homogenous areas. In term of visual
quality, the two behaviours of the original CED and
CED-D modes are very similar and the quantitative
measures in table1 confirm the results. The TV and
bilateral models succeeded in removing noise but
they lead to blur the data.
Table 1: Quantitative measures for denoising 3% and 5%
additive white Gaussian noise in image.
Model PSNR SSIM RMSE
3% of
Gaussian
noise
CED_Weickert
22.51 0.878 0.075
Total Variation (TV)
21.92 0.819 0.080
Bilateral
17.91 0.428 0.127
CED_D
22.31 0.875 0.077
CED_proposed 24.31 0.919 0.060
5% of
Gaussian
noise
CED_Weickert
20.18 0.813 0.098
Total Variation (TV)
20.61 0.731 0.093
Bilateral
15.54 0.405 0.167
CED_D
20.09 0.810 0.099
CED_proposed 22.95 0.880 0.071
4.2 Real Data
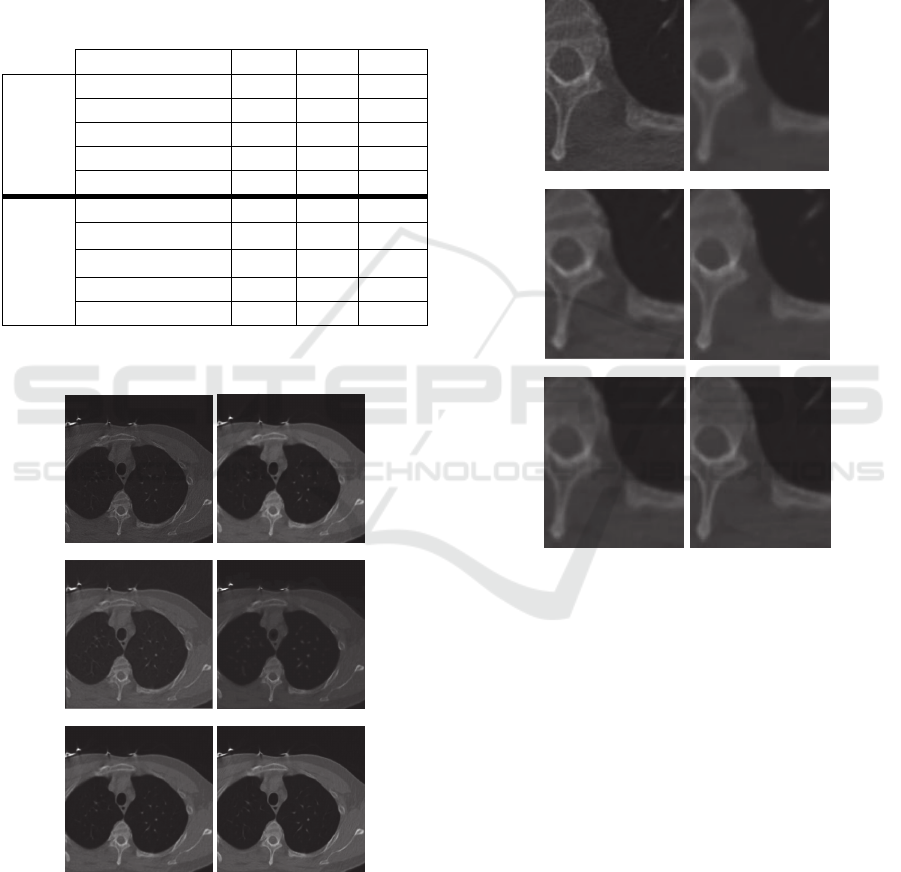
-a- -b-
-c- -d-
-e- -f-
Figure 4: Performance of the diffusion methods on
Transverse Slice of CT data: -a- Original data, -b-
CED_Weickert model (15 iterations), -c- Total Variation
model (15 iterations), -d- Bilateral model, -e- CED_D
model (15 iterations), -f- CED_proposed model (5
iterations).
We evaluate a Cardiac CT coronary angiography test
bolus data for an adult with volume size
(
193512512
). To perform the effectiveness of
our proposed model and other methods, we use a
cross-section for original data and for the results of
denoising model in order to illustrate the behaviour
of filtering methods. The parameters for our model
and for the two others are fixed to:
1
, 1.0
,
5
, 15.0
t and 1
C .
-a- -b-
-c- -d-
-e- -f-
Figure 5: Detail zoom: -a- Original data, -b-
CED_Weickert model, -c- Total Variation model (TV), -d-
Bilateral model, -e- CED_D model, -f- CED_proposed
model.
We realize in figures (Fig. 4, Fig. 5 and Fig. 6),
that the original and the CED-D model reduced
well the noise and blurred the edges but our
proposed model is effective in preserving edges and
removing noise. Moreover, our model has reduced
the number of iterations, while maintaining the
image quality (5 iterations for our model against 15
iterations for the other models), so we can have
better results using less number of iterations which
represent a benefit of saving time.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
106
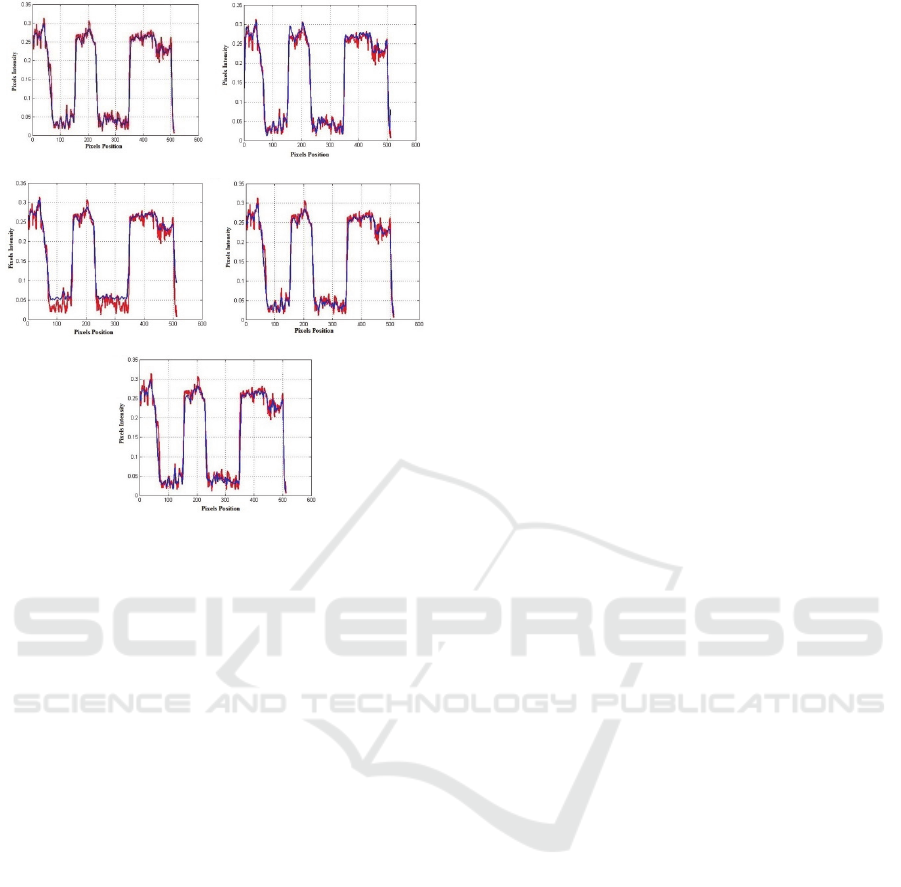
-a- -b-
-c- -d-
-e-
Figure 6: Cross-sectional analysis for the data (red:
original data, blue: denoising method): -a- CED_Weickert
model, -b- Total Variation model (TV), -c- Bilateral
model, -d- CED_D model, -e- CED_proposed model.
5 CONCLUSIONS
In this paper, a new CED model has been proposed
for denoising 3D CT scan data. This new model was
very promising in reducing noise and preserving
edges. Quantitative measures was evaluated in order
to improve the efficiently of the proposed model
compared to other models. In the future work, we
will look forward to generate model for denoising
other kind of 3D medical image such as MRI and
ultrasound data.
REFERENCES
Bakker, P., Van Vliet, L.J., Verbeek, P.W., 2001.
Confidence and curvature estimation of curvilinear
structures in 3-D. Proceedings of the 8
th
ICCV.
Vancuver, Canada.
Frangakis, A. and Hegerl, R., 2001. Noise reduction in
electron tomographic reconstruction using nonlinear
anisotropic diffusion. Journal of Structural Biology.
Kroon, D.J., Slump, C.H., Maal, T., 2010. Optimized
Anisotropic Rotational Invariant Diffusion Scheme on
Cone-beam CT. Medical Image Computing and
Computer-Assistant Intervention, MICCAI.
Magnier, B., Huanyu, X. and Montesinos, P., 2013. Half
Gaussian Kernels Based Shock Filter for Image
Deblurring and Regularization. 8
th
International
Conference on Computer Vision, Imaging and
Computer Graphic Therory and Application. France.
Meijering, E., Niessen, W., Weickert, J. and Viergever,
M., 2002. Diffusion-Enhanced Visualization and
Quantification of Vascular Anomalies in Three-
Dimensional Rotational Angiography: Results of an
In-Vitro Evaluation. Medical Image Analysis.
Mendrik, A., Vonken, E., Rutten, A., Viergever, M., Van
Ginneken, B., 2009. Noise Reduction in Computed
Tomography Scans using 3D Anisotropic Hybrid
Diffusion with Continuous Switch. IEEE Trans. Med.
Imaging.
Perona, P., Malik, J., 1990. Scale-space and edge detection
using anisotropic diffusion. IEEE Trans. Transactions
on Pattern Analysis and Machine Intelligence.
Pop, S., Lavialle, O., Terebes, R., Borda, M., 2007. A
New Partial Differential Equation-Based Approach for
3D Data Denoising and Edge Preserving. Techn-
Electrotechn. et Energ. Bucarest.
Romdhane, F., Benzarti, F., and Amiri, H., 2014. 3D
Medical Images Denoising. In 1
st
International Image
Processing Applications and Systems, Tunisia.
Tschumperlé, D. 2006. Fast Anisotropic Smoothing of
Multi-Valued Images using Curvature-Preserving
PDE’s. International Journal of Computer Vision.
Van Kempen, G.M.P., Van, den Brink, N., Van Vliet, L.J.,
Van Ginkel, M., Verbeek, P.W., Blonk, H., 1999. The
application of a local dimensionality estimator to the
analysis of 3D microscopic network structures.
Scandinavian Conference on Image Analysis.
Greenland.
Wang, Z., Bovik, A., Sheikh, H., Simoncelli, E., 2004.
Image quality assessment: form error visibility to
structural similarity. IEEE Transactions on Image
Processing.
Weickert, J., 1999. Coherence-enhancing diffusion
filtering. International Journal Computer vision.
Denoising 3D Computed Tomography Images using New Modified Coherence Enhancing Diffusion Model
107
