Chaos Analysis of Transcranial Doppler Signals for Feature

Extraction

Ali Ozturk

Computer Engineering Department, KTO Karatay University, Konya, Turkey

Havelsan Inc., Ankara, Turkey

Keywords: Chaos Analysis, TCD Signals, Correlation Dimension, Maximum Lyapunov Exponent, Recurrence Plots,

Chaotic Attractors, Space-Time Separation Plots.

Abstract: In this study, chaos theory tools were used for feature extraction from Transcranial Doppler (TCD) signals.

The surrogates data sets of the TCD signals which were used for the nonlinearity analysis were extracted as

the first feature set. The nonlinear cross prediction errors which were used for the stationary analysis were

also extracted for the TCD signals as another feature set. The chaotic invariant features like correlation

dimension, maximum Lyapunov exponent, recurrence quantification measures etc. give quantitative values

of complexity of the TCD signals. The correlation dimension and maximum Lyapunov exponent were

already used as features for classification of TCD signals in the literature. As another chaotic feature set, the

statistical quantitative values were extracted from the recurrence plots. The correct calculation of the time

delay and the minimum embedding dimension is crucial to correctly estimate all of the chaotic features.

These two data were calculated via mutual information and false nearest neighbours approaches,

respectively. The space-time separation plots were used in order to find the ideal dimension of Theiler

window w which is another important value for the correct estimate of chaotic measures. The reconstructed

chaotic attractors with 3-D embedding and 1-step time delay represent the visual phase space portrait of the

TCD signals. The attractors were also suggested as another candidate feature set.

1 INTRODUCTION

TCD study of the adult intracerebral circulation is

used to evaluate intracranial stenoses, cerebral

arteriovenous malformations, cerebral vasospasm

and cerebral hemodynamics in general (Evans et al..,

1989). The blood flow anomalies in the cerebral

vessels can be visually observed in the sonograms.

However, properly enabling the expert medical staff

to interpret TCD signals is difficult and this prevents

their wider and effective usage in the clinics.

In the literature, the linear features extracted

from Doppler signals via spectral analysis methods

were used for automatic medical diagnosis (Ubeyli

and Guler, 2005; Guler et al., 2002). The spectral

features of TCD signals were used for the

performance comparison of two different artificial

neural networks in (Serhatlioglu et al., 2003) for the

classification of the TCD signals.

There are various studies in which chaos theory

methods were used to analyse the Doppler signals

(Keunen et al., 1994; Vliegen et al., 1996). Keunen

et al., (1996) suggested that the TCD signals of

healthy subjects have an underlying nonlinear

dynamics. It was recognized by Visee et al., (1995)

that the nonlinear phenomena were lost in ischemic

cerebrovascular territory in patients with occlusive

cerebrovascular disease while there was nonlinearity

detected in noncompromised side.

Two chaotic invariant measures, i.e. the

correlation dimension and maximum Lyapunov

exponent, were used for the classification of TCD

signals in (Ozturk and Arslan, 2007; Ozturk et al.,

2008) to compare the performance of various

classifiers. The performance of the chaotic and

linear features were compared on a neuro-fuzzy

classifier in (Ozturk and Arslan, 2015).

If linear methods are used to analyse a time

series which is generated by a nonlinear process,

then some critical features of it can remain

undetected and most of it can be considered as noise.

The non-linear time series analysis (chaos theory)

provided some tools to quantitatively analyse a time

series which is generated by an underlying nonlinear

process. However, in order to apply nonlinear time

168

Ozturk, A.

Chaos Analysis of Transcranial Doppler Signals for Feature Extraction.

DOI: 10.5220/0005693701680174

In Proceedings of the 9th International Joint Conference on Biomedical Engineer ing Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 168-174

ISBN: 978-989-758-170-0

series analysis (chaos theory) methods, it must be

proven that the signals are both nonlinear and

stationary. In (Ozturk and Arslan, 2007), the

surrogates data method was used to detect the

nonlinearity of TCD signals. In this study, The

surrogates data set of the TCD signals were

extracted as the first feature set. The stationarity of

the TCD signals is detected with nonlinear cross

prediction errors method in (Ozturk and Arslan,

2007). In this study, this method was used to extract

the non-linear cross prediction values as another

feature set.

The most famious chaotic features used in the

literature are the maximum Lyapunov exponent and

the correlation dimension. These chaotic measure

will eventually be different for a specific time series

generated by a specific natural phenomea, since

each chaotic attractor will have a different picture in

the embedded phase space. These two features were

also mentioned as a different feature set in this

study.

The recurrence plots are mainly used for

nonstationarity analysis and visualization of time

series. The visual data in the recurrence plots is hard

to interpret. Therefore, recurrence quantification

analysis is necessary to quantify the number and

duration of recurrences which is presented by the

state space trajectory of a dynamical system. The

other proposed feature set in this study is the

statistical quantitative values which are extracted

from the recurrence plots of TCD signals. The time

delay information and minimum embedding

dimension play important role for the correct

extraction of all chaotic features. This is also true for

recurrence quantification analysis. The other

important parameter which effects all of the results

is the Theiler window w and it is estimated from the

space-time separation plots.

The reconstructed 3-D chaotic attractors of the

TCD signals were also presented. These can be used

to extract a different set of features via image

processing methods.

2 MATERIALS AND METHOD

2.1 Hardware

The hardware of the system used for this study

involves a 2 Mhz ultrasound transducer, analog

Doppler unit (Multi Doppler Transducer XX, DWL

Gmb, Uberlingen, Germany), analog/digital

interface board (Sound Blaster Pro-16), and PIII

600 Mhz microprocessor PC with printer. The

Doppler unit is also equipped with imaging software

that makes it possible to focus the sample volume at

a desired location in the temporal region. The signal

obtained from the blood vessel is transferred to a PC

via a 16-bit sound card on an analog/digital interface

board (Ozturk et al., 2008). The signals were then

sampled to 0-255 interval as shown in Figure 1.

2.2 Surrogates Data Set

The method of Iterative Amplitude Adjusted Fourier

Transform (IAAFT) discussed in (Schreiber and

Schmitz, 1996) is used to generate surrogate data

sets. The Fourier-based surrogates depend on the

idea of creating constrained realizations. In this

approach, the measurable properties of the time

series are taken into account. The linear properties of

the time series are specified as in the following



−

Nkni

(1)

The surrogate time series are created by

multiplying the Fourier transform of the data by

random phases and then transforming back to the

time domain as:

Nkni

eSe

−



(2)

Where 0≤α

<2π are independent uniform

random numbers.

2.3 Nonlinear Cross Prediction Errors

Data Set

The method used for the stationarity test of the TCD

signals in (Ozturk and Arslan, 2007) was utilized to

extract the non-linear cross prediction errors as

another feature set. This method divides the time

series into equal parts and the simple nonlinear

prediction algorithm (Hegger et al., 1999) is applied

to the segments to find the one-step ahead prediction

errors. The embedding vectors were obtained by

embedding the time series in 3-D phase space with a

time delay of 1. In the delay embedding space, all

neighbours of 



are taken into account in order to

make a prediction at time +.



∆







(



)

∑



∆



∈



(



)

(3)

Where





(



)

is the number of elements in the

neighbourhood 



(



) of radius

є around the point





The time series was divided into segments S

i=1,..,N. For each two segments S

and S

, the root

Chaos Analysis of Transcranial Doppler Signals for Feature Extraction

169

mean squared error was computed using the

neighbours of S

to predict S

. For i=j, the cross

prediction errors will be smallest, since S

and S

are

identical.

For random time series such as white noise, the

nonlinear cross prediction errors are close to 1. On

the other hand, for a periodic signal which is

generated by sinus function, they are close to 0. For

the time series those are generated by natural

processes, they generally lie in between.

2.4 Recurrence Plots

The other two common methods in nonstationarity

analysis and visualization of time series are the

recurrence plots (Eckmann et al., 1987) (Casdagli,

1997) and the time-seperation plots (Provenzale et

al., 1997). It is difficult to interpret the recurrence

plots due to their complexity (Webber and Zbilut,

1994). The points obtained from a time series

belonging to a stationary process are spreaded over

the plot homogenously, while the points of a time

series belonging to non-stationary process are

grouped around the diagonal (Sprott, 2002). If there

are too many separated points in the plot, this

indicates randomness. This occurs when there is too

much noise in the time series or the embedding

dimension is insufficient. If the points over the

surface have no pattern then the process which

generates the time series has no or very poor

determinism (Kantz and Schreiber, 2005). Zbilut

et.al (1998), extracted some statistical quantitative

values from the recurrence plots. Some of these

values are the surface coverage rate of the points

(REC), the rate of the points parallel to the diagonal

(DET), the length distribution of the points which

form a straight line (ENT) indicating the rate of the

deterministic structures in the time series and the

regression coefficient (TREND) which represents

the relationship between the distance from the

diagonal and the recurrence number. The calculation

of these values takes too long for huge time series.

However, it was observed that for sub-sections of

TCD time series, these values do not differ

significantly and reflect the characteristics of the

original time series.

 =





∑



,



,

(4)

Where N is the total number of points in a

recurrence plot and R

i,j

Є{0,1} depending of the

existence of a point on the i-j coordinates.

 =

∑

()







∑



,



,

(5)

Where 

(



)

is the histogram of the length  of

the diagonal lines.

 = −

∑



(



)

ln()







(6)

Where () corresponds to the diagonal line length.

 =

∑(





/

)(







〈





〉)







∑(





/

)









(7)

Where 



is the maximal number of diagonals

parallel to the main diagonal line.

〈





〉

indicates

the average of the recurrence points 



The values of the time delay, the minimum

embedding dimension and the Theiler window are

important for the calculation of the statistical

quantitative measures mentioned above.

2.5 Space-time Separation Plots

In recurrence plots, the graph of the points which are

closer than a specific ε distance value are obtained

with absolute time. The space-time separation plots

are obtained with relative time. In this kind of plots,

if a vector on the reconstructed attractor has at least

one neighbour in a specific δt interval and Δd

distance, then it is marked as δt – Δd point. By

means of these plots, it is possible to identify the

temporary correlations and to find the dimension of

the Theiler window w which is used in correlation

dimension algorithm of Theiler (1990) and in

Lyapunov exponent estimation of Kantz algorithm

(Kantz, 1994). The first peak point which is close to

the general height in the space-time separation point

generally gives the ideal dimension of Theiler

window w.

2.6 Correlation Dimension

The correlation dimension is computed most

efficiently by the correlation sum (Grassberger and

Procaccia, 1983):

)(

),(



−<=

−−Θ=

wjk

pairs

εε

(8)

Where s

are m-dimensional delay vectors,

pairs

=(N-m+1)(N-m-w+1)/2 is the number of pairs of

points covered by the sums, Θ is the Heaviside step

function and w is the Theiler window (Theiler,

1990). The following power law exists between

embedding dimension m, ball radius ε and

correlation dimension D

),(

εε

∝

(9)

The correlation dimension D

can be defined as

D=lim

→

lim

→

(, ) (10)

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

170

Where



(

, 

)

(,)



(11)

The minimum embedding dimension and the time

delay between embedding vectors are crucial in

order to estimate the correlation dimension correctly.

For the calculation the time delay, the mutual

information method suggested by Fraser and

Swinney (1986) was used. In this method, the

mutual information S is computed for different τ

delay values,



−=

)(

ln)(

(12)

Where p

is the probability to find a time series

value in the i-th interval, and p

(τ) is the joint

probability that an observation falls into the i-th

interval and the observation time τ later falls into the

j-th interval. The time delay τ where the mutual

information S takes the first minimum value is the

optimum delay and is used for embedding.

We used the false nearest neighbors method

proposed in (Hegger et al., 1999) to find the

minimum embedding dimension. This method

includes some small changes to the original

algorithm proposed by (Kennel et al., 1992) to avoid

the wrong results due to the noise in the time series.

Assuming that the standard deviation of the time

series is σ, the threshold of false nearest neighbors is

r and the distance between the vectors of the phase

space is found according to maximum difference,

the false nearest neighbors statistics is calculated as

in the following:

(13)

Where, is the nearest neighbour of the

vector S

and k(n) is the index of the time series

which is different than n and supplying the condition





−



being minimum. The second Heaviside

function in the nominator is used to eliminate the

vectors of which initial distances are higher than σ/r.

The same function also exists in the denominator for

the same reason.

2.7 The Maximal Lyapunov Exponent

In the phase space, the distances between embedding

vectors on attractor do not grow everywhere with the

same rate. They may shrink locally. Therefore, the

maximal Lyapunov exponent calculation will be the

average of the local divergence rates over the whole

embedding vectors.

The algorithm developed by Rosenstein et. al.

(1993) was used to find the maximal Lyapunov

exponent. This algorithm computes the local

divergence rates of the state space distances over the

whole time series data. The stretching factor S is

found for different N values as in following















−=

(14)

Where,







is an embedding vector on the

attractor,





are the neighboring vectors within

diameter ϵ and

is the number of these

neighbors.

The first slope of the curve obtained by plotting

S values for various N values on x-y coordinate

system gives the maximal Lyapunov exponent.

3 EXPERIMENTAL RESULTS

AND DISCUSSION

The profile of the subjects from which the TCD

signals were obtained is given in the following table.

Table 1. The profile of the subjects used in this study.

Males Females

Age

Range

Avg.

Age

Cerebral

aneurysm

12 8 55-65 59.5±0.5

Brain

Hemorrhage

4 6 21-36 27.0±0.5

Cerebral

Oedema

11 11 3-40 25.0±0.5

Brain Tumor 12 18 12-41 29.5±0.5

Healthy 15 8 23-65 31.5±0.5

Summary 54 51 3-65 35.0±0.5

The Iterative Amplitude Adjusted Fourier

Transform (IAAFT) method is used to generate the

surrogate data sets for each TCD signal. A sample

surrogate data set for the TCD signal of a patient

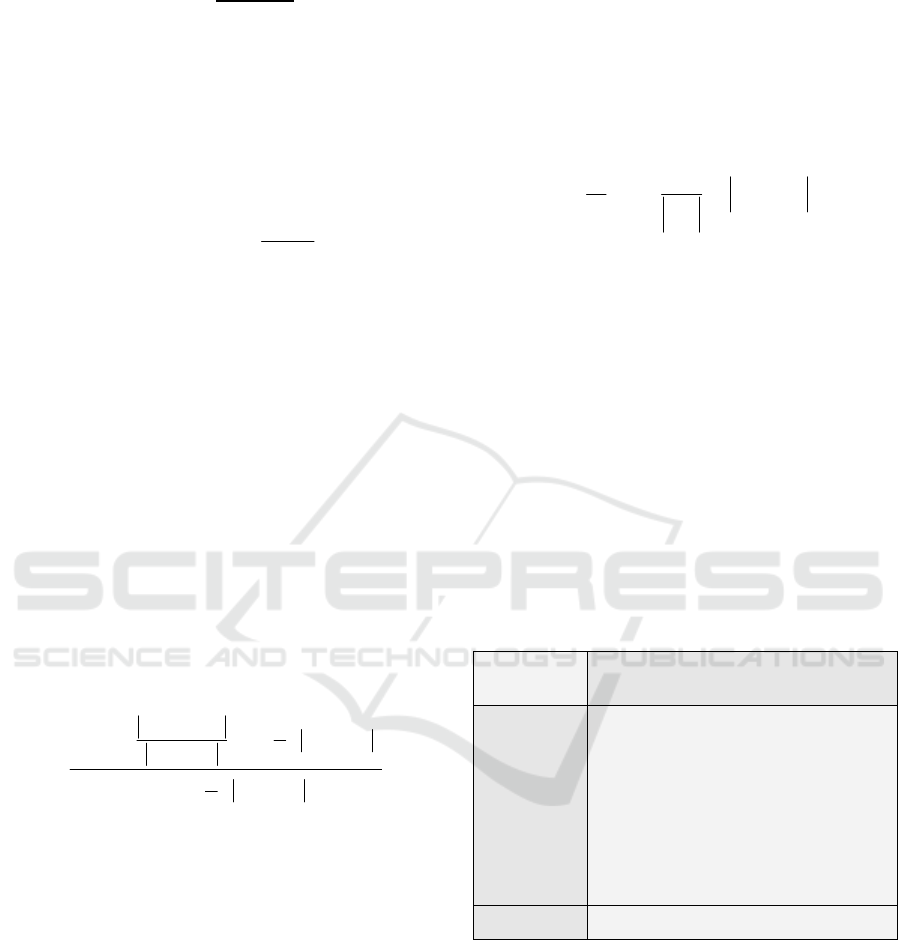
with cerebral aneurysm (Figure 1) is given in Figure

2. It is not easy to visually distinguish the surrogate

data sets from the original TCD signal, but the

surrogates are created with the linear properties via

Fourier transform.



−−













−−Θ













−−Θ













−

)(

)1(

)(

)1(

)(

SYK

)(

Chaos Analysis of Transcranial Doppler Signals for Feature Extraction

171

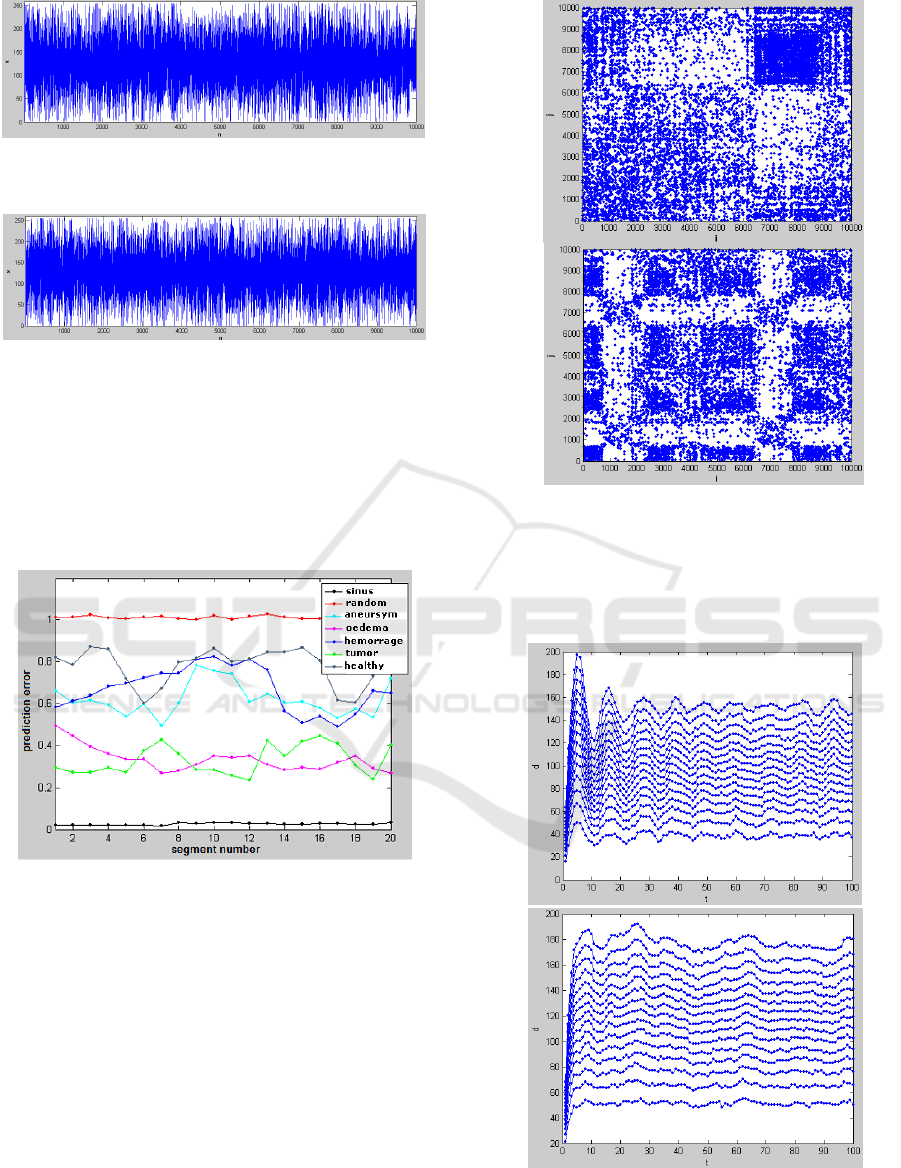
Figure 1: The TCD signal of a patient with cerebral

aneurysm.

Figure 2: The surrogate time series generated for the TCD

signal given in Figure 1.

In the following figure, it can be seen that the

nonlinear cross-prediction error values for the TCD

signals lie between pure deterministic (sinus signal)

and random (Gaussian) time series. These values can

be used as another feature set for the classification of

the TCD signals.

Figure 3: The non-linear prediction errors for sinus,

Gaussian random and one for each TCD signals time

series.

In the following figure, the recurrence-plots

of the TCD signals belonging to different patient

groups are given. As can be seen from the figures,

each patient has a different structure within its

recurrence-plot. The statistical quantitative values

like REC, DET, ENT and TREND were calculated

using the recurrence-plots of the TCD signals. These

values constitute the other chaotic feature set

In the following figure, the space-time

separation plots of the TCD signals belonging to

different patient groups are given. In these plots, the

first peak point which is close to the

Figure 4: Recurrence plots of the TCD signals belonging

to a patient of (a) Hemorrhage and (b) Healthy subject.

general height in the space-time separation

point was used to identify the ideal dimension of

Theiler window w.

Figure 5: The space-time separation plot of the TCD

signal with patient groups a) Oedema (w=50) b) Tumor

(w=40).

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

172

The chaotic attractors embedded in 3-

dimensions for each patient group are given in the

following figure. The first 300 points of TCD signals

were used to draw the attractors in order to enhance

the visuality. The time delay used to draw the

attractors was 1. These chaotic attractor pictures can

be used to extract another feature set for the TCD

signals.

Figure 6: The chaotic attractors of the TCD signals

embedded in 3-dimensions with 1 time delay a) Healthy b)

Oedema.

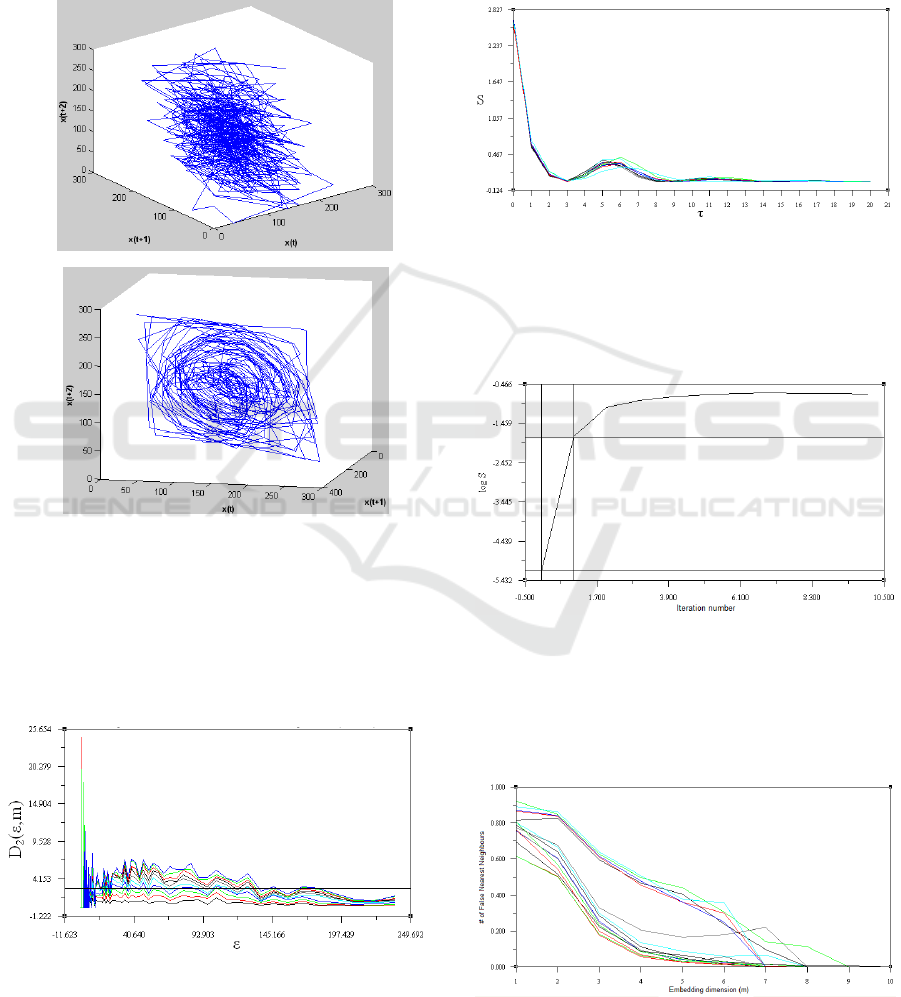
In the following figure, the correlation

dimension estimation for the TCD time series of a

patient with brain hemorrhage is given as an

example.

Figure 7: Correlation dimension estimation of a patient

with brain hemorrhage.

For all of the chaotic features, we need time

delay information which is obtained by mutual

information method. According to this method, the

first delay value τ at which time delayed mutual

information takes the minimum is a good candidate

for a reasonable time delay. In the following figure,

the time delay estimation for the TCD signals with

brain oedema is given.

Figure 8. Time delay value estimation for the patients with

brain oedema.

In the following figure, it is shown how the

maximal Lyapunov is calculated for a patient with

cerebral aneurism.

Figure 9: Maximal Lyapunov exponent estimation for the

TCD signal of a patient with cerebral aneurism.

In the following figure, the minimum

embedding dimension estimation for the TCD

signals with brain tumor is given.

Figure 10: Minimum embedding dimension estimation for

some of the patients with brain tumor.

Chaos Analysis of Transcranial Doppler Signals for Feature Extraction

173

4 CONCLUSIONS

Besides the chaotic invariant measures such as

correlation dimension and maximal Lyapunov

exponent, some other feature sets which can be

extracted with non-linear time series analysis may be

used to further evaluate some of the brain vessel

diseases. The chaotic invariant measures may be

supported with these feature sets. These features

alone or with chaotic measures together may be used

to train a classifier. After the generalization, the

classifier may be used to make automatic diagnosis

of the brain diseases.

The non-linear cross prediction errors of the

TCD signals and the statistical quantitative values

extracted from the recurrence plots can also be used

to train various classifiers in order to make

automated diagnosis of the brain vessel diseases.

The reconstructed 3-D chaotic attractor

pictures can be used to extract another feature set for

the TCD signals.

REFERENCES

Casdagli, M., 1997. Recurrence plots revisited. Physica D.

108:12-44.

Eckmann, J.P., Oliffson, K.S., Ruelle, D., 1987.

Recurrence plots of dynamical systems. Europhys.

Lett. 4(9): 973-977.

Evans, D.H., McDicken, W.N., Skidmore R., Woodcock,

J.P., 1989. Doppler Ultrasound: Physics,

Instrumentation and Clinical Applications. Wiley,

Chichester.

Fraser, A. M., Swinney, H. L. 1986. Independent

coordinates for strange attractors from mutual

information, Phys. Rev. A 33: 1134.

Guler, I., Hardalac, F., Barisci N., 2002. Application of

FFT analyzed cardiac Doppler signals to fuzzy

algorithm, Comp. Biol. Med. 32:435–444.

Grassberger, P., Procaccia, I., 1983. Characterization of

Strange Attractors. Physical Review Letters, 50:346-

349.

Hegger, R., Kantz, H., Schreiber, T., 1999. Practical

implementation of nonlinear time series methods: The

TISEAN package. Chaos, 9: 413.

Kennel, M. B. Brown, R., Abarbanel, H. D. I., 1992.

Determining embedding dimension for phase-space

reconstruction using a geometrical construction.

Physics Rev. A. 45: 340-353.

Keunen, R.W., Pijlman, H.C., Visee, H.F., Vliegen, J.H.,

Tavy, D.L., Stam, K.J., 1994. Dynamical chaos

determines the variability of transcranial Doppler

signals, Neurol. Res. 16: 353–358.

Keunen, R.W., Vliegen, J.H., Stam, C.J., Tavy, D.L.,

1996. Nonlinear transcranial Doppler analysis

demonstrates age-related changes of cerebral

hemodynamics, Ultrasound Med. Biol. 22:383–390.

Kantz, H., 1994. A robust method to estimate the maximal

Lyapunov exponent of a time series. Phys. Lett. A.

185: 77-87.

Kantz, H., Schreiber T., 2005. Nonlinear Time Series

Analysis, Cambridge University Press.

Ozturk, A., Arslan A., 2007. Classification of transcranial

Doppler signals using their chaotic invariant

measures, Computer Methods and Programs in

Biomedicine, 86(2): 171-180.

Ozturk A., Arslan A., Hardalac F., 2008. Comparison of

neuro-fuzzy systems for classification of transcranial

Doppler signals with their chaotic invariant measures,

Expert Systems with Applications, 34(2): 1044-1055.

Ozturk A., Arslan A., 2015. Neuro-fuzzy Classification of

Transcranial Doppler Signals with Chaotic Meaures

and Spectral Parameters, 3

Science and Information

Conference, 591-596.

Provenzale, A., Smith, L. A., Vio, R., Murante, G., 1992.

Distinguishing between low-dimensional dynamics

and randomness in measured time series, Physica D

58, 31.

Schreiber, T., Schmitz, A. 1996. Improved surrogate data

for nonlinearity tests, Phys. Rev. Lett. 77, 635.

Schreiber, T., 1997. Detecting and analysing non-

stationarity in a time series with nonlinear cross-

predictions, Phys. Rev. Lett. 78:843.

Serhatlioglu S., Hardalac F., Guler I., 2003. Classification

of transcranial Doppler signals using artificial neural

network, J. Med. Syst. 27:205–214.

Sprott, J.C., 2002. Chaos and Time-Series Analysis,

Oxford University Pres, New York.

Rosenstein, M. T., Collins, J. J., De Luca, C. J., 1993. A

practical method for calculating largest Lyapunov

exponents from small data sets, Physica D 65,: 117.

Theiler, J., 1990. Estimating fractal dimension. J. Opt.

Soc. Amer. A 7, 1055-1073.

Ubeyli E.D., Guler I., 2005. Adaptive neuro-fuzzy

inference systems for analysis of internal carotid

arterial Doppler signals, Comp. Biol. Med., 35: 687–

702.

Visee, H.F., Keunen, R.W., Pijlman, H.C., Vliegen, J.H.,

Tavy, D.L., Stam, K.J., Giller, C.A., 1995. The

physiological and clinical significance of nonlinear

TCD waveform analysis in occlusive cerebrovascular

disease, Neurol. Res. 17:384–388.

Vliegen, J.H.R., Stam, C.J., Rombouts, S.A.R., Keunen

R.W.M., 1996. Rejection of the ‘filtered noise’

hypothesis to explain the variability of transcranial

Doppler signals: a comparison of original TCD data

with Gaussian-scaled phase randomized surrogate

data sets, Neurol. Res. 18: 19–24.

Webber, C.L. Jr., Zbilut, J.P., 1994. Dynamical

assessment of physiological systems and states using

recurrence plot strategies. Journal of Applied

Physiology. 76:965-973.

Zbilut, J.P., Guiliani, A., Webber, C.L. Jr., 1998.

Recurrence quantification analysis and principle

components in the detection of short complex signals.

Physics Letters A, 237:131-135.

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

174