
A Binary Cuckoo Search Algorithm for Solving Project Portfolio
Problem with Synergy Considerations
Mohammed M. S. El-Kholany and Hisham M. Abdelsalam
Faculty of Computers & Information, Cairo University, 5 Ahmed Zewail Street, Cairo, Egypt
Keywords: Project Portfolio Selection (PPS), Synergy of Project, Cuckoo Search Algorithm.
Abstract: Many companies are moving toward a project-oriented way of managing their businesses while considering
the risk of losing the limited available resources because of selecting incorrect projects to be executed. With
a number of candidate projects larger than those which can be funded, organizations aim to select projects
that maximize benefit and enhance their competitive advantages. These reasons force organizations to
search for more effective techniques to improve their decision with project selection. The consideration of
synergy between projects is not addressed much in literature. This paper proposes new meta-heuristic
technique which is Cuckoo Search Algorithm to solve Project Portfolio Selection problem with synergy
among various projects is considered. Four scenarios are experimented on 0 – 1 optimization problem
contains two constraints budget and segmentation to show performance algorithm through iterations with
changing scenarios in addition to the effect of synergy on projects selection and total benefit for the
organization.
1 INTRODUCTION
An organization decision whether to select a project
for implementation or not is a crucial decision. Such
a decision has a high impact on the organization
resources and its benefit. On one hand the
organization loses resources which are used in
unsuitable projects and, on the other hand, it loses
benefit of more suitable projects that could have
been implemented instead, to achieve more benefit
for organization (Shakhsi-Niaei et al., 2011). This
kind of decisions is called Project Portfolio Selection
(PPS) in which a set of proposed or candidate
projects compete for scarce resources to be
implemented and satisfy all constraints. Project
Portfolio Selection (PPS) is choosing a group of
candidate projects to maximize benefit of
organization (Archer and Ghasemzadeh, 1999).
Research efforts were exerted in this direction to
develop and design models that represent the nature
of the PPS problem and to solve it using either
simulation techniques or optimization techniques.
PPS problem is classified as complex decision
making process due to many factors affecting the
decision such as: determining weights of different
criteria, performance value for each project in
addition to, other qualitative and quantitative factors
should be considered in decision making (Güngör
and Can, 2011). Careful attention should be given
when selecting the set of projects to be implemented,
as every organization tries to achieve its conflicting
organizational objectives while having a limited
amount of resources (Ahn et al., 2010). One of the
factors affecting the decision making process
concerning the PPS problem is the high level of risk
due to uncertainty or incompleteness of information
about the problem.
A recent stream of research was proposed to deal
with uncertainty in portfolio selection decision.
Studies such as (Shakhsi-Niaei et al, 2011) and
(George et al., 2013) proposed a two-stage
techniques that mainly depend on using Monte Carlo
simulation and considering the output of the first
stage as input for the second.
Several Evolutionary Algorithms (EA) were used
to solve the PPS problem since it is classified as NP-
hard and it is difficult to use exact algorithms to
solve it. Some of the EA used to solve this kind of
problem are Scatter Search Algorithm, Genetic
Algorithm (GA), Ant Colony Optimization (ACO)
and Cuckoo Search Algorithm (CS). Scatter Search
algorithm was introduced in (Carazo et al., 2010) to
aid decision maker to select optimal project
130
El-Kholany, M. and Abdelsalam, H.
A Binary Cuckoo Search Algorithm for Solving Project Portfolio Problem with Synergy Considerations.
DOI: 10.5220/0005694201300136
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 130-136
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

portfolio. The model takes into account
interdependencies between projects which are
assessed in groups, also the model takes into
consideration multiple objectives without taking
preferences from decision maker.
Doerner (2004) deployed Ant Colony
Optimization to solve multi-objective PPS with
limited resources. A modified Pareto Ant Colony
Optimization algorithm was introduced by
(Tofighian and Naderi, 2015) in order to solve a PPS
mixed integer linear programming model to
maximize total benefit.
A binary Cuckoo Search Algorithm to solve PPS
was proposed by (El-kholany and Abdelsalam,
2015), it considered two types of constraints budget
and segmentation constraints. The algorithm results
showed that Cuckoo Search was an efficient choice
to solve this type of problem compared to Lingo
software results. Cuckoo Search Algorithm is new
meta-heuristic technique proposed by (Yang and
Deb, 2009) to solve combinatorial and NP-Hard
problems. This algorithm proved its efficiency for
getting solutions better than other heuristics such as
Genetic Algorithm and Particle Swarm Optimization
(Roy and Sinha Chaudhuri, 2013).
A main factor that affects the Project Portfolio
Selection problem is whether or not there is synergy
between the projects. Synergy can be defined as the
complement between two or more projects that
generate additional benefit besides projects’ own
benefit if executed separately. Synergy is powerful
phenomenon to execute projects together to increase
benefit with consuming the fewest available
resources. A framework of IT portfolio selection
was proposed by (Cho and Shaw, 2009) to examine
the importance effect of IT synergy. IT synergy was
classified into three types several sub additive cost,
two-way super-additive and one-way super additive
that used index ,& respectively and effects of
different types were examined and concluded that
firms with high tolerance and moderate are more
likely to obtain IT portfolio than firms with low
tolerance. In (Almeida and Duarte, 2011) a binary
non-linear decision model was proposed to study the
effect of synergy on the PPS decision. ACO is used
to solve PPS problem considering synergy and one
of its special cases where two or more projects
cannot be financially supported in the same time in
(Rivera et al., 2013). A framework considering
synergy between IT projects on the risk and return of
portfolio was proposed in (Cho and Shaw, 2013).
The main focus of this paper is to propose a
cuckoo search algorithm to study the effect of
synergy between projects on project portfolio
selection; considering segmentation and budget
constraints. The data used to perform the study and
test the algorithm was extracted from (Shakhsi-Niaei
et al., 2011) in the case of no synergy used. For
synergy case, the interdependencies data matrix was
generated hypothetically to study the impact of
considering synergy while selecting projects to be
implemented.
Following the introduction, the rest of the paper
is organized as follows. Section 2 covers the
problem formulation as a mathematical model.
Followed by the proposed solution algorithm in
Section 3. While Section 4 provides the results and
numerical analysis of the problem. Finally,
conclusions are given in Section 5.
2 PROBLEM DEFINITION AND
MATHEMATICAL MODEL
The problem considered here is one of the main
problems found in project based organizations. The
problem lies in that there is a set of candidate
projects that the organization should choose from -to
implement- in order to maximize its benefit without
violating any constraints. Two main cases are going
to be covered of this problem, the first is the effect
of executing each project alone on the company’s
total benefit and other is the synergy effect.
2.1 Project Evaluation
The project evaluation consists of two parts, benefit
for each project separately and the second is synergy
evaluation were proposed by (Almeida and Duarte,
2011).
Let’s assume m candidate projects to be
implemented and the evaluation will be based on n
criteria. Each project has performance value for each
criterion where each project is represented by an
array
where each value in the array for
example
, represents the performance value for
project 1 in criterion 2.
=
,
...
,
∀=1,2,….
(1)
Performance value for all projects can be
represented by Matrix Z, where each row represents
project and each column represents criterion j and
is performance value for project in criterion.
=
⋯
⋮⋯⋮
⋯
(2)
A Binary Cuckoo Search Algorithm for Solving Project Portfolio Problem with Synergy Considerations
131

Each criterion is assigned a weight where the
summation of these weights should equal to one
Equation 3.
=
,
,…,
,
=1
(3)
For each project, benefit is evaluated by
multiplying each criterion with performance value
represented by equation (4)
=
∀=1,2,……,
(4)
2.2 Synergy Evaluation
To establish measurement for synergy between
projects, decision maker determines added value
percentage to each project by his experience by
joining other projects in the portfolio. Synergy can
be evaluated by answering two questions
(Damodaran, 2005): (1) what is the form of synergy
expected to take? For example, in economic scale,
will the synergy reduce cost and increase profit? Or
market power, will it increase further growth?
; and (2) when will the synergy effect start?
There are 3 steps to estimate synergy: (1) benefit
for each project is estimated separately; (2) the value
of the combined projects are evaluated, without
synergy by adding values that obtained in first step;
and (3) by expecting rate of growth, combined
projects with synergy is evaluated and the difference
between the value of combined projects without
synergy and value of combined projects with
synergy provides value of synergy.
Relationships between projects can be changed
by changing strategy of company. For example,
organization changed its strategy from increasing
profit to applying legal projects. Legal Projects can
coordinate interactions more effectively than others
that increase profit (Cho and Shaw, 2013) as a result
of this decision maker increases value percentage for
legal projects. Synergy is important feature differs
because from other criteria which involves
interrelated groups of projects, when whole
synergetic group is supported the benefit are bigger
than the same group will be applied separately
(Rivera et al., 2013). Synergy matrix was developed
in matrix (5) to represent synergy between projects.
=
⋯
⋮⋯⋮
⋯
(5)
Where
is degree of contribution of project to
project, in percentage value of project.
2.3 Objective Function
Objective function is to maximize fitness which
evaluated by aggregating benefit and synergy
evaluation in equation (6).
=
+
(6)
D.V
=
1
0
(7)
2.4 Constraints
There are two types of constraints as mentioned in
(Shakhsi-Niaei et al., 2011). The first is budget
constraint equation (8), where the implementation cost
of all the selected projects cannot exceed the available
organizational budget.
≤
(8)
Where
is cost of project to be carried out and
budget is total available budget for organization.
The second type of constraints is segmentation
constraint, where all the projects are classified into
three general categories A, B and C. Each category
must achieve specific percentage from all selected
projects. Equations (9-11) will represent
segmentation constraints.
≤1
(9)
≤2
(10)
≤3
(11)
1,2 and 3 are percentage of candidate
projects to be achieved for each type.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
132

3 PROPOSED SOLUTION
ALGORITHM
3.1 Cuckoo Search Algorithm
Cuckoo Search is new meta-heuristic technique
which simulates behaviour of cuckoo bird which is
laying its eggs on nest for host bird. Cuckoo Female
special way in mimicry colour and pattern of the egg
in order to decrease probability of eggs being
abandoned and increase reproductively. Cuckoo has
skill in the timing of laying eggs by selecting host
bird’s nest just laid its eggs so, cuckoo eggs hatch
earlier than host eggs. Once first child cuckoo is
hatched, it moves randomly and throws other eggs
for host bird which increases probability of cuckoo
to share food with host bird. There are rules applied
in algorithm
• Each Cuckoo lays one egg at time and chosen
nest to dump its egg randomly.
• Nest with best quality will be remained to next
generation.
• Number of nests is fixed, probability of
discovering host bird cuckoo egg Pa
∈
[0,1].
The quality of nests is determined by value of
objective function. For maximization problems, nest
that achieves maximum value for given objective
function will be the best and will continue for next
generation. Figure 1 provides pseudo code for
Cuckoo Search Algorithm.
3.2 Implementation Step
3.2.1 Solution Representation
Cuckoo Search is a multi solution algorithm, each
solution is represented by nest. For the problem at
hand, the solution is represented by length M which
is total number of candidate projects. Available
values for each cell either zero or one. If cell number
assigned to 1 so project will be selected otherwise
project will not be selected.
3.3 Binary Cuckoo Search
Cuckoo Search is meta-heuristic technique designed
to handle continuous variables which are generated
between upper and lower bound however, more
researcher modified it to handle discrete and binary
problems. An improved Cuckoo Search was
proposed in (Feng et al., 2014) for solving knapsack
problem by converting continuous numbers to binary
using sigmoid function as shown in equation 12.
=
1(
)0.5
0
(12)
Where
is real nest number ,
is binary nest
(
)
=
1
(1+
)
3.4 Handling Constraints
The problem on hand has two types of constraints:
budget and segmentation constraints. Two methods
were applied to handle these kinds of constraints.
Greedy Transform Method (GTM) was proposed to
handle the budget constraint as applied in (Feng et
al., 2014), this function depends on calculating
efficiency for each decision variables by dividing
benefit by cost and select most efficient decision
variable as long as constraint is satisfied.
Segmentation handling was proposed by (El-kholany
and Abdelsalam, 2015) to handle second type of
constraints.
3.5 Generation New Solution and
Stopping Criteria
Two ways are applied to generate new solution.
Lévy flight distribution represented in equation 13 is
used to generate new solution. The other way was
proposed by (Feng et al., 2014) and replaced by
function of discovering host bird for cuckoo eggs in
its own nest. Algorithm stopped when it reaches to
predefined maximum number of iterations.
Figure 1: Cuckoo Search Algorithm.
A Binary Cuckoo Search Algorithm for Solving Project Portfolio Problem with Synergy Considerations
133
()
=
+⊕é()
(13)
Where
()
is solution for next generation
()
is solution in current generation
α is transition probability where α>0
lévy (λ) is random walk based on lévy flights.
4 NUMERICAL ANALYSIS
4.1 Case and Data
Data taken from (Shakhsi-Niaei et al., 2011) was
used to test the proposed algorithm. The data used as
it is in case of no synergy between projects. The data
used was deterministic data in the purpose of
simplicity. While for synergy case, the
interdependencies data matrix was generated
hypothetically to study the impact of considering
synergy while selecting projects to be implemented.
The extracted data covers information about 20
candidate projects in R&D department, only a set of
them should be chosen based on 5 different criteria
as follows:
1. Cost: Total cost is required to complete
selected project.
2. Proposed Methodology: efficiency level of
project planning and discipline.
3. Abilities of personnel: level of experience for
project team that is assigned for proposed
project.
4. Scientific and actual capability: level of
education and scientific degree for team and
scientific degree.
5. Technical capability: ability for providing
technical facilities.
As mentioned in equations (9-11) Basic, Developing
and Applied are three categories represented in case
of research centre in Iran, total available budget is
6000 $ r1, r2 and r3 equal 10%, 30% and 60%
respectively and project types have been mentioned
in (14-16). For example, Project 2, 5 and 1 are of
Basic, Developing and Applied.
+
+
+
+
+
+
≤0.1
(14)
+
+
+
≤0.3
(15)
+
+
+
+
+
+
+
+
≤0.6
(16)
Table 1: Synergy Matrix for Scenario 2.
Projects
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1
0.0129 0.0047 0.0182 0.02 0 0.004 0 0.0082 0.0171 0.003 0.011 0 0.0142 0.009 0.001 0.0033 0 0.014 0.003
2
0 0.016 0.0171 0.0029 0.0014 0.0182 0 0.0084 0.0023 0.01 0.0071 0.005 0.0012 0.0213 0.007 0.0017 0 0
3
0.0124 0.0143 0 0.0092 0 0 0.0114 0.0023 0.01 0.0092 0.0045 0.0011 0.0033 0.0029 0.0045 0.022 0.011
4
0.014 0.0061 0.0005 0.0037 0 0.0042 0.0071 0.005 0.0029 0 0.006 0.0291 0.0173 0.003 0 0.0198
5
0.0058 0.0092 0.0058 0 0.0171 0.0419 0.0582 0 0.0044 0.0017 0 0.0631 0.0592 0.0193 0.0839
6
0 0 0.0066 0.0075 0 0.0391 0.0637 0.0039 0 0.0553 0.0794 0.0502 0.0836 0
7
0.0197 0 0 0.0374 0 0.0485 0.031 0.0847 0.045 0 0.0379 0.0883 0.008
8
0.0067 0.0187 0.0384 0.0182 0 0.01 0.0375 0.0274 0.0172 0 0 0.0374
9
0.0182 0 0.0379 0.0576 0.0937 0.0465 0 0.0917 0.0178 0.0112 0.0435
10
0.0176 0.0735 0 0.0818 0 0.0716 0.0183 0.0993 0 0.0375
11
0.0485 0 0.0373 0.0222 0.0188 0 0.0991 0.0737 0.0736
12
0.0118 0.0775 0 0.0884 0.0223 0 0.0919 0.0636
13
0.0226 0 0 0.0732 0.0335 0 0
14
0.0885 0.05 0 0.0449 0.0782 0
15
0
7
29 0 0.0924 0.0394
16
0.0592 0 0.734 0
17
0.304 0 0.055
18
0.0088 0
19
0.0021
20
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
134
Four different scenarios were applied to test how
synergy affects project selection and the company
total benefit:
• Scenario 1 is characterized based on absence of
synergy between projects.
Scenario 2 is applied based on synergy between all
projects together that shown in
• Table 1which assigned based on experts.
• Scenario 3 only project 4 receives
synergistically from other projects.
• Project 18 only contributes synergistically for
all other projects in scenario 4.
4.2 Numerical Results
In Table 2 represents the results of applying the
proposed cuckoo search on the extracted data for the
previously mentioned scenarios. The first column of
the table is the scenario number; the second is the set
of projects selected, while the third represents
the total benefit from implementing the selected
portfolio. The fourth column shows the synergy
gained which was calculated by equation 17 and
finally the total cost of the selected portfolio in the
fifth column.
=
∑
∑
∑
∑
(17)
In the first scenario, it is observed that the
projects selected are those with greatest overall
evaluations where synergy between projects wasn’t
taken into consideration. However, when synergy
was considered in scenario 2, project 11 and project
12 is more attractive than projects 3 and13
respectively, because synergy gain provided by
project 11 is 0.2993 that’s greater than synergy gain
provided by project 3 0.0603, on the other hand
project 12 is more attractive than project 13. In
scenario 3 synergy between projects are cancelled
but only project 4 receives synergistically from all
projects which it makes it more attractive project to
be selected than project 20 which are in type C.
Total benefit increases to 634.298 with increase
of 7%. In scenario 4, project 18 contributes
synergistically for all other projects, it entered to
portfolio instead of project 20 which are in type C
and total benefit increased to 652.423 with 5.8%.
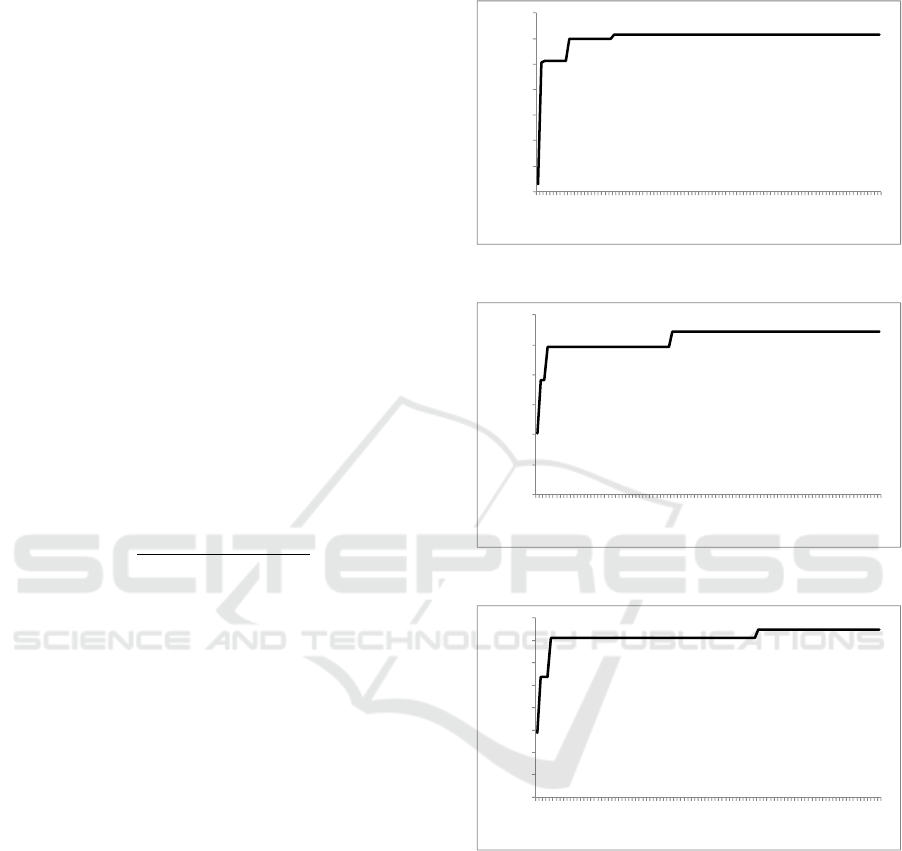
As shown figures 2 – 4 show solution progress
through 100 iterations for scenarios 2 – 4 and
observed that in scenario 2, algorithm got total
benefit 820.01 which is highest value reached at
iteration number 25. On the other hand, scenario 3
takes more time to find maximum solution reached -
Iteration number 41-. Finally, scenario 4 got value of
objective function 652.423 at iteration 65.
Figure 2: Solution Improvement with iteration - Scenario 2.
Figure 3: Solution Improvement with iteration - Scenario 3.
Figure 4:Solution Improvement with iteration - Scenario 4.
5 CONCLUSIONS
The model developed studied the synergy between
projects and provides multi criteria approach for
project portfolio selection. Cuckoo Search algorithm
was proposed to solve the problem considering
synergy relations between projects which were
represented by a matrix. This matrix should be
700
720
740
760
780
800
820
840
1 1223344556677889100
Objective Function
Iteration Number
580
590
600
610
620
630
640
1 1223344556677889100
Objective Function
Iteration Number
615
620
625
630
635
640
645
650
655
1 1223344556677889100
Objective Function
Iteration Number
A Binary Cuckoo Search Algorithm for Solving Project Portfolio Problem with Synergy Considerations
135

Table 2: Scenario Results.
Scenario Portfolio Selected Total Benefit Synergy Gain Total Cost
1
P1 P3 P5 P6 P10 P13
P15 P16 P19 P20
629.28 0 2928
2
P1 P5 P6 P10 P11 P12
P15 P16 P19 P20
820.01 38. 65 % 2896.5
3
P1 P3 P4 P5 P6 P8 P13
P15 P16 P18
634.29 7 % 2947.5
4
P1 P3 P5 P6 P10 P13
P15 P16 P18 P19
652.42 5. 87 % 2949.5
supported by experts or decision makers in order to
be accurate. The solved problem had two types of
constraints: budget and segmentation that were
handled using GTM and Segmentation handling
respectively. Results obtained illustrate the
importance of applying synergy between projects on
the company’s total benefit and the portfolio
selection process. There are several ways to extend
our work is to deal with synergy between groups of
projects in addition to, investigating other types of
Objective functions that also calculate synergy and
considering synergy with multi-objective problems.
REFERENCES
Ahn, M. J., Zwikael, O. & Bednarek, R., 2010.
Technological invention to product innovation: A
project management approach. International Journal
of Project Management, 28(6), pp.559–568.
Almeida, A.T. de & Duarte, M., 2011. A multi-criteria
decision model for selecting project portfolio with
consideration being given to a new concept for
synergies. Pesquisa Operacional, 31(2), pp.301–318.
Archer, N.. N.P. & Ghasemzadeh, F., 1999. An integrated
framework for project portfolio selection.
International Journal of Project Management, 17(4),
pp.207–216.
Carazo, A. F., Gómez, T., Molina, J., Hernández-Díaz, A.
G., Guerrero, F. M., & Caballero, R. (2010). Solving a
comprehensive model for multiobjective project
portfolio selection. Computers & operations
research,37(4), 630-639.
Cho, W. & Shaw, M.J., 2009. Does IT Synergy Matter in
IT Portfolio Selection? ICIS 2009 Proceedings, p.160.
Cho, W. & Shaw, M.J., 2013. Portfolio selection model
for enhancing information technology synergy. IEEE
Transactions on Engineering Management, 60(4),
pp.739–749.
Damodaran, A., 2005. The value of synergy. Available at
SSRN 841486.
El-kholany, M.M.S. & Abdelsalam, H.M., 2015. Optimal
Project Portfolio Selection Using Binary Cuckoo
Search Algorithm. Metaheuristics Internationa
Conference, June..
Feng, Y., Jia, K. & He, Y., 2014. An improved hybrid
encoding cuckoo search algorithm for 0-1 knapsack
problems. Computational intelligence and
neuroscience, 2014, p.1.
George, M., Mavrotas, G. & Pechak, O., 2013. The
trichotomic approach for dealing with uncertainty in
project portfolio selection: combining MCDA,
mathematical programming and Monte Carlo
simulation. International Journal of Multicriteria
Decision Making, 3(1), pp.79–96.
Rivera, G., Gómez, C.G., Fernández, E.R., Cruz, L.,
Castillo, O. & Bastiani, S.S., 2013. Handling of
synergy into an algorithm for project portfolio
selection. In Recent Advances on Hybrid Intelligent
Systems (pp. 417-430). Springer Berlin Heidelberg.
Roy, S. & Sinha Chaudhuri, S., 2013. Cuckoo Search
Algorithm using Lèvy Flight: A Review. International
Journal of Modern Education and Computer Science,
5(12), pp.10–15.
Shakhsi-Niaei, M., Torabi, S. a. A. & Iranmanesh,
S.H.S.H., 2011. A comprehensive framework for
project selection problem under uncertainty and real-
world constraints. Computers & Industrial
Engineering, 61(1), pp.226–237.
Tofighian, A.A. & Naderi, B., 2015. Modeling and solving
the project selection and scheduling. Computers &
Industrial Engineering, 83, pp.30–38.
Yang, X.-S. & Deb, S., 2009. Cuckoo search via Lévy
flights. In Nature & Biologically Inspired Computing,
2009. NaBIC 2009. World Congress on. pp. 210–214.
Güngör, Ş. Ceyda & Erkan Can, G., 2011. A Simulation
Based Optimization Methodology for Information
System Project Selection Problem. In
Trends in the
Development of Machinery and Associated
Technology. pp. 241–244.
Doerner, K., Gutjahr, W.J., Hartl, R.F., Strauss, C. and
Stummer, C., 2004. Pareto ant colony optimization: A
metaheuristic approach to multiobjective portfolio
selection. Annals of operations research, 131(1-4),
pp.79-99.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
136
