Simultaneous Scheduling of Machines and a Single Moving Robot in a

Job Shop Environment by Metaheuristics based Clustered Holonic

Multiagent Model

Houssem Eddine Nouri, Olfa Belkahla Driss and Khaled Gh´edira

Strat´egies d’Optimisation et Informatique Intelligente, Institut Sup´erieur de Gestion de Tunis, Universit´e de Tunis,

41, Avenue de la Libert´e, Cit´e Bouchoucha, Bardo 2000, Tunis, Tunisie

Keywords:

Scheduling, Transport, Robot, Genetic Algorithm, Tabu Search, Holonic Multiagent.

Abstract:

In systems based robotic cells, the control of some elements such as transport robot has some difﬁculties when

planning operations dynamically. The Job Shop scheduling Problem with Transportation times and a Single

Robot (JSPT-SR) is a generalization of the classical Job Shop scheduling Problem (JSP) where a set of jobs

additionally have to be transported between machines by a single transport robot. Hence, the JSPT-SR is

more computationally difﬁcult than the JSP presenting two NP-hard problems simultaneously: the job shop

scheduling problem and the robot routing problem. This paper proposes a hybrid metaheuristic approach based

on clustered holonic multiagent model for the JSPT-SR. Firstly, a scheduler agent applies a Neighborhood-

based Genetic Algorithm (NGA) for a global exploration of the search space. Secondly, a set of cluster agents

uses a tabu search technique to guide the research in promising regions. Computational results are presented

using benchmark data instances from the literature of JSPT-SR. New upper bounds are found, showing the

effectiveness of the presented approach.

1 INTRODUCTION

Scheduling is a ﬁeld of investigation which has known

a signiﬁcant growth these last years. The scheduling

problems appear in all the economic areas, from com-

puter engineering to industrial production and manu-

facturing. The Job Shop scheduling Problem (JSP),

which is among the hardest combinatorial optimiza-

tion problems (Sonmez and Baykasoglu, 1998), is a

branch of the industrial production scheduling prob-

lems. The JSP is known as one of the most popular

research topics in the literature due to its potential to

dramatically decrease costs and increase throughput

(Jones and Rabelo, 1998). The Job Shop schedul-

ing Problem with Transportation times and a Single

Robot (JSPT-SR) is a generalization of the classical

JSP where a set of jobs additionally have to be trans-

ported between machines by a single transport robot.

Hence, the JSPT-SR is more computationally difﬁcult

than the JSP presenting an additional difﬁculty caused

by a set of jobs to be transported by a single robot be-

tween a set of available machines. In the JSPT-SR,

we have to consider two NP-hard problems simulta-

neously: the job shop scheduling problem (Lenstra

and Kan, 1979) and the robot routing problem, which

is similar to the pickup and delivery problem (Lenstra

and Kan, 1981).

For the literature of the Job Shop scheduling Prob-

lem with Transportation times and a Single Robot,

most of the researchers have considered the machine

and robot scheduling as two independent problems.

Therefore, only few researchers have emphasized the

importance of simultaneous scheduling of jobs and

the single robot.

To solve this problem, mathematical formulations

are used to ﬁnd optimal solutions for this problem,

but the complexity of some large instances allowed

to increase the processing time for some important

solutions. (Raman et al., 1986) proposed a mixed

integer programming formulation for this problem,

and they assumed that the robot always returns to the

load/unload station after transferring a load, which re-

duces the ﬂexibility of the robot and inﬂuences the

overall schedule length. An integer programming

model is formulated by (Bilge and Ulusoy, 1995) for

the machine and robot scheduling problems with a

set of time window constraints. According to the

authors, the resulting model is intractable in prac-

tice, because of its nonlinearity and its size. (Cau-

mond et al., 2009) adapted a mathematical formula-

Nouri, H., Driss, O. and Ghédira, K.

Simultaneous Scheduling of Machines and a Single Moving Robot in a Job Shop Environment by Metaheuristics based Clustered Holonic Multiagent Model.

DOI: 10.5220/0005694300510062

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 2, pages 51-62

ISBN: 978-989-758-172-4

tion for a shop scheduling problem with one trans-

porter robot. This formulation differed from the

published works because it considered the maximum

number of jobs authorized in the system, the up-

stream and downstream storage capacities and the

robot loaded/unloaded movements.

Moreover,heuristic and metaheuristic methods of-

fered new opportunity to ﬁnd solutions for this prob-

lem in a reasonable time but they did not guaran-

teed the optimality. (Pundit and Palekar, 1990) imple-

mented a Branch and Bound procedure for a simulta-

neous scheduling of machines and resources handling

in a Job shop environment. But, they did not take

into consideration the violation of precedence rela-

tions between the different machines operations be-

longing to the same job. An iterative heuristic is used

by (Bilge and Ulusoy, 1995) based on the decompo-

sition of the master problem into two sub-problems,

allowing a simultaneous resolution of this scheduling

problem with time windows. (Ulusoy et al., 1997)

adapted a genetic algorithm for this scheduling prob-

lem in a ﬂexible manufacturing system, and where

they used a chromosome representation composed by

two parts, the operation task sequencing and the trans-

port resource assignment. (Anwar and Nagi, 1998)

treated the simultaneous machine and robot schedul-

ing problem using a forward propagation heuristic,

and where they supposed that the robot movements

between cells are considered as additional machines.

A local search algorithm is proposed in (Hurink and

Knust, 2002) and (Hurink and Knust, 2005) for the

job shop scheduling problem with a single robot,

where they supposed that the robot movements can

be considered as a generalization of the travelling

salesman problem with time windows, and additional

precedence constraints must be respected. The used

local search is based on a neighborhood structure in-

spired from (Mastrolilli and Gambardella, 2000) to

make the search process more effective. (Abdel-

maguid et al., 2004) addressed the problem of simul-

taneous scheduling of machines and identical robots

in ﬂexible manufacturing systems, by developing a

hybrid approach composed by a genetic algorithm

and a heuristic. The genetic algorithm is used for

the jobs scheduling problem and the robot assignment

is made by the heuristic algorithm. A hybrid multi-

objective genetic algorithm is proposed by (Reddy

and Rao, 2006) to solve this combined problem, and

considered three minimization objectives, which are

the makespan, mean ﬂow time and mean tardiness.

(Lacomme et al., 2007) studied the job shop schedul-

ing problem with several transport robots, where they

used a local search algorithm based on a neighbour-

hood generated by permutation of two operations or

by assigning another robot to a transport operation.

(Deroussi et al., 2008) addressed the simultaneous

scheduling problem of machines and robots in ﬂex-

ible manufacturing systems, by proposing new solu-

tion representation based on robots rather than ma-

chines. Each solution is evaluated using a discrete

event approach. An efﬁcient neighbouring system is

then implemented into three different metaheuristics:

iterated local search, simulated annealing and their

hybridisation. A differential evolution algorithm is

developed by (Babu et al., 2010) for the machines

and two robots scheduling problem, this algorithm is

inspired by (Storn and Price, 1995) which was pro-

posed for the chebyshev polynomial ﬁtting problem.

(Deroussi and Norre, 2010) considered the ﬂexible

Job shop scheduling problem with transport robots,

where each operation can be realized by a subset of

machines and adding the transport movement after

each machine operation. To solve this problem, an

iterative local search algorithm is proposed based on

classical exchange, insertion and perturbation moves.

Then a simulated annealing schema is used for the ac-

ceptance criterion. A hybrid metaheuristic approach

is proposed by (Zhang et al., 2012) for the ﬂexible Job

Shop problem with transport constraints and bounded

processing times. This hybrid approach is composed

by a genetic algorithm to solve the assignment prob-

lem of operations to machines, and then a tabu search

procedure is used to ﬁnd new improved schedul-

ing solutions. (Lacomme et al., 2013) solved the

machines and robots simultaneous scheduling prob-

lem in ﬂexible manufacturing systems, by adapting a

memetic algorithm using a genetic coding containing

two parts: a resource selection part for machine oper-

ations and a sequencing part for transport operations.

(Zhang et al., 2014) considered the job shop schedul-

ing problem with transport robots and bounded pro-

cessing times. A modiﬁed shifting bottleneck proce-

dure is used coupled with a heuristic for assigning and

sequencing transportation tasks iteratively.

Furthermore, a newly maturing area of the dis-

tributed artiﬁcial intelligence are used, providing

some effective mechanisms for the management of

such dynamic operations in manufacturing environ-

ments, such as the multi agent systems. (Braga et al.,

2008) treated the machines and robots scheduling

problem in ﬂexible manufacturing systems. They

proposed a distributed model based on cooperative

agents, composed by ﬁve agents: an order-agent,

a store-agent, a set of machine-agents and a set of

robot-agents, using negotiation between them in or-

der to obtain a best scheduling solution for this prob-

lem. (Komma et al., 2011) formulated the ma-

chines and robots scheduling problem in ﬂexible man-

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

ufacturing systems as a multi-agent system, allow-

ing to realize an Agent-Based Shop Floor Simulator

(ABSFSim). This simulator is composed by eight

agents classiﬁed into three categories: The ﬁrst cat-

egory containing agents with a single instance such

as the part-generator-agent, the arrival-queue-agent

and departure-agent. A second category taking agents

with multiple instances and a long lifetime such as

the machine-agent, the robot-agent, the node-agent

and segment-agent. And for the third category, it

contained agents with multiple instances and a short

lifetime such as the part-agent. A multi-agent ap-

proach is proposed by (Erol et al., 2012) for robots

and machines scheduling problem within a manufac-

turing system. The proposed multi-agent approach

worked under a real-time environment and generated

feasible schedules using negotiation/bidding mecha-

nisms between agents. This approach is composed by

four agents: a manager-agent, a robot-system-holon,

an order-system-holon and a machine-system-holon.

In this paper, we propose a hybridization of two

metaheuristics based on clustered holonic multiagent

model for the job shop scheduling problem with a

single transport robot. This new approach follows

two principal hierarchical steps, where a genetic al-

gorithm is applied by a scheduler agent for a global

exploration of the search space. Then, a tabu search

technique is used by a set of cluster agents to guide the

research in promising regions. Numerical tests were

made to evaluate the performance of our approach

based on the instances of (Hurink and Knust, 2005),

completed by comparisons with other approaches.

The rest of the paper is organized as follows. In

section 2, we deﬁne the formulation of the JSPT-SR

with its objective function and a simple problem in-

stance. Then, in section 3, we detail the proposed hy-

brid approach with its holonic multiagent levels. The

experimental and comparison results are provided in

section 4. Finally, section 5 ends the paper with a

conclusion.

2 PROBLEM FORMULATION

There is a set of n jobs J = {J

,... ,J

} to be processed

without preemption on a set M = {M

,. .. ,M

}

of m + 1 machines (M

represents the load/unload or

LU station from which jobs enter and leave the sys-

tem). Each job J

is formed by a sequence of ni op-

erations {O

i,1

i,2

,. .. ,O

i,ni

} to be performed succes-

sively according to the given sequence. For each oper-

ation O

i, j

, there is a machine µ

∈ {M

,. .. ,M

} and

a processing time p

associated with it. In addition,

each job J

,. .. ,J

) is composed by ni − 1 trans-

port operations {T

i,1

i,2

,. .. ,T

i,ni−1

} to be made by a

robot R from one machine to another. In fact, for each

transport operation T

i, j

there is two types of move-

ments: travel transport operation and empty transport

operation.

Firstly, travel transport operation t

i, j

,µ

i, j+1

must be

considered for the robot R when an operation O

i, j

processed on machine µ

i, j

and operation O

i, j+1

is pro-

cessed on machine µ

i, j+1

. These transportation times

are job-independentand robot-dependent. Each trans-

portation operation is assumed to be processed by

only one transport robot R which can handle at most

one job at one time. For convenience,t

i, j

,µ

i, j+1

is used

to denote both a transportation operation and a trans-

portation time.

Secondly, empty transport operation t

′

i, j

have to

be considered while the robot R moves from machine

to machine M

without carrying a job. So, it is

possible to assume that t

′

i,i

= 0 and t

i, j

≥ t

′

i, j

As in job shop problems, we assume that sufﬁcient

buffer space exists between machines. This assump-

tion is also stated as an “unlimited input/output buffer

capacity”. Jobs processed on one machine M

are as-

sumed to wait until the robot affected to this transport

operation is available to do it. No additional time is

required to transfer job from machine to the unlimited

output buffer. In a similar way, each machine M

has

an unlimited input buffer to store jobs in waiting to be

processed by it. All data p

, t

i, j

,µ

i, j+1

, t

′

i, j

,µ

i, j+1

are

assumed to be non-negative integers.

The objective is to determine a feasi-

ble schedule which minimizes the makespan

Cmax = Max

j=1,n

} where C

denotes the comple-

tion time of the last operation O

i,ni

of job J

including

the processing times of machine operations and

transport operations.

• Operation completion time

i, j

= t

i, j

,µ

i, j+1

+ t

′

i, j

,µ

i, j+1

(1)

i, j

= p

i, j

(2)

• Job completion time

∑

i=1

i,ni

∑

i,1

i, j

+ T

i, j

(3)

for T

i, j

, j ∈ (1,. .. ,ni− 1)

Makespan = max(C

,. .. ,C

) (4)

Where i = job, j = operation,t

i, j

,µ

i, j+1

= traveling

moving time, t

′

i, j

,µ

i, j+1

= empty moving time, T

i, j

transport operation processing time, p

i, j

= machine

operation processing time.

Simultaneous Scheduling of Machines and a Single Moving Robot in a Job Shop Environment by Metaheuristics based Clustered Holonic

Multiagent Model

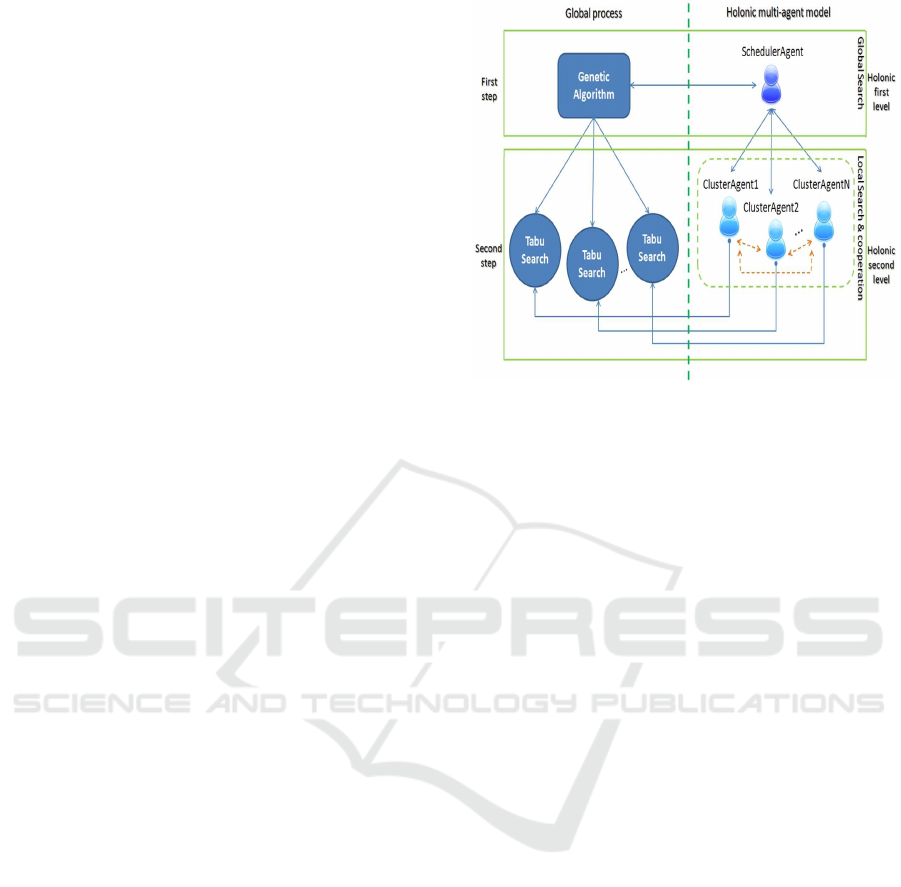
3 HYBRID METAHEURISTICS

BASED CLUSTERED HOLONIC

MULTIAGENT MODEL

(Glover et al., 1995) elaborated a study about the na-

ture of connections between the genetic algorithm and

tabu search metaheuristics, searching to show the ex-

isting opportunities for creating a hybrid approach

with these two standard methods to take advantage

of their complementary features and to solve difﬁ-

cult optimization problems. After this pertinent study,

the combination of these two metaheuristics has be-

come more well-known in the literature, which has

motivated many researchers to try the hybridization

of these two methods for the resolution of different

complex problems in several areas.

(Ferber, 1999) deﬁned a multiagent system as an

artiﬁcial system composed of a population of au-

tonomous agents, which cooperate with each other to

reach common objectives, while simultaneously each

agent pursues individual objectives. Furthermore, a

multiagent system is a computational system where

two or more agents interact (cooperate or compete, or

a combination of them) to achieve some individual or

collectivegoals. The achievement of these goals is be-

yond the individual capabilities and individual knowl-

edge of each agent (Botti and Giret, 2008).

(Koestler, 1967) gave the ﬁrst deﬁnition of the

term “holon” in the literature, by combining the two

Greek words “hol” meaning whole and “on” meaning

particle or part. He said that almost everything is both

a whole and a part at the same time. In fact, a holon

is recursively decomposed at a lower granularity level

into a community of other holons to produce a hol-

archy (Calabrese, 2011). Moreover, a holon may be

viewed as a sort of recursive agent, which is a super-

agent composed by a sub-agents set, where each sub-

agent has its own behavior as a complementary part

of the whole behaviour of the super-agent. Holons

are agents able to show an architectural recursiveness

(Giret and Botti, 2004).

In this work, we propose a hybrid metaheuristic

approach based on clustering processing two general

steps: a ﬁrst step of global exploration using a ge-

netic algorithm to ﬁnd promising areas in the search

space and a clustering operator allowing to regroup

them in a set of clusters. In the second step, a tabu

search algorithm is applied to ﬁnd the best individ-

ual solution for each cluster. The global process of

the proposed approach is implemented in two hierar-

chical holonic levels adopted by a recursive multia-

gent model, named a hybrid Genetic Algorithm with

Tabu Search based on clustered Holonic Multiagent

model (GATS+HM), see Figure 1. The ﬁrst holonic

Figure 1: Hybrid metaheuristics based clustered holonic

multiagent model.

level is composed by a Scheduler Agent which is the

Master/Super-agent, preparing the best promising re-

gions of the search space, and the second holonic

level containing a set of Cluster Agents which are the

Workers/Sub-agents, guiding the search to the global

optimum solution of the problem. Each holonic level

of this model is responsible to process a step of the hy-

brid metaheuristic approach and to cooperate between

them to attain the global solution of the problem.

In fact, the choice of this new metaheuristic hy-

bridization is justiﬁed by that the standard meta-

heuristic methods use generally the diversiﬁcation

techniques to generate and to improve many differ-

ent solutions distributed in the search space, or by

using local search techniques to generate a more im-

proved set of neighbourhood solutions from an ini-

tial solution. But they did not guarantee to attain

promising areas with good ﬁtness converging to the

global optimum despite the repetition of many iter-

ations, that is why they need to be more optimized.

So, the novelty of our approach is to launch a genetic

algorithm based on a diversiﬁcation technique to only

explore the search space and to select the best promis-

ing regions by the clustering operator. Then, apply-

ing the intensiﬁcation technique of the tabu search al-

lowing to relaunch the search from an elite solution

of each cluster autonomously to attain more domi-

nant solutions of the search space. The use of a mul-

tiagent system gives the opportunity for distributed

and parallel treatments which are very complimen-

tary for the second step of the proposed approach.

Indeed, our combined metaheuristic approach fol-

lows the paradigm of “Master” and “Workers” which

are two recursive hierarchical levels adaptable for a

holonic multiagent model, where the Scheduler Agent

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

is the Master/Super-agent of its society and the Clus-

ter Agents are its Workers/Sub-agents.

3.1 Non Oriented Disjunctive Graph

In this work, we chose to use the disjunctive graph of

(Hurink and Knust, 2005) for the job shop problem

with transportation times and one robot. To explain

this graph, a sample problem of three jobs and ﬁve

machines with their transportation times for a single

robot R is presented in Table 1.

Table 1: One instance of job shop problem with a single

robot.

Processing times for each job J

Job1 : M5(1) M4(4)

Job2 : M1(1) M3(6) M2(5)

Job3 : M3(6) M1(3)

Transportation times for the robot R

M1 M2 M3 M4 M5

M1 0 1 2 3 4

M2 1 0 1 2 3

M3 2 1 0 1 2

M4 3 2 1 0 1

M5 4 3 2 1 0

The disjunctive graph G = (V

∪V

,C∪ D

∪ D

see Figure 2, is composed by : a set of vertices V

containing all machine operations, a set of vertices

is the set of transport operations obtained by as-

signing the robot R to each transport operation, and

two dummy nodes 0 and ∗. Also, this graph consists

of: a set of conjunctions C representing precedence

constraints O

i,k

→ t

i,k

,µ

i,k+1

→ O

i,k+1

, undirected dis-

junctions for machines D

, and undirected disjunc-

tions for the transport robot D

. For each job J

, ni− 1

transport operations t

i,k

,µ

i,k+1

are introduced includ-

ing precedence O

i,k

→ t

i,k

,µ

i,k+1

→ O

i,k+1

. In fact,

the robot R may be considered as an additional “ma-

chine” which has to process all these transport opera-

tions. The arcs from machine node to transport node

are weighted with the machine operation durations.

Edges between machine operations represent disjunc-

tions for machine operations which have to be pro-

cessed on the same machine and cannot use it simul-

taneously.

As for the classical job shop, the conjunctions C

model the execution order of operations within ech

job J

. In addition to the classical set of undirected

machine disjunctions D

(all pairs of machine opera-

tions which have to be processed on the same machine

and which are not linked by a directed path), it is nec-

essary to consider the set of undirected robot disjunc-

Figure 2: Non oriented disjunctive graph.

tions D

(all pairs of transport operations which have

to be transported by the robot R and which are not

linked by a directed path). To solve the scheduling

problem it is necessary to turn all undirected arcs in

∪ D

into directed ones, and to assign the robot

R to each transport operation, where the ﬁnal graph

becomes an oriented disjunctive graph.

3.2 Scheduler Agent

The Scheduler Agent (SA) is responsible to process

the ﬁrst step of the hybrid algorithm by using a genetic

algorithm called NGA (Neighborhood-based Genetic

Algorithm) to identify areas with high average ﬁtness

in the search space during a ﬁxed number of iterations

MaxIter, see Figure 3. In fact, the goal of using the

NGA is only to explore the search space, but not to

ﬁnd the global solution of the problem. Then, a clus-

tering operator is integrated to divide the best identi-

ﬁed areas by the NGA in the search space to different

parts where each part is a cluster CL

∈ CL the set of

clusters, where CL = {CL

,CL

,. .. ,CL

}. In addi-

tion, this agent plays the role of an interface between

the user and the system (initial parameter inputs and

ﬁnal result outputs). According to the number of clus-

ters N obtained after the integration of the cluster-

ing operator, the SA creates N Cluster Agents (CAs)

preparing the passage to the next step of the global al-

gorithm. After that, the SA remains in a waiting state

until the reception of the best solutions found by the

CAs for each cluster CL

. Finally, it ﬁnishes the pro-

cess by displaying the ﬁnal solution of the problem.

3.2.1 Individual’s Solution Presentation based

Oriented Disjunctive Graph

The Job Shop scheduling Problem with Transporta-

tion times and a Single Robot is composed by two

Simultaneous Scheduling of Machines and a Single Moving Robot in a Job Shop Environment by Metaheuristics based Clustered Holonic

Multiagent Model

Figure 3: First step of the global process by the Scheduler

Agent.

sub-problems: ﬁrstly the machines and robot selec-

tion, secondly the operationsscheduling problem, that

is why the chromosome representation is encoded in

two parts: Machines and Robot Selection part (MRS),

and Job and Transport operation Sequence part (JTS),

see Figure 4.

Figure 4: The chromosome representation of a scheduling

solution.

The ﬁrst part MRS is a vector V

with a length

L equal to the total number of operations and where

each index represents the selected machine or robot

to process an operation indicated at position p, see

Figure 4 (a). For example p = 3 and p = 7, V

(3)

is the selected machine M

for the operation O

1,2

and V

(7) is the selected robot R

for the operation

2,2

. The second part JTS is a vector V

having

the same length of V

and where each index repre-

sents a machine operation O

i, j

or a transport oper-

ation T

i, j

according to the predeﬁned operations for

each job, see Figure 4 (b). For example this operation

sequence 1-2-1-1-3-2-3-2-3-2-2 can be translated to:

1,1

) → (O

2,1

) → (T

1,1

,R) → (O

1,2

) →

3,1

) → (T

2,1

,R) → (T

3,1

,R) → (O

2,2

) →

3,2

) → (T

2,2

,R) → (O

2,3

). In addition, for

each job J

,. .. ,J

) ni − 1 transport operations are

generated T

1,1

, T

2,1

, T

2,2

and T

3,1

, and scheduled fol-

lowing the presented solution in vector JTS, allowing

to ﬁx the ﬁnal path to be considered by the robot R

during the shop process, see Figure 5.

Figure 5: Final path of the robot R.

Figure 6: Exemple of oriented machine and robot disjunc-

tions.

To model an oriented disjunctive graph we should

consider some rules. Let the example in Figure 6, if

the edge is oriented in the direction O

i,k

→ O

j,k

′

it gets

the weight p

i,k

, else it takes p

j,k

′

in the inverse case.

If an arc is added from T

i,k

to T

j,k

′

, its gets the weight

i,k

i,k+1

′

i,k+1

j,k

′

and t

j,k

′

j,k

′

j,k

′

i,k

it is oriented in the other direction. Thus, basing

on (Hurink and Knust, 2005) we can deﬁne a ﬁxed

machine selection S

called directed Machine Dis-

junctions and a ﬁxed transport selection S

called di-

rected Transport Disjunctions, with their precedence

relations C called operation Conjunctions. So, a

fully oriented disjunctive graph can be obtained us-

ing

S = C ∪ S

∪ S

, which is called a complete se-

lection. In fact, the selections of the two sets of dis-

junctions S

and S

with their set of conjunctions C

are based on the two proposed vectors MRS and JTS,

where MRS allows to present the selected machines

to process job operations and the selected robot to

process transport operations. JTS presents the ex-

ecution order of the job and transport operations in

their selected machines and robot allowing to ﬁx the

ﬁnal Machine and Transport Disjunctions S

∪S

with

their set of Conjunctions C representing the prece-

dence relations between the different operations. The

union C ∪ S

∪ S

S fully describes a solution if the

resulting oriented disjunctive graph G = (V

S) is

acyclic. A feasible schedule can be constructed by

longest path calculation which permits to obtain the

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

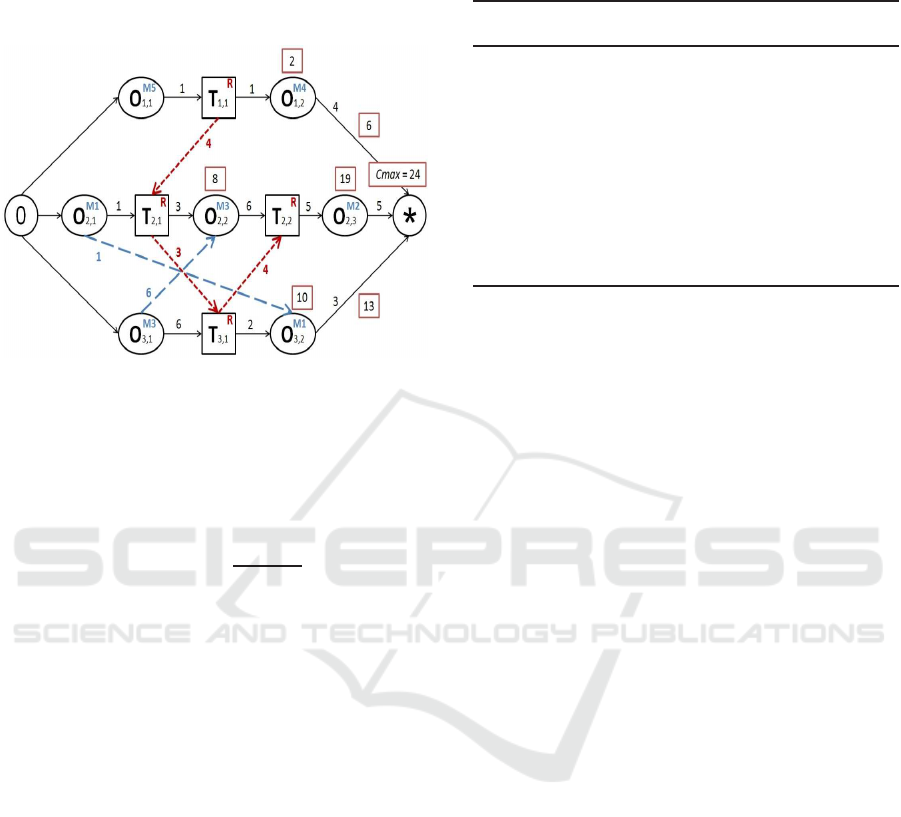
earliest starting time of both machine and transport

operations and fully deﬁnes a semi-active schedule

with the Cmax given by the length of the longest path

from node 0 to *, see Figure 7.

Figure 7: Oriented disjunctive graph.

Noting that the chromosome ﬁtness is calculated

by Fitness(i) which is the ﬁtness function of each

chromosome i and Cmax(i) is its makespan value,

where i ∈ {1, .. ., P} and P is the total population size,

see Equation (5).

Fitness(i) =

Cmax(i)

(5)

3.2.2 Population Initialization

The initial population is generated randomly follow-

ing a uniform law and based on a neighborhood pa-

rameter to make the individual solutions more diver-

siﬁed and distributed in the search space. In fact, each

new solution should have a predeﬁned distance with

all the other solutions to be considered as a new mem-

ber of the initial solution. The used method to deter-

minate the neighborhood parameter is inspired from

(Bozejko et al., 2010), which is based on the permuta-

tion level of operations to obtain the distance between

two solutions. In fact, the dissimilarity distance is cal-

culated by verifying the difference between two chro-

mosomes in terms of the execution order of all the

shop operations O

i, j

and T

i, j

in the Job and Transport

operation Sequence V

(JTS). So, if there is a differ-

ence in the vectorV

, the distance is incremented by 1

because it is in the order of O(1). Let Chrom

(JTS

)

and Chrom

(JTS

) two chromosomes of two differ-

ent scheduling solutions, L is the total number of op-

erations of all jobs and Dist is the dissimilarity dis-

tance. The distance is calculated by verifying the ex-

ecution order difference of the Job and Transport op-

eration Sequence vectors JTS

and JTS

which is in

order of O(1), we give here how to proceed in Algo-

rithm 1 :

Algorithm 1: How to calculate the dissimilarity distance

between two solutions.

1: procedure

2: Dist ← 0,k ← 1

3: for k from 1 to L do

4: if Chrom1(JTS

(k)) 6= Chrom2(JTS

(k))

then

5: Dist ← Dist + 1

6: end if

7: end for

8: return Dist

9: end procedure

Noting that Distmax is the maximal dissimilar-

ity distance and it is calculated by Equation (6), rep-

resenting 100% of difference between two chromo-

somes.

Distmax =

∑

i=1

i,ni

∑

i,1

1 (6)

3.2.3 Selection Operator

The selection operator is used to select the best par-

ent individuals to prepare them to the crossover step.

This operator is based on the ﬁtness function al-

lowing to analyze the quality of each selected solu-

tion. But progressively the ﬁtness values will be sim-

ilar for the most individuals. That is why, we in-

tegrate the neighborhood parameter, where we pro-

pose a new combined parent selection operator named

Fitness-Neighborhood Selection Operator (FNSO) al-

lowing to add the dissimilarity distance parameter

to the ﬁtness function to select the best parents for

the crossover step. The FNSO chooses in each it-

eration two parent individuals until engaging all the

population to create the next generation. The ﬁrst

parent takes successively in each case a solution i,

where i∈ {1,...,P} and P is the total population size.

The second parent obtains its solution j randomly

by the roulette wheel selection method based on the

two Fitness and Neighborhood parameters relative to

the selected ﬁrst parent, where j ∈ {1,. .. ,P} \ {i}

in the P population and where j 6= i. In fact, to use

this random method, we should calculate the Fitness-

Neighborhood total FN for the population, see Equa-

tion (7), the selection probability sp

for each indi-

vidual I

, see Equation (8), and the cumulative prob-

ability cp

, see Equation (9). After that, a random

number r will be generated from the uniform range

[0,1]. If r ≤ cp

then the second parent takes the

ﬁrst individual I

, else it gets the k

individual I

∈

Simultaneous Scheduling of Machines and a Single Moving Robot in a Job Shop Environment by Metaheuristics based Clustered Holonic

Multiagent Model

,. .. ,I

} \ {I

} and where cp

k−1

< r ≤ cp

. For

Equations (7), (8) and (9), k = {1,2,. .. ,P} \ {i}.

• The Fitness-Neighborhood total for the popula-

tion:

FN =

∑

k=1

[1/(Cmax[k] × Neighborhood[i][k])]

(7)

• The selection probability sp

for each individual

1/(Cmax[k] × Neighborhood[i][k])

(8)

• The cumulative probability cp

for each individ-

ual I

∑

h=1

(9)

3.2.4 Crossover Operator

The crossover operator has an important role in the

global process, allowing to combine in each case the

chromosomes of two parents in order to obtain new

individuals and to attain new better parts in the search

space. In this work, this operator is applied only for

the parent chromosome vector V

(JTS).

JTS Crossover. An improved precedence preserv-

ing order-based on crossover (iPOX), inspired from

(Lee et al., 1998), is adapted for the parent opera-

tion vector JTS. This iPOX operator is applied fol-

lowing four steps, a ﬁrst step is selecting two par-

ent operation vectors (JTS

and JTS

) and generat-

ing randomly two job sub-sets Js

/Js

from all jobs.

A second step is allowing to copy any element in

JTS

/JTS

that belong to Js

/Js

into child individ-

ual JTS

′

/JTS

′

and retain them in the same position.

Then the third step deletes the elements that are al-

ready in the sub-set Js

/Js

from JTS

/JTS

. Finally,

ﬁll orderly the empty positions in JTS

′

/JTS

′

with the

reminder elements of JTS

/JTS

in the fourth step,

see the example in the Figure 8.

Figure 8: JTS crossover exemple.

3.2.5 Mutation Operator

The mutation operator is integrated to promote the

children generation diversity. In fact, this operator

is applied on the chromosomes of the new generated

children by the JTS crossover operator.

JTS Mutation. This operator selects randomly two

indexes index

and index

from the vector JTS. Next,

it changes the position of the job number in the index

to the second index

and inversely, see Figure 9.

Figure 9: JTS mutation exemple.

3.2.6 Replacement Operator

The replacement operator has an important role to

prepare the remaining surviving population to be con-

sidered for the next iterations. This operator replaces

in each case a parent by one of its children which has

the best ﬁtness in its current family.

Figure 10: The ﬁnal population transformation by applying

the clustering operator.

3.2.7 Clustering Operator

By ﬁnishing the maximum iteration number Max-

Iter of the genetic algorithm, the Scheduler Agent

applies a clustering operator using the hierarchical

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

clustering algorithm of (Johnson, 1967) to divide

the ﬁnal population into N Clusters, see Figure 10,

to be treated by the Cluster Agents in the second

step of the global process. The clustering operator

is based on the neighbourhood parameter which

is the dissimilarity distance between individuals.

The clustering operator starts by assigning each

individual Indiv(i) to a cluster CL

, so if we have P

individuals, we have now P clusters containing just

one individual in each of them. For each case, we

ﬁxe an individual Indiv(i) and we verify successively

for each next individual Indiv( j) from the remaining

population (where i and j ∈ {1, .. ., P},i 6= j) if the

dissimilarity distance Dist between Indiv(i) and

Indiv( j) is less than or equal to a ﬁxed threshold

Dist fix (representing a percentage of difference X%

relatively to Distmax, see Equation (10)) and where

Cluster(Indiv(i)) 6= Cluster(Indiv( j)). If it is the

case, Merge(Cluster(Indiv(i)),Cluster(Indiv( j))),

else continue the search for new combination with

the remaining individuals. The stopping condition is

by browsing all the population individuals, where we

obtained at the end N Clusters.

Dist fix = Distmax× X% (10)

Figure 11: Distribution of the Cluster Agents in the different

clusters of the search space.

3.3 Cluster Agents

Each Cluster Agent CA

is responsible to apply suc-

cessively to each cluster CL

a local search technique

which is the Tabu Search algorithm to guide the re-

search in promising regions of the search space and

to improve the quality of the ﬁnal population of the

genetic algorithm. In fact, this local search is exe-

cuted simultaneously by the set of the CAs agents,

where each CA starts the research from an elite solu-

tion of its cluster searching to attain new more dom-

inant individual solutions separately in its assigned

Figure 12: Second step of the global process by the Cluster

Agents.

cluster CL

, see Figure 11. The used Tabu Search al-

gorithm is based on an intensiﬁcation technique al-

lowing to start the research from an elite solution in

a cluster CL

(a promising part in the search space) in

order to collect new scheduling sequence minimizing

the makespan. Let E the elite solutionof a clusterCL

′

∈ N(E) is a neighbor of the elite solution E, GL

the Global List of eachCA

to receive new found elite

solutions by the remaining CAs, each CL

plays the

role of the tabu list with a dynamic length and Cmax is

the makespan of the obtained solution. So, the search

process of this local search starts from an elite solu-

tion E using the move and insert method of (Mas-

trolilli and Gambardella, 2000), where each Cluster

Agent CA

changes the execution order of an opera-

tion (O

i, j

if machine operation or T

i, j

if transport oper-

ation) from an index i to another index k in the vector

JTS, searching to generate new scheduling combina-

tion E

′

∈ N(E). After that, verifying if the makespan

value of this new generated solution Cmax(E

′

) dom-

Algorithm 2: The local search process.

1: procedure

2: E ← Elite(CL

)

3: while N(E) 6=

0 do

4: E

′

← Move-and-insert(E) | E

′

∈ N(E) |

′

/∈ CL

5: if Cmax(E

′

) < Cmax(E) and E

′

/∈ GL

then

6: E ← E

′

7: CL

← E

′

8: Send-to-all(E

′

, CA

)

9: end if

10: end while

11: return E

12: end procedure

Simultaneous Scheduling of Machines and a Single Moving Robot in a Job Shop Environment by Metaheuristics based Clustered Holonic

Multiagent Model

inates Cmax(E) (Cmax(E

′

) < Cmax(E)), and if it is

the case CA

saves E

′

in its tabu list (which is CL

)

and sends it to all the other CAs agents to be placed

in their Global Lists GLs(E

′

,CA

), to ensure that it

will not be used again by them as a search point. Else

continues the neighborhood search from the current

solution E. The stopping condition is by attaining the

maximum allowed number of neighbors for a solution

E without improvement, see Figure 12. We give here

how to proceed in Algorithm 2 :

By ﬁnishing this local search step, the CAs agents

terminate the process by sending their last best solu-

tions to the SA agent, which considers the best one of

them as the global solution for the JSPT-SR.

4 EXPERIMENTAL RESULTS

4.1 Experimental Setup

The proposed GATS+HM is implemented in java lan-

guage on a 2.10 GHz Intel Core 2 Duo processor and 3

Gb of RAM memory, where we use the Integrated De-

velopment Environment (IDE) Eclipse to code the al-

gorithm and the multiagent platform Jade (Bellifem-

ine et al., 1999) to create the different agents of our

holonic model. To evaluate its efﬁciency, numeri-

cal tests are made based on the benchmark instances

of (Hurink and Knust, 2005) from the literature of

the JSPT-SR, which consists of two sets P1(6 × 6)

and P2(10× 10) inspired from (Muth and Thompson,

1963). In both instances the number of operations per

job is equal to the number of machines and each job is

processed on each machine exactly once with a ﬁxed

processing time. This shop problem considers a sin-

gle moving robot for all transport operations, where

various test instances were obtained by adding trans-

portation and empty moving times with differentchar-

acteristics.

Due to the non-deterministic nature of the pro-

posed approach, we run it ten independent times for

each case of the (Hurink and Knust, 2005) benchmark

instances in order to obtain signiﬁcant results. The

used parameter settings for our algorithm are adjusted

experimentally and presented as follow: the crossover

probability = 1.0, the mutation probability = 0.5, the

maximum number of iterations = 1000 and the popu-

lation size = 200. The computational results are pre-

sented by three metrics in Table 2, such as the best

makespan, the CPU time of our GATS+HM in min-

utes and the gap between our approach and the best

results in the literature of the JSPT-SR, which is cal-

culated by Equation (11). The Mko is the makespan

obtained by Our approach and Mkc is the makespan

of one of the chosen algorithms for Comparisons.

Gap = [(Mko− Mkc)/Mkc] × 100% (11)

4.2 Experimental Comparisons

To show the efﬁciency of our GATS+HM approach,

we compare its obtained results from the (Hurink

and Knust, 2005) benchmark instances with other al-

gorithms from the literature of the JSPT-SR, which

have obtained the best upper bounds for this prob-

lem. The chosen algorithms are : the one-stage ap-

proach (UB

one

) of (Hurink and Knust, 2005) (with

their known lower bound LB) which obtained the ﬁrst

results in the literature for their proposed instances,

the genetic algorithm-tabu search procedure (GATS)

of (Zhang et al., 2012) and the hybrid memetic algo-

rithm (BFS) of (Lacomme et al., 2013) which are two

recent hybrid metaheuristic approaches.

From Table 2, the comparison results show that

the GATS+HM obtains twelve out of ﬁfteen best re-

sults for the (Hurink and Knust, 2005) instances,

where we attain ten new upper bounds and two sim-

ilar results. Indeed, our algorithm outperforms the

one

in eleven out of ﬁfteen instances with a max-

imum gap of -7,80% for the P02-T5-t2 instance, and

it gets slightly worse result for three instances with a

maximum gap of 1,21% for the P02-D3-d1 instance.

Moreover, our GATS+HM outperforms the BFS in

twelve out of ﬁfteen instances with a maximum gap

of -4,13% for the P02-T2-t1 instance, and it gets

one bad result for the P01-D2-d1 instance with a gap

of 0,68%. For the comparison with the GATS, the

GATS+HM obtains fourteen out of ﬁfteen best results

with a maximum gap of -30,52% for the P02-D2-d1

instance.

By analyzing the computational time in few min-

utes and the comparison results of our approach in

terms of makespan, we can distinguish the efﬁciency

of the new proposed GATS+HM relatively to the lit-

erature of the JSPT-SR. This efﬁciency is explained

by the ﬂexible selection of the promising parts of the

search space by the clustering operator after the ge-

netic algorithm process and by applying the intensi-

ﬁcation technique of the tabu search allowing to start

from a set of elite solutions to attain new more domi-

nant solutions.

5 CONCLUSION

In this paper, we present a new metaheuristic hy-

bridization approach based on clustered holonic

multiagent model, called GATS+HM, for the job

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

Table 2: Results of (Hurink and Knust, 2005) data instances.

Instance LB Gap

one

Gap

one

BFS Gap

BFS

GATS Gap

GATS

GATS+HM

CPU

Time

P01.D1-d1 82 2,44 87 -3,45 87 -3,45 96 -12,50 84 0,30

P01.D1-t1 77 2,60 81 -2,47 81 -2,47 83 -4,82 79 0,27

P01.D2-d1 147 1,36

148 0,68 148 0,68 155 -3,87 149 0,29

P01.D3-d1 213 0,00 217 -1,84 213 0,00 220 -3,18 213 0,28

P01.T2-t1 71 1,41 74 -2,70 74 -2,70 79 -8,86

72 0,26

P01.T3-t0 92 0,00 92 0,00 92 0,00 92 0,00 92 0,19

P02.D1-d1 880 10,57 1044 -6,80 1012 -3,85 1339 -27,33

973 6,15

P02.D1-t0 880 12,50 1042 -4,99 1017 -2,65 1352 -26,78 990 4,26

P02.D1-t1 880 11,36 1016 -3,54 983 -0,31 1337 -26,70

980 4,56

P02.D2-d1 892 12,56 1070 -6,17 1045 -3,92 1445 -30,52 1004 8,53

P02.D3-d1 906 19,54

1070 1,21 1100 -1,55 1516 -28,56 1083 11,45

P02.D5-t2 1167 13,71 1325 0,15 1361 -2,50 1689 -21,43 1327 13,15

P02.T1-t1 874 8,35 1006 -5,86 978 -3,17 1322 -28,37

947 7,14

P02.T2-t1 880 8,18 1015 -6,21 993 -4,13 1279 -25,57 952 7,31

P02.T5-t2 898 13,14 1102 -7,80 1022 -0,59 1339 -24,12

1016 9,25

shop scheduling problem with tansportation times

and a single robot (JSPT-SR). In this approach, a

neighborhood-basedgenetic algorithm is adapted by a

scheduler agent for a global exploration of the search

space. Then, a local search technique is applied by a

set of cluster agents to guide the research in promising

regions of the search space and to improve the quality

of the ﬁnal population. To measure its performance,

numerical tests are made using benchmark data in-

stances from the literature of JSPT-SR, and where

new upper bounds are found showing the effective-

ness of the presented approach. In the future work,

we will search to treat other extensions of the JSPT-

SR, such as the general case of this problem where a

set of robots can be used for the transport oprations,

and by considering the machine assignment problem

for each operation in the shop process. So, the prob-

lem becomes a Flexible Job Shop scheduling Problem

with Tansportation times and Many Robots (FJSPT-

MR). Thus, we will make improvements in the chro-

mosome ﬁrst part MRS to adapt it to this new trans-

formation and study its effects on the makespan.

REFERENCES

Abdelmaguid, T. F., Nassef, A. O., Kamal, B. A., and Has-

san, M. F. (2004). A hybrid ga/heuristic approach

to the simultaneous scheduling of machines and auto-

mated guided vehicles. International Journal of Pro-

duction Research, 42(2):267–281.

Anwar, M. F. and Nagi, R. (1998). Integrated scheduling

of material handling and manufacturing activities for

just-in-time production of complex assemblies. Inter-

national Journal of Production Research, 36(3):653–

681.

Babu, A. G., Jerald, J., Haq, A. N., Luxmi, V. M., and

Vigneswaralu, T. P. (2010). Scheduling of machines

and automated guided vehicles in fms using differen-

tial evolution. International Journal of Production Re-

search, 48(16):4683–4699.

Bellifemine, F., Poggi, A., and Rimassa, G. (1999). Jade -

a ﬁpa-compliant agent framework. In In Proceedings

of the fourth International Conference and Exhibition

on The Practical Application of Intelligent Agents and

Multi-Agent Technology, pages 97–108.

Bilge, U. and Ulusoy, G. (1995). A time window approach

to simultaneous scheduling of machines and material

handling system in an fms. Operations Research,

43(6):1058–1070.

Botti, V. and Giret, A. (2008). ANEMONA: A Multi-

agent Methodology for Holonic Manufacturing Sys-

tems. Springer Series in Advanced Manufacturing.

Springer-Verlag.

Bozejko, W., Uchronski, M., and Wodecki, M. (2010). The

new golf neighborhood for the ﬂexible job shop prob-

lem. In In Proceedings of the International Confer-

ence on Computational Science, pages 289–296.

Braga, R. A. M., Rossetti, R. J. F., Reis, L. P., and Oliveira,

E. C. (2008). Applying multi-agent systems to simu-

late dynamic control in ﬂexible manufacturing scenar-

ios. In European Meeting on Cybernetics and Systems

Research, volume 2, pages 488–493. Austrian Society

for Cybernetic Studies.

Calabrese, M. (2011). Hierarchical-granularity holonic

modelling. Doctoral thesis, Universita degli Studi di

Milano, Milano, Italy.

Caumond, A., Lacomme, P., Moukrim, A., and Tchernev,

N. (2009). An milp for scheduling problems in an fms

with one vehicle. European Journal of Operational

Research, 199(3):706–722.

Deroussi, L., Gourgand, M., and Tchernev, N. (2008). A

simple metaheuristic approach to the simultaneous

scheduling of machines and automated guided vehi-

Simultaneous Scheduling of Machines and a Single Moving Robot in a Job Shop Environment by Metaheuristics based Clustered Holonic

Multiagent Model

cles. International Journal of Production Research,

46(8):2143–2164.

Deroussi, L. and Norre, S. (2010). Simultaneous schedul-

ing of machines and vehicles for the ﬂexible job shop

problem. In International Conference on Metaheuris-

tics and Nature Inspired Computing, pages 1–2.

Erol, R., Sahin, C., Baykasoglu, A., and Kaplanoglu, V.

(2012). A multi-agent based approach to dynamic

scheduling of machines and automated guided vehi-

cles in manufacturing systems. Applied Soft Comput-

ing, 12(6):1720–1732.

Ferber, J. (1999). Multi-Agent Systems: An Introduction

to Distributed Artiﬁcial Intelligence. Addison-Wesley

Longman Publishing Co., Inc., Boston, MA, USA, 1st

edition.

Giret, A. and Botti, V. (2004). Holons and agents. Journal

of Intelligent Manufacturing, 15(5):645–659.

Glover, F., Kelly, J. P., and Laguna, M. (1995). Genetic

algorithms and tabu search: Hybrids for optimization.

Computers and Operations Research, 22(1):111–134.

Hurink, J. and Knust, S. (2002). A tabu search algorithm for

scheduling a single robot in a job-shop environment.

Discrete Applied Mathematics, 119(1-2):181–203.

Hurink, J. and Knust, S. (2005). Tabu search algorithms for

job-shop problems with a single transport robot. Eu-

ropean Journal of Operational Research, 162(1):99–

111.

Johnson, S. C. (1967). Hierarchical clustering schemes.

Psychometrika, 32(3):241–254.

Jones, A. and Rabelo, L. C. (1998). Survey of job shop

scheduling techniques. Tech. rep., National Institute

of Standards and Technology, Gaithersburg, USA.

Koestler, A. (1967). The Ghost in the Machine. Hutchinson,

London, United Kingdom, 1st edition.

Komma, V. R., Jain, P. K., and Mehta, N. K. (2011). An

approach for agent modeling in manufacturing on jade

reactive architecture. The International Journal of Ad-

vanced Manufacturing Technology, 52(9-12):1079–

1090.

Lacomme, P., Larabi, M., and Tchernev, N. (2007).

A disjunctive graph for the job-shop with several

robots. In Multidisciplinary International Conference

on Scheduling : Theory and Applications, MISTA,

pages 285–292, Paris, France.

Lacomme, P., Larabi, M., and Tchernev, N. (2013). Job-

shop based framework for simultaneous scheduling of

machines and automated guided vehicles. Interna-

tional Journal of Production Economics, 143(1):24–

34.

Lee, K., Yamakawa, T., and Lee, K. M. (1998). A ge-

netic algorithm for general machine scheduling prob-

lems. In In Proceedings of the second IEEE inter-

national Conference on Knowledge-Based Intelligent

Electronic Systems, pages 60–66.

Lenstra, J. K. and Kan, A. H. G. R. (1979). Compu-

tational complexity of scheduling under precedence

constraints. Annals of Discrete Mathematics, 4:121–

140.

Lenstra, J. K. and Kan, A. H. G. R. (1981). Complexity of

vehicle routing and scheduling problems. Networks,

11(2):221–227.

Mastrolilli, M. and Gambardella, L. (2000). Effective

neighbourhood functions for the ﬂexible job shop

problem. Journal of Scheduling, 3(1):3–20.

Muth, J. F. and Thompson, G. L. (1963). Industrial Schedul-

ing. International series in management. Prentice-

Hall.

Pundit, R. and Palekar, U. (1990). Job shop scheduling with

explicit material handling considerations. Technical

report, Univ. of Illinois at Urbana-Champaign, Dept.

of M. and I.E.

Raman, N., Talbot, F. B., and Rachamadgu, R. V. (1986).

Simultaneous scheduling of machines and material

handling devices in automated manufacturing. In In

Proceedings of the 2nd ORSA/TIMS Conference on

Flexible Manufacturing Systems, pages 455–466.

Reddy, B. S. P. and Rao, C. S. P. (2006). A hybrid multi-

objective ga for simultaneous scheduling of machines

and agvs in fms. The International Journal of Ad-

vanced Manufacturing Technology, 31(5-6):602–613.

Sonmez, A. I. and Baykasoglu, A. (1998). A new dynamic

programming formulation of (nm) ﬂow shop sequenc-

ing problems with due dates. International Journal of

Production Research, 36(8):2269–2283.

Storn, R. and Price, K. (1995). Differential evolution: A

simple and efﬁcient adaptive scheme for global op-

timization over continuous spaces. Technical report,

International Computer Science Institute, Berkeley.

Ulusoy, G., Erifolu, F. S., and Bilge, U. (1997). A genetic

algorithm approach to the simultaneous scheduling of

machines and automated guided vehicles. Computers

and Operations Research, 24(3):335–351.

Zhang, Q., Manier, H., and Manier, M. A. (2012). A genetic

algorithm with tabu search procedure for ﬂexible job

shop scheduling with transportation constraints and

bounded processing times. Computers and Opera-

tions Research, 39(7):1713–1723.

Zhang, Q., Manier, H., and Manier, M. A. (2014). A modi-

ﬁed shifting bottleneck heuristic and disjunctive graph

for job shop scheduling problems with transportation

constraints. International Journal of Production Re-

search, 52(4):985–1002.

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence