A New Family of Bounded Divergence Measures and Application to

Signal Detection

Shivakumar Jolad

, Ahmed Roman

, Mahesh C. Shastry

, Mihir Gadgil

and Ayanendranath Basu

Department of Physics, Indian Institute of Technology Gandhinagar, Ahmedabad, Gujarat, India

Department of Mathematics, Virginia Tech , Blacksburg, VA, U.S.A.

Department of Physics, Indian Institute of Science Education and Research Bhopal, Bhopal, Madhya Pradesh, India

Biomedical Engineering Department, Oregon Health & Science University, Portland, OR, U.S.A.

Interdisciplinary Statistical Research Unit, Indian Statistical Institute, Kolkata, West Bengal-700108, India

Keywords:

Divergence Measures, Bhattacharyya Distance, Error Probability, F-divergence, Pattern Recognition, Signal

Detection, Signal Classiﬁcation.

Abstract:

We introduce a new one-parameter family of divergence measures, called bounded Bhattacharyya distance

(BBD) measures, for quantifying the dissimilarity between probability distributions. These measures are

bounded, symmetric and positive semi-deﬁnite and do not require absolute continuity. In the asymptotic

limit, BBD measure approaches the squared Hellinger distance. A generalized BBD measure for multiple

distributions is also introduced. We prove an extension of a theorem of Bradt and Karlin for BBD relating

Bayes error probability and divergence ranking. We show that BBD belongs to the class of generalized Csiszar

f-divergence and derive some properties such as curvature and relation to Fisher Information. For distributions

with vector valued parameters, the curvature matrix is related to the Fisher-Rao metric. We derive certain

inequalities between BBD and well known measures such as Hellinger and Jensen-Shannon divergence. We

also derive bounds on the Bayesian error probability. We give an application of these measures to the problem

of signal detection where we compare two monochromatic signals buried in white noise and differing in

frequency and amplitude.

1 INTRODUCTION

Divergence measures for the distance between two

probability distributions are a statistical approach to

comparing data and have been extensively studied in

the last six decades (Kullback and Leibler, 1951; Ali

and Silvey, 1966; Kapur, 1984; Kullback, 1968; Ku-

mar et al., 1986). These measures are widely used in

varied ﬁelds such as pattern recognition (Basseville,

1989; Ben-Bassat, 1978; Choi and Lee, 2003), speech

recognition (Qiao and Minematsu, 2010; Lee, 1991),

signal detection (Kailath, 1967; Kadota and Shepp,

1967; Poor, 1994), Bayesian model validation (Tumer

and Ghosh, 1996) and quantum information theory

(Nielsen and Chuang, 2000; Lamberti et al., 2008).

Distance measures try to achieve two main objectives

(which are not mutually exclusive): to assess (1) how

“close” two distributions are compared to others and

(2) how “easy” it is to distinguish between one pair

than the other (Ali and Silvey, 1966).

There is a plethora of distance measures available

to assess the convergence (or divergence) of proba-

bility distributions. Many of these measures are not

metrics in the strict mathematical sense, as they may

not satisfy either the symmetry of arguments or the

triangle inequality. In applications, the choice of the

measure depends on the interpretation of the metric in

terms of the problem considered, its analytical prop-

erties and ease of computation (Gibbs and Su, 2002).

One of the most well-known and widely used di-

vergence measures, the Kullback-Leibler divergence

(KLD)(Kullback and Leibler, 1951; Kullback, 1968),

can create problems in speciﬁc applications. Specif-

ically, it is unbounded above and requires that the

distributions be absolutely continuous with respect

to each other. Various other information theoretic

measures have been introduced keeping in view ease

of computation ease and utility in problems of sig-

nal selection and pattern recognition. Of these mea-

sures, Bhattacharyya distance (Bhattacharyya, 1946;

Kailath, 1967; Nielsen and Boltz, 2011) and Chernoff

distance (Chernoff, 1952; Basseville, 1989; Nielsen

Jolad, S., Roman, A., Shastry, M., Gadgil, M. and Basu, A.

A New Family of Bounded Divergence Measures and Application to Signal Detection.

DOI: 10.5220/0005695200720083

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 72-83

ISBN: 978-989-758-173-1

and Boltz, 2011) have been widely used in signal

processing. However, these measures are again un-

bounded from above. Many bounded divergence mea-

sures such as Variational, Hellinger distance (Bas-

seville, 1989; DasGupta, 2011) and Jensen-Shannon

metric (Burbea and Rao, 1982; Rao, 1982b; Lin,

1991) have been studied extensively. Utility of these

measures vary depending on properties such as tight-

ness of bounds on error probabilities, information the-

oretic interpretations, and the ability to generalize to

multiple probability distributions.

Here we introduce a new one-parameter (α) fam-

ily of bounded measures based on the Bhattacharyya

coefﬁcient, called bounded Bhattacharyya distance

(BBD) measures. These measures are symmetric,

positive-deﬁnite and bounded between 0 and 1. In

the asymptotic limit (α →±∞) they approach squared

Hellinger divergence (Hellinger, 1909; Kakutani,

1948). Following Rao (Rao, 1982b) and Lin (Lin,

1991), a generalized BBD is introduced to capture

the divergence (or convergence) between multiple dis-

tributions. We show that BBD measures belong to

the generalized class of f-divergences and inherit use-

ful properties such as curvature and its relation to

Fisher Information. Bayesian inference is useful in

problems where a decision has to be made on clas-

sifying an observation into one of the possible array

of states, whose prior probabilities are known (Hell-

man and Raviv, 1970; Varshney and Varshney, 2008).

Divergence measures are useful in estimating the er-

ror in such classiﬁcation (Ben-Bassat, 1978; Kailath,

1967; Varshney, 2011). We prove an extension of

the Bradt Karlin theorem for BBD, which proves the

existence of prior probabilities relating Bayes error

probabilities with ranking based on divergence mea-

sure. Bounds on the error probabilities P

can be

calculated through BBD measures using certain in-

equalities between Bhattacharyya coefﬁcient and P

We derive two inequalities for a special case of BBD

(α = 2) with Hellinger and Jensen-Shannon diver-

gences. Our bounded measure with α = 2 has been

used by Sunmola (Sunmola, 2013) to calculate dis-

tance between Dirichlet distributions in the context of

Markov decision process. We illustrate the applicabil-

ity of BBD measures by focusing on signal detection

problem that comes up in areas such as gravitational

wave detection (Finn, 1992). Here we consider dis-

criminating two monochromatic signals, differing in

frequency or amplitude, and corrupted with additive

white noise. We compare the Fisher Information of

the BBD measures with that of KLD and Hellinger

distance for these random processes, and highlight the

regions where FI is insensitive large parameter devia-

tions. We also characterize the performance of BBD

for different signal to noise ratios, providing thresh-

olds for signal separation.

Our paper is organized as follows: Section I is

the current introduction. In Section II, we recall the

well known Kullback-Leibler and Bhattacharyya di-

vergence measures, and then introduce our bounded

Bhattacharyya distance measures. We discuss some

special cases of BBD, in particular Hellinger distance.

We also introduce the generalized BBD for multi-

ple distributions. In Section III, we show the posi-

tive semi-deﬁniteness of BBD measure, applicability

of the Bradt Karl theorem and prove that BBD be-

longs to generalized f-divergence class. We also de-

rive the relation between curvature and Fisher Infor-

mation, discuss the curvature metric and prove some

inequalities with other measures such as Hellinger

and Jensen Shannon divergence for a special case of

BBD. In Section IV, we move on to discuss applica-

tion to signal detection problem. Here we ﬁrst brieﬂy

describe basic formulation of the problem, and then

move on computing distance between random pro-

cesses and comparing BBD measure with Fisher In-

formation and KLD. In the Appendix we provide the

expressions for BBD measures , with α = 2, for some

commonly used distributions. We conclude the paper

with summary and outlook.

2 DIVERGENCE MEASURES

In the following subsection we consider a measurable

space Ω with σ-algebra B and the set of all probability

measures M on (Ω,B). Let P and Q denote probabil-

ity measures on (Ω,B) with p and q denoting their

densities with respect to a common measure λ. We

recall the deﬁnition of absolute continuity (Royden,

1986):

Absolute Continuity: A measure P on the Borel

subsets of the real line is absolutely continuous with

respect to Lebesgue measure Q, if P(A) = 0, for ev-

ery Borel subset A ∈ B for which Q(A) = 0, and is

denoted by P << Q.

2.1 Kullback-Leibler Divergence

The Kullback-Leibler divergence (KLD) (or rela-

tive entropy) (Kullback and Leibler, 1951; Kullback,

1968) between two distributions P,Q with densities p

and q is given by:

I(P, Q) ≡

plog





dλ. (1)

The symmetrized version is given by

J(P, Q) ≡ (I(P, Q) + I(Q,P))/2

A New Family of Bounded Divergence Measures and Application to Signal Detection

(Kailath, 1967), I(P,Q) ∈ [0, ∞]. It diverges if

∃ x

: q(x

) = 0 and p(x

) 6= 0.

KLD is deﬁned only when P is absolutely contin-

uous w.r.t. Q. This feature can be problematic in nu-

merical computations when the measured distribution

has zero values.

2.2 Bhattacharyya Distance

Bhattacharyya distance is a widely used measure

in signal selection and pattern recognition (Kailath,

1967). It is deﬁned as:

B(P, Q) ≡ −ln



√

pqdλ



= −ln(ρ), (2)

where the term in parenthesis ρ(P,Q) ≡

√

pqdλ

is called Bhattacharyya coefﬁcient (Bhattacharyya,

1943; Bhattacharyya, 1946) in pattern recognition,

afﬁnity in theoretical statistics, and ﬁdelity in quan-

tum information theory. Unlike in the case of KLD,

the Bhattacharyya distance avoids the requirement of

absolute continuity. It is a special case of Chernoff

distance

(P, Q) ≡ −ln



(x)q

1−α

(x)dx



with α = 1/2. For discrete probability distribu-

tions, ρ ∈ [0,1] is interpreted as a scalar product of

the probability vectors P = (

√

,. . .,

√

) and

Q = (

√

,. . .,

√

). Bhattacharyya distance

is symmetric, positive-semideﬁnite, and unbounded

(0 ≤ B ≤ ∞). It is ﬁnite as long as there exists some

region S ⊂ X such that whenever x ∈S : p(x)q(x) 6= 0.

2.3 Bounded Bhattacharyya Distance

Measures

In many applications, in addition to the desirable

properties of the Bhattacharyya distance, bounded-

ness is required. We propose a new family of bounded

measure of Bhattacharyya distance as below,

ψ,b

(P, Q) ≡ −log

(ψ(ρ)) (3)

where, ρ = ρ(P, Q) is the Bhattacharyya coefﬁcient,

(ρ) satisﬁes ψ(0) = b

−1

, ψ(1) = 1. In particular

we choose the following form :

ψ(ρ) =



1 −

(1 −ρ)



b =



α −1



, (4)

where α ∈ [−∞,0) ∪(1,∞]. This gives the measure

(ρ(P, Q)) ≡ −log

(

1−

)

−α



1 −

(1 −ρ)



, (5)

which can be simpliﬁed to

(ρ) =

log

1 −

(1−ρ)

log



1 −



. (6)

It is easy to see that B

(0) = 1, B

(1) = 0.

2.4 Special Cases

1. For α = 2 we get,

(ρ) = −log



1 + ρ



= −log



1 + ρ



(7)

We study some of its special properties in Sec.3.7.

2. α → ∞

∞

(ρ) = −log

−(1−ρ)

= 1 −ρ = H

(ρ), (8)

where H(ρ) is the Hellinger distance (Basseville,

1989; Kailath, 1967; Hellinger, 1909; Kakutani,

1948)

H(ρ) ≡

1 −ρ(P,Q). (9)

3. α = −1

−1

(ρ) = −log



2 −ρ



. (10)

4. α → −∞

−∞

(ρ) = log

(1−ρ)

= 1 −ρ = H

(ρ). (11)

We note that BBD measures approach squared

Hellinger distance when α → ±∞. In general, they

are convex (concave) when α > 1 (α < 0) in ρ, as

seen by evaluating second derivative

∂

(ρ)

∂ρ

−1

log



1 −





1 −

1−ρ



(

> 0 α > 1

< 0 α < 0 .

(12)

From this we deduce B

α>1

(ρ) ≤H

(ρ) ≤B

α<0

(ρ) for

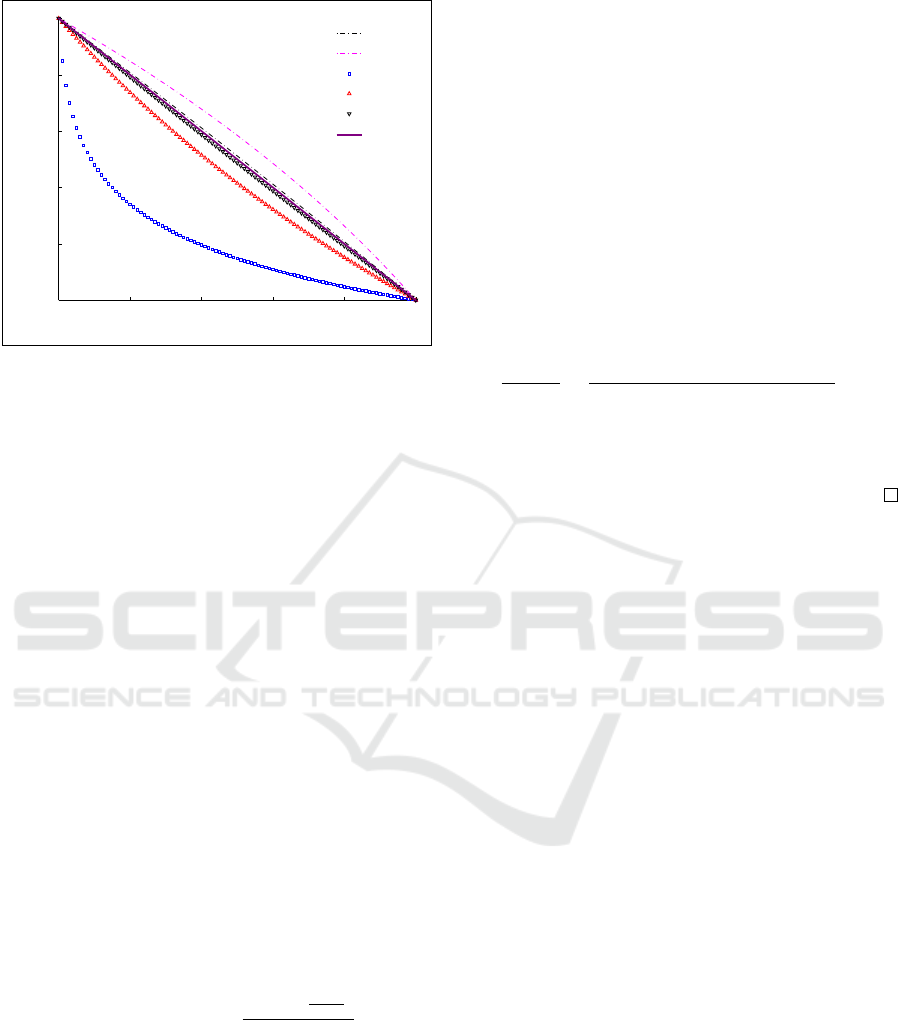
ρ ∈ [0,1]. A comparison between Hellinger and BBD

measures for different values of α are shown in Fig.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

(ρ)

α=−10

−1

1.01

(ρ)

Figure 1: [Color Online] Comparison of Hellinger and

bounded Bhattacharyya distance measures for different val-

ues of α.

2.5 Generalized BBD Measure

In decision problems involving more than two ran-

dom variables, it is very useful to have divergence

measures involving more than two distributions (Lin,

1991; Rao, 1982a; Rao, 1982b). We use the general-

ized geometric mean (G) concept to deﬁne bounded

Bhattacharyya measure for more than two distribu-

tions. The G

({p

}) of n variables p

, p

,. . ., p

with

weights β

,β

,. . .,β

, such that β

≥ 0,

∑

= 1, is

given by

({p

}) =

∏

i=1

For n probability distributions P

,. . .,P

, with

densities p

, p

,. . ., p

, we deﬁne a generalized Bhat-

tacharyya coefﬁcient, also called Matusita measure of

afﬁnity (Matusita, 1967; Toussaint, 1974):

,. . .,P

) =

Ω

∏

i=1

dλ. (13)

where β

≥ 0,

∑

= 1. Based on this, we deﬁne the

generalized bounded Bhattacharyya measures as:

(ρ

,. . .,P

)) ≡

log(1 −

1−ρ

)

log(1 −1/α)

(14)

where α ∈[−∞,0)∪(1,∞]. For brevity we denote it as

(ρ). Note that, 0 ≤ρ

≤1 and 0 ≤B

(ρ) ≤1, since

the weighted geometric mean is maximized when all

the p

’s are the same, and minimized when any two

of the probability densities p

’s are perpendicular to

each other.

3 PROPERTIES

3.1 Symmetry, Boundedness and

Positive Semi-deﬁniteness

Theorem 3.1. B

(ρ(P, Q)) is symmetric, positive

semi-deﬁnite and bounded in the interval [0, 1] for

α ∈ [−∞,0) ∪(1,∞].

Proof. Symmetry: Since ρ(P,Q) = ρ(Q,P), it fol-

lows that

(ρ(P, Q)) = B

(ρ(Q,P)).

Positive-semideﬁnite and boundedness: Since

(0) = 1, B

(1) = 0 and

∂B

(ρ)

∂ρ

αlog(1 −1/α) [1 −(1 −ρ)/α]

< 0

for 0 ≤ ρ ≤ 1 and α ∈ [−∞, 0) ∪(1, ∞], it follows that

0 ≤ B

(ρ) ≤ 1. (15)

3.2 Error Probability and Divergence

Ranking

Here we recap the deﬁnition of error probability and

prove the applicability of Bradt and Karlin (Bradt and

Karlin, 1956) theorem to BBD measure.

Error Probability: The optimal Bayes error proba-

bilities (see eg: (Ben-Bassat, 1978; Hellman and Ra-

viv, 1970; Toussaint, 1978)) for classifying two events

with densities p

(x) and p

(x) with prior prob-

abilities Γ = {π

,π

} is given by

min[π

(x),π

(x)]dx. (16)

Error Comparison: Let p

(x) (i = 1,2) be param-

eterized by β (Eg: in case of Normal distribution

β = {µ

,σ

;µ

,σ

} ). In signal detection literature,

a signal set β is considered better than set β

for the

densities p

(x) , when the error probability is less for

β than for β

(i.e. P

(β) < P

(β

)) (Kailath, 1967).

Divergence Ranking: We can also rank the param-

eters by means of some divergence D. The signal

set β is better (in the divergence sense) than β

, if

) > D

In general it is not true that D

) >

) =⇒ P

(β) < P

(β

). Bradt and Karlin

proved the following theorem relating error probabil-

ities and divergence ranking for symmetric Kullback

Leibler divergence J:

A New Family of Bounded Divergence Measures and Application to Signal Detection

Theorem 3.2 (Bradt and Karlin (Bradt and Karlin,

1956)). If J

) > J

), then ∃a set of prior

probabilities Γ = {π

,π

} for two hypothesis g

for which

(β,Γ) < P

(β

,Γ) (17)

where P

(β,Γ) is the error probability with parameter

β and prior probability Γ.

It is clear that the theorem asserts existence, but

no method of ﬁnding these prior probabilities. Kailath

(Kailath, 1967) proved the applicability of the Bradt

Karlin Theorem for Bhattacharyya distance measure.

We follow the same route and show that the B

(ρ)

measure satisﬁes a similar property using the follow-

ing theorem by Blackwell.

Theorem 3.3 (Blackwell (Blackwell, 1951)).

(β

,Γ) ≤ P

(β,Γ) for all prior probabilities Γ if

and only if

[Φ(L

)|g] ≤ E

[Φ(L

)|g],

∀ continuous concave functions Φ(L), where

= p

(x,β)/p

(x,β) is the likelihood ratio and

[Φ(L

)|g] is the expectation of Φ(L

) under the

hypothesis g = P

Theorem 3.4. If B

(ρ(β)) > B

(ρ(β

)), or equiva-

lently ρ(β) < ρ(β

) then ∃ a set of prior probabilities

Γ = {π

,π

} for two hypothesis g

, for which

(β,Γ) < P

(β

,Γ). (18)

Proof. The proof closely follows Kailath (Kailath,

1967). First note that

√

L is a concave function of

L (likelihood ratio) , and

ρ(β) =

∑

x∈X

(x,β)p

(x,β)

∑

x∈X

(x,β)

= E

. (19)

Similarly

ρ(β

) = E

(20)

Hence, ρ(β) < ρ(β

) ⇒

< E

. (21)

Suppose assertion of the stated theorem is not true,

then for all Γ, P

(β

,Γ) ≤ P

(β,Γ). Then by Theorem

3.3, E

[Φ(L

)|g

] ≤E

[Φ(L

)|g

] which contradicts

our result in Eq. 21.

3.3 Bounds on Error Probability

Error probabilities are hard to calculate in general.

Tight bounds on P

are often extremely useful in prac-

tice. Kailath (Kailath, 1967) has shown bounds on P

in terms of the Bhattacharyya coefﬁcient ρ:

2π

−

1 −4π

≤ P

≤



−



√

ρ,

(22)

with π

+ π

= 1. If the priors are equal π

= π

the expression simpliﬁes to



1 −

1 −ρ



≤ P

≤

ρ. (23)

Inverting relation in Eq. 6 for ρ(B

), we can get the

bounds in terms of B

(ρ) measure. For the equal prior

probabilities case, Bhattacharyya coefﬁcient gives a

tight upper bound for large systems when ρ →0 (zero

overlap) and the observations are independent and

identically distributed. These bounds are also useful

to discriminate between two processes with arbitrar-

ily low error probability (Kailath, 1967). We suppose

that tighter upper bounds on error probability can be

derived through Matusita’s measure of afﬁnity (Bhat-

tacharya and Toussaint, 1982; Toussaint, 1977; Tous-

saint, 1975), but is beyond the scope of present work.

3.4 F-divergence

A class of divergence measures called f-divergences

were introduced by Csiszar (Csiszar, 1967; Csiszar,

1975) and independently by Ali and Silvey (Ali and

Silvey, 1966) (see (Basseville, 1989) for review).

It encompasses many well known divergence mea-

sures including KLD, variational, Bhattacharyya and

Hellinger distance. In this section, we show that

(ρ) measure for α ∈ (1,∞], belongs to the generic

class of f-divergences deﬁned by Basseville (Bas-

seville, 1989).

F-divergence (Basseville, 1989). Consider a measur-

able space Ω with σ-algebra B. Let λ be a measure on

(Ω,B) such that any probability laws P and Q are ab-

solutely continuous with respect to λ, with densities p

and q. Let f be a continuous convex real function on

, and g be an increasing function on R. The class

of divergence coefﬁcients between two probabilities:

d(P, Q) = g



Ω





qdλ



(24)

are called the f-divergence measure w.r.t. functions

( f , g) . Here p/q = L is the likelihood ratio. The term

in the parenthesis of g gives the Csiszar’s (Csiszar,

1967; Csiszar, 1975) deﬁnition of f-divergence.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

The B

(ρ(P, Q)) , for α ∈ (1,∞] measure can be writ-

ten as the following f divergence:

f (x) = −1 +

1 −

√

, g(F) =

log(−F)

log(1 −1/α)

, (25)

where,

F =

Ω



−1 +



1 −



qdλ

Ω





−1 +



−

√



dλ

= −1 +

1 −ρ

. (26)

and

g(F) =

log(1 −

1−ρ

)

log(1 −1/α)

= B

(ρ(P, Q)). (27)

3.5 Curvature and Fisher Information

In statistics, the information that an observable ran-

dom variable X carries about an unknown parameter θ

(on which it depends) is given by the Fisher informa-

tion. One of the important properties of f-divergence

of two distributions of the same parametric family

is that their curvature measures the Fisher informa-

tion. Following the approach pioneered by Rao (Rao,

1945), we relate the curvature of BBD measures to

the Fisher information and derive the differential cur-

vature metric. The discussions below closely follow

(DasGupta, 2011).

Deﬁnition. Let {f (x|θ); θ ∈ Θ ⊆ R}, be a family of

densities indexed by real parameter θ, with some reg-

ularity conditions ( f (x|θ) is absolutely continuous).

(φ) ≡ B

(θ,φ) =

log(1 −

1−ρ(θ,φ)

)

log(1 −1/α)

(28)

where ρ(θ,φ) =

f (x|θ) f (x|φ)dx

Theorem 3.5. Curvature of Z

(φ)|

φ=θ

is the Fisher

information of f (x|θ) up to a multiplicative constant.

Proof. Expand Z

(φ) around theta

(φ) = Z

(θ) + (φ −θ)

(φ)

dφ

(φ −θ)

(φ)

dφ

+ . . .

(29)

Let us observe some properties of Bhattacharyya co-

efﬁcient : ρ(θ,φ) = ρ(φ,θ), ρ(θ,θ) = 1, and its

derivatives:

∂ρ(θ,φ)

∂φ



φ=θ

∂

∂θ

f (x|θ)dx = 0, (30)

∂

ρ(θ,φ)

∂φ



φ=θ

= −



∂ f

∂θ



dx +

∂

∂θ

f dx

= −

f (x|θ)



∂log f (x|θ)

∂θ



= −

(θ). (31)

where I

(θ) is the Fisher Information of distribution

f (x|θ)

(θ) =

f (x|θ)



∂log f (x|θ)

∂θ



dx. (32)

Using the above relationships, we can write down

the terms in the expansion of Eq. 29 Z

(θ) =

0 ,

∂Z

(φ)

∂φ



φ=θ

= 0, and

∂

(φ)

∂φ



φ=θ

= C(α)I

(θ) > 0, (33)

where C(α) =

−1

4αlog(1−1/α)

> 0

The leading term of B

(θ,φ) is given by

(θ,φ) ∼

(φ −θ)

C(α)I

(θ). (34)

3.6 Differential Metrics

Rao (Rao, 1987) generalized the Fisher information

to multivariate densities with vector valued parame-

ters to obtain a “geodesic” distance between two para-

metric distributions P

of the same family. The

Fisher-Rao metric has found applications in many ar-

eas such as image structure and shape analysis (May-

bank, 2004; Peter and Rangarajan, 2006) , quantum

statistical inference (Brody and Hughston, 1998) and

Blackhole thermodynamics (Quevedo, 2008). We de-

rive such a metric for BBD measure using property of

f-divergence.

Let θ,φ ∈ Θ ⊆ R

, then using the fact that

∂Z(θ,φ)

∂θ



φ=θ

= 0, we can easily show that

∑

i, j=1

∂

∂θ

dθ

+ ··· =

∑

i, j=1

i j

dθ

+ . . . .

(35)

The curvature metric g

i j

can be used to ﬁnd the

geodesic on the curve η(t), t ∈ [0,1] with

C = η(t) : η(0) = θ η(1) = φ. (36)

Details of the geodesic equation are given in many

standard differential geometry books. In the con-

text of probability distance measures reader is re-

ferred to (see 15.4.2 in A DasGupta (DasGupta, 2011)

A New Family of Bounded Divergence Measures and Application to Signal Detection

for details) The curvature metric of all Csiszar f-

divergences are just scalar multiple KLD measure

(DasGupta, 2011; Basseville, 1989) given by:

i j

(θ) = f

(1)g

i j

(θ). (37)

For our BBD measure

(x) =



−1 +

1 −

√



4αx

3/2

(1) = 1/4α. (38)

Apart from the −1/log(1 −

), this is same as C(α)

in Eq. 34. It follows that the geodesic distance for our

metric is same KLD geodesic distance up to a multi-

plicative factor. KLD geodesic distances are tabulated

in DasGupta (DasGupta, 2011).

3.7 Relation to Other Measures

Here we focus on the special case α = 2, i.e. B

(ρ)

Theorem 3.6.

≤ H

≤ log4 B

(39)

where 1 and log4 are sharp.

Proof. Sharpest upper bound is achieved via taking

sup

ρ∈[0,1)

(ρ)

. Deﬁne

g(ρ) ≡

1 −ρ

−log

(1 + ρ)/2

. (40)

We note that g(ρ) is continuous and has no singulari-

ties whenever ρ ∈ [0, 1). Hence

(ρ) =

1−ρ

1+ρ

+ log(

1+ρ

)

log

ρ+1

log2 ≥ 0.

It follows that g(ρ) is non-decreasing and hence

sup

ρ∈[0,1)

g(ρ) = lim

ρ→1

g(ρ) = log(4). Thus

≤ log4. (41)

Combining this with convexity property of B

(ρ) for

α > 1, we get

≤ H

≤ log4 B

Using the same procedure we can prove a generic ver-

sion of this inequality for α ∈ (1,∞] , given by

(ρ) ≤ H

≤ −αlog



1 −



(ρ) (42)

Jensen-Shannon Divergence: The Jensen differ-

ence between two distributions P,Q, with densities

p,q and weights (λ

,λ

); λ

+ λ

= 1, is deﬁned as,

,λ

(P,Q) = H

(λ

p + λ

q) −λ

(p) −λ

(q),

(43)

where H

is the Shannon entropy. Jensen-Shannon di-

vergence (JSD) (Burbea and Rao, 1982; Rao, 1982b;

Lin, 1991) is based on the Jensen difference and is

given by:

JS(P, Q) =J

1/2,1/2

(P, Q)

plog



p + q



+ q log



p + q



dλ (44)

The structure and goals of JSD and BBD measures

are similar. The following theorem compares the two

metrics using Jensen’s inequality.

Lemma 3.7 Jensen’s Inequality: For a convex func-

tion ψ, E[ψ(X)] ≥ ψ(E[X]).

Theorem 3.8 (Relation to Jensen-Shannon mea-

sure). JS(P, Q) ≥

log2

(P, Q) −log2

We use the un-symmetrized Jensen-Shannon met-

ric for the proof.

Proof.

JS(P, Q) =

p(x)log

2p(x )

p(x) + q(x)

= −2

p(x)log

p(x) + q(x)

2p(x )

≥−2

p(x)log

p(x) +

q(x)

2p(x )

(since

√

p + q ≤

√

p +

√

−2log

p(X) +

q(X)

2p(X )

By Jensen’s inequality

E[−log f (X)] ≥ −log E[ f (X)], we have

−2log

p(X) +

q(X)

2p(X )

≥

−2 log E

p(X) +

q(X)

2p(X )

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

Hence,

JS(P, Q) ≥ −2log

p(x)



p(x) +

q(x)



2p(x)

= −2 log

1 +

p(x)q(x)

−log 2

= 2



(p(x ), q(x))

log2



−log 2

log2

(P, Q) −log2. (45)

4 APPLICATION TO SIGNAL

DETECTION

Signal detection is a common problem occurring in

many ﬁelds such as communication engineering, pat-

tern recognition, and Gravitational wave detection

(Poor, 1994). In this section, we brieﬂy describe the

problem and terminology used in signal detection. We

illustrate though simple cases how divergence mea-

sures, in particular BBD can be used for discrimi-

nating and detecting signals buried in white noise of

correlator receivers (matched ﬁlter). For greater de-

tails of the formalism used we refer the reader to

review articles in the context of Gravitational wave

detection by Jaranowski and Kr

olak(Jaranowski and

olak, 2007) and Sam Finn (Finn, 1992).

One of the central problem in signal detection is to

detect whether a deterministic signal s(t) is embedded

in an observed data x(t), corrupted by noise n(t). This

can be posed as a hypothesis testing problem where

the null hypothesis is absence of signal and alternative

is its presence. We take the noise to be additive , so

that x(t) = n(t) + s(t). We deﬁne the following terms

used in signal detection: Correlation G (also called

matched ﬁlter) between x and s, and signal to noise

ratio ρ (Finn, 1992; Budzy

nski et al., 2008).

G = (x|s), ρ =

(s,s), (46)

where the scalar product (.|.) is deﬁned by

(x|y) := 4ℜ

∞

˜x( f ) ˜y

∗

( f )

N( f )

d f . (47)

ℜ denotes the real part of a complex expression, tilde

denotes the Fourier transform and the asterisk * de-

notes complex conjugation.

N is the one-sided spec-

tral density of the noise.

For white noise, the probability densities of G when

respectively signal is present and absent are given by

(Budzy

nski et al., 2008)

(G) =

√

2πρ

exp



−

(G −ρ

)

2ρ



, (48)

(G) =

√

2πρ

exp



−

2ρ



(49)

4.1 Distance between Gaussian

Processes

Consider a stationary Gaussian random process X,

which has signals s

or s

with probability densities

and p

respectively of being present in it. These

densities follow the form Eq. 48 with signal to noise

ratios ρ

and ρ

respectively. The probability den-

sity p(X) of Gaussian process can modeled as limit

of multivariate Gaussian distributions. The diver-

gence measures between these processes d(s

) are

in general functions of the correlator (s

−s

)

(Budzy

nski et al., 2008). Here we focus on distin-

guishing monochromatic signal s(t) = A cos(ωt + φ)

and ﬁlter s

(t) = A

cos(ω

t + φ) (both buried in

noise), separated in frequency or amplitude.

The Kullback-Leibler divergence between the sig-

nal and ﬁlter I(s,s

) is given by the correlation (s −

|s −s

I(s,s

) =(s −s

|s −s

) = (s|s) + (s

) −2(s|s

)

=ρ

+ ρ

−2ρρ

[hcos(∆ωt)icos(∆φ)

−hsin(∆ωt)isin(∆φ)], (50)

where hi is the average over observation time [0, T ].

Here we have assumed that noise spectral density

N( f ) = N

is constant over the frequencies [ω,ω

The SNRs are given by

, ρ

. (51)

(for detailed discussions we refer the reader to

Budzynksi et. al (Budzy

nski et al., 2008)).

The Bhattacharyya distance between Gaussian

processors with signals of same energy is ( Eq 14 in

(Kailath, 1967)) just a multiple of the KLD B = I/8.

We use this result to extract the Bhattacharyya coefﬁ-

cient :

ρ(s,s

) = exp



−

(s −s

|s −s

)



(52)

4.1.1 Frequency Difference

Let us consider the case when the SNRs of signal and

ﬁlter are equal, phase difference is zero, but frequen-

cies differ by ∆ω. The KL divergence is obtained by

A New Family of Bounded Divergence Measures and Application to Signal Detection

evaluating the correlator in Eq. 50

I(∆ω) = (s −s

|s −s

) = 2ρ



1 −

sin(∆ωT )

∆ωT



(53)

by noting hcos(∆ωt)i =

sin(∆ωT )

∆ωT

and hsin(∆ωt)i =

1−cos(∆ωT )

∆ωT

. Using this, the expression for BBD family

can be written as

(∆ω) =

log



1 −



1 −e

−



1−

sin(∆ωT )

∆ωT





log



1 −



(54)

As we have seen in section 3.4, both BBD and KLD

belong to the f-divergence family. Their curvature for

distributions belonging to same parametric family is a

constant times the Fisher information (FI) (see Theo-

rem: 3.5). Here we discuss where the BBD and KLD

deviates from FI, when we account for higher terms

in the expansion of these measures.

The Fisher matrix element for frequency g

ω,ω



∂logΛ

∂ω



= ρ

/3 (Budzy

nski et al., 2008),

where Λ is the likelihood ratio. Using the relation for

line element ds

∑

i, j

i j

dθ

and noting that only

frequency is varied, we get

ds =

ρT ∆ω

√

. (55)

Using the relation between curvature of BBD measure

and Fisher’s Information in Eq.34, we can see that for

low frequency differences the line element varies as:

(∆ω)

C(α)

∼ ds.

Similarly

√

∼ ds at low frequencies. However, at

higher frequencies both KLD and BBD deviate from

the Fisher information metric. In Fig. 2, we have plot-

ted ds,

√

and

(∆ω)/C(α) with α = 2 and

Hellinger distance (α → ∞) for ∆ω ∈(0, 0.1). We ob-

serve that till ∆ω = 0.01 (i.e. ∆ωT ∼ 1), KLD and

BBD follows Fisher Information and after that they

start to deviate. This suggests that Fisher Informa-

tion is not sensitive to large deviations. There is not

much difference between KLD, BBD and Hellinger

for large frequencies due to the correlator G becom-

ing essentially a constant over a wide range of fre-

quencies.

4.1.2 Amplitude Difference

We now consider the case where the frequency and

phase of the signal and the ﬁlter are same but they dif-

fer in amplitude ∆A (which reﬂects in differing SNR).

Figure 2: Comparison of Fisher Information, KLD, BBD

and Hellinger distance for two monochromatic signals dif-

fering by frequency ∆ω, buried in white noise. Inset shows

wider range ∆ω ∈ (0, 1) . We have set ρ = 1 and chosen

parameters T = 100 and N

= 10

Figure 3: Comparison of Fisher information line element

with KLD, BBD and Hellinger distance for signals differing

in amplitude and buried in white noise. We have set A = 1,

T = 100 and N

= 10

The correlation reduces to

(s −s

|s −s

) =

(A + ∆A)

−2

A(A + ∆A)T

(∆A)

. (56)

This gives us I(∆A) =

(∆A)

, which is the same

as the line element ds

with Fisher metric ds =

T /2N

∆A. In Fig. 3, we have plotted ds,

√

and

(∆ω)/C(α) for ∆A ∈ (0,40). KLD and FI

line element are the same. Deviations of BBD and

Hellinger can be observed only for ∆A > 10.

Discriminating between two signals s

requires

minimizing the error probability between them. By

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

Theorem 3.4, there exists priors for which the prob-

lem translates into maximizing the divergence for

BBD measures. For the monochromatic signals dis-

cussed above, the distance depends on parameters

(ρ

,ρ

,∆ω, ∆φ). We can maximize the distance for a

given frequency difference by differentiating with re-

spect to phase difference ∆φ (Budzy

nski et al., 2008).

In Fig. 4, we show the variation of maximized BBD

for different signal to noise ratios (ρ

,ρ

), for a ﬁxed

frequency difference ∆ω = 0.01. The intensity map

shows different bands which can be used for setting

the threshold for signal separation.

Detecting signal of known form involves minimiz-

ing the distance measure over the parameter space of

the signal. A threshold on the maximum “distance”

between the signal and ﬁlter can be put so that a detec-

tion is said to occur whenever the measures fall within

this threshold. Based on a series of tests, Receiver Op-

erating Characteristic (ROC) curves can be drawn to

study the effectiveness of the distance measure in sig-

nal detection. We leave such details for future work.

Figure 4: BBD with different signal to noise ratio for a

ﬁxed. We have set T = 100 and ∆ω = 0.01.

5 SUMMARY AND OUTLOOK

In this work we have introduced a new family of

bounded divergence measures based on the Bhat-

tacharyya distance, called bounded Bhattacharyya

distance measures. We have shown that it belongs

to the class of generalized f-divergences and inher-

its all its properties, such as those relating Fishers In-

formation and curvature metric. We have discussed

several special cases of our measure, in particular

squared Hellinger distance, and studied relation with

other measures such as Jensen-Shannon divergence.

We have also extended the Bradt Karlin theorem on

error probabilities to BBD measure. Tight bounds on

Bayes error probabilities can be put by using proper-

ties of Bhattacharyya coefﬁcient.

Although many bounded divergence measures

have been studied and used in various applications, no

single measure is useful in all types of problems stud-

ied. Here we have illustrated an application to signal

detection problem by considering “distance” between

monochromatic signal and ﬁlter buried in white Gaus-

sian noise with differing frequency or amplitude, and

comparing it to Fishers Information and Kullback-

Leibler divergence.

A detailed study with chirp like signal and colored

noise occurring in Gravitational wave detection will

be taken up in a future study. Although our measures

have a tunable parameter α, here we have focused on

a special case with α = 2. In many practical appli-

cations where extremum values are desired such as

minimal error, minimal false acceptance/rejection ra-

tio etc, exploring the BBD measure by varying α may

be desirable. Further, the utility of BBD measures is

to be explored in parameter estimation based on min-

imal disparity estimators and Divergence information

criterion in Bayesian model selection (Basu and Lind-

say, 1994). However, since the focus of the current

paper is introducing a new measure and studying its

basic properties, we leave such applications to statis-

tical inference and data processing to future studies.

ACKNOWLEDGEMENTS

One of us (S.J) thanks Rahul Kulkarni for insightful

discussions, Anand Sengupta for discussions on ap-

plication to signal detection, and acknowledge the ﬁ-

nancial support in part by grants DMR-0705152 and

DMR-1005417 from the US National Science Foun-

dation. M.S. would like to thank the Penn State Elec-

trical Engineering Department for support.

REFERENCES

Ali, S. M. and Silvey, S. D. (1966). A general class of co-

efﬁcients of divergence of one distribution from an-

other. Journal of the Royal Statistical Society. Series

B (Methodological), 28(1):131–142.

Basseville, M. (1989). Distance measures for signal pro-

cessing and pattern recognition. Signal processing,

18:349–369.

Basu, A. and Lindsay, B. G. (1994). Minimum disparity

estimation for continuous models: efﬁciency, distri-

butions and robustness. Annals of the Institute of Sta-

tistical Mathematics, 46(4):683–705.

Ben-Bassat, M. (1978). f-entropies, probability of er-

A New Family of Bounded Divergence Measures and Application to Signal Detection

ror, and feature selection. Information and Control,

39(3):227–242.

Bhattacharya, B. K. and Toussaint, G. T. (1982). An upper

bound on the probability of misclassiﬁcation in terms

of matusita’s measure of afﬁnity. Annals of the Insti-

tute of Statistical Mathematics, 34(1):161–165.

Bhattacharyya, A. (1943). On a measure of divergence

between two statistical populations deﬁned by their

probability distributions. Bull. Calcutta Math. Soc,

35(99-109):4.

Bhattacharyya, A. (1946). On a measure of divergence be-

tween two multinomial populations. Sankhy

a: The In-

dian Journal of Statistics (1933-1960), 7(4):401–406.

Blackwell, D. (1951). Comparison of experiments. In Sec-

ond Berkeley Symposium on Mathematical Statistics

and Probability, volume 1, pages 93–102.

Bradt, R. and Karlin, S. (1956). On the design and compar-

ison of certain dichotomous experiments. The Annals

of mathematical statistics, pages 390–409.

Brody, D. C. and Hughston, L. P. (1998). Statistical geom-

etry in quantum mechanics. Proceedings of the Royal

Society of London. Series A: Mathematical, Physical

and Engineering Sciences, 454(1977):2445–2475.

Budzy

nski, R. J., Kondracki, W., and Kr

olak, A. (2008).

Applications of distance between probability distribu-

tions to gravitational wave data analysis. Classical

and Quantum Gravity, 25(1):015005.

Burbea, J. and Rao, C. R. (1982). On the convexity of

some divergence measures based on entropy func-

tions. IEEE Transactions on Information Theory,

28(3):489 – 495.

Chernoff, H. (1952). A measure of asymptotic efﬁciency for

tests of a hypothesis based on the sum of observations.

The Annals of Mathematical Statistics, 23(4):pp. 493–

507.

Choi, E. and Lee, C. (2003). Feature extraction based

on the Bhattacharyya distance. Pattern Recognition,

36(8):1703–1709.

Csiszar, I. (1967). Information-type distance measures

and indirect observations. Stud. Sci. Math. Hungar,

2:299–318.

Csiszar, I. (1975). I-divergence geometry of probability dis-

tributions and minimization problems. The Annals of

Probability, 3(1):pp. 146–158.

DasGupta, A. (2011). Probability for Statistics and Ma-

chine Learning. Springer Texts in Statistics. Springer

New York.

Finn, L. S. (1992). Detection, measurement, and gravita-

tional radiation. Physical Review D, 46(12):5236.

Gibbs, A. and Su, F. (2002). On choosing and bounding

probability metrics. International Statistical Review,

70(3):419–435.

Hellinger, E. (1909). Neue begr

undung der theo-

rie quadratischer formen von unendlichvielen

ver

anderlichen. Journal f

ur die reine und angewandte

Mathematik (Crelle’s Journal), (136):210–271.

Hellman, M. E. and Raviv, J. (1970). Probability of Error,

Equivocation, and the Chernoff Bound. IEEE Trans-

actions on Information Theory, 16(4):368–372.

Jaranowski, P. and Kr

olak, A. (2007). Gravitational-wave

data analysis. formalism and sample applications: the

gaussian case. arXiv preprint arXiv:0711.1115.

Kadota, T. and Shepp, L. (1967). On the best ﬁnite set

of linear observables for discriminating two gaussian

signals. IEEE Transactions on Information Theory,

13(2):278–284.

Kailath, T. (1967). The Divergence and Bhattacharyya Dis-

tance Measures in Signal Selection. IEEE Transac-

tions on Communications, 15(1):52–60.

Kakutani, S. (1948). On equivalence of inﬁnite product

measures. The Annals of Mathematics, 49(1):214–

224.

Kapur, J. (1984). A comparative assessment of various mea-

sures of directed divergence. Advances in Manage-

ment Studies, 3(1):1–16.

Kullback, S. (1968). Information theory and statistics. New

York: Dover, 1968, 2nd ed., 1.

Kullback, S. and Leibler, R. A. (1951). On information

and sufﬁciency. The Annals of Mathematical Statis-

tics, 22(1):pp. 79–86.

Kumar, U., Kumar, V., and Kapur, J. N. (1986). Some

normalized measures of directed divergence. Inter-

national Journal of General Systems, 13(1):5–16.

Lamberti, P. W., Majtey, A. P., Borras, A., Casas, M., and

Plastino, A. (2008). Metric character of the quan-

tum Jensen-Shannon divergence . Physical Review A,

77:052311.

Lee, Y.-T. (1991). Information-theoretic distortion mea-

sures for speech recognition. Signal Processing, IEEE

Transactions on, 39(2):330–335.

Lin, J. (1991). Divergence measures based on the shannon

entropy. IEEE Transactions on Information Theory,

37(1):145 –151.

Matusita, K. (1967). On the notion of afﬁnity of several dis-

tributions and some of its applications. Annals of the

Institute of Statistical Mathematics, 19(1):181–192.

Maybank, S. J. (2004). Detection of image structures using

the ﬁsher information and the rao metric. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

26(12):1579–1589.

Nielsen, F. and Boltz, S. (2011). The burbea-rao and bhat-

tacharyya centroids. IEEE Transactions on Informa-

tion Theory, 57(8):5455–5466.

Nielsen, M. and Chuang, I. (2000). Quantum computation

and information. Cambridge University Press, Cam-

bridge, UK, 3(8):9.

Peter, A. and Rangarajan, A. (2006). Shape analysis using

the ﬁsher-rao riemannian metric: Unifying shape rep-

resentation and deformation. In Biomedical Imaging:

Nano to Macro, 2006. 3rd IEEE International Sympo-

sium on, pages 1164–1167. IEEE.

Poor, H. V. (1994). An introduction to signal detection and

estimation. Springer.

Qiao, Y. and Minematsu, N. (2010). A study on in-

variance of-divergence and its application to speech

recognition. Signal Processing, IEEE Transactions

on, 58(7):3884–3890.

Quevedo, H. (2008). Geometrothermodynamics of black

holes. General Relativity and Gravitation, 40(5):971–

984.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

Rao, C. (1982a). Diversity: Its measurement, decomposi-

tion, apportionment and analysis. Sankhya: The In-

dian Journal of Statistics, Series A, pages 1–22.

Rao, C. R. (1945). Information and the accuracy attainable

in the estimation of statistical parameters. Bull. Cal-

cutta Math. Soc., 37:81–91.

Rao, C. R. (1982b). Diversity and dissimilarity coefﬁcients:

A uniﬁed approach. Theoretical Population Biology,

21(1):24 – 43.

Rao, C. R. (1987). Differential metrics in probability

spaces. Differential geometry in statistical inference,

10:217–240.

Royden, H. (1986). Real analysis. Macmillan Publishing

Company, New York.

Sunmola, F. T. (2013). Optimising learning with trans-

ferable prior information. PhD thesis, University of

Birmingham.

Toussaint, G. T. (1974). Some properties of matusita’s mea-

sure of afﬁnity of several distributions. Annals of the

Institute of Statistical Mathematics, 26(1):389–394.

Toussaint, G. T. (1975). Sharper lower bounds for discrimi-

nation information in terms of variation (corresp.). In-

formation Theory, IEEE Transactions on, 21(1):99–

100.

Toussaint, G. T. (1977). An upper bound on the probability

of misclassiﬁcation in terms of the afﬁnity. Proceed-

ings of the IEEE, 65(2):275–276.

Toussaint, G. T. (1978). Probability of error, expected

divergence and the afﬁnity of several distributions.

IEEE Transactions on Systems, Man and Cybernetics,

8(6):482–485.

Tumer, K. and Ghosh, J. (1996). Estimating the Bayes

error rate through classiﬁer combining. Proceedings

of 13th International Conference on Pattern Recogni-

tion, pages 695–699.

Varshney, K. R. (2011). Bayes risk error is a bregman di-

vergence. IEEE Transactions on Signal Processing,

59(9):4470–4472.

Varshney, K. R. and Varshney, L. R. (2008). Quanti-

zation of prior probabilities for hypothesis testing.

IEEE TRANSACTIONS ON SIGNAL PROCESSING,

56(10):4553.

APPENDIX

BBD Measures of Some Common Distributions.

Here we provide explicit expressions for BBD B

, for

some common distributions. For brevity we denote

ζ ≡ B

• Binomial :

P(k) =





(1 − p)

n−k

, Q(k) =





(1 −q)

n−k

bin

(P,Q) = −log

1 + [

√

pq +

(1 − p)(1 −q)]

(57)

• Poisson :

P(k) =

−λ

, Q(k) =

−λ

poisson

(P,Q) = −log

1 + e

−(

√

−

√

)

(58)

• Gaussian :

P(x) =

√

2πσ

exp

−

(x −x

)

2σ

Q(x) =

√

2πσ

exp

−

(x −x

)

2σ

Gauss

(P,Q) = 1 −log

1 +

2σ

+ σ

exp

−

−x

)

4(σ

+ σ

)

(59)

• Exponential : P(x) = λ

−λ

, Q(x) = λ

−λ

exp

(P, Q) = −log

(

)

2(λ

+ λ

)

. (60)

• Pareto : Assuming the same cut off x

P(x) =

(

for x ≥ x

0 for x < x

(61)

Q(x) =

(

for x ≥ x

0 for x < x

(62)

pareto

(P, Q) = −log

(

√

)

2(α

+ α

)

. (63)

A New Family of Bounded Divergence Measures and Application to Signal Detection