
Extraction of Temporal Gait Parameters using a Reduced Number of
Wearable Accelerometers
Mohamed Boutaayamou
1,2
, Vincent Denoël
1
,
Olivier Brüls
1
, Marie Demonceau
3
, Didier Maquet
3
,
Bénédicte Forthomme
1
, Jean-Louis Croisier
1
, Cédric Schwartz
1
, Jacques G. Verly
2
and Gaëtan Garraux
4,5
1
Laboratory of Human Motion Analysis, University of Liège (ULg), Liège, Belgium
2
INTELSIG Laboratory, Department of Electrical Engineering and Computer Science, ULg, Liège, Belgium
3
Department of Rehabilitation and Movement Sciences, ULg, Liège, Belgium
4
Movere Group, Cyclotron Research Center, ULg, Liège, Belgium
5
Department of Neurology, University Hospital Center, Liège, Belgium
Keywords: Gait Analysis, Wearable Accelerometers, Wavelet Analysis, Validation, Gait Segmentation, Gait Events,
Heel-off, Heel Strike, Toe Strike, Toe-off, Heel Clearance, Stance Time, Swing Time, Stride Time.
Abstract: Wearable inertial systems often require many sensing units in order to reach an accurate extraction of
temporal gait parameters. Reconciling easy and fast handling in daily clinical use and accurate extraction of
a substantial number of relevant gait parameters is a challenge. This paper describes the implementation of a
new accelerometer-based method that accurately and precisely detects gait events/parameters from
acceleration signals measured from only two accelerometers attached on the heels of the subject’s usual
shoes. The first step of the proposed method uses a gait segmentation based on the continuous wavelet
transform (CWT) that provides only a rough estimation of motionless periods defining relevant local
acceleration signals. The second step uses the CWT and a novel piecewise-linear fitting technique to
accurately extract, from these local acceleration signals, gait events, each labelled as heel strike (HS), toe
strike (TS), heel-off (HO), toe-off (TO), or heel clearance (HC). A stride-by-stride validation of these
extracted gait events was carried out by comparing the results with reference data provided by a kinematic
3D analysis system (used as gold standard) and a video camera. The temporal accuracy ± precision of the
gait events were for HS: 7.2 ms ± 22.1 ms, TS: 0.7 ms ± 19.0 ms, HO: −3.4 ms ± 27.4 ms, TO:
2.2 ms ± 15.7 ms, and HC: 3.2 ms ± 17.9 ms. In addition, the occurrence times of right/left stance, swing,
and stride phases were estimated with a mean error of −6 ms ± 15 ms, −5 ms ± 17 ms, and −6 ms ± 17 ms,
respectively. The accuracy and precision achieved by the extraction algorithm for healthy subjects, the
simplification of the hardware (through the reduction of the number of accelerometer units required), and
the validation results obtained, convince us that the proposed accelerometer-based system could be extended
for assessing pathological gait (e.g., for patients with Parkinson’s disease).
1 INTRODUCTION
Wearable inertial systems have been proposed to
measure gait events and to estimate temporal gait
parameters (e.g., Willemsen et al. 1990; Aminian et
al., 1999; Selles et al., 2005; Lee et al. 2007;
Godfrey et al., 2008). Compared to conventional gait
analysis techniques, such as optoelectronic motion
capture systems and instrumented walkways, these
systems are not limited to controlled laboratory
environment; they can handle gait analysis in an
entirely natural setting with the possibility to obtain
gait parameters over longer walking distances (e.g.,
Khandelwal and Wickström 2014). The hardware
part of inertial systems, such as accelerometer units,
includes low-cost, small, and lightweight sensing
units with generally low power consumption (e.g.,
Stamatakis et al., 2011). With an appropriate
algorithm, these inertial systems are particularly
suitable for assessing gait in a clinical environment
(e.g., Salarian et al., 2004; Rueterbories et al., 2010).
Yet, these systems often need many sensing units
to achieve reasonable accuracy and precision in the
extraction of gait events/parameters. Arranging these
Boutaayamou, M., Denoël, V., Brüls, O., Demonceau, M., Maquet, D., Forthomme, B., Croisier, J-L., Schwartz, C., Ver ly, J. and Garraux, G.
Extraction of Temporal Gait Parameters using a Reduced Number of Wearable Accelerometers.
DOI: 10.5220/0005696900570066
In Proceedings of the 9th International Joint Conference on Biomedical Engineer ing Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 57-66
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
57

sensor units on lower limbs (e.g., feet) in a manner
that is acceptable for clinical gait analysis remains a
challenge.
We have previously developed and validated a
signal processing algorithm to automatically extract
gait events in healthy walking – labelled as heel
strike (HS), toe strike (TS), heel-off (HO), and toe-
off (TO) – from acceleration signals measured by
four accelerometer units attached to heels and toes
(Boutaayamou et al., 2015a). The algorithm
exploited distinctive and remarkable features in
these acceleration signals to identify and extract gait
events with good accuracy and precision.
In this paper, we present a new signal processing
algorithm that extracts the same gait events from
only two accelerometers, i.e., one on each shoe, at
the level of the heel. Our approach to the
aforementioned problem consists therefore in
reducing the number of accelerometer units by
eliminating the two units on the toes. We also extend
the previous algorithm to detect a new gait event,
i.e., the time of heel clearance (HC) which is an
important gait event that can refine the swing phase.
In addition, we consider the validation on a stride-
by-stride basis of the proposed algorithm on a group
of healthy people during normal walking. In this
validation, we compare the results (i.e., measured
gait events and calculated temporal gait parameters
of interest) to reference data provided by a kinematic
3D system (used as gold standard) and a video
camera.
2 METHOD
2.1 Wearable Accelerometer System
Acceleration signals during walking were recorded
by a wearable, wireless accelerometer-based
hardware system which includes several small three-
axis accelerometer units (2 cm x 1 cm x 0.5 cm), a
transmitter module, and a receiver module
(Stamatakis et al., 2011; Boutaayamou et al., 2015a)
(Figure 1). This system can measure accelerations
up to ±12 g (where g = 9.81 m/s² is value of the
gravitational acceleration) along its three sensitive
axes: x (horizontal), y (transverse), and z (vertical).
In this study, two accelerometer units were tightly
attached on the right and left feet, i.e., one on each
shoe at the level of the heel. The right and left
accelerometers were synchronized. Accelerometers
were connected to the transmitter module positioned
on the waist. The wires between accelerometers and
(a) (b)
Figure 1: (a) The wearable accelerometer-based hardware
system. (b) Schematic illustration of the placement of a
wearable accelerometer (either for right or left foot) and
the direction of axes.
the transmitter module were tightly strapped around
the legs so as to avoid disturbing the subject
movements. Acceleration signals were recorded at
200 Hz. All data were analyzed using Matlab 7.6.0
(MathWorks, Natick, MA, USA).
2.2 Subjects and Gait Tests Procedure
Gait signals were recorded during walking tests
performed by seven young and healthy subjects
without any previous injury of the lower limbs
((mean ± standard deviation) age = 27 ± 2.6 years;
height = 181 ± 7 cm; weight = 78 ± 9 kg). All of
them provided informed consent. The gait tests
procedure of this study is similar to the one reported
in (Boutaayamou et al., 2015a). Before we started
the measurements, subjects took sufficient time to
get used to the instrumentation tools and the
experimental procedure. During the tests, they were
asked to walk on a 12–m long track, at their
preferred, self-selected, usual speed. Each subject
performed several gait tests of 60 s. Subjects wore
their own regular shoes. All of the walking tests
were performed at the Laboratory of Human Motion
Analysis of the University of Liège, Belgium.
2.3 Wavelet Analysis: Segmentation of
Acceleration Signals
In the present study, we use a segmentation method
that we have previously developed (Boutaayamou et
al., 2015b) to identify gait patterns from only heel
acceleration signals, thereby reducing the number of
wearable accelerometers and allowing for a robust
extraction of the gait events/parameters (see Sec.
2.4). This segmentation method is based on the
continuous wavelet transform (CWT) to isolate (1)
time intervals where the heel acceleration is close to
zero, from (2) time intervals the accelerometers are
moving. The wavelet coefficient C(a,b) of the CWT
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
58
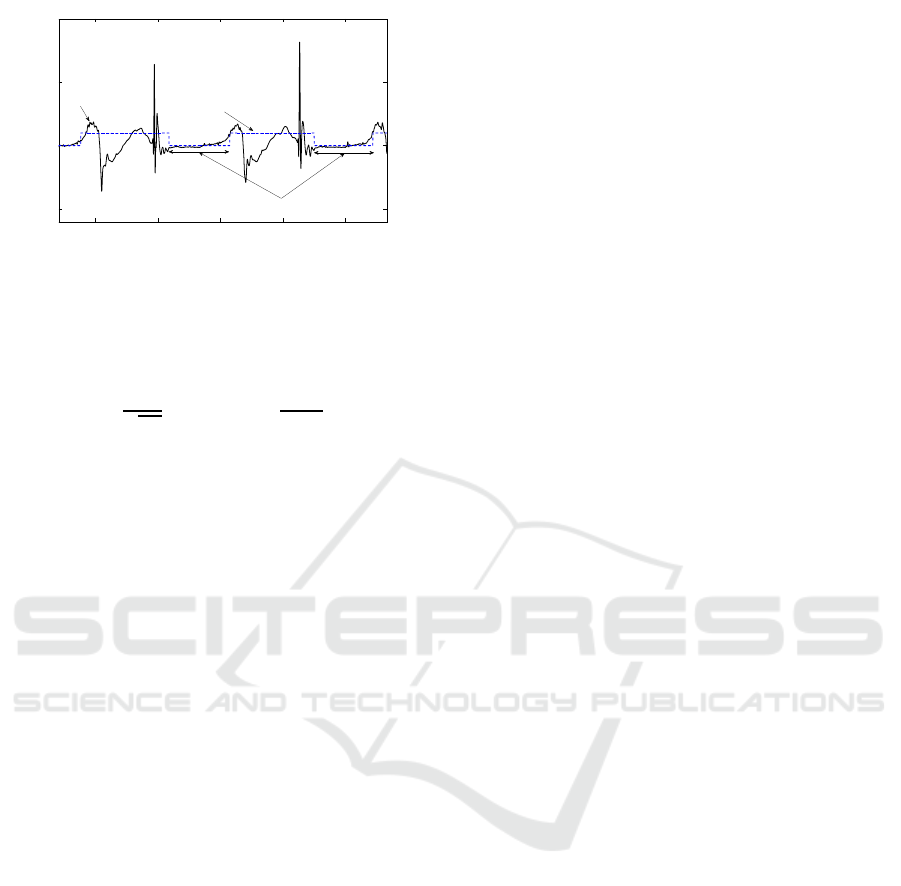
Figure 2: Rough estimation of heel flat/non-flat phases
using the gait segmentation based on the continuous
wavelet transform.
of a signal s(t) is defined as
(,)=
1
|
|
(
)
∗
−
,
(1)
where a (≠0) and b (∈ℝ) are the scale and location
parameters, respectively,
∗
is the complex
conjugate of the mother wavelet function , and t is
the time. Compressing a (small values of a) tracks
high frequencies changes whereas stretching a (large
values of a) tracks low frequencies. C(a,b) thus
measures the similarity between the signal s(t) and
the scaled and shifted versions of , with larger
values indicating higher similarity. The wavelet
(Mexican hat) is chosen here as the mother
wavelet .
The detailed description of the developed
segmentation method is not the focus of this study.
Rather, we consider the results of its application to
the vertical acceleration signal measured at the level
of the heel. We therefore obtain a “heel binary
function” that roughly estimate heel flat phases
(motionless periods) and heel non-flat phases. A
typical result of the binary function is shown in
Figure 2 (dashed lines). The segmentation method
has the advantage that it avoids to look directly for
specific gait events. The segmentation only
determine rough heel flat/non-flat phases in which
gait events of interest can be further extracted with
good accuracy.
2.4 New Signal Processing Algorithm
In order to estimate precisely gait parameters such as
the durations of the stance, swing, and stride phases
during a gait cycle (i.e., the duration of a stride), it is
necessary to detect, for each foot, the precise
moments of gait events of interest during the same
gait cycle. These gait events are characterized by
distinctive and remarkable features on heel
acceleration signals. Depending on the nature of
these features, a suitable method is employed in the
present study to accurately extract gait events. For
clarity, we consider only one foot. It is obvious that
the algorithm could be applied in the same way for
both feet.
Times of occurrence of HS
accel
, TS
accel
, HO
accel
,
TO
accel
, and HC
accel
are identified mainly from the
acceleration signals in sagittal plane, i.e., with
respect to the x-axis and z-axis accelerations denoted
by z
and x
, respectively. The subscripts accel, ref,
and h refer to our method, to the reference methods,
and to the heel, respectively.
2.4.1 Gait Events Identification
We now describe the main steps of the detection
following the chronological occurrence order of
healthy gait events (i.e., not the order that the
algorithm follows to extract these events).
a) The time of the heel strike event: HS
accel
In the present study, we adapt the method
described in (Boutaayamou et al., 2015a) to detect
HS
accel
as follows:
• At HS
accel
, the heel acceleration signal
is subject
to abrupt changes (Figure 3a). To detect HS
accel
,
we only consider the segment defined as the
second half of the heel non-flat phase. In this
segment, HS
accel
is identified using the magnitude
of z
filtered with a 4
th
-order zero-lag Butterworth
high-pass filter (cutoff frequency=10 Hz). HS
accel
is detected as the time of occurrence of the
maximum value of the magnitude of this filtered
(Figure 3a). As pointed out in (Boutaayamou et
al., 2015a), the determination of HS
accel
is robust
with respect to this filtering step, since HS
accel
occurs rapidly with a frequency larger than 10 Hz.
b) The time of the toe strike event: TS
accel
TS
accel
can be extracted from the heel
acceleration signal as the accelerometer is sensitive
enough to measure the acceleration movement of the
foot when the toe hits the ground. The main steps to
estimate TS
accel
are as follows:
• As TS
accel
occurs after HS
accel
and before HO
accel
,
we seek TS
accel
in the segment [HS
accel
, 0.4*HS
accel
+0.6* HO
accel
] (the procedure for extracting HO
accel
is explained in c)). TS
accel
is automatically detected
using x
and z
restricted to this segment. The
resulting local signals are then filtered with a 4
th
-
order zero-lag Butterworth low-pass filter (cutoff
frequency = 20 Hz), and integrated twice in order
to calculate their associated position signals. The
33.5 34 34.5 35 35.5
−5
0
5
10
Time [s]
Acceleration [g]
Heel flat phases
Heel binary function
˙z˙
h
Extraction of Temporal Gait Parameters using a Reduced Number of Wearable Accelerometers
59

drift related to this double integration is limited
since the latter is performed in a small time
interval. We then apply a piecewise-linear fitting
method to each of these position signals. This
method estimates a location of convex curvature in
a signal using two linear segment that best fit this
signal in the least-square sense (Appendix)
(Boutaayamou et al., 2015a). The times of
resulting convex curvatures in the two position
signals are denoted t
1
and t
2
. It is then assumed that
TS
accel
is estimated as the mean of t
1
and t
2
(Figure 3b).
c) The time of the heel-off event: HO
accel
HO
accel
is automatically detected in the segment
that lies between 125 ms after HS
accel
and 70 ms
before TO
accel
(the extraction method of TO
accel
is
described in d)). We adapt the method presented in
(Boutaayamou et al., 2015a) to detect HO
accel
from
z
as follows:
• We consider the local signal obtained from the
restriction of z
to the previous segment. This
local signal is then filtered with a 4
th
-order zero-
lag Butterworth low-pass filter (cutoff
frequency = 20 Hz). This filtering step does not
alter the physical significance of the local signal
(Boutaayamou et al., 2015a). Since this signal
corresponds to a slow movement (some
milliseconds before and after HO
accel
), there is no
critical peak to be detected that could be removed
erroneously in this filtering step (Boutaayamou et
al., 2015a). A double integration of this local
acceleration signal is then performed to calculate
the corresponding position signal. The drift that
could be generated from this double integration is
negligible since the latter is carried out in a small
time interval. We apply the aforementioned
piecewise-linear fitting method twice to the
resulting local position signal in order to estimate
successive locations of convex curvature in this
local position signal. The time of the last location
of convex curvature is our estimate of HO
accel
(Figure 3c).
d) The time of the toe-off event: TO
accel
• At TO
accel
, the direction of motion of the ankle
joint changes from plantarflexion to dorsiflexion in
the sagittal plane (Whittle, 1996). It is assumed
that TO
accel
corresponds to the time when a zero
crossing of the vertical heel acceleration signal
occurs after the beginning of the non-flat
phase (Figure 3d).
e) The time of the heel clearance event: HC
accel
• HC
accel
is defined as the moment when the
minimum clearance between the heel
accelerometer and the ground is achieved during
the swing phase. We consider distinctive vertical
heel acceleration features that indicate where
HC
accel
can be found in the time and frequency
domains. These features are rather sharp negative
peaks in z
(Figure 3e) involving some mid
frequencies. In order to extract HC
accel
, we apply
the CWT (see Sec. 2.3) to the local signal defined
as the restriction of z
to the neighbourhood of
these features. The CWT is indeed adapted for
identifying HC
accel
because it allows detection of a
specified frequency at a specified time. The
previous local signal is then decomposed into
wavelet packages. The wavelet (Mexican hat) is
used as the mother wavelet to extract HC
accel
as it
is similar to the pattern of the aforementioned
features. A typical result is depicted in Figure 3e.
2.4.2 Extraction of Temporal Gait
Parameters
Temporal gait parameters, such as durations of the
stance, swing, and stride phases, are calculated on
the basis of the previous gait events as follows:
• Right stance duration (time between right HS
(HS
right
) and right TO (TO
right
) during stride i)
Right stance = TO
right
( i ) – HS
right
( i ) .
• Left stance duration (time between left HS (HS
left
)
and left TO (TO
left
) during stride i)
Left stance = TO
left
( i ) – HS
left
( i ) .
• Right swing duration (time between HS
right
of
stride i+1 and TO
right
of stride i)
Right swing = HS
right
( i+1 ) – TO
right
( i ) .
• Left swing duration (time between HS
left
of
stride i+1 and TO
left
of stride i)
Left swing = HS
left
( i+1 ) – TO
left
( i ) .
• Right stride duration (time between two
consecutive right HSs)
Right stride = HS
right
( i+1 ) – HS
right
( i ) .
• Left stride duration (time between two consecutive
left HSs)
Left stride = HS
left
( i+1 ) – HS
left
( i ) .
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
60
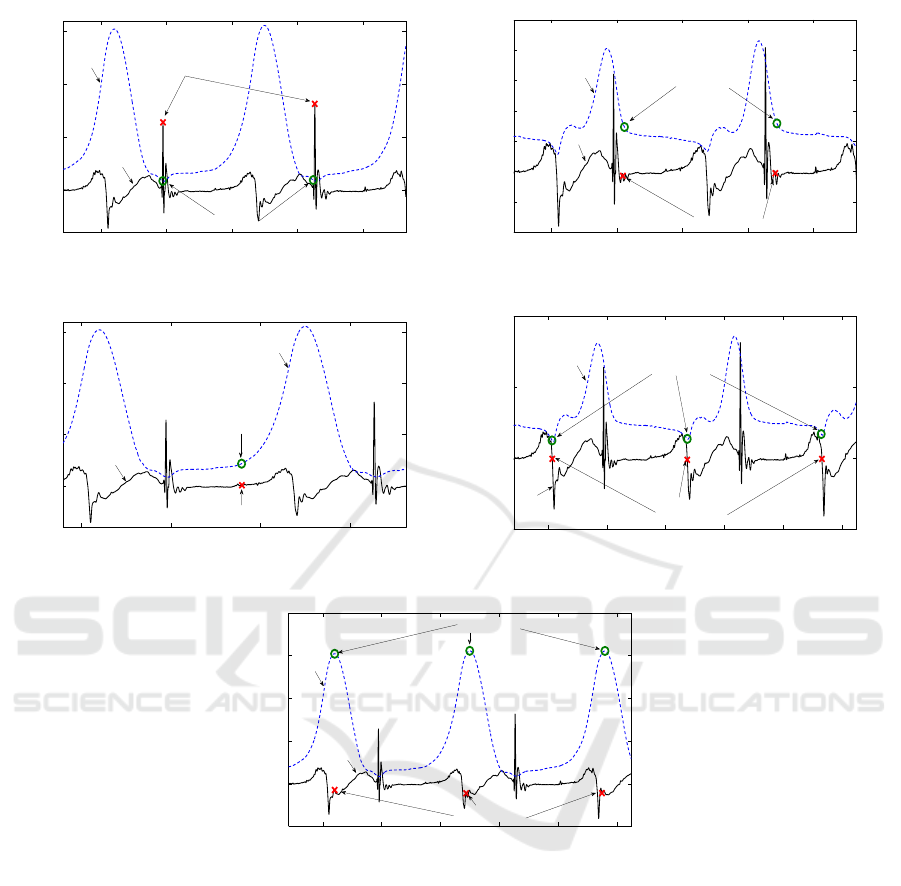
(a) (b)
(c) (d)
(e)
Figure 3: Vertical heel acceleration signal (i.e., z
measured by our accelerometer system) and reference kinematic signals
(i.e., the vertical heel position z
and the vertical toe position z
measured by the Codamotion system). The gait events, i.e.,
(a) HS, (b) TS, (c) HO, (d) TO, and (e) HC, detected by our method and by reference methods are shown on each signal
during typical consecutive strides.
2.5 Stride-by-stride Validation Method
2.5.1 Reference Data
A kinematic 3D analysis system (Codamotion
system; Charnwood Dynamics; Rothley, UK) and a
video camera provided reference data to validate, on
a stride-by-stride basis, the gait parameters/events
determined by our method.
The kinematic system is based on active optical
technology; it can accurately measure the 3D
positions of active markers placed in the body
locations of interest. We collected kinematic data at
the level of the heel and the toe of each foot at
400 Hz. The heel marker was placed upon the heel
accelerometer. The video camera (30 fps) was
placed close to the track such that the pointing
direction is approximately perpendicular to the
sagittal plan.
Kinematic data were used to validate, on a stride-
by-stride basis, the gait events HS
accel
,
TS
accel
,
33.5 34 34.5 35 35.5
0
5
10
15
Time [s]
Acceleration [g] − Position [x20 cm]
z
h
˙z˙
h
z
h
(HS
ref
)
˙z˙
h
(HS
accel
)
33.5 34 34.5 35 35.5
−4
−2
0
2
4
6
8
10
Time [s]
Acceleration [g] − Position [x20 cm]
z
t
˙z˙
h
z
t
(TS
ref
)
˙z˙
h
(TS
accel
)
33.5 34 34.5 35
0
5
10
15
Time [s]
Acceleration [g] − Position [x20 cm]
z
h
˙z˙
h
(HO
accel
)
z
h
(HO
ref
)
˙z˙
h
33.5 34 34.5 35 35.5 36
−5
0
5
10
Time [s]
Acceleration [g] − Position [x20 cm]
˙z˙
h
˙z˙
h
(TO
accel
)
z
t
(TO
ref
)
z
t
33.5 34 34.5 35 35.5 36
−5
0
5
10
15
20
Time [s]
Acceleration [g] − Position [x20 cm]
z
h
z
h
(HC
ref
)
˙z˙
h
(HC
accel
)
˙z˙
h
Extraction of Temporal Gait Parameters using a Reduced Number of Wearable Accelerometers
61
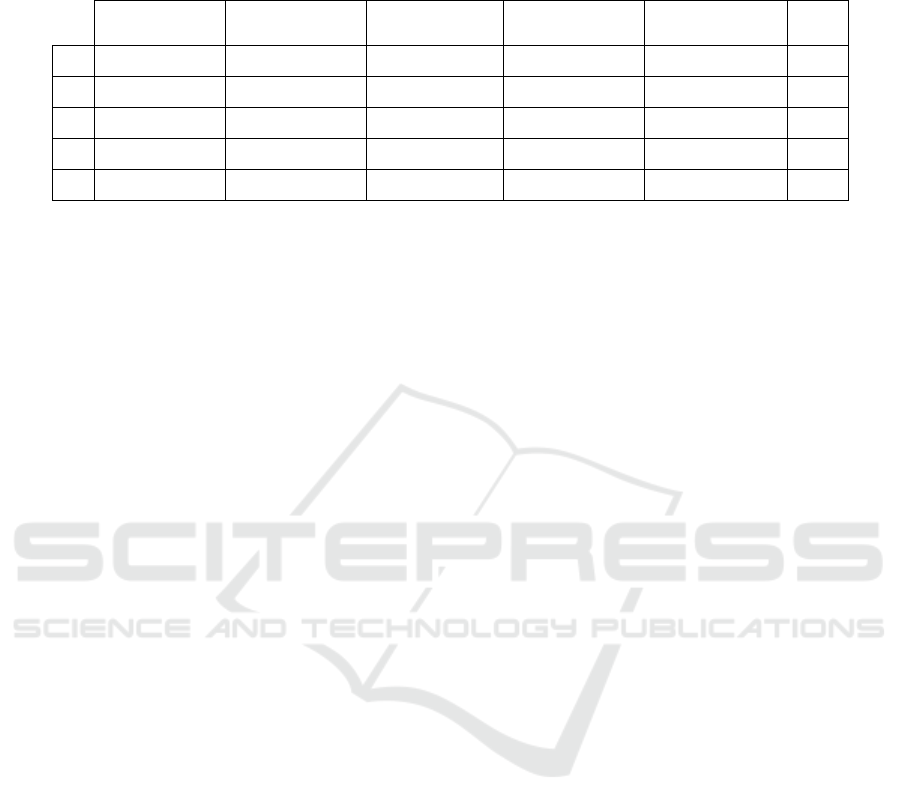
Table 1: The results of our method are compared to the results of reference methods considering several consecutive strides.
This evaluation is given as the accuracy (mean of the differences), the precision (std. dev. of the differences), limits of
agreement, 95% confidence interval (CI) of the differences, and 95% CI of the lower and upper limits of agreement.
Accuracy (ms)
(precision (ms))
Limits of
agreements (ms)
95% CI of the
differences (ms)
95% CI of the
lower limits (ms)
95% CI of the
upper limits (ms)
No. of
events
HS
7.2(22.1) −36.250.7] 5.6 8.8] −38.9 −33.5] 47.953.4]
771
TS
0.7(19.0)
−36.638.0] −0.9 2.3] −39.3 −33.9] 35.340.7] 567
HO
−3.4(27.4)
−57.250.3] −8.2 1.3] −66.5 −49.9] 43.159.7] 126
TO
2.2(15.7) −28.633.0] 1.1 3.3] −30.5 −26.8] 31.234.9]
819
HC
3.2(17.9)
−31.938.3] 1.9 4.4] −34.7 −30.5] 36.941.1] 839
TO
accel
,
and HC
accel
. Reference gait events HS
ref
and
TO
ref
, were obtained by the kinematic method
reported in (Boutaayamou et al., 2014). HS
ref
and
TO
ref
were extracted solely from measured heel and
toe coordinates during overground walking (Figures
3a and 3d). TS
ref
was extracted from the vertical toe
position signal (Boutaayamou et al., 2015a) in each
gait cycle (Figure 3b). HC
ref
was detected as the time
of the local maximum of heel clearance (Figure 3e).
The video camera provided HO
ref
.
2.5.2 Evaluation Method
We evaluated the level of agreement between our
method and the reference methods by quantifying
the accuracy, precision, absolute error, and intraclass
correlation coefficient (ICC). Accuracy and
precision were computed as the mean and standard
deviation (std. dev.), respectively, of the differences
between the gait events for each stride, i.e.,
HS
accel
– HS
ref
, TS
accel
– TS
ref
, HO
accel
– HO
ref
,
TO
accel
– TO
ref
, and HC
accel
– HC
ref
. The absolute
error was calculated as the mean and std. dev. of
absolute values of the previous differences. The ICC
evaluates the statistical agreement between our
method and the reference methods. A Bland-Altman
analysis was also carried out.
3 RESULTS
Table 1 provides a quantitative one-by-one
comparison of gait events. Because of the limited
number of extracted reference events and the
variation of some reference patterns among subjects,
the sample size for the compared gait events was not
always the same but ranged between 126 and 839
events. During some gait tests, we observed that
some markers – used to record reference kinematic
signals – detached from the shoes. We therefore
excluded the associated gait events from the
analysis. In addition, we emphasize that HO
ref
was
obtained only by the video camera. The extraction of
HO
ref
is thus limited to one stride during a given gait
test. The total number of HO
ref
(here 126) is
therefore much smaller than that of HS
ref
, TS
ref
,
TO
ref
, and HC
ref
. The four latter reference data were
indeed extracted from consecutive strides.
The accuracy and precision of gait events
detection ranged from −3.4 ms to 7.2 ms, and
15.7 ms to 27.4 ms, respectively. Given the
sampling frequency of 200 Hz of the recorded heel
accelerations for both feet, the accuracy and the
precision of detection are less than durations of 2
frames (10 ms) and 6 frames (30 ms), respectively.
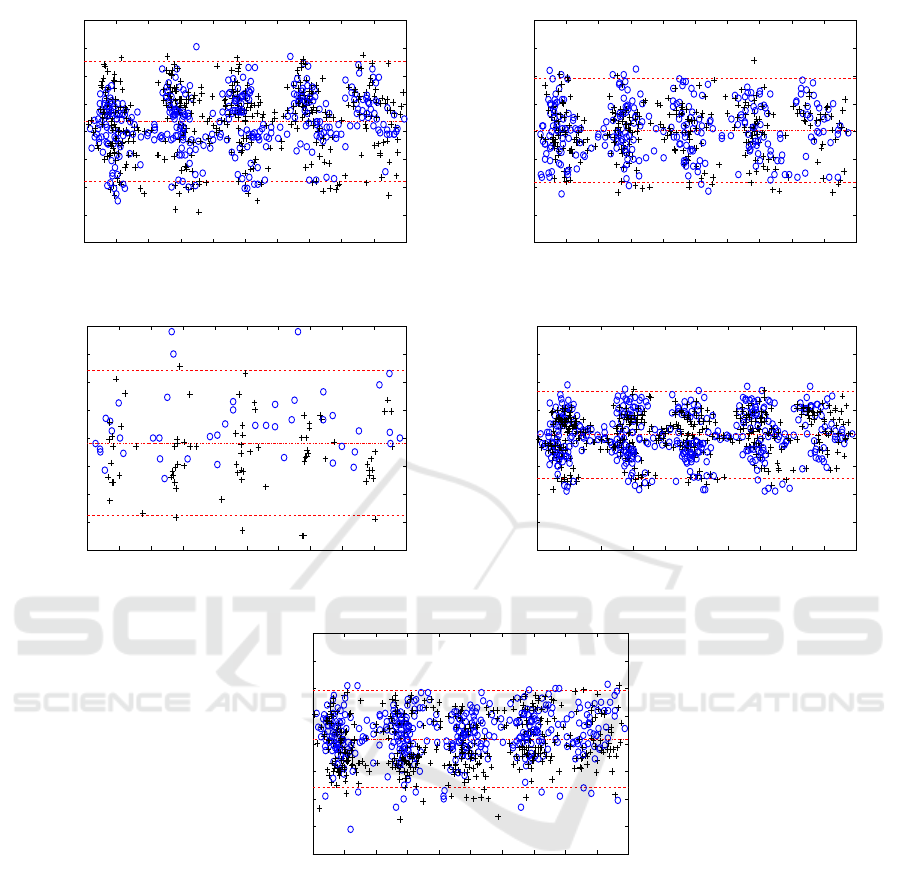
Figure 4 shows the Bland-Altman plots of gait
events differences. We observe small systematic
biases in accordance with the accuracy of detection
provided in Table 1. The proposed method tends to
detect earlier gait events except for HO. In addition,
the limits of agreement (i.e., mean ± 1.96 std. dev.)
and their associated 95% confidence interval exhibit
small variations in the times of gait events (Table 1).
Table 2 shows the results of durations of stance,
swing, and stride phases calculated by our method
and by the reference method (i.e., provided by the
Codamotion system) for the right and left feet. These
temporal parameters could be estimated with a mean
absolute error less than 15 ms. The ICC coefficient
was larger than 0.95 for both stance time and stride
time, and larger than 0.87 for swing time.
Figure 5 shows the Bland-Altman plots of the
temporal parameters for the right and left feet. Most
differences of these temporal parameters are within
the 1.96 std. dev. lines.
4 DISCUSSION
We have presented a new signal processing
algorithm that extracts relevant temporal gait
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
62
(a) (b)
(c) (d)
(e)
Figure 4: Bland−Altman plots of the gait events, i.e., (a) HS, (b) TS, (c) HO, (d) TO, and (e) HC, measured using our
method and reference methods, with mean (dash-dotted line in the middle) of differences HS
accel
– HS
ref
, TS
accel
– TS
ref
,
HO
accel
– HO
ref
, TO
accel
– TO
ref
, and HC
accel
– HC
ref
. 95% of these differences are between the lines ± 1.96 std. dev. (dashed
lines). (o) and (
+) refer to gait events measured at the right foot and those measured at the left foot, respectively.
parameters/events from only two accelerometers
attached to the right and left feet, i.e., one on each
shoe at the level of the heel.
The new algorithm is versatile enough to detect
gait events. The algorithm is based on the CWT and
an original piecewise-linear fitting method. Those
methods allow for an automatic and robust
extraction of gait events from relevant local
acceleration signals. The algorithm was validated by
comparing results obtained by our method to those
obtained by a kinematic 3D system (used as gold
standard) and a video camera. The experimental
results show a good agreement between our
algorithm and the reference, and demonstrate an
accurate and precise detection of HS, TS, HO, TO,
and HC in a group of healthy people during normal
walking. In addition, the algorithm computes the
time of stance, swing, and stride phases with a good
10 15 20 25 30 35 40 45 50 55 60
−80
−60
−40
−20
0
20
40
60
80
(
HS
accel
+HS
re
f
)/
2
[
s
]
HS
accel
−HS
ref
[ms]
10 15 20 25 30 35 40 45 50 55 60
−80
−60
−40
−20
0
20
40
60
80
(TS
accel
+TS
re
f
)/2[s]
TS
accel
−TS
ref
[ms]
10 15 20 25 30 35 40 45 50 55 60
−80
−60
−40
−20
0
20
40
60
80
(HO
accel
+HO
re
f
)/2[s]
HO
accel
−HO
ref
[ms]
10 15 20 25 30 35 40 45 50 55 60
−80
−60
−40
−20
0
20
40
60
80
(TO
accel
+TO
re
f
)/2[s]
TO
accel
−TO
ref
[ms]
10 15 20 25 30 35 40 45 50 55 60
−80
−60
−40
−20
0
20
40
60
80
(HC
accel
+HC
re
f
)/2[s]
HC
accel
−HC
ref
[ms]
Extraction of Temporal Gait Parameters using a Reduced Number of Wearable Accelerometers
63
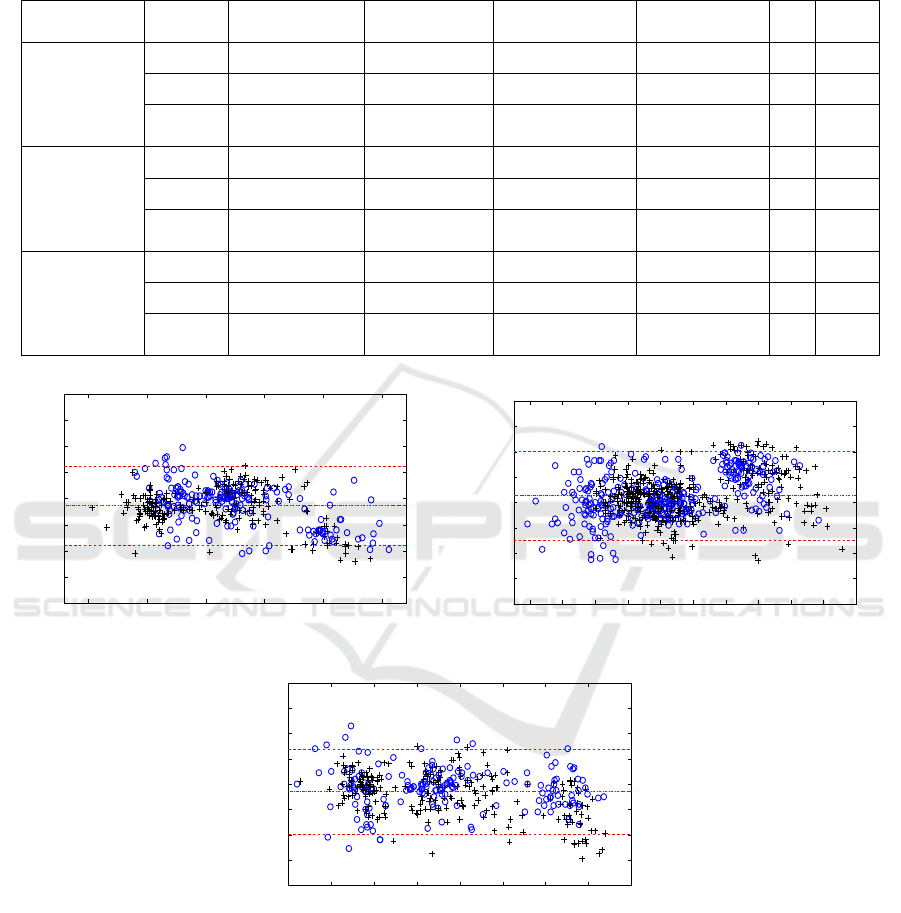
Table 2: Results of right/left stance, swing, and stride phase durations calculated by our method are compared to those
obtained by a reference kinematic system, Codamotion, used as gold standard. This comparison is given as the difference of
the estimated values (mean error), the mean of the absolute error (abs. error), and the intraclass correlation
coefficient (ICC).
Gait
parameters
Foot Accelerometers Codamotion Mean error Abs. error ICC No. of
strides
Stance time (s)
Right
0.6700.047 0.674 0.055 −0.0040.016 0.0120.011
0.95 188
Left
0.6560.052 0.662 0.055 −0.0060.015 0.0120.010
0.95 220
Right
and left
0.6620.050 0.668 0.055 −0.0060.015 0.0120.010
0.95 408
Swing time (s)
Right
0.4040.042 0.399 0.035 0.0050.018 0.0140.012
0.89 336
Left
0.4180.038 0.413 0.035 0.0050.018 0.0140.011
0.87 383
Right
and left
0.4120.041 0.407 0.035 −0.0050.017 0.0140.011
0.88 719
Stride time (s)
Right
1.0800.092 1.083 0.092 −0.0030.016 0.0120.011
0.98 181
Left
1.0810.090 1.089 0.098 −0.0080.018 0.0150.013
0.98 227
Right
and left
1.0800.090 1.087 0.095 −0.0060.017 0.0130.012
0.98 408
(a) (b)
(c)
Figure 5: Bland−Altman plots of the temporal gait parameters, i.e., (a) stance time, (b) swing time, and (c) stride time
estimated during consecutive strides by our method and the gold standard method. (o) and (
+
) refer to right and left gait
parameters, respectively.
accuracy and precision.
Previous studies reported results of gait
parameters during the normal walk. Compared to
stance time calculated in (Selles et al., 2005) (i.e.,
15 ms ± 41 ms), in (Rampp et al., 2015) (i.e.,
9 ms ± 69 ms), and in (Salarian et al., 2004) (i.e.,
5.9 ms ± 29.6 ms), the accuracy is similar but the
precision is improved in our method (i.e.,
−6 ms ±15 ms). Similar accuracy and better
precision in stride time are also found in our method
0.55 0.6 0.65 0.7 0.75 0.8
−80
−60
−40
−20
0
20
40
60
80
(Stance time
accel
+Stance time
ref
)/2[s]
Stance time
accel
−Stance time
ref
[ms]
0.32 0.34 0.36 0.38 0.4 0.42 0.44 0.46 0.48 0.5 0.52
−80
−60
−40
−20
0
20
40
60
80
(Swing time
accel
+Swing time
ref
)/2[s]
Swing time
accel
−Swing time
ref
[ms]
0.9 0.95 1 1.05 1.1 1.15 1.2 1.25 1.3
−80
−60
−40
−20
0
20
40
60
80
(Stride time
accel
+Stride time
ref
)/2[s]
Stride time
accel
−Stride time
ref
[ms]
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
64

(i.e., −6 ms ± 17 ms) compared to (Rampp et al.,
2015) (i.e., 2 ms ± 68 ms) and to (Salarian et al.,
2004) (i.e., 2.2 ms ± 23.2 ms). In addition, the
accuracy of swing time in (Rampp et al., 2015) (i.e.,
−8 ms ± 45 ms) is similar to our results but the
precision is improved in our method (i.e.,
−5 ms ±17 ms). Compared to commercial trunk
accelerometer systems (e.g., (Auvinet et al., 1999)),
which only provide global gait features, our system
is capable to extract stride-by-stride parameters. The
stride-by-stride extraction may be a huge advantage
in the gait analysis of some specific population such
as Parkinson’s disease patients who experience
freezing of gait, a sudden and brief episodic
alteration of strides regulation.
Participants did not complain about the hardware
system during the gait tests. They all reported that
wires and accelerometers did not interfere with their
gait. Since only two accelerometers were attached to
heels and wires were behind the legs of the
participants during walking, these participants did
not notice or complain about the system.
It is noteworthy that all accelerometers of the
used hardware system were synchronized. The
algorithm can thus extract other important gait
parameters such as the times of initial double
support, terminal double support, double support,
and right/left steps.
Based on TS and HO, the algorithm can extract
the durations of the sub-phases of the stance phase,
namely: (1) loading response duration (time from
HS of one foot to TS of the same foot); (2) foot-flat
duration (time from TS of one foot to HO of the
same foot); and (3) push-off duration (time from HO
of one foot to TO of the same foot). In addition, HC
can be used to refine the swing phase duration.
The proposed ambulatory accelerometer system
was capable of measuring temporal gait parameters
in a very large number of strides without the need of
controlled laboratory conditions. We believe that our
novel accelerometer-based system offers
perspectives for use in a routine clinical practice to
deal with abnormal gait (e.g., gait of patients with
Parkinson’s disease).
5 CONCLUSIONS
We presented a new signal processing algorithm that
reduces the number of wearable accelerometers for
estimating temporal gait parameters. The advantages
of this method can be summarized as follows:
• Only two accelerometers are required, i.e., one for
each shoe at the level of the heel. This contributes
to a simplification of our wearable accelerometer-
based system, thus resulting in reducing the costs
and time needed to attach the system on body.
• This algorithm is validated for consecutive strides
during normal walking. The validation used
reference data provided by a kinematic system
(used as gold standard) and a video camera.
• Compared to previous studies, the proposed
method performs equally well or better in terms of
accuracy and precision of detection of temporal
gait parameters such as times of swing, stance, and
stride phases.
The extension of this method to the study of
pathological gait (e.g., gait of patients with
Parkinson’s disease) is now in progress. The method
promises to allow an objective quantification of gait
parameters in routine clinical practice.
ACKNOWLEDGEMENTS
The authors wish to acknowledge the contribution of
J. Stamatakis and B. Macq through the design of the
accelerometer-based hardware system used in the
present study. The authors would like also to thank
all the participants to the gait tests of this study.
REFERENCES
Aminian, K., Rezakhanlou, K., De Andres, E., Fritsch, C.,
Leyvraz, P.-F., and Robert, P. (1999). Temporal
feature estimation during walking using miniature
accelerometers: an analysis of gait improvement after
hip arthroplasty. Medical and Biological Engineering
and computing, 37(6):686–691.
Auvinet, B., Chaleil, D., and Barrey, E. (1999). Analyse
de la marche humaine dans la pratique hospitalière par
une méthode accélérométrique. Revue du Rhumatisme,
66(7–9) :447–457.
Boutaayamou, M., Schwartz, C., Denoël, V., Forthomme,
B., Croisier, J.-L., Garraux, G., Verly, J., and Brüls,
O. (2014). Development and validation of a 3D
kinematic-based method for determining gait events
during overground walking. In IEEE International
Conference on 3D Imaging, pages 1–6.
Boutaayamou, M., Schwartz, C., Stamatakis, J., Denoël,
V., Maquet, D., Forthomme, B., Croisier, J.-L., Macq,
B., Verly, J., Garraux, G., and Brüls, O. (2015a).
Development and validation of an accelerometer-
based method for quantifying gait events. Medical
Engineering and Physics, 37:226–232.
Boutaayamou, M., Denoël, V., Verly, J., Garraux, G., and
Brüls, O. (2015b). Gait segmentation using continuous
wavelet transform for extracting validated gait events
from accelerometer signals. In Biomedica 2015–The
Extraction of Temporal Gait Parameters using a Reduced Number of Wearable Accelerometers
65

European Life Sciences Summit.
Godfrey, A., Conway, R., Meagher, D., and ÓLaighin, G.
(2008). Direct measurement of human movement by
accelerometry. Medical Engineering and Physics,
30(10):1364–1386.
Forsman, P. M., Toppila, E. M., and Hæggström, E. O.
(2009). Wavelet analysis to detect gait events. In IEEE
EMBC, pages 424–427.
Khandelwal, S., and Wickström, N. (2014). Identification
of gait events using expert knowledge and continuous
wavelet transform analysis. In Proceedings of the
International Conference on Bio-inspired Systems and
Signal Processing, pages 197–204.
Lee, J.-.A., Cho S.-H., Lee J.-W., Lee K.-H., and Yang H.-
K. (2007). Wearable accelerometer system for
measuring the temporal parameters of gait. In
Proceedings of the 29th Annual International
Conference of the IEEE EMBS, pages 23-26.
Rampp, A., Barth, J., Schülein, S., Gaßmann, K.-G.,
Klucken, J., and Eskofier, B. M. (2015). Inertial
sensor-based stride parameter calculation from gait
sequences in geriatric patients. IEEE Transactions on
Biomedical Engineering, 62(4):1089–1097.
Rueterbories, J., Spaich., E.G., Larsen, B., and Andersen
O.K. (2010). Methods for gait event detection and
analysis in ambulatory systems. Medical Engineering
and Physics, 32(6):545–552.
Salarian, A., Russmann, H., Vingerhoets, F.J.G.,
Dehollain, C., Blanc, Y., Burkhard P.R., and Aminian,
K. (2004). Gait assessment in Parkinson’s disease:
toward an ambulatory system for long-term
monitoring. IEEE Transactions on Biomedical
Engineering, 51(8):1434–1443.
Selles, R.W., Formanoy, M.A.G., Bussmann, J.B.J.,
Janssens, P.J., and Stam, H.J. (2005). Automated
estimation of initial and terminal contact timing using
accelerometers; development and validation in
transtibial amputees and controls. IEEE Transactions
on Neural Systems and Rehabilitation Engineering,
13(1):81–88.
Stamatakis, J., Crémers, J., Maquet, D., Macq, B., and
Garraux, G. (2011). Gait feature extraction in
Parkinson’s disease using low-cost accelerometers. In
Proceedings of the Annual International Conference
of the IEEE Engineering in Medicine and Biology
Society, pages 7900–7903.
Whittle, W. (1996). Clinical gait analysis: a review.
Human Movement Science, 15:369–387.
Willemsen, A.T.M., Bloemhof, F., and Boom, H.B.
(1990). Automatic stance-swing, phase detection from
accelerometer data for peroneal nerve stimulation.
IEEE Transactions on Biomedical Engineering,
37(12):1201–8.
APPENDIX
We present the piecewise-linear fitting method used
to estimate the locations of the convex curvature in a
signal (Sec. 2.4.1). For this, we consider a given
signal =
(
)
,(
),…, (
) defined
in a time interval=
,
,…,
, where is the
total number of samples of . This method first
computes the coefficients of piecewise-linear
functions with two linear segments that best fit
in the least-square sense, leading to the computation
of least-square errors. The minimum of these least-
square errors is then determined and the associated
piecewise-linear function provides two linear
segments that intersect at the breakpoint
(
,(
)
)
. The main steps to determine the
breakpoint
(
,(
)
)
are as follows:
• For each =1,…,, one computes the
coefficients
,
,
,and
of a piecewise-linear
function
that best fits by minimizing
=((
)
−
(
))²,
(2)
where
()=
∗+
,∈
,
],
∗+
,∈
]
,
]
.
(3)
This error can be expressed as
=
‖
−
‖
,
(4)
where
=
,
=
⋮
1
⋮
1
,
=
(
)
⋮
(
)
i
f
∈
,
],
and
=
,
=
⋮
1
⋮
1
,
=
(
)
⋮
(
)
i
f
∈
]
,
]
.
The normal equations associated with (4) are
=
.
(5)
Solving (5) leads to the coefficients
,
,
,and
.
• Finally, one obtains the breakpoint
(
,(
)
)
by determining the minimum of the
least-square errors, i.e.,
=
,…,
(
)
.
(6)
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
66
