A Mutual Inﬂuence-based Learning Algorithm

Stefan Rudolph, Sven Tomforde and J

org H

ahner

Organic Computing Group, University of Augsburg, Eichleitnerstr. 30, 86159, Augsburg, Germany

Keywords:

Mutual Inﬂuence, Q-Learning, Distributed W-Learning, Smart Cameras, Adaptive Control.

Abstract:

Robust and optimized agent behavior can be achieved by allowing for learning mechanisms within the un-

derlying adaptive control strategies. Therefore, a classic feedback loop concept is used that chooses the best

action for an observed situation – and learns the success by analyzing the achieved performance. This typi-

cally reﬂects only the local scope of an agent and neglects the existence of other agents with impact on the

reward calculation. However, there are signiﬁcant mutual inﬂuences among agents population. For instance,

the success of a Smart Camera’s control strategy depends (in terms of person detection or 3D-reconstruction)

largely on the current strategy performed by its spatially neighbors. In this paper, we compare two concepts to

consider such inﬂuences within the adaptive control strategy: Distributed W-Learning and Q-Learning in com-

bination with mutual inﬂuence detection. We demonstrate that the performance can be improved signiﬁcantly,

if taking detected inﬂuences into account.

1 INTRODUCTION

In order to cope with dynamic and potentially un-

known conditions, the control of agent behavior is

typically equipped with learning capabilities. This

has been shown to result in more robust and self-

optimizing behavior (Panait and Luke, 2005). In most

cases, the learning concept relies on a local ﬁtness

measurement. This means that each agent can judge

how good or bad its own performance is by measur-

ing the state of its environment, and without taking

global knowledge into account. The problem with this

concept is that it assumes a direct effect of actions to

performance and neglects signiﬁcant other inﬂuences.

The most important inﬂuence might come from other

neighbored agents – measuring the current state of the

environmental conditions might be a result of others’

action.

Consider a Smart Camera (SC) Network (Valera

and Velastin, 2005; Rinner et al., 2008) as exam-

ple: Each SC can adapt its behavior in terms of pan,

tilt, and zoom. The adaptive control mechanism has

to cover different tasks, ranging from person detec-

tion to tracking throughout the network and to 3D-

reconstruction of suspicious persons. Obviously, the

current strategy of its neighbors in close spatial vicin-

ity has signiﬁcant inﬂuence on the success: (a) if it

observes the same area, the person detection is less

successful since one of both SCs does not report a

novel detection event, and (b) if it does not share the

same ﬁeld of view, a 3D-reconstruction is not possi-

ble.

Within this paper, we discuss our approach to

explicitly detect such mutual inﬂuences by identify-

ing correlations between the neighbors’ conﬁguration

and the own performance. This information is then

included in the situation description of the learning

mechanism which is responsible for deciding about

the current conﬁguration. The basic idea is here that

as soon as inﬂuences are detected, the system should

be able to learn how to take this information into

account – without manually implementing a counter

strategy.

The remainder of this paper is organized as fol-

lows: Section 2 describes the methodological basis

by explaining our system model, the approach to de-

tect mutual inﬂuences among distributed agents, and

a brief introduction of the utilized learning algorithm.

Afterwards, Section 3 evaluates the approach in com-

parison to the state-of-the-art, where inﬂuences are

learned implicitly within the learning algorithm. This

is done based on a simulation of a Smart Camera

Network, where mutual inﬂuences within the con-

trol strategies can be observed. Section 4 gives an

overview of the state-of-the-art. Finally, Section 5

summarizes the paper and gives an outlook to future

work.

Rudolph, S., Tomforde, S. and Hähner, J.

A Mutual Inﬂuence-based Learning Algorithm.

DOI: 10.5220/0005697001810189

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 1, pages 181-189

ISBN: 978-989-758-172-4

181

2 METHOD

In this section, we introduce the mutual inﬂuences de-

tection and how it can be used to design more efﬁcient

learning algorithms. This is structured as follows. In

Section 2.1, we give an introduction to the notion of

mutual inﬂuence, and the applied detection method.

Afterwards, Section 2.2 explains how the mutual in-

ﬂuence information can be exploited in a learning al-

gorithm.

2.1 Mutual Inﬂuence

As brieﬂy scratched in the previous section, we want

to utilize a mutual inﬂuence detection algorithm in or-

der to improve the efﬁciency of learning algorithms.

In order to deﬁne what is meant with this brief de-

scription of mutual inﬂuence, this section outlines our

utilized system model which is inspired from stan-

dard machine learning notions. Despite the back-

ground in machine learning, the methodology is as-

sumed to be applicable to all systems covering the ba-

sic system model. Afterwards, we continue this sec-

tion with the presentation of the mutual inﬂuence de-

tection algorithm. The method of the measurement

of mutual inﬂuences has originally been proposed in

(Rudolph et al., 2015a), therefore, we keep the de-

scription rather short in this work.

2.1.1 System Model

We start with a set of agents {A

, . . . , A

}, where

each agent can assume different conﬁgurations. Such

a conﬁguration typically consists of different parts.

Consider a router as a simple example: The router

can take varying conﬁgurations into account, such as

the processed network protocol or parameter settings

(i.e. for time-out intervals, buffer sizes, etc.). We de-

ﬁne the whole conﬁguration space of an agent A

cartesian product C

= c

× ··· × c

, where c

i j

are

the parts of the conﬁguration. A further assumption is

that the particular conﬁgurations of individual agents

are non-overlapping, meaning each agent has its own

set of conﬁgurations, c

i j

6= c

for all deﬁned i 6= k, j, l.

This does not mean that the conﬁguration parts have

to be completely disjoint in structure and values of the

contained variables. For instance, two routers might

have the possibility to conﬁgure the time-out interval,

which would lead to the same set of possible conﬁg-

urations in these attributes, but on different devices.

Such a relation is explicitly allowed within the model.

Besides the conﬁguration space, we need to consider a

further element: the local performance measurement.

In order to apply the proposed method, each agent has

to estimate the success of its decisions at runtime –

as a response to actions taken before. This is real-

ized based on a feedback mechanism – with feedback

possibly stemming from the environment of the agent

(i.e. direct feedback) or from manual assignments (i.e.

indirect feedback). This resembles the classic rein-

forcement model, where the existence of such a per-

formance measurement (mostly called reward) is one

of the basic assumptions, cf., e.g., (Wiering and van

Otterlo, 2012).

2.1.2 Measurement

Given the described system model, we continue with

the actual methodology for the measurement of mu-

tual inﬂuences. The goal is to identify those parts

of the conﬁguration of the neighboring agents that

have inﬂuence on the agent itself. Thereby, we focus

on spatially neighbored agents (such as the cameras

in the motivating example) – but the methodology is

not restricted to this kind of neighborhood (i.e., “vir-

tual neighborhoods” are also possible – for instance,

routers in a data communication network). After the

identiﬁcation of inﬂuencing conﬁguration parts, they

can be addressed by a designer or by a self-adapting

system itself.

In general, we are typically not interested in the ques-

tion if an agent as a whole is inﬂuencing (some of)

its neighbors, since the beneﬁt of this information is

negligible. In contrast, we want to detect speciﬁc

conﬁguration parameters whose optimal usage strat-

egy is somehow inﬂuenced by the current settings of

the neighbored agents. The basic idea of the algo-

rithm is to make use of stochastic dependency mea-

sures that estimate associations and relations between

the conﬁguration parts of an agent and the perfor-

mance of a second agent. These dependency mea-

sures are designed to ﬁnd correlations between two

random variables X and Y . As suggested in (Rudolph

et al., 2015a), we use the Maximal Information Coefﬁ-

cient (MIC – (Reshef et al., 2011), see next subsection

for details).

If using only dependency measures, the proposed

method does not completely tackle the previously in-

troduced notion of mutual inﬂuence. This method

alone has some issues since the conﬁguration of the

agent itself is not taken into account. We explain this

problem and present a solution to resolve this issue in

Section 2.1.4.

2.1.3 Maximal Information Coefﬁcient

The Maximal Information Coefﬁcient (MIC) is a mea-

sure of dependence between two real valued random

variables. It has been introduced by Reshef et al.

(2011) and is based on the Mutual Information that

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

182

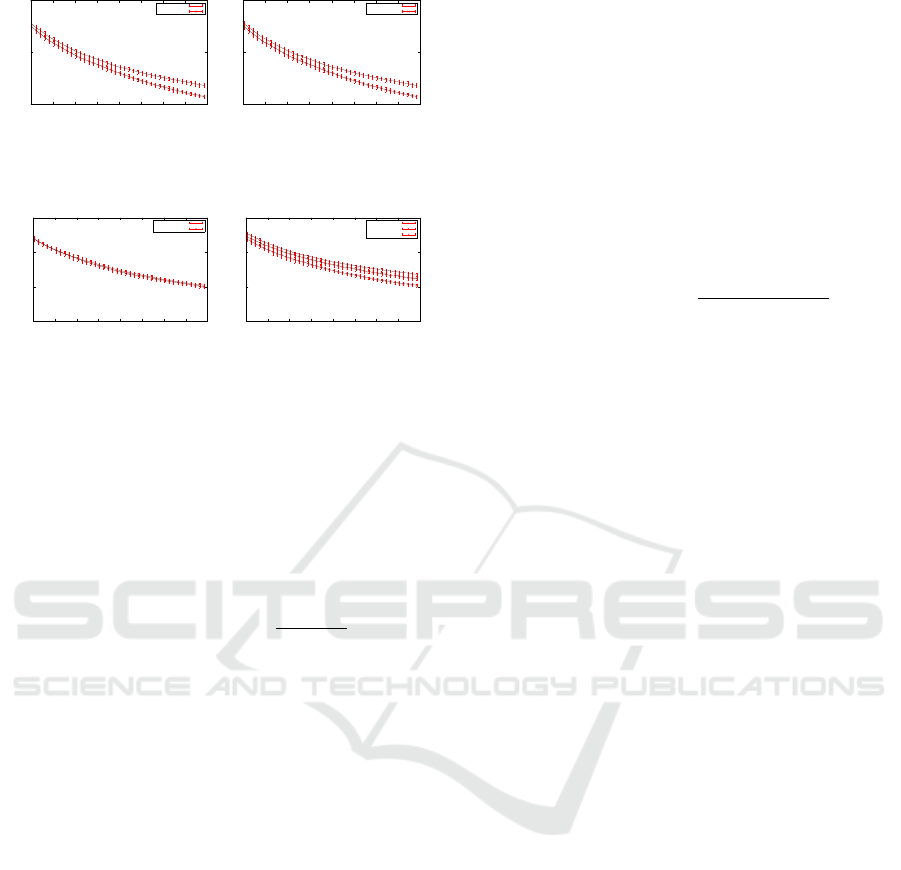
0.125

0.25

0.5

10000 15000 20000 25000 30000 35000 40000 45000 50000

Influence

Steps

Pan Camera 1

Pan Camera 2

(a) The inﬂuence of the

pan of Camera 1 and 2 on

Camera 0.

0.125

0.25

0.5

10000 15000 20000 25000 30000 35000 40000 45000 50000

Influence

Steps

Tilt Camera 1

Tilt Camera 2

(b) The inﬂuence of the

tilt of Camera 1 and 2 on

Camera 0.

0.0625

0.125

0.25

0.5

10000 15000 20000 25000 30000 35000 40000 45000 50000

Influence

Steps

Zoom Camera 1

Zoom Camera 2

zoom of Camera 1 and 2

on Camera 0.

0.0625

0.125

0.25

0.5

10000 15000 20000 25000 30000 35000 40000 45000 50000

Influence

Steps

Pan Camera 1

Tilt Camera 1

Zoom Camera 1

(d) The inﬂuences of the

pan, tilt and zoom of Cam-

era 1 on Cam 0.

Figure 1: The results of the inﬂuence measurement based

on 20 independent runs. The graphs show the Inﬂuence of

the different conﬁguration parts on Camera 0.

goes back to Shannon and Weaver (1949). Therefore,

we start with a short introduction of the Mutual Infor-

mation and then present the MIC in detail.

The mutual information is deﬁned as:

I(X;Y ) =

∑

x∈X

∑

y∈Y

p(x, y) log



p(x, y)

p(x)p(y)



, (1)

where p(x, y) is the joint probability distribution of

the discrete random variables X and Y variables.

In addition, p(x) and p(y) are the corresponding

marginal distributions. The measure quantiﬁes how

much information about X can be retrieved from the

realization of Y and vice versa. The mutual informa-

tion gives values ≥ 0 and only equals to zero if the two

random variables are stochastically completely inde-

pendent. An important advantage of this technique

compared to other measures, such as, Pearson Corre-

lation Coefﬁcient (Pearson, 1895) or Kendall tau rank

correlation coefﬁcient (Olofsson, 2011), is the pos-

sibility to ﬁnd non-linear dependencies. Often, the

probability distributions p(x), p(y), and p(x, y) are

unknown and have to be estimated in order to calcu-

late the mutual information. In the discrete case, this

is mostly done with the straight forward method of

counting the frequency of occurrence of the different

events.

An adaption of the mutual information for continuous

has been presented with the MIC. It picks up a pos-

sibility of avoiding the density estimation in the con-

tinuous case. That is the binning of samples, mean-

ing the data is sorted into bins based on their similar-

ity. Afterwards, the probability distributions are esti-

mated for the bins. This again is an easy counting of

frequency and the data is essentially discretized. The

resulting distributions are used for the calculation of

the discrete variant of the mutual information. The

problem is that the manual choice of the bins is time

consuming and can lead to deceptive results if not ap-

propriate. Therefore, MIC has been equipped with a

concept of always using the bins that lead to the max-

imal mutual information. Finding this bin conﬁgura-

tion is computational heavy – which resulted in the

utilization of a heuristic to tackle the problem. As a

result, MIC is deﬁned as:

MIC(X ;Y ) = max

I(X;Y )

log(min(n

, n

))

, (2)

where n

and n

denote the number of bins for X and

Y . The divisor log(min(n

, n

)) gives the maximal

achievable mutual information given the number of

bins and thus is used as normalizing factor. B typi-

cally denotes a function of the sample size N and lim-

its the number of bins. This is necessary to avoid triv-

ial partitioning, such as creating a single bin for each

data point that most of the time create relatively high

values for the mutual information. The initial paper

introducing MIC proposes to use B = N

0.6

based on

the described experiments.

In general, MIC shows some interesting properties.

Similar to the mutual information, it is deﬁned for val-

ues ≥ 0. In particular, it equals zero only if the ran-

dom variables are completely independent. Further-

more, it is normalized and shows a good equitability

in simulation results, i.e., that different types of asso-

ciation in the data can be compared.

2.1.4 Consideration of Own Conﬁguration

As mentioned before, the use of dependency mea-

sures for the detection of inﬂuences is not straight

forward in some cases. The issue appears if the own

conﬁguration of the agent A is essential for the deter-

mination of the inﬂuence of an agent B on A. This is if

the conﬁguration of B and the performance of A with-

out taking into account the conﬁguration of A lead to

a distribution that does not indicate a dependency be-

tween them, but, there is an inﬂuence of B on A. This

inﬂuence can then by revealed by using multiple esti-

mators of the inﬂuence for the different conﬁgurations

of A. The effect can be observed in already rather sim-

ple examples. One is given with example calculations

of the mutual inﬂuence in (Rudolph et al., 2015a). For

the measurement, it is sufﬁcient to use two estimators

and group the samples of all available conﬁgurations

to the two estimators. But, sometimes the usage of

more estimator can lead to a faster detection, as shown

in (Rudolph et al., 2015b).

A Mutual Inﬂuence-based Learning Algorithm

183

Camera 2

Camera 1

Camera 0

(a) A top view on the

experimental setup

with the pontenially

observable areas of

the cameras. The red

areas show a possible

conﬁguration of the

current ﬁeld of view.

Camera 1

Camera 0

Camera 2

(b) A 3-dimensional illus-

tration of the experimental

setup. We see agray ﬂoor

with orange blocks that rep-

resent targets. The targets

are moving from left to right

and vice versa. The observ-

ing cameras are depicted

with their current ﬁeld of

view.

Figure 2: The experimental setup.

2.2 The Learning Algorithm

In this section, the reinforcement learning algorithm

is presented. We chose the Q-Learning algorithm

(Watkins and Dayan, 1992) as the basis of this work,

since it is (i) well-known in the reinforcement learn-

ing domain and (ii) it has already been successfully

applied in the Smart Camera domain, cf. (Rudolph

et al., 2014). The algorithm has then been enhanced

using the inﬂuence information of the system by

adapting the state space of the learning algorithm in

order to reﬂect the actual inﬂuences in the system.

The remainder of the section gives an introduction to

Q-Learning (see Section 2.2.1) and describes the de-

tails of the modiﬁcation for application in the Smart

Camera domain.

2.2.1 Q-Learning

The Q-Learning algorithm is a basic Reinforcement

Learning technique that is well known and stud-

ied intensively. It has originally been proposed by

Watkins and Dayan (1992). Like all RL techniques,

Q-learning tries to solve the general RL Problem, i.e.,

to ﬁnd an optimal policy for a given problem with re-

spect to the long term reward r ∈ R. The main idea

is to ﬁnd a Quality-function Q : S × A → R that ap-

proximates the reward for each state-action pair and

takes into account the long term reward. To reach this

goal, the value for each state-action-pair is initialized

according to some of the various proposed methods,

e.g., they are all set to a ﬁxed value or they are set to

a random value, and afterwards updated according to

the rule

t+1

, a

) = Q

, a

)

+ α



t+1

+ γmax

t+1

, a) − Q

, a

)



(3)

where Q

(s, a) denotes the old Q-Value and Q

t+1

(s, a)

the new one, each for a given state-action pair (s, a).

Furthermore, r

t+1

denotes the reward received in time

step t + 1 and therefore is the immediate reward for

the action a

taken in time step t. The discount factor

γ ∈ [0, 1) determines the fraction of estimated future

rewards that is taken into account in the present step.

The learning rate α ∈ (0, 1] determines how much the

current experience, i.e. the current reward, is taken

into account for approximating the Q-value.

2.2.2 Including Mutual Inﬂuence Information

After the presentation of the Q-learning algorithm, we

depict how this information can be exploited to create

a MI-based learning algorithm. Although we used Q-

Learning as example for a learning algorithm, other

techniques can be utilized as well.

The main idea is to include the parts of the conﬁg-

uration of a neighbor that have an inﬂuence on itself

within its own state space. Considering two agents A

and A

with conﬁguration space C

= c

1,1

× c

1,2

and

= c

2,1

× c

2,2

, where the inﬂuence measurement in-

dicates that conﬁguration part c

2,1

has a signiﬁcant in-

ﬂuence on agent A

, we introduce this conﬁguration

part in the state space of it. The agent is then able

to react to the actual conﬁguration of its neighboring

agent.

Looking into a more concrete example, we con-

sider the Smart Camera domain that is also used for

the experiments following later in Section 3. Follow-

ing (Rudolph et al., 2014), a Q-learning algorithm

can be designed by deﬁning the situation and action

parts: (a) the current pan, tilt and zoom conﬁgura-

tions are used as situation (i.e., the state space), and

(b) changes to these values (in terms of deﬁned de-

gree steps) serve as action space. More precisely,

the states for each of the cameras can be of the form

[pan

,tilt

, zoom

] and the actions could be the in-

crease of pan, tilt or zoom, or the decease of pan,

tilt or zoom, or no change to pan, tilt or zoom, i.e.,

of the form [X

i,pan

, X

i,tilt

, X

i,zoom

], where X

i,p

could be

increase, decrease or no change. The actual conﬁg-

uration space of each camera would then also con-

sist of the [pan, tilt, zoom] conﬁgurations. But, the

conﬁguration space and state space are conceptually

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

184

different and are not necessarily the same. Assum-

ing that the pan of Camera 1 has a signiﬁcant in-

ﬂuence on Camera 0, we can apply the above de-

scribed method of the enhancement of the state space

of Camera 1. The new states could then have the

form [pan

,tilt

, zoom

, pan

]. This enhancement of

the state space will allow the camera to consider the

conﬁguration of its neighboring camera.

3 EVALUATION

In this section, we present the evaluation of the novel

algorithm. First, we introduce the evaluation setting

that is settled in the Smart Camera domain in Sec-

tion 3.1. Afterwards, we show the results of the mea-

surement of the inﬂuence in Section 3.2. Then a learn-

ing algorithm for the comparison of the performance

of the algorithm is introduced in Section 3.3. At least,

we show the results of the mutual inﬂuence-based al-

gorithm and the comparison algorithm in Section 3.4.

3.1 Evaluation Setting

For the evaluation, we chose a Smart Camera appli-

cation setting that requires a collaboration in order

to reach an optimal result. Therefore, we deﬁne the

goals: (i) detect new targets, and (ii) create 3D mod-

els of targets in an area (i.e., the goal is to provide a

stereo reconstruction of suspicious persons). There is

some research on techniques that allow to construct a

3D model from 2D pictures from different angles, see

(Menze and Muhle, 2012; Menze et al., 2013) for an

example.

The experimental setup is depicted in Figure 2.

There (in particular in Figure 2a), we see a top down

view on three cameras, marked as black dots. Around

them, we see circles in different colors that show the

potential observable areas of the cameras. We can see

that a collaboration between Camera 0 and 1 is neces-

sary for an optimal behavior of the cameras. Camera 2

is not involved with the other two cameras. Therefore,

a collaboration is not helpful. In Figure 2b, we see a

3D model of the scene with example targets added,

represented as orange boxes. In the scenario, the tar-

gets move from left to right and leave the scene or

from right to left and leave the scene.

In the performance measure, we reﬂect the goals

mentioned before. We rate the detection of a before

unobserved target with a performance of 1 and the ob-

servation of multiple cameras with a performance of

2.5 while one or multiple cameras could observe mul-

tiple targets which are then added up. We chose the

difference between the two possible observations in

order to reﬂect that a 3D reconstruction of an target is

much more valuable. Experiments with other weight-

ings between the two goals have shown only minor

effects on the mutual inﬂuence detection.

3.2 Measurement of Inﬂuence

Before the MI-based algorithm can be applied, it is

necessary to gather the MI information for the sce-

nario. The measurement of inﬂuence presented here

is based on the results in in (Rudolph et al., 2015a).

However, we present them here again in short since

they are necessary for the understanding of the fol-

lowing results. Exemplary, we show the inﬂuence

information for Camera 0. The values for the dif-

ferent parts of the conﬁguration of Camera 1 and 2

are shown in Figure 1a, 1b and 1c. We see that the

pan and tilt of Camera 1 are clearly more inﬂuencing

than the counterparts of Camera 2. In Figure 1d, we

can observe the comparison of the three parts of Cam-

era 1. Here, the pan again has the highest measured

inﬂuence, followed by the tilt. The inﬂuence of the

zoom of Camera 1 is rather marginal, since the aver-

age is higher starting from 10, 000 steps.

3.3 Comparison Algorithm

As basis for a meaningful comparison, we chose the

Distributed W-Learning algorithm (DWL) since it is a

comparatively new reinforcement learning technique

and is especially designed for multi agent systems.

Furthermore, it has already been applied to a similar

learning task in the Smart Camera domain (Rudolph

et al., 2014). It has originally been proposed by

Dusparic and Cahill (2010). It borrows the ideas

of Q-Learning and W-Learning and extends them

with a cooperative mechanism. Since Q-learning has

been outlined in Section 2.2.1, we now introduce W-

Learning (see Section 3.3.1) and on this basis, DWL

is introduced (see Section 3.3.2).

3.3.1 W-Learning

An extension of Q-learning is W-learning. It was

introduced by Humphrys (1995) and addresses the

problem of a too large state space, i.e. there are too

many states to handle in terms of memory, or the

learning will be slowed down too much through the

large number of states that have to be visited in or-

der to learn the optimal policy and therefore makes

the algorithm inapplicable. The proposed solution for

this problem is to split the state space according to

different goals. For every part there is a dedicated

Q-Learner that approximates the value of the state-

A Mutual Inﬂuence-based Learning Algorithm

185

action pairs. For the update of the Q-values Equa-

tion 3 is used. In order to decide which W-Learner

is allowed to execute its proposed action, for each W-

Learner a separate W-value is introduced. It is up-

dated using the equation

i,t+1

) = (1 − α)W

i,t

)

+ α



i,t+1

, a

) − r

i,t+1

+ γmax

i,t+1

t+1

, a

)



(4)

where W

i,t

(s) denotes the former mentioned W-value

for W-learner i at time t for state s. The parameters

α and γ are as in the Q-learning update equation (i.e.

Equation 3) the learning rate and the discount factor.

Equally, Q

(s, a) is the Q-value at time t for the state-

action pair (s, a). For the selection of the action to

execute the W-learner with the highest W-value has

to be found. The action that has the highest Q-value

within this W-learner is selected and executed.

3.3.2 Distributed W-Learning

LP

Q‐Learning

W‐Learning

Executeaction

proposedby

highestW‐Value

Action

W‐Value

LP

Q‐Learning

W‐Learning

Action

W‐Value

RP

Q‐Learning

W‐Learning

Action

W‐Value

RP

Q‐Learning

W‐Learning

Action

W‐Value

Figure 3: The Architecture of DWL.

In (Dusparic and Cahill, 2010), Distributed W-

learning (DWL) is introduced. It is an adaption of

the W-learning idea to distributed systems. Since they

often create huge state spaces in most cases, a cen-

tral optimization is not viable. Therefore, DWL in-

troduces a W-learning process for each agent in the

system and enhances it with remote W-learner. The

architecture of the DWL decision process is depicted

in Figure 3. The remote W-learner work similar to the

former introduced W-learners, now denoted as local

W-learner. The difference of the remote W-learner

is that they use the state and reward of the neighbor

agents to determine a proposed action. Through this

mechanism, the neighbors can inﬂuence each others

action and are assumed to ﬁnd an optimal policy for

the whole system. For some applications it might be

useful to not value the opinion of the neighbors as

high as the own. Therefore, to determine the local

W-values, we use the same method as in W-learning,

but, to determine the W-values of the remote poli-

cies a cooperation coefﬁcient 0 ≤ C ≤ 0 is introduced

as a weight. Using a low C leads to a more selﬁsh

behavior. A high value for C lets the agent take its

neighbors suggestions more into account. Other then

stated in (Dusparic and Cahill, 2010), C = 0 does not

lead to a fully non-cooperative behavior, since the W-

values could be (and in practice sometimes are) neg-

ative. Just multiplying the remote W-values by C will

not lead to the desired result. Therefore, in the case

of a negative W-value, we divide by C.

3.4 Results

Here, we present the results of the different algo-

rithms. We start with some information about the re-

sults that apply for all algorithms and then present

the results for DWL in Sec 3.4.1. Then, we show

the performance results of the MI-based algorithm in

Section 3.4.2 and discuss the results in Section 3.4.3.

Since Q-learning introduces two variables, the learn-

ing rate α and the discount factor γ, we would like

to ﬁnd an optimal parameter set for the task. How-

ever, due to computational reasons it is not possible

to run full parameter studies including the collabora-

tion factor c in DWL. Therefore, we run experiments

with a single camera to ﬁnd a parameter set for α and

γ that allows an optimal learning behavior. We found

that α = 0.3 and γ = 0.6 fulﬁlls this requirement and

therefore used it for both algorithms, DWL and the

MI-based algorithm.

For each setting, i.e., for DWL each parameter

setting and for the MI-based algorithm each situa-

tion setting, we made 20 independent runs that last

500,000 steps and use the average for the graphs, typ-

ically enhanced with the standard deviation.

3.4.1 DWL

100

120

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Cooperation Coefficient

Average Performance in last 20000 steps

Figure 4: The results for DWL.

The results using the DWL algorithm are shown in

Figure 4. Each bar shows the average performance of

the last 20,000 steps. We see that a value of 0.2 for the

Collaboration Coefﬁcient C gives the maximum value

of about 96 regarding the performance measure given

in Section 3.1. For the minimum value of 0.0 for C

DWL is equivalent to basic Q-learning and therefore

has no collaboration mechanism any more. It gives a

value of about 83. A collaboration factor of 0.1 and

0.3 also give a viable performance compared to the

maximum value. Looking at a higher values, i.e. 0.4

and higher, we see that the collaboration does have

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

186

a negative effect since it rather achieves the perfor-

mance of non-collaborative behaviour, i.e. with C=0.

3.4.2 MI-based Algorithm

The results for the MI-based algorithm are presented

in Figure 5. The data is enhanced with the standard

deviation. In Figure 5a, we see the performance of

the Q-Learning algorithm with the states of Camera 0

extended by the pan conﬁguration of Camera 1. We

can observe that a signiﬁcantly higher performance

as by DWL of approximately 225 is reached meaning

that the introduced collaboration allows the system to

ﬁnd optimal strategies. Furthermore, the introduction

of the pan is already sufﬁcient to reach this goal. In

Figure 5b and 5c, the graphs are similarly shaped to

the one that only considers the pan. However, the

differences are in the details. If more conﬁguration

parts are introduced in the states of Camera 1, we

see that the performance rises slower in the beginning

(between 150, 000 and 300, 000 steps). But later on

(between 300, 000 and 500, 000) the micro improve-

ments are learned faster if all conﬁguration parts are

included. In Figure 5d, we can observe the results for

the inclusion of the tilt of Camera 1 in the states of

Camera 0 without the consideration of pan. We see

that a near optimal behavior is not found very often,

but at least sometimes. The learning of a near opti-

mal behavior explains the jump in the graph at around

230, 000 steps and consequently a much higher stan-

dard deviation afterwards. However, most runs con-

tinue to process a strategy with a sub-optimal perfor-

mance, resulting in an averaged reward of approxi-

mately 90. In Figure 5e, the runs with only the zoom

of Camera 1 integrated in the states of Camera 0 are

shown, respectively. The results again are far from

optimal, but show that few runs can ﬁnd a near op-

timal strategy. That again causes the jump at around

120000 steps.

3.4.3 Discussion

The presented results show that the MI-based ap-

proach clearly outperforms all other approaches.

DWL can give better results than a non-collaborative

algorithm for some parameter settings. However, it

is far from an optimal behavior even after a learn-

ing phase of 500,000 steps. Concluding the results

of the MI-based algorithm, we see that the mutual in-

ﬂuence detection method has accurately identiﬁed the

most inﬂuencing part of the conﬁguration and there-

fore allows to learn optimal behavior. This can be

seen since the runs with the pan included clearly out-

perform DWL and a non-collaborative learning. We

have also seen that the inclusion of the less inﬂuenc-

100

150

200

250

300

0 50000 100000 150000 200000 250000 300000 350000 400000 450000 500000

System Performance

Steps

System Performance

(a) The graphs show the

system perfomance when

the pan angle of Camera 1

is integrated in the state

space of Camera 0.

100

150

200

250

300

0 50000 100000 150000 200000 250000 300000 350000 400000 450000 500000

System Performance

Steps

System Performance

(b) The graphs show the

system perfomance when

the pan and tilt angle of

Camera 1 is integrated in

the state space of Cam-

era 0.

100

150

200

250

300

0 50000 100000 150000 200000 250000 300000 350000 400000 450000 500000

System Performance

Steps

System Performance

system perfomance when

the pan and tilt angle, and

the zoom of Camera 1

is integrated in the state

space of Camera 0.

100

110

120

130

0 50000 100000 150000 200000 250000 300000 350000 400000 450000 500000

System Performance

Steps

System Performance

(d) The graphs show the

system perfomance when

only the tilt angle of Cam-

era 1 is integrated in the

state space of Camera 0.

100

110

120

0 50000 100000 150000 200000 250000 300000 350000 400000 450000 500000

System Performance

Steps

System Performance

(e) The graphs show the

system perfomance when

only the zoom of Camera 1

is integrated in the state

space of Camera 0.

Figure 5: The results for the 3D-reconstruction scenario

using the MI-based algorithm. The graphs show the sys-

tem performance for the three conﬁgurations. Each graph

is based on 20 runs with different random seeds. The line

shows the average system performance and the error bars

show the standard deviation.

ing parts (tilt and zoom) does improve the results, too.

But this latter improvement is less strong compared to

the usage of just pan, which has been identiﬁed as less

effective by the MI detection method beforehand.

4 RELATED WORK

In literature, several approach that try to formalize

the mutual inﬂuences can be found. Most of these

approaches focus on the inﬂuence through direct or

indirect interactions. For instance, a model for inter-

actions is proposed by Keil and Goldin (2003), but a

method to detect the implicit interactions is not pro-

vided. Another approach is to use stit logic for model-

A Mutual Inﬂuence-based Learning Algorithm

187

ing the interactions in multi agent systems (Broersen,

2010). The focus of this work is on the system spec-

iﬁcation and veriﬁcation and therefore differs much

from the focus of our work. In (Logie et al., 2008), a

data mining approach for the detection of mutual in-

ﬂuences in multi agent systems is proposed. Unfortu-

nately, this is a position paper without concrete meth-

ods and results and no following works have been

published, yet.

The presented method has similarities with the fea-

ture selection approach that originates in supervised

learning and, recently, there are some promising at-

tempts for the adaption to systems with performance

measurement, i.e. the reinforcement learning domain,

such as (Parr et al., 2008; Bishop and Miikkulainen,

2013; Hachiya and Sugiyama, 2010; Nguyen et al.,

2013). All of these works have in common that they

do not match the presented idea of a self-adapting and

self-organizing system. In particular, they do not con-

sider autonomic entities that interact and try to maxi-

mize the system utility based on what they can sense

from their local environment and their local status. In

contrast, they focus on the selection of features from

given input sets for the particular learning algorithms.

Within this work, we focus on the detection of the in-

ﬂuence of the conﬁgurations of other system entities.

Furthermore, a variety of contributions can be found

in literature with a focus on multi agent learning

(Stone and Veloso, 2000). These works all belong

to one of two categories: (i) team learning where a

single learner is used for all the agents or (ii) con-

current learner where each agent has an own learner

(Panait and Luke, 2005). In this work, we show how

an optimal learning structure can be found in order

to ensure an optimal learning behavior. We applied

the technique to Q-Learning. However, other learn-

ing techniques, possibly especially designed for multi

agent systems, can beneﬁt from the mutual inﬂuence

information as well.

There are several stochastic dependency measures

that could be considered. The probably most promi-

nent instance is the Pearson Correlation Coefﬁcient

(Pearson, 1895). In addition, a variety of further mea-

sures with a similar scope exist. In order to decrease

the number of candidates to be applied for the detec-

tion task, we considered the following list of char-

acteristics that deﬁne the requirements for this pur-

pose: (i) The dependency measure should be able

to ﬁnd nonlinear dependencies between random vari-

ables. (ii) The dependency measure should only be

zero if there is no dependency between the random

variables. (iii) The dependency measure should be

able to handle discrete and continuous random vari-

ables.

The MIC fulﬁlls these criteria most appropriately.

There are also other dependency measures that meet

the criteria, such as, mutual information (Shannon

and Weaver, 1949) or distance covariance (Szkely

et al., 2007). But, some rather famous dependency

measures are excluded by these criteria.

5 CONCLUSION

Based on the observation that an increasing part of

technical systems is characterized by explicit and im-

plicit dependencies among distributed entities, this

paper presented a concept for optimizing the adapta-

tion strategy of an internal control mechanism guiding

the agent’s behavior. The idea is to explicitly identify

correlations between the particular conﬁguration set-

tings of a neighbored entity and the own performance

measurement. We introduced a method to derive such

correlation measures at runtime and integrate the cor-

responding information within the decision logic of

the learning agent. To illustrate the possible impact,

we chose Q-Learning as simple model-free reinforce-

ment technique that is applied to learn a situation-

action mapping online.

To demonstrate the improved performance, we

compared the developed technique with D-Learning,

which is a standard technique that combines Q-

Learning-based online reinforcement learning ap-

proaches with similar learners for neighbor impact.

In contrast to our concept, an integrated technique

is performed. The evaluation showed that our ap-

proach that turns implicit in explicit dependency re-

lations achieves a signiﬁcant better performance and

illustrated this within simulations of a Smart Camera

scenario.

Future work mainly deals with more sophisticated

solutions regarding the utilization of mutual inﬂuence

information. On the one hand, this refers to other and

more complex learning techniques – especially rule-

based learning techniques that have to consider mu-

tual inﬂuence estimations within their condition parts.

On the other hand, more sophisticated approaches

with respect to scalability issues are investigated. In

this context, fast pre-estimators that identify reliably

which entity is most probably having inﬂuence are de-

veloped.

REFERENCES

Bishop, J. and Miikkulainen, R. (2013). Evolutionary

feature evaluation for online reinforcement learning.

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

188

In Computational Intelligence in Games (CIG), 2013

IEEE Conference on, pages 1–8.

Broersen, J. M. (2010). CTL.STIT: enhancing ATL

to express important multi-agent system veriﬁcation

properties. In 9th International Conference on Au-

tonomous Agents and Multiagent Systems (AAMAS

2010), Toronto, Canada, May 10-14, 2010, Volume 1-

3, pages 683–690.

Dusparic, I. and Cahill, V. (2010). Distributed w-learning:

Multi-policy optimization in self-organizing systems.

In Proceedings of the 3rd IEEE International Con-

ference on Self-Adaptive and Self-Organizing Systems

(SASO). IEEE.

Hachiya, H. and Sugiyama, M. (2010). Feature selection

for reinforcement learning: Evaluating implicit state-

reward dependency via conditional mutual informa-

tion. In Balczar, J. L., Bonchi, F., Gionis, A., and Se-

bag, M., editors, ECML/PKDD (1), volume 6321 of

Lecture Notes in Computer Science, pages 474–489.

Springer.

Humphrys, M. (1995). W-learning: Competition among

selﬁsh q-learners. Technical report.

Keil, D. and Goldin, D. Q. (2003). Modeling indirect

interaction in open computational systems. In 12th

IEEE International Workshops on Enabling Technolo-

gies (WETICE 2003), Infrastructure for Collabora-

tive Enterprises, 9-11 June 2003, Linz, Austria, pages

371–376.

Logie, R., Hall, J. G., and Waugh, K. G. (2008). Towards

mining for inﬂuence in a multi agent environment.

In Abraham, A., editor, IADIS European Conf. Data

Mining, pages 97–101. IADIS.

Menze, M., Klinger, T., Muhle, D., Metzler, J., and Heipke,

C. (2013). A stereoscopic approach for the associ-

ation of people tracks in video surveillance systems.

PFG Photogrammetrie, Fernerkundung, Geoinforma-

tion, 2013(2):83–92.

Menze, M. and Muhle, D. (2012). Using Stereo Vision

to Support the Automated Analysis of Surveillance

Videos. ISPRS - International Archives of the Pho-

togrammetry, Remote Sensing and Spatial Informa-

tion Sciences, pages 47–51.

Nguyen, T., Li, Z., Silander, T., and Leong, T. Y. (2013).

Online feature selection for model-based reinforce-

ment learning. In Dasgupta, S. and Mcallester, D., edi-

tors, Proceedings of the 30th International Conference

on Machine Learning (ICML-13), volume 28, pages

498–506. JMLR Workshop and Conference Proceed-

ings.

Olofsson, P. (2011). Probability, Statistics, and Stochastic

Processes. Wiley.

Panait, L. and Luke, S. (2005). Cooperative multi-agent

learning: The state of the art. Autonomous Agents and

Multi-Agent Systems, 11(3):387–434.

Parr, R., Li, L., Taylor, G., Painter-Wakeﬁeld, C., and

Littman, M. L. (2008). An analysis of linear models,

linear value-function approximation, and feature se-

lection for reinforcement learning. In Proceedings of

the 25th International Conference on Machine Learn-

ing, ICML ’08, pages 752–759, New York, NY, USA.

ACM.

Pearson, K. (1895). Notes on regression and inheritance

in the case of two parents. Proceedings of the Royal

Society of London, 58(1):240 – 242.

Reshef, D. N., Reshef, Y. A., Finucane, H. K., Grossman,

S. R., McVean, G., Turnbaugh, P. J., Lander, E. S.,

Mitzenmacher, M., and Sabeti, P. C. (2011). De-

tecting novel associations in large data sets. Science,

334(6062):1518–1524.

Rinner, B., Winkler, T., Schriebl, W., Quaritsch, M., and

Wolf, W. (2008). The evolution from single to per-

vasive smart cameras. In Distributed Smart Cameras,

2008. ICDSC 2008. Second ACM/IEEE International

Conference on, pages 1–10.

Rudolph, S., Edenhofer, S., Tomforde, S., and H

ahner, J.

(2014). Reinforcement learning for coverage opti-

mization through ptz camera alignment in highly dy-

namic environments. In Proceedings of the Inter-

national Conference on Distributed Smart Cameras,

ICDSC ’14, pages 19:1–19:6, New York, NY, USA.

ACM.

Rudolph, S., Tomforde, S., Sick, B., and H

ahner, J. (2015a).

A mutual inﬂuence detection algorithm for systems

with local performance measurement. In Proceedings

of the 9th IEEE Conference on Self-Adaptive and Self-

Organizing Systems (SASO). IEEE Press, to appear.

Rudolph, S., Tomforde, S., Sick, B., Heck, H., Wacker, A.,

and H

ahner, J. (2015b). An online inﬂuence detection

algorithm for organic computing systems. In Proceed-

ings of the 28th GI/ITG International Conference on

Architecture of Computing Systems ARCS Workshops.

Shannon, C. and Weaver, W. (1949). The Mathemati-

cal Theory of Communication. University of Illinois

Press.

Stone, P. and Veloso, M. (2000). Multiagent systems: A sur-

vey from a machine learning perspective. Autonomous

Robots, 8(3):345–383.

Szkely, G. J., Rizzo, M. L., and Bakirov, N. K. (2007). Mea-

suring and testing dependence by correlation of dis-

tances. Ann. Statist., 35(6):2769–2794.

Valera, M. and Velastin, S. (2005). Intelligent distributed

surveillance systems: a review. Vision, Image and Sig-

nal Processing, IEE Proceedings -, 152(2):192–204.

Watkins, C. J. C. H. and Dayan, P. (1992). Technical note

q-learning. Machine Learning, 8:279–292.

Wiering, M. and van Otterlo, M., editors (2012). Reinforce-

ment Learning: State-of-the-Art (Adaptation, Learn-

ing, and Optimization). Springer Verlag, Berlin / Hei-

delberg, Germany. ISBN-13: 978-3642276446.

A Mutual Inﬂuence-based Learning Algorithm

189