
Classification of Dust Elements by Spatial Geometric Features
A. Proietti, M. Panella, E. D. Di Claudio, G. Jacovitti and G. Orlandi
Department of Information Engineering, Electronics and Telecommunications,
University of Rome “La Sapienza”, Via Eudossiana 18, 00184 Rome, Italy
Keywords:
Dust Analysis, Classification, Feature Extraction, CMOS Sensor.
Abstract:
Management of air quality is an important task in many human activities. It is carried out mainly by installing
ventilation and filtering facilities. In order to ensure efficiency, these systems must be designed after the
knowledge of key environmental parameters, such as size and type of particles and fibres present in the air.
In this paper, we propose a new method for the classification of dust particles and fibres based on a minimal
set of geometric features extracted from binary images of dust elements, captured by a very cheap imaging
system. The proposed technique is discussed and tested. Experimental results obtained by real-measured data
are presented, showing satisfactory performance by using several well-known classifiers.
1 INTRODUCTION
Maintenance of air quality in indoor environments is
relevant for safety and health of people, but also for
the protection of property and works. The local au-
thorities and the international organizations have en-
acted specific regulations and instruments for control-
ling the indoor air quality and the levels of pollutants
and harmful agents, e.g., the environmental and air
quality laws by International Organization for Stan-
dardization (ISO, 2010).
Agents affecting the air quality level can be clas-
sified on the basis of three characteristics: origin, na-
ture and effects. As regard for the origin, we can dis-
tinguish between indoor contaminants (arising from
people, combustion, machining by-products and ma-
terial degradation) and outdoor contaminants (parti-
cles collected through the windows, ventilation ducts,
etc.). Based on the nature, we can distinguish among
gases and vapours, organic fragments of plants, an-
imal sources, micro-organisms, mineral particulate
(dust, fumes, machining residuals) and liquids (fog
and suspensions). From effects viewpoint, we can dis-
tinguish among pollutants causing physiological stim-
uli (such as smells), stress (such as headaches or fa-
tigue) and diseases (such as irritation, allergies, muta-
tions, or cancer).
In order to obtain the desired quality, a suitable
artificial or natural ventilation can be provided to re-
move or dilute the contaminants by mixing and re-
distributing air. To this purpose, it is necessary to
consider the type of pollutants to be removed, their
size, shape and other physical properties, the air flow
speed, etc. In the case when ventilation is insufficient,
due to high level of pollutants, the air quality must
be controlled by filtering to minimize the concentra-
tion of particles and micro-organisms. Pollutants are
trapped by filters (i.e., porous partition) according to
four basic mechanisms:
• sieve effect, occurring when the space between
the filter fibres (or netting, wire mesh, etc.) is
smaller than the diameter of the particles;
• direct interception, taking place when particles
striking the filter surface are trapped;
• inertial impact, occurring when particles are
blocked within the tortuous channels of the filter
media;
• diffusion deposit, which occurs when the particles
are so small that they spread by Brownian motion
and remain in the filter.
The combination of these mechanisms establishes
the overall efficiency of an air filter. It is evident that
the correct design of the filtering equipment relies on
a correct evaluation of the size and nature of the dust
elements. In particular, it is important to distinguish
between particulate and fibres to prevent and correct
the pollution phenomenon.
Classification is a common task in many scientific
fields (Rizzi et al., 2008; Panella and Martinelli, 2011;
Maisto et al., 2013; Scardapane et al., 2015). Regard-
ing particle shape recognition, a classifier based on
Proietti, A., Panella, M., Claudio, E., Jacovitti, G. and Orlandi, G.
Classification of Dust Elements by Spatial Geometric Features.
DOI: 10.5220/0005697502470254
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 247-254
ISBN: 978-989-758-173-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
247
a mixture of Gaussian models (Panella et al., 2003;
Parisi et al., 2007) was employed for automatic recog-
nition of biological particles in microscopic images
(Ranzato et al., 2007), starting from digital images
of airborne pollen. An approach based on harmonic
wavelet transform (Drolon et al., 2000) was applied
for the analysis of wear and erosion phenomena act-
ing on particles. An approach based on fuzzy kernel-
based membership functions (Panella et al., 2001)
was applied for shape classification (Proietti et al.,
2016). Other traditional methods for monitoring the
dust (Baron, 2001; Camuffo, 2013; Ghedini et al.,
2011) rely on physical and chemical analyses (spec-
trometry, spectroscopy, etc.).
An original and cheap met hod for the imaging of
dust samples was introduced in (Proietti et al., 2014),
by using a high resolution optical CMOS sensor di-
rectly exposed to the air flow (i.e., without a lens).
Using this device, dust elements adhering to the sen-
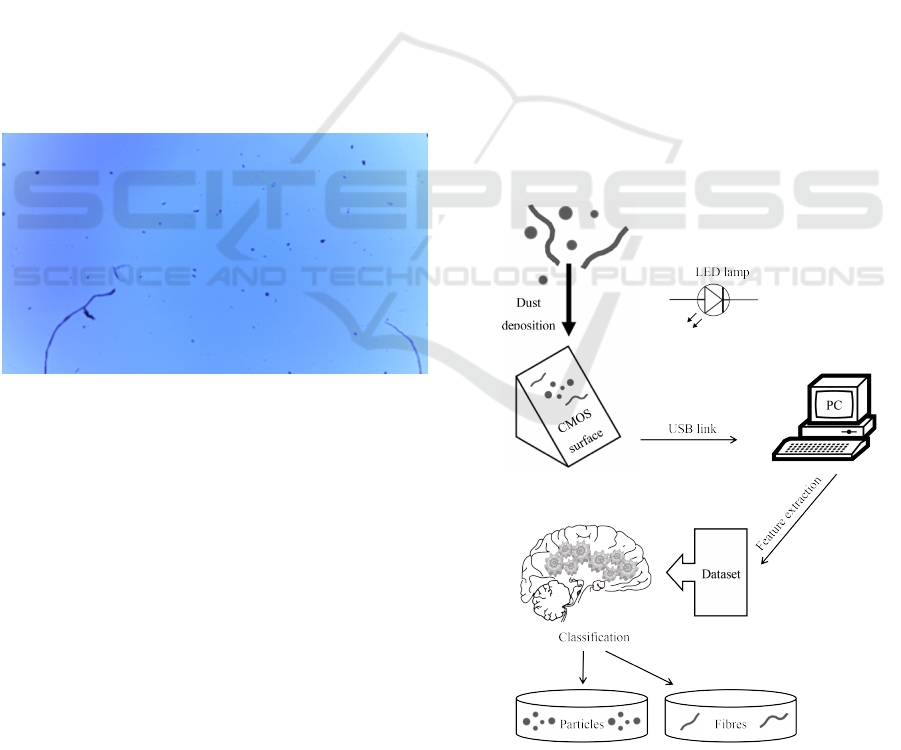
sor and backlit by a LED source (see Figure 1) appear
as shadows, that can be employed for effective dust
analysis. The sensor is periodically cleaned before
each acquisition cycle.
Figure 1: A typical dust deposition image collected by the
CMOS sensor.
This basic technique enables to perform analy-
sis of dust elements, according to their size and two
fundamental typologies, herein referred to as parti-
cles and fibres, respectively characterized by a round
shape or an elongated structure. In this paper the task
is accomplished using just three geometric features.
The selected features reflect properties of back-
lit dust shadows. The size and the elongation of the
particle are jointly quantified by a pair of features,
i.e., the perimeter length and the perimeter/area ratio
(isoperimetric index). The third feature is the varimax
norm, a novel and powerful feature recently presented
in (Di Claudio et al., 2015), which measures the reg-
ularity of the shadow contour. It appears determinant
to obtain high discrimination power.
As proven by the experiments, the three selected
features are largely independent and generate well-
separable clusters in the feature space, leading very
robust classification performance when applied to
state of the art trained classifiers.
The proposed approach differs from similar tasks
reported in the literature (e.g., character recognition),
since it does not perform template matching with pre-
set shapes.
In Sect. 2 we describe the feature extraction strat-
egy starting from the dust deposition image, as well
as the resulting feature space for training a classi-
fier. The setup of the classification experiment on
the considered dataset is illustrated in Sect. 3. In
Sect. 4 the numerical results obtained from the appli-
cation of several well-known classifiers on the mea-
sured dataset are discussed, in order to assess the ef-
fectiveness of dust characterization and compare the
performances of the selected approaches.
2 FEATURE EXTRACTION
The proposed method employs pattern recognition
techniques based on a set of geometric features ex-
tracted from the images collected by the above men-
tioned CMOS sensor-based acquisition system (Proi-
etti et al., 2014), as illustrated in Figure 2.
Figure 2: A schematic overview of the employed acquisi-
tion system based on CMOS imaging sensor.
Dust directly deposits on a naked imaging sen-
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
248

sor. The shadows projected by the illuminating LEDs
(showed in Figure 3) are processed to yield binary im-
ages (see Figure 4), using auxiliary processing tools,
such as background subtraction, equalization, filter-
ing and thresholding (Proietti et al., 2014). Each ele-
ment is extracted using a morphological analysis and
subsequently classified on the basis of some well-
defined features.
Figure 3: A collection of dust samples extracted from an
acquired image.
Figure 4: The binary image resulting from the preprocess-
ing and binarization of dust deposition in Figure 1.
First, connected components of the binary image
are isolated (see Fig. 5). These components are sets of
pixels of value 1 surrounded by pixels of value 0. The
search for connected components is performed by a
classical procedure (Gonzalez et al., 2004).
Figure 5: An example of a silhouette of a dust element and
of its boundary.
In substance, the connected components are the
silhouettes of each single dust element. Due to the
image nature and to the short time between clean op-
erations, the occurrence of the superposition of two
silhouettes is a rare event, so that its effect on the
global statistics is neglected.
Specifically, silhouette is separately classified
based on the following three features.
1. Length b of the silhouette boundary. It is evalu-
ated by a special version of the Moore neighbour
tracing algorithm, adopting Jacob’s stopping cri-
teria (Reddy et al., 2012). This procedure returns
a new binary image composed by only the bound-
ary pixels q
i
, wherein the inner ones are set to zero
(see Fig. 5). Hence, the boundary length is calcu-
lated as:
b =
L−1
∑
i=0
q
i
. (1)
where L is the total number of the one valued pix-
els in the connected component. Note that b is
not a geometrical measure, since its value only ap-
proximates the length of the silhouette perimeter.
2. Isoperimetric index g defined as:
g =
b
2
4πL
. (2)
The meaning of this index is related to the isoperi-
metric theorem (Bogomolny, 1987). It assumes
the minimum value (equal to one) for a circular
shape. In substance, it is an estimate of the sil-
houette roundness.
On the end, L approximates the effective area of
the dust silhouette if multiplied by the area σ
2
of
each pixel, where σ is the pixel pitch of the used
CMOS optical sensor. The σ parameter is criti-
cal for the minimum detectable particle size. In
the present setting, the sensor is characterized by
σ = 3 µm, allowing to barely detect the PM10 par-
ticulate.
Since the value of b does not exactly represent the
silhouette perimeter, the sample value of g is also
approximated.
3. Varimax norm v of the differences δ
ϕl
between
the orientation consecutive tangents of the silhou-
ette boundary, estimated using a two-stage fast
smoothing procedure as described in (Di Claudio
et al., 2015). The varimax norm is then defined as
follows:
V = b
∑
b
l=1
δ
ϕl
− µ
4
n
∑
b
l=1
δ
ϕl
− µ
2
o
2
, (3)
Classification of Dust Elements by Spatial Geometric Features
249

where
µ =
1
b
b
∑
l=1
δ
ϕl
. (4)
represents the average curvature of the particle.
The varimax norm measures the roughness of the
silhouette boundary and, in particular, assumes
high values in the presence of abrupt changes of
its orientation, typical of fibres. This original fea-
ture is determinant for the discrimination power
of the whole procedure.
3 SETUP FOR CLASSIFICATION
In order to evaluate the effectiveness of the proposed
features system, some classification tests were per-
formed. Starting from a real dust images acquisi-
tion similarly to the example in Fig. 4, several dust
particles and fibres using the procedure discussed in
Sect. 2 were collected. As a result, 400 real dust ele-
ments (54 fibres and 346 particles, representing a re-
alistic distribution of dust deposition elements), anno-
tated with a classification by experts, were produced
in order to build a preliminary archive for training and
testing classification procedure (this database will be
available for testing other methods after request to
the first author). Thanks to the wide variety of col-
lected dust elements (in terms of size, shape, convex-
ity/concavity, irregularity, etc.), the adopted dataset
seems a valid basis for the assessment and the per-
formance evaluation of classification techniques.
The values of the features used in this work are
statically summarized in Table 1, where the mini-
mum, maximum, mean and the standard deviation are
reported.
In Figure 6, the distribution of the size of the parti-
cles, calculated as the diameter of the equivalent circle
having the same area L of the silhouette, is displayed.
Likewise, in Figure 7, the distribution of the size of
the fibres, approximated by its half length (b/2), is
reported.
As far as particles/fibres classification is con-
cerned, the discussed feature set was employed. In
order to represent data within the unitary 3-D space,
the whole dataset was normalized on each feature in-
dependently between 0 and 1 as follows:
x
m
←−
x
m
− α
ω − α
, m = 1... M , (5)
where x
m
is the generic feature (i.e., b, g or v), M is
the number of patterns in the dataset and
ω = arg max
m=1...M
{x
m
} , α = arg min
m=1...M
{x
m
}, (6)
are the maximum and minimum value that the fea-
tures x
m
can assume. This normalization is essential
to balance the respective amplitudes at the classifier
input to improve numerical conditioning.
As a result, the dataset consists of a matrix con-
taining 400 rows and 3 columns (three features for
each element), plus an additional column represent-
ing the class label annotated by experts (i.e., particle
or fibre) and used as a benchmark. The classification
was performed in the overall space (b,g,v) and in the
subspaces generated by the three single features (b),
(g) and (v) and by the features pairs (b, g), (b,v) and
(g,v), resulting in seven different datasets.
Figure 6: The particles distribution versus the diameter of
the equivalent circle of area L.
Figure 7: The fibres distribution versus the length (com-
puted as the semi-boundary).
As a preliminary analysis, a singular value de-
composition (SVD) was performed (Golub and Loan,
1989). Overall, the SVD analysis of the considered
datasets demonstrated that the chosen features were
nearly mutually uncorrelated over the dataset itself.
Moreover, the use of SVD-rotated features in classifi-
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
250

Table 1: Numerical overview of the features extracted from the considered dust dataset.
Feature
Attribute b g v
min 15.00 0.68 1.07
max 893.00 16.18 33.22
mean 74.23 1.63 2.51
std. dev. 129.14 2.57 3.34
cation tasks did not provide performance advantages
over the raw feature set and therefore was not pursued
further.
4 EXPERIMENTAL RESULTS
To test the classification capabilities of the proposed
features, they were fed as inputs to the standard clas-
sifiers described in the following:
• the Linear Discriminant Analysis (Fisher, 1938),
which tries to characterize a dataset using a linear
polynomial in order to separate patterns in two or
more classes;
• the Quadratic Discriminant Analysis
(Krzanowski, 1988), similarly to the LDA,
it tries to characterize a dataset using a quadratic
polynomial;
• the Nearest Neighbour (k-NN) approach (Cover
and Hart, 1967), which assigns a class based on
the most frequent class among the pattern neigh-
bourhood;
• the Naive Bayes classifier (Langley et al., 1992),
which is a classification algorithm based on the
Bayes’ theorem, supposing a strong independence
among features;
• the Classification And Regression Tree (CART)
classifier (Lawrence and Wright, 2001), which
operates by recursively splitting the data until
ending points are achieved using some preset cri-
teria;
• the Probabilistic Neural Network (PNN) classifier
(Specht, 1990), based on a four layers neural net-
work employing Bayesian decision-making the-
ory;
• the Fuzzy Inference Systems (FIS) classifier (Tak-
agi and Sugeno, 1985), which relies on the use of
fuzzy logic and fuzzy sets theory to achieve clas-
sification tasks (Liparulo et al., 2013).
The tests were performed using the above men-
tioned datasets and a stratified ten-fold cross-
validation (Purushotham and Tripathy, 2012), using
a uniform patterns split into groups of the same size.
Figure 8: The 2-D projections of the classified (b, g,v) dust
dataset using the Naive Bayes classifier: blacks dots are pat-
terns classified as fibres; grey dots are patterns classified as
particles.
Classification of Dust Elements by Spatial Geometric Features
251
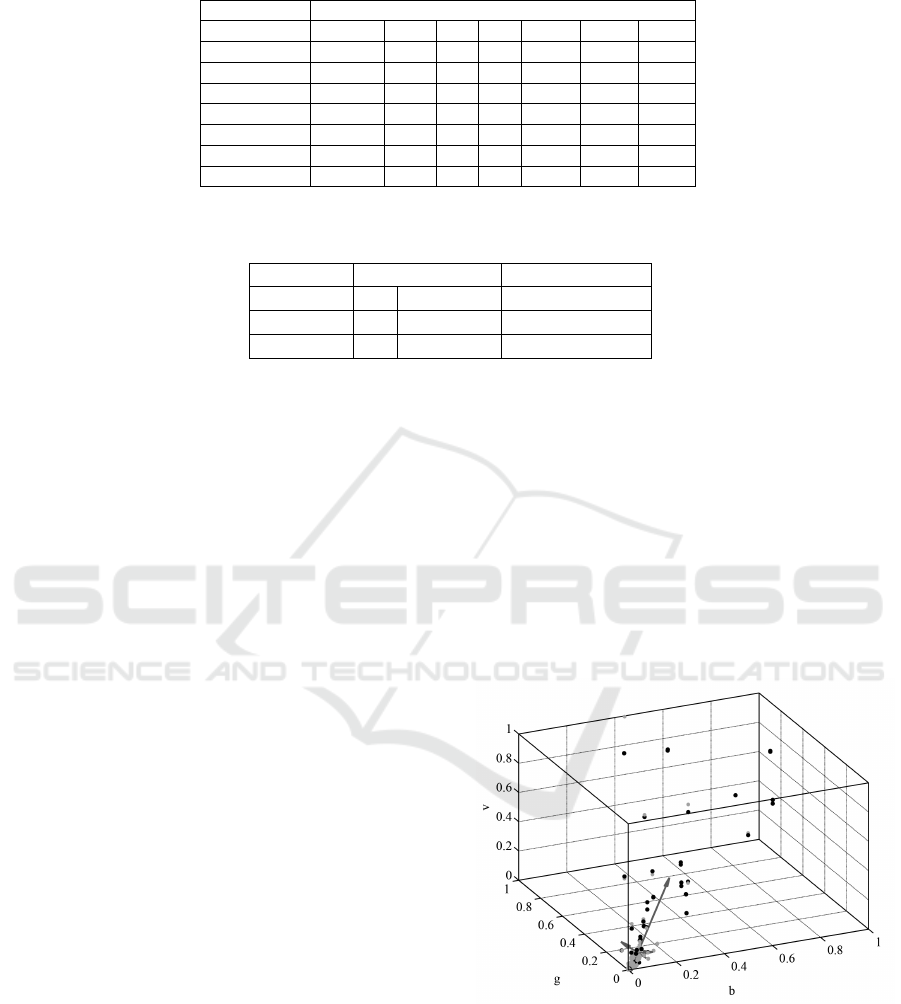
Table 2: Average performance over 50 trials for every classifier applied to the proposed set/subset of features.
Error rate (%)
Classifier (b,g,v) b g v (b,g) (b,v) (g,v)
LDA 5.2 5.2 5.2 4.8 5.2 5.2 4.8
QDA 3.3 3.3 2.9 4.8 3.8 3.3 3.8
k-NN 2.4 2.4 4.5 4.3 2.4 2.4 2.9
Naive Bayes 1.8 3.3 2.1 3.3 2.9 2.1 2.1
CART 3.3 3.8 2.4 4.7 2.9 3.3 2.9
PNN 5.2 6.7 5.2 8.5 5.2 5.2 5.2
FIS 4.3 16.2 3.8 9.5 4.8 4.3 3.3
Table 3: Confusion matrix resulting from the Naive Bayes classifier using the (b,g,v) dataset. F is the fibres class, P is the
particles class.
Estimated class Intra-class error
True class F P (%)
F 52 2 3.7
P 5 341 1.5
The numerical parameters to be set in advance for the
used classifiers have been determined using an inner
ten-fold cross-validation on each training subset: the
value of k in k-NN varied in the range (2,10), using
Euclidean distance. The value of the spread in PNN
varied in the interval (0.05,1) with a step of 0.05;
the number of rules within the FIS classifier varied in
the range (1,10). The following choices were made
within the used classifiers: for k-NN we set k = 3.
For the Naive Bayes classifier, the normal distribu-
tion with diagonal covariance was adopted as prior.
For the PNN the spread of the radial basis functions
was set to 0.1. The FIS classifier consisted of five
Mamdani-type fuzzy rules (Mamdani and Assilian,
1975).
The results in terms of misclassification errors for
each classifier and for every dataset, among all the
possible combinations of the proposed features, are
reported in Table 2. Since the training of some clas-
sifiers depends upon a random initialization of model
parameters, the averages over 50 different trials of the
above ten-fold cross-validation were performed.
The proposed approach for dust characterization
achieves valuable performances in terms of error rate
(i.e., below 5% of error) for most classification mod-
els and independently of the combination of features
in the dataset. A remarkable exception is constituted
by the FIS classifier if the single features b or v or the
pair (b,v) is involved.
In particular, the best performance was obtained
by the Naive Bayes classifier using the overall fea-
tures space (b,g,v), with an error rate smaller than
2%. The high performance of this classifier was not
unexpected, considering the low correlation among
the employed features. The confusion matrix related
to the results obtained through the Naive Bayes classi-
fier is reported in Table 3. Two fibres are misclassified
as particles, with an intra-class error of 3.7% within
the total 54 samples of fibres. Five particles are mis-
classified as fibre, with an intra-class error of 1.5%
within the total 346 samples of particles.
A 3-D plot of the classification results is shown
in Figure 9. The principal directions resulting from
the previously discussed SVD analysis were also re-
ported. In Figure 8, all the 2-D projections of the clas-
sified (b,g,v) dust dataset onto the three coordinate
planes are shown. It is interesting to note that the two
considered classes are well separable, even if it is im-
possible to employ for this purpose a simple spherical
or ellipsoidal surface.
Figure 9: A 3-D plot in the normalized (b,g,v) feature space
of the classified dust dataset using the Naive Bayes classi-
fier. Blacks dots are patterns classified as fibres and grey
dots are patterns classified as particles.
The approach proposed therein was compared to
other techniques: the early standard approach based
on grey-valued image analysis (Proietti et al., 2014)
and the approach based only on contour analysis
(Di Claudio et al., 2015). The results are reported in
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
252

Table 4: Comparison of the proposed approach (geometric features) with respect to other techniques: an early standard
approach based on grey-valued images analysis (Proietti et al., 2014), the approach based only on contour analysis (Di Claudio
et al., 2015) and an approach based on binary template matching (Proietti et al., 2015).
Algorithms Error rate
Geometric features 2%
Grey-valued images 15%
Contour analysis 4%
Template matching 9%
Table 4. Observe that the performance of the present
approach exceeds the performance of the said ones by
a sizeable margin.
As far as the computational costs are concerned,
the time required by all these algorithms for perform-
ing the classification task is comparable. They are less
than 100µs, referring to a x64 Intel(R) Core(TM) i7-
2600K CPU running at 3.40 GHz with 8 GB, 1333
MHz RAM.
Moreover, let us mention that an approach based
on binary template matching (Proietti et al., 2015)
was also tried in previous works (Proietti et al., 2015).
However, this technique yielded a misclassification
error greater than 9% with a much higher computa-
tional time.
5 CONCLUSIONS
A new approach for the classification of dust on the
basis of their size and typology (particles and fibres)
based on geometric features extracted from binary im-
ages was presented. The approach represents an ef-
fective choice in terms of speed and accuracy and re-
quires a very simple acquisition device.
Since the involved algorithms are essentially
multiplication-free, the global classification tech-
nique is very fast and energy saving. Hence, it is ideal
in distributed sensor networks and especially in wire-
less scenarios, where the processing power consump-
tion is a major problem, since the classification task
competes with the energy spent for communication
among sensing devices and image acquisition.
The aim of this paper is to propose a novel ap-
proach to features selection for fibres classification.
In the paper, encouraging results on real dataset by us-
ing well-known classification models have been pre-
sented. A deep assessment of more complex scenar-
ios, with different datasets and different classifiers,
will be considered in future contributions. Also, fu-
ture works will entail the use of enhanced optics over
the CMOS sensors to capture even smaller particles
and more detailed classification.
REFERENCES
Baron, P. (2001). Measurement of airborne fibers: A review.
Industrial Health, 39(2):39–50.
Bogomolny, A. (1987). On the perimeter and area of fuzzy
sets. Fuzzy Sets and Systems, 23(2):257 – 269.
Camuffo, D. (2013). Microclimate for Cultural Heritage:
Conservation, Restoration, and Maintenance of In-
door and Outdoor Monuments. Elsevier Science,
Boston.
Cover, T. and Hart, P. (1967). Nearest neighbor pattern clas-
sification. Information Theory, IEEE Transactions on,
13(1):21–27.
Di Claudio, E., Jacovitti, G., Orlandi, G., and Proietti, A.
(2015). Fast classification of dust particles from shad-
ows. In ICPRAM 2015 - 4th International Confer-
ence on Pattern Recognition Applications and Meth-
ods, Proceedings, volume 2, pages 241–247.
Drolon, H., Druaux, F., and Faure, A. (2000). Particles
shape analysis and classification using the wavelet
transform. Pattern Recognition Letters, 21(67):473 –
482.
Fisher, R. A. (1938). The statistical utilization of multiple
measurements. Annals of Eugenics, 8(4):376–386.
Ghedini, N., Ozga, I., Bonazza, A., Dilillo, M., Cachier, H.,
and Sabbioni, C. (2011). Atmospheric aerosol moni-
toring as a strategy for the preventive conservation of
urban monumental heritage: The florence baptistery.
Atmospheric Environment, 45(33):5979 – 5987.
Golub, G. and Loan, C. V. (1989). Matrix Computations.
John Hopkins University Press, Baltimore, USA, 2nd
edition.
Gonzalez, R. C., Woods, R. E., and Eddins, S. L. (2004).
Digital image processing using matlab. Upper Saddle
River, N. J: Pearson Prentice Hall.
ISO (2010). Cleanrooms and associated controlled envi-
ronments - part 1: Classification of air cleanliness by
particle concentration. ISO/DIS 14644-1.
Krzanowski, W. J., editor (1988). Principles of Multivariate
Analysis: A User’s Perspective. Oxford University
Press, Inc., New York, NY, USA.
Langley, P., Iba, and, W., and Thompson, K. (1992). An
analysis of bayesian classifiers. In Proceedings of the
Tenth National Conference on Artificial Intelligence,
AAAI’92, pages 223–228. AAAI Press.
Lawrence, R. L. and Wright, A. (2001). Rule-based classifi-
cation systems using classification and regression tree
(cart) analysis. Photogrammetric engineering and re-
mote sensing, 67(10):1137–1142.
Classification of Dust Elements by Spatial Geometric Features
253

Liparulo, L., Proietti, A., and Panella, M. (2013). Fuzzy
membership functions based on point-to-polygon dis-
tance evaluation. In Fuzzy Systems (FUZZ), 2013
IEEE International Conference on, pages 1–8. IEEE.
Maisto, M., Panella, M., Liparulo, L., and Proietti, A.
(2013). An Accurate Algorithm for the Identification
of Fingertips Using an RGB-D Camera. IEEE Jour-
nal on Emerging and Selected Topics in Circuits and
Systems, 3(2):272–283.
Mamdani, E. and Assilian, S. (1975). An experiment in
linguistic synthesis with a fuzzy logic controller. In-
ternational Journal of Man-Machine Studies, 7(1):1 –
13.
Panella, M. and Martinelli, G. (2011). Neural networks with
quantum architecture and quantum learning. Inter-
national Journal of Circuit Theory and Applications,
39(1):61–77.
Panella, M., Rizzi, A., and Martinelli, G. (2003). Refining
accuracy of environmental data prediction by MoG
neural networks. Neurocomputing, 55(3-4):521–549.
Panella, M., Rizzi, A., Mascioli, F. F., and Martinelli,
G. (2001). ANFIS synthesis by hyperplane cluster-
ing. In Proceedings of Joint IFSA World Congress
and NAFIPS International Conference (IFSA/NAFIPS
2001), volume 1, pages 340–345. IEEE.
Parisi, R., Cirillo, A., Panella, M., and Uncini, A. (2007).
Source localization in reverberant environments by
consistent peak selection. In Proceedings of IEEE
International Conference on Acoustics, Speech, and
Signal Processing (ICASSP 2007), volume I, pages I–
37–I–40. IEEE.
Proietti, A., Leccese, F., Caciotta, M., Morresi, F., Santa-
maria, U., and Malomo, C. (2014). A new dusts sen-
sor for cultural heritage applications based on image
processing. Sensors (Switzerland), 14(6):9813–9832.
Proietti, A., Liparulo, L., Leccese, F., and Panella, M.
(2016). Shapes classification of dust deposition using
fuzzy kernel-based approaches. Measurement, 77:344
– 350.
Proietti, A., Panella, M., Leccese, F., and Svezia, E. (2015).
Dust detection and analysis in museum environment
based on pattern recognition. Measurement, 66(0):62
– 72.
Purushotham, S. and Tripathy, B. (2012). Evaluation of
classifier models using stratified tenfold cross valida-
tion techniques. Communications in Computer and
Information Science, 270 CCIS(PART II):680–690.
Ranzato, M., Taylor, P., House, J., Flagan, R., LeCun,
Y., and Perona, P. (2007). Automatic recognition of
biological particles in microscopic images. Pattern
Recognition Letters, 28(1):31 – 39.
Reddy, P. R., Amarnadh, V., and Bhaskar, M. (2012).
Evaluation of stopping criterion in contour tracing
algorithms. International Journal of Computer Sci-
ence and Information Technologies (IJCSIT), 3:3888–
3894.
Rizzi, A., Buccino, M., Panella, M., and Uncini, A. (2008).
Genre classification of compressed audio data. In Pro-
ceedings of IEEE MMSP 2008, pages 654–659. IEEE.
Scardapane, S., Wang, D., Panella, M., and Uncini,
A. (2015). Distributed learning for random vec-
tor functional-link networks. Information Sciences,
301:271–284.
Specht, D. F. (1990). Probabilistic neural networks. Neural
Networks, 3(1):109 – 118.
Takagi, T. and Sugeno, M. (1985). Fuzzy identification of
systems and its applications to modeling and control.
IEEE Transactions on Systems, Man and Cybernetics,
15(1):116–132.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
254
