Unsupervised Clustering of Hyperspectral Images of Brain Tissues by

Hierarchical Non-negative Matrix Factorization

Bangalore Ravi Kiran

, Bogdan Stanciulescu

and Jesus Angulo

Centre de Robotique(CAOR), MINES ParisTech, PSL-Research University, Paris, France

Centre de Morphologie Mathematique(CMM), MINES ParisTech, PSL-Research University, Fontainebleau, France

Keywords:

Hyperspectral Image, Unsupervised Clustering, Brain Tissue, Non-negative Matrix Factorization.

Abstract:

Hyperspectral images of high spatial and spectral resolutions are employed to perform the challenging task of

brain tissue characterization and subsequent segmentation for visualization of in-vivo images. Each pixel is

high-dimensional spectrum. Working on the hypothesis of pure-pixels on account of high spectral resolution,

we perform unsupervised clustering by hierarchical non-negative matrix factorization to identify the pure-

pixel spectral signatures of blood, brain tissues, tumor and other materials. This subspace clustering was

further used to train a random forest for subsequent classiﬁcation of test set images constituent of in-vivo and

ex-vivo images. Unsupervised hierarchical clustering helps visualize tissue structure in in-vivo test images

and provides a inter-operative tool for surgeons. Furthermore the study also provide a preliminary study of the

classiﬁcation and sources of errors in the classiﬁcation process.

1 INTRODUCTION

Medical Hyperspectral imaging (MHSI) is a non-

invasive and non-ionizing modality used in robust tis-

sue identiﬁcation, characterization achieved reason-

able classiﬁcation and localization accuracy in of var-

ious kinds of cancerous tissues on account of vast

improvements in spectral and spatial imaging reso-

lutions (Lu and Fei, 2014). Discriminating cancer-

ous and normal tissues with Near Infra-Red (NIR)

spectroscopy has been an active topic in the past

two decades. (Panasyuk et al., 2007) study the use

of MHSI for identifying residual tumor in a resec-

tion bed and to indicate regions requiring more re-

section. (Lu et al., 2014) use HSI in-vivo to achieve

tumor identiﬁcation in tumor bearing mice. (Liu

et al., 2011) study localization of tumor tissue on

the tongue of human patients using a tunable HSI

camera. In this study we study the characteriza-

tion and identiﬁcation of brain tissues by perform-

ing joint clustering and un-mixing. We also demon-

strate the utility of the hierarchical clustering as a vi-

sual aid for inter-operative(IoP) procedures (Schulder

and Carmel, 2003) in the resection of cancerous tis-

sue. Though one should note that the standard in IoP

brain tumor surgery modality has been MRI, it is pre-

cise but a costly technology. Hyperspectral images

are cheaper and furthermore faster to acquire.

The primary goal of this paper is to address the

common problem of lack of an exact ground truth la-

bels in the hyperspectral images in-vivo. This pro-

duces a challenging problem of hyperspectral image

segmentation and classiﬁcation. Our solution consists

in generating unsupervised clustering that can serve

as a stable identiﬁcation and labeling, for a subse-

quent semi-supervised classiﬁcation. Further we note

that, it is unrealistic to obtain a well localized marker

of tumors, in-vivo, during a surgical procedure, in

view of different constraints of space and time. Fi-

nally we also do not know the exact spectrum of can-

cerous and normal tissue at this stage of our study. We

do note that from previous studies on different tumor

types, normal and cancerous tissue spectra are close

(see subsection 4), and are difﬁcult to distinguish.

We thus characterize the tissue by clustering their

spectrum in similar subspaces. This helps visualize

different structures in the tissue as well as locate tu-

mors and related structures. Unsupervised clustering

is rarely followed, for such problems, but given that

we operate at high spatial and spectral resolutions, we

stand to gain some useful information. We use the

clustering of ex-vivo tumors with surrounding tissue,

blood and other structures as a target model we pre-

dict the location of tumors in in-vivo images. Finally,

the clustering will also be used as tool by surgeons

and pathology to label the tissues to generate ground

Kiran, B., Stanciulescu, B. and Angulo, J.

Unsupervised Clustering of Hyperspectral Images of Brain Tissues by Hierarchical Non-negative Matrix Factorization.

DOI: 10.5220/0005697600770084

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 2: BIOIMAGING, pages 77-84

ISBN: 978-989-758-170-0

Figure 1: We classify the input images into three categories: In-vivo images (during surgery), Ex-vivo images (extracted tumor

after surgery) and material cubes (carefully windowed regions containing only surgical material). Black plastic rings markers

highlight the locations of healthy tissue and a tumor tissue in a scene. The ex-vivo images serve as localized target that ensure

the presence of tumor tissue in a localized window. We partition the operations into a training and test set, after which we

perform hierarchical clustering on the test images. The H2NMF clustering algorithm also performs unmixing and calculates

the endmembers for each cluster. We use clusters at a particular level to train a random forest classiﬁer. We demonstrate the

classiﬁcation on other ex-vivo and in-vivo images in the test set. The ﬂow-diagram at the bottom illustrates all the steps in our

study.

truth data.

The primary contributions of the paper include the

identiﬁcation of pure-spectrum or pure-pixels of ma-

terials using VNIR camera images of brain tumors by

applying the hierarchical clustering by 2-rank NMF

approximation (Gillis et al., 2015). Pure-pixels are

found at the leaves of this hierarchical structure and

correspond to rank-1 matrices. This is discussed in

section 2. We use the unsupervised clustering as su-

pervised labels to identify these pure-pixels in the

in-vivo images by training a decision forest. See

ﬁgure 1 for a summary of the work-ﬂow. The or-

ganization of the paper is as follows. We describe

brieﬂy the imaging setup in this section, in section

2 we provide a brief introduction to endmember ex-

traction, the separable non-negative matrix factoriza-

tion(NMF) and the hierarchical NMF decomposition

algorithm (Gillis et al., 2015) employed in this study.

Imaging Setup: The medical imaging demon-

strator consists of two camera pairs covering differ-

ent parts of the spectrum at different spatial reso-

lutions, a VNIR (visible-to-near-infrared) and NIR

(near-infrared cameras) cameras. The VNIR cam-

era captures 826 spectral bands, in the spectral range

of 400-1000 nm with a spectral resolution of 2-3

nm, and each pixel has a dimension of 0.1287 mm

x 0.1287 mm. While the NIR camera captures 172

spectral bands, in the spectral range of 900-1700 nm,

each pixel has a dimension of 0.48 mm x 0.48 mm.

We shall work with the VNIR camera images mainly

since they consist of precise spectral information. The

increment in wavelength is 1.9285 nm for the current

setup. Images are calibrated using a standard white

and dark reference.

In this study we work on hyperspectral images

from a VNIR camera with a very high spatial and

spectral resolution. Images were obtained of the brain

tissue and brain tumors, in-vivo (brain tissue open

during surgery) and ex-vivo (extracted brain tumor on

surgical table). Images were obtained over 20 opera-

tions. The images from both cameras were obtained

during the surgical procedure. The information of the

type of tumor and other associated patient information

was missing during the current paper’s study. This

will be discussed more in detail. The images were

taken during the surgical procedure (in-vivo) and right

after the procedure outside the body (ex-vivo) with

the extracted tumor placed under the camera. In this

paper we restrict our study to the VNIR camera im-

ages due to their high spectral and spatial resolution.

2 UNMIXING

Hyperspectral unmixing is the problem of inferring

which are the materials in the scene (visible directly

or visible as a mixture) by the general process of di-

mensionality reduction. This basically consists in de-

composing a hyperspectral image X = [x

, x

, ...x

]

with n pixels, where each pixel x

is p-dimensional

spectrum. The two elements of the decomposition

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

Figure 2: Segmentation Hierarchy showing a tumor ex-vivo decomposed at different levels r = 1 to 32 of the hierarchical

2-rank decomposition (H2NMF) algorithm. The 2-rank approximation divisional step is used is to arrive with a unit rank

matrices and the leaves of the hierarchical decomposition. The labels in the segmentations are consistently colored to match

with the tree nodes. They help show the persistence of a subspace/clustering visually. This tree structure gives an visual idea of

the structure of the tissue, labels in that are close in terms subspaces branch. By viewing the endmembers (spectra) at different

levels, we can infer visually that blood is a dominant material in the scene (blue peak around 400nm). The shallow clusters

correspond to submatrices of low approximation error which close to rank-1 and thus correspond to a single tissue/material.

are a set of r reference spectra or endmembers and

W = [w

, w

, ...w

] and their relative proportions at

each pixel(abundances) H = [h

, h

, ...h

], where, w

is a p-dimensional spectrum and h

is r-dimensional

coefﬁcient weights. The spectrum at a pixel is a con-

vex composition of endmembers. This imposes two

conditions: Firstly the abundances need to be positive

and the sum of abundances by each endmember sum

to unity at each pixel (Ma et al., 2014). The goal of

the hyperspectral unmixing(HU) or endmember ex-

traction process is to obtain the spectrum that corre-

sponds to “pure” materials in the scene. This can be

a complex problem based on the physical interactions

between the materials, rays and the reﬂections. We

assume the Linear mixing model(LMM) for its inher-

ent simplicity and popularity in the remote sensing

community. The model assumes that at a given pixel

location the incident ray interacts only with one mate-

rial in the true site of the pixel. Given the spectral and

spatial resolution of the VNIR camera, this assump-

tion seems to be a reasonable.

Separable NMF: Endmember extraction is well stud-

ied as a problem of non-negative matrix factoriza-

tion problem since it respects the endmember con-

straints. It is written as a matrix factorization problem

X ≈ W H, where this approximation is often evaluated

by minimizing the Frobenius norm of the residual

kX −WHk

. Independent of how the decomposition

is calculated the NMF, geometrically it generates the

vectors h

(endmembers) whose simplicial cone con-

tains all the data points {x

} ∈ X. There can be many

cones possible and the decomposition is non-unique.

In case of high spatial and spectral resolution of HSI

cubes, one can make the hypothesis that there exists

pixels in the image which themselves form the bound-

ing vertices of the a convex cone, and thus directly

the endmembers. Physically this means that given a

pixel spectrum we can infer the material it contains

and be sure that its contribution is from a single ma-

terial. This is called the separability condition (Gillis

and Luce, 2014) under which we obtain a unique and

tractable decomposition of the NMF problem. Geo-

metrically, the separability condition reformulates the

NMF problem as that of ﬁnding the extreme rays of

the conical hull of a ﬁnite set of vectors. Given a HSI

cube X ∈ R

n×p

, we can write its separable NMF de-

composition as

X = W H = W [I

, H

]Π (1)

where W ∈ R

m×r

, H

> 0, Π is a permutation matrix,

which rotates the r different endmembers. Columns

of W are the endmembers, while the entry H(i, j) are

the abundances/scalar coefﬁcient of the ith endmem-

ber at the jth pixel in X. Geometrically this corre-

sponds to the convex hull of the columns of X.

Hierarchical Two-rank NMF: The hierarchical two

rank NMF (H2NMF) ﬁrst introduced in the paper

(Gillis et al., 2015) aims at obtaining a rank-1 sub-

matrix by hierarchical application of a NMF decom-

position. The decomposition step consists of a, ﬁrst

projecting the data points on to the ﬁrst two eigen

vectors, and thus a 2-d cone, by calculating the singu-

lar value decomposition(SVD). Second, the direction

matrix is approximated by a separable NMF decom-

positions, namely the SPA (Gillis and Luce, 2014) of

the data points under decomposition.

This yields pure-pixels in the HSI cube approxi-

mating the ﬁrst principle component. The goal is to

Unsupervised Clustering of Hyperspectral Images of Brain Tissues by Hierarchical Non-negative Matrix Factorization

ﬁnally arrive with a set of leaves which which are of

rank. This corresponds to pure-pixel or a single ma-

terial. Though this hierarchical method is provided,

the stopping condition for the growth of the hierarchy

is not provided. Instead this is a parameter of the al-

gorithm that determines the number of endmembers

being extracted. At each step of this divisional hier-

archical clustering step, the approximation error min-

imized is (Gillis et al., 2015),

= σ

(X(:, K

))+σ

(X(:, K

))−σ

(X(:, K

)) (2)

where σ

refers to the ﬁrst singular value of the ma-

trices, and K

corresponds to the indices of the parent

and K

, K

are indices of the child clusters in the bi-

nary split. This approximation error corresponds to

the rank approximation of input cluster or matrix.

The split is decided by choosing line after the pro-

jection on to a 2-d cone. This is chosen by parameter

∗

(see algorithm 1) so as to have a balanced set of

points across the split (Gillis et al., 2015) as well a

clusters with elements that are homogeneous.

The H2NMF algorithm apart from clustering per-

forms unmixing by generating and endmember asso-

ciated with each cluster. To evaluate the endmem-

ber corresponding to a cluster that is supposed to be

a rank-1 approximation of sub-matrices, we follow

(Gillis et al., 2015)’s measure. Mean removed spec-

tral angle(MRSA) is deﬁned for any two pairs of spec-

tra x, y as:

φ(x, y) =

arccos



(x − ¯x)

(y − ¯y)

kx − ¯xk

ky − ¯yk



∈ [0, 1] (3)

where for a vector z ∈ R

, ¯z =

∑

i=1

. The MRSA

provides the a measure to compare the pure-pixel

in the input sub-matrix and its endmember spectrum

produced by a rank-2 NMF decomposition. We use

MRSA to evaluate the homogeneity of the hierarchi-

cal clustering at different levels.

We use the H2NMF algorithm (see Algo. 1) to

provide a hierarchical subspace decomposition of the

ex-vivo cubes to recover the pure-pixels by varying

the level of decomposition. The decomposition is ro-

bust to noise and calculates quickly, given the huge

sizes of the datasets (X’s size is several 100000 pixels

× 800 wavelengths). Secondly we visualize the hier-

archical clustering structure which provides us a way

to localize different tissue based on their paths in the

hierarchy. In ﬁgure 2 we can observe from the clus-

tering and the endmembers that, blood (endmember

spectrum in blue, peaking around 400 nm for r = 4,

8, 12) at various levels of the hierarchy. Continuing

further r > 8 we see that the tissues themselves are

seen to have different layers and structuring of these

layers.

3 EXPERIMENTS AND ANALYSIS

We partition the operations (numbered 1-20) into a

two disjoint sets: ﬁrst the training set over which we

perform unsupervised clustering and subsequent clas-

siﬁer training, second the test set over which we pre-

dict the cluster labels. We predict both on in-vivo and

ex-vivo images from different operations in the test

set to evaluate the validity of the different cluster la-

bels. The training set consists of ex-vivo images, ma-

terial cubes and certain windows from In-vivo images

that contain synthetic surgical materials such as cot-

ton, plastic cables and straps, as demonstrated in ﬁg-

ure 1. The training set also contains supplementary

tissue information such skull and surrounding tissues.

Ideally this process captures the dictionary of materi-

als to be clustered in the same subspace.

Training Set: The training set is a union of pix-

els from images of the tumor ex-vivo and dictionary

of materials such as plastic and cotton, from the train-

ing subset of operations. We denote the training im-

ages by X

train

∈ R

N×p

, where N are the total num-

ber of pixels in the training set images together, and

p = 826 is the dimensionality of the spectra at each

pixel. The ex-vivo and material cubes in the test set

will be clustered together so as to separate the dif-

Algorithm 1: H2NMF (Gillis et al., 2015).

1: procedure H2NMF(X ∈ R

p×n

)

2: K

← {1, 2, ..., n} and K

←

0 for 2 ≤ i ≤ r

3: (K

), K

) = 2-rank-Split(X, K

)

4: while k < r do

 Iterate until r-clusters are reached

5: j = arg max

i=[1,2...r]

from eq(2)

 pick cluster j with largest error

6: K

= K

, K

= K

 update cluster j into j and k

7: (K

, K

) = splitting(X, K

)

8: (K

, K

) = splitting(X, K

)

9: return K

 cluster indices forming hierarchy

10: procedure SPLITTING(X ∈ R

p×n

, K ⊂

{1, 2, ...n})

11: [W, H] = rank2NMF(X(:, K ))

 Projection onto 2-d cone

12: x(i) =

H(1,i)

H(1,i)+H(2,i)

13: Compute split parameter δ

∗

 parameter

trades-off balanced split and cluster homogeneity

14: K

= {K (i)|x(i) ≥ δ

∗

}

15: K

= {K (i)|x(i) < δ

∗

}

16: return K

, K

 return 2-sets of

indices corresponding to two sub-matrices of the

input-matrix X.

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

Figure 3: H2NMF clustering on the training set X

train

which consists of input ex-vivo tumor tissue HSI cube and on materials.

We in this case the ring on a cotton, and a cable in scene with open cranium and healthy tissues. This labeling with the

corresponding HSI cubes serves as the training set for constructing the random forest classiﬁer.

ferent pure-pixels corresponding to different materi-

als The training set does not contain any in-vivo im-

ages since images containing the target tumor samples

shall remain unlabelled and not part of a class.

Test Set: The test set consists of both types of

images: Images ex-vivo of the tumor, and images in-

vivo from operations not in the training set. We refer

to the different test cubes/images as X

and their cor-

responding classiﬁcation map by the random forest as

We use algorithm (1) described in section 2 to per-

form hierarchical clustering of the training-images.

The principal goal here is to visualize the tissue struc-

ture as decomposed by the hierarchical clustering and

aid a surgeon or expert in annotating these images.

Another important goal is to determine the depth of

the hierarchy at which we are able to separate the

tumor, blood, tissues and materials and extract their

endmembers or spectral signatures.

3.1 Cluster Evaluation

In this section we compare the performance of

H2NMF, the clustering method used in our study,

with respect to other clustering algorithms: hier-

archical K-means(HKM), hierarchical spherical K-

means(HSKM). For the cases of NMF when used as

a clustering method, one does not explicitly use a dis-

tance function or dissimilarity (Kuang, 2014). The

prediction strength (Tibshirani and Walther, 2005) is

a well suited measure for cluster validation for NMF-

based clustering because it does not rely on a distance

function. Here we introduce a method similar to the

one described in (Kuang, 2014) to evaluate the NMF.

Given matrix X we split them into X

train

, X

train

over

which we obtain NMF decompositions, giving us

argminkX

train

−W

train

argminkX

test

−W

test

(4)

Now the prediction error can be obtained by solving

the non-negative least-squares problem for

predict

= argminkX

test

−W

train

(5)

We then compare the maximum abundance values in

test

, H

predict

to check which endmember index con-

tributed the most, and use this a measure of prediction

strength. This is because the H2NMF algorithm pro-

vides decomposition with one dominant endmember.

This is a variant on the classical prediction strength

measure (Tibshirani and Walther, 2005). We demon-

strate the results for the three hierarchical clustering

algorithms. The prediction strength provides us a way

to calculate the optimal number of clusters. Figure 4

demonstrates the prediction strength calculated over

random samples of the training set X

train

. This mea-

sure could also provide a reasonable guide in deter-

mining which clusters to split, aside the approxima-

tion error. We plot the maximum value of MRSA

from equation (3) for different number of clusters in

in ﬁgure 4. This demonstrates how far the pure-pixel

in cluster in a given level of hierarchy from its rank-2

NMF approximation. The ﬁgure also shows the plot

of the average approximation error in eq. 2 over dif-

ferent leaf sub-matrices for the three hierarchical clus-

tering algorithms. Both of these measures provide us

a tool to asses if the spectrum and sub-matrix at a leaf

are well approximated by a pure-pixel. Finally, we

evaluate the hierarchical clusters intrinsically by us-

ing the gap statistic (Tibshirani and Walther, 2005)

Unsupervised Clustering of Hyperspectral Images of Brain Tissues by Hierarchical Non-negative Matrix Factorization

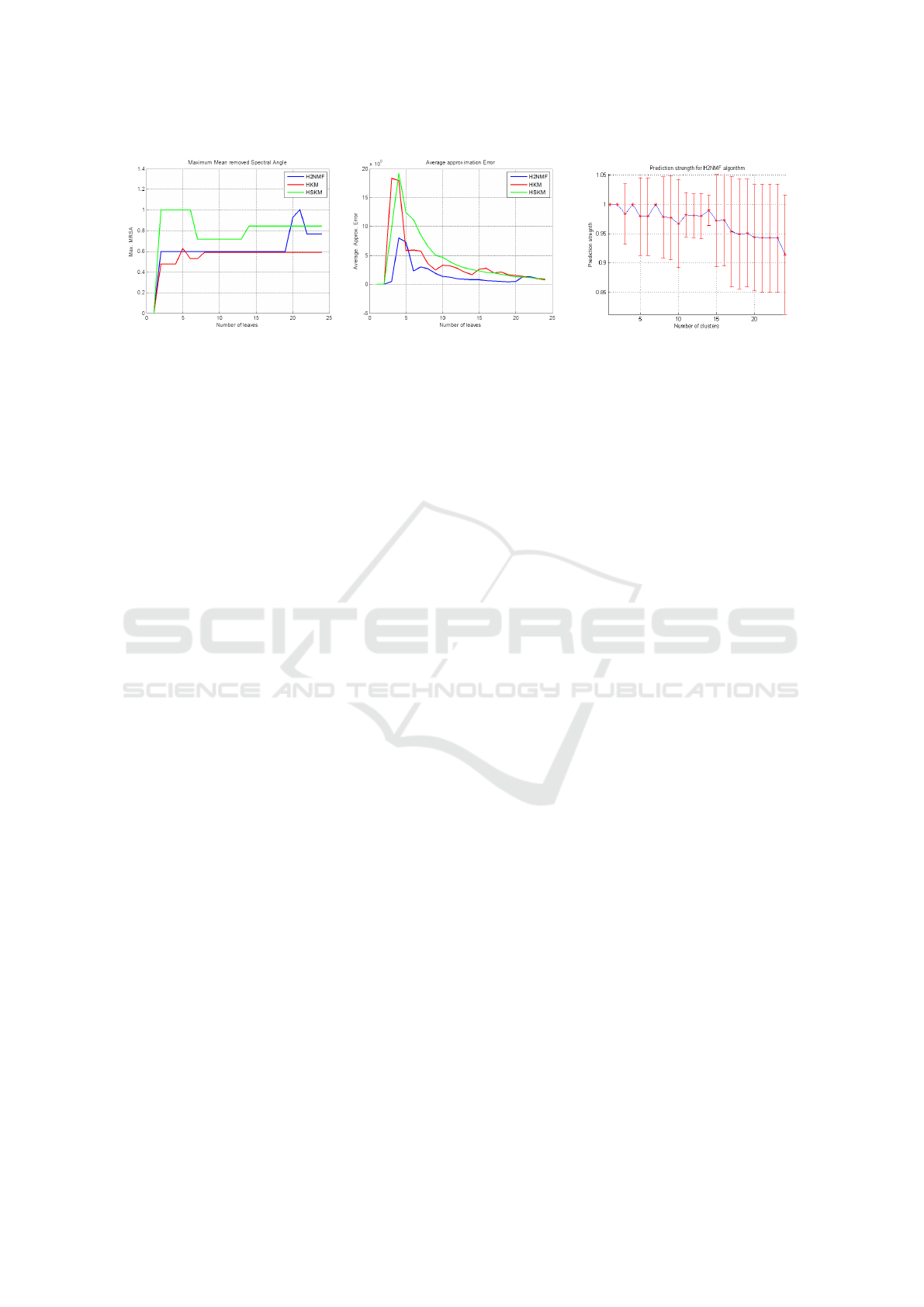
Figure 4: Left: the variation of the maximum MRSA(mean-removed spectral angle) to evaluate the homogeneity of clusters

in terms of endmember signature. This is evaluated across the three hierarchical clustering algorithms: H2NMF, HSKM,

HKM. We observe that all the three algorithms provide a good. Center: ﬁgure also shows the variation approximation error in

equation (2) with increasing leaves for three hierarchical clustering algorithms. Right: Plot demonstrating the mean prediction

strength calculated using the NMF decomposition. The red bars show the variance of the prediction strength. Optimal clusters

are chosen based on the maximum of the prediction strength. Here for example it is 14.

which using the average pairwise dissimilarity per

cluster to evaluate the number of clusters graphically,

by looking for an elbow.

We now train the resulting clustering on the train-

ing set X

train

. We use the Matlab’s implementation of

the random forest to train the Random forest(RF) with

the weak learner set to axis-aligned-hyperplane. We

ﬁrst cut the subspace hierarchy by choosing the num-

ber of clusters r, and then use the clusters as labels to

train the RF-classiﬁer.

The predictions of the RF-classiﬁer are shown in

ﬁgure 5 when trained on two different levels of clus-

tering. We remark here that the actual subspace hi-

erarchy obtained by a sequence rank-2 NMF decom-

positions, is not completely approximated by the RF-

classiﬁer. Nevertheless we do see a reasonable seg-

mentation. The rings shown in the in-vivo images

correspond to physical markers that were placed and

localize healthy and tumor tissues for evaluation pur-

poses. We do not obtain a single cluster label that

might correspond to tumor. To improve the classiﬁ-

cation it would be ideal to integrate the structure of

the subspace hierarchy. This can be done by learning

a random forest for each level in the hierarchy. This

would of course be costly. A more principled solu-

tion would be to minimize an appropriate loss func-

tion that approximates the original subspace hierar-

chy.

The resulting segmentation from the classiﬁer pro-

vides ﬁrstly the stable pure signatures of different ma-

terials in the ex-vivo tumors. The results are veriﬁed

basically by checking the presence of unique label (or

sets of labels) in a ring (1)) in the in-vivo images.

The tissue samples within these rings have been ver-

iﬁed posteriori by pathology. One ring is assured to

surround a cancerous tissue sample, while the other

a healthy one. In this setup there was estimate of

the depth cancerous and its uniform exposure to the

VNIR-camera. This is tough to ensure during critical

surgeries. The color-map of the classiﬁcation result in

ﬁgure 5 correspond to the color-map of the unsuper-

vised clustering in ﬁgure 3. The semantic meaning

of the labels is temporary and the color-map further

requires veriﬁcation by a surgeon or pathology ex-

pert, to which ﬁnally a more sensible name shall be

attached. But it is evident that we are able to identify

plastic surgical materials, cotton.

4 ISSUES

Spectral Proximity of Benign and Malignant Tis-

sues: (Sahu et al., 2013) study differentiation be-

tween benign and malignant tumors in canine mam-

mary tumors, and detect tumors using a imaging spec-

trometer. Ovarian tissue characterization and tumor

differentiation (Utzinger et al., 2001), were performed

using NIR spectroscopy. The results showed that both

slope and intensity of reﬂectance spectra may have

the ability to discriminate normal from abnormal con-

ditions of the ovary. Slopes between 510 nm and

530 nm were most discriminatory for ovaries, while

630 nm to 900 nm in the study on kidneys (Peswani,

2007). The differences between malignant and benign

tissues in human breast tissues, have been attributed to

the metabolic difference due to the presence of more

oxy-hemoglobin, lipids and water. These elements

were used as the spectral markers considered for the

additive construction of the spectrum. (Kukreti et al.,

2010). This proximity in the spectral response of nor-

mal, benign and malignant tumor plays an crucial role

in classiﬁcation of tumors pixels. In our study, due

the lack of information on the actual spectrum of tu-

mor tissues we are unable to provide a good division

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

Figure 5: Results of the classiﬁcation on the test set which consists of Ex-vivo images and In-vivo images test-set. Two sets

of classiﬁcation maps are shown, the top image tile corresponding to learning the labels by cutting the subspace tree at r = 18

clusters and the bottom tile at r = 24. We observe that there are different tissue structures and materials found in the original

clustering in ﬁgure 3. It would be ideal to have a cluster/endmember corresponding to the tumor, though we remark that it

is not obvious to extract them or check for their existence. We can also notice that there are sets of labels co-occurring in

the marker rings though no trivial or consistent co-occurrence that can ensure a tumor detection. We can also notice in the

ﬁgure that certain materials have been approximated by the same subspace cluster: the cotton and the plastic. This can also be

visually conﬁrmed by look at the subspace tree. Discriminating materials in this subspace tree structure is a crucial analysis

tool. As already mentioned, multiple classiﬁers are needed to approximate well the subspace clustering hierarchy. This would

merge the two levels of classiﬁcation in this image into a more precise classiﬁcation map.

of the subspace and the subsequent reﬁnement of de-

cision boundary between normal and possible cancer-

ous tissue.

Specular Reﬂections. Specular reﬂections are a

prime problem in all our clustering and classiﬁcation

steps and contributes to mis-classiﬁcation. Specular

reﬂection occurs when the light source can be seen

as a direct reﬂection on the surface of the tissue un-

der study. The pixels affected by specular reﬂection

contain mainly the light source and may or may not

contain sufﬁcient information on the reﬂectance of the

tissue under study. These reﬂected rays may also be

suspect of undergoing multiple reﬂections. An exam-

ple is shown in ﬁgure 6.

Figure 6: An in-vivo image and its classiﬁcation map with

the specular reﬂection marked in dotted red ellipse. This

phenomena is not restricted to the optical range.

5 CONCLUSION

In this paper we applied and studied the hierarchi-

cal rank-2 NMF unmixing and clustering to segment

Unsupervised Clustering of Hyperspectral Images of Brain Tissues by Hierarchical Non-negative Matrix Factorization

brain tissue structure in an unsupervised setting. Sub-

sequently we have tried to train a random forest to

learn the structure of the subspace clusters.

Subspace Learning and Spatial Features:

Though the classiﬁer can’t discriminate between nor-

mal tissues and tumor spectra, it provides a good seg-

mentation of the tissues and surgical materials in the

scene. The H2NMF hierarchy provides a hierarchy of

low rank sub-matrices that contain pure-pixels, and in

this case correspond to different brain tissues. This

cluster hierarchy can further be used by a surgeon in

loop to search more pertinent subspaces and feed the

results back to the classiﬁer. We have seen the effect

of learning classiﬁers on different levels of the hier-

archical clustering. Though this produces reasonable

segmentations, it does not approximate the subspace

hierarchy exactly. We will study how to deﬁne loss

functions to encode this structure. Given that the dif-

ference in spectrum between tumor tissues and nor-

mal tissues are small, and prone to noise and varia-

tions across patients, building a robust spatial struc-

ture descriptor is important. One of the results of

our study points to the fact that the tissue structures

surrounding a tumor is a key feature. There is al-

ready evidence that in the micro-scale these normal

and cancerous tissues have a different toplogical ar-

rangement (Dvorak, 2003). This structural informa-

tion of tumor is useful to obtain a better detector for

cancerous tisues in hyperspectral images, since spec-

trum alone is not sufﬁcient to classify them robustly.

Spatio-spectral features have been used in (Lu et al.,

2014), though our aim in the future is to use the spatial

features extracted by scattering-transform (Bruna and

Mallat, 2013) on the different abundance maps ex-

tracted by the hierarchical clustering algorithm. This

enables us to perform a principled search for features

across various scales.

ACKNOWLEDGEMENT

This work has been supported in part by the Euro-

pean Commission through the FP7 FET Open pro-

gramme ICT-2011.9.2, by the European Project HE-

LICoiD “HypErspectral Imaging Cancer Detection”

under Grant Agreement 618080.

REFERENCES

Bruna, J. and Mallat, S. (2013). Invariant scattering con-

volution networks. IEEE Trans. Pattern Anal. Mach.

Intell., 35(8):1872–1886.

Dvorak, H. F. (2003). How tumors make bad blood ves-

sels and stroma. The American journal of pathology,

162(6):1747–1757.

Gillis, N., Kuang, D., and Park, H. (2015). Hierarchi-

cal clustering of hyperspectral images using rank-two

nonnegative matrix factorization. IEEE T. Geoscience

and Remote Sensing, 53(4):2066–2078.

Gillis, N. and Luce, R. (2014). Robust near-separable

nonnegative matrix factorization using linear opti-

mization. Journal of Machine Learning Research,

15:1249–1280.

Kuang, D. (2014). Nonnegative matrix factorization for

clustering. PhD thesis, Georgia Institute of Technol-

ogy.

Kukreti, S., Cerussi, A. E., Tanamai, W., Hsiang, D.,

Tromberg, B. J., and Gratton, E. (2010). Characteriza-

tion of metabolic differences between benign and ma-

lignant tumors: High-spectral-resolution diffuse opti-

cal spectroscopy. Radiology, 254(1):277–284.

Liu, Z., Wang, H., and Li, Q. (2011). Tongue tumor de-

tection in medical hyperspectral images. Sensors,

12(1):162–174.

Lu, G. and Fei, B. (2014). Medical hyperspectral imaging:

a review. Journal of biomedical optics, 19(1):010901–

010901.

Lu, G., Halig, L., Wang, D., Qin, X., Chen, Z. G., and Fei,

B. (2014). Spectral-spatial classiﬁcation for nonin-

vasive cancer detection using hyperspectral imaging.

Journal of biomedical optics, 19(10):106004–106004.

Ma, W.-K., Bioucas-Dias, J., Chan, T.-H., Gillis, N., Gader,

P., Plaza, A., Ambikapathi, A., and Chi, C.-Y. (2014).

A signal processing perspective on hyperspectral un-

mixing: Insights from remote sensing. Signal Pro-

cessing Magazine, IEEE, 31(1):67–81.

Panasyuk, S., Yang, S., Faller, D., Ngo, D., Lew, R., Free-

man, J., and Rogers, A. (2007). Medical hyperspectral

imaging to facilitate residual tumor identiﬁcation dur-

ing surgery. Cancer Biol Ther, pages 439–46.

Peswani, D. L. (2007). Detection of Positive Can-

cer Margins Intra-operatively During Nephrectomy

and Prostatectomy Using Optical Reﬂectance Spec-

troscopy. ProQuest.

Sahu, A., McGoverin, C., Pleshko, N., Sorenmo, K., and

Won, C.-H. (2013). Hyperspectral imaging system

to discern malignant and benign canine mammary tu-

mors. In SPIE Defense, Security, and Sensing, pages

87190W–87190W. International Society for Optics

and Photonics.

Schulder, M. and Carmel, P. W. (2003). Intraoperative

magnetic resonance imaging: impact on brain tumor

surgery. Cancer Control, 10(2):115–124.

Tibshirani, R. and Walther, G. (2005). Cluster validation

by prediction strength. Journal of Computational and

Graphical Statistics, 14(3):511–528.

Utzinger, U., Brewer, M., Silva, E., Gershenson, D., Blast,

R. C., Follen, M., and Richards-Kortum, R. (2001).

Reﬂectance spectroscopy for in vivo characterization

of ovarian tissue. Lasers in surgery and medicine,

28(1):56–66.

BIOIMAGING 2016 - 3rd International Conference on Bioimaging