Graph Fragmentation Problem

Juan Piccini, Franco Robledo and Pablo Romero

Laboratorio de Probabilidad y Estad

ıstica, Instituto de Matem

atica y Estad

ıstica, Prof. Ing. Rafael Laguardia (Imerl),

Facultad de Ingenier

ıa, Universidad de la Rep

ublica, Julio Herrera y Reissig 565, Montevideo, Uruguay

Keywords:

Graph Theory, Combinatorial Optimization Problem, Metaheuristics, GRASP, Path Relinking.

Abstract:

A combinatorial optimization problem called Graph Fragmentation Problem (GFP) is introduced. The decision

variable is a set of protected nodes, which are deleted from the graph. An attacker picks a non-protected

node uniformly at random from the resulting subgraph, and it completely affects the corresponding connected

component. The goal is to minimize the expected number of affected nodes S. The GFP ﬁnds applications

in ﬁre ﬁghting, epidemiology and robust network design among others. A Greedy notion for the GFP is

presented. Then, we develop a GRASP heuristic enriched with a Path-Relinking post-optimization phase.

Both heuristics are compared on the lights of graphs inspired by a real-world application.

1 INTRODUCTION

In robust network design, the major cause of con-

cern is connectivity. The goal is to ﬁnd a mini-

mum cost design, meeting high connectivity require-

ments. Network connectivity is a rich ﬁeld of knowl-

edge, and the related literature is vast (Monma et al.,

1990; Stoer, 1993). However, in several real-world

applications a malfunctioning or affection of a sin-

gle element is immediately propagated to neighbor-

ing elements. This is the case of ﬁre ﬁghting, elec-

tric shocks, epidemic propagations, etc., where an in-

correct protection scheme might have catastrophic ef-

fects. In this paper, an abstract setting of the previous

problems is presented as a combinatorial optimiza-

tion problem. The reader can ﬁnd problems related

with graph partitioning, which are similar in nature

to ours in (Borgatti, 2006), (Ortiz-Arroyo, 2010). In

(Borgatti, 2006), the author studies a combinatorial

problem inspired in game theory, where key players

are protected (deleted) in order to cope with network

attackers. Several scores are proposed in order to cap-

ture a notion of network resilience. In (Ortiz-Arroyo,

2010), an entropy-based score is considered for net-

work resilience. In this article we consider a score

which is slightly different to that of Borgatti. Ad-

ditionally, we mathematically prove sufﬁcient condi-

tions for a solution to be optimal. These properties

are then used as part of a GRASP heuristic. The doc-

ument is organized in the following manner. Section 2

formally presents the Graph Fragmentation Problem.

Desired properties of candidate solutions are included

in Section 3. A Greedy notion and a more sophisti-

cated heuristic for the GFP is developed in Section 4.

Section 5 shows the results of both heuristics in a real-

world application, while Section 6 presents conclud-

ing remarks.

2 GRAPH FRAGMENTATION

PROBLEM

We are given a simple graph G = (V, E) and a bud-

get constraint B. The decision variable is a subset

∗

, called protected nodes, which will be deleted

from the graph. The result is an induced subgraph

= (V

,E(V

)), with V

= V −V

∗

. A node v ∈ V

uniforlmy chosen at random, and the full component

from G

that contains v is affected, this is, damaged

by an atacker or an accident that starts at v.

The goal is to choose the set V

∗

: |V

∗

| ≤ B in order

to minimize the expected value (or Score) of affected

nodes. If the resulting graph G

is partitioned into

k connected components with orders n

,.. .,n

such

that n = |V

|, then the Graph Fragmentation Prob-

lem (GFP) is the following combinatorial optimiza-

tion problem:

min

∗

Sc(G

) =

∑

i=1

, (1)

s.t.|V

∗

| ≤ B, (2)

being p

the probability of the event v ∈ V

, being

v the node uniformly chosen at random.

Piccini, J., Robledo, F. and Romero, P.

Graph Fragmentation Problem.

DOI: 10.5220/0005697701370144

In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 137-144

ISBN: 978-989-758-171-7

137

3 PROPERTIES

In this section, we study properties of the FGP.

Observe that the best case occurs when only a

singleton is affected, so Sc(G

) ≥ 1. The equality is

achieved if and only if G

consists of isolated nodes.

Furthermore, if n

max

denotes the number of nodes

from the largest component, then Sc(G

) ≤ n

max

its deﬁnition.

Recall that the union between graphs

= (V

) and G

= (V

) is the graph

G = (V

∪V

∪E

), and it is denoted G = G

∪G

A counterintuitive result is that a uniformly random

node protection strategy might lead to a worse

solution. In fact, let us consider G = K

∪ K

, being

the complete graph with n nodes. The score is

Sc(G) =

× 2 +

× 4 =

. However, if we pick

v ∈ K

then Sc(G − v) =

× 1 +

× 4 =

, so

Sc(G − v) > Sc(G).

The intuition suggests that it is better to disconnect

the graph whenever possible, this is, to protect nodes

in such a way that the resulting subgraphs has as many

components as possible. Then, only few nodes will be

affected. This property explains the name of the prob-

lem. These results are mathematically formalized in

the following paragraphs.

Proposition 1 (Load Balancing). The best resulting

graph G

among all feasible graphs with k compo-

nents and identical order n should have balanced

components: n

= n/k, ∀i = 1, ...,k.

Proof. The score is precisely Sc(G

) =

kxk

, being

x = (n

,.. ., n

), kxk

and kxk

the respective Eu-

clidean and 1-norm for vector x. We should minimize

the Euclidean distance in the hyperplane kxk

= n

constant, whose normal vector is

−→

1 ∈ R

, with all

unit coordinates. The optimum is found in the orthog-

onal projection of the null vector onto the polyhedra:

opt

−→

0 +

−→

1 k

−→

1 k

−→

Now, let us determine whether it is better to pro-

tect an additional node. Let G be an arbitrary graph

with k components and cardinalities n

,.. ., n

, and

n =

∑

j=1

. If we delete some node v from the ﬁrst

component (observe that the labels are not relevant for

analysis), there are two cases:

a) The number of connected components is the

same.

b) The number of connected components is in-

creased.

First, assume that Condition [a] holds. Then:

Sc(G − v) − Sc(G) =

∑

i=2

)

n − 1

− 1)

n − 1

−

)

n − 1

+ B

− B,

being A = 1/n

∑

i=2

)

, B

= (n

− 1)

/(n − 1) and

B = n

/n. As a consequence, Sc(G − v) < Sc(G) if

and only if n

meets the following inequality:

P(n

) = (n

)

− 2nn

+ (1 + A)n < 0 (3)

Observe that the minimum (or the highest score re-

duction) is achieved when n

= n, this is, when G is

connected. In that case Sc(G − v) − Sc(G) = 1. We

have proved the following

Proposition 2 (Best Singleton). If there is no cut-

node, the best node protection belongs to the highest

connected component.

Proof. The polynomial P is monotonically decreas-

ing with respect to n

Let n

max

be the size of the highest connected com-

ponent. Studying the sign of P(n

max

), there is a posi-

tive score reduction if and only if:

max

≥ n −

n(n − 1 − A). (4)

We will see that this inequality always holds:

Proposition 3 (Single Balancing). If G does not

present a cut-node, then there exists v such that

Sc(G − v) < Sc(G).

Proof. Inequality 4 occurs if and only if nA + n

max

≤

n(2n

max

− 1). But nA + n

max

∑

= nSc(G), so

Inequality 4 holds if and only if Sc(G) ≤ 2n

max

− 1.

But Sc(G) ≤ n

max

≤ 2n

max

− 1 always holds.

Let us now focus our study to Condition [b], and

denote by v a cut-node in G. First of all, observe that a

node-protection in a balanced way always produces a

score reduction. However, in some cases, the deletion

of a cut node is not a good idea. Consider for instance

G = C

∪ P

, being C

an cycle with 9 nodes and P

an elementary path with 3 nodes, and v the central

node from P

. Then, we have that Sc(G) =

, but Sc(G − v) =

+ 2 ×

= 7 +

so Sc(G − v) > Sc(G). However, if we choose a cut-

node v from a component with n

nodes, such that

P(n

) < 0, then the score is decreased. Furthermore,

the score reduction is even better than in the case of

no cut-node.

Proposition 4 (Fragmentation). If G presents a cut-

node v ∈ V

where |V

| = n

and P(n

) < 0, then

Sc(G − v) < Sc(G). Furthermore, if v

∈ V is not a

cut-node, then Sc(G − v) < Sc(G −v

) < Sc(G).

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

138

Proof. If V

− {v} = V

∪V

, n

+ n

= n

− 1, then

)

+ (n

)

< (n

− 1)

. This implies that the score

reduction is even larger than in a non cut-node dele-

tion. A similar argument is met when the cut node

produces more than two components. As a conse-

quence, the score reduction is even larger than the

protection of a non-cut-node from V

. By Proposi-

tion 3, a score reduction is achieved if v

is not a cut-

node.

Theorem 1 (Score Reduction). Consider an arbi-

trary graph G = (V,E). There is some v ∈ V such

that Sc(G − v) < Sc(G), unless G consists of isolated

nodes.

Proof. This is a Corollary of Single Balancing and

Fragmentation. We always pick a node v from the

largest connected component with n

max

nodes. If v

is not a cut node, by Proposition 4 we have Sc(G −

v) < Sc(G). Otherwise, by Proposition 3 the score

reduction is even larger, so Sc(G − v) < Sc(G) again.

In both cases a score reduction is produced.

4 HEURISTICS

Combinatorial optimization problems arise in sev-

eral real-world problems (economics, telecommuni-

cation, transport, politics, industry), were human be-

ings have the opportunity to choose among several

options. Usually, that number of options cannot be

exhaustively analyzed, mainly because its number in-

creases exponentially with an input size of the system.

Much work has been done over the last six decades to

develop optimal seeking methods that do not explic-

itly require an examination of each alternative, giving

shape to the ﬁeld of Combinatorial Optimization (Pa-

padimitriou and Steiglitz, 1982). Several combinato-

rial problems belong to the N P -Hard class, or the

search space is sufﬁciently large to admit an exact

algorithm, and a smart search technique should be

considered exploiting the real structure of the prob-

lem via heuristics. Optimality is not guaranteed, but

compromised at the cost of computational efﬁciency.

Metaheuristics are an abstraction of search method-

ologies which are widely applicable to optimization

problems. The most promising are Simulated An-

nealing (Kirkpatrick, 1984), Tabu Search (Glover,

1989), Genetic Algorithms (Goldberg, 1989), Vari-

able Neighborhood Search (Hansen and Mladenovic,

2001), GRASP (Feo and Resende, 1989), Ant Colony

Optimization (Dorigo, 1992) and Particle Swarm Op-

timization (Kennedy and Eberhart, 1995), among oth-

ers. The interested reader can ﬁnd a list of metaheuris-

tics and their details in the Handbook of Metaheuris-

tics (Gendreau and Potvin, 2010).

In this section, we develop a Greedy notion and

a Grasp heuristic enriched with a Path Reliking post-

optimization stage. First, we review basic elements of

Grasp and Path Relinking.

4.1 GRASP

Greedy Randomized Adaptive Search Procedure

(GRASP) is a multi-start or iterative process (Lin and

Kernighan, 1973), where feasible solutions are pro-

duced in a ﬁrst phase, and neighbor solutions are

explored in a second phase. The best overall solu-

tion is returned as the result. The ﬁrst implemen-

tation is due to Tomas Feo and Mauricio Resende,

were the authors address a hard set covering problem

arising for Steiner triple systems (Feo and Resende,

1989). They introduce adaptation and randomness

to the classical Greedy heuristic for the set covering

problem (where P

,.. ., P

cover the set J = {1,.. ., m}

and the objective is to ﬁnd the minimum cardinality

set I ⊂ {1,..., n} such that ∪

i∈I

= J).

It is a powerful metaheuristic to address hard

combinatorial optimization problems, and has been

succesfully implemented in particular to several

telecommunications problems, such as Internet Tele-

phony (Srinivasan et al., 2000), Cellular Sys-

tems (Amaldi et al., 2003a; Amaldi et al., 2003b),

Cooperative Systems (Romero, 2012), Connectiv-

ity (Canuto et al., 2001) and Wide Area Network de-

sign (Robledo Amoza, 2005). Here we will sketch

the GRASP metaheuristic based on the work from

Mauricio Resende and Celso Ribeiro, which is use-

ful as a template to solve a wide family of combi-

natorial problems (Resende and Ribeiro, 2003; Re-

sende and Ribeiro, 2014). Consider a ground set

E = {1,.. .,n}, a feasible set F ⊆ 2

for the optimiza-

tion problem min

A⊆E

f (A), and an objective func-

tion f : 2

→ R. The Pseudo-code 1 illustrates the

main blocks of a GRASP procedure for minimiza-

tion, where Max

Iterations iterations are performed,

α ∈ [0,1] is the quantity of randomness in the process

and N is a neighborhood structure of solutions (basi-

cally, a rule that deﬁnes a neighbor of a certain solu-

tion). The cycle includes Lines 1 − 5, and the best so-

lution encountered during the cycle is ﬁnally returned

in Line 6. Lines 2 and 3 represent respectively the

Construction and Local Search phases, whereas the

partially best solution is updated in Line 4.

A general approach for the Greedy Randomized

Construction is speciﬁed in Pseudo-code 2. Solution

S is empty at the beginning, in Line 1, and an auxiliary

set C has the potential elements to be added to S. A

Graph Fragmentation Problem

139

Algorithm 1: S = GRASP(MaxIterations, N ).

1: for k = 1 to Max Iterations do

2: S ← Greedy Randomized(α)

3: S ← Local Search(S,N )

4: U pdate Solution(S)

5: end for

6: return S

carefully chosen element from C is picked up dur-

ing each iteration of the While loop (Lines 3 − 9),

which is ﬁnished once a feasible solution is met. A

Greedy construction would choose c

min

, which is the

element with the lowest cost to be added to the par-

tial non-feasible solution (Line 4). On the other hand,

max

is the most expensive element to be added (Line

5). The Restricted Candidate List RCL is deﬁned in

Line 6, and has all the elements whose cost are be-

low a certain threshold (see Line 6). In Line 7, an

element from the RCL is uniformly picked at random

and added to the solution S. The process is repeated

until a feasible solution S is found. It is worth to no-

tice the effect of the input parameter α ∈ [0,1]. When

α = 0, the Greedy construction is retrieved. On the

contrary, α = 1 means a completely random construc-

tion. Therefore, the parameter α imposes a trade-off

between diversiﬁcation and greediness.

Algorithm 2: S = Greedy Randomized(α).

1: S ←

2: C ← E

3: while C 6=

0 do

4: c

min

← min

c∈C

f (S ∪ {c})

5: c

max

← max

c∈C

f (S ∪ {c})

6: RCL ← {c ∈ C : f (S ∪ {c}) ≤ f (S ∪ {c

min

}) +

α( f (S ∪ {c

max

}) − f (S ∪ {c

min

}))}

7: S ← S ∪Random(RCL)

8: U pdate(C)

9: end while

10: return S

The Greedy Randomized Construction does not

provide guarantee of local optimality. For that rea-

son, a Local Search phase is ﬁnally introduced, in or-

der to return a locally optimal solution (which could

be incidentally globally optimal). In order to deﬁne

this phase, a rule to deﬁne neighbors of a certain so-

lution is mandatory, called a neighborhood structure.

A better neighbor solution is iteratively picked until

no improvement is possible. A general local search

phase is presented in pseudo-code 3.

The success of the local search phase strongly de-

pends on the quality of the starting solution, the com-

putational cost for ﬁnding a better local solution, and

naturally, on the richness of the neighborhood struc-

ture. The interested reader can ﬁnd valuable literature

and GRASP enhancements.

Algorithm 3: S = Local Search(S,N ).

1: H(S) = {X ∈ N (S) : f (X) < f (S)}

2: while H(S) 6=

0 do

3: S ← ChooseIn(H)

4: H(S) = {X ∈ N (S) : f (X) < f (S)}

5: end while

6: return S

4.2 Greedy for the GFP

Usually, once we face a new combinatorial optimiza-

tion problem, a Greedy notion is developed. In spe-

ciﬁc combinatorial structures, Greedy produces the

globally optimum solution. Greedy heuristic builds

a solution in a stepwise manner. The best step is

chosen whenever possible. Therefore, Greedy tries

to build the global optimum by means of the best lo-

cal steps. Naturally, Greedy rarely produces the best

solution (see for instance its performance in the cele-

brated Traveling Salesman Problem).

In our problem, Greedy iteratively applies the best

node protection. Function ChooseBestNode ﬁnds v

such that v = argmin

{Sc(G − w)}. Greedy is sup-

ported by Theorem 1, and the score reduction is guar-

anteed for the GFP.

Algorithm 4: G

out

= Greedy(G, B).

1: for i = 1 : B do

2: v ← ChooseBestNode(G)

3: G ← G − v

4: end for

5: G

out

← G

6: return G

out

A linear search among all nodes w ∈ V is de-

veloped in order to ﬁnd the best node protection in

Greedy. Observe that if there is no cut node, a node

is picked uniformly at random from the largest con-

nected component, since they produce the same score

reduction. In order to trade computational effort, we

propose an alternative algorithm that always improves

the score. It is supported by Proposition 3.

Algorithm 5: G

out

= Balance(G,B).

1: for i = 1 : B do

2: V

max

← LargestComponent(G

out

)

3: v ← ChooseRandom(V)

4: G ← G − {v}

5: end for

6: G

out

← G

7: return G

out

Balance iteratively picks nodes from the largest

connected component. Observe that no score evalu-

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

140

ation is required, hence, the computational effort is

below that of Greedy.

4.3 Grasp for the GFP

We already have a Greedy notion for the GFP, and a

Balance heuristic. Both reduce the score in each iter-

ation. A key point is to note that a fragmentation in

large components always improves the score. There-

fore, Separator function ﬁnds the node-connectivity

for a given connected graph. It returns a node separa-

tor set V

aux

of the largest component V

max

Algorithm 6: G

out

= Grasp(G,B, α).

1: G

out

← G

2: Counter ← B

3: LocalImprove ← True

4: while Counter > 0 do

5: if random < α then

6: v = RandomNode(G)

7: G

out

← G

out

− v

8: else

9: V

max

← LargestComponent(G

out

)

10: V

aux

← Separator(G,V

max

)

11: if Counter ≥ |V

aux

| then

12: G

out

← G

out

−V

aux

13: Counter ← Counter − |V

aux

14: end if

15: end if

16: end while

17: while Improve(G) = True do

18: (G

out

,LocalImprove) ← Swap(G

out

,G)

19: end while

20: return G

out

The construction phase is ﬁrst applied (Lines 1-

15) and then, a Local Search phase takes place (Lines

16-18). The graph (G

out

) and number of remaining

nodes to protect (Counter) are initialized in Lines 1-2.

Nodes are protected in a While loop (Lines 3-15). If a

uniform random variable over the compact set [0,1] is

greater than the input α (Line 4), a random node v is

then picked and removed (Lines 5-6). Otherwise, the

largest component is selected (Line 8), and the node

separator in that component is found (Line 9). If it

is feasible, that node separator is removed from the

graph (Lines 10-12). Finally, a Local Search phase

takes place. It guarantees a local optimum solution.

The core is Swap function, explained in the following

lines.

Non-protected nodes are those from the ﬁrst ar-

gument G

(Line 1), while the remaining nodes be-

long to the difference V (G

) −V (G

) (see Line 2). A

Boolean constant determines whether there exists

Algorithm 7: (G

out

,Improve) = Swap(G

1: {v

,... ,v

n−B

} ← V (G

)

2: {v

n−B+1

,... ,v

} ← V (G

) −V (G

)

3: Improve ← False

4: G

out

← G

5: for i = 1 : B do

6: for j = 1 : n − B do

7: G

aux

← (G

out

+ v

n−B+i

) − v

8: reduction ← E(G) −E(G

aux

)

9: if reduction > 0 then

10: G

out

← G

aux

11: Improve ← True

12: break

13: end if

14: end for

15: end for

16: return (G

out

,Improve)

some improvement or not (Line 3). Iteratively, all

(protected,non-protected) pairs are considered and

switched to see whether there is some improvement

or not (block of Lines 5-15). If there is some im-

provement, LocalImprovement is set to True (Line

11) and iterative process is ﬁnished (Line 12). The

pair (G

out

,Improve) is returned. It is worth to remark

that G

out

= G

if and only if G

is a local optimum.

Otherwise, the best ﬁrst movement is produced.

4.4 Path Relinking

Thanks to the randomization introduced to the Grasp

heuristic, new solutions are obtained with different

runs. Then, once we consider a pool {G

,.. ., G

} of

s elite solutions (they are the best solutions obtained

using N >> s runs), new solutions could be found via

elementary paths in the graph G of solutions. In this

case, the node set of G is the induced subgraph of G

with precisely n −B nodes. Two solutions G

and G

are incident if and only if there is a single swap that

moves one solution into the other (i.e., if they differ

in one node).

Algorithm 8: Pool = Relinking(G

,...,G

1: S ← (G

,... ,G

)

2: for all (u,v) ∈ Pool do

3: Path ← ShortestWalk(u,v)

4: S

u,v

← Best(Path)

5: S ← S ∪{S

u,v

}

6: end for

7: Pool ← SelectBest(r,S)

8: return Pool

Relinking receives a pool of r solutions and

returns another pool of r solutions, with better

Graph Fragmentation Problem

141

score.New candidate solutions S

u,v

are found for ev-

ery pair of elite solutions u and v. The best r solutions

are returned.

4.5 Main Algorithm

The main algorithm combines Grasp strength and a

Path relinking post-optimization stage, in a straight-

forward fashion.

Algorithm 9: G

out

= Main(G, B, N

1: S ←

2: for i = 1 : N

3: G

← Grasp(G,B)

4: S ← S ∪G

5: end for

6: (G

,... ,G

) ← Best(r, S)

7: for i = 1 : N

8: (G

,... ,G

) ← Relinking(G

,... ,G

)

9: end for

10: G

out

← SelectBest(1,{G

,... ,G

})

11: return G

out

5 RESULTS

In order to highlight the effectiveness of our three

heuristics, we introduce Greedy, Balance and Main

to three real-life graphs. These graphs G

USA

FON

and G

PEG

represent respectively the neighborhood of

the states from USA, a real Fiber Optic Network and

a part of a real Power Electric Grid. In all cases, it

is highly desirable to minimize the risk of the neigh-

boring elements, once a failure or catastrophic event

occurs. Thanks to the randomization effect during

Balance call, the performance of different runs is vari-

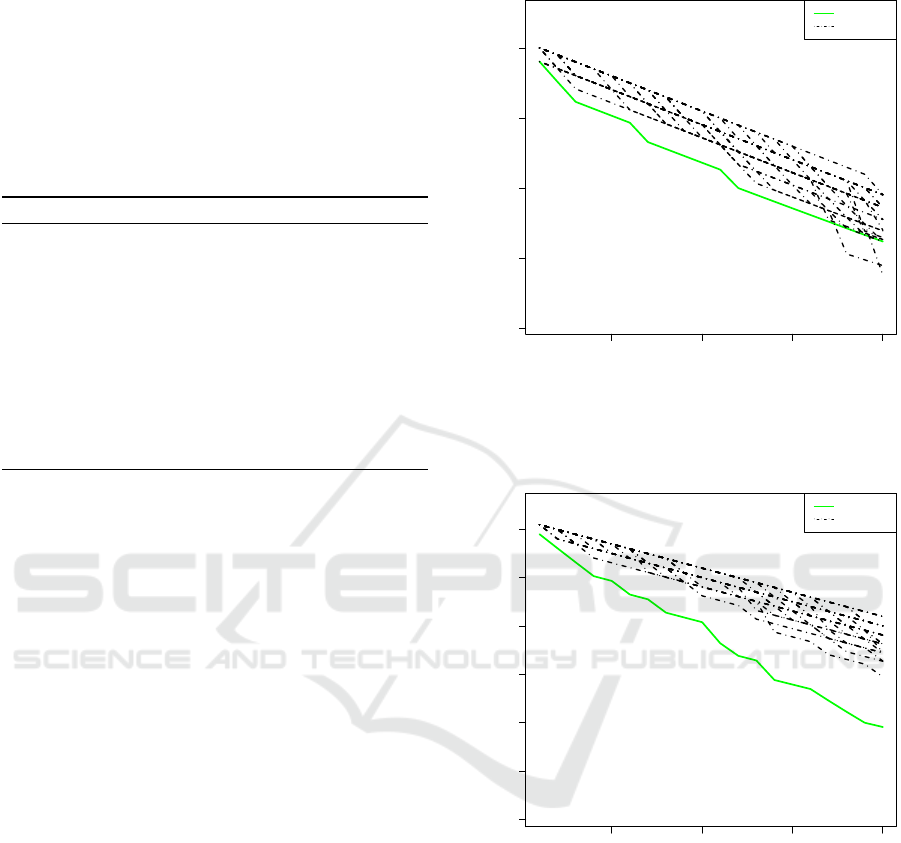
able. Figures 1, 2 and 3 show the score of Greedy

(solid line) and the scores of 30-runs of Balance

(dashed lines) versus Main with N

= N

= 30, r = 6,

α = 0.5. The score for the different heuristics is ex-

pressed as a function of the budget B. Red point’s

abcissa is the cost reached by Main after removing 20

nodes. Runs were made on a computer Dell Inspiron-

N4010 with 1.8 GiB of memory, proccesor Intel Core

i3 CPU M380 @ 2.53 GHz x 4, 64 bit’s OS. CPU

times are 0.924 min. for G

USA

, 1.065 min. for G

FON

and 13.021 min. for G

PEG

It can be appreciated that our Main heuristic out-

performs both naive solutions Greedy and Balance,

under all possible budgets. Even though Balance

has a reduced computational cost, its performance

presents a large gap with respect to Greedy heuris-

tic. Figures 4, 5 and 6 show the pruning result for the

different heuristics and graphs under study.

5 10 15 20

0 10 20 30 40

Performance Analysis−Neighborhood Graph

Removed nodes

Score

Greedy

Balance

●

Main

Figure 1: Greedy (solid) vs. 30 Balance runs (dashed) for

the Neighborhood Graph.

5 10 15 20

0 10 20 30 40 50 60

Performance Analysis−Fiber Optic Graph

Removed nodes

Score

Greedy

Balance

●

Main

Figure 2: Greedy (solid) vs. 30 Balance runs (dashed) for

the Fiber Optic Graph.

6 CONCLUSIONS

The Graph Fragmentation Problem (GFP) has been

introduced. The goal is to protect (remove) B nodes

from a graph G, in such a way that a random attack to

an arbitrary node v affects the lowest expected num-

ber of nodes (where the whole connected component

from v is affected). The GFP ﬁnds applications to ﬁre

ﬁghting, highly virulent epidemic propagations and

electric shocks, among others.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

142

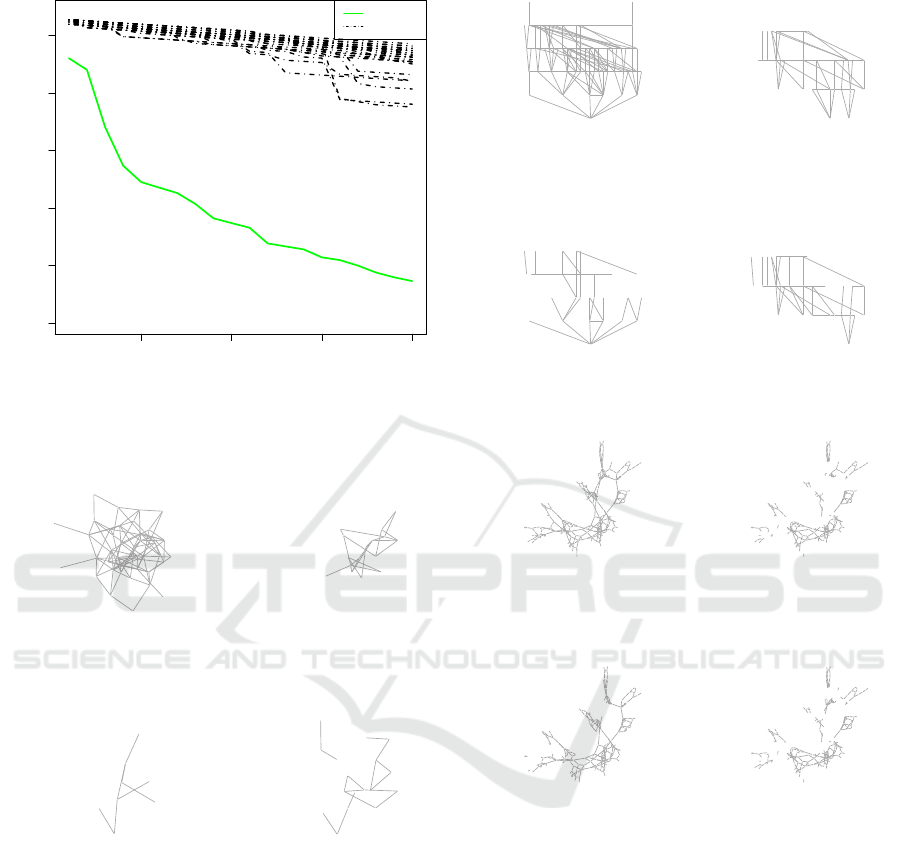
5 10 15 20

0 50 100 150 200 250

Performance Analysis−IEEE300 Graph

Removed nodes

Score

Greedy

Balance

●

Main

Figure 3: Greedy (solid) vs. 30 Balance runs (dashed) for

the IEEE 300 Graph.

●

Neighborhood Graph, Sc= 41

●

After Greedy, Sc= 12.429

●

After Balance, Sc= 15.571

●

After Main, Sc= 3.762

Figure 4: Graph G

USA

when α = 1/2.

In this paper, elementary properties of the GFP

were studied. Speciﬁcally, graph fragmentation and

balancing are good strategies. Together, they deﬁne

a Greedy notion for the problem. Furthermore, we

proved that Greedy achieves improvement in each it-

eration (i.e., in each node protection). A more sophis-

ticated Grasp heuristic enriched with a Path Relinking

post-optimization scheme has been developed. The

effectiveness of our more sophisticated heuristic has

been tested on a real-life networks.

As a future work, we would like to establish the

intractability of GFP and develop different heuristics.

●

● ●

●

● ● ●

●● ● ●

● ●

●

●●●

●

● ●

●

● ●

●

●●

●

●●

●

● ●

●●

●

● ●

Fiber Optic Graph, Sc= 62

●

● ● ●

●

●●

●

● ● ●

●

●●

●

● ●

●

● ●

●●

●

● ●

After Greedy, Sc= 19.095

●

● ●

●

● ●

●

●●

●

●● ●

●

● ●

●● ●

●

After Balance, Sc= 40.048

● ● ●

●

● ● ●

●

● ● ●

●

●●

●

● ●

●

● ●

●●

●

● ●

After Main, Sc= 15.524

Figure 5: Graph G

FON

when α = 1/2.

●

IEEE300 Graph, Sc= 265

●

After Greedy, Sc= 36.396

●

After Balance, Sc= 227.408

●

After Main, Sc= 35.343

Figure 6: Graph G

PEG

when α = 1/2.

REFERENCES

Amaldi, E., Capone, A., and Malucelli, F. (2003a). Plan-

ning UMTS base station location: Optimization mod-

els with power control and algorithms. IEEE Transac-

tions on Wireless Communications, 2(5):939–952.

Amaldi, E., Capone, A., Malucelli, F., and Signori, F.

(2003b). Optimization models and algorithms for

downlink UMTS radio planning. In Wireless Com-

munications and Networking, (WCNC’03), volume 2,

pages 827–831.

Borgatti, S. (2006). Identifying sets of key players in a so-

cial network. Computational & Mathematical Orga-

nization Theory, 12:21–34.

Canuto, S., Resende, M., and Ribeiro, C. (2001). Lo-

Graph Fragmentation Problem

143

cal search with perturbation for the prize-collecting

Steiner tree problems in graphs. Networks, 38:50–58.

Dorigo, M. (1992). Optimization, Learning and Natural

Algorithms. PhD thesis, DEI Politecnico de Milano,

Italia.

Feo, T. A. and Resende, M. G. C. (1989). A probabilistic

heuristic for a computationally difﬁcult set covering

problem. Operations Research Letters, 8(2):67 – 71.

Gendreau, M. and Potvin, J.-Y. (2010). Handbook of Meta-

heuristics. Springer Publishing Company, Incorpo-

rated, 2nd edition.

Glover, F. (1989). Tabu search - part i. INFORMS Journal

on Computing, 1(3):190–206.

Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-

timization and Machine Learning. Addison-Wesley

Longman Publishing Co., Inc., Boston, MA, USA, 1st

edition.

Hansen, P. and Mladenovic, N. (2001). Variable neighbor-

hood search: Principles and applications. European

Journal of Operational Research, 130(3):449–467.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. In Proceedings of the IEEE International

Conference on Neural Networks, volume 4, pages

1942–1948. IEEE.

Kirkpatrick, S. (1984). Optimization by simulated an-

nealing: Quantitative studies. Journal of Statistical

Physics, 34(5):975–986.

Lin, S. and Kernighan, B. W. (1973). An Effective Heuristic

Algorithm for the Traveling-Salesman Problem. Op-

erations Research, 21(2):498–516.

Monma, C. L., Munson, B. S., and Pulleyblank, W. R.

(1990). Minimum-weight two-connected spanning

networks. Mathematical Programming, 46(1-3):153–

171.

Ortiz-Arroyo, D. (2010). Discovering sets of key players

in social networks, in Computational Social Network

Analysis, Chp. 2. Springer London.

Papadimitriou, C. H. and Steiglitz, K. (1982). Com-

binatorial optimization: algorithms and complexity.

Prentice-Hall, Inc., Upper Saddle River, NJ, USA.

Resende, M. G. C. and Ribeiro, C. C. (2003). Greedy Ran-

domized Adaptive Search Procedures. In F. Glover

and G. Kochenberger, editors, Handbook of Metha-

heuristics, Kluwer Academic Publishers.

Resende, M. G. C. and Ribeiro, C. C. (2014). Grasp:

Greedy randomized adaptive search procedures. In

Burke, E. K. and Kendall, G., editors, Search Method-

ologies, pages 287–312. Springer US.

Robledo Amoza, F. (2005). GRASP heuristics for Wide

Area Network design. PhD thesis, INRIA/IRISA, Uni-

versit

e de Rennes I, Rennes, France.

Romero, P. (2012). Mathematical analysis of schedul-

ing policies in Peer-to-Peer video streaming networks.

PhD thesis, Facultad de Ingenier

ıa, Universidad de la

Rep

ublica, Montevideo, Uruguay.

Srinivasan, A., Ramakrishnan, K., Kumaram, K., Arava-

mudam, M., and Naqvi, S. (2000). Optimal design

of signaling networks for Internet telephony. In Pro-

ceedgins of the IEEE INFOCOM 2000.

Stoer, M. (1993). Design of Survivable Networks. Lecture

Notes in Mathematics. Springer.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

144