
A Survey of Internet Energy Efficiency Metrics
Kerry Hinton
1
and Fatemeh Jalali
2
1
Centre for Energy Efficient Telecommunications, University of Melbourne, Parkville, Australia
2
IBM Research, Melbourne, Australia
Keywords: Energy Consumption, Energy Efficiency, Communications Networks, Telecommunications Services,
Internet Services.
Abstract: Several metrics have been widely applied to quantify the “energy efficiency” of the Internet and ICT. In this
paper we analyse and compare these metrics when applied to telecommunication network equipment,
networks and services. We show that different metrics can imply different, and possibly conflicting,
strategies for improving energy efficiency. Some guidelines are suggested for the appropriate application of
these metrics.
1 POWER & ENERGY MODELS
1.1 Equipment Power Model
The dependence of power consumption, P(t), at time
t, on traffic throughput, C(t), for network equipment
can be written in a generic “affine” form
(Vishwanath, et al. 2014 ):
max idle
idle idle
max
PP
Pt P ECt P Ct
C
(1)
Where P
idle
is the power consumption with no
throughput (i.e. C(t) = 0), C
max
is the maximum
throughput of the network element and P
max
is the
power consumption when C(t) = C
max
. In (1) the
linear slope E = (P
max
– P
idle
)/C
max
has dimensions of
energy per bit. We shall refer to this slope as the
“incremental energy per bit”.
1.2 Network Power Model
Using (1), the total network power, P
Ntwk
, is the sum
of the equipment power;
,
1
E
N
Ntwk idle j j j
j
Pt P ECt
(2)
where N
E
is the number of network elements, P
idle,j
,
E
j
and C
j
(t) are the idle power, incremental energy
per bit and throughput of the j-th network element
respectively.
We have
j
C
j
≥ C
Ntwk
, because most traffic flows
will go through multiple network elements. If we
identify all network traffic flows with a service,
including network management, control and
monitoring traffic, then we can write
1
S
N
k
Ntwk
k
Ct Ct
(3)
where N
(S)
is the number of services, k is the index
for the service and C
(k)
is the traffic (bits/sec) for the
k-th service. We also have for the traffic through the
j-th network element:
11
SS
NN
kkk
jj j
kk
Ct C t C t
(4)
where C
j
(k)
=
j
(k)
C
(k)
is the traffic through the j-th
network element due to service k. (
j
(k)
is the
proportion of service traffic C
(k)
that propagates
through network element j.) Note that for a service k,
we also have C
(k)
≤
j
C
j
(k)
.
1.3 Service Power Model
The “fundamental unit” of the Internet (as far as its
end users are concerned) is “service” (e.g. SaaS,
IaaS, Google Docs, Dropbox, etc). There has been a
growing interest in the power consumption of
services over recent years (Chan, C., et al., 2012).
From (1) we see the power consumption of a
network element has an idle power component, P
idle
,
Today, most wireline network equipment has P
idle
≥
Hinton, K. and Jalali, F.
A Survey of Internet Energy Efficiency Metrics.
In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 243-251
ISBN: 978-989-758-184-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
243

0.8P
max
(Vishwanath, A., et al. 2014). For much of
the “Layer 0” and “Layer 1” equipment P
idle
= P
max
.
To allocate power to services, we need an approach
for allocating a proportion of P
idle
to each service
traffic flow propagating through a network element.
If
,
k
idle j
Pt
is the idle power allocated to service k in
network element j, we expect the sum over all
services through that element to satisfy
,,
1
k
idle j idle j
k
P
Pt
(5)
One way to fulfil this requirement, is to apply the
same linear proportionality rule to the idle power as
found for the incremental power in (1). That is, we
set
,
kk
idle j j
PtCt
. Using (5),
,
k
idle j
Pt
has the
form:
,,
k
kj
idle j idle j
j
Ct
PtP
Ct
(6)
With this rule, the overall power consumption of the
k-th service, P
(k)
(t) provided by the network is
,
1
E
N
idle j
kk
jj
j
j
P
Pt ECt
Ct
(7)
It is important to note that this is not the only
approach available. For example, we could set
,,
ksrv
idle j idle j j
PtP N t
where N
j
(srv)
(t) is the number
of services through network element j at time t. A
disadvantage of this approach is that N
j
(srv)
(t) can be
awkwardly large for core network equipment.
2 EFFICIENCY METRICS
The ITU has described an energy-efficiency metric
in ITU-T Rec. L.1330 as (ITU-T 2012(a) ):
“The energy efficiency metric is typically defined as
the ratio between the functional unit and the energy
necessary to deliver the functional unit.”
This definition results in a metric with units
“bits/Joule”. ITU-T Rec. L.1330 also recognises that
“The inverse metric, energy divided by functional
unit, could be used as an alternative.”
We shall focus on “energy per bit” metrics.
2.1 Standardised Metrics
Energy efficiency metrics currently used in
standards documents are based on the ratio of power
to traffic for a number, M, of pre-defined load levels
of the equipment (Minoli, D., 2011). For example,
the ECR-VL is defined by the ratio,
11
MM
mm m m
mm
ECR a P a C
(8)
Where ∑
m
a
m
= 1, P
m
and C
m
are the power and the
pre-defined loads indexed by m. The values of P
m
and C
m
are specified in the definition and depend
upon the type of network element.
For a network element, placing (1) into (8) gives
idle
max m m
m
P
ECR E
Cab
(9)
Where b
m
= C
m
/C
max
. Example values for b
m
are: b
1
=
1, b
2
= 0.5, b
3
= 0.3, b
4
= 0.1 and b
5
= 0 with
corresponding weights a
1
= 0.1, a
2
= 0.5, a
3
= 0.3, a
4
= 0 and a
5
= 0.1 (Minoli, D., 2011).
There are several problems with this and similar
metrics (TEER, EER and TEEER) (Minoli, D.,
2011). First, although these definitions include
averages over loads, they effectively correspond to a
single load; therefore the value does not incorporate
the impact of traffic variation over the diurnal cycle.
Another is seen by considering two routers with
the (approximately) same C
max
but different values
for P
idle
and E. Let the values for the routers be
P
idle,1
, E
1
and P
idle,2
E
2
respectively and P
idle,2
=
xP
idle,1
where x is constant. Then we get the same
ECR value for both routers provided:
,1
21
1
idle
max m m
m
P
EE x
Cab
(10)
If we set x = 0 router 2 is load proportional (i.e.
P
idle,2
= 0) which is viewed as desirably energy
efficient. However it still has the same ECR as
router 1 which may have large idle power.
Using the value for x given by
1
,1
1
max
mm
m
idle
EC
x
ab
P
(11)
in (10) gives E
2
= 0 which is often considered
energy inefficient but will still have the same ECR
as router 1. Hence ECR type metrics do not reflect
the idea of “energy efficiency” very well.
Finally, the metric defined in (8) does not lend
itself to being applied to networks or services. It is
not clear how to apply this metric to a collection of
interconnected network elements. Even less apparent
is how to apply this metric to service that may be
one of many propagating through an element.
SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems
244

2.2 Defining Energy Efficiency
In this work we will study a range of metrics that
have been proposed and applied (Schien, D, and
Preist, C. 2014)(GreenTouch, 2015)(Baliga, J., et al.
2009). We will implement them in a manner that is
applicable to network elements, networks and
services. Simple energy/bit efficiency metrics that
have been employed in the literature are:
a) “Instantaneous energy per bit” defined by the
ratio of the instantaneous power to throughput:
1
Pt
Ht
Ct
(12)
This metric has been adopted in a range of “bottom-
up” metrics used to calculate the energy efficiency
of the Internet at peak load (Baliga, J., et al. 2009) or
at time t (Chiaraviglio, L., et al., 2009). When
P
idle
≠ 0,
1
H(t) will vary over the diurnal cycle.
b) “Energy per bit” defined by the ratio of total
energy, E(T), consumed over duration T to total bit
throughput. B(T), over duration T:
2
0
0
()
T
T
T
T
Ptdt
P
T
HT
TC
Ctdt
E
B
(13)
In this equation the time integral is over duration T
from a pre-determined origin time. The GreenTouch
consortium uses 1/(
2
H(T)) with T = 1 year for the
years 2010 and 2020 (GreenTouch, 2015). In (13)
X
T
=
T
X(t)dt/T.
Some “top-down” metrics use (13), with E(T)
determined from information such as equipment
deployment inventory data and energy consumption
and B(T) is an assessment of the total network traffic
(Schien, D, and Preist, C. 2014).
c) “Mean instantaneous energy per bit” was
proposed in (ITU-T 2012(b)), although that
document contains a mathematical error. The
average the instantaneous metric over time duration
T is defined by:
31
0
1
T
T
T
Pt
P
HT dt Ht
TCt C
(14)
Other metrics have been defined, for example
mobile network researchers have used power per
unit area (Tombaz, S. et al. 2013). Due to lack of
space, in this work we will focus on the energy per
bit metrics,
1
H,
2
H and
3
H, listed above.
2.3 Uses of Metrics
Metrics are most frequently used for improvement
(i.e developing strategies to change the value of the
metric for a system), benchmarking (comparing the
value of a metric for the systems being
benchmarked) or estimating energy consumption.
When used for improvement, the choice of metric
will directly impact the strategies adopted for
“improvement”. When used for benchmarking, the
choice of metric will determine what we mean when
we say one system is “better” than another.
Therefore, the choice of metric is important.
3 DIURNAL CYCLES
Diurnal traffic cycles result from the fact that many
users are typically “off-line” and “on-line” during
common times over a 24 hour period. An example of
a diurnal cycle for an Australian city (taken from an
edge router traffic log) is shown by the solid line in
Fig. 1. Also shown is a pure sinusoidal
approximation (dashed line) of the 24 hour diurnal
cycle. In general, traffic diurnal cycles can
dramatically vary in shape; however they all have a
cyclic profile.
For the purposes of comparing the general
characteristics of these metrics we shall use a “first-
order” sinusoidal approximation for the diurnal
cycle of the k-th service’s traffic flow (in bits/sec) of
the form
cos 2
kkk k
mean
CtC C tT
(15)
with T = 24 hours. In (15)
k
mean
C
is the mean traffic
for the k-th service flow over duration T and C
(k)
the variation away from the mean for the k-th flow.
The phase
(k)
accounts for the fact that the diurnal
cycles of the individual services may not be
synchronized (i.e. different services will have a
different time of peak traffic). Using (15) enables the
calculation of closed forms for the metrics above.
Figure 1: Example of a 7 day diurnal cycle from a
commercially deployed router (solid line) and a first-order
sinusoidal approximation (dashed line).
A Survey of Internet Energy Efficiency Metrics
245

The form in (15) can be applied to equipment
and networks. From (3) the time dependence of the
total network traffic is the sum of all the service
traffics:
1
cos 2
cos 2
S
Ntwk mean,Ntwk Ntwk Ntwk
N
kk k
mean
k
CtC C tT
CC tT
(16)
Similarly, from (4) the total traffic for the j-th
network element, C
j
(t), will have the form:
1
1
cos 2
cos 2
cos 2
S
S
jmean,jj j
N
kk k
mean, j j
k
N
kk k k
jmean
k
Ct C C tT
CC tT
CC tT
(17)
The
terms correspond to the location of the peak
load within the diurnal cycle relative to a fixed
arbitrary origin. Setting the time origin to time t
0
(hours) then if the peak traffic occurs at time t
peak
,
we have
= 2
(t
peak
– t
0
)/24.
For a network or element in which the flows are
synchronized (i.e. all flows have the same peak
traffic time) we have
,,
11
,,,,
11
SS
SS
NN
kk
mean Ntwk mean max Ntwk max
kk
NN
kk
mean j mean j max j max j
kk
CCCC
CCCC
(18)
However, with unsynchronized flows, we get
1
1/ 2
2
1
cos
cos 2
S
SSS
N
k
Ntwk mean
k
NNN
kklkl
kkll
Ntwk
Ct C
CCC
tT
(19)
where
1
11
tan sin cos
S
S
N
N
kk k k
Ntwk
kk
CC
(20)
A corresponding form can be written for C
j
(t).
Assuming the differences (
(k)
–
(l)
) is are not all
zero, then comparing a network with many
synchronized flows to the same network with many
unsynchronized flows we find,
,,
Ntwk Ntwk
mean Ntwk mean Ntwk
s
ynch unsynch
CC
CC
(21)
Taking this further, if the phases,
(k)
, are
uniformly, randomly distributed
1/ 2
2
,
k
Ntwk
Sk
mean Ntwk
unsynch
mean
C
C
C
NC
(22)
From this we see that as the number of
unsynchronised flows increases the network traffic
maximum, given by C
mean,Ntwk
+ C
Ntwk
, reduces to
the mean, C
mean,Ntwk
;
max,
,,
,
lim
lim 1
S
S
Ntwk
N
Ntwk
mean Ntwk mean Ntwk
N
mean Ntwk
C
C
CC
C
(23)
This means the depth of the diurnal cycle reduces
when increasingly many unsynchronised traffic
flows are brought together. This result applies to any
single network element, network facility or overall
network that deals with many service flows.
The results in (21) (22) and (23) tell us that
facilities dealing with highly synchronised traffic
(such as serving only a local time-zone) are likely to
experience a relatively deeper diurnal cycle than
those dealing with unsynchronised traffic (such as
traffic from geographically diverse regions around
the globe).
Diurnal cycle depth plays an important role when
improving energy efficiency, because networks are
dimensioned to accommodate peak traffic (C
max
). In
legacy networks equipment remains fully energised
24/7, therefore dimensioning network for peak load
means that during off-peak hours equipment is lowly
utilised which is less energy inefficient (i.e. higher
energy per bit) than at peak time.
In new generation networks, a widely proposed
strategy is to implement low energy (sleep) states
during “off-peak” times to improve energy
efficiency (Mahadevan, P. et al., 2009). The depth of
the diurnal cycle is important because it indicates
how much equipment can be powered-down during
off peak times (GreenTouch, 2015).
4 THE METRICS
4.1 Network Equipment
Without a loss of generality, we can drop the phase
term when applying the diurnal cycle to the traffic
through a network element. For the j-th network
element, we have
SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems
246

,
1
,
,
2
,
,
3
1/2 1/2
,,
cos 2
idle j
jj
mean j j
idle j
jj
mean j
idle j
jj
min j max j
P
Ht E
CC tT
P
HT E
C
P
HT E
CC
(24)
where C
min,j
= C
mean,j
- C
j
. To calculate
3
H
j
(T) we
have used Item 3.613.1 from (Gradshteyn, I. Ryzhik,
I. 1980).
We note that C
mean
= C
T
, therefore we could
interpret the difference between
2
H(T) and
3
H(T)
results from the former using the arithmetic mean of
the traffic C(t) whereas the latter uses the geometric
mean (for sinusoidal traffic load).
Figure 2: Plot of the ratio
3
H(T)/
2
H(T) showing that the
metric
3
H(T) reflects the impact of durations of low
utilisation on network energy/bit metric for equipment in
which idle power dominates.
Comparing
2
H
j
(T) and
3
H
j
(T) in (24) we note that
3
H
j
(T) reflects the impact of traffic variation over a
diurnal cycle where-as
2
H
j
(T) does not. We see this
by calculating the ratio
3
H
j
(T)/
2
H
j
(T) over a range
diurnal cycle depths (C
min
/C
max
) for the network
element traffic as shown in Fig. 2.
2
H
j
(T) is constant
with respect to the ratio (C
min
/C
max
) where-as
3
H
j
(T)
exposes the impact of periods of low utilisation
which correspond to low values of (C
min
/C
max
).
4.2 Networks
For a network using (2) and (3) we have
,
1
1
,
2
cos
cos 2
E
N
idle j j mean, j j j
j
Ntwk
mean Ntwk Ntwk
t
PEC C
T
Ht
CC tT
(25)
,
1
2
,,
E
N
idle j j mean, j
Eidle mean
j
EE E
Ntwk
mean Ntwk mean Ntwk
PEC
NP EC
HT
CC
(26)
3
,
1/2 1/ 2
1
,,
1/2 1/ 2
,,
1/2 1/ 2
,,
1
1cos
E
N
Ntwk idle j
j
min Ntwk max Ntwk
max Ntwk min Ntwk
j
jmean,j j
mean, j
max Ntwk min Ntwk
HT P
CC
CC
C
EC
C
CC
(27)
The notation X
E
represents an average over
network elements, defined by
1
1
E
N
j
E
j
E
XX
N
(28)
The approximations in (26) and (27)is justified by
the fact that E
j
and C
j
are independent random
variables hence EC
E
E
E
C
E
.
In
3
H
Ntwk
(T),
j
is measured relative to the
network peak traffic time, that is
j
= 2
(t
peak,j
–
t
peak,Ntwk
)/24. To calculate (27) we have used Items
2.554.2 and 2.553.2 from (Gradshteyn, I. Ryzhik, I.
1980).
From (27) the factors that feed into
3
H
Ntwk
(T) are
the relative depths of the traffic diurnal cycles,
C/C
mean
, and the degree of synchronisation of the
traffic flows,
(k)
(see (17)). To acquire an
appreciation of the impact of these parameters on the
metrics, a mesh network simulation was constructed.
The simulated network consisted of 50 inter-
connected network elements (N
E
= 50) each with a
power profile given by (1) with a range of values for
P
idle
(randomly selected in the range 1kW to 1.5kW)
and E (randomly selected in the range 0.5 nJ/bit to 2
nJ/bit). These values are typical of current
generation router and switch technology (Van
Heggegham, W., et al., 2012). The network carries
500 sinusoidal service flows (N
(S)
= 500), with mean
flow data rates randomly distributed over the range
0.5 Gbit/s ≤ C
mean
≤ 2 Gbit/s. Each flow travels
through 10 network elements randomly selected
from the 50 elements in the simulation. No flow
travels through the same element more than once.
Although the simulation is a mesh network, the
architecture is not a major influence because the
overall power consumption is determined by the
equipment along the service flow paths not the
global network architecture.
The synchronisation of the flows is parametrised
by quantity b with the phase of the flows chosen
randomly over the range -b
≤
(k)
≤ b
. For highly
synchronised flows we set b = 0.1. For totally
desynchronised flows we set b = 1. The simulation is
run for values of b from 0.1to 1.0 in steps of 0.1.
To parametrise the diurnal cycle depth, C/C
mean
the flows are distributed randomly over a range
C/C
mean
to C/C
mean
+ 0.2 with values of C/C
mean
A Survey of Internet Energy Efficiency Metrics
247

from 0.1 to 0.8 in steps of 0.1.
For the case of synchronised flows and a deep
diurnal cycle in the simulated network, the value of
1
H
Ntwk
(t) can vary dramatically over the diurnal
cycle. For the simulated network described above, at
peak traffic time, we get
1
H
Ntwk
(t
peak
) 66 nJ/bit. At
the time of minimum traffic (t
trough
)
1
H
Ntwk
(t
trough
)
910 nJ/bit. Therefore using this metric requires
careful consideration of the time at which it is
measured. Measuring at peak traffic time will give a
low estimate for typical energy per bit. From (25)
and (26), for a totally desynchronised network we
have
1
H
Ntwk
(t)
2
H
Ntwk
(T) for all t over the diurnal
cycle. For the simulated network, this situation gives
1
H
Ntwk
(t)
2
H
Ntkw
(T) 113 nJ/bit.
The values of
2
H
Ntwk
(T) and
3
H
Ntwk
(T) (T = 24
hours) for ranges of cycle depth, C/C
mean
, and
synchronisation, b, are shown by the surface plot in
Fig. 3. The top left region of the surface plots
corresponds to highly synchronised service traffic
flows with relatively deep diurnal cycles. We see
that
3
H
Ntwk
(T) reflects the impact of periods of low
network utilisation that occur in networks with
highly synchronised traffic and a deep diurnal cycle.
In contrast
2
H
Ntwk
(T)
3
H
Ntwk
(T) for networks that
are desynchronised or have shallow diurnal cycles.
Figure 3: Surface plots of
2
H
Ntwk
(T) and
3
H
Ntwk
(T) for
values of synchronicity parameter b and diurnal cycle
depth C/C
mean
.
4.3 Services
Using the equations above, for the k-th service
,
11
11
()
EE
NN
k k idle j k
jjjj
jj
j
P
Ht E Ht
Ct
(29)
2
1/ 2 1/ 2
,,
,
1/ 2 1/2
1/ 2 1/ 2
1
,,
,,
1
1cos
E
E
k
k
k
N
max j min j
jidlej k
j
k
j
min j max j
max j min j
mean
N
k
jj
j
HT
CC
P
C
CC
CC
C
E
(30)
,
3 3
1/2 1/ 2
11
,,
EE
NN
kkidlej k
jjjj
jj
min j max j
P
HT E HT
CC
(31)
In (30)
j
(k)
is the offset between the peak traffic time
of the j-th network and the peak traffic time of the k-
th service.
If all the services in the network are similarly
synchronised (i.e. no service is significantly out of
synch with all the other services) we get for all k;
,
2
1
,
E
k
N
k j idle j k
jj
j
mean j
P
HT E
C
(32)
To graphically display the dependence of
2
H
(k)
(T)
and
3
H
(k)
(T) on the parameters C/C
mean
and b, we
average over the k-index; i.e. over the services
giving;
1
S
N
S
kkS
XX
k
HT HTN
(33)
where X is 2 or 3.
Plotting the simulation results for
2
H
(k)
(T)
(S)
and
3
H
(k)
(T)
(S)
, we get identical surface plots as in fig.
3. That is, for the simulation scenario
2
H
Ntwk
(T) =
2
H
(k)
(T)
(S)
and
3
H
Ntwk
(T) =
3
H
(k)
(T)
(S)
. This can be
shown to hold in general provided all of C
mean,j
fall
within a limited range of values.
It is important to note that
X
H
(k)
(T)
X
H
Ntwk
(T)
only applies when all the services are all similarly
synchronised such that the phase,
(k)
, of each
service is within a given range (parametrised by b)
of all other services.
For a service that is significantly out of
synchronisation with the other services, the value of
2
H
(k)
(T) is significantly greater. For example,
consider a service k for which
(k)
well away from
zero and
(l)
0 for all l ≠ k. In this case the network
is highly synchronised with only flow k well out of
synch. In this situation, C
max,j
>> C
min,j
for all j.
Using (30) we get
2
,
1/2 1/2
11
,,
,
1/2 1/2
11
,,
1
2
EE
EE
k
k
k
NN
jidlej k k
jj
k
jj
min j max j
mean
k
NN
jidlej k k
jj
jj
min j max j
HT
P
C
E
CC
C
P
E
CC
(34)
SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems
248
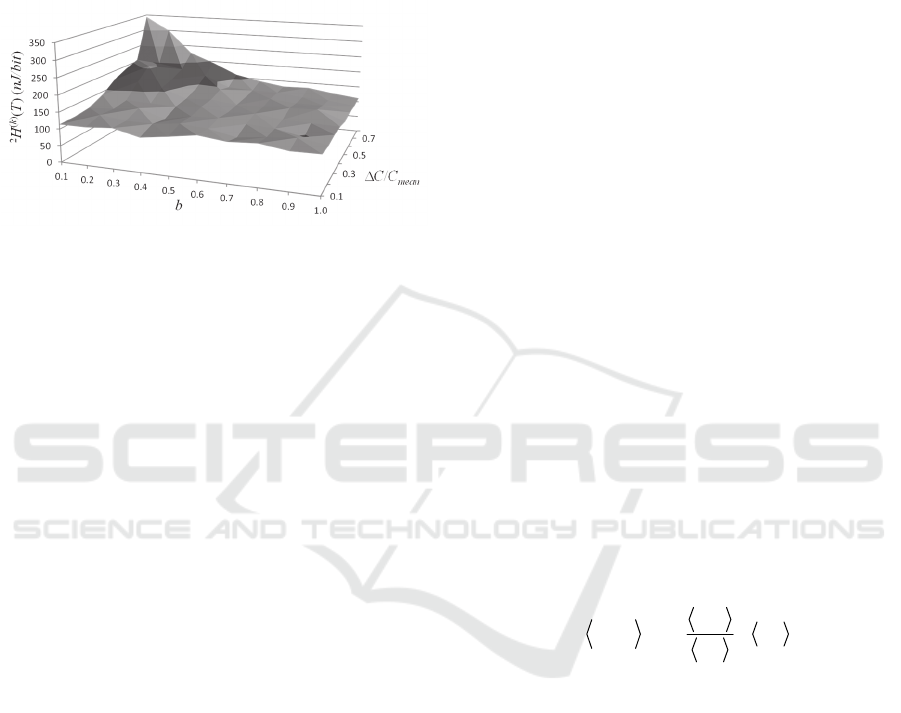
Fig. 4 is a surface plot of
2
H
(k)
(T) for a service
with
(k)
=
for all values of b. We see that an out-
of-synch service has much higher energy per bit than
the other, (in-synch) services when the network is
highly synchronised. As the degree of
synchronisation reduces or the diurnal cycle depth
reduces,
2
H
(k)
(T) reduces to that of the other services.
Figure 4: Surface plot for
2
H
(k)
(T) for a service (
) out of
phase with all other services in the network. Low values of
b correspond to all other flows across the network being
highly synchronised.
Comparing Fig. 3(a) and Fig. 4, we see that service
operators wishing to minimise the energy per bit of
their service will want to avoid being significantly
out-of-synch with the majority of services. This will
lead to service providers trying to synchronise their
services with everyone else. This, in turn, will lead
to deeper diurnal cycles and the resulting over-
dimensioning of the network, mentioned in Section
4, and consequential increase in energy
consumption.
5 APPLICATIONS
The expressions for the H metrics above are all
based on a pure sinusoidal diurnal cycle. In real
networks the diurnal cycle is not a pure sinusoid.
However, generalising these metrics to arbitrary
diurnal cycle profiles is relatively simple. For
1
H(t),
we just replace the sinusoid with the actual diurnal
cycle from collected traffic data. Because
2
H
j
(T) and
2
H
Ntwk
(T) only involve C
mean
, these are directly
applicable to any diurnal cycle profile.
The
2
H
(k)
(t) and
3
H metrics involve quantities
C
max
, C
min
, C and
. To generalise these metrics we
replace these values, in the metric definitions, with
their means over multiple diurnal cycles: C
max
D
,
C
min
D
, C
D
and
D
which can be extracted from
traffic data collected over multiple days. Where a
quantity is raised to a power, a, we replace X
a
by
(X
D
)
a
. Our discussion from now on can be applied
to these generalised forms.
As discussed above, metrics
1
H(t) and
2
H(T) are
already widely used where-as the
3
H(T) metric is
not. The advantage provided by the
3
H(T) metric is
that it quantifies the impact of the shape of the
diurnal cycle and its relationship to other traffic
flows (via C
max
, C
min
and
). This enables us to
quantify the impact of changing traffic profiles on
energy efficiency of networks and services.
Although the energy efficiency metrics have
primarily been created to provide a quantitative
measure of “energy efficiency” (ITU-T 2012 (a))(
Coroama, V. Hilty, L. 2014), they have been also
used to estimate the power consumption of
equipment, networks and services (Baliga, J., et al.
2009)(Van Heggegham, W., et al.,
2012)(Vishwanath, A., et al. 2015). We will now
consider some issues with these applications
5.1 Deployed Networks
The application of the metrics above in real
networks can be very problematic due to
unavailability of or difficulty in attainting the
required data. In particular, evaluating these metrics
for a network or service may require collection of a
significant amount of data not readily available.
Therefore approximations for the metrics can make
evaluation easier, although possibly at the cost of
reduced accuracy. Also, the inter-relationships
between the metrics may allow the data collected for
one metric to be used to evaluate another.
Using (26) we can show that
2
1
idle
Ntwk hops E
E
P
HN E
C
(35)
where N
hops
is the mean number of hops for service
traffic across the network. This form aligns with the
expressions for edge and core network energy
efficiency in (Baliga, J., et al. 2009)(Van
Heggegham, W., et al., 2012).
As discussed above, the simulation results show
the
2
H metric for a network is approximately equal
to the mean
2
H metric across the services, that is:
2
H
Ntwk
(T)
2
H
(k)
(T)
(S)
. The results also show the
variance
(S)
of the services satisfies
(S)
(
X
H
(k)
(T)) < 0.1
X
H
(k)
(T)
(S)
. This means that, to a
first order approximation, provided all the services
in the network are roughly synchronised to the same
degree (i.e. no services are significantly out of
synchronisation with the other services), we have
22
k
Ntwk
HT H T
(36)
A Survey of Internet Energy Efficiency Metrics
249

for most of the services transported by the network.
Similar results hold for
3
H
(k)
(T) and
3
H
Ntwk
(T). In this
case, we can use the
2
H metric of a service to
estimate the
2
H metric of a network or vice versa.
5.2 Estimating Power Consumption
Using energy efficiency to estimate power or energy
consumption is based on the principle that the
power, P, consumed by a network element, network
or service with energy efficiency H joules/bit with
traffic load C bit/sec is given by P = HC (Baliga, J.,
et al. 2009)(Van Heggegham, W., et al., 2012). The
energy consumption is given by Q = HB where B is
the number of bits transferred (Vishwanath, A., et al.
2015).
Although this appears to be intuitive, as we have
seen above, there are multiple choices for evaluating
H. Many authors have used the definition
H’ = P
max
/C
max
where the values of P
max
and C
max
are
based on data provided in equipment specification
sheets or some form of measurement (Baliga, J., et
al. 2009)(Van Heggegham, W., et al., 2012).
In some cases the utilisation U has been included
to give H” = P
max
/UC
max
(Makkes, M., et al., 2013)
where the “utilisation”, U = C(t)/C
max
.
In most cases, H is used to calculate the power or
energy consumption of a service or user, based upon
a data rate for the service or user, C
(k)
(t). Therefore,
the appropriate equation is (7). Noting that
P
max
= P
idle
+ EC
max
, we get
,,
,,
1
1
k max j idle j k
j
max j max j j
PP
Pt Ct
CCUt
(37)
where the j-sum is over equipment along the path of
the service data.
We see that for load proportional equipment
(P
idle
0), H’ is appropriate and for constant power
equipment (P
idle
P
max
) the H’’ is appropriate.
Comparing (13) and (14),
2
H(T) is more
appropriate to calculate the power or energy
consumption of a service because it has the form
P
T
/C
T
and a service is typically parametrised with
C
T
or B(T). Provided the conditions for (36) to hold
are satisfied (see Sec. 8.1) we will have
2
2
,
kk
Ntwk
TT
kk
Ntwk
PHTC
THT T
EB
(38)
This approach has been widely used (Vishwanath,
A., et al. 2015) to estimate power or energy
consumption of a variety of Internet services.
As shown in Sec. 7, (38) is only accurate if the
service in question is not out-of-synch with the other
network flows. Therefore using (38) to estimate the
energy consumption of out-of-synch services (such
as off-peak data transfer services) is inappropriate.
This will also apply to services that travel through
time-zones out-of-synch with their originator.
6 CONCLUSIONS
As a measure for energy efficiency, we have shown
that, even for a given network and the values of
metrics
1
H,
2
H and
3
H can be significantly different.
For example, in a network with somewhat
synchronised traffic, the using the
1
H metric at peak
traffic hour will give a very different value to the
2
H
metric. Therefore, comparing these metrics can be
problematic (Coroama, V. Hilty, L. 2014)( Schien,
D, Preist, C. 2014).
When used to benchmark or improve energy
efficiency, we see that desynchronising traffic flows
reduces the
3
H
metrics. Therefore, according to these
metrics we can improve the energy efficiency of a
network element by desynchronising its traffic
flows. In contrast desynchronising flows has no
impact on
2
H
j
(T) and
2
H
Ntwk
(T).
On the other hand,
2
H
(k)
(T) indicates service
providers should endeavour to synchronise their
service flows with any oscillation in the diurnal
cycle. If all service providers do this, the diurnal
cycle will increase in depth which will impact
network dimensioning. Hence the choice of metric
influences strategy choice for improvement and even
using the same metric in different situations may
lead to different (and possibly conflicting) strategies.
We have also shown that, in certain
circumstances, energy efficiency metrics can be used
to estimate power or energy consumption. However,
this must be done with care and particular note of
how synchronised the service traffic is with other
traffic in the network.
As the energy consumption of the Internet and
ICT increases over the coming years, energy
efficiency metrics will play an important role in
mitigating this increase. In this paper we have
summarised some of the subtleties that need to be
considered in the application of these metrics.
REFERENCES
Baliga, J., et al. 2009, “Energy Consumption in Optical IP
Networks”,
IEEE Jour Lightwave Technol, Vol.27,
No.13, p.2391.
SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems
250

Chan, C., et al., 2012 “Methodologies for assessing the
use-phase power consumption and greenhouse gas
emissions of telecommunications network services”
Environ. Sci. Technol., Vol.47, No.1, p.485.
Chiaraviglio, L., et al., 2009 “Energy-Aware Backbone
Networks: A Case Study”, ICC Workshop.
Coroama, V. Hilty, L. 2014, “Assessing Internet energy
intensity: A review of methods and results”,
Environmental Impact Assessment Review, Vol. 45,
p.63.
Gradshteyn, I. Ryzhik, I. 1980, “Table of Integreals, Series
and Products”, Academic Press.
GreenTouch, 2015 “Reducing the Energy Consumption in
Networks by up to 98% by 2020”
White paper, June.
ITU-T 2012 (a), L.1310 “Energy efficiency metrics and
measurement methods for telecommunications
equipment”
ITU-T 11/2012.
ITU-T 2012(b) Y.3022 (08/2012), “Measuring Energy in
Networks”
Mahadevan, P. et al., 2009 “Energy aware network
operations”, IEEE INFOCOM’09, p.25.
Makkes, M., et al., 2013 “A decision framework for
placement of applications in clouds that minimizes
their carbon footprint”
Jour. Cloud Computing, Vol.2,
No. 21.
Minoli, D., 2011 “Designing Green Networks and
Network Operations” CRC Press.
Schien, D, Preist, C. 2014 “Approaches to Energy
Intensity of the Internet”,
IEEE Communications
Magazine, Nov.
p.130.
Tombaz, S. et al. 2013, “Energy Efficiency Assessment of
Wireless Access Networks Utilizing Indoor Base
Stations”,
PIMRC 2013, p. 3105.
Van Heggegham, W., et al., 2012, “Power consumption
modelling in optical multilayer networks”, Photonic
Network Communications, Vol.24, No.2, p.86.
Vishwanath, A., et al. 2014 “Modelling Router Energy
Consumption in High-Capacity Routers and
Switches”,
IEEE JSAC., Vol.32, No.8, p.1524.
Vishwanath, A., et al. 2015 “Energy Consumption
Comparison of Interactive Cloud-Based and Local
Applications”,
IEEE JSAC, Vol.33, No.4, p.616.
A Survey of Internet Energy Efficiency Metrics
251
