A Framework for Creating Realistic Synthetic Fluorescence

Microscopy Image Sequences

Matsilele Mabaso

, Daniel Withey

and Bhekisipho Twala

MDS(MIAS), Council for Scientific and Industrial Research, Pretoria, South Africa

Department of Electrical and Electronic Engineering, University of Johannesburg,

Auckland Park, Johannesburg, South Africa

Keywords: Synthetic Image Sequences, Microscopy Bioimaging, Spot Detection.

Abstract: Fluorescence microscopy imaging is an important tool in modern biological research, allowing insights into

the processes of biological systems. Automated image analysis algorithms help in extracting information

from these images. Validation of the automated algorithms can be done with ground truth data based on

manual annotations, or using synthetic data with known ground truth. Synthetic data avoids the need to

annotate manually large datasets but may lack important characteristics of the real data. In this paper, we

present a framework for the generation of realistic synthetic fluorescence microscopy image sequences of

cells, based on the simulation of spots with realistic motion models, noise models, and with the use of real

background from microscopy images. Our framework aims to close the gap between real and synthetic

image sequences. To study the effect of real backgrounds, we compared three spot detection methods using

our synthetic image sequences. The results show that the real background influences spot detection,

reducing the effectiveness of the spot detection algorithms, indicating the value of synthetic images with a

realistic background in system validation.

1 INTRODUCTION

Advances in bioimaging based on fluorescence

microscopy have become fundamental in biomedical

and medical research. The use of fluorescence

microscopy and specific staining methods makes the

biological molecules to appear as bright particles

called spots. These bright particles are local intensity

maxima whose intensity level is significantly

different from their neighbourhood. This technique

generates a huge amount of data which is degraded

by factors such as noise and non-uniformity in the

background. Automated image analysis algorithms

are used to study and analyse these images.

Evaluation of these algorithms in real image datasets

requires manual annotation to estimate the ground

truth. However, the process of manual annotation

requires an expert to follow hundreds of spots

moving in an image sequence. This process can be

tedious, susceptible to errors and the ground truth

varies when repeated.

To avoid the problem of manual annotation,

several studies (Genovesio et al., 2006; Sbalzarini

and Koumoutsakos, 2005; Smal et al., 2010; Yoon et

al., 2008; Ruusuvuori et al., 2008; Ruusuvuori et al.,

2010; Rezatifighi et al., 2013) introduced the use of

synthetic image sequences to simulate real

microscopy images. The use of synthetic images

became popular because they contain the ground

truth data and give the opportunity to compare and

validate the results of automated methods. Most

existing frameworks for the creation of synthetic

image sequences (Feng et al., 2011; Smal et al.,

2010; Smal et al., 2008) make certain assumptions,

such as: no background structures, fixed shape for

spots and fixed signal to noise ratio.

(a) (b)

Figure 1: A selection of images with multiple spots. (a)

real fluorescence microscopy image, and (b) synthetic

image with a real background. The background in (b) was

obtained from a different study.

Mabaso, M., Withey, D. and Twala, B.

A Framework for Creating Realistic Synthetic Fluorescence Microscopy Image Sequences.

DOI: 10.5220/0005699200850092

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 2: BIOIMAGING, pages 85-92

ISBN: 978-989-758-170-0

These assumptions make creations of synthetic

images simpler; however, they do not fully reflect

the complexity of real images.

In this work, we describe a powerful framework

for creating realistic synthetic image sequences. The

approach presented in this study is based on the use

of real microscopy image sequences, unlike other

frameworks that simulate the entire image sequence.

Instead of learning the background and trying to

simulate it, our framework makes use of real

microscopy images with synthetic spots. To simulate

our spots we place a Gaussian profile directly into

the real image. These will result in partially-

synthetic image sequences. The proposed framework

is described for 2D images but can also be extended

to 3D.

This paper is organized as follows: Section 2

gives some related work, followed by Section 3

which explains the framework strategy, then Section

4 and 5 present the experimental set-up and results,

and, finally, Section 6 concludes the study.

2 RELATED WORK

There exist several studies for the creation of

synthetic sequences of microscopy images.

Smal (Smal, 2015) proposed a framework that

can mimic images acquired using fluorescence

microscopy. The procedure can simulate background

structures and spots, however, it does not fully

mimic the background of real images, and spot

motion is not considered. Another study (Genovesio

et al., 2006) generated synthetic images using a

mixture of Gaussians to form the background. Their

study modelled some image properties however, it

lacked the properties of a real background structures.

Similar to (Genovesio et al., 2006), (Yoon et al.,

2008) proposed a framework which can model the

movements of spots in microscopy images.

However, (Yoon et al., 2008) did not take into

account the background in microscopy images.

There exist few methods which can model the

effects of image noise, spot motion, and realistic

background in synthetic microscopy images. The

work by (Smal, 2015) can model noise and

background but the motion of spots was not

considered. Another work by (Rezatifighi et al.,

2013) uses HDome transformation (Vincent, 1993)

to estimate the background in real microscopy image

sequences. Although, their study can model spot

motion and noise, it still lacks important

characteristics of real data.

A recent study by (Chenouard et al., 2014)

compared the performance of different tracking

methods using synthetic image sequences. Their

sequences contained spots moving in random walk

with varying velocities, and Gaussian noise was

used to simulate the kind of noise found in

microscopy images. However, the disadvantage of

their sequences is lack of background structures.

One of the major conclusions in their study is the

need for synthetic image sequences with realistic

background.

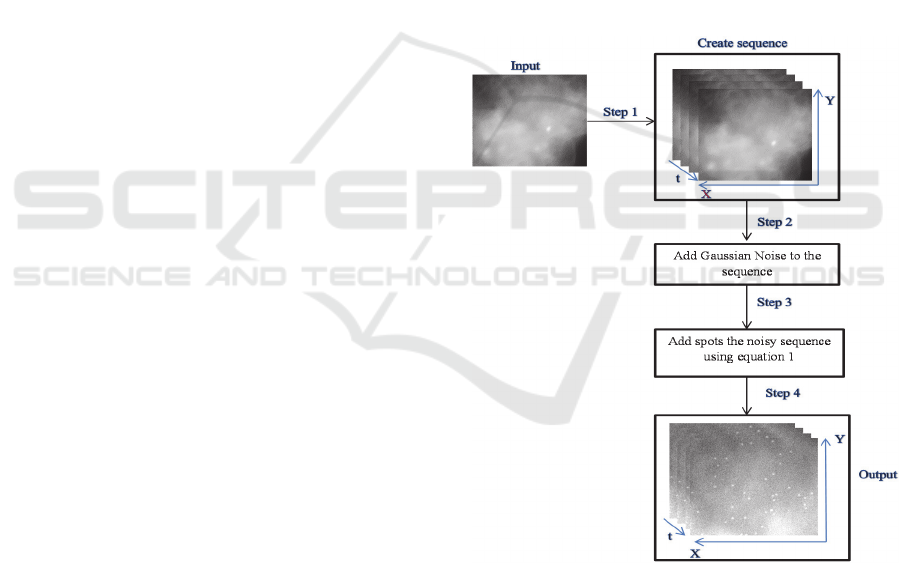
3 OUR FRAMEWORK

To generate our realistic synthetic image sequences,

we propose an improved framework as shown in,

Figure 2, which is able to create realistic synthetic

image sequences of fluorescence microscopy.

Figure 2: A diagram showing the steps involved in our

framework for the creation of synthetic image sequences.

3.1 Reference Data

An example of a real microscopy image with mRNA

spots is shown in Figure 1(a).

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

3.2 Background Modelling

Existing work on creating synthetic image sequences

are based on estimating the background either by

using HDome (Vincent, 1993) or Gaussian mixture

model (Genovesio et al., 2006). The disadvantage of

estimating the background is that it will still be

different from the real background. In our

framework, instead of simulating the background,

we make use of real microscopy images (without

spots) and add the spots. The real images were

obtained from our collaborator, the Synthetic

Biology Research Group at the CSIR.

3.3 Spot Model

Fluorescence microscopy images contain a number

of bright particles (spots) superimposed on an

uneven background, as shown in Figure(a). The

most common approach to model these spots is to fit

a Gaussian intensity profile (Cheezum et al., 2001;

Zhang et al., 2007; Carter et al., 2005). In this work,

we considered a 2D Gaussian function with four

parameters, the position,  and , standard

deviation, and peak intensity. The model for a single

spot is given by:





,













































(1)

The parameters, 



,



describes the width of the

spots, and, , the spot amplitude. In order to model

an isotropic spot, the parameters, 



and 



were set

to be equal.

3.4 Spot Motion Models

The movements of spots in microscopy imaging can

be described using some statistical models of

motion. A number of studies (Genovesio et al.,

2006; Feng et al., 2011; Rezatifighi et al., 2013)

suggested the use of three kinds of models to

describe the kinds of spot movements in microscopy

images (Genovesio et al., 2006). The models

include random walk, first order linear extrapolation,

and second order linear extrapolation, modelling

Brownian motion, constant speed, and constant

acceleration movements, respectively, which are

motions representative of biological motion

(Lakadamyali et al., 2003). To model the movement

of spots using the above mentioned motion models,

we used a plugin developed by (Chenouard, 2015)

3.5 Noise Generation

There exists many noise sources in microscopy

imaging which affects the image quality. To

simulate the kind of noise found in microscopy

imaging, we used additive Gaussian noise with mean

of zero and varying standard deviation, ~μ

0,



. Gaussian models are commonly used

models in microscopy imaging.

3.6 Signal to Noise Ratio

The quality of images can be expressed in terms of

signal to noise ratio (SNR). The SNR measures the

amount of noise in image and is widely used in

image processing. The signal to noise ratio was

defined as the ratio of spot intensity, 



, divided

by the noise standard deviation, 



;











(2)

4 EXPERIMENTAL SET-UP

4.1 Synthetic Sequences

The framework presented in this study is capable of

simulating different kinds of microscopy image

sequences. In order to study the effect of real

background on synthetic image sequences, we

created two types of synthetic image scenarios. The

first scenario consisted of image sequences with no

background structures (named NOBGND) and the

second scenario consisted of synthetic sequences

with real fluorescence background structures.

BGND refers to background. For the second

scenario four realistic synthetic image sequences

(named, BGND0, BGND1, BGND2 and BGND3)

were created by varying the background as shown

in, Figure 3, All the scenarios were corrupted by

Gaussian noise, with the mean of zero and varying

standard deviation {2.86, 5, 10, 20}. The following

signal to noise ratios (SNR) levels were explored {7,

4, 2, 1} where the spot intensity was 20 gray levels.

Each synthetic image sequence created was of 100

time steps with image dimension of 512 by 512

pixels. The density of spots in each image of a

sequence was on the order of {50-100} and the spots

motion models were governed by Brownian motion.

The spot numbers, dynamics, start and end were

randomized in order to mimic the kinds of properties

in real microscopy images. MATLAB was used to

A Framework for Creating Realistic Synthetic Fluorescence Microscopy Image Sequences

add spots, and the OMERO.matlab-4.3.3 toolbox

was used to read and save images.

4.2 Detection Methods

In order to study the effect of real background on

synthetic image sequence, we compared results from

three spot detection methods applied to our synthetic

image sequences. These methods were chosen based

on their implementation availability and they were

also being used in different comparison studies

(Ruusuvuori et al., 2010; Smal et al., 2010). The

detection algorithms compared are, Isotropic

Undecimated Wavelet Transform (IUWT) (Olivo-

Marin, 2008), Feature Point Detection (FPD)

(Sbalzarini and Koumoutsakos, 2005) and HDome

Transformation (Smal et al., 2010; Vincent, 1993).

A detailed description of each method is found in

Appendix A.

4.3 Performance Measure

In order to test the performance of the three

detection methods, we computed several measures:

true positives (TP), false positives (FP) and false

negatives (FN). True positives are detected spots

that correspond to the ground-truth spots. If the

detected spot does not correspond to the ground

truth it is considered as a false positive. A missed

ground truth spot is considered as a false negative.

Two performance measures are considered in this

study, Recall and Precision (Allalou et al., 2010).

Recall measures the ratio of correctly detected spots

overall ground-truth spots, and is defined as:

(a)

(b)

(c)

(d)

(e)

Figure 3: Examples of synthetic image sequences created

using our framework. (a) NOBGND, and (b) BGND0, (c)

BGND1, (d) BGND2, and (e) BGND3.















(3)

Precision measures the ratio of correctly detected

spots among all detected spots and defined as:















(4)

Where 



the number of true positives is, 



the number of false negatives and 



the number of

false positives.

Then, the 



measure is computed as a

weighted average of the two measures, precision and

recall:





2









(5)

A good detection method should have the value of





approaching one.

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

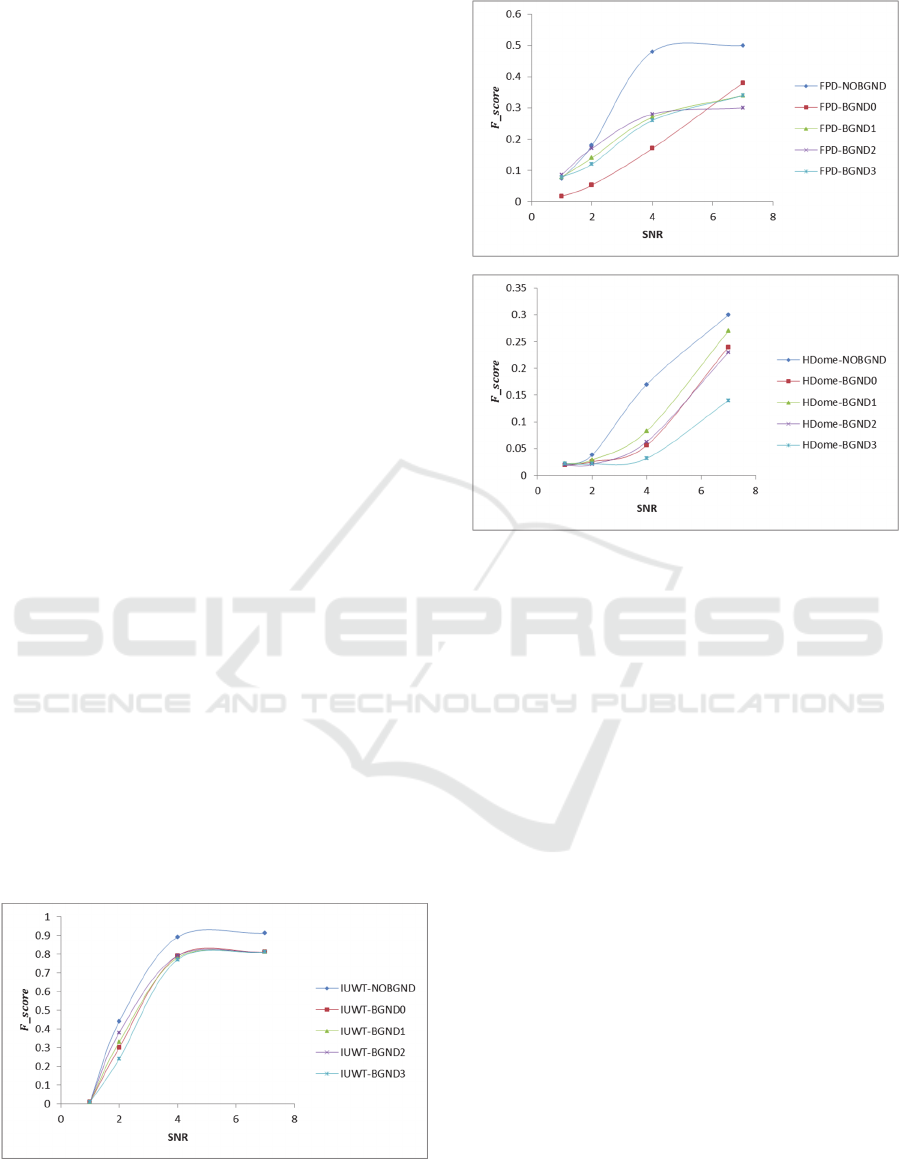
5 EXPERIMENTAL RESULTS

We evaluate the performance of three detection

methods using synthetic image sequences consisting

of five experimental scenarios. The first scenario

consisted of image sequences with no background

structures, NOBGND. This will help with the

evaluation of the performance of the algorithms as a

function of image noise (SNR). The second to fifth

scenario consisted of image sequences with a real

background (BGND0, BGND1, BGND2 and

BGND3). The second to fifth experimental scenarios

were used to evaluate the performance of the

methods as a function of real background and image

noise. In all the scenarios, the spot motion was

governed by Brownian motion. For each method, the

performance measures, Recall, Precision and 



were computed. It’s important to mention that the

only difference between image scenarios was the

background, and all other properties were the same.

Figure 4 shows the results of all detection

methods in terms of 



. The results show that all

methods performed well on NOBGND sequences

compared to sequences with a background. It is

noted that the HDome and FPD methods fail to

reach 



nearly one on NOBGND test case at

SNR=7; because the challenges of handling

overlapping spots. It turns out that the performance

of the algorithms decreases when the real

background is introduced. The decrease in

performance of the algorithms could be explained by

the increase in the number of false positives (FP)

and false negatives (FN) detected by the algorithms

when the background is introduced, and thus

affecting the 



. In all experiments, the IUWT

method performed better compared to other

methods. However at SNR=2 or below all methods

drop in performance for all experiments.

(a)

(b)

(c)

Figure 4: The curves of 



versus SNR for the detection

methods applied to two synthetic image scenarios as

described in Section 4.1. (a) IUWT, (b) FPD and, (c)

HDome. All methods perform less well with realistic

background.

6 CONCLUSIONS

In this work we presented a framework for the

simulation of fluorescence microscopy images

sequences and also study the effect of real

background on synthetic image sequences. The

framework improves the modelling of real

microscopy image sequences by including realistic

spots, realistic noise, and realistic motion with real

image background. The synthetic image sequences

created using this framework offer a better way to

evaluate different detection and tracking algorithms

since the ground truth is available. Our evaluation

results showed that the performance of three

detection methods is reduced when tested with

synthetic image sequences exhibiting realistic

background, compared to the sequences which had

no background. This showed that the real

background has an effect on spot detection algorithm

performance. The performance of the detection

methods is reduced in the presence of background

structures.

A Framework for Creating Realistic Synthetic Fluorescence Microscopy Image Sequences

ACKNOWLEDGEMENTS

This work was carried out with the financial support

of the Council for Scientific and Industrial Research

(CSIR) and the Electrical and Electronic

Engineering Department at the University of

Johannesburg, South Africa. We would also like to

thank the Synthetic Biology research group at the

CSIR for providing us with real microscopy images.

REFERENCES

Allalou, A., Pinidiyaarachchi, A. and Wählby, C. (2010)

'Robust signal detection in 3D fluorescence

microscopy ', Cytometry, vol. 77A, no. 1, pp. 86-96.

Carter, B.C., Shubeita, G.T. and Gross, S.P. (2005)

'Tracking single particles: a user-friendly quantitative

evaluation', Physical Biology, vol. 2, no. 1, pp. 60-72.

Cheezum, M.K., Walker, W.F. and Guilford, W.H. (2001)

'Quantitative comparison of algorithms for tracking

single fluorescent particle', Biophysical Journal, vol.

81, pp. 2378-2388.

Chenouard, N. (2015) Particle tracking benchmark

generator, [Online], Available:

http://icy.bioimageanalysis.org/plugin/Particle_trackin

g_benchmark_generator [1 September 2015].

Chenouard, N., Ihor, S., de Chaumont, F., Maska, M.,

Sbalzarini, I.F., Gong, Y., Cardinale, J., Carthel, C.,

Coraluppi, S., Winter, M., Cohen, A.R., Godinez,

W.J., Rohr, K., Kalaidzidis, Y., Liang, L., Duncan, J.,

Shen, H., Xu, Y., Magnusson, K.E., Jalden, J. et al.

(2014) 'Objective comparison of particle tracking

methods', Nature Methods, vol. 11, no. 3, pp. 281-290.

Crocker, J.C. and Grier, D.G. (1996) 'Methods of Digital

Video Microscopy for Colloidal Studies', Journal of

Colloid and Interface Science 179, pp. 298-310.

Feng, L., Xu, Y., Yang, Y. and Zheng, X. (2011) 'Multiple

dense particle tracking in fluorescence microscopy

images based on multidimensional assignment',

Journal of Structural Biology, vol. 173, pp. 219-228.

Genovesio, A., Liendl, T., Emiliana, V., Parak, W.J.,

Coppey-Moisan, M. and Olivo-Marin, J.-C. (2006)

'Multiple particle tracking in 3d+t microscopy:

Method and application to the tracking of endocytosed

quantum dots', IEEE Transactions on Image

Processing, vol. 15, no. 5, pp. 1062-1070.

Lakadamyali, M., Rust, M.R., Babcock, H.P. and Zhuang,

X. (2003) 'Visualizing infection of individual

influenza viruses', Proceedings of the National

Academy of Science of the United States of America,

9280-9285.

Olivo-Marin, J.-C. (2008) 'Extraction of spots in biological

images using multiscale products', Pattern

Recognition, vol. 35, no. 9, pp. 1989-1996.

Rezatifighi, S.H., Pitkeathly, W.T., Goud, S., Hartley, R.,

Mele, K., Hughes, W.E. and Burchfield, J.G. (2013) 'A

framework for generating realistic synthetic sequences

of total internal reflection fluorescence microscopy

images', 10th IEEE International Symposium on

Biomedical Imaging, 157-160.

Ruusuvuori, P., Äijö, T., Chowdhury, S., Garmaendia-

Torres, C., Selinummi, J., Birbaumer, M., Dudley,

A.M., Pelkmans, L. and Yli-Harja, O. (2010)

'Evaluation of methods for detection of fluorescence

labeled subcellular objects in microscope images',

BMC Bioinformatics, vol. 11, pp. 1-17.

Ruusuvuori, P., Lehmussola, A., Selinummi, J., Rajala, T.,

Huttunen, H. and Yli-Harja, O. (2008) 'Benchmark set

of synthetic images for validating cell image analysis

algorithms', Proceedings of the 16th European Signal

Processing Conference, EUSIPCO.

Sbalzarini, I.F. and Koumoutsakos, P. (2005) 'Feature

Point Tracking and Trajectory Analysis for Video

Imaging in Cell Biology', Journal of Structural

Biology, vol. 151, no. 2, pp. 182-195.

Smal, I. (2015) Synthetic data generator

, September,

[Online], Available:

http://smal.ws/wp/software/synthetic-data-generator/.

Smal, I., Loog, M., Niessen, W. and Meijering, E. (2010)

'Quantitative comparison of spot detection methods in

fluorescence microscopy', IEEE Trans on Medical

Imaging, vol. 29, no. 2, pp. 282-301.

Smal, I., Meijering, E., Draegenstein, K., Galjart, N.,

Grigoriev, I., Akhmanova, A., van Royen, M.,

Houtsmuller, A.B. and Niessen, W. (2008) 'Multiple

object tracking in molecular bioimaging by Rao-

Blackwellized marginal particle filtering', Medical

Image Analysis , vol. 12, no. 6, pp. 764-777.

Vincent, L. (1993) 'Morphological grayscale

reconstruction in image analysis: Applications and

efficient algorithms ', IEEE Trans Image Process, vol.

2, pp. 176-201.

Yoon, J.W., Bruckbauer, A., Fitzgerald, W.J. and

Klenerman, D. (2008) 'Bayesian inference for

improved single molecule fluorescence tracking',

Biophysical Journal, vol. 94, pp. 4932-4947.

Zhang, B., Zerubia, J. and Olivo-Marin, J.-C. (2007)

'Gaussian approximations of fluorescence microscope

PSF models', Applied Optics, vol. 46, no. 10, pp. 1-34.

APPENDIX-A

Spot Detection Methods

Isotropic Undecimated Wavelet Transform

The method of IUWT was proposed in (Olivo-

Marin, 2008) for the detection of spots in biological

images. The algorithm is based on the assumption

that spots will be present at each scale of wavelet

decomposition and thus will appear in the multiscale

product. The ́ trous wavelet transform step is based

on the convolution of the image , row by row

and column by column with a symmetric low pass

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

filter 



1,4,6,4,1



⁄

, resulting in a smoothed

image 



,. This process is repeated for  scale

levels, augmenting the filter with 2



1 zeros

between taps in each case. The corresponding

wavelet coefficients, 



,, are given as:







,









,









,



0



(6)

Then a hard thresholding step is applied to reduce

the effect of noisy wavelet coefficients.









,









,, 



,



0, 



,



(7)

With 







, where 



is the standard deviation of

noisy wavelet coefficients at scale  and 3.

Thus, after hard thresholding, a multiscale

product of each wavelet coefficient is computed to

get a correlation image, 



,,







,







,





(8)

This correlation image 





,



, is binarized with

equation (9) and the resulting connected components

yield the final particles detected.





,

255, 





,







0, 

(9)

Where, 



, is the predetermined detection level. A

spot is accepted only at positions where the

correlation is above 



Feature Point Detection

The method of feature point detection was proposed

in (Crocker and Grier, 1996) and used for the

detection of bright particles in (Sbalzarini and

Koumoutsakos, 2005). The algorithm consists of

four steps:

1) Image Restoration: this step corrects the

imperfection in the image by using a box-car

average estimation and simultaneously enhances

spot-like structures by convolving with a

Gaussian kernel. The convolution kernel is given

by:





























4









21







(10)

where 





and are normalization factors, 



defines

the kernel width and  is a user-tunable constant,

thus the final image after restoration is given by:







,







,



















,





(11)

where , and , are pixel coordinates in the

image and kernel, respectively.

2) Estimating the Particle Location: this is done

by locating local intensity maxima in the filtered

image, 



,. A local maximum is considered

to be a spot if it has the highest intensity within a

local window and the intensity is in the 



highest percentile. These local maximum are

identified using a gray scale dilation with a disc

as the structural element. Then pixels of the

filtered image with the same value as the dilation

transformed image are taken as candidate

locations.

3) Refining the Particle Location: this step

reduces the standard deviation of the position

measurement. It is based on the assumption that

the local intensity maximum of the point  at





,



 is near the geometric center 



,



 of

the spot. The offset is approximated by the

distance to the gray-level centroid in the filtered

image, 



,:













































,























(12)

Factor 



, is the sum of all pixels values over

feature point  given as:





















,







.













(13)

Then the refined location estimate is determined as:







,





















,







.

(14)

4) Non-particle Discrimination: this step rejects

false identifications from sources such as auto

fluorescence and dust. This step is based on the

intensity moments of order 0 and 2, and

identifies true particles as those within a cluster

in the 



,



plane.

HDOME

The method of HDome transformation was proposed

in (Vincent, 1993) and used in biological application

in (Smal et al., 2010). The method is based on the

mathematical morphology:





,







,













,







where 



,



 denotes the results of

subtracting a constant, h, from a gray-scale image

A Framework for Creating Realistic Synthetic Fluorescence Microscopy Image Sequences

,, and 







,



 is the morphological

reconstruction of the gray-scale image, , from





,



. The gray-level reconstruction is

obtained by geodesic dilation of 



,



 under

,. The algorithm starts by reducing

background noise by convolving the original gray

scale image with a LoG filter and simultaneously

enhancing particles. Then HDome method is applied

to the filtered image to keep spots of height superior

to the threshold .

BIOIMAGING 2016 - 3rd International Conference on Bioimaging