
GPS Trajectory Data Enrichment based on a Latent Statistical Model
Akira Kinoshita
1
, Atsuhiro Takasu
2
, Kenro Aihara
2
, Jun Ishii
3
, Hisashi Kurasawa
3
, Hiroshi Sato
3
,
Motonori Nakamura
3
and Jun Adachi
2
1
The University of Tokyo, 2-1-2 Hitotsubashi, Chiyoda, Tokyo, Japan
2
National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda, Tokyo, Japan
3
NTT Network Innovation Laboratories, 3-9-11 Midoricho, Musashino, Tokyo, Japan
Keywords:
GPS Trajectory Data, Interpolation, Latent Statistical Model, Moving Mode Estimation.
Abstract:
This paper proposes a latent statistical model for analyzing global positioning system (GPS) trajectory data.
Because of the rapid spread of GPS-equipped devices, numerous GPS trajectories have become available,
and they are useful for various location-aware systems. To better utilize GPS data, a number of sensor data
mining techniques have been developed. This paper discusses the application of a latent statistical model
to two closely related problems, namely, moving mode estimation and interpolation of the GPS observation.
The proposed model estimates a latent mode of moving objects and represents moving patterns according to
the mode by exploiting a large GPS trajectory dataset. We evaluate the effectiveness of the model through
experiments using the GeoLife GPS Trajectories dataset and show that more than three-quarters of covered
locations were correctly reproduced by interpolation at a fine granularity.
1 INTRODUCTION
Because of the rapid spread of mobile devices
equipped with a global positioning system (GPS),
location information is combined with a wide vari-
ety of data and effectively exploited to realize new
location-aware systems as well as to make existing
systems smarter. For example, recommender systems
utilize GPS data in several tasks, such as location-
aware shopping recommendations (Yang et al., 2008)
and tourism recommendations (Cao et al., 2010).
Location information is key information for intelli-
gent transportation systems such as traffic monitoring
(Schnitzler et al., 2014) and incident detection (Ki-
noshita et al., 2015).
To utilize location information effectively, a num-
ber of sensor data mining methods have been pro-
posed, with the moving mode estimation method of-
ten discussed in the literature. When analyzing user
behavior, the means of traveling are useful. How-
ever, most GPS data do not contain such informa-
tion. Zheng et al. (Zheng et al., 2010a) proposed a
mode-prediction method in which they first detected
a mode-change point in a trajectory and then assigned
a mode to each segment of the trajectory. Latent vari-
ables are often introduced to detect the mode. Yu
et al. (Yu and Kobayashi, 2003) proposed a moving
mode prediction method based on an extended hid-
den Markov model (HMM) where a moving mode is
represented by a hidden state of the HMM. They as-
sumed that the modes represent purposes and means
of traveling such as driving, shopping, etc.
There has also been a growing interest in trajec-
tory pattern mining. Giannotti et al. (Giannotti et al.,
2007) proposed a frequency-based method, where
they found popular areas and frequent moving pat-
terns from trajectories. Monreale et al. (Monreale
et al., 2009) extended this study for location predic-
tion. They extracted the moving pattern represented
by tree-structured data called a T-pattern tree from the
training data, and then predicted the position based on
the moving patterns.
Although the amount of GPS data is extremely
large, we still need to enrich the data in various as-
pects. For example, the sampling rate is limited for
saving the consumption of energy, which causes a
sparsity problem for some analyses. Sampling every
few seconds, for instance, is not sufficient for identi-
fying the route of a car that is moving fast. In addi-
tion, some sensing data could be missing because of
transmission failure.
This paper discusses two GPS data enrichment
Kinoshita, A., Takasu, A., Aihara, K., Ishii, J., Kurasawa, H., Sato, H., Nakamura, M. and Adachi, J.
GPS Trajectory Data Enrichment based on a Latent Statistical Model.
DOI: 10.5220/0005699902550262
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 255-262
ISBN: 978-989-758-173-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
255

problems, namely, interpolation of GPS trajectories
and traveling mode estimation.
When the sampling frequency is not high enough
for analysis, GPS trajectories are interpolated in space
and time. From the spatial point of view, there are
several approaches to estimate locations and paths of
GPS data. Many of them form a trajectory curve
from discrete GPS position data. Brunsdon (Bruns-
don, 2007) applied a principal curve detection tech-
nique (Biau and Fischer, 2012) to trace paths from
GPS data. Sankararaman et al. (Sankararaman et al.,
2013) extracted trajectory curve segments from tra-
jectories, where a frequent portion of the trajectories
is extracted by the dynamic time warping-based sim-
ilarity. When moving objects are supposed to be on
the road, map matching is useful for interpolation,
and many studies have investigated the map-matching
problem. Feng and Timmermans (Feng and Tim-
mermans, 2013) proposed a map-matching method
of GPS data based on the Bayesian belief network.
Karagiorgou and Pfoser (Karagiorgou and Pfoser,
2012) proposed a map generation method where they
detected intersections and then made a road network
by connecting them. Hao et al. (Hao et al., 2014)
proposed a probabilistic model to estimate the vehi-
cle driving state, such as idling and acceleration, to
estimate precisely the location at any time.
From the temporal point of view, Yang et al. (Yang
et al., 2013) proposed the extended Gaussian mixture
model (GMM) to estimate the traveling time of vehi-
cles, where GMM is used to represent the probability
density function of traveling time. Wang et al. (Wang
et al., 2014) proposed a tensor-based method of trav-
eling time.
The present paper proposes a statistical model for
interpolating GPS sensing points. It introduces trav-
eling modes to describe a movement behavior that
varies according to the transportation means, with the
expectation of improvement in interpolation accuracy.
To exploit the training trajectories labeled with trav-
eling modes, we applied the semi-supervised learning
technique to obtain an effective model and evaluated
the model effectiveness using real data.
2 MODEL FOR GPS
TRAJECTORY ENRICHMENT
2.1 Trajectory
As moving objects generally travel on a road, ob-
served GPS points are often mapped onto the road
by a map-matching technique (e.g., (Goh et al., 2012;
Wei et al., 2012)). However, the observed location is
usually erroneous and the map-matching result is not
always correct. In addition, people sometimes get out
of the road network such as in a park. Therefore, we
describe the location of moving objects by a grid. We
first partition a 2-dimensional space into cells each
of which represents an equal-sized and mutually ex-
cluded rectangle. Let G denote the grid, i.e., the set of
cells in which objects move. We represent the loca-
tion of a moving object by a cell g ∈ G, meaning that
the object is somewhere in the cell.
Given a grid G, the movement of a moving object
is described by the cells it passes through and by the
traveling time for each cell. Let g
i
be the i-th cell that
the object passes through. Once the object enters a
cell g
i
, it travels in it for time t
i
, then moves to the next
cell g
i+1
. Therefore, the trajectory of a moving object
is defined as a pair (g, t), where g
:
= hg
1
, g
2
, . . . , g
l
i is
a location sequence, t
:
= ht
1
, t
2
, . . . , t
l
i is a traveling
time sequence, and l is the length of both sequences.
2.2 Traveling Mode
Moving objects, particularly people, change location
by walking or by various means of transportation such
as a vehicle. Even when an object moves by the same
means, its behavior may be different according to its
location. For example, people tend to walk quickly in
a business district to go to work, whereas they tend
to walk more slowly in a commercial district. We in-
troduce a set M of modes to distinguish the behavior
patterns. Note that the mode is latent because we can-
not observe it explicitly. A moving object may change
its traveling mode at any time while traveling, but it
makes the model too complicated. Therefore, in this
paper, we assume that the moving object travels with
the same mode in a cell. The traveling mode depends
on the location. For example, the “train” mode is
likely to be chosen on a railway, while the “car” mode
is likely to be chosen on an expressway. Therefore,
for each cell g, we introduce a multinomial probabil-
ity distribution with parameter θ
g
:
= (θ
gm
)
m∈M
. The
probability of the traveling mode m ∈ M of an object
in a cell g is:
p(m | g)
:
= θ
gm
. (1)
2.3 Traveling Time of Moving Objects
The traveling time varies according to the traveling
mode and location as well as the individual charac-
teristics. To avoid the sparsity problem in parameter
estimation, we ignore the differences between indi-
viduals. For each mode m in a cell g, we describe the
distribution of traveling time t in terms of a univari-
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
256

ate Gaussian distribution with mean µ
gm
and variance
σ
gm
2
, i.e.,
p(t | g, m)
:
= N (t; µ
gm
, σ
gm
2
)
=
1
p
2πσ
gm
2
exp
−
(t − µ
gm
)
2
2σ
gm
2
. (2)
Taking a marginal distribution, the traveling time t to
pass through g follows a Gaussian mixture distribu-
tion:
p(t | g) =
∑
m∈M
θ
gm
N (t;µ
gm
, σ
gm
2
). (3)
2.4 Moving Direction
To predict the future location of a moving object, we
introduce a probability distribution for the next cell to
move into.
Suppose a moving object is in a cell g and consider
the probability distribution over the adjacent cells.
The probability distribution should depend on the cell
itself because of traffic constraints such as “no right
turn” and attractors such as popular shops. It should
also depend on the traveling mode. If a moving ob-
ject is traveling by train, it tends to go straight to the
next cell. On the other hand, if the moving object is
walking, it may move to various directions.
From this observation, we introduce the probabil-
ity distribution of the direction of an adjacent cell to
which a moving object moves. Let D be a set of di-
rections of adjacent cells: {north, east, south, west}.
When a moving object in mode m is in a cell g, we as-
sume that its moving direction d ∈ D follows a multi-
nomial distribution with parameter φ
gm
:
= (φ
gmd
)
d∈D
,
namely,
p(d | g, m)
:
= φ
gmd
. (4)
Now, the trajectory of a moving object is redefined as
a triple (g, t, d), where d
:
= hd
1
, d
2
, . . . , d
l
i is the mov-
ing direction sequence and d
i
is the moving direction
from the i-th cell g
i
.
2.5 Likelihood of a Trajectory
Let x
:
= (g, t, d) be a trajectory. The moving object
takes only one of the traveling modes for each cell,
although they are latent. Let m
i
be the traveling mode
in the i-th cell and y
:
= hm
1
, m
2
, . . . , m
l
i be the mode
sequence for the trajectory x. Then, the complete-data
likelihood of the model is given as follows:
p(x, y) =
l
∏
i=1
p(t
i
| g
i
, m
i
) · p(d
i
| g
i
, m
i
) · p(m
i
| g
i
)
=
l
∏
i=1
N (t
i
;µ
g
i
m
i
, σ
g
i
m
i
2
) · θ
g
i
m
i
· φ
g
i
m
i
d
i
. (5)
3 PARAMETER ESTIMATION
We adopt a maximum a posteriori (MAP) estimation
for learning the prediction model. Let us first intro-
duce the conjugate priors for each probability distri-
bution. The symmetric Dirichlet distribution with the
parameter α (respectively β) is used for the multino-
mial distributions for the mode (respectively the mov-
ing direction), whereas the Gaussian-gamma distribu-
tion with the parameters ν, η, a, and b is used for
the traveling time distribution. Now the generative
process of the model parameters is to choose them as
follows:
1. θ
g
∼ Dir(α) for each g ∈ G,
2. φ
gm
∼ Dir(β) for each g ∈ G and m ∈ M,
3. (µ
gm
, (σ
gm
2
)
−1
) ∼ GaussianGamma(ν, η, a, b) for
each g ∈ G and m ∈ M.
The observed trajectory data are considered to be
generated under these parameters. Most of them are
unlabeled, i.e., their mode is unknown. Let X
u
denote
a set of unlabeled trajectories. The generative process
of X
u
is as follows.
4. For each observation in each trajectory in X
u
,
(a) m ∼ Multi(θ
g
),
(b) d ∼ Multi(φ
gm
),
(c) t ∼ N (µ
gm
, σ
gm
2
).
On the other hand, we can obtain a portion of labeled
data where the mode of observation is known as in the
GeoLife dataset (Zheng et al., 2009). Let X
l
denote a
set of labeled trajectories. The generative process of
X
l
is as follows.
5. For each observation in each trajectory in X
l
,
(a) d ∼ Multi(φ
gm
),
(b) t ∼ N (µ
gm
, σ
gm
2
),
where m is the labeled mode.
For simplicity, we denote the set of parameters
used in our model by Θ:
Θ
:
=
{θ
g
}
g∈G
, {φ
gm
, µ
gm
, σ
gm
2
}
g∈G,m∈M
. (6)
Using both labeled and unlabeled data, Θ can be esti-
mated by solving the following formula including two
weight parameters λ
l
and λ
u
that control the effect
of labeled and unlabeled data, respectively (Gr
¨
onroos
et al., 2014):
arg max
Θ
[ln p(Θ) + λ
l
ln p(X
l
| Θ) + λ
u
ln p(X
u
| Θ)].
(7)
Although we are in a semi-supervised situation, the
estimate of Θ can be computed by an expectation–
maximization (EM) algorithm. In the remainder of
GPS Trajectory Data Enrichment based on a Latent Statistical Model
257

this section, we derive the MAP estimator, concentrat-
ing on differences from the ordinary textbook treat-
ments (Bishop, 2006; Zhu and Goldberg, 2009) be-
cause of lack of space.
The Q function for our model is given by
Q(Θ,
ˆ
Θ) =
∑
x∈X
u
|x|
∑
i=1
∑
m∈M
p(m | x
i
,
ˆ
Θ)ln p(x
i
, m | Θ),
(8)
where
p(m | x
i
,
ˆ
Θ) ∝
ˆ
θ
g
i
m
·
ˆ
φ
g
i
md
i
· N (t
i
| ˆµ
g
i
m
,
ˆ
σ
g
i
m
2
), (9)
p(x
i
, m | Θ) = θ
g
i
m
· φ
g
i
md
i
· N (t
i
| µ
g
i
m
, σ
g
i
m
2
), (10)
and
ˆ
Θ refers to the parameters estimated in the previ-
ous EM iteration. The E step computes Equation (9)
for each observation x
i
:
= (g
i
, t
i
, d
i
) in the unlabeled
training dataset X
u
for each mode m ∈ M.
According to Equation (7), the objective function
to be maximized in the M step is given by
F(Θ)
:
= ln p(Θ)+λ
l
ln p(X
l
| Θ)+ λ
u
Q(Θ,
ˆ
Θ). (11)
The first term is rewritten using the priors we intro-
duced above, as follows:
ln p(Θ) =
∑
g∈G
ln p(θ
g
| α) +
∑
g∈G,m∈M
ln p(φ
gm
| β)
+
∑
g∈G,m∈M
ln p
µ
gm
,
σ
gm
2
−1
| ν, η, a, b
.
(12)
The second term is the weighted log-likelihood of the
labeled training data. Using Equation (5), we obtain
ln p(X
l
| Θ) =
∑
g∈G,m∈M
N
gm
lnθ
gm
+
∑
g∈G,m∈M,d∈D
N
gmd
lnφ
gmd
+
∑
g∈G,m∈M
N
gm
∑
j=1
lnN (t
j
| µ
gm
, σ
gm
2
),
(13)
where N
gm
is the number of labeled observations in
the cell g with the mode label m, N
gmd
is the number
of labeled observations whose direction is d in the cell
g with the mode label m, and t
j
is the j-th labeled
observation value of the travel time in the cell g with
the mode label m. The third term is the weighted Q
function, which can be rewritten as follows:
Q(Θ,
ˆ
Θ) =
∑
g∈G,d∈D
N
gd
∑
j=1
∑
m∈M
γ
gmd j
·
lnθ
gm
+ ln φ
gmd
+ln N (t
j
| µ
gm
, σ
gm
2
)
, (14)
where N
gd
is the number of unlabeled observations in
the cell g whose direction is d, x
j
:
= (g, t
j
, d) is the
j-th unlabeled observation value in the cell g with the
direction d, and γ
gmd j
:
= p(m | x
j
,
ˆ
Θ). Because the
parameters θ
g
and φ
gm
have a constraint, respectively,
Equation (11) is maximized by introducing Lagrange
multipliers and setting its partial derivative to zero.
The update equations are derived as follows:
θ
gm
∝ α − 1 + λ
l
N
gm
+ λ
u
∑
d∈D
N
gd
∑
j=1
γ
gmd j
, (15)
φ
gmd
∝ β − 1 + λ
l
N
gmd
+ λ
u
N
gd
∑
j=1
γ
gmd j
, (16)
µ
gm
=
νη + λ
l
∑
N
gm
j=1
t
j
+ λ
u
∑
d∈D
∑
N
gd
j=1
γ
gmd j
t
j
η + λ
l
N
gm
+ λ
u
∑
d∈D
∑
N
gd
j=1
γ
gmd j
,
(17)
σ
gm
2
=
S
2a − 1 + λ
l
N
gm
+ λ
u
∑
d∈D
∑
N
gd
j=1
γ
gmd j
, (18)
where
S
:
= 2b + η(µ
gm
− ν)
2
+ λ
l
N
gm
∑
j=1
(t
j
− µ
gm
)
2
+ λ
u
∑
d∈D
N
gd
∑
j=1
γ
gmd j
(t
j
− µ
gm
)
2
.
(19)
4 INTERPOLATION
Now assume that we have the total traveling time
t
Σ
:
=
∑
l
i=1
t
i
instead of the traveling time sequence
t. Let x
0
be a triple (g, t
Σ
, d). As each t
i
follows
a Gaussian distribution N (µ
g
i
m
i
, σ
g
i
m
i
2
), the sum of
normally distributed variables t
Σ
obeys the Gaussian
distribution N (µ
x
0
,y
, σ
x,y
2
), where
µ
x
0
,y
=
∑
i
µ
g
i
m
i
, σ
x
0
,y
2
=
∑
i
σ
g
i
m
i
2
. (20)
Therefore,
p(x
0
, y) = p(t
Σ
| g, y) ·
l
∏
i=1
p(d
i
| g
i
, m
i
) · p(m
i
| g
i
)
= N (t
Σ
;µ
x
0
,y
, σ
x
0
,y
2
) ·
l
∏
i=1
θ
g
i
m
i
· φ
g
i
m
i
d
i
. (21)
Using two distant GPS observations, the total trav-
eling time t
Σ
and the first and last cells of the location
sequence g can be calculated directly. Given a set of
possible location sequences {g}, a corresponding set
of possible moving direction sequences {d}, a set of
possible traveling mode sequences {y}, we can ob-
tain the maximum-likelihood trajectory, i.e., the most
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
258

probable g, d, and y, using Equation (21), whereby
the observations are interpolated. On the assumption
that the trajectory travels n
ew
cells along the east–west
direction and n
ns
cells along the north–south direc-
tion via the shortest path, the cardinality of the search
space is
(n
ew
+ n
ns
)!
n
ew
!n
ns
!
|M|
n
ew
+n
ns
. (22)
5 EXPERIMENTAL RESULTS
5.1 Experimental Setup
We used GeoLife GPS Trajectories Version 1.3
(Zheng et al., 2008; Zheng et al., 2010b; Zheng et al.,
2009) for evaluating the proposed latent model. This
dataset consisted of trajectories of 182 users. The tra-
jectories of 69 users were associated with a traveling
mode in walk, run, bike, bus, taxi, car, subway, train,
airplane. Therefore, the number of modes |M| was 9.
Figure 1: The experimental object region, which is a rect-
angle with side lengths of about 50 km in Beijing (map tiles
©OpenStreetMap contributors, CC BY-SA 2.0).
We chose data inside the area of central Beijing
shown in Figure 1, where observed GPS data were
not sparse. We generated trajectories by concatenat-
ing observations in chronological order whenever the
time gap between two consecutive observations was
10 s or less.
Next, we converted the original GeoLife trajectory
data into our trajectory form described in Section 2.1.
Figure 2 illustrates the method of conversion. We first
split the area into cells with a width of 0.0006° of lon-
gitude and height of 0.0005° of latitude. Each cell g is
a rectangle with side lengths of about 50 m. An origi-
nal GeoLife trajectory is a sequence of spatiotemporal
points. We converted the trajectory by finding all the
•
•
•
•
•
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
Observed point
Linear-interpolated point
Converted cell
Figure 2: Trajectory conversion from the GeoLife dataset.
The color of a converted cell indicates the travel time within
it.
Table 1: Transportation modes and their priors.
mode mean speed ν [s] η a b
walk 1 km/h 180.0 10
−6
1 2
run 4 km/h 45.0 10
−6
1 2
bike 10 km/h 18.0 10
−6
1 2
bus 15 km/h 12.0 10
−6
1 2
taxi 20 km/h 9.0 10
−6
1 2
car 30 km/h 6.0 10
−6
1 2
subway 40 km/h 4.5 10
−6
1 2
train 60 km/h 3.0 10
−6
1 2
airplane 900 km/h 0.2 10
−6
1 2
cells through which it passes and calculating the trav-
eling time for each cell by linear interpolation. We
used 90% of the converted dataset for training and the
residual 10% of the data was used for the test. The
training dataset included nine-tenths of consecutive
trajectories for each user.
5.2 Model Parameter Estimation
We estimated the model parameters by MAP esti-
mation. There were 4,462,614 observations from
186,617 cells in the training dataset. We used prior
parameters for each mode, as shown in Table 1, which
we chose arbitrarily. The value of ν was determined
by dividing 50 m, which is equal to the length of a
side of a cell, by the mean travel speed we assumed
(Table 1). We also used prior and weight parameters:
α = β = 2.0, λ
u
= 0.5, λ
l
= 1.0.
We implemented the EM algorithm described
above using OpenMP for multiprocessing. The EM
algorithm has iterated the E step and the M step until
the improvement in log-likelihood fell below 0.01%.
The estimation was executed on our 32-core Xeon
computer. The EM algorithm was finished in nine it-
erations taking 11.3 s.
Figure 3 shows the estimated parameters; only
GPS Trajectory Data Enrichment based on a Latent Statistical Model
259
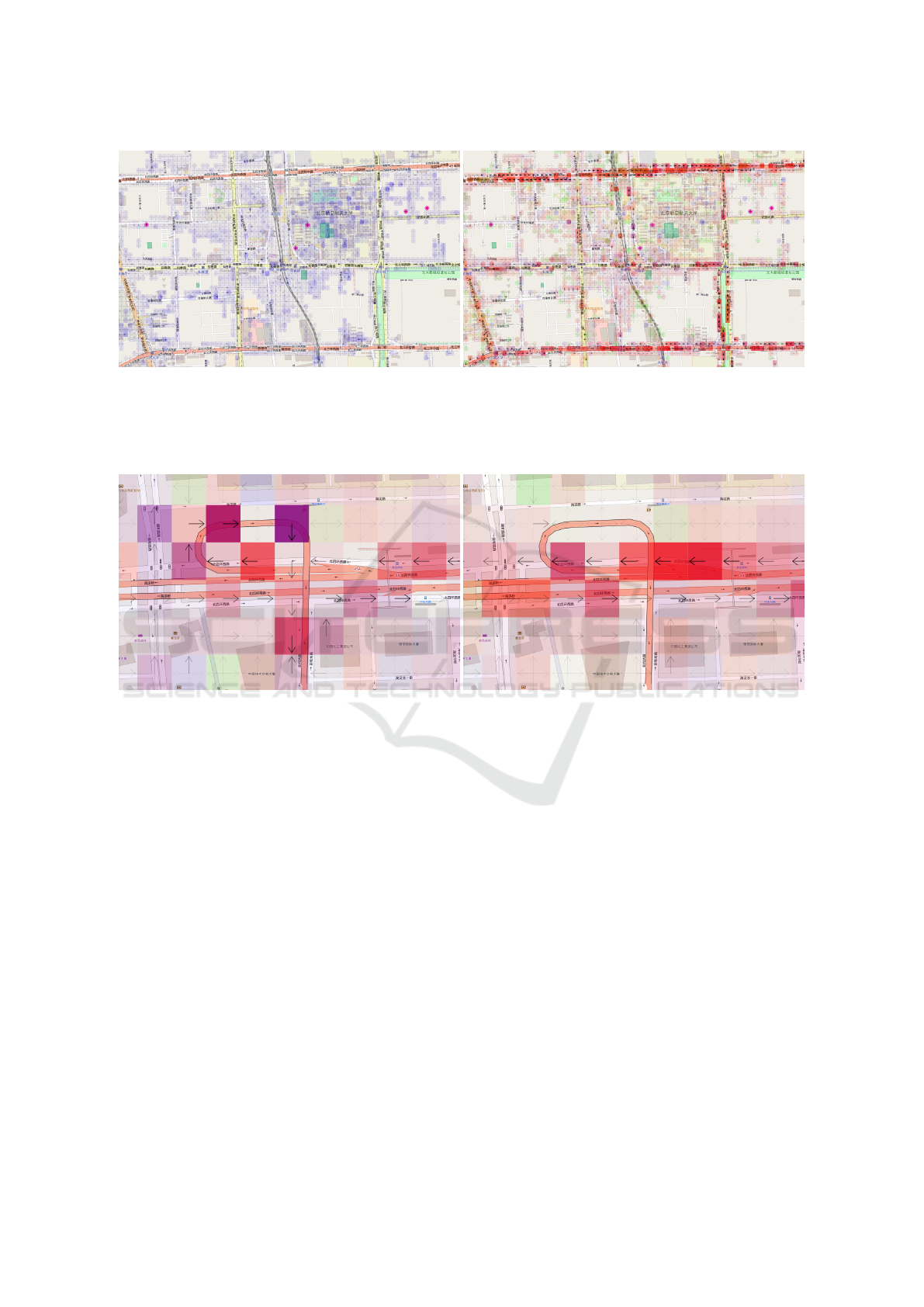
(a) Run. (b) Train.
Figure 3: Estimated model parameters for each cell for each traveling mode (map tiles ©OpenStreetMap contributors, CC
BY-SA 2.0). Two of nine modes are shown because of space limitations. The color of a cell indicates the mean travel time
µ
gm
. Green represents short travel time (1.8 s), red is moderate travel time (3.6 s), and blue is long travel time (∞ s). The
opacity of a cell indicates θ
gm
, the probability that the mode m is chosen in the cell g (opaquer is higher).
(a) Slower mode. (b) Faster mode.
Figure 4: Enlarged view of estimated model parameters around Zhongguancun exit on the North 4th Ring Road (expressway)
(map tiles ©OpenStreetMap contributors, CC BY-SA 2.0). The parameters µ
gm
and θ
gm
are shown in the same way as in
Figure 3, while arrows in a cell indicate φ
gmd
, the probability that the direction d is chosen with the mode m in the cell g
(bolder is higher).
two of nine modes are shown because of space limi-
tations. As can be seen, there are regional differences
of traveling mode tendencies: slower modes tend to
appear around local streets, while faster modes are
likely to appear on arteries or railways. Figure 4 is
an enlarged view, showing the differences in moving
direction and mean travel time between two different
modes. The moving direction is also learned, so that
a trajectory travels on the right side of wide roads and
that it takes different routes depending on the mode.
5.3 Interpolation and Traveling Mode
Estimation
We evaluated the performance of our interpolation
method. As our algorithm has high complexity, we
prepared a 3x5 dataset by collecting all subtrajecto-
ries that travel three cells along a north–south or
east–west direction and five cells along the orthog-
onal direction via the shortest path. For each sub-
trajectory in the 3x5 dataset, we estimated the inter-
mediate cells given its first and last cells and its to-
tal travel time. The cardinality of the search space
was 2,410,616,376. The interpolation was finished
in 1 min for each subtrajectory using our 72-core
Xeon computer and the OpenMP technology. We
evaluated the interpolation performance by recall, i.e.,
the number of correctly interpolated cells divided by
the number of the total intermediate cells that actu-
ally included observation data of the original GeoLife
dataset.
In the test dataset, there were 8,276 subject sub-
trajectories and the recall was 78.8% (38,695 suc-
cess/49,092 cells). Although we did not conduct any
parameter tuning, more than three-quarters of the in-
terpolations were successful. There is an ample room
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
260

walk
run
bike
bus
taxi
car
subway
train
airplane
estimated mode
walk
run
bike
bus
taxi
car
subway
train
airplane
true mode
29
4
18 37
12
26 82
97
78
0 0 0 0 0 0 0 0 0
3
2
25 16 8 13 26 3
21
0 0
9
8
4 2
8 0
1
10 0
4 2
5 8 38 30 25
27
0
4
5
19
85
112
189 159
11
0 0 0 0 6 8 8
7
11 2 1
16 3 18
22 24
36
0 0 0 0 0 0 0 0 0
Figure 5: Confusion matrix of traveling mode estimation.
0 10 20 30 40 50
traveling time [sec]
walk
run
bike
bus
taxi
car
subway
train
airplane
Figure 6: Distribution of traveling time for each mode.
for improving performance by giving better priors and
weight parameters when the model is learned. On the
other hand, our interpolation method has high com-
plexity and is not scalable. Further work is being car-
ried out to improve the scalability of the algorithm.
Of the 3x5 subtrajectories in the test dataset, 309
have traveling mode labels. Our interpolation algo-
rithm estimated the traveling mode for each cell at
the same time as determining the cells. The accuracy
of the traveling mode was 12.9% (184 success/1,427
correctly interpolated cells). Figure 5 shows the con-
fusion matrix.
One possible reason for the poor accuracy of trav-
eling mode estimation is that the distribution of trav-
eling time was similar for all traveling modes. Fig-
ure 6 shows box plots of traveling time over the whole
dataset for each traveling mode. Here it can be seen
that the distributions of some modes, car and train for
example, were similar. This calls for further discus-
sion on feature selection. Another possible problem
is the labeling quality in the dataset. For example, a
GeoLife trajectory shown in Figure 7 was labeled as
“airplane” mode, but its movement was unnatural for
an airplane because it traveled along expressways, ar-
teries, and local streets. As the interpolation in this
experiment was conducted only in the spatial aspect,
Figure 7: A GeoLife trajectory labeled as “airplane” mode
(map tiles ©OpenStreetMap contributors, CC BY-SA 2.0).
it remains a challenge for future research to enrich tra-
jectories in the temporal aspect. Improving the perfor-
mance of traveling mode estimation would assist this
kind of trajectory enrichment.
6 CONCLUSION
We have studied the problem of GPS trajectory en-
richment, namely, interpolation and traveling mode
estimation. We developed a statistical model where
the traveling time and the moving direction depended
on both the location and the latent traveling mode,
whereas the mode also depended on the location. We
derived formulas to estimate the MAP parameters of
the model using GPS observation data which can in-
clude some observations with traveling mode labels.
Our method was applied to the GeoLife dataset. The
results showed that our model could describe the char-
acteristics of movements depending on location and
traveling mode and that more than three-quarters of
covered locations were correctly reproduced by inter-
polation at a fine granularity. Future work will in-
clude the development of a more computationally ef-
ficient interpolation algorithm, optimization of the set
of traveling modes, and feature selection.
ACKNOWLEDGEMENTS
This work was supported by CPS-IIP Project in the
research promotion program for national-level chal-
lenges “Research and development for the realization
of next-generation IT platforms” by the Ministry of
Education, Culture, Sports, Science and Technology,
Japan.
GPS Trajectory Data Enrichment based on a Latent Statistical Model
261

REFERENCES
Biau, G. and Fischer, A. (2012). Parameter selection
for principal curves. IEEE Trans. Inf. Theory,
58(3):1924–1939.
Bishop, C. M. (2006). Mixture Models and EM. In Pat-
tern Recognit. Mach. Learn., chapter 9, pages 423–
460. Springer, New York, NY, USA.
Brunsdon, C. (2007). Path estimation from GPS tracks. In
Proc. 9th Int. Conf. GeoComputation, Maynooth, Ire-
land.
Cao, L., Luo, J., Gallagher, A., Jin, X., Han, J., and Huang,
T. S. (2010). A worldwide tourism recommendation
system based on geotagged web photos. In 2010
IEEE Int. Conf. Acoust. Speech Signal Process., pages
2274–2277, Dallas, Texas, USA. IEEE.
Feng, T. and Timmermans, H. J. P. (2013). Map matching of
GPS data with Bayesian belief networks. Proc. East.
Asia Soc. Transp. Stud., 9.
Giannotti, F., Nanni, M., Pedreschi, D., and Pinelli, F.
(2007). Trajectory pattern mining. In Proc. 13th
ACM SIGKDD Int. Conf. Knowl. Discov. Data Min.
(KDD ’07), pages 330–339, San Jose, California,
USA. ACM.
Goh, C. Y., Dauwels, J., Mitrovic, N., Asif, M. T., Oran,
A., and Jaillet, P. (2012). Online map-matching based
on Hidden Markov model for real-time traffic sensing
applications. In 15th Int. IEEE Conf. Intell. Transp.
Syst., pages 776 – 781, Anchorage, Alaska, USA.
IEEE.
Gr
¨
onroos, S.-A., Virpioja, S., Smit, P., and Kurimo,
M. (2014). Morfessor FlatCat: An HMM-based
method for unsupervised and semi-supervised learn-
ing of morphology. In Proc. COLING 2014, 25th Int.
Conf. Comput. Linguist. Tech. Pap., pages 1177–1185,
Dublin, Ireland.
Hao, P., Boriboonsomsin, K., Wu, G., and Barth, M. (2014).
Probabilistic model for estimating vehicle trajectories
using sparse mobile sensor data. In 2014 IEEE 17th
Int. Conf. Intell. Transp. Syst. (ITSC ’14), pages 1363–
1368, Qingdao, China. IEEE.
Karagiorgou, S. and Pfoser, D. (2012). On vehicle tracking
data-based road network generation. In Proc. 20th Int.
Conf. Adv. Geogr. Inf. Syst. (SIGSPATIAL ’12), pages
89–98, Redondo Beach, California. ACM.
Kinoshita, A., Takasu, A., and Adachi, J. (2015). Real-time
traffic incident detection using a probabilistic topic
model. Inf. Syst., 54:169–188.
Monreale, A., Pinelli, F., Trasarti, R., and Giannotti, F.
(2009). WhereNext: A location predictor on trajectory
pattern mining. In Proc. 15th ACM SIGKDD Int. Conf.
Knowl. Discov. Data Min. (KDD ’09), pages 637–646,
Paris, France. ACM.
Sankararaman, S., Agarwal, P. K., Mølhave, T., Pan, J.,
and Boedihardjo, A. P. (2013). Model-driven match-
ing and segmentation of trajectories. In Proc. 21st
ACM SIGSPATIAL Int. Conf. Adv. Geogr. Inf. Syst.
(SIGSPATIAL ’13), pages 234–243, Orlando, Florida.
ACM.
Schnitzler, F., Artikis, A., Weidlich, M., Boutsis, I.,
Liebig, T., Piatkowski, N., Bockermann, C., Morik,
K., Kalogeraki, V., Marecek, J., Gal, A., Mannor,
S., Kinane, D., and Gunopulos, D. (2014). Het-
erogeneous stream processing and crowdsourcing for
traffic monitoring: Highlights. In Proc. Eur. Conf.
Mach. Learn. Princ. Pract. Knowl. Discov. Databases
(ECML PKDD ’14), pages 520–523, Nancy, France.
Springer Berlin Heidelberg.
Wang, Y., Zheng, Y., and Xue, Y. (2014). Travel time esti-
mation of a path using sparse trajectories. In Proc.
20th ACM SIGKDD Int. Conf. Knowl. Discov. data
Min. (KDD ’14), pages 25–34, New York, New York,
USA. ACM.
Wei, H., Wang, Y., Forman, G., Zhu, Y., and Guan, H.
(2012). Fast Viterbi map matching with tunable
weight functions. In Proc. 20th Int. Conf. Adv. Geogr.
Inf. Syst. (SIGSPATIAL ’12), pages 613–616, Redondo
Beach, California. ACM.
Yang, Q., Wu, G., Boriboonsomsin, K., and Barth, M.
(2013). Arterial roadway travel time distribution es-
timation and vehicle movement classification using a
modified Gaussian mixture model. In 16th Int. IEEE
Conf. Intell. Transp. Syst. (ITSC ’13), pages 681–685,
The Hague, The Netherlands. IEEE.
Yang, W.-S., Cheng, H.-C., and Dia, J.-B. (2008). A
location-aware recommender system for mobile shop-
ping environments. Expert Syst. Appl., 34(1):437–
445.
Yu, S.-Z. and Kobayashi, H. (2003). A hidden semi-Markov
model with missing data and multiple observation se-
quences for mobility tracking. Signal Processing,
83:235–250.
Zheng, Y., Chen, Y., Li, Q., Xie, X., and Ma, W.-Y. (2010a).
Understanding transportation modes based on GPS
data for web applications. ACM Trans. Web, 4(1):1:1–
1:36.
Zheng, Y., Li, Q., Chen, Y., Xie, X., and Ma, W.-Y. (2008).
Understanding mobility based on GPS data. In Proc.
10th Int. Conf. Ubiquitous Comput. (UbiComp ’08),
pages 312–321, Seoul, Korea. ACM.
Zheng, Y., Xie, X., and Ma, W.-Y. (2010b). GeoLife: A
collaborative social networking service among user,
location and trajectory. Bull. Tech. Comm. Data Eng.,
33(2):32–39.
Zheng, Y., Zhang, L., Xie, X., and Ma, W.-Y. (2009). Min-
ing interesting locations and travel sequences from
GPS trajectories. In Proc. 18th Int. Conf. World Wide
Web (WWW ’09), pages 791–800, Madrid, Spain.
ACM.
Zhu, X. and Goldberg, A. B. (2009). Introduction to Semi-
Supervised Learning. Morgan & Claypool.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
262
