
A Comparative Study on Outlier Removal from a Large-scale Dataset
using Unsupervised Anomaly Detection
Markus Goldstein and Seiichi Uchida
Department of Advanced Information Technology, Kyushu University,
744 Motooka, Nishi-ku, Fukuoka, 819-0395, Japan
Keywords:
Outlier Removal, Unsupervised Anomaly Detection, Handwritten Digit Recognition, Large-scale Dataset,
Data Cleansing, Influence of Outliers.
Abstract:
Outlier removal from training data is a classical problem in pattern recognition. Nowadays, this problem
becomes more important for large-scale datasets by the following two reasons: First, we will have a higher
risk of “unexpected” outliers, such as mislabeled training data. Second, a large-scale dataset makes it more
difficult to grasp the distribution of outliers. On the other hand, many unsupervised anomaly detection methods
have been proposed, which can be also used for outlier removal. In this paper, we present a comparative study
of nine different anomaly detection methods in the scenario of outlier removal from a large-scale dataset.
For accurate performance observation, we need to use a simple and describable recognition procedure and
thus utilize a nearest neighbor-based classifier. As an adequate large-scale dataset, we prepared a handwritten
digit dataset comprising of more than 800,000 manually labeled samples. With a data dimensionality of
16×16 = 256, it is ensured that each digit class has at least 100 times more instances than data dimensionality.
The experimental results show that the common understanding that outlier removal improves classification
performance on small datasets is not true for high-dimensional large-scale datasets. Additionally, it was found
that local anomaly detection algorithms perform better on this data than their global equivalents.
1 INTRODUCTION
Outliers are instances in a dataset, which deviate
clearly from the norm. It seems to be logical to elimi-
nate outliers before classification takes place. Indeed,
this was the main motivation of Grubbs (Grubbs,
1969), when he developed his first outlier test. At that
time, parametric classification models like a simple
Gaussian fit were very sensitive to outliers. With the
development of more sophisticated classification al-
gorithms, for example the Support Vector Machines
(SVM) (Sch
¨
olkopf and Smola, 2002) or Artificial
Neural Networks (ANN) (Mehrotra et al., 1997), the
need for outlier removal decreased. The reason for
this trend was that these classifiers are not very sensi-
tive to outliers in the dataset any more, or have even
built-in outlier suppression techniques. However, the
research for the detection of outliers experienced a re-
vival from the year 2000 onwards, when many new
methods have been developed for anomaly detection.
In this research area, one is typically interested in the
anomalies (the outliers) itself, not primarily in their
removal. Anomalies can carry important information
for a variety of applications and are therefore of inter-
est in intrusion detection (Portnoy et al., 2001), medi-
cal diagnosis (Lin et al., 2005), fraud detection (Geb-
hardt et al., 2013) and surveillance (Basharat et al.,
2008).
Today, the terms outlier and anomaly are mainly
used as a synonym, whereas the removal of outliers
from a dataset is also often referred to as data cleans-
ing and the search for the outliers as anomaly detec-
tion. In the anomaly detection research domain, three
different learning modes based on the availability of
labels exist (Chandola et al., 2009; Goldstein, 2014).
In the case of having a fully labeled dataset with the
labels normal and anomalous, supervised anomaly
detection algorithms are used, which is very similar
to a standard classification task. Second, if a dataset
contains only normal data and no anomalies, semi-
supervised anomaly detection algorithms could be ap-
plied. In this setup, typically a model of the norm is
learned and the deviation of the test data to that model
is used as an indicator for abnormality. A well-known
semi-supervised anomaly detection algorithm is the
One-class SVM (Sch
¨
olkopf et al., 1999). The third
setup is unsupervised anomaly detection. Here, no
assumption about the data is made and it is only ana-
Goldstein, M. and Uchida, S.
A Comparative Study on Outlier Removal from a Large-scale Dataset using Unsupervised Anomaly Detection.
DOI: 10.5220/0005701302630269
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 263-269
ISBN: 978-989-758-173-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
263

lyzed using its internal structure. The result of todays
unsupervised anomaly detection algorithms is often a
score instead of a binary label such that the results
can be ranked and further processing can draw more
sophisticated conclusions.
Unsupervised anomaly detection is in general a
challenging task since it is solely based on intrinsic
information and does not have a ground truth to opti-
mize a decision boundary. In this context, is is also of-
ten hard to decide what actually should be considered
as an anomaly and what not. An important concept is
the differentiation between global and local anoma-
lies. Global anomalies are suspicious instances with
respect to the whole dataset whereas local anomalies
are only noticeable with respect to their immediate
neighborhood. More information and detailed exam-
ples can be found in (Goldstein, 2014). Please note
that anomaly detection algorithms focus on the detec-
tion on either global or local anomalies.
Of course, unsupervised anomaly detection algo-
rithms can also be used for data cleansing by remov-
ing the top anomalies from the training data. In this
work, we utilize a variety of unsupervised anomaly
detection algorithms in order to study the effect of
outlier removal on handwritten character recognition.
The goal of this research is to gain a deeper under-
standing of the importance of anomalies in a dataset,
not the improvement of classification accuracy. The
use of a large-scale dataset is of particular interest to
us in order to learn whether anomalies have signifi-
cant influence at all in this situation.
2 RELATED WORK
Outlier detection and removal for improving accu-
racy has been studied extensively (Barnett and Lewis,
1994). In this context, it is important to stress out that
there exist multiple views of what an outlier is. Es-
pecially in research conducted on focusing on clas-
sification performance improvement, data instances
close to the decision boundary and also misclassifi-
cations are named outliers. It is correct that these
are outliers with respect to a classification problem,
but these instances are not necessarily outliers in a
statistical sense. This view on addressing an inter-
class anomaly detection is also often understood as
a preprocessing step for classification (Sharma et al.,
2015).
This research focuses on an intra-class outlier def-
inition, which is a more statistical perspective. This
more general view can also be used to boost clas-
sification, but it detects also outliers far away from
decision boundaries. Although these anomalies will
very likely have no influence on classification per-
formance, they might still be of particular interest.
In the application scenario of handwritten character
recognition, this could be mislabeled data, errors in
scanning, segmentation and binarization as well as
strong image distortions. Prior experiments were per-
formed (Smith and Martinez, 2011) with unsuper-
vised anomaly detection for outlier removal similar to
this work, but evaluation was only based on two un-
supervised anomaly detection algorithms (k-NN and
LOF) as well as a restriction on small datasets due to
implementation restrictions as stated by the authors.
Concerning handwritten digits, it was found (Guyon
et al., 1996) that outlier removal improves recognition
performance for a small dataset with less than 8,000
instances. In this work, we want to verify whether
this is still true for a large-scale dataset or whether
nowadays the huge amount of data compensates out-
lier elimination.
3 METHODOLOGY
3.1 Anomaly Detection
A huge variety of unsupervised anomaly detection
algorithms exit today. A comprehensive overview
as well as a categorization is presented by (Chan-
dola et al., 2009). The vast majority of the differ-
ent approaches is very resource demanding in terms
of time and memory. For our primary goal, the
analysis of a large-scale dataset, only a small sub-
set of algorithms can be utilized. In this work, the
algorithms will not be described in detail. Instead,
we only briefly summarize their main characteristics.
As a categorization attempt, the algorithms might be
classified in three main groups: (1) Nearest-neighbor
based methods, (2) Clustering-based methods and (3)
Statistical methods. Statistical methods can again
be sub-classified into parametric or non-parametric
methods such as histograms (Goldstein and Dengel,
2012), Kernel-density estimation (Turlach, 1993) or
Gaussian Mixture Models (Lindsay, 1995). Besides
that, other methods based on classification techniques
exist, such as Support Vector Machines (Amer et al.,
2013) or autoencoders (Hawkins et al., 2000). Due
to its complexity, most of the methods are not suit-
able for large-scale datasets. For that reason, we use
the histogram-based HBOS (Goldstein and Dengel,
2012) algorithm from this group only.
For the nearest-neighbor based approaches, the
global k-NN algorithm (Ramaswamy et al., 2000;
Angiulli and Pizzuti, 2002), the well-known Lo-
cal Outlier Factor (LOF) (Breunig et al., 2000), the
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
264

Connectivity-based Outlier Factor (COF) (Tang et al.,
2002), the Local Outlier Probability (LoOP) (Kriegel
et al., 2009) as well as the Influenced Outlierness
(INFLO) (Jin et al., 2006) were selected. Please note
that the k-NN algorithm is global and all the remain-
ing ones focus on detecting local anomalies. The idea
of LOF is to estimate a local density of a data instance
and then comparing it with the local densities of the k
neighbors. This procedure results in a spherical den-
sity estimation. COF works similar to LOF, but the
density estimation uses a minimum spanning tree ap-
proach instead. INFLO addresses a problem arising
in LOF, when clusters of different densities are close
to each other. In contrast, LoOP has a different ba-
sic approach using probabilities to identify anomalies.
Here, the local density is estimated by a half-Gaussian
distribution.
For the clustering-based approaches, the
Clustering-based Local Outlier Factor (CBLOF) (He
et al., 2003) and a modified version uCBLOF (Amer
and Goldstein, 2012) are the representative candi-
dates. The basic idea is to cluster the data using
k-means, remove too small clusters and afterwards
use the distance of each instance to the centroid
as an anomaly score. In CBLOF, additionally a
weighting factor is utilized according to the cluster’s
size. The Local Density Cluster-based Outlier
Factor (LDCOF) (Amer and Goldstein, 2012) also
uses k-means clustering as a basis, but additionally
estimates the cluster’s local density for computing the
anomaly score. In contrast to the CBLOF variants,
this procedure can be considered as taking local
cluster densities better into account. Additionally,
the Clustering-based Multivariate Gaussian Outlier
Score (CMGOS) (Goldstein, 2014) carries out this
idea further and uses the Mahalanobis distance for
computing the anomaly score. Since k-means clus-
tering is not deterministic, multiple runs might lead
to different anomaly detection results making it hard
to compare the different algorithms. For that reason,
the k-means clustering algorithm was performed 10
times and the most stable result was chosen as a basis
for all the clustering-based algorithms.
All used algorithms are available within an open
source anomaly detection plug-in
1
of the Rapid-
Miner (Mierswa et al., 2006) data mining software.
One goal of this implementation is the focus on large-
scale dataset processing.
3.2 Classification
After utilizing the anomaly detection algorithms on
the training data, our goal is to remove anomalies
1
More information and download at http://git.io/vnD6n
from the training set and study the effect on the clas-
sification results using the test set for evaluation. Our
hypothesis is, that removing strong anomalies should
increase the classification performance.
As already stated in the introduction, our focus is
not to tweak recognition rates, but to gain insight of
the internal structure of the large-scale data. For this
reason, we explicitly chose a classifier being sensitive
to anomalies in order to immediately study their ef-
fect. To this end, we choose a one-nearest-neighbor
classifier for evaluation. This has the big advantage
that a single removed outlier might directly influence
the classification result. Of course, we are aware that
using a k-NN approach would be in general much bet-
ter and more robust with respect to maximizing clas-
sification performance.
As a distance measure, the Hamming distance was
used. It is intuitively interpretable and corresponds to
the Euclidean distance on binarized images.
4 EVALUATION
4.1 Dataset
Our large-scale character image dataset comprises in
total 819,725 handwritten digit images, separated ran-
domly into a 614,794 instances for anomaly detection
and training as well as 204,931 instances for the test
set. The size of each character image is 16 × 16 pixel
resulting in a feature vector of 256. The distribution
of the digits is not balanced since the data was pulled
from a real-world environment and the digit “0” oc-
curred approximately three times more often than the
other digits. The data has been binarized and was la-
beled manually. It is unknown if the labeling is abso-
lutely accurate. Also, the number of different writers
in the dataset is unknown.
4.2 Experimental Setup
First, the unsupervised anomaly detection algorithm
is applied separately on each of the 10 classes in the
training set. This results in 10 different lists with
scores describing the “outlierliness” of each instance.
These lists are then merged together and sorted by the
anomaly score. This ensures that the statistically most
significant anomaly ranks top in this list, regardless
of its class. All nine algorithms presented in Sec-
tion 3.1 were used for evaluation with the exception
of CBLOF. The reason why CBLOF was excluded is
that it weights the resulting score with the cluster size.
Since the digit “0” occurs more often in the data, all
outliers from this class are ranked first. However, the
A Comparative Study on Outlier Removal from a Large-scale Dataset using Unsupervised Anomaly Detection
265

unweighted version uCBLOF (Amer and Goldstein,
2012) was used instead. In a second step, the top N
outliers are removed and the performance of the one-
nearest-neighbor classifier using the reduced training
set is evaluated on the test set. For N, the following
numbers were selected: 4, 8, 16, 32, 64, 128, 256,
512, 600, 1200, 1800, 2400, 3000, 3600, 4200, 4800,
5400 and 6000. The last value for N corresponds to
approximately removing 1% of the training data. The
reason for a more dense evaluation for small N is the
assumption that the classification performance will
increase when removing the most obvious anomalies.
4.3 Anomaly Detection Results
The results of the anomaly detection algorithms can-
not directly be evaluated quantitatively due to the fact
that there is no ground truth. Nevertheless, we can
show the top anomalies detected by plotting the im-
ages with the highest scores. Figure 1 shows exem-
plary the top-10 result of the k-NN global anomaly
detection algorithm for all classes. The anomalies are
ordered according to their score with the highest score
on the left column. It can be seen that the anomaly
detection results are reasonable. For the class “8” the
two top anomalies seem to be mislabeled instances.
Also, the top-3 anomalies of the digit “5” might be
worth considering a mislabeling. The results of the
local outlier factor (LOF) algorithm are illustrated in
Figure 2 as a representative of a local anomaly de-
tector. As mentioned in the introduction, global and
local anomalies may differ a lot. It can be seen nicely
that some global anomalies cannot be detected by
LOF, for example for the digit “8”, but for the dig-
its “1”, “2” and “4” new interesting anomalies show
up. The results are also remarkable since it has been
shown that local anomaly detection algorithms tend to
perform worse than global algorithms on large-scale
datasets (Goldstein, 2014).
4.4 Classification Results
First, the results of the unsupervised anomaly detec-
tion algorithms were sorted according to their outlier
score. Then, the top N anomalies of that list were re-
moved from the training data and the performance of
the 1-NN classifier was measured. Since the dataset
is very large, removing few instances does not lead
to a huge change in the classification accuracy mea-
sured as a percentage. For this reason, absolute num-
bers were used in the following plots. Please keep in
mind that classification improvement is not our goal
at all, and that the presented insignificant change with
respect to accuracy should only be interpreted as a
Figure 1: The top-10 anomalies of the large-scale dataset
for every digit. The results have been computed using the
global k-NN method.
Figure 2: Showing the top-10 anomalies using the LOF al-
gorithm. Some global anomalies are not detected.
trend to answer the question of the effect of outlier
removal. Figure 4 and 5 show the classification re-
sults of all algorithms, whereas the latter is a mag-
nified view to verify our hypothesis that removing
the most obvious anomalies should increase recog-
nition performance. The plots also show a baseline,
among which no anomalies are removed as well as
a random strategy when N instances are removed by
chance from the training data.
The results were very astonishing to us. First of
all it can be seen that the performances of the differ-
ent anomaly detection algorithms differ a lot. While
typically the global k-NN and the LOF deliver good
results on average, the earlier performs very poorly
on our large-scale dataset. The results also show that
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
266

202720
202740
202760
202780
202800
202820
202840
202860
0 1000 2000 3000 4000 5000 6000
Correctly classified test data
Removed anomalies from training data
baseline
random
LOF
k-NN
INFLO
COF
LoOP
HBOS
uCBLOF
CMGOS
LDCOF
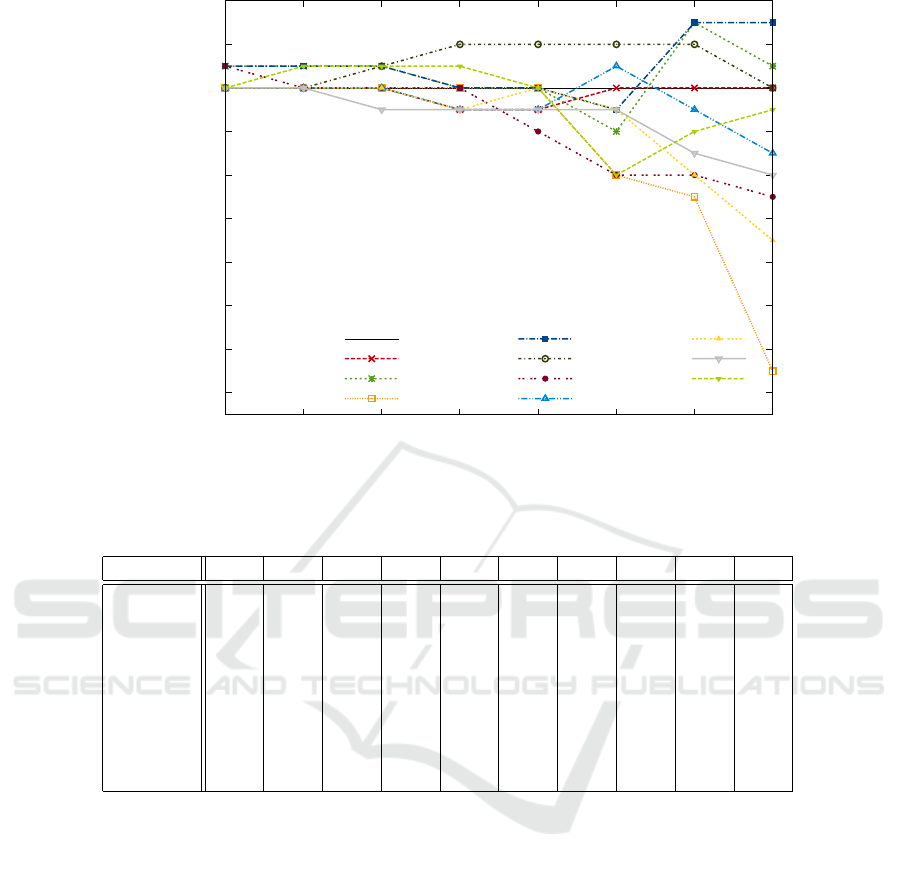
Figure 4: Results of the one-nearest-neighbor classifier after removing the top-N anomalies using nine different unsupervised
anomaly detection algorithms.
Figure 3: The 10 most normal digit images of each digit
class for comparison determined using the global k-NN.
INFLO performs best on our dataset being at the same
time the only one improving classification accuracy
in total. Figure 4 also illustrates that local anomaly
detection algorithms perform much better than the
global algorithms (4 lowest curves).
The most important result to us is that we could
not verify our initial hypothesis. Removing anoma-
lies, even only the most prominent ones, does not
guarantee an improvement of classification accuracy.
On the contrary, chances are high that removing
anomalies is going to drop recognition performance
if too many of them are removed.
Table 1 shows the percentage of each digit class
among the top-1000 anomalies for each of the evalu-
ated algorithms. Some of the algorithm have a strong
bias to detect anomalies of a specific class, whereas
the digits “0” and “1” seems to have on average more
detected anomalies than the other digits.
5 CONCLUSIONS
In this paper we evaluated the effect of removing
intra-class anomalies from a large-scale handwritten
digit dataset. Nine different unsupervised anomaly
detection algorithms have been used in order to cover
a wide range, taking global and local approaches
into account as well as covering all the basic under-
lying mathematical methodologies. A one-nearest-
neighbor classifier was then used to evaluate the ef-
fect of anomaly removal from the training data with
respect to classification accuracy. The goal was not to
tweak the accuracy but to derive a general statement
about the usefulness of anomaly removal. For smaller
datasets, it was shown previously that outlier removal
is beneficial. Our experiments showed that remov-
ing anomalies from large-scale character datasets is in
general not a good idea. Summarizing our results, the
benefit from removing the obvious anomalies is very
low compared to the risk of dropping performance
A Comparative Study on Outlier Removal from a Large-scale Dataset using Unsupervised Anomaly Detection
267
202836
202838
202840
202842
202844
202846
202848
202850
202852
202854
4 8 16 32 64 128 256 512
Correctly classified test data
Removed anomalies from training data
baseline
random
LOF
k-NN
INFLO
COF
LoOP
HBOS
uCBLOF
CMGOS
LDCOF
Figure 5: Magnified view of Figure 4 showing the effect of the most important anomalies.
Table 1: Outlier class distribution. The percentage of anomalies among the top-1000 for each anomaly detection algorithm.
0 1 2 3 4 5 6 7 8 9
LOF 5.2 63.0 5.0 3.4 1.1 1.4 5.6 5.8 2.1 7.4
k-NN 3.9 0.1 8.1 9.4 16.5 11.5 4.1 1.5 42.1 2.7
INFLO 3.8 71.3 3.6 2.4 0.7 0.7 5.2 4.9 1.5 5.9
COF 2.2 71.9 4.3 1.4 2.4 1.3 4.2 3.0 1.6 7.7
LoOP 15.2 14.7 16.3 7.3 8.2 6.0 7.6 10.2 7.6 6.9
HBOS 21.7 6.2 0.1 11.4 0.9 5.6 18.7 18.3 3.3 13.8
uCBLOF 35.4 1.1 3.6 7.5 6.5 7.3 11.5 9.0 11.1 7.0
CMGOS 28.4 6.1 5.2 8.5 3.7 10.1 8.8 7.2 12.7 9.3
LDCOF 11.4 53.4 0.3 5.7 0.1 1.0 8.8 7.1 0.3 11.9
due to removing too many important instances. When
comparing our anomaly removal with a random re-
moval strategy, it is even possible to state that anoma-
lies are very important for the classification accuracy
and should remain in the large-scale dataset.
However, our experiments additionally showed
that unsupervised anomaly detection algorithms can
be used to manually review the top anomalies – on our
dataset we gained insight about incorrectly labeled in-
stances, found upside-down images as well as images
which can be considered as noise.
ACKNOWLEDGEMENTS
This research is supported by The Japan Science and
Technology Agency (JST) through its “Center of In-
novation Science and Technology based Radical In-
novation and Entrepreneurship Program (COI Pro-
gram)”.
REFERENCES
Amer, M. and Goldstein, M. (2012). Nearest-neighbor
and clustering based anomaly detection algorithms for
rapidminer. In Simon Fischer, I. M., editor, Pro-
ceedings of the 3rd RapidMiner Community Meeting
and Conferernce (RCOMM 2012), pages 1–12. Shaker
Verlag GmbH.
Amer, M., Goldstein, M., and Abdennadher, S. (2013). En-
hancing one-class support vector machines for unsu-
pervised anomaly detection. In Proceedings of the
ACM SIGKDD Workshop on Outlier Detection and
Description (ODD ’13), pages 8–15, New York, NY,
USA. ACM Press.
Angiulli, F. and Pizzuti, C. (2002). Fast outlier detection in
high dimensional spaces. In Elomaa, T., Mannila, H.,
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
268

and Toivonen, H., editors, Principles of Data Mining
and Knowledge Discovery, volume 2431 of Lecture
Notes in Computer Science, pages 43–78. Springer
Berlin / Heidelberg.
Barnett, V. and Lewis, T. (1994). Outliers in Statistical
Data. Wiley Series in Probability & Statistics. Wiley.
Basharat, A., Gritai, A., and Shah, M. (2008). Learning
object motion patterns for anomaly detection and im-
proved object detection. In Computer Vision and Pat-
tern Recognition. (CVPR 2008). IEEE Conference on,
pages 1–8. IEEE Computer Society Press.
Breunig, M. M., Kriegel, H.-P., Ng, R. T., and Sander, J.
(2000). LOF: Identifying density-based local outliers.
In Proceedings of the 2000 ACM SIGMOD Interna-
tional Conference on Management of Data, pages 93–
104, Dallas, Texas, USA. ACM Press.
Chandola, V., Banerjee, A., and Kumar, V. (2009).
Anomaly detection: A survey. ACM Computing Sur-
veys, 41(3):1–58.
Gebhardt, J., Goldstein, M., Shafait, F., and Dengel, A.
(2013). Document authentication using printing tech-
nique features and unsupervised anomaly detection. In
Proceedings of the 12th International Conference on
Document Analysis and Recognition (ICDAR 2013),
pages 479–483. IEEE Computer Society Press.
Goldstein, M. (2014). Anomaly Detection in Large
Datasets. Phd-thesis, University of Kaiserslautern,
Germany.
Goldstein, M. and Dengel, A. (2012). Histogram-based out-
lier score (hbos): A fast unsupervised anomaly detec-
tion algorithm. In W
¨
olfl, S., editor, KI-2012: Poster
and Demo Track, pages 59–63. Online.
Grubbs, F. E. (1969). Procedures for Detecting Outlying
Observations in Samples. Technometrics, 11(1):1–21.
Guyon, I., Matic, N., and Vapnik, V. (1996). Discovering
informative patterns and data cleaning. Advances in
Knowledge Discovery and Data Mining, pages 181–
203.
Hawkins, S., He, H., Williams, G. J., and Baxter, R. A.
(2000). Outlier detection using replicator neural net-
works. In Proceedings of the 4th International Con-
ference on Data Warehousing and Knowledge Dis-
covery (DaWaK 2000), pages 170–180, London, UK.
Springer-Verlag.
He, Z., Xu, X., and Deng, S. (2003). Discovering cluster-
based local outliers. Pattern Recognition Letters,
24(9-10):1641–1650.
Jin, W., Tung, A., Han, J., and Wang, W. (2006). Ranking
outliers using symmetric neighborhood relationship.
In Ng, W.-K., Kitsuregawa, M., Li, J., and Chang, K.,
editors, Advances in Knowledge Discovery and Data
Mining, volume 3918 of Lecture Notes in Computer
Science, pages 577–593. Springer Berlin / Heidelberg.
Kriegel, H.-P., Kr
¨
oger, P., Schubert, E., and Zimek, A.
(2009). Loop: Local outlier probabilities. In Proceed-
ing of the 18th ACM Conference on Information and
Knowledge Management (CIKM ’09), pages 1649–
1652, New York, NY, USA. ACM Press.
Lin, J., Keogh, E., Fu, A., and Herle, H. V. (2005). Approx-
imations to magic: Finding unusual medical time se-
ries. In In 18th IEEE Symposium on Computer-Based
Medical Systems (CBMS), pages 23–24. IEEE Com-
puter Society Press.
Lindsay, B. (1995). Mixture Models: Theory, Geometry,
and Applications. NSF-CBMS Regional Conference
Series in Probability and Statistics. Institute of Math-
ematical Statistics, Penn. State University.
Mehrotra, K., Mohan, C. K., and Ranka, S. (1997). Ele-
ments of Artificial Neural Networks. MIT Press, Cam-
bridge, MA, USA.
Mierswa, I., Wurst, M., Klinkenberg, R., Scholz, M.,
and Euler, T. (2006). Yale: Rapid prototyping for
complex data mining tasks. In Proceedings of the
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining (KDD 2006), pages
935–940, New York, NY, USA. ACM Press.
Portnoy, L., Eskin, E., and Stolfo, S. (2001). Intrusion de-
tection with unlabeled data using clustering. In In Pro-
ceedings of ACM CSS Workshop on Data Mining Ap-
plied to Security (DMSA-2001), pages 5–8.
Ramaswamy, S., Rastogi, R., and Shim, K. (2000). Efficient
algorithms for mining outliers from large data sets. In
Proceedings of the 2000 ACM SIGMOD International
Conference on Management of Data (SIGMOD ’00),
pages 427–438, New York, NY, USA. ACM Press.
Sch
¨
olkopf, B. and Smola, A. J. (2002). Learning with Ker-
nels: Support Vector Machines, Regularization, Op-
timization, and Beyond. Adaptive Computation and
Machine Learning. MIT Press, Cambridge, MA.
Sch
¨
olkopf, B., Williamson, R. C., Smola, A. J., Shawe-
Taylor, J., and Platt, J. C. (1999). Support vector
method for novelty detection. In Advances in Neu-
ral Information Processing Systems 12 (NIPS), pages
582–588. The MIT Press.
Sharma, P. K., Haleem, H., and Ahmad, T. (2015). Improv-
ing classification by outlier detection and removal. In
Emerging ICT for Bridging the Future - Proceedings
of the 49th Annual Convention of the Computer So-
ciety of India CSI Volume 2, volume 338 of Advances
in Intelligent Systems and Computing, pages 621–628.
Springer International Publishing.
Smith, M. and Martinez, T. (2011). Improving classification
accuracy by identifying and removing instances that
should be misclassified. In Neural Networks (IJCNN),
The 2011 International Joint Conference on, pages
2690–2697.
Tang, J., Chen, Z., Fu, A., and Cheung, D. (2002). Enhanc-
ing effectiveness of outlier detections for low density
patterns. In Chen, M.-S., Yu, P., and Liu, B., editors,
Advances in Knowledge Discovery and Data Mining,
volume 2336 of Lecture Notes in Computer Science,
pages 535–548. Springer Berlin / Heidelberg.
Turlach, B. A. (1993). Bandwidth selection in kernel den-
sity estimation: A review.
A Comparative Study on Outlier Removal from a Large-scale Dataset using Unsupervised Anomaly Detection
269
