
Fully Automated Soft Contact Lens Detection from NIR Iris Images
Balender Kumar
1
, Aditya Nigam
2
and Phalguni Gupta
3
1
Department of Computer Science and Engineering, Indian Institute of Technology Kanpur (IITK), Kanpur, India
2
School of Computer Science and Electrical Engineering, Indian Institute of Technology Mandi (IIT Mandi), Mandi, India
3
National Institute of Technical Teacher’s & Research (NITTTR), Salt Lake, Kolkata, India
Keywords:
Iris, Contact Lens, Hough Transform, Soft Contact Lens, Multi-scale Line Tracking.
Abstract:
Iris is considered as one of the best biometric trait for human authentication due to its accuracy and perma-
nence. However easy iris spoofing raise the risk of false acceptance or false rejection. Recent iris recognition
research has made an attempt to quantify the performance degradation due to the use of contact lens. This
study proposes a strategy to detect soft contact lens in visual pictures of the eye obtained using NIR sensor.
The lens border is detected by considering small annular ring-like area near the outer iris boundary and lo-
cating candidate points while traversing along the lens perimeter. The system performance is evaluated over
public databases such as IIITD-Cogent, UND 2010, IIITD-Vista along with our self created IITK database.
The rigorous experimentation revels the superior performance of the proposed system as compared with other
existing techniques.
1 INTRODUCTION
In present world scenario, with bigger threats to the
whole human race by several terrorist organizations
around the world, ensuring human security is a huge
challenge. Therefore automated human identification
and verification are the basic requirements in order
to provide secure and restricted access. There are
several ways by which it can be realized such as to-
ken and knowledge based, but they can be very easily
lost or circumvented. Several biometrics based so-
lution has now been deployed to ensure robust and
accurate human identification and verification. Many
physiological biometric traits such as face, palmprint
(Nigam and Gupta, 2014b), knuckleprint (Badrinath
et al., 2011; Nigam and Gupta, 2011), fingerprint,
face, iris (Nigam and Gupta, 2012), ear (Nigam and
Gupta, 2014c) are well suited hence studied exten-
sively. But it is observed that no trait can adequately
support and deliver a system with desired perfor-
mance. Hence recently many multimodal systems
are proposed (Nigam and Gupta, 2015), (Nigam and
Gupta, 2014a), (Nigam and Gupta, 2013a) suggesting
different combinations of knuckleprint, iris, palmprint
images in order to achieve better accuracy.
Image quality is another key factor which is very
relevant in such systems but its computation is very
difficult as its a very subjective task. Not much work
is reported, investigating the quality of iris (Nigam
et al., 2013), knuckleprint (Nigam and Gupta, 2013b)
and palmprint images.
Out of all the available biometric traits, arguably
iris can be considered as one of the best biometric trait
for human authentication process, as it contain highly
distinguishable texture (Flom and Safir, 1987). Also
iris pattern remain unchanged after the age of two and
does not degrade over time and environment. Perfor-
mance wise it is best but it is vulnerable to spoofing
via printed contact lenses. Also the system perfor-
mance degrades severely while subjects wear contact
lens (Lovish et al., 2015; Yadav et al., 2014; Kohli
et al., 2013). Contact lenses are of two types cosmetic
contact lens and Non-cosmetic or soft contact lens.
Soft contact lens detection is an important and chal-
lenging problem to preventing spoofing as compared
to cosmetic lens due to absence of any extra texture.
Very limited amount of work is done in this area. In
this work we deal with detection of soft contact lens
based on faint edge detection using line tracking.
There are some techniques available to detect
cosmetic contact lens which is easier to discrimi-
nate. Soft contact lens are texture-less and transpar-
ent hence are very difficult to differentiate. Most of
the time they are unrecognizable even by humans in
NIR images. The sole available clues are faintly vis-
ible lens boundaries. Thermal images has been used
Kumar, B., Nigam, A. and Gupta, P.
Fully Automated Soft Contact Lens Detection from NIR Iris Images.
DOI: 10.5220/0005702005890596
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 589-596
ISBN: 978-989-758-173-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
589
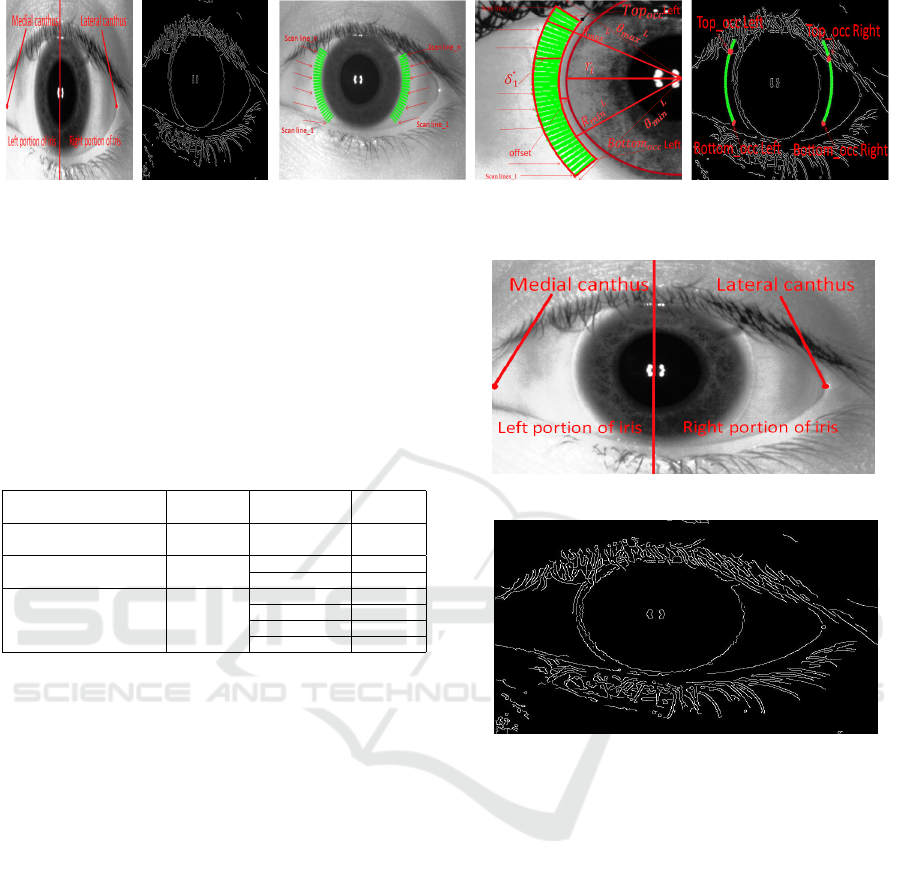
(a) Original Img. (b) Edge Map. (c) Scan-lines. (d) Annotated. (e) Top/Bot Occl. (L/R)
Figure 1: Overview of Occlusion Exclusion, showing Edge Map and Left/Right Occlusion.
in (Kywe et al., 2006) to detect contact lens using
temperature variations. Basic edge extraction algo-
rithms has been utilized in (Erdogan and Ross, 2013)
to detect abrupt intensity changes and to extract con-
tact lens border. Texture features has been utilized
in (Yadav et al., 2014; Kohli et al., 2013) to obtain
impressive contact lens detection performance. Some
recent previous results are tabulated in Table 1.
Table 1: Previous Work on Soft Contact Lens Detection.
Cite Technique
Used
Database Result
(Kywe et al., 2006) Thermo-
Vision
39 Subject 50-66%
(Erdogan and Ross, 2013)
Edge ICE 2005 72-76%
Detection MBGC 68.8-70%
(Yadav et al., 2014)
IIITD Cogent 56.66%
Texture IIITD Vista 67.52%
Features UND I(2013) 65.41%
UND II(2013) 67%
2 OCCLUSION EXCLUSION
FROM LENS
Eyelids and eyelashes are two major challenges in de-
tecting contact lens as they occlude significant iris re-
gions. Particularly eyelid occlusion detection helps to
set dynamic angle range which depends on the visibil-
ity of contact lens as lens cannot be beyond the eyelid
boundaries. We detect occlusion from contact lens
area using Canny edge detector with a high threshold
(an overview of occlusion exclusion is shown in Fig.
1). Since sclera is white and texture-less there cannot
be any edge points. If some edge points are present
on sclera they must be due to eyelashes and eyelids.
Based on these edge points dynamic angle range is
defined ensuring that our algorithm never crosses the
eyelid boundaries.
Iris image I is segmented by algorithm proposed
in (Bendale et al., 2012), that uses Hough trans-
form and Integro differential operator to obtain cen-
ter (C
x
,C
y
) and the distance between center to limbus
boundary r
i
. An edge map of iris image using Canny
is generated using higher threshold and false edges
Figure 2: Original Annotated Image.
Figure 3: Edge Map of Original Image.
are removed by excluding those connected compo-
nent that are less than P pixels in size as shown in Fig-
ure 3. Now an arrangement of scan-lines (Fig. 4) is
characterized with in the radius range {R
L
min
to R
L
max
}
and {R
R
min
to R
R
max
} for left and right iris portion re-
spectively, as shown in Figure 5 and defined below:
R
L
min
= (r
i
+ δ
1
+ o f f set) (1)
R
L
max
= (R
L
min
+ δ
3
) (2)
R
R
min
= (r
i
+ δ
2
+ o f f set) (3)
R
R
max
= (R
R
min
+ δ
4
) (4)
where, δ
1
, δ
2
are the difference between the max-
imum possible radius of the lens and minimum pos-
sible radius of iris for left and right iris portions re-
spectively. The values of δ
3
, δ
4
are discussed in next
subsection. The details of occlusion exclusion proce-
dure has been given in Algorithm 1, used to estimate
Top
occ
and Bottom
occ
as shown in Fig. 6.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
590

Figure 4: Scan Line Arrangement.
Figure 5: Annotated Image version.
Figure 6: Top and Bottom Occlusion (Left/Right) portion.
2.1 Parameter Selection
Human iris diameter lies in the range of 10.2 to
13.0 mm with its expected value as 12 mm (Caroline
and Andre, 2002) whereas soft contact lens diameter
ranges from 13mm to 15mm (Details-a, 2010). How-
ever, diameter of an iris fluctuates from 4 to 8 mm
in the dark and 2 to 4 mm in bright light (Details-b,
2010). For calculating δ
1
and δ
2
, 1 mm is assumed to
be equivalent to 3.779 pixels. Ideally based on heuris-
tics δ
1
(in pixels) should be equal to 3.779 times the
difference between maximum possible contact lens
radius and minimum possible iris radius. But due to
dark and bright/light effect it can be much more. For
this work it is observed that they can vary from 25 to
35 pixel for UND, IIITD-Cogent, IIIT-Vista and IITK
contact lens databases. Ideally δ
1
= δ
2
, but the lens
may be misplaced or shifted towards left or right. In
case of right shifting, δ
2
is greater than δ
1
and vice-
versa. Also, empirically δ
3
and δ
4
values depending
Algorithm 1: Occlusion Exclusion from Lens Area.
Require: I: Iris image, (C
x
,C
y
,r
i
): center and radius.
Ensure: Bottom
occ
: Minimum range of θ, Top
occ
:
Maximum range of θ.
Part A: Define
1: θ
L
min
,θ
R
min
: (5 ∗
π
4
),(
π
4
) //min angle for left,right
2: θ
L
max
,θ
R
max
: (7 ∗
π
4
),(3 ∗
π
4
) //max angle for
left,right
3: R
L
min
: (r
i
+ δ
1
+o f f set) //min radius for left
4: R
L
max
: (R
L
min
+ δ
3
) //max radius for left
5: R
R
min
: (r
i
+ δ
2
)+offset //min radius for right
6: R
R
max
: (R
R
min
+ δ
4
) //max radius for right
7: S: S is 1-D array used to store current scan line
for corresponding θ, for given range.
8: H(θ): H is 1-D Array to store number of non zero
entries corresponding scan line.
Part B: Steps
9: I
E
: Edge map of (I) using canny edge detector
// False edges are eliminated from an edge map
by removing small connected component (having
pixels less than P).
10: for θ = θ
min
:θ
max
do
11: // θ
min
=θ
L
min
, θ
max
=θ
L
max
for left side and
θ
min
=θ
R
min
, θ
max
=θ
R
max
for right side.
12: count=0;
13: for r = R
min
:R
max
do
14: // R
min
=R
L
min
, R
max
=R
L
max
for left side and
R
min
=R
R
min
, R
max
=R
R
max
in case of right side.
15: a = C
x
+r×cosθ
16: b = C
y
+r×sinθ
17: if(I
E
(a,b)!=0)
18: count = count+1
19: end if
20: end for
21: if(count ≥ T ) // T is threshold which varies
database to database.
22: H(θ) =1
23: else
24: H(θ) =0
25: end for
26: [Bottom
occ
,Top
occ
] = MaxMargin(H)
27: // Find the index in array H containing the max-
imum number of consecutive zeros and return its
corresponding index angles
28: return (Bottom
occ
,Top
occ
)
on visible part of contact lens can be fixed. Experi-
mentally they are found to follow: o f f set ≥ 0 and δ
3
,δ
4
∈ {1,10}. If δ
3
, δ
4
are greater than 10, then one
have to shrink our angle range because we are going
toward medial canthus or lateral canthus as shown in
Figs 2, 5 which will degrade the accuracy substan-
tially.
Fully Automated Soft Contact Lens Detection from NIR Iris Images
591
These scan-lines are within a radius range as dis-
cussed above, as well as they are also with in an an-
gular region ranging from {θ
L
min
=
5∗π
4
to θ
L
max
=
7∗π
4
}
and {θ
R
min
=
π
4
to θ
R
max
=
3∗π
4
} for left and right iris
portion respectively, with an angular distance of 1
◦
between any two consecutive scan lines (as shown in
Figure 5). Hence we are working on specified annu-
lar region of thge binary edge-map to estimate the top
and bottom occlusion.
Observation: The scan-line over sclera have
very few edge pixels, on the other hand if current
scan-line intersects eyelashes or eyelid then it is
bound to have non-zero edge pixels. Hence for each
scan-line (say at an angle θ) count the number of
edge (non-zero) pixels. If this count is greater then
a threshold T then that scan-line is occluded else it is
not occluded.
In order to estimate top and bottom occlusion an-
gle, we computed two maximally distant (in terms of
angular distance) scan-lines between which each and
every scan-line is having edge pixels less than T (i.e
not occluded). The lower angle is called Bottom
occ
which represent lower eyelid or eyelashes and the
higher index angle called Top
occ
which represent the
upper eyelid or eyelashes as shown in Figure 6.
3 SOFT CONTACT LENS
DETECTION
Soft contact lens detection is very challenging and
only available hint is the faint lens boundaries. Hence
the proposed SCLD algorithm uses Multi Scale Line
Tracking (MSLT ) Algorithm (Vlachos and Dermatas,
2010), which was initially used to segment retinal
vessels. This algorithm can detect very faint edges
and can extract soft contact lens boundaries. The
steps involved in MSLT algorithm are given in Al-
gorithm 2.
Output of MSLT gives lines of variable size and
diameter based on the visibility of the contact lens
border. MSLT algorithm returns a binary image in
which the lens border lines are clearly visible on the
sclera portion, if contact lens is present as shown in
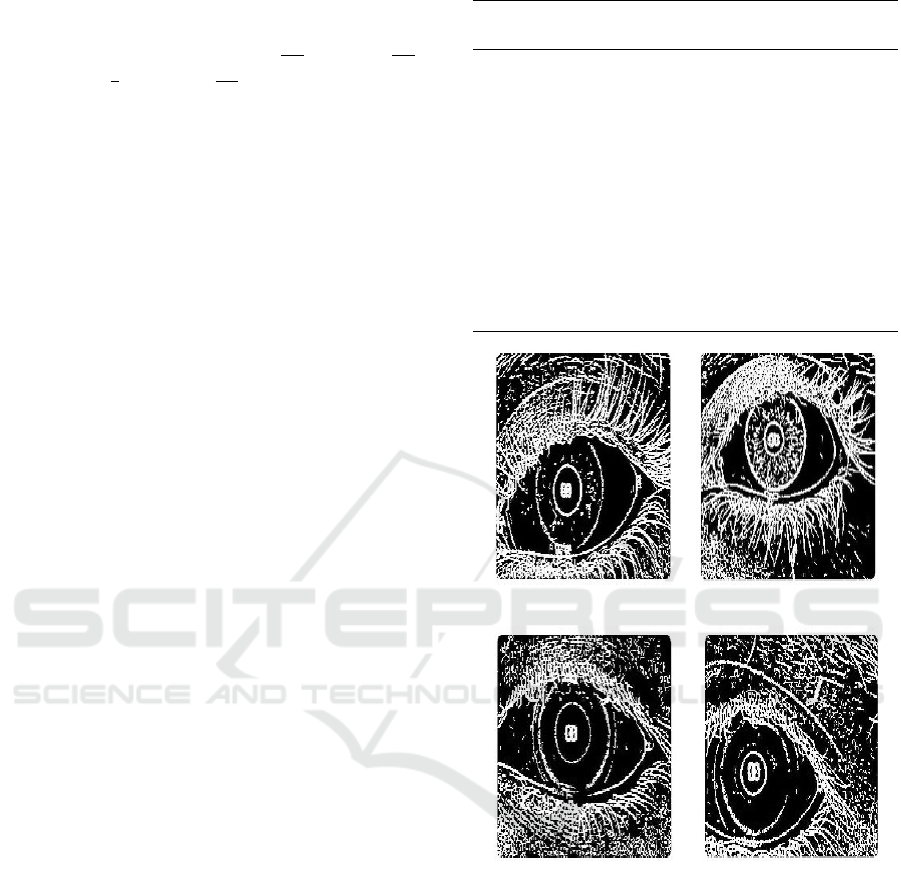
Figures 7 and 8. There must be some edge-lines
due to the presence of eyelid/eyelashes. Hence oc-
clusion exclusion from contact lens area is done as
discussed in Section 2. After applying MSLT algo-
rithm we compute two feature viz. Maximum edge
line Maximum Hough Votes, that are used to detect
contact lens as discussed below.
An arrangement of arc-lines (scan-lines are ra-
dially outward in horizontal direction Figure 4) as
shown in Figure 9(a) are characterized (arc-lines are
Algorithm 2: Steps involved in MSLT Algorithm (Vlachos
and Dermatas, 2010).
1: Brightness Normalization.
2: Automated selection of initial seed pixels.
3: Initialize confidence array for boundary tracking.
4: Populating confidence array by adding most suit-
able boundary pixels.
5: Repeat this process for each scale. (Multi-scale
boundary tracking)
6: Initial rough estimation of boundary network.
7: Smoothing using Median filter to remove irregu-
larities.
8: Finally morphological directional filtering is per-
formed in five different directions.
Figure 7: MSLTA algorithm based Masks (No Lens).
Figure 8: MSLTA based Masks (Soft Contact Lens).
vertical along an arc at some angle and radius) in an
angular range of {θ
L
min
to θ
L
max
} and {θ
R
min
to θ
R
max
} for
left and right iris portions respectively, at 1
◦
angular
distance. These arc-lines are of radius ranging from
{R
L
min
to R
L
max
} form left and {R
R
min
to R
R
max
} for right
portion at an angular distance of 1
◦
between any two
consecutive arc-line as shown in Figure 9(b) and dis-
cussed in previous Section for scan-lines. Every arc-
line between an angle range of {Bottom
occ
to Top
occ
}
is considered since it is not occluded. Algorithm 3 can
be used to detect soft contact lens using line tracking.
3.1 Feature Computation
Out of all arc-line the one which has got the maximum
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
592

Algorithm 3: Soft Contact Lens Detection (SCLD) using
Line Tracking.
Require: I: Iris image, (C
x
,C
y
): Iris Center , r
i
: Iris
radius, Bottom
occ
, Top
occ
.
Ensure: Two parameter, H1: Max Hough
Voting,Max
linesize
: Size of the contact lens
in contact lens iris image.
Define:
1: θ
L
min
, θ
R
min
: (5 ∗
π
4
),(
π
4
) //min angle for left and
right side.
2: θ
L
min
, θ
R
min
: (7 ∗
π
4
),(3 ∗
π
4
) // max angle for left
and right side.
3: R
L
min
: (r
i
)+offset //min radius for left side.
4: R
L
max
: (r
i
+ δ
1
) //max radius for left side.
5: R
R
min
: (r
i
)+offset //min radius for right side.
6: R
R
max
: (r
i
+ δ
2
) //max radius for right side.
Steps:
7: I:Apply Gaussian filter on (I)
8: I1:Apply MLSTA Algorithm(I) (Vlachos and
Dermatas, 2010).
9: H1=0,Max
linesize
=0.
10: for r = R
min
:R
max
do // R
min
=R
L
min
, R
max
=R
L
max
in case of left side and
// R
min
=R
R
min
, R
max
=R
R
max
in case of right side.
11: count=0;
12: for θ = θ
min
:θ
max
do // θ
min
=θ
L
min
,
θ
max
=θ
L
max
in case of left side and
// θ
min
=θ
R
min
, θ
max
=θ
R
max
in case of right side.
13: if(θ≥Bottom
occ
and Top
occ
≥ θ) // Con-
sidering lines within the range
// of top and bottom occlusion
14: a = C
x
+r×cosθ.
15: b = C
y
+r×sinθ.
16: if(I1(a,b)!=0)
17: count = count+1 //Store corresponding
Co-ordinate into x
i
,y
i
// and radius into r
1
.
18: end if
19: end if
20: end for
21: Max
linesize
=max(Max
linesize
,count) //Store
corresponding Max
linesize
Co-ordinate and r into
X
i
,Y
i
Co-ordinate and R
1
.
22: end for
23: [H1] = Hough Voting(X
i
,Y
i
,R
1
);
24: return (H1,Max
linesize
)
number of edge pixels (MEP) (pixels that are proba-
ble candidates of lens) has been selected, and the
(a) Arc-Lines.
(b) Annotation.
(c) Left/Right Reg.
Figure 9: Arc-line Arrangement.
value of MEP is used as our first feature. Also to
ensure circular shape Hough voting is used. The cen-
ter and radius for which maximum number of Hough
votes (MHV ) are obtained has been selected, and the
value of MHV is used as the second feature. These
features can be seen as a likelihood of soft contact
lens. Both MEP and MHV values must be high in
case of soft contact lens and vice-versa as shown in
Figure 10. The overall flow diagram of the complete
Soft Contact Lens Detection (SCLD) is shown in Fig-
ure 11.
Algorithm 4 can be used to perform Hough voting
in order to extract features. All parameters used in
this experimentation are reported in Table 2.
4 EXPERIMENTAL ANALYSIS
In this section experimental analysis of the proposed
system is presented.
4.1 Dataset
The system performance is tested over IIITD (Yadav
et al., 2014; Kohli et al., 2013), UND and self cre-
ated contact lens databases, acquired using FA2 and
Fully Automated Soft Contact Lens Detection from NIR Iris Images
593
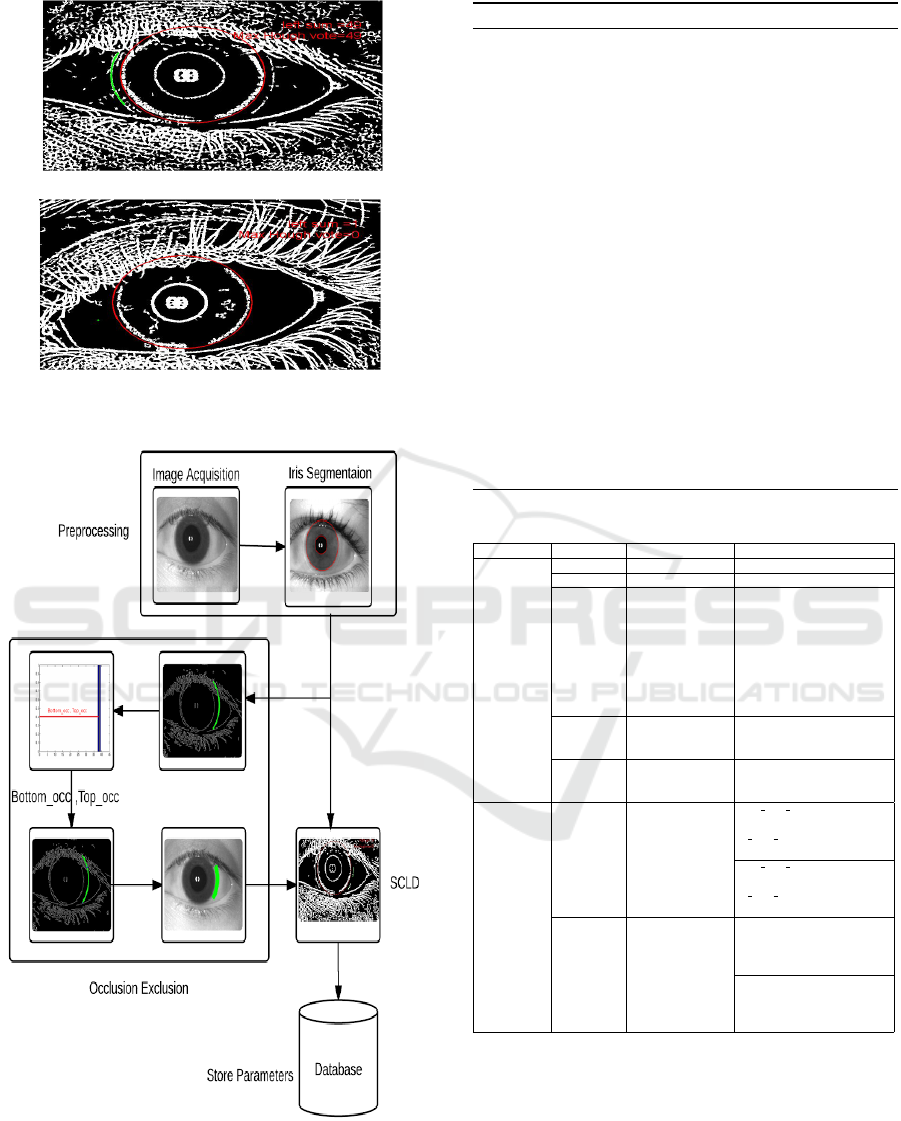
(a) Soft Contact Lens.
(b) No Contact Lens.
Figure 10: Pixels selected using M EP and MHV features.
Figure 11: Soft Contact Lens Detection(SCLD) using Line
Tracking.
LG − 4000 iris sensors. The images are acquired in 3
conditions:
Algorithm 4: Hough Voting.
Require: (X
i
,Y
i
): Co-ordinate of the selected line,
R
1
: Radius of selected line
Ensure: H1: Max Hough Voting pixel from accumu-
lator array.
Steps:
1: for every edge pixel (X
i
,Y
i
) do
2: for each possible radius value R
1
do
3: for each possible gradient direction Θ do
//or use estimated gradient at (X
i
,Y
i
).
4: a = X
i
−r∗cosΘ
5: b = Y
i
+r∗sinΘ
6: H[a,b,r]+=1;
7: end for
8: end for
9: H1=max(H) //Select maximum voting pixel
10: end for
11: return (H1)
Table 2: Description of Parameter Values.
Algorithm Parameter Description Value
Parameter
common to
all algorithm
r
i
Iris radius(in pixel) (Bendale et al., 2012)
(C
x
,C
y
) Iris Center(in pixel) (Bendale et al., 2012)
δ
1
, δ
2
δ
1
, δ
2
(in pixels)
is the difference
between the maximum
possible radius of the
lens and minimum
possible radius of the
iris, where radius
of contact lens and
iris in millimeter(mm).
25 - 35
δ
3
, δ
4
Constant fix by
experimental
analysis (in pixels)
0-10
o f f set
Constant fix by
experimental
analysis (in pixels)
0-10
1.Occlusion
Exclusion in
Contact Lens
Area.
2.Soft Contact
Lens Detection
(SCLD) using
Line Tracking.
θ: [θ
min
,θ
max
]
Scan line interval
[5 ∗
π
4
, 7 ∗
π
4
]
for left portion of iris
[
π
4
, 3 ∗
π
4
]
for right portion of iris
[5 ∗
π
4
, 7 ∗
π
4
]
for left portion of iris
[
π
4
, 3 ∗
π
4
]
for right portion of iris
r: [R
min
, R
max
] Scan line size
[r
i
+δ
1
+o f f set, r
i
+o f f set+δ
1
+ δ
3
]
for left portion of iris.
[r
i
+δ
1
+o f f set, r
i
+o f f set+δ
1
+δ
3
]
for right portion of iris
[r
i
+o f f set, r
i
+δ
1
]
for left portion of iris.
[r
i
+o f f set, r
i
+δ
2
]
for right portion of iris.
• Soft contact lens iris images [’Y ’]
• Colored/Textured lens iris images [’C’]
• Normal iris images without lens [’N’]
We have only considered no contact lens and soft
contact lens images i.e. [’N’,’Y ’] classes and binary
classification has been done. The features values as
define earlier as MEP and MHV are computed for
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
594
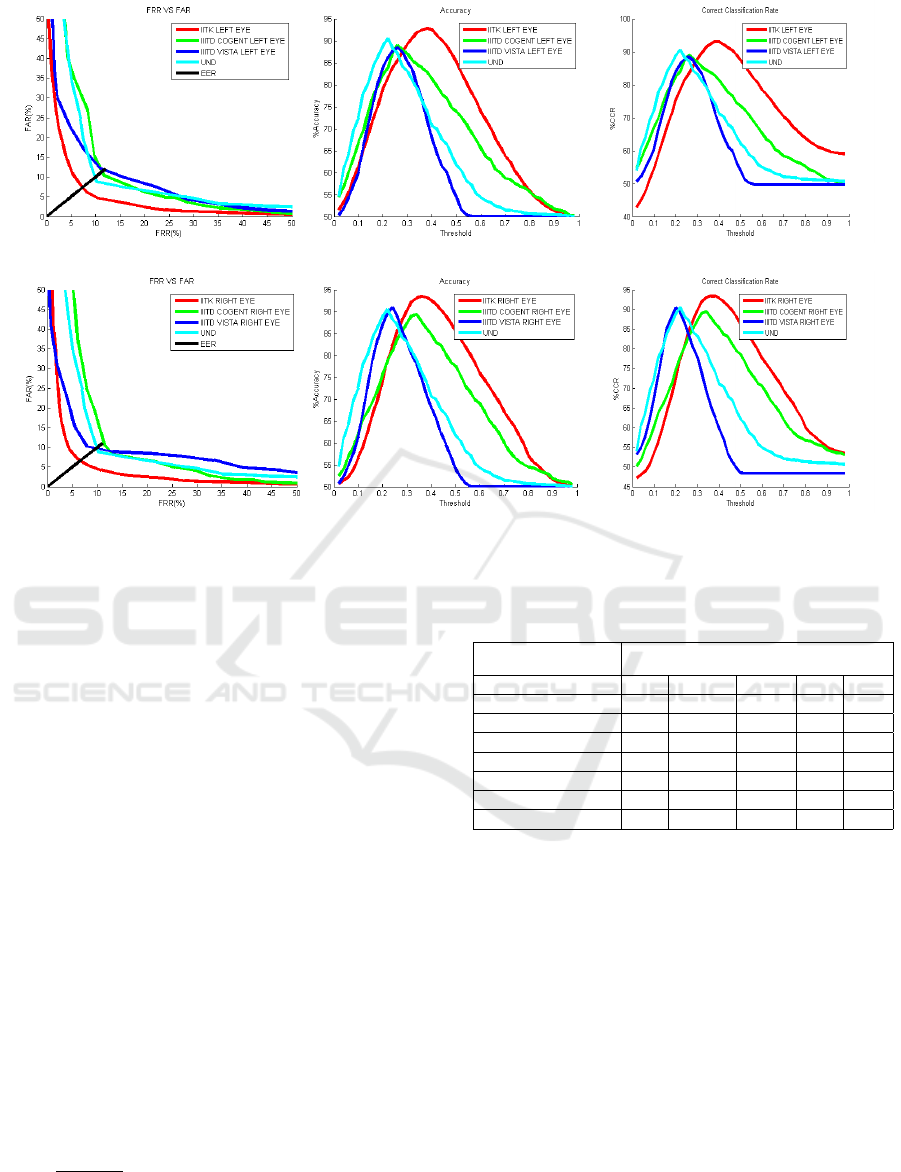
(a) EER (Left Eye). (b) Accuracy (Left Eye). (c) CCR (Left Eye).
(d) EER (Right Eye). (e) Accuracy (Right Eye). (f) CCR (Right Eye).
Figure 12: Comparative Analysis for both eyes.
every image. Their values are normalized so as to de-
fine a weighing scheme that can give a single score,
ranging between {0 to 1}. Finally this normalized
weighted score is used for contact lens detection.
4.2 Threshold Selection
In order to estimate the best possible thresholding pa-
rameters all databases are partitioned into two parts,
training and testing. Best suited threshold value for
the above mentioned normalized weighted score is
computed over the training images by checking ev-
ery value with in the range of {0 to 1}. Finally, the
value of threshold at which the system performance
got maximized (T
best
), over training data, has been
used for testing the proposed system over test dataset.
Prediction: Left over 34% data has been used as
testing dataset. In the similar way as defined above,
weighted normalized feature score has been calcu-
lated and compared against pre-computed threshold
value T
best
, for contact lens decision making.
The system performance is analyzed using stan-
dard parameters viz. CCR, Accuracy, FRR, FAR,
EER and shown in Table 3. Accuracy is defined as
100 −
FAR+FRR
2
. To best of our knowledge this is the
first work performing two class binary classification
to detect soft contact lens over IIITD Vista, IIITD Co-
gent and UND database hence there is no available al-
Table 3: Performance Analysis across Various databases us-
ing SCLD Line Tracking approach.
Descriptor SCLD using Line Tracking
Database CCR Accuracy FAR FRR EER
IITK Left Eye 92.99 92.81 6.21 8.15 7.56
IITK Right Eye 93.39 93.43 7.25 5.86 6.56
IIITD Vista Left Eye 88.44 88.43 12.1951 10.94 11.56
IIITD Vista Right Eye 90.99 90.94 10.22 7.88 9.05
IIITD Cogent Left Eye 88.96 88.96 10.40 11.66 11.03
IIITD Cogent Right Eye 89.48 89.35 10.41 11.49 10.95
UND 90.54 90.53 8.77 10.16 9.46
gorithm to compare. The EER and accuracy on these
database using soft contact lens detection using Line
Tracking algorithm is shown in Table 3 and in Fig-
ures 12. It is observed that proposed system can han-
dle small amount of uneven illumination also. The
EER over our database has been found to be low as
it is collected under controlled environmental condi-
tions.
5 CONCLUSION
In this work fully automatic soft contact lenses de-
tection algorithm is proposed using NIR sensor. The
lens border is detected by considering small annular
ring-like area near the outer iris boundary and locat-
ing candidate points while traversing along the lens
Fully Automated Soft Contact Lens Detection from NIR Iris Images
595

perimeter. Multi-Scale Line Tracking (MSLT) based
faint edge detection algorithm is used and features
like number of edge pixels (MEP) and number of
Hough votes (MHV ) are used for classification. Ex-
periments are conducted on publicly available IIITD-
Vista, IIITD-Cogent, UND 2010 and our indigenous
database. Results of the experiment indicate that pro-
posed method outperforms previous soft lens detec-
tion techniques.
ACKNOWLEDGEMENTS
Authors would like to thank Indian Institute of Tech-
nology Mandi and IITK for providing funds, intellec-
tual help and guidance.
REFERENCES
Badrinath, G., Nigam, A., and Gupta, P. (2011). An ef-
ficient finger-knuckle-print based recognition system
fusing sift and surf matching scores. In Informa-
tion and Communications Security, volume 7043 of
Lecture Notes in Computer Science, pages 374–387.
Springer Berlin Heidelberg.
Bendale, A., Nigam, A., Prakash, S., and Gupta, P.
(2012). Iris segmentation using improved hough
transform. In Emerging Intelligent Computing Tech-
nology and Applications, volume 304 of Communi-
cations in Computer and Information Science, pages
408–415. Springer Berlin Heidelberg.
Caroline, P. and Andre, M. (2002). The effect of corneal di-
ameter on soft lens fitting, part 2. Contact Lens Spec-
trum, 17(5):56–56.
Details-a (2010). Soft Contact Lens Diameter. Accessed:
2015-5-13.
Details-b (2010). Biometrics Data Sets. http://www3.
nd.edu/∼cvrl/CVRL/Data_Sets.html. Accessed:
2015-06-5.
Erdogan, G. and Ross, A. (2013). Automatic detection of
non-cosmetic soft contact lenses in ocular images. In
SPIE Defense, Security, and Sensing, pages 87120C–
87120C. International Society for Optics and Photon-
ics.
Flom, L. and Safir, A. (1987). Iris recognition system. US
Patent 4,641,349.
Kohli, N., Yadav, D., Vatsa, M., and Singh, R. (2013). Re-
visiting iris recognition with color cosmetic contact
lenses. In Proceedings of International Conference
on Biometrics (ICB), pages 1–7. IEEE.
Kywe, W. W., Yoshida, M., and Murakami, K. (2006).
Contact lens extraction by using thermo-vision. In
18th International Conference on Pattern Recognition
(ICPR), volume 4, pages 570–573. IEEE.
Lovish, Nigam, A., Kumar, B., and Gupta, P. (2015). Ro-
bust contact lens detection using local phase quan-
tization and binary gabor pattern. In 16th Interna-
tional Conference Computer Analysis of Images and
Patterns, CAIP 2015, Valletta, Malta, September 2-4,
pages 702–714.
Nigam, A. and Gupta, P. (2011). Finger knuckleprint based
recognition system using feature tracking. In Bio-
metric Recognition, volume 7098 of Lecture Notes in
Computer Science, pages 125–132. Springer Berlin
Heidelberg.
Nigam, A. and Gupta, P. (2012). Iris recognition using con-
sistent corner optical flow. In 11th Asian Conference
on Computer Vision, Daejeon, Korea, November 5-9,
2012, Revised Selected Papers, Part I, pages 358–369.
Nigam, A. and Gupta, P. (2013a). Multimodal personal
authentication system fusing palmprint and knuck-
leprint. volume 375 of Communications in Computer
and Information Science, pages 188–193.
Nigam, A. and Gupta, P. (2013b). Quality assessment of
knuckleprint biometric images. In 20th International
Conference on Image Processing (ICIP), pages 4205–
4209.
Nigam, A. and Gupta, P. (2014a). Multimodal personal au-
thentication using iris and knuckleprint. In Intelligent
Computing Theory, volume 8588 of Lecture Notes in
Computer Science, pages 819–825. Springer Interna-
tional Publishing.
Nigam, A. and Gupta, P. (2014b). Palmprint recognition
using geometrical and statistical constraints. In 2nd
International Conference on Soft Computing for Prob-
lem Solving (SocProS 2012), December 28-30, 2012,
volume 236 of Advances in Intelligent Systems and
Computing, pages 1303–1315. Springer India.
Nigam, A. and Gupta, P. (2014c). Robust ear recognition
using gradient ordinal relationship pattern. In Com-
puter Vision - ACCV 2014 Workshops - Singapore,
Singapore, November 1-2, 2014, Revised Selected Pa-
pers, Part III, pages 617–632.
Nigam, A. and Gupta, P. (2015). Designing an accurate
hand biometric based authentication system fusing
finger knuckleprint and palmprint. Neurocomputing,
151, Part 3:1120 – 1132.
Nigam, A., T., A., and Gupta, P. (2013). Iris classification
based on its quality. In Intelligent Computing Theo-
ries, volume 7995 of Lecture Notes in Computer Sci-
ence, pages 443–452. Springer Berlin Heidelberg.
Vlachos, M. and Dermatas, E. (2010). Multi-scale retinal
vessel segmentation using line tracking. Computer-
ized Medical Imaging and Graphics, 34(3):213–227.
Yadav, D., Kohli, N., Doyle, J., Singh, R., Vatsa, M., and
Bowyer, K. W. (2014). Unraveling the effect of tex-
tured contact lenses on iris recognition. IEEE Trans-
actions on Information Forensics and Security.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
596
