
Strategies for Phylogenetic Reconstruction
For the Maximum Parsimony Problem
Karla E. Vazquez-Ortiz, Jean-Michel Richer and David Lesaint
LERIA, University of Angers, 2 Boulevard Lavoisier 49045, Angers Cedex 01, France
Keywords:
Phylogenetic Reconstruction, Maximum Parsimony, GPU, Simulated Annealing, Path-relinking.
Abstract:
The phylogenetic reconstruction is considered a central underpinning of diverse field of biology like: ecology,
molecular biology and physiology. The main example is modeling patterns and processes of evolution. Ma-
ximum Parsimony (MP) is an important approach to solve the phylogenetic reconstruction by minimizing the
total number of genetic transformations, under this approach different metaheuristics have been implemented
like tabu search, genetic and memetic algorithms to cope with the combinatorial nature of the problem. In
this paper we review different strategies that could be added to existing implementations to improve their effi-
ciency and accuracy. First we present two different techniques to evaluate the objective function by using CPU
and GPU technology, then we show a Path-Relinking implementation to compare tree topologies and finally
we introduces the application of these techniques in a Simulated Annealing algorithm looking for an optimal
solution.
1 INTRODUCTION
According to the scientific community of biology,
nowadays there are about 5 to 100 millions species of
organisms living on Earth. Phylogeny is the univer-
sal proposition accepted that suggests all organisms
on Earth are genetically related, and the genealogical
relationships of living things can be represented by a
vast evolutionary tree called phylogenetic tree or, in
short, a phylogeny (Hennig, 1966). The phylogeny
studies the origin and the progressive evolution of a
group of n species and it deduces how they change
through time.
In order to study the evolutionary relationships
between different groups of organisms, phylogenetic
uses the information of biological macromolecules
(DNA, RNA and proteins) represented by characters,
with this information it deduces the evolutionary re-
lationships of the studied groups and represents them
as phylogenetic trees.
The problem of reconstructing molecular phylo-
genetic trees has become an important field of study in
Bioinformatics and has many practical applications in
population genetics, whole genome analysis, and the
search for genetic predictors of disease (Hillis et al.,
1996; Sridhar et al., 2007).
In the literature there exist different methods to
solve the phylogenetic reconstruction, nevertheless
we focus our attention in a cladistic method based on
the Maximum Parsimony (MP) criterion. Parsimony
is used to test the homologous nature of similarities by
finding the phylogenetic tree which best accounts for
all of the similarities. Under this context MP is con-
sidered as one of the most suitable evaluation criterion
for phylogenies (Penny et al., 1982; Sober, 1993).
In the next section we will show the definition of
Fitch parsimony, which is used as an objective func-
tion to evaluate the phylogenetic trees, in this defi-
nition all changes have the same cost (Felsenstein,
2003).
2 PROBLEM STATEMENT
Let S be a set {S
1
,S
2
,...,S
n
} composed of n se-
quences of length k over a predefined alphabet A .
A binary rooted phylogenetic tree T = (V,E) is used
to represent their ancestral relationships. It consists
of a set of nodes V = {v
1
,...,v
r
} and a set of edges
E ⊆ V × V = {{u,v}|u,v ∈ V }. The set of nodes
V (|V | = (2n − 1)) is partitioned into two subsets: I
that contains n −1 internal nodes (or hypothetical an-
cestors) each having 2 descendants; and L which is
composed of the n taxa that are leaves of the tree, i.e.
nodes with no descendant.
The parsimony sequence z = {z
1
,··· ,z
k
} for each
226
Vazquez-Ortiz, K., Richer, J-M. and Lesaint, D.
Strategies for Phylogenetic Reconstruction - For the Maximum Parsimony Problem.
DOI: 10.5220/0005702902260236
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 226-236
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

internal node z = f (x,y) ∈ I, whose descendants are
x = {x
1
,··· ,x
k
} and y = {y
1
,··· ,y
k
}, is calculated
with the following expression:
∀i,1 ≤ i ≤ k, z
i
=
x
i
∪ y
i
, if x
i
∩ y
i
=
/
0
x
i
∩ y
i
, otherwise
(1)
Then, the parsimony score of the sequence z un-
der Fitch optimality criterion (Fitch, 1971; Hartigan,
1973) is defined as follows:
φ(z) =
k
∑
i=1
C
i
where C
i
=
1, if x
i
∩ y
i
=
/
0
0, otherwise
(2)
and the parsimony score for the tree t is obtained as
follows:
φ(t) =
∑
∀z∈I
φ(z) . (3)
Thus, the Maximum Parsimony (MP) problem
consists in finding a tree topology t
∗
for which φ(t
∗
)
is minimum, i.e.,
φ(t
∗
) = min{φ(t) : t ∈ T } , (4)
where T is the set composed of all the possible tree
topologies also known as the search space of the pro-
blem.
Because of its equivalence with the combinatorial
optimization problem known as the Steiner tree pro-
blem on hypercubes, MP is considered NP-complete
(Gusfield, 1997). The Steiner tree problem on hyper-
cubes is NP-complete (Foulds and Graham, 1982).
This essentially means that no algorithm that solves
all instances quickly is likely to be found.
The MP problem has been exactly solved for very
small instances (n ≤ 10) using a branch & bound al-
gorithm (B&B) originally proposed by Hendy and
Penny (Hendy and Penny, 1982). One of the most
recent applications of B&B to solve MP is XMP, a
new program for finding exact MP trees, which uses
B&B with optimized vectorized inner loops (White
and Holland, 2011) on highly parallel distributed-
memory computers. For their experiments they used
real and synthetic instances from (Bader et al., 2006)
and other real datasets. Those instances have between
12 and 36 taxa which is relatively small.
Reconfigurable computing has been used to solve
exactly MP problem (Kasap and Benkrid, 2011), but
it supports instances of maximum 12 taxa. The exact
methods are limited by the number of taxa which is
relatively small. This algorithms becomes impractical
when the number of studied species n increases, since
the size of the search space suffers a combinatorial
explosion. Indeed, for a set of n taxa, the number of
rooted tree topologies is given by the following ex-
pression (Xiong, 2006):
|T | = (2n − 3)!/2
n−2
(n − 2)! (5)
Therefore, there is a need for heuristic methods to
address the MP problem in reasonable time. However,
as expressed by Goloboff (Goloboff, 1999): the use
of local search is not efficient enough to find a global
optimum in the case of large data sets, because there
exist some composite optima called islands (Maddi-
son, 1991) which makes the overall problem hard to
solve.
In 2003, Barker presented LVB, software which
implemented a multi-start Simulated Annealing al-
gorithm for solving the MP problem (Barker, 2003).
Later, an updated version of LVB was released in
2010 (Barker, 2012). This new version adds a hill-
climbing phase at the end of each Simulated Annea-
ling search and a new stop condition.
Ribeiro and Vianna (Ribeiro and Vianna, 2005)
in 2005 applied a greedy randomized adaptive search
procedure (GRASP) for solving the MP problem
and showed that this algorithm had the best per-
formance with respect to the state-of-the-art algo-
rithms. Different evolutionary algorithms were also
reported for the MP problem. Among them we found
GA+PR+LS, a genetic algorithm hybridized with lo-
cal search which employs Path-Relinking to imple-
ment a progressive crossover operator (Ribeiro and
Vianna, 2009). Go
¨
effon and Hao (Richer et al.,
2009) introduced a memetic algorithm called Hy-
dra which yields the best-known solutions for a set
of 20 benchmark instances proposed in (Ribeiro and
Vianna, 2005).
TNT (Tree analysis using New Technology) is
probably the fastest and one of the most effective
and complete parsimony analysis program for the MP
problem. TNT is known for finding better trees se-
veral thousands times faster than other software. TNT
uses many search strategies (Goloboff, 2002) coming
from genetic algorithms, local search and supertrees.
During the local search phases based on SPR and
TBR, TNT can visit millions of trees in a very short
time as it is based on Gladstein’s incremental down-
pass optimization (Gladstein, 1997).
This paper describes three techniques to help im-
prove the search for solutions of better quality: a
CUDA implementation of the algorithm that evaluates
the parsimony score of a phylogenetic tree, a bottom-
up implementation of Path-Relinking for phyloge-
netic trees that enables to efficiently compare two
trees and to give an estimation of the distance between
them in terms of the number of transformations from
one tree to another. Finally we discuss the design of
a Simulated Annealing (SA) algorithm tailored to the
MP problem in order to find near-optimal solutions.
The rest of this paper is organized as follows. In
section 3 the techniques used for the evaluation of
Strategies for Phylogenetic Reconstruction - For the Maximum Parsimony Problem
227

the objective function are discussed in detail using
CUDA. Then, a Path-Relinking implementation is
described in section 4. A Simulated Annealing al-
gorithm is presented in the section 5 where we com-
pare its performance with respect to LVB, an exis-
ting SA implementation (Barker, 2003; Barker, 2012)
and three other representative state-of-the-art algo-
rithms: GA+PR+LS (Ribeiro and Vianna, 2009),
TNT (Goloboff et al., 2008) and Hydra (Go
¨
effon,
2006). Finally, the last section shows the results of
our implementations.
3 EVALUATION OF MAXIMUM
PARSIMONY OBJECTIVE
FUNCTION
The evaluation function is one of the key elements
for the successful implementation of metaheuristic
algorithms because it is in charge of guiding the
search process toward good solutions in a combina-
torial search space.
During the search of an optimal solution, the eva-
luation function is used during different phases:
• When an initial solution is built by a greedy
method, the evaluation function is used to add
every taxon x in a node z that minimizes the in-
crease of its parsimony score φ(z), during this
step, the algorithm counts the number of unions
between the sequence of the new taxon and the
sequence of every taxon in the tree, in order to
know which is the best position. The new taxon
is joined in the site that represents the minimum
parsimony score. This process is repeated until
all taxa are joined to the tree, at the end we will
have the parsimony score of the phylogenetic tree.
• When the initial tree or the current solution s is
clipped using some neighborhood function; it is
not necessary to recalculate the parsimony score
of the whole tree because each node has its se-
quence and parsimony score, so the new parsi-
mony score of the tree is calculated from the node
where the sub-tree will be inserted until the root.
To avoid unnecessary calculations, the parsimony
score of each node is tested against the parsimony
score of the best tree found s
?
. If this score is ex-
ceeded, the score computation is canceled to pro-
ceed with the next tree rearrangement (Ronquist,
1998a; Goloboff, 1993).
3.1 CPU Implementation
In this section we describe the implementation details
to efficiently compute the parsimony score φ(t) of a
tree using the SIMD units of the CPU. The Fitch algo-
rithm (see algorithm 1) is the function that consumes
the most of time in a search algorithm for the MP
problem resolution. This function is called to com-
pute the score and the hypothetical sequences z for
each node of the tree including the root to obtain the
parsimony score. We can implement this function by
Algorithm 1: Fitch’s scoring algorithm for two se-
quences x and y.
input: x,y: array[k] of character
output: z: array[k] of character, mutations: number
of mutations
1 mutations ← 0
2 i ← 0
3 while i < k do
4 z[i] ← x[i] | y[i]
5 if z[i] = 0 then
6 mutations ← mutations + 1
7 z[i] ← x[i] & y[i]
8 end
9 i ← i + 1
10 end
11 return mutations
taking full advantage of the core of the x86 processors
that have a SSE (SIMD Streaming Extension) or AVX
(Advanced Vector Extensions) unit which enables to
treat data as vectors. The use of vectors enables the
application of the same operation on different data at
the same time. Intel processors offer on a 32-bits ar-
chitecture a set of 8 SSE registers of 128 bits or 8
AVX registers of 256 bits long. If we represent a nu-
cleotide with one byte, in the case of DNA, then a SSE
register can store and handle 16 bytes (nucleotides) at
a time (resp. 32 with AVX). In the case of proteins, it
is necessary to use 32 bits integers to represent the 20
different amino acids, so a SSE register can handle 4
integers (resp. 8 with AVX).
In order to efficiently perform the union and inter-
section of algorithm 1, each character is represented
by a power of 2. For nucleotides the different symbols
are (-, A, C, G, T, ?). We represent the gap symbol -
by 2
0
= 1, until T 2
4
= 16. The undefined character ?
which can represent any other character is then coded
by the value 31 = 1+2+···+16. With this represen-
tation the union can be performed by the binary-OR
(|) and the intersection by the binary-AND (&).
The experiments we have carried out (Richer,
2008) show that the vectorization of Fitch’s function
gives a 90% speedup on Intel Core 2 Duo processors,
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
228

while other architectures (Pentium II/III/4, Pentium-
M, Athlon 64, Sempron) provide 70 to 80% improve-
ment. This improvement then enables to divide the
overall computation time of a program by a factor of
3 to 4. A first pseudo-code was given in (Ronquist,
1998b) for PowerPC processors, then (Richer, 2008)
released the code for Intel and AMD processors.
Finally, note that the processors (Intel Core i5
or i7, AMD Phenom) introduce the SSE4.2 instruc-
tions set that contains the popcnt instruction which
counts the number of bits set to one in a general
purpose register. This instruction is used essentially
to determine the number of mutations that occur
when we perform the union between x[i:i+15] and
y[i:i+15]. By replacing the implementation of
popcnt by the native SSE4.2 instruction, the experi-
ments we have carried out show an overall improve-
ment of 95% (on an Intel Core i7 860 processor) com-
pared to the basic implementation.
The introduction of the AVX and then AVX2 ins-
tructions set in 2013 by Intel enabled to use vec-
tors of 256 bits. We have rewritten the SSE4.2 ver-
sion in AVX2 but could only gain 1% compared to
the SSE4.2 version on Intel Haswell processors. For
more details please see (Richer, 2013).
3.2 GPU Implementation
On an architectural point of view, the GPU can be
considered as a powerful coprocessor that the CPU
uses to achieve massively parallel treatments. The
CPU has nevertheless some SIMD (Single Instruction
Multiple Data) units (SSE, AVX) that can perform
computations in parallel but they can only handle 4
(or 8 in the case of AVX) 32 bits integers or simple
precision floating point values.
The combination of CPU and GPU is powerful
because CPUs consist of a few cores optimized for
serial processing, while GPUs consist of thousands
of smaller, more efficient cores designed for parallel
performance. However the GPU must be fed with
enough data to reach its full potential, that is the rea-
son that makes the CPU more efficient than the GPU
by processing small data instances.
3.2.1 Tree Representation
We use a static or flat representation of the tree to
speed up the treatments and to obtain coalesced me-
mory transaction when all of the threads in a half-
warp access global memory at the same time. A node
is represented by a structure of four integers, namely:
L,R,P,N which are the index of the Left and Right
offspring and the index of the Parent. The N field is
used only for data alignment in memory but also con-
tains the index of the node (see figure 1).
S1 S2
I1 S3
I2
L R P N
S1
S2
S3
I1
I2
−1 −1 0
1
2
3
4
3
−1
−1
−1
−1
0 1
3 2
3
4
4
−1
Figure 1: Flat tree representation.
The first n (here n = 3) nodes contain the leaves
(for example: S1, S2, S3) that have no offspring so
the fields L and R are set to -1. The rest of the n − 1
nodes are internal nodes. The root node (here I2) has
no parent so the field P is set to -1. The two basic
operations on the tree which are the degraph of a sub-
tree and the regraph on a branch must be implemented
carefully in order to avoid a false interpretation of the
score. For example if we put I2 before I1 in the ta-
ble of figure 1, the result will be wrong because I1
appears before I2 in the tree when we go from the
leaves to the root.
3.2.2 Data Storage
We store the initial and the hypothetical sequences in
a matrix of (2n − 1) × k characters or integers called
data on the GPU. The first n rows will not be modi-
fied as they contain the initial sequences, the other
rows will be modified by the kernel to compute the
hypothetical sequences.
3.2.3 Kernel
The code of the kernel consists in computing each in-
ternal sequence by assigning to each thread a column
of the matrix M. We start from the first internal se-
quence at index n and then we move back towards the
root (see listing 1). The input parameters are N(= n)
the number of leaves of the tree, K the length of the se-
quences, data as described in the previous subsection.
The output parameter is an array called mutations
which will record the number of mutations for each
column of the sequences. This array is stored on the
GPU. The flat tree is obtained from constant memory
(variable gpu tree) for efficiency reason as the tree is
a read-only structure.
Listing 1: Kernel to compute the parsimony score of a tree
φ(t).
1 g l o b a l vo i d k e r n e l ( i n t N, i n t K ,
2 C h a r a c t e r ∗ d a t a ,
3 i n t ∗ m u t a t i o n s ) {
Strategies for Phylogenetic Reconstruction - For the Maximum Parsimony Problem
229

4 i n t t i d = blockDim . x ∗ b l o c k I d x . x
5 + t h r e a d I d x . x ;
6 i n t l o c a l m u t a t i o n = 0 ;
7 i n t n o d e i d = N ;
8
9 w h i l e ( g p u t r e e [ n o d e i d ] . P != −1) {
10 i n t l e f t n o d e i d =
11 g p u t r e e [ n o d e i d ] . L ;
12 i n t r i g h t n o d e i d =
13 g p u t r e e [ n o d e i d ] . R ;
14 C h a r a c t e r x i = d a t a [ l e f t n o d e i d ∗
15 K + t i d ] ;
16 C h a r a c t e r y i = d a t a [ r i g h t n o d e i d ∗
17 K + t i d ] ;
18 C h a r a c t e r z i = x i & y i ;
19 i f ( z i == 0 ) {
20 ++ l o c a l m u t a t i o n ;
21 z i = x i | y i ;
22 }
23 d a t a [ n o d e i d ∗ K + t i d ] = z i ;
24 ++ n o d e
i d ;
25 }
26
27 i f ( t i d < K) {
28 m u t a t i o n s [ t i d ] = l o c a l m u t a t i o n ;
29 } e l s e {
30 m u t a t i o n s [ t i d ] = 0 ;
31 }
32 }
The call to the kernel is presented on listing 2. First,
the tree to evaluate called cpu tree is copied to the
constant memory area on the GPU gpu tree. After
the execution of the kernel, the mutations are copied
from the GPU to the CPU then they are summed on
the CPU to obtain the parsimony score φ(t).
Listing 2: Call to kernel and sum of mutations.
1 cudaMemcpyToSymbol ( ” g p u t r e e ” ,
2 c p u t r e e , ( 2 ∗N−1) ∗ s i z e o f ( Node ) , 0 ,
3 cudaMem cpyHost ToDevice ) ;
4 k e r n e l <<<g r i d , b l o c k >>>(N, K, g p u d a t a ,
5 g p u m u t a t i o n s ) ;
6 Memcpy ( c p u m u t a t i o n s , g p u m u t a t i o n s ,
7 s i z e o f ( i n t ) ∗ K,
8 cud aMemcpy DeviceToHost ) ) ;
9 i n t c o s t = a c c u m u l a t e (& c p u m u t a t i o n s [ 0 ] ,
10 &c p u m u t a t i o n s [K] , 0 ) ;
3.3 Results
We have implemented a simple benchmark in order
to compare the CPU and GPU efficiency. The pro-
gram takes as input the number of sequences and the
number of residues of the sequences. The sequences
are randomly generated. We then randomly generate
50 different trees and perform 1000 evaluations of the
parsimony score for each tree. Results were obtained
on the latest Intel CPU architecture (Haswell - Core
Table 1: Results in seconds for different number of se-
quences (n) and lengths (k) for 64 bits architecture.
taxa (n) length (k) i5 4570 GTX 770 Tesla K20 speed up
8 bits data
64 1024 0.03 1.43 1.89 -
32768 1.59 5.41 5.07 -
100000 12.50 15.01 11.81 1.05
200000 36.80 28.90 22.45 1.63
512 1024 0.42 6.14 9.56 -
32768 38.70 26.36 26.76 1.44
100000 125.26 82.50 68.49 1.82
200000 252.39 161.75 131.77 1.91
32 bits data
64 1024 0.17 1.43 1.86 -
32768 17.48 6.78 6.71 -
100000 58.83 20.33 18.10 3.25
200000 120.76 39.89 35.35 3.41
512 1024 1.69 6.55 11.05 -
32768 162.60 38.23 43.09 3.77
100000 508.90 127.55 122.06 4.15
200000 1022.30 261.94 243.17 4.2
i5-4570 running at 3.20 GHz with AVX2), a common
GPU (GTX 770) and a high end GPU (Tesla K20).
From table 1 we can notice that as the length of
the sequences and the number of sequences increases
the GPU implementation becomes more efficient than
the CPU one. This is generally the case when dea-
ling with small arrays for which vectorization is more
efficient than parallelization. Furthermore, GPU are
the preferred solution for computations with floating
point values but also for bytes and integers to some
extent.
4 A BOTTOM-UP
IMPLEMENTATION OF
PATH-RELINKING
Path-Relinking (PR), has proved unusually effective
for solving a wide range of optimization problems
from both classical and real world settings. PR ope-
rates with a population of good solutions. Given two
solutions called source and guiding, PR consists in
transforming the source solution into the guiding so-
lution (Glover et al., 2000). The aim of PR is to gen-
erate a path from the source to the guiding solution in
order to possibly find a better solution.
PR was implemented in a top-down recursive ver-
sion by (Ribeiro and Vianna, 2009), this implemen-
tation starts from the root of the tree and compares
the left and right subtrees of the source and guiding
solution respectively. It moves all the taxa from left
subtree of the source solution that are represented in
the right subtree of the guiding solution to the right
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
230
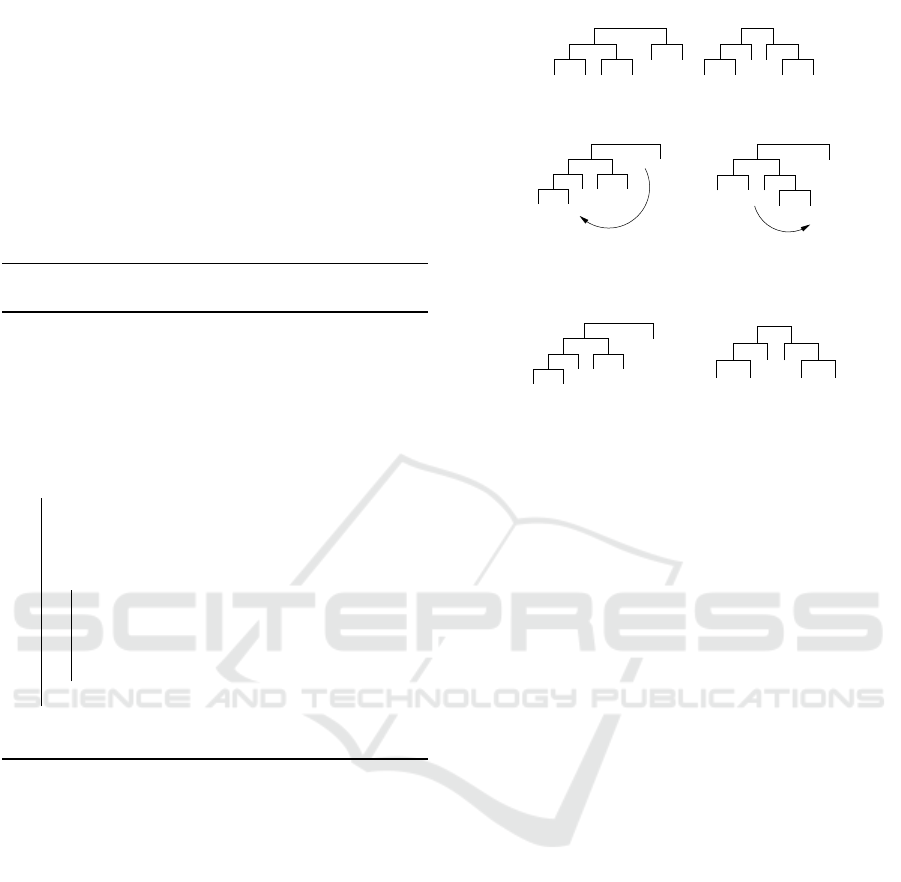
subtree of the source solution and conversely. This
procedure requires a lot of modifications and moves
of the taxa.
We have implemented a bottom-up iterative so-
lution (V
´
azquez-Ortiz et al., 2014) which compares
the subtrees present in the source and guiding solu-
tions (see Figure 2). For this the subtrees of each so-
lution are ordered by their number of leaves and we
start to compare subtrees of size 2, then subtrees of
size 3, and so on (see Algorithm 2).
Algorithm 2: Path-Relinking with bottom-up itera-
tive implementation.
input: s: source tree, g : guiding tree
output: number of transformations
1 reorder(s) ;
2 reorder(g) ;
3 trans f ormations ← 0;
4 Ω
g
← ordered set of subtrees of guiding tree g;
5 change ← true;
6 while change do
7 Ω
s
← ordered set of subtrees of source tree
s;
8 change ← f alse ;
9 if ∃ t = (X,Y) ∈ Ω
g
− Ω
s
then
10 change ← true ;
11 degraph Y and regraph on X in s;
12 trans f ormations ←
trans f ormations + 1;
13 end
14 end
15 return trans f ormations
Consider the example of Figure 2 (a) where we
can see the source and guiding trees. First the algo-
rithm starts with subtrees of size 2 in (b) it inserts the
leave B on the node (A, F), then it transforms the node
(C,E) into the node (E,F). In the same way it con-
tinues with the subtrees of size 3 in (d) and (e).
4.1 Complexity
The complexity of the algorithm can be computed as
follows: given n, the number of taxa of the problem,
the reordering of the guiding tree needs 2n − 1 com-
parisons and the computation of Ω
g
can be done in
2n − 1 operations. The main loop will be executed a
certain number of times, let’s say p times, and we will
need to compute Ω
s
, find a missing subtree (the ma-
ximum will be n comparisons) and perform a degraph
and regraph (1 transformation). This adds up to:
p × (2n − 1 + n + 1) + 3 × (2n − 1) ' 3n × (p + 2)
B
C
FA E
D
guiding tree
F
D
EA C
B
source tree
(a) Source and guiding trees.
F EC
A B
D
(b) First modifi-
cation resulting in
(A,B) on source.
A B C
D
E F
(c) Modification re-
sulting in (E,F).
A B
E F
D
C
(d) Modification re-
sulting in ((A,B),C).
B
C
FA E
D
(e) Modification re-
sulting in (D,(E,F)).
Figure 2: Example of Bottom-Up Path-Relinking with
source and guiding trees.
In the worst case p = n, so the worst case com-
plexity is O(n
2
) for the bottom-up implementation.
4.2 Results
4.2.1 Benchmark
We report results for a problem called zilla that was
originally obtained from the chloroplast gene rbcL
(Chase et al., 1993) and it contains 500 taxa of 759
DNA residues. Its best parsimony score of 16,218 was
found first by TNT.
We compare the results of the bottom-up - iterative
implementation explained in this article - with the top-
down with minimization - recursive implementation
from the article of (Ribeiro and Vianna, 2009) - with
optimization on regraph, i.e. when a leaf is regraphed
all possible branches are tested and we keep the first
one that minimizes the score of the tree.
4.2.2 Experiments
The experimentations were performed on
an Intel Core i5-4570 and the program
was coded in Java 1.7, it is part of a soft-
ware called Arbalet (http://www.info.univ-
angers.fr/pub/richer/ur.php?arbalet). In table 2
we report for each implementation the number of
transformations (degraph + regraph), the execution
time in seconds, the number of times the source
tree had a score inferior or equal to the guiding tree
(#Equal) and the number of times the source tree had
Strategies for Phylogenetic Reconstruction - For the Maximum Parsimony Problem
231

a score strictly inferior to the guiding tree (#Less)
during the generation of the path.
Note that the source tree has a higher score than
the guiding tree. This is not necessary for the bottom-
up method for which we can invert the trees. However
this is required by the top-down with minimization im-
plementation.
In Table 2, with the bottom-up implementation the
path between the two trees of score 16,218 (called
16,218 and 16,218
b
) was built with 24 transforma-
tions in 0.1 seconds. During the transformation pro-
cess the source tree had a best score (of 16,218) 13
times among the 24 transformations.
With the top-down with minimization algorithm
the construction of the path of the tree of score 21,727
into the tree of score 16,611 has needed 1528 trans-
formations and took 22.4 seconds. It also lead to the
generation of 586 trees of score under 16,611. This
means that the top-down with minimization algorithm
can sometimes help find a tree of lower score than the
guiding tree.
5 SIMULATED ANNEALING
Simulated Annealing (SA) is a general-purpose
stochastic optimization technique that has proved to
be an effective tool for the approximation of global
optimal solutions to many NP-hard optimization pro-
blems. In this section we present an improved im-
plementation of a SA algorithm (see Algorithm 3)
where we applied the CPU implementation to eva-
luate the objective function because the GPU imple-
mentation requires static memory and our SA uses dy-
namic memory. We add the Path-Relinking algorithm
in the neighborhood function. The main difference
of our implementation with respect to SA of LVB
(Barker, 2003; Barker, 2012) occurs in the neighbor-
hood function (line 8) which has been tailored to be
more specific for the MP problem. Our SA employs
a composed neighborhood function combining stan-
dard neighborhood relations for trees with a stochastic
descent algorithm on the current solution, while LVB
randomly selects a neighbor s
0
∈ T of the current so-
lution s.
Based on previous experimentations (Vazquez-
Ortiz, 2011; Richer, 2013) we have extracted the main
components of the SA algorithm and we have used the
best values for each parameter in order to provide an
efficient version of our algorithm:
• Initial solution: we use the neighbor joining (NJ)
algorithm
• Initial temperature: T
i
= 6.0
Algorithm 3: SA algorithm.
input: N : neighborhood, f : fitness function,
MCL : Markov Chain length, α :
cooling scheme, T
i
: initial temperature,
T
f
: final temperature
output: s
?
the best solution found
1 s
0
← GenerateInitialSolution();
2 s ← s
0
;
3 s
∗
← s
0
;
4 t ← T
i
;
5 while t > T
f
do
6 i ← 0;
7 while i < MCL do
8 s
0
← GenerateNeighbor(s,i,N );
9 ∆ f ← f (s
0
) − f (s);
10 generate a random u ∈ [0,1];
11 if (∆ f < 0) or (e
−∆ f /t
> u) then
12 s ← s
0
;
13 if f (s
0
) < f (s
∗
) then
14 s
∗
← s
0
;
15 end
16 end
17 i ← i + 1;
18 end
19 t ← αt;
20 end
21 return s
∗
• cooling schedule: we use a dynamic version of
the geometrical cooling schedule with a rehea-
ting system, where the temperature decreases by
a cooling factor of α = 0.99 at each step using
the relation t = αt. If the best-so-far solution is
not improved during 40 consecutive temperature
decrements, the current temperature t is increased
by a factor β = 1.4 using the function t = βt. In
our implementation this reheat mechanism can be
applied at most max reheat = 3 times, since it re-
presents a good trade-off between efficiency and
quality of solutions found.
• Stop condition: the algorithm terminates when the
current temperature t reaches T
f
= 0.0001
• Markov chain length MCL: for each temperature
t, the maximum number of visited neighboring so-
lutions is MCL. It depends directly on the parame-
ters n and k of the studied instance, since we have
observed that more moves are required for bigger
trees (Vazquez-Ortiz, 2011). For this experiment
we used MCL = 40 × (n + k)
• Neighborhood function: we use Subtree Pruning
and Regrafting (SPR) (Swofford et al., 1996). It
cuts a branch of the tree and reinserts the resulting
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
232

Table 2: Results of Path-Relinking for Bottom-Up and Top-Down implementations (Times in seconds).
Bottom-Up Top-Down With Minimization
source / guiding Trans. Time #Equal #Less Trans. Time #Equal #Less
16218
b
/ 16218 24 0.10 13 0 74 0.85 21 0
16219 / 16218 32 0.14 2 0 343 4.08 3 0
16250 / 16218 97 0.40 3 0 1519 25.32 2 0
16401 / 16218 151 0.60 2 0 1474 25.36 2 0
16611 / 16218 186 0.75 2 0 1225 19.57 2 0
21727 / 16218 446 1.68 2 0 1241 18.70 2 0
16250 / 16219 92 0.37 2 0 1418 24.70 1 0
16401 / 16219 152 0.61 2 0 1390 23.74 1 0
16401 / 16250 162 0.63 1 0 1203 19.74 1 0
16611 / 16250 144 0.56 1 0 1233 35.78 3 0
21727 / 16250 449 1.71 1 0 1196 19.65 1 0
16611 / 16401 202 0.79 3 0 1216 47.75 2 1
21727 / 16611 455 1.84 2 0 1528 22.40 593 586
subtree elsewhere, generating a new internal node.
For each tree there exist 2(n − 3)(2n − 7) possi-
ble SPR neighbors (Allen and Steel, 2001) which
makes it a medium size neighborhood. N = SPR.
5.1 Computational Experiments
5.1.1 Benchmark Instances and Performance
Assessment
For our experiments we use 20 instances randomly
generated by (Ribeiro and Vianna, 2005), their gene-
rator takes as parameters the number of taxa, the num-
ber of characters, and the ratio of indefinition, which
corresponds to the fraction of undefined characters in
each taxon. Instances with larger ratios of indefini-
tion are harder. The number of taxa in these instances
ranges from 45 to 75, the number of characters from
61 to 159, and the ratio of indefinition from 20% to
50%. In the Table 3 we can see their characteristics,
in the columns two and three n represents the num-
ber of sequences and k their length, in the two last
columns we show the percentage of indefinition and
similarity.
The criteria used for evaluating the performance
of the algorithms are the same as those used in the
literature: the best parsimony score found for each
instance (smaller values are better) and the expended
CPU time in seconds.
5.2 Comparison of our SA with the
State-of-the-Art Procedures
In this experiment a performance comparison of the
best solutions achieved by our SA with respect to
those produced by LVB (Barker, 2012) GA+PR+LS
Table 3: Characteristics of the instances.
Instance n k Indefinition (%) Similarity (%)
tst01 45 61 20 67
tst02 47 151 30 76
tst03 49 111 40 82
tst04 50 97 50 88
tst05 52 75 20 68
tst06 54 65 30 75
tst07 56 143 40 82
tst08 57 119 50 87
tst09 59 93 20 68
tst10 60 71 30 75
tst11 62 63 40 82
tst12 64 147 50 87
tst13 65 113 20 69
tst14 67 99 30 76
tst15 69 77 40 82
tst16 70 69 50 88
tst17 71 159 20 68
tst18
73 117 30 76
tst19 74 95 40 82
tst20 75 79 50 87
(Ribeiro and Vianna, 2009), TNT (Goloboff et al.,
2008) and Hydra (Go
¨
effon, 2006) was carried out
over the test-suite described in section 5.1.1.
The results from this experiment are depicted in
Table 4. Column 1 indicates the instance, the best
solutions found by LVB and its average CPU time are
in the second column, GA+PR+LS, TNT and Hydra,
in terms of parsimony score Φ are listed in the next
three columns. Note that for TNT this corresponds to
the best result over 30 runs. Columns 6 to 9 present
the best (B), average (Avg.), and standard deviation
(Dev.) of the parsimony score attained by our SA in
30 independent executions, as well as its average CPU
time in seconds. Finally, the difference (δ) between
the best result produced by our our SA algorithm and
the best-known solution produced by either TNT or
Strategies for Phylogenetic Reconstruction - For the Maximum Parsimony Problem
233

Table 4: Performance comparison among our SA, LVB, GA+PR+LS, TNT and Hydra over 20 standard benchmark instances.
LVB our SA
Instance Score T GA+PR+LS TNT Hydra B Avg. Dev. T δ
tst01 551 39.20 547 545 545 545 545.13 0.43 1407.57 0
tst02 1370 10.90 1361 1354 1354 1354 1355.30 0.97 1938.23 0
tst03 846 74.80 837 834 833 833 833.43 0.56 2506.30 0
tst04 595 1047.10 590 589 588 587 588.23 0.80 1341.17 -1
tst05 798 26.60 792 789 789 789 789.00 0.00 2007.90 0
tst06 605 189.80 603 597 596 596 596.57 0.56 1164.27 0
tst07 1281 84.50 1274 1273 1269 1269 1270.83 1.63 4063.80 0
tst08 875 2648.70 862 856 852 852 853.33 1.27 2884.73 0
tst09 1152 47.30 1150 1145 1144 1141 1144.73 1.09 3237.53 -3
tst10 732 408.90 722 720 721 720 720.80 0.70 2288.00 -1
tst11 551 3578.70 547 543 542 541 542.21 0.72 3807.79 -1
tst12 1234 593.70 1225 1219 1211 1208 1215.27 2.76 3668.40 -3
tst13 1533 41.60 1524 1516 1515 1515 1517.77 1.91 2514.20 0
tst14 1175 454.10 1171 1162 1160 1160 1163.03 1.82 2847.13 0
tst15 764 12427.40 758 755 752 752 753.90 1.11 4808.63 0
tst16 560 64487.00 537 531 529 529 531.00 1.23 3268.20 0
tst17 2464 40.60 2469 2453 2453 2450 2456.00 2.63 8020.23 -3
tst18 1543 179.90 1531 1522 1522 1521 1525.67 3.96 4451.37 -1
tst19 1036 3081.10 1024 1017 1013 1012 1016.23 2.14 6875.30 -1
tst20 687 56240.00 671 666 661 659 662.82 1.44 7149.43 -2
Avg. 1017.60 7285.90 1009.75 1004.30 1002.45 1001.65 1004.06 1.39 3512.51
Hydra is shown in the last column.
The analysis of the information presented in Table
4 lead us to the next observations: First, LVB (Barker,
2012) and GA+PR+LS (Ribeiro and Vianna, 2009)
return worse solutions than Hydra, TNT and our SA.
Second, the solutions provided by the proposed SA
algorithm improve all the solutions of LVB (pre-
vious SA implementation). On average our SA pro-
vided solutions with parsimony score smaller (com-
pare Columns 6 and 7) and it attained improve the
results produced by Hydra (Go
¨
effon, 2006) on 9 best-
known solutions and to reach its results for the 11 re-
maining instances. TNT is the fastest software and
will solve a problem in a few seconds. We have no-
ticed that LVB has a erratic behavior. For example,
the resolution of problem tst15 can take from 3 min
to 14 hours and the time spent for the resolution is not
in accordance with the discovery of a better solution:
3 min to reach a solution of score 779 and 3 hours to
reach a solution of score 780.
Thus, as this experiment confirms, our SA al-
gorithm is an effective alternative for solving the
MP problem, compared with the three representative
state-of-art algorithms: GA+PR+LS, TNT and Hydra.
6 CONCLUSIONS
In this paper we have described three techniques to
help improve phylogenetic reconstruction with MP:
the first one is related to the implementation and the
evaluation of the score of a tree, the second is a stra-
tegy that could help get solutions of better quality or
could be used to compare trees. The third technique is
an adaptation of the Simulated Annealing metaheuris-
tic tailored to MP that efficiently could integrate the
two other strategies. From the experimentations of
this three implementations we could conclude sepa-
rately:
• CPU and GPU implementations: we have pre-
sented the implementation details of the evalua-
tion of the parsimony score of a tree on a CPU and
a GPU. The results obtained show that for a small
number of sequences of short length the CPU is
faster than the GPU. But for an important number
of sequences with a long length the GPU becomes
much faster than the CPU. This will be very in-
teresting for phylogenies based on multi-genes or
whole genomes where sequences can have from
thousands to millions of residues.
• Path-Relinking: we have described an implemen-
tation of PR in the context of Phylogenetic Recon-
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
234

struction with Maximum Parsimony. Confronted
to other existing implementations our method
does not allow to find trees with a better score
which is the aim of Path-Relinking but represents
an interesting tool to compare the topologies of
the source and guiding trees. The bottom-up ite-
rative implementation that we have described is
faster than the top-down recursive implementa-
tions and can serve as a measure of distance be-
tween trees and could be applied to any other con-
text.
• Simulated annealing: we have presented an im-
proved Simulated Annealing algorithm to find
near-optimal solutions for the MP problem un-
der the optimality criterion of Fitch. In the
experiments our algorithm was carefully com-
pared with an existing Simulated Annealing
implementation (LVB) (Barker, 2003; Barker,
2012), and other three state-of-the-art algorithms
GA+PR+LS, TNT and Hydra. The results show
that our SA is able to consistently improve the
best results produced by LVB, obtaining in cer-
tain instances important reductions in the parsi-
mony score. Compared with the state-of-the-art
algorithm called Hydra (Go
¨
effon, 2006) our SA
algorithm was able to improve on 9 previous best-
known solutions and to equal these results on the
other 11 selected benchmark instances. Further-
more, it was observed that the solution cost found
by our SA presents a relatively small standard de-
viation, which indicates the precision and robust-
ness of the proposed approach.
As future work we suggest to integrate the CUDA
evaluation technique into our implementation of Sim-
ulated Annealing for MP an use the Path-Relinking
technique to determine local optima during the de-
crease of the temperature in order to avoid unsuccess-
ful evaluations of many trees.
7 AVAILABILITY
The C++ source code for the SA algorithm and Path-
Relinking can be found on sourceforge.net under the
biosbl project. The code for the GPU implementation
is freely available from the website of Jean-Michel
Richer. It should run under all Unix/Linux platforms
(http://www.info.univ-angers.fr/pub/richer/rec.php).
REFERENCES
Allen, B. J. and Steel, M. (2001). Subtree transfer opera-
tions and their induced metrics on evolutionary trees.
Annals of Combinatorics, 5(1):1–15.
Bader, D. A., Chandu, V. P., and Yan, M. (2006). Exactmp:
An efficient parallel exact solver for phylogenetic tree
reconstruction using maximum parsimony. In Parallel
Processing, 2006. ICPP 2006. International Confer-
ence on, pages 65–73. IEEE.
Barker, D. (2003). LVB: parsimony and simulated annea-
ling in the search for phylogenetic trees. Bioinformat-
ics, 20(2):274–275.
Barker, D. (2012). LVB homepage.
Chase, M. W., Soltis, D. E., Olmstead, R. G., Morgan,
D., Les, D. H., Mishler, B. D., Duvall, M. R., Price,
R. A., Hills, H. G., Qiu, Y., Kron, K. A., Rettig,
J. H., Conti, E., Palmer, J. D., Manhart, J. R., Sytsma,
K. J., Michaels, H. J., Kress, W. J., Karol, K. G.,
Clark, W. D., Hedren, M., Gaut, B. S., Jansen, R. K.,
Kim, K., Wimpee, C. F., Smith, J. F., Furnier, G. R.,
Strauss, S. H., Xiang, Q., Plunkett, G. M., Soltis, P. S.,
Swensen, S. M., Williams, S. E., Gadek, P. A., Quinn,
C. J., Eguiarte, L. E., Golenberg, E., Learn, G. H.,
Graham, S. W., Barrett, S. C. H., Dayanandan, S., and
Albert, V. A. (1993). Phylogenetics of seed plants:
An analysis of nucleotide sequences from the plastid
gene rbcl. Annals of the Missouri Botanical Garden,
80(3):528–580.
Felsenstein, J. (2003). Inferring phylogenies. Sinauer As-
sociates.
Fitch, W. (1971). Towards defining course of evolution:
minimum change for a specified tree topology. Sys-
tematic Zoology, 20:406–416.
Foulds, L. R. and Graham, R. L. (1982). The steiner pro-
blem in phylogeny is np-complete. Advances in Ap-
plied Mathematics, 3(1):43–49.
Gladstein, D. S. (1997). Efficient incremental character op-
timization. Cladistics, 13(1-2):21–26.
Glover, F., Laguna, M., and Mart, R. (2000). Fundamen-
tals of scatter search and path relinking. Control and
Cybernetics, 39:653–684.
Go
¨
effon, A. (2006). Nouvelles heuristiques de voisinage
et m
´
em
´
etiques pour le probl
`
eme maximum de parci-
monie. PhD thesis, LERIA, Universit
´
e d’Angers.
Goloboff, P. (1999). Analyzing large data sets in reason-
able times: solutions for composite optima. Cladis-
tics, 15:415–428.
Goloboff, P. (2002). Techniques for analyzing large data
sets. In DeSalle R., G. G. and Wheeler W., e., editors,
Techniques in Molecular Systematics and Evolution,
page 7079. Brikhuser Verlag, Basel.
Goloboff, P. A. (1993). Nona, version 2.0. Computer Pro-
gram and Manual Distributed by the Author.
Goloboff, P. A., Farris, J. S., and Nixon, K. C. (2008). Tnt,
a free program for phylogenetic analysis. Cladistics,
24(5):774–786.
Gusfield, D. (1997). Algorithms on strings, trees, and se-
quences: Computer science and computational biol-
ogy. Cambridge University Press, 1st. edition.
Hartigan, J. A. (1973). Minimum mutation fits to a given
tree. Biometrics, 29:53–65.
Strategies for Phylogenetic Reconstruction - For the Maximum Parsimony Problem
235

Hendy, M. D. and Penny, D. (1982). Branch and bound
algorithms to determine minimal evolutionary trees.
Mathematical Biosciences, 59(2):277–290.
Hennig, W. (1966). Phylogenetic systematics. Phylogeny.
University of Illinois Press, Urbana.
Hillis, D. M., Moritz, C., and Mable, B. K. (1996). Molecu-
lar systematics. Sinauer Associates Inc., Sunderland,
MA, 2nd. edition.
Kasap, S. and Benkrid, K. (2011). High performance phy-
logenetic analysis with maximum parsimony on re-
configurable hardware. Very Large Scale Integration
(VLSI) Systems, IEEE Transactions on, 19(5):796–
808.
Maddison, D. R. (1991). The discovery and importance of
multiple islands of most-parsimonious trees. System-
atic Zoology, 40(3):315–328.
Penny, D., Foulds, L. R., and Hendy, M. D. (1982). Test-
ing the theory of evolution by comparing phyloge-
netic trees constructed from five different protein se-
quences. Nature, 297:197–200.
Ribeiro, C. C. and Vianna, D. S. (2005). A GRASP/VND
heuristic for the phylogeny problem using a new
neighborhood structure. International Transactions in
Operational Research, 12(3):325–338.
Ribeiro, C. C. and Vianna, D. S. (2009). A hybrid ge-
netic algorithm for the phylogeny problem using path-
relinking as a progressive crossover strategy. In-
ternational Transactions in Operational Research,
16(5):641–657.
Richer, J.-M. (2008). Three new techniques to im-
prove phylogenetic reconstruction with maximum
parsimony. Technical report, LERIA, University of
Angers, France.
Richer, J.-M. (2013). Improvevement of fitch function for
maximum parsimony in phylogenetic reconstruction
with intel avx2 assembler instructions. Technical re-
port, LERIA, University of Angers, France.
Richer, J. M., Go
¨
effon, A., and Hao, J. K. (2009). A
memetic algorithm for phylogenetic reconstruction
with maximum parsimony. Lecture Notes in Computer
Science, 5483:164–175.
Ronquist, F. (1998a). Fast fitch-parsimony algorithms for
large data sets. Cladistics, 14(4):387–400.
Ronquist, F. (1998b). Fast fitch-parsimony algorithms for
large data sets. Cladistics, 14(4):387–400.
Sober, E. (1993). The nature of selection: Evolutionary
theory in philosophical focus. University Of Chicago
Press.
Sridhar, S., Lam, F., Blelloch, G. E., Ravi, R., and Schwartz,
R. (2007). Direct maximum parsimony phylogeny re-
construction from genotype data. BMC Bioinformat-
ics, 8(472).
Swofford, D. L., Olsen, G. J., Waddell, P. J., and Hillis,
D. M. (1996). Phylogeny reconstruction. In Molec-
ular Systematics, chapter 11, pages 411–501. Sinauer
Associates, Inc., Sunderland, MA, 2nd. edition.
Vazquez-Ortiz, K. E. (2011). Metaheur
´
ısticas para la res-
oluci
´
on del problema de m
´
axima parsimonia. Mas-
ter’s thesis, LTI, Cinvestav - Tamaulipas, Cd. Vitoria,
Tamps. Mexico.
V
´
azquez-Ortiz, K. E., Richer, J.-M., Lesaint, D., and
Rodriguez-Tello, E. (2014). A bottom-up implemen-
tation of path-relinking for phylogenetic reconstruc-
tion applied to maximum parsimony. In Computa-
tional Intelligence in Multi-Criteria Decision-Making
(MCDM), 2014 IEEE Symposium on, pages 157–163.
IEEE.
White, W. T. J. and Holland, B. R. (2011). Faster exact ma-
ximum parsimony search with xmp. Bioinformatics,
27(10):1359–1367.
Xiong, J. (2006). Essential Bioinformatics. Cambridge Uni-
versity Press, 1st. edition.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
236
