
On the Decomposition of Min-based Possibilistic Influence Diagrams
Salem Benferhat
1
, Hadja Faiza Khellaf-Haned
2
and Ismahane Zeddigha
2
1
CRIL, Universit
´
e d’Artois, Rue Jean Souvraz, SP 18 62307, Lens Cedex, France
2
RIIMA, Universit
´
e des Sciences et de la Technologie Houari Boumediene, BP 32 El Alia Bab Ezzouar, Alger, Alg
´
erie
Keywords:
Decision Theory, Possibility Theory, Possibilistic Networks, Possibilistic Influence Diagrams.
Abstract:
Min-based possibilistic influence diagrams allow a compact modelling of decision problems under uncertainty.
Uncertainty and preferential relations are expressed on the same structure by using ordinal data. Like proba-
bilistic influence diagrams, min-based possibilistic influence diagrams contain three types of nodes: chance,
decision and utility nodes. Uncertainty is described by means of possibility distributions on chance nodes and
preferences are expressed as satisfaction degrees on utility nodes.
In many applications, it may be natural to represent expert knowledge and preferences separately and treat all
nodes similarly. This paper shows how an influence diagram can be equivalently represented by two possibilis-
tic networks: the first one represents knowledge of an agent and the second one represents agent’s preferences.
Thus, the decision evaluation process is based on more compact possibilistic network.
1 INTRODUCTION
Decision making under uncertainty (Whalen, 1984),
(Denardo et al., 2012), (Anzilli, 2013), (Dubois et al.,
2013) plays an important role in Artificial Intelligence
(AI) applications. Several decision making tools have
been developed to assist decision makers in their
tasks: simulation techniques, dynamic programming
(Sniedovich, 2010), logical decision models (Dubois
et al., 1998) and graphical decision models (Zhang,
2013), (Garcia and Sabbadin, 2006). Using graphical
models, authors in (Boutouhami and Khellaf, 2015)
have proposed an approximate approach for comput-
ing optimal qualitative possibilistic optimistic deci-
sion in the context of optimistic criteria. They showed
that it comes down to computing a normalization de-
gree of the moral graph associated to the resulting
graph obtained by merging preferences and knowl-
edge represented by two min-based possibilistic net-
works.
This paper also focuses on graphical decision
models which provide efficient decision tools by al-
lowing a compact representation of decision prob-
lems under uncertainty (Shenoy, 1994). Most of de-
cision graphical models are based on Influence Dia-
grams (ID) (Howard and Matheson, 1984), (Zhang,
1998) for representing decision maker’s beliefs and
preferences on sequences of decisions to be made
under uncertainty. The evaluation of Influence Di-
agrams ensures optimal decisions while maximizing
the decision maker’s expected utilities (Tatman and
Shachter, 1990), (Zhang, 1998), (Dubois and Prade,
1988). Min-based (or qualitative) possibilistic Influ-
ence Diagrams ”PID” (Garcia and Sabbadin, 2006)
allow a gradual expression of both agent’s prefer-
ences and knowledge. The graphical part of possi-
bilistic Influence Diagrams is exactly the same as the
one of standard Influence Diagrams. Uncertainty is
expressed by possibility degrees and preferences are
considered as satisfaction degrees.
Unlike probabilistic decision theory which is
based on one expected utility criteria to evaluate opti-
mal decisions, a qualitative possibilistic decision the-
ory (Dubois et al., 1999), (Dubois et al., 2001) of-
fers several qualitative utility criteria for decision ap-
proaches under uncertainty. Among these criteria,
one can mention the pessimistic and optimistic utili-
ties proposed in (Dubois and Prade, 1995), the binary
utility proposed in (Giang and Shenoy, 2005), etc.
As standard Influence Diagrams, direct (Garcia and
Sabbadin, 2006) and an indirect methods (Garcia and
Sabbadin, 2006), (Guezguez et al., 2009) have been
proposed to evaluate a min-based PID. Besides, Influ-
ence Diagrams represent agent’s beliefs and prefer-
ences on the same structure and they operate on three
types of nodes: chance, decision and utility nodes.
In practice, it will be easier for an agent to express
its knowledge and preferences separately. Further-
Benferhat, S., Khellaf-Haned, H. and Zeddigha, I.
On the Decomposition of Min-based Possibilistic Influence Diagrams.
DOI: 10.5220/0005703501170128
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 117-128
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
117

more, it is more simple to treat all nodes in the same
way. In (Benferhat et al., 2013), authors have pro-
posed a new compact graphical model for represent-
ing decision making under uncertainty based on the
use of possibilistic networks. Agent’s knowledge and
preferences are expressed in qualitative way by two
distinct qualitative possibilistic networks. This new
representation, for decision making under uncertainty
based on min-based possibilistic networks, benefits
from the simplicity of possibilistic networks.
In this paper, we show how to decompose an ini-
tial min-based Influence Diagram into two min-based
possibilistic networks: the first one represents agent’s
beliefs and the second one encodes its preferences.
Then, we define the required steps for splitting a qual-
itative Influence Diagram into two min-based possi-
bilistic networks preserving the same possibility dis-
tribution and the same qualitative utility. This proce-
dure allows us to obtain a more compact (in terms
of dependence) qualitative possibilistic network for
computing optimal decisions. This decomposition
process provides also the opportunity to exploit the in-
ference algorithms (Ajroud et al., 2012), (Amor et al.,
2003) developed for min-based possibilistic networks
to solve qualitative Influence Diagrams.
The rest of this paper is organized as follows:
next section briefly recalls basic concepts of possibil-
ity theory, min-based possibilistic networks and min-
based PID. Section 3 describes how the decompo-
sition process can be efficiently used for encoding
an Influence Diagram into two possibilistic networks.
Section 4 gives related works. Section 5 concludes
the paper.
2 BACKGROUND
2.1 Basic Concepts of Possibility Theory
This section gives a brief refresher on possibility the-
ory (Dubois and Prade, 1988) which is issued from
fuzzy sets theory (Zadeh, 1978).
Let X = {X
1
, ..., X
N
} be a set of variables. We de-
note by D
X
i
= {x
i1
, ..., x
in
} the domain associated with
the variable X
i
. x
i j
denotes the jth instance of X
i
. The
universe of discourse is denoted by Ω = ×
X
i
∈V
D
X
i
,
which is the Cartesian product of all variables domain
in X . Each element ω ∈ Ω is called an interpretation
which represents a possible state of Ω. It is denoted
by ω = (x
1i
, ..., x
N j
). φ, ψ... represent events, namely
subsets of Ω.
A basic element in a possibility theory is the no-
tion of possibility distribution π which corresponds to
a mapping from Ω to the scale [0, 1]. This distribution
encodes available knowledge on real world. π(ω) = 1
means that ω is completely possible and π(ω) = 0
means that it is impossible for ω to represent the real
world. A possibilistic scale can be interpreted in or-
dinal or numerical way. A possibility distribution π is
said to be normalized, if max
ω
π(ω) = 1.
Given a possibility distribution π on the universe
discourse Ω, two dual measures are defined for each
event φ ⊆ Ω: Possibility measure Π(φ) and Neces-
sity measure N(φ). The first one evaluates to what
extent φ is consistent with our knowledge encoded
by π, namely Π(φ) = max
ω∈Ω
{π(ω) : ω |= φ}. The sec-
ond one, evaluates at which level φ is certainly im-
plied by our knowledge represented by π, namely
N(φ) = 1 − Π(¬φ).
The possibilistic conditioning consists in the revi-
sion of our initial knowledge, encoded by a possibility
distribution π by the arrival of a new certain informa-
tion φ ⊆ Ω. The initial distribution π is then replaced
by another one, denoted π
0
= π(. | φ). The two inter-
pretations relative to the possibilistic scale (qualita-
tive and quantitative) induce two definitions of possi-
bilistic conditioning (Amor et al., 2002), (Bouchon-
Meunier et al., 2002): product-based conditioning
and min-based conditioning. In this paper, we use the
last one defined by:
π(ω |
min
φ) =
1 If π(ω) = Π(φ) and ω |= φ
π(ω) If π(ω) < Π(φ) and ω |= φ
0 oterhwise
(1)
Similarly, possibility theory offers several defini-
tions of independence relation (Amor et al., 2002),
(de Campos and Huete, 1999). As we interpret the un-
certainty scale in ordinal manner, we will used the so-
called min-based independence relation, initially de-
fined as a non-interactivity relation by Zadeh (Zadeh,
1978). This relation is obtained by using the min-
based conditioning (Equation 1) and it is defined by:
∀x, y, z Π(x ∧ y | z) = min(Π(x | z), Π(y | z)). (2)
2.2 Min-based Possibilistic Networks
In a possibility theory framework, there are two ways
to define possibilistic networks according to the possi-
bilistic conditioning. In this paper, we only focus on
min-based possibilistic networks. A min-based pos-
sibilistic network (Borgelt et al., 1998) over a set of
variables X denoted by ΠG
min
= (G, π) is character-
ized by:
1. A Graphical Component: which is represented
by a Directed Acyclic Graph (DAG) where nodes
correspond to variables and arcs represent depen-
dence relations between variables.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
118

2. Numerical Components: these components
quantify different links in the DAG by using lo-
cal possibility distributions for each node X in the
context of its parents denoted by Par(X). More
precisely:
• For every root node X (Par(X) =
/
0), uncer-
tainty is represented by a priori possibility de-
gree π(x) for each instance x ∈ D
X
, such that
max
x∈Ω
π(x) = 1.
• For the rest of the nodes (Par(X ) 6=
/
0), uncer-
tainty is represented by the conditional possi-
bility degree π(x | u
X
) for each instance x ∈
D
X
and for any instance u
X
∈ D
Par(X)
(where
D
Par(X)
represents the Cartesian product of
all variables domain in Par(X)), such that
max
x∈Ω
π(x | u
X
) = 1, for any u
X
.
The set of a priori and conditional possibility degrees
induces a unique joint possibility distribution π
G
de-
fined by:
π
G
(X
1
, ..., X
N
) = min
i=1..N
π(X
i
| U
i
). (3)
The most common task performed on possibilistic
networks is the possibilistic inference which consists
in determining how the realization of specific values
of some variables called (observations or evidence)
affects the remaining variables (Huang and Darwiche,
1996).
2.3 Min-based Possibilistic Influence
Diagrams
Like standard Influence Diagrams (Lauritzen and
Nilsson, 2001)(Zhang, 2013), PID
s
have two compo-
nents: the graphical part which is exactly the same
as the one of standard Influence Diagrams and the
numerical part which consists in evaluating different
links in the graph. The uncertainty is expressed by
possibility degrees and preferences are considered as
satisfaction degrees.
In a min-based possibilistic Influence Dia-
gram (qualitative possibilistic ID), denoted by
ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
), both agent’s knowledge and
preferences are expressed in a qualitative setting. This
is achieved by ordering the different states of the
world and providing a preference relation between
different consequences.
1. A Graphical Component: which is represented
by a DAG, denoted by G
ID
= (X , A) where X =
C ∪ D ∪U represents a set of variables containing
three different kinds of nodes: chance, decision
and utility nodes. A is a set of arcs representing
either causal influences or information influences
between variables.
• Chance Nodes: are represented by cir-
cles. They represent state variables X
i
∈ C =
{X
1
, ..., X
n
}. Chance nodes reflect uncertain
factors of a decision problem. A combination
x = {x
1i
, ..., x
n j
} of state variable values repre-
sents a state.
• Decision Nodes: are represented by rectangles.
They represent decision variables D
j
∈ D =
{D
1
, ..., D
p
} which depict decision options. A
combination d = {d
1i
, ..., d
p j
} of values repre-
sents a decision.
• Utility Nodes: or value nodes V
k
∈ V =
{V
1
, ...,V
q
} are represented by diamonds. They
represent local utility functions (local satisfac-
tion degrees) µ
k
∈ {µ
1
, ..., µ
q
}.
A conventional assumption that an Influence Di-
agram must respect is that utility nodes have no
children.
2. Numerical Components: After specifying the
structure of an Influence Diagram, uncertainty is
described by means of a priori and conditional
possibility distributions relative to chance nodes.
Possibility distributions are defined on the scale
L = [0, 1] and they are assumed to be normalized.
In addition, decision maker should quantify value
nodes, on utility scale U, to express their utilities
(which may not be normalized). These compo-
nents quantify different links in the DAG as fol-
lows:
• For every chance node X ∈ C , uncertainty is
represented by:
– If X is a root node, then a priori possibility
degree π
ID
(x) will be associated for each in-
stance x ∈ D
X
, such that max
x∈D
X
π
ID
(x) = 1.
– If X has parents, the conditional possibil-
ity degree π
ID
(x | u
X
) will be associated for
each instance x ∈ D
X
and u
X
∈ D
Par(X)
=
×
X
j
∈Par(X)
D
X
j
, such that max
x∈D
X
π
ID
(x | u
x
) = 1,
for any u
X
.
• Decision nodes are not quantified. Indeed, a
value of decision node D
j
is deterministic, it
will be fixed by the decision maker.
Once a decision d = {d
1i
, ..., d
p j
} ∈ D is fixed,
chance nodes of the min-based Influence Dia-
gram form a qualitative possibilistic network in-
duces a unique joint conditional possibility dis-
tribution relative to chance node interpretations
x = {x
1i
, ..., x
n j
}, in the context of d.
π
ID
min
(x | d) = min
i=1..n
π
ID
(x
il
| u
X
i
). (4)
On the Decomposition of Min-based Possibilistic Influence Diagrams
119

where x
il
∈ D
X
i
and u
X
i
∈ D
Par(X
i
)
=
×
X
m
∈Par(X
i
),D
j
∈Par(X
i
)
D
X
m
∪ D
D
j
.
• For each utility node V
k=1..q
∈ V , ordinal val-
ues µ
k
(u
V
k
) are assigned to every possible in-
stantiations u
V
k
of the parent variables Par(V
k
).
Ordinal values µ
k
represent satisfaction degrees
associated with local instantiations of parents
variables.
The global satisfaction degree µ
ID
min
(x, d) relative
to the global instantiation (x, d) of all variables
(chance and decision nodes) can be computed as
the minimum of the local satisfaction degrees:
µ
ID
min
(x, d) = min
k=1..q
µ
k
(u
V
k
). (5)
where u
V
k
∈ D
Par(V
k
)
= ×
X
i
∈Par(V
k
),D
j
∈Par(V
k
)
D
X
i
∪
D
D
j
.
A qualitative Influence Diagram is evaluated in or-
der to identify the optimal strategy δ
∗
, maximizing
one of the possibilistic qualitative utilities. In fact, a
strategy δ assigns an instantiation d to each global in-
stantiation x of the state variables.
3 DECOMPOSITION OF
MIN-BASED POSSIBILISTIC
INFLUENCE DIAGRAM
This section discusses the main contributions of this
paper. Our aim is to show that a qualitative PID
can be modelled by two possibility distributions, one
representing agent’s beliefs and the other represent-
ing the qualitative utility. So, we propose a decom-
position process of min-based possibilistic Influence
Diagram ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
) into two min-based
possibilistic networks:
1. Agent’s knowledge ΠK
min
= (G
K
, π). This qual-
itative possibilistic network should codify the
same joint conditional possibility distribution π
ID
min
induced by the PID.
2. Agent’s preferences ΠP
min
= (G
P
, µ). Again, this
preference-based possibilistic network must cod-
ify the same qualitative utility µ
ID
min
induced by the
PID.
In what follows, the decomposition process of the
Influence Diagram ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
) into two
qualitative possibilistic networks is presented.
3.1 The Construction of a
Knowledge-based Qualitative
Possibilistic Network
The knowledge-based qualitative possibilistic net-
work ΠK
min
= (G
K
, π) encodes agent’s beliefs. It in-
duces a unique possibility distribution π
K
using Equa-
tion 3. The graphical component G
K
of the new qual-
itative possibilistic network ΠK
min
is defined on the
set of variables Y = X ∪ D = {Y
1
, ...,Y
n+p
} of chance
and decision nodes (where n = |X | and p = |D|). The
construction of such network is performed in three
steps:
• Each decision node D
j
will be transformed into
a chance node representing the total ignorance,
namely:
∀D
j
∈ D, π(d
jl
| u
D
j
) = 1. (6)
for each instance d
jl
∈ D
D
j
and u
D
j
∈ D
Par(D
j
)
• All state nodes remain unchanged:
∀X
i
∈ C , π(x
il
| u
X
i
) = π
ID
(x
il
| u
X
i
) (7)
for each instance x
il
∈ D
X
i
and u
X
i
∈ D
Par(X
i
)
.
• All utility nodes {V
1
, ...,V
q
} and their associated
edges are removed.
The building of the knowledge-based possibilistic
network ΠK
min
can be summarized by Algorithm 1.
The new min-based possibilistic network ΠK
min
=
Data: ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
), a min-based
PID.
Result: ΠK
min
= (G
K
, π), knowledge-based
network.
begin
foreach D
j
∈ D do
Transform each decision node D
j
into
chance node using Equation 6.
end
foreach X
i
∈ C do
Quantify each chance node X
i
using
Equation 7.
end
Remove utility nodes {V
1
, ...,V
q
}.
end
Algorithm 1: Building knowledge-based network.
(G
K
, π) induces a unique joint possibility distribution
π
K
defined by the min-based chain rule (Equation 3).
The following proposition ensures that the joint pos-
sibility distribution induced by the new possibilistic
network ΠK
min
encodes the same states represented
by the Influence Diagram ΠID
min
.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
120
Proposition 1. Let ΠK
min
= (G
K
, π) be a min-based
possibilistic network obtained using Algorithm 1. The
joint possibility distribution π
K
induced by ΠK
min
is
equal to the one induced by the Influence Diagram
ΠID
min
. Namely,
π
K
(Y
1
, ...,Y
n+p
) = π
ID
min
(X
1
, ..., X
n
| D
1
, ..., D
p
)
= min
X
i
∈C
π
ID
(X
i
| U
i
)
(8)
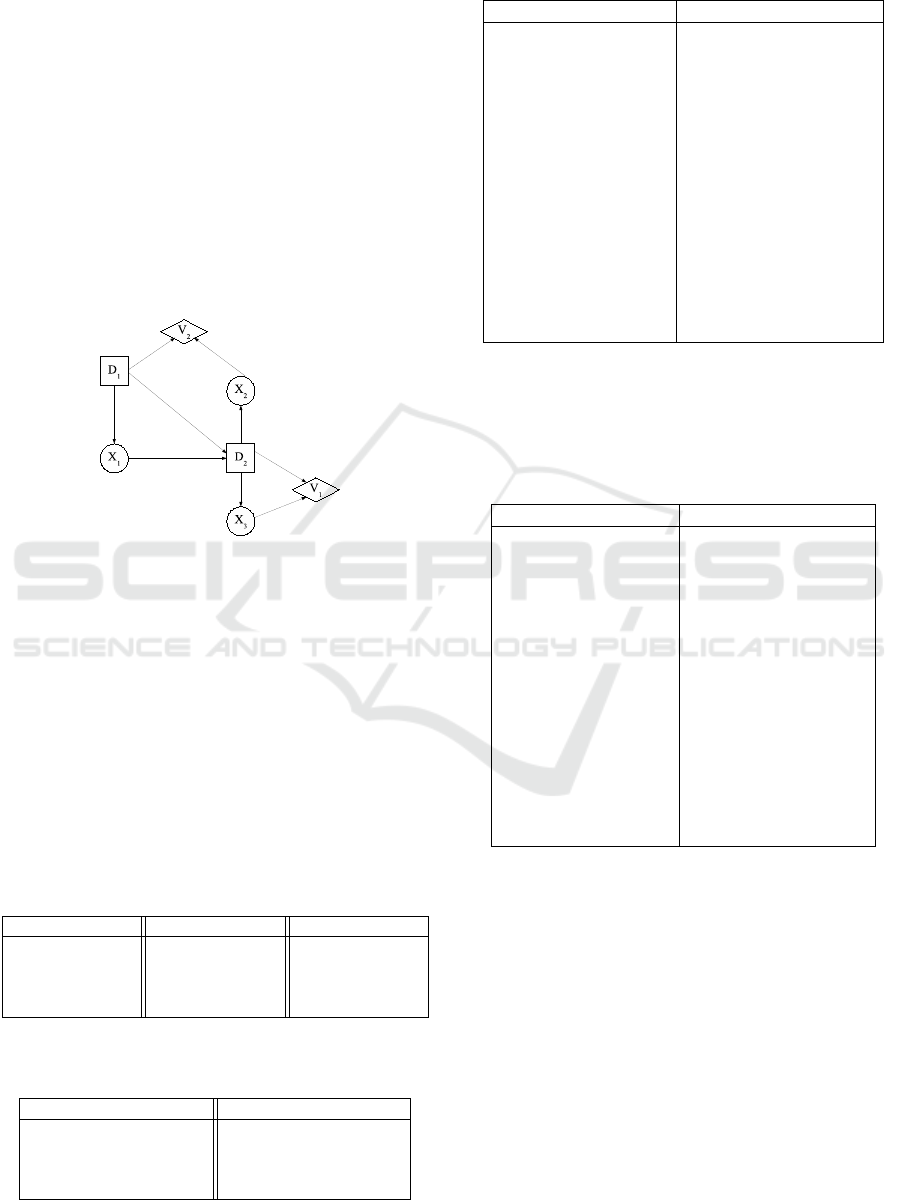
Example 1. Let us consider a simple decision prob-
lem represented by a min-based Influence Diagram
ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
). The graphical component
G
ID
is given by Figure 1. It contains three chance
nodes C = {X
1
, X
2
, X
3
}, two decision nodes D =
{D
1
, D
2
} and two utility nodes V = {V
1
,V
2
}. We sup-
pose that all variables are binary.
Figure 1: An example of influence diagram.
The numerical components are represented by
conditional possibility distributions associated with
chance nodes X
1
, X
2
, X
3
and qualitative utilities for
the value node V
1
and V
2
, in the context of their par-
ents. Indeed, conditional possibilities are represented
in Tables 1. Utilities for V
1
and V
2
are represented in
Table 2. It should be noted that utilities for V
2
is not
normalized.
The joint conditional possibility distribution π
ID
min
induced by the Influence Diagram ΠID
min
, using
Equation 4, is given by Table 3.
Table 1: Initial possibility distributions π
ID
on X
1
| D
1
, X
2
|
D
2
and X
3
| D
2
.
X
1
D
1
π
ID
(X
1
| D
1
) X
2
D
2
π
ID
(X
2
| D
2
) X
3
D
2
π
ID
(X
3
| D
2
)
x
1
d
1
1 x
2
d
2
.3 x
3
d
2
1
x
1
¬d
1
.4 x
2
¬d
2
1 x
3
¬d
2
1
¬x
1
d
1
.2 ¬x
2
d
2
1 ¬x
3
d
2
.4
¬x
1
¬d
1
1 ¬x
2
¬d
2
.4 ¬x
3
¬d
2
.8
Table 2: Initial qualitative utilities µ
1
on X
3
, D
2
and µ
2
on
X
2
, D
1
.
X
3
D
2
µ
1
(X
3
, D
2
) X
2
D
1
µ
2
(X
2
, D
1
)
x
3
d
2
.2 x
2
d
1
.5
x
3
¬d
2
.3 x
2
¬d
1
.9
¬x
3
d
2
1 ¬x
2
d
1
.1
¬x
3
¬d
2
0 ¬x
2
¬d
1
.4
Table 3: The joint conditional possibility distribution π
ID
min
on X
1
, X
2
, X
3
given D
1
, D
2
.
X
1
X
2
X
3
D
1
D
2
π
ID
min
X
1
X
2
X
3
D
1
D
2
π
ID
min
x
1
x
2
x
3
d
1
d
2
.3 ¬x
1
x
2
x
3
d
1
d
2
.2
x
x
x
1
1
1
x
x
x
2
2
2
x
x
x
3
3
3
d
d
d
1
1
1
¬
¬
¬d
d
d
2
2
2
1
1
1 ¬x
1
x
2
x
3
d
1
¬d
2
.2
x
1
x
2
x
3
¬d
1
d
2
.3 ¬x
1
x
2
x
3
¬d
1
d
2
.3
x
1
x
2
x
3
¬d
1
¬d
2
.4 ¬
¬
¬x
x
x
1
1
1
x
x
x
2
2
2
x
x
x
3
3
3
¬
¬
¬d
d
d
1
1
1
¬
¬
¬d
d
d
2
2
2
1
1
1
x
1
x
2
¬x
3
d
1
d
2
.3 ¬x
1
x
2
¬x
3
d
1
d
2
.2
x
1
x
2
¬x
3
d
1
¬d
2
.8 ¬x
1
x
2
¬x
3
d
1
¬d
2
.2
x
1
x
2
¬x
3
¬d
1
d
2
.3 ¬x
1
x
2
¬x
3
¬d
1
d
2
.3
x
1
x
2
¬x
3
¬d
1
¬d
2
.4 ¬x
1
x
2
¬x
3
¬d
1
¬d
2
.8
x
x
x
1
1
1
¬
¬
¬x
x
x
2
2
2
x
x
x
3
3
3
d
d
d
1
1
1
d
d
d
2
2
2
1
1
1 ¬x
1
¬x
2
x
3
d
1
d
2
.2
x
1
¬x
2
x
3
d
1
¬d
2
.3 ¬x
1
¬x
2
x
3
d
1
¬d
2
.2
x
1
¬x
2
x
3
¬d
1
d
2
.4 ¬
¬
¬x
x
x
1
1
1
¬
¬
¬x
x
x
2
2
2
x
x
x
3
3
3
¬
¬
¬d
d
d
1
1
1
d
d
d
2
2
2
1
1
1
x
1
¬x
2
x
3
¬d
1
¬d
2
.4 ¬x
1
¬x
2
x
3
¬d
1
¬d
2
.4
x
1
¬x
2
¬x
3
d
1
d
2
.4 ¬x
1
¬x
2
¬x
3
d
1
d
2
.2
x
1
¬x
2
¬x
3
d
1
¬d
2
.4 ¬x
1
¬x
2
¬x
3
d
1
¬d
2
.2
x
1
¬x
2
¬x
3
¬d
1
d
2
.4 ¬x
1
¬x
2
¬x
3
¬d
1
d
2
.4
x
1
¬x
2
¬x
3
¬d
1
¬d
2
.4 ¬x
1
¬x
2
¬x
3
¬d
1
¬d
2
.4
The global satisfaction degree
µ
ID
min
(D
1
, D
2
, X
1
, X
2
, X
3
) generated by the Influ-
ence Diagram ΠID
min
can be computed using
Equation 5. The results are reported in Table 4.
Table 4: Global qualitative utilities µ
ID
min
(D
1
, D
2
, X
1
, X
2
, X
3
).
D
1
D
2
X
1
X
2
X
3
µ
ID
min
D
1
D
2
X
1
X
2
X
3
µ
ID
min
d
1
d
2
x
1
x
2
x
3
.2 ¬d
1
d
2
x
1
x
2
x
3
.2
d
1
d
2
x
1
x
2
¬x
3
.5 ¬d
1
d
2
x
1
x
2
¬x
3
.9
d
1
d
2
x
1
¬x
2
x
3
.1 ¬d
1
d
2
x
1
¬x
2
x
3
.2
d
1
d
2
x
1
¬x
2
¬x
3
.1 ¬d
1
d
2
x
1
¬x
2
¬x
3
.4
d
1
d
2
¬x
1
x
2
x
3
.2 ¬d
1
d
2
¬x
1
x
2
x
3
.2
d
1
d
2
¬x
1
x
2
¬x
3
.5 ¬d
1
d
2
¬x
1
x
2
¬x
3
.9
d
1
d
2
¬x
1
¬x
2
x
3
.1 ¬d
1
d
2
¬x
1
¬x
2
x
3
.2
d
1
d
2
¬x
1
¬x
2
¬x
3
.1 ¬d
1
d
2
¬x
1
¬x
2
¬x
3
.4
d
1
¬d
2
x
1
x
2
x
3
.3 ¬d
1
¬d
2
x
1
x
2
x
3
.3
d
1
¬d
2
x
1
x
2
¬x
3
0 ¬d
1
¬d
2
x
1
x
2
¬x
3
0
d
1
¬d
2
x
1
¬x
2
x
3
.1 ¬d
1
¬d
2
x
1
¬x
2
x
3
.3
d
1
¬d
2
x
1
¬x
2
¬x
3
0 ¬d
1
¬d
2
x
1
¬x
2
¬x
3
0
d
1
¬d
2
¬x
1
x
2
x
3
.3 ¬d
1
¬d
2
¬x
1
x
2
x
3
.3
d
1
¬d
2
¬x
1
x
2
¬x
3
0 ¬d
1
¬d
2
¬x
1
x
2
¬x
3
0
d
1
¬d
2
¬x
1
¬x
2
x
3
.1 ¬d
1
¬d
2
¬x
1
¬x
2
x
3
.3
d
1
¬d
2
¬x
1
¬x
2
¬x
3
0 ¬d
1
¬d
2
¬x
1
¬x
2
¬x
3
0
We propose to decompose the Influence Diagram
ΠID
min
given in Figure 1 into two qualitative pos-
sibilistic networks. The first min-based possibilistic
network ΠK
min
= (G
K
, π) describes agent’s knowl-
edge, the second one ΠP
min
= (G
P
, µ) will express its
preferences.
Let us proceed to build the knowledge-based network
ΠK
min
= (G
K
, π) using Algorithm 1. The graphical
component G
K
is given by Figure 2. In fact, the
graphical component G
K
corresponds to the Influence
Diagram of Figure 1 from which we removed the util-
ity nodes.
Using Algorithm 1, the initial possibility distribu-
tion associated with ΠK
min
are given by Tables 5, 6
and 7.
On the Decomposition of Min-based Possibilistic Influence Diagrams
121
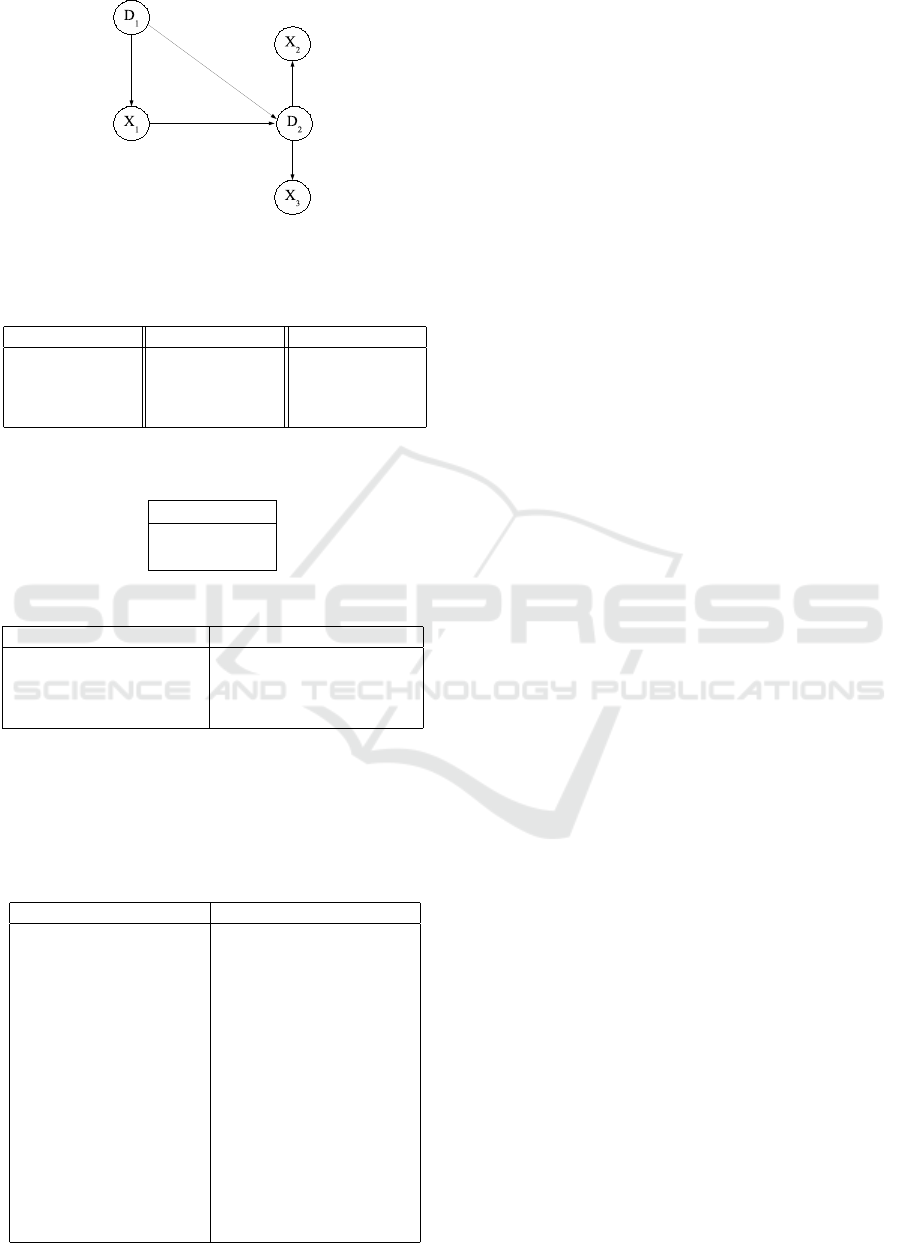
Figure 2: Knowledge-based possibilistic network.
Table 5: Initial possibility distribution ΠK
min
on X
1
| D
1
,
X
2
| D
2
and X
3
| D
2
.
X
1
D
1
π(X
1
| D
1
) X
2
D
2
π(X
2
| D
2
) X
3
D
2
π(X
3
| D
2
)
x
1
d
1
1 x
2
d
2
.3 x
3
d
2
1
x
1
¬d
1
.4 x
2
¬d
2
1 x
3
¬d
2
1
¬x
1
d
1
.2 ¬x
2
d
2
1 ¬x
3
d
2
.4
¬x
1
¬d
1
1 ¬x
2
¬d
2
.4 ¬x
3
¬d
2
.8
Table 6: Initial possibility distribution ΠK
min
on D
1
.
D
1
π(D
1
)
d
1
1
¬d
1
1
Table 7: Initial possibility distribution ΠK
min
on D
2
| D
1
X
1
.
D
2
D
1
X
1
π(D
2
| D
1
X
1
) D
2
D
1
X
1
π(D
2
| D
1
X
1
)
d
2
d
1
x
1
1 ¬d
2
d
1
x
1
1
d
2
d
1
¬x
1
1 ¬d
2
d
1
¬x
1
1
d
2
¬d
1
x
1
1 ¬d
2
¬d
1
x
1
1
d
2
¬d
1
¬x
1
1 ¬d
2
¬d
1
¬x
1
1
Table 8 contains the joint possibility distribution
π
K
(using Equation 3) induced by the min-based pos-
sibilistic network ΠK
min
.
Table 8: The joint possibility distribution
π
K
(X
1
, X
2
, X
3
, D
1
, D
2
).
X
1
X
2
X
3
D
1
D
2
π
K
X
1
X
2
X
3
D
1
D
2
π
K
x
1
x
2
x
3
d
1
d
2
.3 ¬x
1
x
2
x
3
d
1
d
2
.2
x
1
x
2
x
3
d
1
¬d
2
1 ¬x
1
x
2
x
3
d
1
¬d
2
.2
x
1
x
2
x
3
¬d
1
d
2
.3 ¬x
1
x
2
x
3
¬d
1
d
2
.3
x
1
x
2
x
3
¬d
1
¬d
2
.4 ¬x
1
x
2
x
3
¬d
1
¬d
2
1
x
1
x
2
¬x
3
d
1
d
2
.3 ¬x
1
x
2
¬x
3
d
1
d
2
.2
x
1
x
2
¬x
3
d
1
¬d
2
.8 ¬x
1
x
2
¬x
3
d
1
¬d
2
.2
x
1
x
2
¬x
3
¬d
1
d
2
.3 ¬x
1
x
2
¬x
3
¬d
1
d
2
.3
x
1
x
2
¬x
3
¬d
1
¬d
2
.4 ¬x
1
x
2
¬x
3
¬d
1
¬d
2
.8
x
1
¬x
2
x
3
d
1
d
2
1 ¬x
1
¬x
2
x
3
d
1
d
2
.2
x
1
¬x
2
x
3
d
1
¬d
2
.3 ¬x
1
¬x
2
x
3
d
1
¬d
2
.2
x
1
¬x
2
x
3
¬d
1
d
2
.4 ¬x
1
¬x
2
x
3
¬d
1
d
2
1
x
1
¬x
2
x
3
¬d
1
¬d
2
.4 ¬x
1
¬x
2
x
3
¬d
1
¬d
2
.4
x
1
¬x
2
¬x
3
d
1
d
2
.4 ¬x
1
¬x
2
¬x
3
d
1
d
2
.2
x
1
¬x
2
¬x
3
d
1
¬d
2
.4 ¬x
1
¬x
2
¬x
3
d
1
¬d
2
.2
x
1
¬x
2
¬x
3
¬d
1
d
2
.4 ¬x
1
¬x
2
¬x
3
¬d
1
d
2
.4
x
1
¬x
2
¬x
3
¬d
1
¬d
2
.4 ¬x
1
¬x
2
¬x
3
¬d
1
¬d
2
.4
It can be checked that the joint possibility distribu-
tion π
K
associated to the knowledge-based possibilis-
tic network ΠK
min
is the same as the one induced by
the possibilistic Influence Diagram ΠID
min
(see Table
3).
3.2 Building Preference-based
Qualitative Possibilistic Network
The second qualitative possibilistic network ΠP
min
=
(G
P
, µ) represents agent’s preferences associated with
the qualitative utility. ΠP
min
induces a unique quali-
tative utility µ
P
using Equation 3. This section shows
that this qualitative utility is equal to the qualitative
utility µ
ID
min
(Equation 5) encoded by the Influence Di-
agram ΠID
min
.
The graphical component G
P
of the new quali-
tative possibilistic network ΠP
min
is defined on the
set of variables Z = {Z
1
, ..., Z
m
} ⊂ X ∪ D of chance
and decision nodes. The set of nodes Z represents
the union of the parent variables of all utility nodes
{V
1
, ...,V
q
} in the Influence Diagram. Namely, Z =
{Z
1
, ..., Z
m
} = Par(V
1
) ∪ ... ∪ Par(V
q
), where m =
|Par(V
1
) ∪ ... ∪ Par(V
q
)| presents the total of parent
variables of all utility nodes in ΠID
min
.
During the construction phase of the graph G
P
, we
need to make sure that the generated graph is a DAG
structure. We should also avoid the creation of loops
at the merging step of the evaluation process (Benfer-
hat et al., 2013). So, before enumerating the decom-
position process of an Influence Diagram ΠID
min
, the
notion of topological order generated by a DAG is re-
called:
Definition 1. A Directed Acyclic Graph is a linear
ordering of its nodes such that for every arc from node
X
i
to node X
j
, X
i
comes before X
j
in the ordering. Any
DAG has at least one topological ordering.
Construction algorithms are known for construct-
ing a topological ordering of any DAG in linear time.
The usual algorithm for topological ordering consists
in finding a ” start node” which have no incoming
edges. Then, edges outgoing this node must be re-
moved. This process will be repeated until all nodes
will be visited.
Example 2. The DAG G
ID
(X , A) associated with the
Influence Diagram given in Example 1 has two valid
topological ordering:
• D
1
, X
1
, D
2
, X
2
, X
3
,
• D
1
, X
1
, D
2
, X
3
, X
2
.
which are equivalent to:
D
1
≺ X
1
≺ D
2
≺ X
2
X
3
.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
122

We first propose a naive solution that requires a
pretreatment step which consists to reduce all utility
nodes into a single one. This node will inherit the
parents of all value nodes. A more advanced solution
preserving the initial structure will then be proposed.
Hence, operating on the initial structure of the Influ-
ence Diagram induces a more compact representation.
3.2.1 Decomposition Process with a Single
Utility Node
The first solution consists in reducing all utility nodes
into a single one. Hence, it amounts to perform pre-
treatment on the initial Influence Diagram before its
decomposition. Formally, the pretreatment step con-
sists on the reduction of the number of value nodes to
one, noted V
r
, that will inherit the parents of all value
nodes (Par(V
1
), ..., Par(V
q
)) ie Par(V
r
) = Par(V
1
) ∪
... ∪ Par(V
q
). The utility value associated to the new
utility node V
r
corresponds to the minimum of utili-
ties, which corresponds to the global satisfaction de-
gree, namely:
µ
r
(u
V
r
) = µ
ID
min
(x, d) = min
k=1..q
µ
k
(u
V
k
). (9)
where u
V
r
∈ D
Par(V
r
)
and u
V
k
∈ D
Par(V
k
)
.
Once this step is accomplished, the min-based
possibilistic network ΠP
min
= (G
P
, µ) encoding
agent’s preferences is built as follows:
• Select an arbitrary node, denoted Z
k
∈ Par(V
r
)
to be a child of the remaining parent variables
Par(V
r
)\Z
k
. This selection must be in agreement
with the order generated by the DAG associated
with the reduced Influence Diagram. This means
that the selected node Z
k
must be the last in the
topological ordering induced by the reduced In-
fluence Diagram.
• Create arcs from all the remaining nodes
{Par(V
r
) − Z
k
} to the node Z
k
.
• Each node Z
j
6= Z
k
will be associated a total igno-
rance possibility distribution, namely:
∀z
jl
∈ D
Z
j
, µ(z
jl
) = 1. (10)
• The node Z
k
will be quantified as follows:
∀z
kl
∈ D
Z
k
, ∀u
Z
k
∈ D
Par(Z
k
)
,
µ(z
kl
| u
Z
k
) = µ
ID
min
(u
V
r
). (11)
The construction of preference-based possibilistic
network ΠP
min
can be summarized by algorithm 2.
The following proposition indicates that the min-
based possibilistic network ΠP
min
= (G
P
, µ) con-
structed from the previous steps, codifies the same
qualitative utility encoded by the qualitative Influence
Diagram ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
).
Data: {V
1
, Par(V
1
)}, ..., {V
q
, Par(V
q
)}, utility nodes
and their parents in the qualitative Influence
Diagram.
Result: ΠP
min
= (G
P
, µ), preference-based
possibilistic network.
begin
Z ← {Par(V
1
) ∪ ... ∪ Par(V
q
)}.
Reduce all utility nodes to a single node V
r
.
Select a node Z
k
∈ Par(V
r
) to be child of the
remaining parent variables according to the
topological ordering induced by the reduced
ID.
Create arcs from {Par(V
r
)\Z
k
} to Z
k
.
Quantifying chance node Z
k
using Equation 11
foreach Z
j
6= Z
k
do
Quantifying Z
j
using Equation 10.
end
end
Algorithm 2: Construction of preference-based possi-
bilistic network.
Proposition 2. Let ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
) be a min-
based possibilistic Influence Diagram. Let ΠP
min
=
(G
P
, µ) be a min-based possibilistic network obtained
using Algorithm 2. The joint qualitative utility µ
P
in-
duced by ΠP
min
is equivalent to the one induced by
the Influence Diagram ΠID
min
. Namely,
µ
P
(Z
1
, ..., Z
m
) = µ
ID
min
(X
1
, ..., X
n
, D
1
, ..., D
p
). (12)
Example 3. Let us continue Example 1. Applying the
solution based on a single node utility, we propose to
build the preference-based network ΠP
min
= (G
P
, µ)
encoding agent’s preferences. The pretreatment step
consists in reducing V
1
and V
2
to one utility node de-
noted V
r
. The new utility node inherits the parents of
old utility nodes V
1
and V
2
, namely D
1
, X
1
, D
2
and X
2
.
The reduced Influence Diagram is given by Figure 3.
Figure 3: Min-based possibilistic Influence Diagram with
single utility node.
Using Algorithm 2, the graphical component G
P
will be defined on set of variables Z = Par(V
r
) =
{X
2
, X
3
, D
1
, D
2
}. As already mentioned, an arbitrary
node must be selected from Z to be a child of the
remaining parent variables. The choice of this node
must be in accordance with the topological ordering
On the Decomposition of Min-based Possibilistic Influence Diagrams
123

induced by the reduced Influence Diagram. First, we
give the topological ordering induced by the reduced
Influence Diagram (Figure 3 ):
D
1
≺ X
1
≺ D
2
≺ X
2
X
3
.
Then, two nodes are worn candidates for this choice:
X
2
or X
3
, let X
3
be this node. The graphical compo-
nent G
P
is given by Figure 4.
Figure 4: Preference-based possibilistic network.
The conditional possibility distribution µ(X
3
|
D
1
D
2
X
2
) associated to X
3
is defined using Equation
11. The results are mentioned in Table 9. Possibility
distributions on other nodes {D
1
, D
2
, X
2
} are uniform
(see Table 10).
Table 9: Initial possibility distribution ΠP
min
on X
3
|
D
1
D
2
X
2
.
X
3
D
1
D
2
X
2
µ(X
3
| D
1
D
2
X
2
) X
3
D
1
D
2
X
2
µ(X
3
| D
1
D
2
X
2
)
x
3
d
1
d
2
x
2
.2 ¬x
3
d
1
d
2
x
2
.5
x
3
d
1
d
2
¬x
2
.9 ¬x
3
d
1
d
2
¬x
2
.1
x
3
d
1
¬d
2
x
2
.3 ¬x
3
d
1
¬d
2
x
2
0
x
3
d
1
¬d
2
¬x
2
.1 ¬x
3
d
1
¬d
2
¬x
2
0
x
3
¬d
1
d
2
x
2
.2 ¬x
3
¬d
1
d
2
x
2
.9
x
3
¬d
1
d
2
¬x
2
.2 ¬x
3
¬d
1
d
2
¬x
2
.4
x
3
¬d
1
¬d
2
x
2
.3 ¬x
3
¬d
1
¬d
2
x
2
0
x
3
¬d
1
¬d
2
¬x
2
.3 ¬x
3
¬d
1
¬d
2
¬x
2
0
Table 10: Initial possibility distribution ΠP
min
on D
1
, D
2
and X
2
.
D
1
µ(D
1
) D
2
µ(D
2
) X
2
µ(X
2
)
d
1
1 d
2
1 x
2
1
¬d
1
1 ¬d
2
1 x
2
1
Using Equation 3, the preference-based possi-
bilistic network ΠP
min
induces the joint qualitative
utility µ
P
given by Table 11.
As illustrated by Tables 9 and 11, the conditional
possibility distribution µ(X
3
| D
1
D
2
X
2
) is the same as
the joint qualitative utility induced by the preferences-
based possibilistic network ΠP
min
. Therefore, we con-
clude that the proposed solution which consists in re-
ducing the initial Influence Diagram do not allow a
compact representation of agent’s preferences.
Table 11: The joint qualitative utility µ
P
(D
1
, D
2
, X
1
, X
2
, X
3
).
D
1
D
2
X
1
X
2
X
3
µ
P
D
1
D
2
X
1
X
2
X
3
µ
P
d
1
d
2
x
1
x
2
x
3
.2 ¬d
1
d
2
x
1
x
2
x
3
.2
d
1
d
2
x
1
x
2
¬x
3
.5 ¬d
1
d
2
x
1
x
2
¬x
3
.9
d
1
d
2
x
1
¬x
2
x
3
.1 ¬d
1
d
2
x
1
¬x
2
x
3
.2
d
1
d
2
x
1
¬x
2
¬x
3
.1 ¬d
1
d
2
x
1
¬x
2
¬x
3
.4
d
1
d
2
¬x
1
x
2
x
3
.2 ¬d
1
d
2
¬x
1
x
2
x
3
.2
d
1
d
2
¬x
1
x
2
¬x
3
.5 ¬d
1
d
2
¬x
1
x
2
¬x
3
.9
d
1
d
2
¬x
1
¬x
2
x
3
.1 ¬d
1
d
2
¬x
1
¬x
2
x
3
.2
d
1
d
2
¬x
1
¬x
2
¬x
3
.1 ¬d
1
d
2
¬x
1
¬x
2
¬x
3
.4
d
1
¬d
2
x
1
x
2
x
3
.3 ¬d
1
¬d
2
x
1
x
2
x
3
.3
d
1
¬d
2
x
1
x
2
¬x
3
0 ¬d
1
¬d
2
x
1
x
2
¬x
3
0
d
1
¬d
2
x
1
¬x
2
x
3
.1 ¬d
1
¬d
2
x
1
¬x
2
x
3
.3
d
1
¬d
2
x
1
¬x
2
¬x
3
0 ¬d
1
¬d
2
x
1
¬x
2
¬x
3
0
d
1
¬d
2
¬x
1
x
2
x
3
.3 ¬d
1
¬d
2
¬x
1
x
2
x
3
.3
d
1
¬d
2
¬x
1
x
2
¬x
3
0 ¬d
1
¬d
2
¬x
1
x
2
¬x
3
0
d
1
¬d
2
¬x
1
¬x
2
x
3
.1 ¬d
1
¬d
2
¬x
1
¬x
2
x
3
.3
d
1
¬d
2
¬x
1
¬x
2
¬x
3
0 ¬d
1
¬d
2
¬x
1
¬x
2
¬x
3
0
3.2.2 Decomposition Process based on the Initial
Influence Diagram
The main limitation of the first solution, presented in
Section 3.2.1 and inspired from the work proposed in
(Guezguez, 2012), concerns the reduction of all util-
ity nodes into a single one that will inherit the parents
of all value nodes. So, we suggest to preserve the ini-
tial structure. The solution proposed in this section
is to try to have the structure of a preference-based
network as close as possible to the initial structure of
the Influence Diagram. Hence, as we will see, oper-
ating on the initial structure of the Influence Diagram
allows a more compact representation than if we have
used the reduced Influence Diagram.
The min-based possibilistic network ΠP
min
=
(G
P
, µ) encoding agent’s preferences is built progres-
sively as follows:
• For each utility node V
k
∈ V = {V
1
, ...,V
q
}, de-
fine an order between parent variables. More pre-
cisely, this order is induced by the DAG associ-
ated with the initial Influence Diagram.
Example 4. Let us consider the Influence Dia-
gram given in Example 1 Figure 1. The parent
variables of utility node V
2
are D
1
and X
2
. We
recall that the Influence Diagram ΠID
min
induces
the following order:
D
1
≺ X
1
≺ D
2
≺ X
3
X
2
.
Then, an order can be defined between parent
variables D
1
and X
2
as follows:
D
1
≺ X
2
• For each utility node V
k
∈ V = {V
1
, ...,V
q
}, a set
of nodes is defined, among the parent variables of
V
k
where each node is eligible to be a child of the
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
124

remaining parent variables. The candidate nodes
are those that appear in the last row of the order
list generated in the previous step. Indeed, re-
specting the order induced between the parents of
each utility node enables us to avoid the creation
of loops at the merging step of the evaluation pro-
cess (Benferhat et al., 2013). Each candidate node
can have one of the three following status:
1. Either it has not yet been introduced in the DAG
G
P
under construction.
2. Or it represents a root node in the DAG part
already built.
3. Or it represents a child.
• One node, denoted Z
k
must be selected from the
candidate set generated in the previous step. For
more compact representation of the DAG G
P
un-
der construction, the selected node must satisfy as
a priority the first or second property (not yet in-
troduced or root node). If the selected node Z
k
do
not yet appear in the DAG G
P
under construction,
then we must first integrate it in G
P
. In the same
way, parent variables that have not yet been inte-
grated in G
P
must be created. Finally, arcs from
the remaining parent variables to Z
k
must be cre-
ated.
If the selected node Z
k
already appears in the DAG
G
P
under construction as a root node, then we
must only integrate the remaining parent variables
that are not yet included in G
P
and create arcs
from the remaining parent variables to Z
k
.
Then, we proceed to compute the conditional pos-
sibility distribution µ(Z
k
| U
Z
k
). In both situations
(1 or 2), the conditional possibility distribution
µ(Z
k
| U
Z
k
) associated to the node Z
k
is defined
as follows:
∀z
kl
∈ D
Z
k
, ∀u
Z
k
∈ D
Par(Z
k
)
,
µ(z
kl
| u
Z
k
) = µ
k
(u
V
k
). (13)
If such a node does not exist (all candidate nodes
are already children), then we choose the node
with a minimum number of parents in order to
have more compact representation. The condi-
tional possibility distribution µ(Z
k
| U
Z
k
) associ-
ated to the node Z
k
is defined as follows:
∀z
kl
∈ D
Z
k
, ∀u
Z
k
∈ D
Par(Z
k
)
,
µ(z
kl
| u
Z
k
) = min[µ(z
kl
| u
Z
k
), µ
k
(u
V
k
)]. (14)
• For each node Z
j
different from the selected node
Z
k
will be associated a total ignorance possibility
distribution, namely:
∀z
jl
∈ D
Z
j
, µ(z
jl
) = 1. (15)
The construction of preference-based possibilistic
network ΠP
min
can be summarized by Algorithm 3.
The proposed algorithm generates the qualitative
min-based possibilistic network ΠP
min
= (G
P
, µ) step
by step. Indeed, for each utility node, the algorithm
selects the candidate parents that can be a child of the
remaining parents in the DAG G
P
under construction.
These candidate nodes appear in the last rank of the
topological ordering generated by the ID. Among the
candidates, if there exists a node that has not yet been
introduced in G
P
or it presents a root node, so it will
be selected as the child of the remaining parent vari-
ables in the DAG G
P
under construction. Otherwise,
if such node does not exist then it means that all candi-
date nodes are already integrated in the DAG G
P
and
Data: {V
1
, Par(V
1
)}, ..., {V
q
, Par(V
q
)}, utility nodes
and their parents in the qualitative influence
diagram.
Result: ΠP
min
= (G
P
, µ), preference-based
possibilistic network.
begin
Z ←
/
0. /* Set of integrated variables in G
P
*/
Child ←
/
0.
foreach V
k
∈ {V
1
, ...,V
q
} do
List − order(V
k
) ← {Par(V
k
)} ordered in
the same way that the order induced by
ΠID
min
.
Candidate(V
k
) ← { the variables with the
last rank in the List − order(V
k
)}.
Select a variable Z
k
∈ Candidate(V
k
) and
Z
k
6∈ Child.
if Z
k
exists then
Child ← Child ∪ {Z
k
}./*Z
k
presents
child in G
P
*/
Create nodes Par(V
k
) 6∈ Z./*creating
nodes that not appear in G
P
*/
Create arcs from {Par(V
k
) − Z
k
} to
Z
k
./*creating arcs from the remaining
parent variables to the selected node
Z
k
*/
Quantifying chance node Z
k
using
Equation 13
else
Select a variable Z
k
∈ Candidate(V
k
)
and |Par(Z
k
)| in G
P
is the smallest.
Create nodes Par(V
k
) 6∈ Z.
Create arcs from {Par(V
k
) − Z
k
} to Z
k
.
Quantifying chance node Z
k
using
Equation 14
end
foreach Z
j
∈ Par(V
k
) and Z
j
6= Z
k
do
if Z
j
6∈ Child then
Quantifying chance node Z
j
using
Equation 15
end
end
end
end
Algorithm 3: Preference-based possibilistic network.
On the Decomposition of Min-based Possibilistic Influence Diagrams
125

they have parents (they present child). According to
the selected node status (not integrated, root or child)
an utility will be associated to this node. A total igno-
rance possibility distribution will be associated with
the remaining parent variables.
It is evident that the last solution which operates
on the initial ID structure (which does not require the
reduction of utility nodes to a single utility one) al-
lows a compact representation of the qualitative util-
ity.
It should be noted that in the case of an ID with
multiple utility nodes having no common parents,
the preference-based qualitative possibilistic network
will in fact be disconnected. Indeed, each component
of the graph encodes local satisfaction degrees asso-
ciated to one utility node.
The following proposition shows that the qualitative
possibilistic network ΠP
min
= (G
P
, µ), built follow-
ing the previous steps, encodes the same qualitative
utility encoded by the qualitative Influence Diagram
ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
).
Proposition 3. Let ΠID
min
(G
ID
, π
ID
min
, µ
ID
min
) be a min-
based PID. Let ΠP
min
= (G
P
, µ) be a preferences-
based possibilistic network obtained using Algorithm
3. The joint qualitative utility µ
P
induced by ΠP
min
is
equal to the one induced by ΠID
min
. Namely,
µ
P
(Z
1
, ..., Z
m
) = µ
ID
min
(X
1
, ..., X
n
, D
1
, ..., D
p
). (16)
4 RELATED WORKS
In possibilistic framework, few works exist on deci-
sion making. A possibilistic adaptation of the well
known ID has been proposed in (Garcia and Sab-
badin, 2006) (Guezguez et al., 2009) (Zhang, 2013),
etc. Both knowledge and utilities are described in
a same graphical structure using ordinal data. Like
the probabilistic ID, the PID
s
contain three types of
nodes: chance, decision and utility nodes. Uncer-
tainty is described by means of possibility distribu-
tions on chance nodes and preferences are expressed
as satisfaction degrees on utility nodes. To compute
optimal decisions, two methods have been proposed
in literature for evaluating qualitative PID: direct and
an indirect once. A direct method uses initial struc-
tures but require additional computations in order to
update possibility distribution tables (Garcia and Sab-
badin, 2006). Also, in (Garcia and Sabbadin, 2006),
an indirect method has been proposed which consists
to transform a PID into a decision tree. Recently, in
(Guezguez et al., 2009) a new indirect method has
been proposed to evaluate PID based on the transfor-
mation of this latter into qualitative possibilistic net-
work. It should be noted that the proposed solution
reduces utility nodes in a single one. On this new
structure the inference process will be made.
Recently in (Benferhat et al., 2013), authors have
proposed a new possibilistic graphical model for han-
dling decision problems under uncertainty. The pro-
posed solution for representing decision making un-
der uncertainty is based on the use of min-based pos-
sibilistic networks. It suggested to encode agent’s
knowledge and preferences by two distinct qualitative
possibilistic networks. The first one encodes a joint
possibility distribution representing available knowl-
edge and the second one encodes the qualitative util-
ity. This new representation is in agreement with the
semantic definition of a qualitative decision problem
given in (Dubois et al., 1999). This new represen-
tation for decision making under uncertainty based
on min-based possibilistic networks, benefits from the
simplicity of possibilistic networks. Indeed, the com-
putation of optimal decision is performed using infer-
ence process in a unified way. Unlike the solution pro-
posed in (Guezguez et al., 2009) for computing opti-
mal decisions, the decomposition process allows us to
obtain more compact representation. In fact, the pos-
sibilistic network issued from the fusion phase (Ben-
ferhat et al., 2013) is based on more compact repre-
sentation of the qualitative utility.
5 CONCLUSIONS
This paper concerns the decomposition of a Possi-
bilistic Influence Diagram into two possibilistic net-
works: the first expresses agent’s knowledge and the
second encodes its preferences. This procedure al-
lows a simple representation of decision problems un-
der uncertainty. Indeed, the decomposition process
described in this paper offers a natural way to express
knowledge and preferences of a agent separately in
unified way using only one type of nodes. And in
order to perform the decomposition process, an algo-
rithm has been proposed and has confirmed that the
new model based on the possibilistic networks (Ben-
ferhat et al., 2013) for representing decision making
has the capacity to encode any decision problem. The
proposed algorithm ensures a more compact represen-
tation of the graph used in evaluation phase for com-
puting optimal decisions.
As future work, we plan to extend the proposed
graphical model for the representation of decision
problems to deal with more complex problems involv-
ing sequential decisions. Indeed, one of the attractive
benefits of Possibilistic Influence Diagrams consists
on their ability of dealing sequential decisions.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
126

ACKNOWLEDGEMENTS
This work has received supports from the french
Agence Nationale de la Recherche, ASPIQ project
reference ANR-12-BS02-0003. This work has also
received support from the european project H2020
Marie Sklodowska-Curie Actions (MSCA) research
and Innovation Staff Exchange (RISE): AniAge
(High Dimensional Heterogeneous Data based An-
imation Techniques for Southeast Asian Intangible
Cultural Heritage Digital Content), project number
691215.
REFERENCES
Ajroud, A., Omri, M., Youssef, H., and Benferhat, S.
(2012). Loopy belief propagation in bayesian net-
works : origin and possibilistic perspectives. CoRR,
abs/1206.0976.
Amor, N. B., Benferhat, S., Dubois, D., Mellouli, K., and
Prade, H. (2002). A theoretical framework for pos-
sibilistic independence in a weakly ordered setting.
International Journal of Uncertainty, Fuzziness and
Knowledge-Based Systems, 10(2):117–155.
Amor, N. B., Benferhat, S., and Mellouli, K. (2003). Any-
time propagation algorithm for min-based possibilis-
tic graphs. Soft Comput., 8(2):150–161.
Anzilli, L. (2013). A possibilistic approach to invest-
ment decision making. International Journal of Un-
certainty, Fuzziness and Knowledge-Based Systems,
21(02):201–221.
Benferhat, S., Khellaf, F., and Zeddigha, I. (2013). A pos-
sibilistic graphical model for handling decision prob-
lems under uncertainty. In The 8th conference of the
European Society for Fuzzy Logic and Technology,
EUSFLAT, Milano, Italy.
Borgelt, C., Gebhardt, J., and Kruse, R. (1998). Inference
methods. In Handbook of Fuzzy Computation, chapter
F1.2. Institute of Physics Publishing, Bristol, United
Kingdom.
Bouchon-Meunier, B., Coletti, G., and Marsala, C. (2002).
Independence and possibilistic conditioning. Annals
of Mathematics and Artificial Intelligence, 35:107–
123.
Boutouhami, K. and Khellaf, F. (2015). An approximate
possibilistic graphical model for computing optimistic
qualitative decision. In In proceedings of the Interna-
tional Conference on Artificial Intelligence and Appli-
cations AIFU, Dubai UAE, pages 183–196.
de Campos, M. L. and Huete, F. J. (1999). Indepen-
dence concepts in possibility theory. Fuzzy Sets Syst.,
103:487–505.
Denardo, E., Feinberg, E., and Rothblum, U. (2012). Split-
ting in a finite markov decision problem. SIGMET-
RICS Performance Evaluation Review, 39(4):38.
Dubois, D., Berre, D. L., Prade, H., and Sabbadin, R.
(1998). Logical representation and computation of op-
timal decisions in a qualitative setting. In AAAI-98,
pages 588–593.
Dubois, D., Fargier, H., and Prade, H. (2013). Decision-
making under ordinal preferences and comparative
uncertainty. CoRR, abs/1302.1537.
Dubois, D., Godo, L., Prade, H., and Zapico, A. (1999).
On the possibilistic decision model: from decision un-
der uncertainty to case-based decision. International
Journal of Uncertainty, Fuzziness and Knowledge-
Based Systems, 7(6):631–670.
Dubois, D. and Prade, H. (1988). Possibility Theory: An
Approach to Computerized Processing of Uncertainty
. Plenum Press, New York.
Dubois, D. and Prade, H. (1995). Possibility theory as a
basis for qualitative decision theory. In Proceedings
of the 14th international joint conference on Artificial
intelligence - Volume 2, pages 1924–1930, San Fran-
cisco, CA, USA. Morgan Kaufmann Publishers Inc.
Dubois, D., Prade, H., and Sabbadin, R. (2001). Decision-
theoretic foundations of qualitative possibility the-
ory . European Journal of Operational Research,
128(3):459–478.
Garcia, L. and Sabbadin, R. (2006). Possibilistic influence
diagrams. In 17th European Conference on Artifi-
cial Intelligence (ECAI’06), pages 372–376, Riva del
Garda, Italy. IOS Press.
Giang, P. and Shenoy, P. (2005). Two axiomatic approaches
to decision making using possibility theory. European
Journal of Operational Research, 162(2):450–467.
Guezguez, W. (2012). Possibilistic Decision Theory:
From Theoretical Foundations to Influence Diagrams
Methodology. Phd thesis, Paul Sabatier University,
France.
Guezguez, W., Amor, N. B., and Mellouli, K. (2009). Qual-
itative possibilistic influence diagrams based on qual-
itative possibilistic utilities. European Journal of Op-
erational Research, 195(1):223–238.
Howard, R. and Matheson, J. (1984). Influence Diagrams.
In Readings on the Principles and Applications of De-
cision Analysis, pages 721–762. Strategic Decisions
Group.
Huang, C. and Darwiche, A. (1996). Inference in belief net-
works: A procedural guide. Int. J. Approx. Reasoning,
15(3):225–263.
Lauritzen, S. and Nilsson, D. (2001). Representing and
solving decision problems with limited information.
Manage. Sci., 47(9):1235–1251.
Shenoy, P. (1994). A comparison of graphical techniques
for decision analysis. European Journal of Opera-
tional Research, 78:1–21.
Sniedovich, M. (2010). Dynamic Programming: Founda-
tions and Principles; 2nd ed. Pure and Applied Math-
ematics. CRC Press, Hoboken.
Tatman, J. and Shachter, R. (1990). Dynamic programming
and influence diagrams. IEEE Transactions on Sys-
tems, Man and Cybernetics, 20(2):365–379.
Whalen, T. (1984). Decision making under uncertainty
with various assumptions about available informa-
tion. IEEE Trans. on systems, Man and Cybernetics,
(14):888–900.
On the Decomposition of Min-based Possibilistic Influence Diagrams
127

Zadeh, L. (1978). Fuzzy sets as a basis for a theory of pos-
sibility. Fuzzy Sets and Systems, 1:3–28.
Zhang, N. (1998). Probabilistic inference in influence di-
agrams. In Computational Intelligence, pages 514–
522.
Zhang, N. (2013). Probabilistic inference in influence dia-
grams. CoRR, abs/1301.7416.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
128
