Predicting Glaucomatous Progression with Piecewise Regression Model

from Heterogeneous Medical Data

Kyosuke Tomoda

, Kai Morino

, Hiroshi Murata

, Ryo Asaoka

and Kenji Yamanishi

Graduate School of Information Science and Technology, The University of Tokyo, Tokyo 133–8656, Japan

Graduate School of Medicine, The University of Tokyo, Tokyo 133–8655, Japan

Keywords:

Glaucoma, Intraocular Pressure, Heterogeneity, Collective Method, Piecewise Linear Regression Model.

Abstract:

This study aims to accurately predict glaucomatous visual-ﬁeld loss from patient disease data. In general, med-

ical data show two kinds of heterogeneity: 1) internal heterogeneity, in which the phase of disease progression

changes in an individual patient’s time series dataset; and 2) external heterogeneity, in which the trends of

disease progression differ among patients. Although some previous methods have addressed the external

heterogeneity, the internal heterogeneity has never been taken into account in predictions of glaucomatous

progression. Here, we developed a novel framework for dealing with the two kinds of heterogeneity to pre-

dict glaucomatous progression using a piecewise linear regression (PLR) model. We empirically demonstrate

that our method signiﬁcantly improves the accuracy of predicting visual-ﬁeld loss compared with existing

methods, and can successfully treat the two kinds of heterogeneity often observed in medical data.

1 INTRODUCTION

1.1 Motivation of our Study

The aim of our study is to construct a novel method

for the treatment of heterogeneous medical data in the

prediction of disease progression. We speciﬁcally fo-

cus on data from patients with glaucoma to predict

visual-ﬁeld loss progression. Medical datasets are

heterogeneous from the following two aspects: exter-

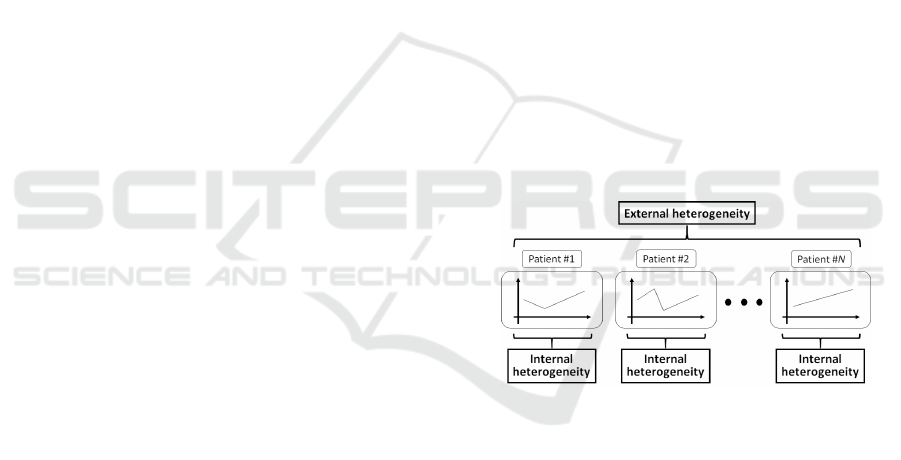
nal heterogeneity and internal heterogeneity (Fig. 1).

External heterogeneity generally refers to the rela-

tionship of measured data among patients; e.g., the

rates of the disease progression differ from patient

to patient. By contrast, internal heterogeneity occurs

within an individual patient; e.g., changes in the phase

of disease progression over time. Therefore, in order

to obtain comprehensive knowledge and trends from

medical data, a method for appropriately dealing with

the characteristic heterogeneity is required.

It is not straightforward to treat heterogeneous

medical data because these two kinds of heterogene-

ity must be resolved in different ways. The main

challenge in this respect is due to the speciﬁc struc-

ture of large medical datasets. Although the datasets

are often composed of data from a large number of

patients, data for each patient are usually limited be-

Figure 1: The two kinds of heterogeneity observed in medi-

cal datasets. External heterogeneity is caused by differences

among patients, whereas internal heterogeneity is caused by

changes in each patient’s state over time.

cause of the high costs related to diagnosis, both for

the patients and clinicians. In particular, a detailed

medical examination requires well-trained clinicians,

special medical equipment, and a long period of diag-

nosis. In this paper, we refer to this speciﬁc structure

of medical data as medical-data-structure-difﬁculty.

This difﬁculty limits the ability to construct a reliable

predictive model for each patient using only the pa-

tient’s information. One way to solve this problem

is to take advantage of hidden relationships among

patients. However, mining for such hidden relation-

ships is often difﬁcult because of the heterogeneous

nature of medical data described above. Therefore,

accurate analysis of medical data requires a method

for overcoming the two heterogeneity problems and

Tomoda, K., Morino, K., Murata, H., Asaoka, R. and Yamanishi, K.

Predicting Glaucomatous Progression with Piecewise Regression Model from Heterogeneous Medical Data.

DOI: 10.5220/0005703900930104

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 5: HEALTHINF, pages 93-104

ISBN: 978-989-758-170-0

the medical-data-structure-difﬁculty simultaneously.

Various methods have been proposed to over-

come the medical-data-structure-difﬁculty in a med-

ical dataset, which have mostly involved incorporat-

ing information from other patients to improve the

prediction accuracy (Liang, Z. et al., 2013; Maya,

S. et al., 2014; Murata, H. et al., 2014; Morino, K.

et al., 2015). Therefore, appropriate information is

collected from a patient dataset and a tuned predic-

tor is constructed for the target patient. We here refer

to these types of methods as “collective methods.” In

collective methods, we should carefully analyze the

heterogeneity to collect data appropriately. Most of

the existing collective methods for dealing with data

from glaucoma patients have focused on resolving the

external heterogeneity problem. We here propose a

new collective method that achieves the better pre-

diction accuracy than existing methods, because our

method can cope with both the external and internal

heterogeneity in the medical dataset.

Glaucoma data, the focus of our study, criti-

cally contain both kinds of heterogeneity as well

as the medical-data-structure-difﬁculty mentioned

above. Glaucoma is an eye disease that causes pro-

gressive damage to a patient’s visual ﬁeld, which can

ultimately lead to blindness, and is the second-leading

cause of blindness worldwide (Kingman, S., 2004).

Quigley et al. (Quigley, H. A. and Broman, A. T.,

2006) estimated that nearly 80 million people will

suffer from glaucoma by 2020. The glaucomatous

visual-ﬁeld loss is considered to be irreversible, but

glaucomatous progression can be delayed with appro-

priate treatment. Therefore, suggesting an appropriate

treatment plan at an early stage of disease progres-

sion is a critical factor for improving patients’ quality

of life. Accordingly, the development of methods for

the early prediction of glaucoma progression is par-

ticularly important for effectively treating the disease.

Most of the existing glaucoma prediction meth-

ods involve analyses of visual-ﬁeld data, which are

associated with the aforementioned medical-data-

structure-difﬁculty and external heterogeneity prob-

lem. However, in reality, the rate of glaucomatous

progression changes over time for each eye (inter-

nal heterogeneity). Therefore, to improve prediction,

a novel collective method is required to deal with

the internal heterogeneity of data (within-eye level)

in addition to the external heterogeneity (between-

eye level). The internal heterogeneity can be poten-

tially captured with intraocular pressure (IOP) data.

This is based on clinical evidence that the progres-

sion rate of glaucoma increases with an increase in

the IOP value (AGIS Investigators, 2010; Collabora-

tive Normal-Tension Glaucoma Study Group, 1998;

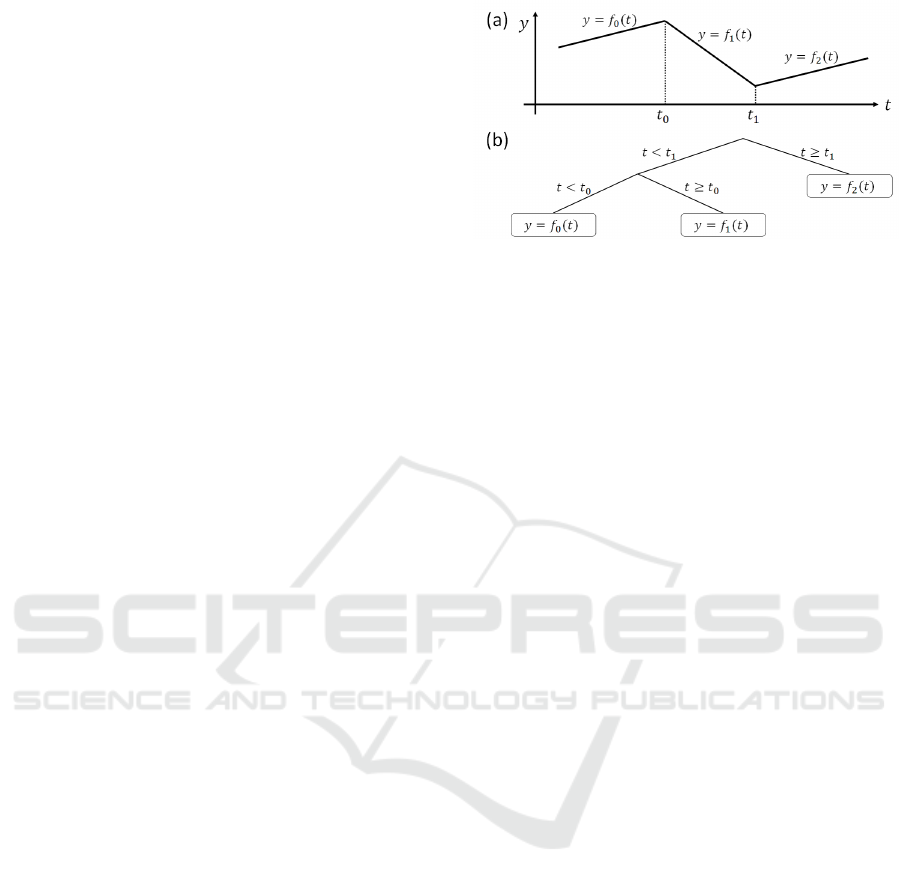
Figure 2: Schematic ﬁgure of the piecewise linear regres-

sion model. (a) The piecewise linear regression. (b) The

tree structure expression corresponding to the piecewise lin-

ear regression lines shown in (a).

Satilmis, M. et al., 2003). However, previous col-

lective models for predicting glaucomatous progres-

sion (Liang, Z. et al., 2013; Maya, S. et al., 2014;

Murata, H. et al., 2014) have been trained only with

visual-ﬁeld data. In this paper, we outline the ﬁrst ap-

plication of IOP data to the prediction of glaucoma

progression and achieve good prediction accuracy.

1.2 Heterogeneity of Glaucoma Data

Here, we introduce the heterogeneity of glaucoma.

Internal Heterogeneity: The progression rate

of glaucoma essentially changes over several time

points, even when considering the time series of

one eye. Clinical knowledge suggests that the pro-

gression rate of glaucoma varies because of high

IOP values (AGIS Investigators, 2010; Collabora-

tive Normal-Tension Glaucoma Study Group, 1998;

Satilmis, M. et al., 2003). This internal heterogeneity

can be difﬁcult to detect because only limited data can

be obtained from the target eye at certain time points.

Our proposed novel collective method resolves this

internal heterogeneity difﬁculty by using IOP data.

External Heterogeneity: Glaucoma data are

highly variable among eyes from the following four

perspectives: (1) the disease stage at initial diagnosis;

(2) the progression rate of glaucoma; (3) the average

and ﬂuctuation levels of IOP; (4) the minimum level

of IOP that affects the progress of glaucoma.

1.3 Novelty and Signiﬁcance

The novelty and signiﬁcance are summarized below.

1) A Novel Framework for Solving the Het-

erogeneity Problems of Medical Data with a Col-

lective Method. We here propose a novel collec-

tive piecewise linear regression (PLR) model to si-

multaneously deal with the two kinds of heterogene-

ity of medical data and the medical-data-structure-

HEALTHINF 2016 - 9th International Conference on Health Informatics

difﬁculty. In general, a PLR model is suitable for

dealing with the internal heterogeneity problem of

medical data; however, it cannot be easily applied to

the problem of glaucoma progression prediction. A

PLR model (Fig. 2(a)) can be interpreted as a tree-

structured model (Fig. 2(b)); i.e., the edges carry

information about the segmentation, and the nodes

carry information about the regression lines. This

model is powerful because it can reﬂect the complex

features of medical data by breaking it down into sev-

eral pieces. However, this beneﬁt comes with a disad-

vantage in that piecewise regression requires a large

dataset for good prediction even if the complexity of

the model or the depth of the tree structure is ap-

propriately controlled. Therefore, the medical-data-

structure-difﬁcultyis a barrier to effectivelyanalyzing

the data with existing PLR methods. Our proposed

method overcomes the problems of medical data.

A) Application of a Collective PLR Model with

Medical-data-structure-difﬁculty. Our proposed

method can be used to train a PLR model with hetero-

geneous medical data. As described above, only lim-

ited data can be obtained for each patient from a large

medical dataset owing to the medical-data-structure-

difﬁculty. Although effective training algorithms for

a tree-structured model with a very large dataset have

been intensively investigated (Natarajan, R. and Ped-

nault, E., 2002; Vogel, D. S. et al., 2007), there have

been few studies conducted to develop a training al-

gorithm for this type of “big data.” Therefore, our

current study sheds new light on this common prob-

lem and offers a potential solution.

B) A Useful Framework for the Overall Optimiza-

tion of a Piecewise Regression Model Consider-

ing External Heterogeneity. Our novel method opti-

mizes the piecewise model as well as each regression

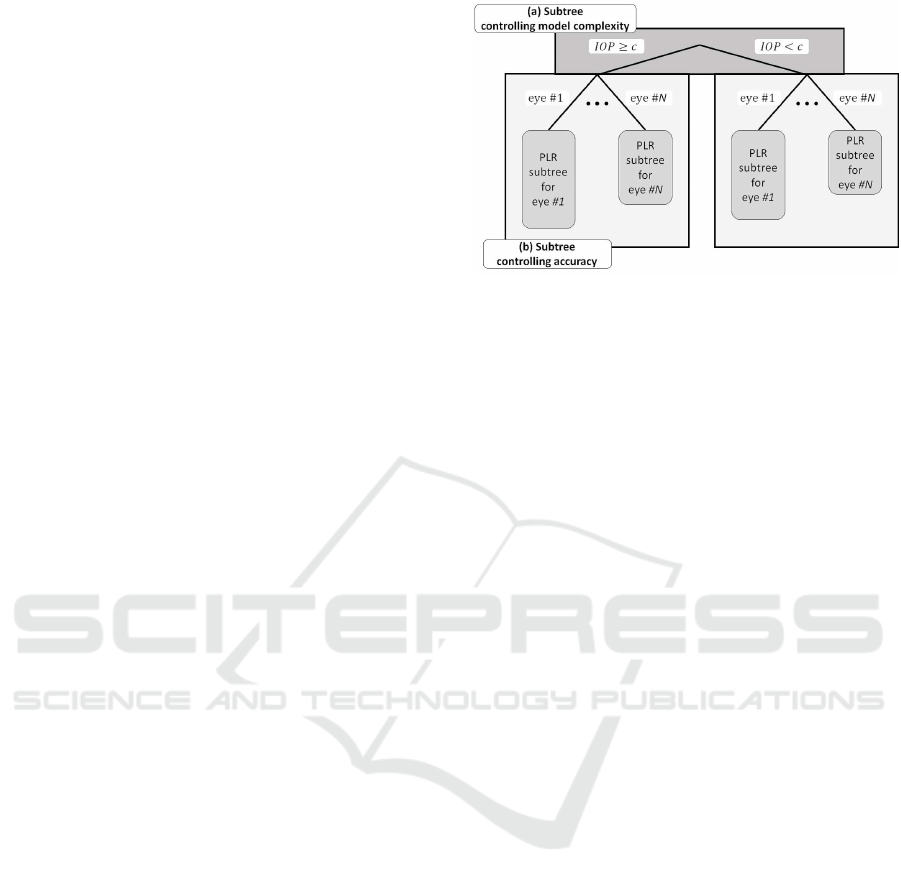
line for each piece simultaneously. Our model (Fig. 3)

consists of two parts: one that controls the model’s

complexity, and the other that controls the model’s

prediction accuracy. This clearly divided model struc-

ture enables the use of other collective regression al-

gorithms besides those employed in this paper (Liang,

Z. et al., 2013). We describe this feature in greater

detail in Sec. 3.2. We optimized the whole model, in-

cluding the segmentation and regression parameters,

using data from similar eyes. We did this optimiza-

tion by applying the statistical model selection crite-

ria. Speciﬁcally, we examined a number of existing

information criteria to investigate which gave the best

prediction accuracy.

C) Good Framework of the Collective Piecewise

Regression for Tackling Internal Heterogeneity.

For the collective piecewise regression, our proposed

method provides a good framework that can effec-

Figure 3: Hierarchical tree structure of our IOP-based

piecewise model. The structure of the model can be sep-

arated into two parts (a) controlling the model complexity

and (b) controlling the model accuracy. The PLR model for

each eye also has its tree structure as shown in Fig. 2(b).

tively deal with internal heterogeneity. Our model

was carefully designed to collect data of similar eyes

while coping with the internal heterogeneity related to

disease progression over time. Our method involves

segmentation of time-series data, even within one pa-

tient’s time course, followed by calculation of the re-

gression lines for each piece. We assume that the gra-

dient parameters for each piece in the same state are

common and that the intercept parameters for each

piece are different, so that the internal heterogeneity

can be accurately expressed (see Step 4 in Fig. 5). We

note that our model does not have only common gra-

dient parameters but individualized intercept parame-

ters to reﬂect each patient’s characteristics. This in-

dividualization cannot be realized by simply sharing

the parameters with all the patients. Hence, our model

can represent each patient’s glaucoma progression ef-

ﬁciently.

2) Big Impact on the Medical Field of Glau-

coma

A) First Application of IOP to the Prediction of

Glaucoma Progression. To the best of our knowl-

edge, our proposed model represents the ﬁrst appli-

cation of IOP to the prediction of glaucoma progres-

sion. In existing analyses (Liang, Z. et al., 2013;

Maya, S. et al., 2014; Murata, H. et al., 2014; Maya,

S. et al., 2015; Holmin, C. and Krakau, C. E. T.,

1982; Zhu, H. et al., 2014), only visual-ﬁeld data

have been used for prediction. Although clinical stud-

ies suggest the importance of IOP to understand dis-

ease progression (AGIS Investigators, 2010; Collabo-

rative Normal-Tension Glaucoma Study Group, 1998;

Satilmis, M. et al., 2003), the high external hetero-

geneity of IOP has limited its application to predictive

models (see Sec. 1.2). We believe that this difﬁculty

can be overcome with our novel collective method,

which is expected to have a great impact on the med-

Predicting Glaucomatous Progression with Piecewise Regression Model from Heterogeneous Medical Data

ical ﬁeld of glaucoma.

B) Wide Applicability to other Glaucomatous Pre-

diction Models based on Visual-ﬁeld Data. Any ex-

isting glaucoma prediction method can be converted

into an IOP-based piecewise prediction model using

our framework, which should increase its impact in

the medical ﬁeld of glaucoma. As mentioned in point

1-B), our model was developedusing a general frame-

work. Therefore, our model is not only applicable to

various existing glaucoma prediction models but also

to models that will be developed in the future. This

wide applicability is practically important for the fu-

ture progress of glaucoma prediction, since any great

prediction model will lose its value after an improved

method is proposed. Owing to its clearly segmentable

structure, our model will be able to embrace other

models, indicating that it has a long life span, and is

ﬂexible and widely applicable.

1.4 Related Works

Conventionally, linear regression analyses of visual-

ﬁeld time-series data for each eye have been used

to predict the glaucomatous progression (Holmin, C.

and Krakau, C. E. T., 1982). However, simple lin-

ear regression for time series of an individual eye is

not effective when the number of data points is small,

which is often the case for clinical data. Although var-

ious regression models have been applied to the pre-

diction with only data from a target eye, the prediction

accuracy was limited due to the shortage of data (Fu-

jino Y. et al., 2015; Taketani Y. et al., 2015). Thus, we

must overcome this shortage for better prediction.

To make up for this deﬁciency in clinical data,

some recent studies have proposed collective meth-

ods that exploit visual-ﬁeld data from other eyes to

predict the glaucomatous progression in a target eye

at an early stage of disease. These studies also pro-

posed some methods for coping with the external het-

erogeneity and medical-data-structure-difﬁculty from

a data-mining point of view. Liang et al. (Liang, Z.

et al., 2013) proposed a spatio-temporal clustering-

based method. They collected similar eyes in terms

of their spatial and temporal feature of progression.

Then, they used data from the eyes similar to the tar-

get eye for prediction. Zhu et al. (Zhu, H. et al., 2014)

used Bayesian inference to reﬂect the spatial correla-

tion of progression. Maya et al. (Maya, S. et al., 2014)

used tensor decomposition and a multitask-learning

method to extract multiple features from a heteroge-

neous glaucoma dataset. Murata et al. (Murata, H.

et al., 2014) used Bayesian linear regression to utilize

the measurements of other eyes when making predic-

tions of a target eye. Maya et al. (Maya, S. et al.,

Figure 4: Schematic ﬁgure of the glaucomatous pro-

gression. The total deviation (TD) values on a vi-

sual ﬁeld are schematically shown in shades of gray.

Darker mesh shades indicate a more defective visual

ﬁeld. The overall aim was to predict TD values at

each mesh at a given target time. 2015) proposed

a hierarchical minimum description length (MDL)-

based clustering method for ﬁnding progression pat-

terns, and substituted the clusters used in Liang et

al. (Liang, Z. et al., 2013) with their newly discovered

clusters to more effectivelypredict glaucomatous pro-

gression. However, all of these studies focused on ex-

ternal heterogeneity and did not address the problem

of internal heterogeneity.

To overcome the internal heterogeneity problem,

we employed a PLR model for predicting glaucoma-

tous progression. As we mentioned above, a PLR

model potentially deals with the internal heterogene-

ity problem. However, it is widely known that sufﬁ-

cient data within an appropriate range are required in

order to appropriately estimate each regression line.

Therefore, a large dataset should be used in the learn-

ing phase, which can sometimes cause problems in

applying this model to real situations. Although sev-

eral studies have focused on training models for a tree

structure with a massive dataset (Natarajan, R. and

Pednault, E., 2002; Vogel, D. S. et al., 2007), there is

barely any information on training a PLR model un-

der a situation of medical-data-structure-difﬁculty.

1.5 Organization

The rest of this paper is organized as follows. In Sec-

tion 2, we introduce some prior knowledge for under-

standing glaucomatous progression. In Section 3, we

present our proposed framework for training a collec-

tive PLR model for tackling the internal and external

heterogeneity. The results of experiments conducted

to evaluate our framework with glaucoma dataset are

described in Section 4. Finally, we provide an overall

conclusion and summary of our method in Section 5.

2 PRELIMINARIES

2.1 Prediction of Glaucoma

Our aim was to predict the visual-ﬁeld loss precisely

at a given target time, as depicted in Fig. 4. In our

dataset, the visual-ﬁeld data were measured on 74

meshes of a visual ﬁeld to obtain a total deviation

(TD) value. This value represents the differences in

the measured light sensitivity on each mesh compared

to age-matched normative data. A negative TD value

HEALTHINF 2016 - 9th International Conference on Health Informatics

Figure 4: Schematic ﬁgure of the glaucomatous progres-

sion. The total deviation (TD) values on a visual ﬁeld are

schematically shown in shades of gray. Darker mesh shades

indicate a more defective visual ﬁeld. The overall aim was

to predict TD values at each mesh at a given target time.

means that the sensitivity is worse than the normative

sensitivity; thus, the TD value decreases as glaucoma

progresses. The rates of progression differ among

the meshes on a visual ﬁeld; therefore, the TD value

needs to be predicted independently for each mesh.

2.2 Effect of High IOP

Several ophthalmological studies have shown a re-

lationship between IOP and glaucoma progression.

The AGIS Investigators (AGIS Investigators, 2010)

found that a group of patients with glaucomatous

eyes and high IOP lost their visual ﬁelds more

quickly than patients with lower IOP. The Collabo-

rative Normal-Tension Glaucoma Study Group (Col-

laborative Normal-Tension Glaucoma Study Group,

1998) observed that the rate of glaucoma progression

in the eyes of patients undergoing treatment, which

involves reduction in IOP, was signiﬁcantly lower

than that of patients not receiving treatment for IOP

reduction. Satilmis et al. (Satilmis, M. et al., 2003)

demonstrated that the rate of glaucoma progression

was related to the standard deviation in IOP.

Considering these results, the rates of the progres-

sion greatly change at some time points that can be

detected with IOP values. This means that the internal

heterogeneity in the glaucoma dataset can be captured

with IOP. However, the relationship between IOP and

the degree of glaucoma progression has not yet been

fully investigated in ophthalmology. Hence, we do

not employ the raw value of IOP as an explanatory

variable but rather discretize it into “high” and “low”

states to make segmentations of time series according

to whether the undelying IOP is high or low. Further,

the discretization of IOP into the ”two” states makes it

effcient to estimate the parameters of the model. This

is because the more states we separate IOP into, the

smaller the size of each piece becomes.

3 PROPOSED METHOD

3.1 Concept of Proposed Method

Our method makes it possible to decide the appropri-

ate thresholds for separating time series and express

the internally heterogeneous progress of glaucoma.

We optimize the thresholds using an information cri-

terion and estimate gradient and intercept parameters

for each of the separated piece. The outline of our

method is described below. Figure 5 helps to under-

stand its procedure. We note that the following proce-

dure was applied to one prediction-target eye.

Step 1: Normalization for the External Hetero-

geneity of IOP. The mean and standard deviation of

the IOP distribution are highly variable among eyes.

Therefore, the IOP distribution of each eye was nor-

malized to effectively analyze the external hetero-

geneity of IOP.

Step 2: Selection of an IOP Threshold Value c. An

IOP threshold value c is selected to construct the PLR

model from a possible list of IOP threshold values.

We note that a threshold value that has in the previous

iterations is not selected again for model construction.

Step 3: Division of the Visual-ﬁeld Time Series into

Pieces. The state of an eye (high- or low-IOP state)

is decided using the given IOP threshold c. At each

time point when visual-ﬁeld data are recorded, if the

standardized IOP score is larger than the given c, the

IOP state at that time point is determined to be in a

high-IOP state (see Sec. 3.4). The time series is then

divided into pieces when the state changes. This pro-

cedure reﬂects actual clinical knowledge based on the

internal heterogeneity of glaucoma progression.

Step 4: Construction of PLR Models using Our

Collective Method. A PLR model was constructed

using our proposed collective method with the di-

vided pieces. First, a set of similar eyes E was se-

lected to estimate the parameters of the PLR mod-

els. In this case, the training dataset consisted of

|E| eyes that showed similar behavior to the target

eye. In this study, we employed an existing clustering

method (Liang, Z. et al., 2013) to collect data from

similar eyes. However, another collective method

could be used for the same process. Next, we trained

the PLR model only using the eye set E. For each

piece, we ﬁt a linear function of time; i.e., we esti-

mate the gradient and intercept parameters. We ap-

plied the same gradient parameters to pieces in the

same IOP state. On the other hand, the intercept pa-

rameters were individually determined for each piece.

This proper estimation of the gradient and intercept

parameters is the key for effectively constructing a

PLR model (see Sec. 3.5).

Predicting Glaucomatous Progression with Piecewise Regression Model from Heterogeneous Medical Data

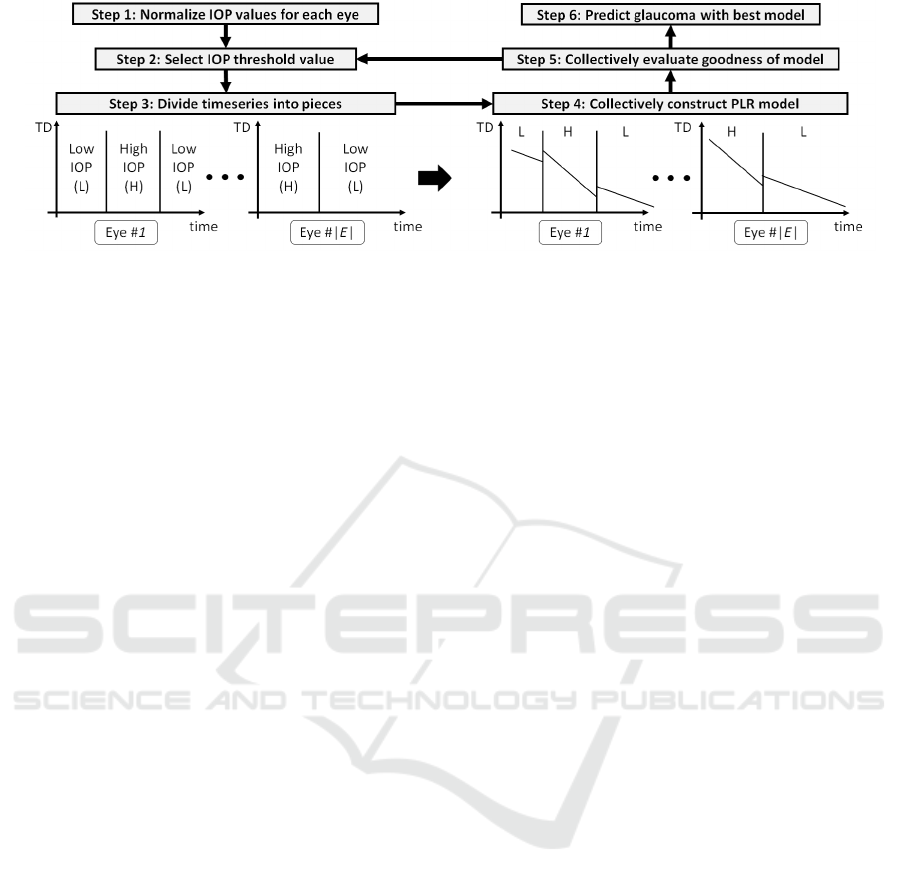
Figure 5: Flow of our algorithm. First, we calculate the standard scores of IOP in Step 1. Then, we iteratively obtain one PLR

model by changing IOP threshold values c in Steps 2-5. Finally, we determine the best PLR model based on an information

criterion and predict the glaucoma progression in Step 6. We note that the gradients corresponding to the same IOP state are

the same for all the eyes belonging to the eye set E composed of eyes similar to the target eye.

Step 5: Evaluation of the Generated PLR Models.

Different PLR models were generated when a differ-

ent threshold c was chosen. Therefore, the best c is

required to obtain the best PLR model. We evaluated

the quality of the generated PLR models on the basis

of statistical model selection criteria. If all possible

thresholds were already selected, the best PLR model

was chosen as the predictor of the target eye, which

was then applied to Step 6. Otherwise, Steps 2-5 were

repeated to construct a new PLR model.

Step 6: Prediction of progression with the best

PLR model. The visual-ﬁeld loss of the target eye

was predicted with the best PLR model incorporat-

ing both the external and internal heterogeneity of the

glaucoma dataset.

3.2 Shared and Unshared Parts of Our

Collective Method

Our collectivemethod is different from those that sim-

ply use data from other eyes for prediction of a tar-

get eye. The important difference is that we carefully

estimated the model parameters shared among other

eyes.

In the Model Selection Phase (Fig. 3 (a)): The ﬁt-

ness and simplicity of the model are evaluated from

the overall model. The threshold value for the stan-

dardized IOP is common to all similar eyes. This

value is decided by considering the whole model and

each of the predictors for each eye.

In the Estimation Phase (Fig. 3 (b)): The gradient

parameter is shared among each piece in the same

IOP state; therefore, this parameter is estimated using

the data from all similar eyes. Meanwhile, the inter-

cept parameters differ among each piece; therefore,

this parameter is estimated for each eye individually.

This modeling procedure allows for the internal het-

erogeneity of progression to be expressed precisely.

3.3 Problem Settings

Let N denote the number of observed eyes, t

i, j

the

time of the jth measurement of the ith eye, and n

the

number of measurements for the ith eye. We repre-

sent the vector of the TD values measured at t

i, j

= (y

(1)

i, j

,..., y

(K)

i, j

) ∈ R

, where K is the number of

meshes on a visual ﬁeld, and p

i, j

∈ R is the IOP value

at t

i, j

. We set T

:= (t

i,1

,...,t

i,n

), Y

:= (y

i,1

,..., y

i,n

and P

:= (p

i,1

,..., p

i,n

). The whole measured dataset

is represented as D := {(T

),...,(T

)}.

We predict the TD value at an arbitrary time point af-

ter the last measurement, given a dataset of N eyes

that includes measurement time, TD and IOP values.

3.4 Judging the IOP State

As mentioned in Sec. 2.2, the higher the IOP, the more

rapidly glaucoma progresses; therefore, the progres-

sion rate changes at certain time points depending on

ﬂuctuations in IOP. To model this internal heterogene-

ity, we propose an IOP-based PLR model. The two

IOP states are deﬁned as the high-IOP state (denoted

as H) and the low-IOP state (denoted as L).

However, IOP also shows external heterogeneity.

To overcome this problem, we focused on the tem-

poral differences within the IOP time series for each

eye. For the ith eye, we used a standardized score

˜p

i, j

= (p

i, j

− ¯p

)/σ

at t

i, j

calculated with the mean ¯p

and standard deviation σ

of IOP. Through this nor-

malization of the external heterogeneity of IOP, the

IOP data from other eyes can be treated in the same

manner. Let s

i, j

denote the IOP state of the ith eye at

time t

i, j

, then s

i, j

is deﬁned as

i, j

(

H, (if ˜p

i, j

≥ c),

L, (if ˜p

i, j

< c),

where c is the threshold constant. Figure 6(a) displays

HEALTHINF 2016 - 9th International Conference on Health Informatics

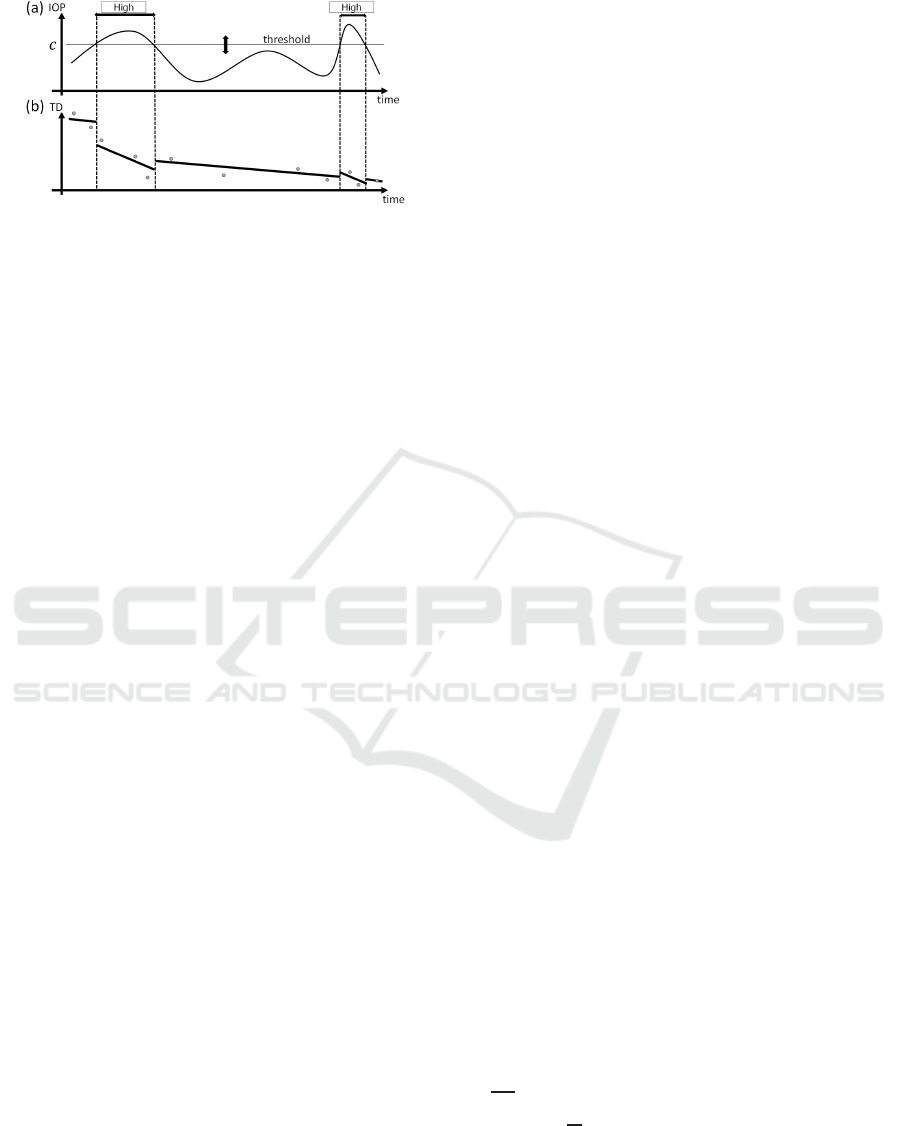
Figure 6: Concept of the proposed method. (a) The time-

series data were divided into intervals with high- or low-IOP

states using the threshold c. (b) The PLR model was trained

based on these intervals. The gradients of the lines within

the same IOP states were the same, and these regression

lines were allowed to be disconnected from the subsequent

lines. The dots on the graph represent the data points.

the classiﬁcation protocol. Here, we represent I

i,k

(k =

1,... , L

) as the set of indices in the interval where

the IOP state remains the same among the series of

IOP states s

= {s

i, j

}

j=1

, calculated as shown above.

We denote L

as the number of intervals for the ith

eye. We further assume that this threshold constant is

common between the target eye and similar eyes.

It is worth noting that the training data should not

be partitioned from the target eye data for the follow-

ing two reasons: ﬁrst, it is difﬁcult to estimate the cor-

rect IOP state, because of the very limited data from

the target eye with a small number of diagnoses; sec-

ond, if the data from the target eye are partitioned,

the number of visual-ﬁeld data points for the target

eye will be too small to construct the PLR model, be-

cause segmenting the data would further decrease the

amount of training data. Thus, we did not partition

the time series of the target eye, and assumed that it

was in a low-IOP state. This assumption is valid and

realistic, because the interval for the high-IOP state is

usually very short, and therefore the progression after

the ﬁnal measurement should be in the low-IOP state.

3.5 IOP-based Collective PLR Model

Once the visual-ﬁeld data for each eye are divided us-

ing the standardized IOP scores, a segmented time-

series dataset is obtained for each eye, or a tree struc-

ture, as shown in Fig. 3. For each high- and low-IOP

state, the proposed model represents a different rate

of progression, or the internal heterogeneity of pro-

gression. Fig. 6 (b) shows our PLR model as applied

to Liang et al.’s method (Liang, Z. et al., 2013).

Liang et al. (Liang, Z. et al., 2013) proposed a

spatio-temporal clustering-based linear-regression

model using data from other eyes. They assumed

the same glaucomatous progression within the

same cluster. Here, we show an application of our

developed PLR model to the temporal-shift linear

regression method (TSLR) using k-NN as a clustering

method (Liang, Z. et al., 2013) . They extracted the

feature vector of ith eye via singular value decompo-

sition of the matrix Y

to collect data from the eyes

similar to the target eye. They recognized the ﬁrst

left-singular vector of Y

as the spatial feature vector

of ith eye, and the k-nearest eyes in the spatial feature

vector space are collected as the similar-eyes cluster.

Let E ⊂ {1,...,N} denote the set of indices within a

cluster, and let w

i,k

and b

i,k

denote the gradient and

intercept of the kth piece of the regression line for

the ith eye, respectively. Then, the assumption above

can be formulated as ∀i, j ∈ E, ∀k,h s.t. s

i,k

= s

j,h

S, ∃w

, w

(l)

i,k

= w

(l)

j,h

= w

(l)

, where S ∈ {H,L}. As

stated above, the intercept parameters are not shared

among pieces in the same IOP state within all the eyes

in E, while the gradient parameter is shared. This

gap enables speciﬁcity for each piece and can reﬂect

the internal heterogeneity. Then, the optimal param-

eters

(l)

= (w

(l)

,σ

(l)

,{b

(l)

i,S,k

}) are calculated as

(l)

argmin

∑

i∈E

∑

k=1

∑

j∈I

i,k

(l)

i, j

−



(l)

i, j

+ b

(l)

i,S,k

o

where σ

(l)

is the standard deviation of the above

errors. Hereafter, we omit the mesh index l for sim-

plicity since each mesh is processed independently.

3.6 Evaluating the Generated Models

As shown above, several tree-structured PLR mod-

els could be obtained with respect to each threshold

value c. The easiest way to evaluate the models is

to select the one with the smallest residual sum of

squares (ERROR). However, this can result in over-

ﬁtting, because the ERROR becomes smaller as the

tree structure of the PLR models deepens and more

detailed data are trained. Therefore, we chose the

best model based on information criteria, consider-

ing a trade-off between simplicity and ﬁtness of a

model. Toward this end, the Akaike Information Cri-

terion (AIC) (Akaike, H., 1973), Bayesian Informa-

tion Criterion (BIC) (Schwarz, G., 1978), and Mini-

mum Description Length Criterion (MDL) (Rissanen,

J., 1986) are well-known information criteria.

The log-likelihood function for the TSLR is

calculated for each IOP state S as logL(φ

| D) =

−

2σ

∑

i∈E

∑

k=1

∑

j∈I

i,k



i, j

− (w

i, j

+ b

i,S,k

)



−

logσ

−

log(2π), where φ

:= (w

,σ

,{b

i,S,k

})

and n

denote the parameters and the number of data

points for the IOP state S, respectively. Therefore,

AIC, BIC, and MDL are calculated as follows:

Predicting Glaucomatous Progression with Piecewise Regression Model from Heterogeneous Medical Data

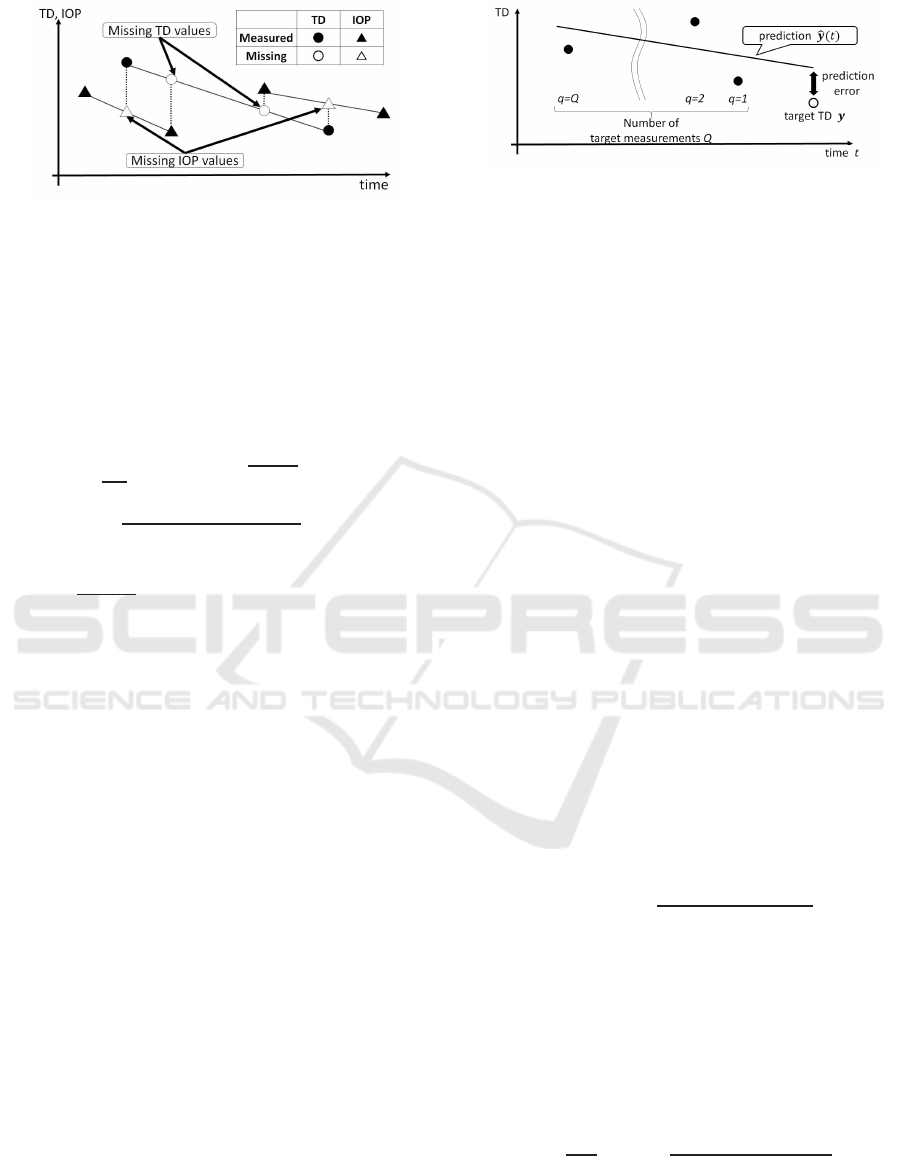
Figure 7: Interpolation of missing TD and IOP values.

AIC = −2logL(φ

| D) + 2

∑

i∈T

+ 2

BIC = −2logL(φ

| D) +

∑

i∈T

+ 2

log

∑

i∈T

MDL = −logL(φ

| D) +

∑

i∈T

+ 2

log

∑

i∈T

arcsinx+ x

1− x

V/U

where U =

p−

∑

i=1

)

/2, V is the vari-

ance of all time stamps in IOP state S, and

C = 2

∏

i=1



1/(b

) − 1/(a

)



∏

i=1

−

)/(P

+1), where (a

), (a

), and (a

) rep-

resent the upper and lower bounds of the gradient w

intercept b

, and standard deviation σ

, respectively.

We designate p as the squared sum of time stamps,

as the sum of time stamps in the ith interval, P

the number of pieces, and n

as the quantity of data in

ith interval. The best model and the best threshold are

determined by minimizing the sum of the criteria for

the high- and low-IOP states.

4 EXPERIMENTS

4.1 Data and Parameters

The dataset used in this paper was provided by the De-

partment of Ophthalmology,The University of Tokyo.

This dataset includes visual-ﬁeld data and IOP data

obtained from N = 939 glaucomatous eyes. The

visual-ﬁeld data (TD values) were measured with the

Humphrey Field Analyzer (Carl Zeiss Meditec AG,

Dublin, CA, USA), using the SITA-standard 30-2

method (K = 74), controlling for the effects of in-

creasing age on the degree of visual-ﬁeld loss. There-

fore, the TD value should decrease if glaucoma has

progressed. The TD values were within the range

Figure 8: Predicting the last measurement of a target eye.

We use Q data points from the target eye for training in

addition to data from other eyes.

[−37.0, 4.0] (median: -4, mean: -8.662, standard de-

viation: 10.56). The mean number of measurements

of TD and IOP for each patient was around 11 and 21,

respectively. The standardized-score threshold was

set within [0.1,3.0] (step: 0.1).

4.2 Data Interpolation

Our method requires both visual-ﬁeld data and IOP

data for each data point. However, most data points

only contain one or the other measure. To facilitate

the use of the dataset, we employed linear interpola-

tion to ﬁll in the missing data using the two neighbor-

ing measurements for the missing measurement, as

shown in Fig. 7. We used these preprocessed data in

all of the experiments, even when IOP values were not

required. The gap between the time stamp from the

last measurement in the training dataset and the target

dataset was within [28.9,889] (median: 227, mean:

258, standard deviation: 117) days.

4.3 Evaluation of Prediction Accuracy

We predict the TD value at the last measurement for

the target eye using the previous Q data points with

data from another N − 1 eyes, as depicted in Fig. 8.

We set Q = 1, . . . ,6. The prediction accuracy was

evaluated with the Root Mean Square Error (RMSE):

RMSE

∑

d=1

(d)

− ˆy

(d)

)

/K,

where y

(d)

and ˆy

(d)

denote the measured and predicted

TD value for the dth mesh of the ith eye, respectively.

Smaller RMSE means better prediction. We also eval-

uated the accuracy of prediction gained in applying

our meta-algorithm to existing methods based on the

Improvement Rate (IR):

IR =

100

∑

i=1



1−

(RMSE

of applied)

(RMSE

of original)



Greater IR indicates larger enhancement of predic-

tion accuracy among N eyes by applying our meta-

algorithm.

HEALTHINF 2016 - 9th International Conference on Health Informatics

100

In the following sections, we evaluate the efﬁ-

cacy of our proposed method applied to Liang et al.’s

method(Liang, Z. et al., 2013) in terms of RMSE

and IR. We deﬁne the optimal selection procedure as

BEST that achieves the smallest RMSE by choosing

the optimal model for each eye; i.e., BEST selects the

best model from all the generated models on the basis

of the TD value to be predicted. We employed leave-

one-out cross-validation in the following analyses.

4.4 Experiment 1: The Best Use of IOP

Experimental Settings: There are several options to

employ IOP information in our method, including the

use of raw values, raw deviations, and standardized

scores. Here, we show the superiority of using the

standardized scores to the other two options in terms

of improvement in prediction accuracy for the BEST

procedure. The thresholds for the raw value and raw

deviation were set within [10, 30] (step: 1) and [0.1,3]

(step: 0.1), respectively. Both units are mmHg.

Results: Table 1 displays the median, mean, and

10%-trimmed mean of the RMSEs using our method

with the three analytical approaches of IOP. As for

the mean and 10%-trimmed mean, the standardized

score signiﬁcantly improved prediction accuracy for

all Q according to a one-sided Student’s t-test. There

was no signiﬁcant difference in terms of the median.

Table 2 shows the proportion of cases in which our

method using the standardized IOP scores performed

better in terms of prediction compared to that using

the other two scores. The use of our standardized

scores signiﬁcantly outperformed the use of the other

two according to a one-sided binomial test.

4.5 Experiment 2: Best Information

Criterion

Experimental Settings: We compared the ERROR,

AIC, BIC, and MDL to determine which criterion is

most suitable for prediction with our method. We also

analyzed the BEST case as reference.

Results: Table 3 presents the median and mean

RMSEs of the predictions obtained with the model for

the ERROR, AIC, BIC, MDL, and BEST. The MDL

performed signiﬁcantly better than the others in terms

of the mean RMSEs at the 1% signiﬁcance level with

a one-sided Student’s t-test in most cases, while it

performed better at the 5% signiﬁcance level when

Q = 3. As for the case of the median RMSEs, the

MDL performed well in most cases but there was no

signiﬁcant difference. Table 4 shows the proportionof

cases in which our method using the four criteria most

accurately predicted the value. A one-sided binomial

test veriﬁed that the MDL signiﬁcantly outperformed

the other criteria at the 0.1% level in all the cases.

4.6 Experiment 3: Effectiveness of IOP

Experimental Settings: We compared our method

as applied to the original Liang et al.’s method (Liang,

Z. et al., 2013) with the original to investigate the im-

provement in predictive ability. Based on the results

of Experiment 2, we used the MDL. In addition, we

compared our method with the BEST to evaluate the

predictive potential obtained by introducing the IOP.

Results: Table 5 shows the median, mean, and

10%-trimmed mean of the RMSEs for predictions ob-

tained with our proposed method compared to the

original method. As for the mean, the Student’s t-test

veriﬁed that our model signiﬁcantly outperformed the

original at the 0.1% level when the null hypothesis

IR = 0 was set for both trimmed and non-trimmed

cases. For the median, a Mann-Whitney-Wilcoxon

test veriﬁed that our model exceeded the predictive

power of the original at the 5% level except when

we set Q = 1. Table 6 shows the proportion of cases

in which our method predicted the value most accu-

rately. A binomial test determined that our method

was signiﬁcantly better than the original. The results

shown in Tables 5 and 6 revealed that our method ap-

plied with the BEST procedure is highly signiﬁcantly

superior to the original for prediction accuracy.

4.7 Discussion

Experiment 1: The use of a standardized IOP score

was more effective compared to the use of raw IOP

values or deviations as an indicator of the IOP state.

We believe that this is because the usual state of the

IOP differs from eye to eye; thus a standardized score

can normalize IOP values across eyes, whereas the

raw value and deviation cannot. With the three indi-

cators of IOP, we segmented the IOP states into high

and low states. The fact that the standardized score

was the best indicator of the IOP states indicates a

method for controlling for the heterogeneous differ-

ences among individuals; i.e., solving the external

heterogeneity of IOP. Thus, the scores could correctly

represent the fundamental states of most eyes.

Experiment 2: The results suggested that MDL was

a better choice for improving predictions compared

to others. This result could be due to the following

factors. The framework of MDL, which can take the

structure of a model into account by calculating the

optimal code length, ﬁts well with the property of

our PLR model owing to its clear tree structure (see

Fig. 3). Indeed, several studies have shown that the

Predicting Glaucomatous Progression with Piecewise Regression Model from Heterogeneous Medical Data

101

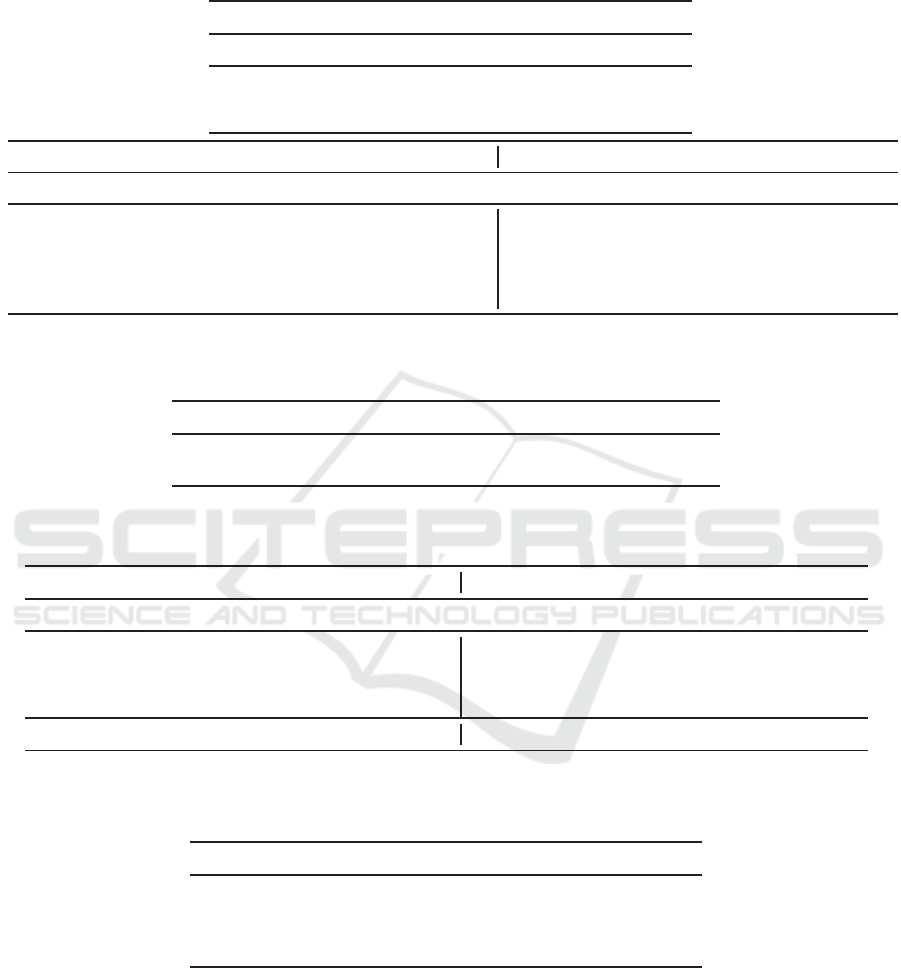
Table 1: Median, mean, and 10%-trimmed mean of RMSEs using the raw values, raw deviations, and standardized scores

of the IOP for each eye. The BEST optimal selection procedure was used for prediction. The symbol ♯ indicates statistical

signiﬁcance at the 0.1 % level.

Q 1 2 3 4 5 6

(a) Median RMSEs

Std. score 4.026 3.834 3.726 3.673 3.652 3.621

Raw val. 4.112 3.879 3.828 3.759 3.756 3.716

Raw dev. 4.139 3.861 3.770 3.739 3.724 3.666

Q 1 2 3 4 5 6 1 2 3 4 5 6

(b) Mean RMSEs (c) 10%-trimmed Mean RMSEs

Std. score 4.314 4.081 3.991 3.969 3.933 3.875 4.161 3.918 3.809 3.775 3.750 3.708

Raw val. 4.376 4.144 4.054 4.029 3.998 3.939

4.226 3.984 3.872 3.838 3.817 3.771

IR 1.463♯ 1.563♯ 1.576♯ 1.606♯ 1.707♯ 1.834♯

1.262♯ 1.402♯ 1.376♯ 1.391♯ 1.472♯ 1.834♯

Raw dev. 4.456 4.184 4.091 4.100 4.023 3.946

4.241 3.977 3.879 3.851 3.811 3.756

IR 1.550♯ 1.252♯ 1.300♯ 1.501♯ 1.139♯ 1.214♯

0.880♯ 0.803♯ 0.862♯ 0.830♯ 0.777♯ 0.844♯

Table 2: Proportion (%) of cases for which our proposed standardized score of IOP yielded better prediction performance.

Cases for the BEST procedure are shown. The symbol ♯ indicates statistical signiﬁcance at the 0.1 % level.

Q 1 2 3 4 5 6

v.s. Raw val. 70.54♯ 71.27♯ 69.28♯ 71.41♯ 70.20♯ 73.64♯

v.s. Raw dev. 63.70♯ 61.26♯ 61.44♯ 62.65♯ 62.03♯ 62.74♯

Table 3: Median and mean of RMSEs for predictions with the models selected according to the ERROR/AIC/BIC/MDL, and

the possible best model (BEST). The symbols ∗ and † indicate statistical signiﬁcance at 5% and 1 %, respectively.

Q 1 2 3 4 5 6 1 2 3 4 5 6

(a) Median RMSEs (b) Mean RMSEs

ERROR 4.461 4.179 4.097 4.083 4.104 4.085 4.738 4.509 4.425 4.425 4.391 4.322

AIC 4.461 4.179 4.096 4.088 4.104 4.087

4.737 4.508 4.425 4.425 4.391 4.323

BIC 4.456 4.173 4.101 4.083 4.099 4.092

4.731 4.505 4.424 4.423 4.387 4.320

MDL 4.422 4.163 4.113 4.087 4.064 4.076

4.682† 4.471† 4.394* 4.388† 4.351† 4.291†

BEST 4.026 3.834 3.726 3.673 3.652 3.621 4.314 4.081 3.991 3.969 3.934 3.875

Table 4: Proportion (%) of cases for which each criterion gave the best performance for prediction. The symbol ♯ indicates

statistical signiﬁcance at the 0.1 % level.

Q 1 2 3 4 5 6

ERROR 17.26 16.77 17.76 15.80 17.55 15.97

AIC 14.98 13.53 14.75 15.80 13.40 15.26

BIC 19.33 19.81 21.74 19.19 19.63 20.96

MDL 48.43♯ 49.89♯ 45.75♯ 49.20♯ 49.43♯ 47.81♯

MDL works well for tree-structured models (Mehta,

M. et al., 1995; Robnik-

Sikonja, M. and Kononenko,

I., 1998). In addition, extremely ineffective models

were not selected when using the MDL, as implied by

the fact that there were signiﬁcant differences in the

mean, but almost no differences in the median.

Meanwhile, because the MDL is difﬁcult to calcu-

late analytically, it is difﬁcult to apply the MDL to our

proposed method for complex models such as Murata

et al.’s model (Murata, H. et al., 2014). However, suf-

ﬁciently accurate results were gained with our method

just using ERROR This might be because we assumed

that the gradients of each piece were the same in the

same IOP state, which worked as a kind of regularizer

of the parameters. This result suggests that using ER-

ROR is a feasible solution for more complex models.

HEALTHINF 2016 - 9th International Conference on Health Informatics

102

Table 5: Median, mean, and 10%-trimmed mean of RMSEs. Liang et al.’s method (Liang, Z. et al., 2013) is referred to as the

“original”, and our method as applied to the original method is referred to as the “proposed”. The symbols ∗ and ♯ indicate

statistical signiﬁcance at the 5% and 0.1 % level, respectively.

Q 1 2 3 4 5 6

(a) Median RMSEs

Original 4.557 4.386 4.246 4.261 4.241 4.205

Proposed (MDL) 4.422 4.163* 4.113* 4.087* 4.064* 4.076*

Proposed (BEST) 4.026♯ 3.834♯ 3.726♯ 3.673♯ 3.652♯ 3.621♯

Q 1 2 3 4 5 6 1 2 3 4 5 6

(b) Mean RMSEs (c) 10%-trimmed Mean RMSEs

Original 369.8 566.6 300.0 262.1 391.4 235.4 4.681 4.487 4.394 4.357 4.317 4.266

Proposed

4.682 4.471 4.394 4.388 4.351 4.291

4.525 4.299 4.208 4.181 4.155 4.116

(MDL)

IR 4.541♯ 5.177♯ 4.985♯ 4.853♯ 4.205♯ 4.182♯

2.670♯ 2.944♯ 2.932♯ 3.108♯ 2.811♯ 2.833♯

Proposed

4.314 4.081 3.991 3.969 3.934 3.875

4.161 3.918 3.809 3.775 3.750 3.708

(BEST)

IR 12.78♯ 14.19♯ 14.54♯ 14.83♯ 14.32♯ 14.50♯

10.92♯ 11.95♯ 12.49♯ 12.76♯ 12.54♯ 12.89♯

Table 6: Proportion (%) of cases in which our method applied to Liang et al.’s method is superior to the original method based

on MDL and BEST. The ♯ indicates that the values are statistically signiﬁcant at the 0.1 % level.

Q 1 2 3 4 5 6

Proposed (MDL) 71.41♯ 71.38♯ 71.57♯ 71.74♯ 72.74♯ 67.63♯

Proposed (BEST) 99.24♯ 99.35♯ 99.78♯ 99.45♯ 99.23♯ 99.11♯

Experiment 3: Table 5 demonstrates that the appli-

cation of our proposed method to the original Liang

et al.’s method showed much better performance than

the original method. Moreover, our method achieved

better prediction accuracy with small Q. It is well-

known that high IOP exacerbates the progression of

glaucoma (see Sec. 2.2). Therefore, data incorporat-

ing eyes at different IOP states can be anomalous for

long-term prediction of the original method. In our

method, such noise is excluded by segmenting the

data with IOP values, which cannot be realized in the

original method. Therefore, we suppose that this sep-

aration of the data enables our method to produce ac-

curate predictions with less data owing to its stronger

power of expression and purity of the training data.

Table 6 also indicates that our method with MDL

represents a signiﬁcant improvement over the orig-

inal, and that it can help to improve the outcome

for a large number of eyes. However, about 30 %

of patients would not beneﬁt from our method judg-

ing from the results. This demonstrates that the best

model is not always selected with MDL, and that there

is still room for improvement in considering informa-

tion criteria. Nonetheless, Table 6 shows that insofar

as our framework exploits the IOP and copes with ex-

ternal and internal heterogeneity, it offers more accu-

rate predictions compared to existing methods.

Overall Discussion: We have shown the efﬁcacy of

our collective PLR model in predicting the progres-

sion of glaucoma. Since our method can be applied

to other existing methods, it is expected to serve as an

improvement of current methods by exploiting sup-

plemental data. However, there is still room for im-

provement in the model-selection phase, because the

accuracy of the prediction with the BEST procedure

was much better than that when using other informa-

tion criteria. One possible explanation for this result

is the small number of data entries for the high-IOP

state, making it difﬁcult to comprehensively evaluate

the model for this state. Thus, our future work will fo-

cus on such situations to improvethe proposed model.

5 CONCLUSION

We have proposed a novel collective PLR method

that copes with external and internal heterogeneity as

well as the medical-data-structure-difﬁculty of medi-

cal datasets. Existing methods cannot cope with the

internal heterogeneity, i.e., a situation where the rate

of progression for individual eyes changes over time.

We have dealt with this internal heterogeneity using

Predicting Glaucomatous Progression with Piecewise Regression Model from Heterogeneous Medical Data

103

a PLR model based on clinical knowledge regarding

the relationship between IOP and the rate of glauco-

matous progression (AGIS Investigators, 2010; Col-

laborative Normal-Tension Glaucoma Study Group,

1998; Satilmis, M. et al., 2003). Our method can

also deal with the external heterogeneity and medical-

data-structure-difﬁculty by incorporating a collective

method. Therefore, our method is a novel extension

of previous collective methods from both theoretical

and practical aspects, which increases prediction ac-

curacy. Similarly, other methods (Maya, S. et al.,

2014; Murata, H. et al., 2014) are expected to be im-

proved by incorporation of our method.

Medical datasets are commonly plagued by high

levels of heterogeneity, and we have here proposed

a new method that shows good performance in over-

coming this heterogeneity in a glaucoma dataset for

effective predictions of disease progression. We be-

lieve that our method can be extended to tackle simi-

lar difﬁculties in other medical datasets and we have

provided standardized directions for such analyses.

ACKNOWLEDGEMENTS

We thank Mr. Fujino and Ms. Taketani at the De-

partment of Ophthalmology,The University of Tokyo,

for their useful advice. This work was supported by

CREST, JST.

REFERENCES

AGIS Investigators (2010). The advanced glaucoma in-

tervention study (AGIS): 7. the relationship between

control of intraocular pressure and visual ﬁeld de-

terioration. American Journal of Ophthalmology,

130:429–440.

Akaike, H. (1973). Information theory and an extension

of the maximum likelihood principle. In Proceedings

of the 2nd International Symposium on Information

Theory, pages 267–281.

Collaborative Normal-Tension Glaucoma Study Group

(1998). Comparison of glaucomatous progression be-

tween untreated patients with normal-tension glau-

coma and patients with therapeutically reduced in-

traocular pressures. American Journal of Opthalmol-

ogy, 126(4):487–497.

Fujino Y., Murata H., Mayama C., and Asaoka R. (2015).

Applying “lasso” regression to predict future visual

ﬁeld progression in glaucoma patients. Investigative

Ophthalmology & Visual Science, 56(4):2334–2339.

Holmin, C. and Krakau, C. E. T. (1982). Regression anal-

ysis of the central visual ﬁeld in chronic glaucoma

cases. Acta Ophthalmologica, 60(2):267–274.

Kingman, S. (2004). Glaucoma is second leading cause of

blindness globally. Bulletin of the World Health Or-

ganization, 82(11):887–888.

Liang, Z., Tomioka, R., Murata, H., Asaoka, R., and Ya-

manishi, K. (2013). Quantitative prediction of glau-

comatous visual ﬁeld loss from few measurements.

In Proceedings of the 2013 IEEE 13th International

Conference on Data Mining 2013, pages 1121–1126.

Maya, S., Morino, K., and Yamanishi, K. (2014). Predicting

glaucoma progression using multi-task learning with

heterogeneous features. In Proceedings of the 2014

IEEE International Conference on Big Data, pages

261–270.

Maya, S., Morino, K., and Yamanishi, K. (2015). Discov-

ery of glaucoma progressive patterns using hierarchi-

cal MDL-based clustering. In Proceedings of the 21st

ACM SIGKDD Conference on Knowledge Discovery

and Data Mining, pages 1979–1988.

Mehta, M., Rissanen, J., and Agrawal, R. (1995). MDL-

based decision tree pruning. In Proceedings of the

1st ACM SIGKDD Conference on Data Mining, pages

216–221.

Morino, K., Hirata, Y., Tomioka, R., Kashima, H., Ya-

manishi, K., Hayashi, N., Egawa, S., and Aihara,

K. (2015). Predicting disease progression from short

biomarker series using expert advice algorithm. Sci-

entiﬁc Reports, 5:8953.

Murata, H., Araie, M., and Asaoka, R. (2014). A new ap-

proach to measure visual ﬁeld progression in glau-

coma patients using variational bayes linear regres-

sion. Investigative Ophthalmology & Visual Science,

55:8386–8392.

Natarajan, R. and Pednault, E. (2002). Segmented regres-

sion estimators for massive data sets. In Proceedings

of the 2nd SIAM International Conference on Data

Mining, pages 566–582.

Quigley, H. A. and Broman, A. T. (2006). The number of

people with glaucoma worldwide in 2010 and 2020.

British Journal of Ophthalmology, 90(3):262–267.

Rissanen, J. (1986). Stochastic complexity and modeling.

Annals of Statistics, 14(3):1080–1100.

Robnik-

Sikonja, M. and Kononenko, I. (1998). Pruning re-

gression trees with MDL. In Proceedings of the 13th

European Conference on Artiﬁcial Intelligence, pages

455–459.

Satilmis, M., Org¨ul, S., Doubler, B., and Flammer, J.

(2003). Rate of progression of glaucoma correlates

with retrobulbar citation and intraocular pressure.

American Journal of Ophthalmology, 135(5):664–

669.

Schwarz, G. (1978). Estimating the dimension of a model.

Annals of Statistics, 6(2):461–464.

Taketani Y., Murata H., Fujino Y., Mayama C., and Asaoka

R. (2015). How many visual ﬁelds are required to pre-

cisely predict future test results in glaucoma patients

when using different trend analyses? Investigative

Ophthalmology & Visual Science, 56(6):4076–4082.

Vogel, D. S., Asparouhov, O., and Scheffer, T. (2007). Scal-

able look-ahead linear regression trees. In Proceed-

ings of the 13th ACM SIGKDD Conference on Knowl-

edge Discovery and Data Mining, pages 757–764.

Zhu, H., Russell, R. A., Saunders, L. J., Ceccon, S.,

Garway-Health, D. F., and Crabb, D. P. (2014). De-

tecting changes in retinal function analysis with non-

stationary weibull error regression and spatial en-

hancement (ANSWERS). PLOS ONE, 9(1):e85654.

HEALTHINF 2016 - 9th International Conference on Health Informatics

104