Branch-and-Bound Optimization of a Multiagent System for Flow

Production using Model Checking

Stefan Edelkamp and Christoph Greulich

University of Bremen, Institute for Artiﬁcial Intelligence, Am Fallturm 1, 28359 Bremen, Germany

Keywords:

Multiagent Systems, Model Checking, Optimization, Branch-and-Bound, Autonomous Production.

Abstract:

In this paper we propose the application of a model checker to evaluate a multiagent system that controls

the industrial production of autonomous products. As the ﬂow of material is asynchronous at each station,

queuing effects arise as long as buffers provide waiting room. Besides validating the design of the system,

the core objective of this work is to ﬁnd plans that optimize the throughput of the system. Instead of mapping

the multiagent system directly to the model checker, we model the production line as a set of communicating

processes, with the movement of items modeled as communication channels. Experiments shows that the

model checker is able to analyze the movements of autonomous products for the model, subject to the partial

ordering of the product parts. It derives valid and optimized plans with several thousands of steps using

constraint branch-and-bound.

1 INTRODUCTION

The ongoing transformation of production indus-

tries causes a paradigm shift in manufacturing pro-

cesses towards new technologies and innovative con-

cepts, called cyber, smart, digital or connected fac-

tory (Bracht et al., 2011). The sector is entering its

fourth revolution, characterized by a merging of com-

puter networks and factory machines. At each link

in the production and supply chains, tools and work-

stations communicate constantly via the Internet and

local networks. Machines, systems, and products ex-

change information both among themselves and with

the outside world.

Flow Production Systems are installed for prod-

ucts that are produced in high quantities. By opti-

mizing the ﬂow of production, manufacturers hope to

speed up production at a lower cost, and in a more en-

vironmentally sound way. In manufacturing practice

there are not only series ﬂow lines (with stations ar-

ranged one behind the other), but also more complex

networks of stations at which assembly operations are

performed (assembly lines). The considerable dif-

ference from ﬂow lines, which can be analyzed by

known methods, is that a number of required compo-

nents are brought together to form a single unit for

further processing at the assembly stations. An as-

sembly operation can begin only if all required parts

are available.

Performance Analysis of ﬂow production systems

is generally needed during the planning phase regard-

ing the system design, when the decision for a con-

crete conﬁguration of such a system has to be made.

The planning problem arises, e.g., with the introduc-

tion of a new model or the installation of a new manu-

facturing plant. Because of the investments involved,

an optimization problem arises. The expenditure for

new machines, for buffer or handling equipment, and

the holding costs for the expected work-in-process

face revenues from sold products. The performance

of a concrete conﬁguration is characterized by the

throughput, i.e., the number of items that are pro-

duced per time unit. Other performance measures are

the expected work in process or the idle times of ma-

chines or workers.

In this paper we consider assembly-line networks

with stations, which are represented as a directed

graph. Between any two successive nodes in the net-

work, we assume a buffer of ﬁnite capacity. In the

buffers between stations and other network elements,

work pieces are stored, waiting for service. At assem-

bly stations, service is given to work pieces. Travel

time is measured and overall time is to be optimized.

Our running case study is the so called Z2, a phys-

ical monorail system for the assembling of tail-lights.

Unlike most production systems, Z2 employs agent

technology to represent autonomous products and as-

sembly stations. The techniques developed, however,

will be applicable to most ﬂow production systems.

We formalize the production ﬂoor as a system of com-

Edelkamp, S. and Greulich, C.

Branch-and-Bound Optimization of a Multiagent System for Flow Production using Model Checking.

DOI: 10.5220/0005705100270037

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 1, pages 27-37

ISBN: 978-989-758-172-4

municating processes and apply the state-of-the-art

model checker Spin (Holzmann, 2004) for analyzing

its behavior. Using optimization mechanisms imple-

mented on top of Spin, additional to the veriﬁcation

of the correctness of the model, we exploit its explo-

ration process for optimization of production ﬂow.

For the optimization Via Model Checking we use

many new language features from the latest version

of the Spin model checker including loops and na-

tive c-code veriﬁcation. The main contribution of

this text, however, is general cost-optimization via

branch-and-bound. The optimization approach orig-

inally invented for Spin was designed for state space

trees (Ruys and Brinksma, 1998; Ruys, 2003), while

the proposed new approach also supports state space

graphs, crucially reducing the running time and mem-

ory consumption of the algorithm, rendering other-

wise intractable models to become analyzable.

The paper is structured as follows. First, we con-

sider related work on agent-based industrial (ﬂow)

production, on model checking multiagent systems

(MASs), and on planning via model checking. Next,

we introduce the industrial case study, and its mod-

eling as well as its simulation as an MAS. The sim-

ulator is used to measure the increments of the cost

function to be optimized. Then, we turn to the intri-

cacies of the Promela model speciﬁcation and the pa-

rameterization of Spin, as well as to the novel branch-

and-bound optimization scheme. In the experiments

we validate the conciseness and effectiveness of the

model and the taken approach.

2 RELATED WORK

Especially in open, unpredictable, dynamic, and com-

plex environments, MASs are applied to determine

adequate solutions for transport problems. For ex-

ample, agent-based commercial systems are used

within the planning and control of industrial pro-

cesses (Dorer and Calisti, 2005; Himoff et al., 2006),

as well as within other areas of logistics (Fischer et al.,

1996; B

urckert et al., 2000). A comprehensive survey

is provided by (Parragh et al., 2008).

Flow line analysis is often done with queuing the-

ory (Manitz, 2008; Burman, 1995). Pioneering work

in analyzing assembly queuing systems with synchro-

nization constraints analyzes assembly-like queues

with unlimited buffer capacities (Harrison, 1973). It

shows that the time an item has to wait for synchro-

nization may grow without bound, while limitation of

the number of items in the system works as a control

mechanism and ensures stability. Work on assembly-

like queues with ﬁnite buffers all assume exponen-

tial service times (Bhat, 1986; Lipper and Sengupta,

1986; Hopp and Simon, 1989).

2.1 Model Checking Multiagent

Systems

Model checking production ﬂow is rare. Timed au-

tomata were used for simulating material ﬂow in agri-

cultural production (Helias et al., 2008). There are,

however, numerous attempts to apply model checking

to validate the work of MASs.

The LORA framework (Wooldridge, 2000;

Wooldridge, 2002) uses labeled transition and Kripke

systems for characterizing the behavior of the agents

(their belief, their desire and their intention), and tem-

poral logics for expressing their interplay, as well as

for the progression of knowledge. Alternatives con-

sider an MAS as a game, in which agents –either in

separation or cooperatively– optimize their individual

outcome (Safﬁdine, 2014). Communication between

the agents is available via writing to and reading from

channels, or via common access to shared variables.

Other formalization approaches include work in the

context of the MCMAS tool by Lomuscio

. Recently,

there has been some approaches to formalize MASs

as planning problems (Nissim and Brafman, 2013).

2.2 Planning and Model Checking

Since the origin of the term artiﬁcial intelligence, the

automated generation of plans for a given task has

been seen as an integral part of problem solving in

a computer. In action planning (Nau et al., 2004),

we are confronted with the descriptions of the initial

state, the goal (states) and the available actions. Based

on these we want to ﬁnd a plan containing as few ac-

tions as possible (in case of unit-cost actions, or if no

costs are speciﬁed at all) or with the lowest possible

total cost (in case of general action costs).

The process of fully-automated property valida-

tion and correctness veriﬁcation is referred to as

model checking (Clarke et al., 2000). Given a formal

model of a system M and a property speciﬁcation φ

in some form of temporal logic like LTL (Gerth et al.,

1995), the task is to validate, whether or not the spec-

iﬁcation is satisﬁed in the model, M |= φ. If not, a

model checker usually returns a counterexample trace

as a witness for the falsiﬁcation of the property.

Planning and model checking have much in com-

mon (Giunchiglia and Traverso, 1999; Cimatti et al.,

1997). Both rely on the exploration of a potentially

large state space of system states. Usually, model

http://vas.doc.ic.ac.uk/software/mcmas/

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

checkers only search for the existence of speciﬁca-

tion errors in the model, while planners search for

a short path from the initial state to one of the goal

states. Nonetheless, there is rising interest in planners

that prove insolvability (Hoffmann et al., 2014), and

in model checkers to produce minimal counterexam-

ples (Edelkamp and Sulewski, 2008).

In terms of leveraging state space search, over the

last decades there has been much cross-fertilization

between the ﬁelds. For example, based on Sat-

plan (Kautz and Selman, 1996) bounded model check-

ers exploit SAT and SMT representations (Biere et al.,

1999; Armando et al., 2006) of the system to be

veriﬁed, while directed model checkers (Edelkamp

et al., 2001; Kupferschmid et al., 2006) exploit pan-

ning heuristics to improve the exploration for falsiﬁ-

cation; partial-order reduction (Valmari, 1991; Gode-

froid, 1991) and symmetry detection (Fox and Long,

1999; Lluch-Lafuente, 2003) limit the number of suc-

cessor states, while symbolic planners (Cimatti et al.,

1998; Jensen et al., 2001; Edelkamp and Reffel, 1998)

apply functional data structures like BDDs to repre-

sent sets of states succinctly.

3 CASE STUDY: Z2

One of the few successful real-world implementations

of a multiagent ﬂow production is the so called Z2

production ﬂoor unit (Ganji et al., 2010; Morales

Kluge et al., 2010). The Z2 unit consists of six work-

stations where human workers assemble parts of au-

tomotive tail-lights. The system allows production of

certain product variations and reacts dynamically to

any change in the current order situation, e.g., a de-

crease or an increase in the number of orders of a cer-

tain variant. As individual production steps are per-

formed at the different stations, all stations are in-

terconnected by a monorail transport system. The

structure of the transport system is shown in Fig-

ure 1. On the rails, autonomously moving shuttles

carry the products from one station to another, de-

pending on the products’ requirements. The monorail

system has multiple switches which allow the shut-

tles to enter, leave or pass workstations and the cen-

tral hubs. The goods transported by the shuttles are

also autonomous, which means that each product de-

cides on its own which variant to become and which

station to visit. This way, a decentralized control of

the production system is possible.

The modular system consists of six different

workstations, each is operated manually by a human

worker and dedicated to one speciﬁc production step.

At production steps III and V, different parts can be

Figure 1: Assembly scenario for tail-lights (Morales Kluge

et al., 2010).

Figure 2: Assembly states of tail lights.(Ganji et al., 2010).

used to assemble different variants of the tail-lights

as illustrated in Fig. 2. At the ﬁrst station, the ba-

sic metal-cast parts enter the monorail on a dedicated

shuttle. The monorail connects all stations, each sta-

tion is assigned to one speciﬁc task, such as adding

bulbs or electronics. Each tail-light is transported

from station to station until it is assembled com-

pletely.

From the given case study, we derive a more gen-

eral notation of ﬂow production for an assembly-line

network. System progress is non-deterministic and

asynchronous, while the progress of time is moni-

tored.

Deﬁnition 1 (Flow Production). A ﬂow production

ﬂoor is a 6-tuple F = (A, E, G,≺, S, Q) where

• A is a set of all possible assembling actions

• P is a set of n products; each P

∈ P, i ∈ {1, . . . , n},

is a set of assembling actions, i.e., P

⊆ A

• G = (V, E, w, s,t) is a graph with start node s, goal

node t, and weight function w : E → IR

≥0

• ≺ = (≺

, . . . , ≺

) is a vector of assembling plans

with each ≺

⊆ A × A, i ∈ {1, . . . , n}, being a par-

Branch-and-Bound Optimization of a Multiagent System for Flow Production using Model Checking

tial order

• S ⊆ E is the set of assembling stations induced by

a labeling ρ : E → A ∪

0, i.e., S = {e ∈ E | ρ(e) 6=

• Q is a set of (FIFO) queues of ﬁnite size |Q| < ∞

together with a labeling ψ : E → Q

Products P

, i ∈ {1, . . . , n}, travel through the net-

work G, meeting their assembling plans/order ≺

⊆

A × A of the assembling actions A. For deﬁning the

cost function we use the set of predecessor edges

Pred(e) = {e

= (u, v) ∈ E | e = (v, w)}.

Deﬁnition 2 (Run, Plan, and Path). Let F =

(A, E, G, ≺, S, Q) be a ﬂow production ﬂoor. A run π

is a schedule of triples (e

, , t

, l

) of edges e

, queue

insertion positions l

, and execution time-stamp t

j ∈ {1, . . . , n}. The set of all runs is denoted as

Π. The run partitions into a set of n plans π

, l

), . . . , (e

, l

), one for each product P

, i ∈

{1, . . . , n}. Each plan π

corresponds to a path, start-

ing at the initial node s and terminating at goal node

t in G.

3.1 Multiagent System Simulation

In the real-world implementation of the Z2 system,

every assembly station, every monorail shuttle and ev-

ery product is represented by a software agent. Even

the RFID readers which keep track of product posi-

tions are represented by software agents which decide

when a shuttle may pass or stop. The agent represen-

tation is based on the well-known Java Agent Devel-

opment Kit (JADE) and relies heavily on its FIPA-

compliant messaging components.

Most agents in this MAS resemble simple reﬂex

agents as deﬁned by Russell and Norvig (2010) .

These agents just react to requests or events which

were caused by other agents or the human workers in-

volved in the manufacturing process. In contrast, the

agents which represent products are actively working

towards their individual goal of becoming a complete

tail-light and reaching the storage station. In order

to complete its task, each product has to reach sub-

goals which may change during production as the or-

der situation may change. The number of possible ac-

tions is limited by sub-goals which already have been

reached, since every possible production step has pre-

conditions as illustrated in ﬁgure 3.

The product agents constantly request updates re-

garding queue lengths at the various stations and the

overall order situation. The information is used to

compute the utility of the expected outcome of every

action which is currently available to the agent. High

utility is given when an action leads to fulﬁllment of

Figure 3: Preconditions of the various manufacturing

stages.

an outstanding order and takes as little time as possi-

ble. Time, in this case, is spent either on actions, such

as moving along the railway or being processed, or on

waiting in line at a station or a switch. By inferring

a MATLAB server, each agent individually makes its

decisions by applying a Fuzzy Logic model (Rekers-

brink et al., 2007).

More generally, the objective of products in such

a ﬂow production system can be formally described

as follows.

Deﬁnition 3 (Product Objective, Travel and Waiting

Time). The objective for product i is to minimize

max

1≤i≤n

wait(π

) + time(π

over all possible paths with initial node s and goal

node t, where

• time(π

) is the travel time of product P

, deﬁned as

the sum of edge costs time(π

) =

∑

e∈π

w(e), and

• wait(π

) the waiting time, deﬁned as wait(π

) =

∑

(e,t,l),(e

)∈π

∈Pred(e)

t − (t

+ w(e

)).

The Z2 MAS was developed strictly for the pur-

pose of controlling the Z2 monorail hardware setup.

Nonetheless, due to its hardware abstraction layer

(Morales Kluge et al., 2010), the Z2 MAS can be

adapted into other hardware or software environ-

ments. By replacing the hardware with other agents

and adapting the monorail infrastructure into a di-

rected graph, the Z2 MAS can be transferred to a vir-

tual simulation environment (Greulich et al., 2015).

Such an environment, which treats the original Z2

agents like black boxes, can easily be hosted by the

JADE-based event-driven MAS simulation platform

PlaSMA

. Experiments show how close the execu-

tions of the simulated and the real-world scenarios

match.

For this study, we provided the PlaSMA model

with timers to measure the time taken between two

graph nodes. Since the hardware includes many RFID

readers along the monorail, which all are represented

by an agent and a node within the simulation, we sim-

pliﬁed the graph and kept only three types of nodes:

http://plasma.informatik.uni-bremen.de/

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

Figure 4: Weighted graph model of the assembly scenario.

switches, production station entrances and production

station exits. The resulting abstract model of the sys-

tem is a weighted graph (see Fig.4), where the weight

of an edge denotes the traveling/processing time of

the shuttle between two respective nodes.

4 FORMAL SPECIFICATION

Promela is the input language of the model checker

Spin

, the ACM-awarded popular open-source soft-

ware veriﬁcation tool, designed for the formal veri-

ﬁcation of multi-threaded software applications, and

used by thousands of people worldwide. Promela

deﬁnes asynchronously running communicating pro-

cesses, which are compiled to ﬁnite state machines.

It has a c-like syntax, and supports bounded channels

for sending and receiving messages.

Channels in Promela follow the FIFO principle.

Therefore, they implicitly maintain order of incoming

messages and can be limited to a certain buffer size.

Consequently, we are able to map edges to commu-

nication channels. Unlike the original Z2 MAS, the

products are not considered to be decision making en-

tities within our Promela model. Instead, the products

are represented by messages which are passed along

the node processes, which resemble switches, station

entrances and exits.

Unlike the original MAS and the resembling

PlaSMA simulation, the Promela model is designed

to apply a branch-and-bound optimization to eval-

uate the optimal throughput of the original system.

Instead of local decision making, the various node

agents have certain nondeterministic options of han-

dling incoming messages, each leading to a different

system state. The model checker systematically com-

putes these states and memorizes paths to desirable

outcomes when it ends up in a ﬁnal state. As men-

tioned before, decreasing production time for a given

http://spinroot.com/spin/whatispin.html

number of products increases the utility of the ﬁnal

state.

We derive a formal model of the Z2 multiagent

systems as follows. First, we deﬁne global setting on

the number of stations and number of switches. We

also deﬁne the data type storing the index of the shut-

tle/product to be byte.

In the Promela model, production nodes are real-

ized as processes and edges between the nodes by the

following channels.

chan entrance_to_exit[STATIONS]= [1] of {shuttle};

chan exit_to_switch[STATIONS]= [BUFFERSIZE] of {shuttle};

chan switch_to_switch[SWITCHES]= [BUFFERSIZE] of {shuttle};

chan switch_to_entrance[STATIONS]=[BUFFERSIZE]of{shuttle};

As global variables, we also have bit-vectors for

the different assemblies being processed.

bit metalcast[SHUTTLES];

bit electronics[SHUTTLES];

bit bulb[SHUTTLES];

bit seal[SHUTTLES];

bit cover[SHUTTLES];

Additionally, we have a bit-vector that denotes

when a shuttle with a fully assembled item has ﬁnally

arrived at its goal location. A second bit-vector is used

to set for each shuttle whether it has to acquire a col-

ored or a clear bulb.

bit goals[SHUTTLES];

bit color[SHUTTLES];

A switch is a process that controls the ﬂow of the

shuttles. In the model, a non-deterministic choice is

added to either enter the station or to continue trav-

eling onwards on the cycle. Three of four switching

options are made available, as immediate re-entering

a station from its exit is prohibited.

proctype Switch(byte in; byte out; byte station)

{

shuttle s;

:: exit_to_switch[station]?s; switch_to_switch[out]!s;

:: switch_to_switch[in]?s; switch_to_switch[out]!s;

:: switch_to_switch[in]?s; switch_to_entrance[station]!s;

}

The entrance of a manufacturing station takes the

item from the according switch and moves it to the

exit. It also controls that the manufacturing complies

with the capability of the station.

First, the assembling of product parts is different

at each station, in the stations 1 and 3 we have the

insertion of bulbs (station 1 provides colored bulbs,

station 3 provides clear bulbs), station 2 assembles

the seal, station 4 the electronics and station 0 the

cover. Station 5 is the storage station where empty

metal casts are placed on the monorail shuttles and

Branch-and-Bound Optimization of a Multiagent System for Flow Production using Model Checking

ﬁnished products are removed to be taken into stor-

age.

Secondly, there is a partial order of the respective

product parts to allow ﬂexible processing and a better

optimization based on the current load of the ongoing

production.

proctype Entrance(byte station)

{

shuttle s;

:: switch_to_entrance[station]?s;

entrance_to_exit[station]!s

:: (station == 4) -> electronics[s] = 1;

:: (station == 3 && !color[s]) -> bulb[s] = 1;

:: (station == 2)-> seal[s] = 1;

:: (station == 1 && color[s]) -> bulb[s] = 1;

:: (station == 0 && seal[s]

&& bulb[s] && electronics[s])-> cover[s] = 1;

:: (station == 5 && cover[s]) -> goals[s] = 1;

:: else

}

An exit is a node that is located at the end of a sta-

tion, at which assembling took place. It is connected

to the entrance of the station and the switch linked to

it.

proctype Exit(byte station)

{

shuttle s;

:: entrance_to_exit[station]?s;

exit_to_switch[station]!s;

}

A hub is a switch that is not connected to a sta-

tion but provides a shortcut in the monorail network.

Again, three of four possible shuttle movement op-

tions are provided

proctype Hub(byte in1; byte out1; byte in2; byte out2)

{

shuttle s;

:: switch_to_switch[in1]?s; switch_to_switch[out1]!s;

:: switch_to_switch[in1]?s; switch_to_switch[out2]!s;

:: switch_to_switch[in2]?s; switch_to_switch[out1]!s;

}

In the initial state, we start the individual pro-

cesses, which represent nodes and hereby deﬁne the

network of the monorail system. Moreover, initially

we have that the metal cast of each product is already

present on its carrier, the shuttle. The coloring of the

tail-lights can be deﬁned at the beginning or in the

progress of the production. Last, but not least, we ini-

tialize the process by inserting shuttles on the starting

rail (at station 5).

init {

atomic {

byte i;

c_code { cost = 0; }

c_code { best_cost = 100000; }

for (i : 0 .. (SHUTTLES)/2)){ color[i] = 1; }

for (i : 0 .. (SHUTTLES-1)) { metalcast[i] = 1; }

for (i : 0 .. (STATIONS-1)) { run Entrance(i);

run Exit(i); }

run Switch(7,0,5); run Switch(0,1,4);

run Switch(1,2,3); run Switch(3,4,2);

run Switch(4,5,1); run Switch(5,6,0);

run Hub(2,3,8,9); run Hub(6,7,9,8);

for (i : 0 .. (SHUTTLES-1)) { exit_to_switch[5]!i; }

}

We also heavily made use of the term atomic,

which enhances the exploration for the model

checker, allowing it to merge states within the search.

In difference to the more aggressive d step keyword,

in an atomic block all communication queue action

are still blocking, so that we chose to use an atomic

block around each loop.

5 CONSTRAINED

BRANCH-AND-BOUND

OPTIMIZATION

There are different options for ﬁnding optimized

schedules with the help of a model checker that have

been proposed in the literature. First, as in the Soldier

model of (Ruys and Brinksma, 1998), rendezvous

communication to an additional synchronized process

has been used to increase cost, dependent on the tran-

sition chosen, together with a specialized LTL prop-

erty to limit the total cost for the model checking

solver. This approach, however, turned out to be lim-

ited in its ability. An alternative proposal for branch-

and-bound search is based on the support of native c-

code in Spin (introduced in version 4.0) (Ruys, 2003).

One running example is the traveling salesman prob-

lem (TSP), but the approach is generally applicable

to many other optimization problems. However, as

implemented, there are certain limitations to the scal-

ability of state space problem graphs. Recall that the

problem graph induced by the TSP is in fact a tree,

generating all possible permutations for the cities.

Inspired by (Edelkamp et al., 2001; Brinksma and

Mader, 2000) and (Ruys, 2003) we applied and im-

proved branch-and-bound optimization within Spin.

Essentially, the model checker can ﬁnd traces of sev-

eral hundreds of steps and provides trace optimiza-

tion by ﬁnding the shortest path towards a counterex-

ample if run with the parameter ./pan -i. How-

ever, these traces are step-optimized, and not cost-

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

optimized. Therefore, Ruys (2003) proposed the in-

troduction of a variable cost.

c_state "int best_cost" "Hidden"

c_code { int cost; }

c_track "cost" "sizeof(int)" "Matched"

While the cost variable increases the amount of

memory required for each state, it also limits the

power of Spins built-in duplicate detection, as two

otherwise identical states are considered different if

reached by different accumulated cost. If the search

space is small, so that it can be explored even for

the enlarged state vector, then this option is sound

and complete, and ﬁnally returns the optimal solution

to the optimization problem. However, as with our

model, it might be that there are simply too many rep-

etitions in the model so that introducing cost to the

state vector leads to a drastic increase in state space

size, so that otherwise checkable instances now be-

come intractable. We noticed that even by concentrat-

ing on safety properties (such as the failed assertion

mentioned), the insertion of costs causes troubles.

5.1 Constrained Branching

For our model, cost has to be tracked for every shuttle

individually. The variable cost of the most expensive

shuttle indicates the duration of the whole production

process. Furthermore, the cost total provides insight

regarding unnecessary detours or long waiting times.

Hence, minimizing both criteria are the optimization

goals of this model. Again, a more general formaliza-

tion can be derived from our case study as follows.

Deﬁnition 4 (Overall Objective). With cost(π

) =

wait(π

) + time(π

), as overall objective function we

have min

π∈Π

max

1≤i≤n

cost(π

)

= min

π∈Π

max

1≤i≤n

∑

e∈π

w(e)

∑

(e,t,l),(e

)∈π

∈Pred(e)

t − (t

+ w(e

))

= min

π∈Π

max

1≤i≤n,(e,t,l)∈π

t + w(e)

subject to the side constraints that

• time stamps on all runs π

, l

). . . (e

, l

), i ∈ {1, . . . , n} are

monotonically increasing, i.e., t

≤ t

for all

1 ≤ l < k ≤ m.

• after assembling all products are complete,

i.e., all assembling actions have been executed,

so that for all i ∈ {1, . . . , n} we have P

∪

)∈π

{ρ(e

)}

• the order of assembling product P

on path π

, l

). . . (e

, l

), i ∈ {1, . . . , n}, is pre-

served, i.e., for all (a, a

) ∈≺

and a = ρ(e

), a

ρ(e

) we have j < k,

• all insertions to queues respect their sizes, i.e., for

all π

= (e

, l

). . . (e

, l

), i ∈ {1, . . . , n}, we

have that 0 ≤ l

< |ψ(e

)|.

In Promela, every do-loop is allowed to contain

an unlimited number of possible options for the model

checker to choose from. The model checker randomly

chooses between the options, however, it is possible

to add an i f -like condition to an option: If the ﬁrst

statement of a do option holds, Spin will start to exe-

cute the following statements, otherwise, it will pick

a different option.

Since the model checker explores any possible

state of the system, many of these states are techni-

cally reachable but completely useless from an opti-

mization point of view. In order to reduce state space

size to a manageable level, we add constraints to the

relevant receiving options in the do-loops of every

node process.

Peeking into the incoming queue to ﬁnd out,

which shuttle is waiting to be received is already con-

sidered a complete statement in Promela. Therefore,

we exploit C-expressions (c expr) to combine sev-

eral operations into one atomic statement. For every

station t and every incoming channel q, a function

prerequisites(t, q) determines, if the ﬁrst shuttle in q

meets the prerequisites for t, as given by Figure 3.

shuttle s;

:: c_expr{prerequisites(Px->q,Px->t)} ->

channel[q]?s;

channel[out]!;

For branch-and-bound optimization, we now fol-

low the guidelines of (Ruys, 2003). This enables the

model checker to print values to the output, only if

the values of the current max cost and sum cost have

improved.

c_code {

if (max < best_cost ||

(max == best_cost && sum < best_sum_cost) {

best_cost = max;

best_sum_cost = sum;

putrail();

Nr_Trails--;

};

}

5.2 Process Synchronization

Due to the nature of the state space search of the

model checker, node agents in the Promela model do

not make decisions. Nonetheless, the given Promela

model is a distributed simulation consisting of a vary-

ing number of processes, which potentially inﬂuence

each other if executed in parallel.

Branch-and-Bound Optimization of a Multiagent System for Flow Production using Model Checking

In parallel simulation, different notions of time

have to be considered. Physical time is the time

of occurrence of real world events, simulation time

(or virtual time) is the adaptation of physical time

into the simulation model. Furthermore, wall clock

time refers to the real-world time which passes dur-

ing computation of the simulation.

Consequently, we introduce an integer array

waittime[SHUTTLES] to the Promela model. It en-

ables each shuttle to keep track of its local virtual

time (LVT), as the wait time will be increased by the

cost of each action as soon as the action is executed.

However, parallel execution allows faster processes to

overtake slower processes, even though the LVT of

the slower process is lower. While Spin maintains the

order of products and their respective costs implicitly

by the FIFO queues as long as the products are passed

along in a row, the so called causality problem (Fuji-

moto, 2000) emerges, as soon as products part ways

at any switch node.

We addressed this problem by introducing an

event-based time progress to the Promela model.

Whenever a shuttle s travels along one of the edges,

the corresponding message is put into a channel and

the waiting time waittime(s) of the respective shuttle

is increased by the cost of the given edge. The receiv-

ing process is not allowed to take the message out of

the channel, until the waiting time of the shuttle has

passed.

Again, we introduce an atomic C function

canreceive(q), which returns true only if the ﬁrst ele-

ment s of q has waittime(s) ≤ 0, changing the receiv-

ing constraint to the following.

shuttle s;

:: c_expr{canreceive(Px->q) &&

prerequisites(Px->q, Px->t)} ->

channel[q]?s;

waittime[s]+=next_step_cost;

channel[out]!s;

Within Spin, a global Boolean variable timeout

is deﬁned, which is automatically set to true when all

current processes are unable to proceed, e.g. because

they cannot receive a message. Consequently, when

waittime(p) > 0 for every shuttle p, all processes will

be blocked and timeout will be set to true. As sug-

gested by Bo

sna

cki and Dams (1998) , we add a pro-

cess that computes time progress whenever timeout

occurs. Unlike Bo

sna

cki and Dams, however, we ap-

ply an event-driven discrete time model as described

in Algorithm 1. To further constrain branching, the

time-managing process also asserts that the time does

not exceed the best cost, since worse results do not

need to be explored completely.

active proctype timemanager() {

:: timeout -> c_code{ increasetime(); };

assert(currenttime < best_cost);

}

Algorithm 1: Increase simulation time.

1: procedure INCREASETIME

2: minimum ← ∞

3: delta ← 1

4: for all p ∈ products do

5: if 0 < waittime(p) < minimum then

6: minimum ← waittime(p)

7: if minimum < ∞ then

8: delta ← minimum

9: for all p ∈ products do

10: if waittime(p) − delta ≥ 0 then

11: waittime(p) ← waittime(p) − delta

12: else

13: waittime(p) ← 0

6 EVALUATION

In this section, we present results of a series of experi-

ments executing the Promela model. We compare the

results with the outcomes of the JADE-based simula-

tion of the original hardware implementation. Unlike

the original MAS, the Promela model does not rely on

local decision making but searches for an optimal so-

lution systematically. Therefore, the Promela model

resembles a centralized planning approach. Conse-

quently, we compare the centralized solution with the

original distributed MAS solution. The comparison

should be dealt with care: while a simulation exe-

cutes one run in a complex system, model checking

explores all possible runs in a simpliﬁed system.

For executing the model checking, we chose ver-

sion 6.4.3 of Spin. For the standard setting of trace

optimization for safety checking (option -DSAFETY),

we compiled the model as follows.

./spin -a z2.pr;

gcc -O2 -DREACH -DSAFETY -o pan pan.c;

./pan -i -m30000

Parameter -i stands for the incremental optimiza-

tion of the counterexample length. We regularly in-

creased the maximal tail length with option -m, as in

some cases of our running example, the traces turned

out to be longer than the standard setting of at most

10000 steps. Option -DREACH is needed to warrant

minimal counterexamples at the end.

We used two different machines for the experi-

ments: First, a common notebook with an Intel(R)

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

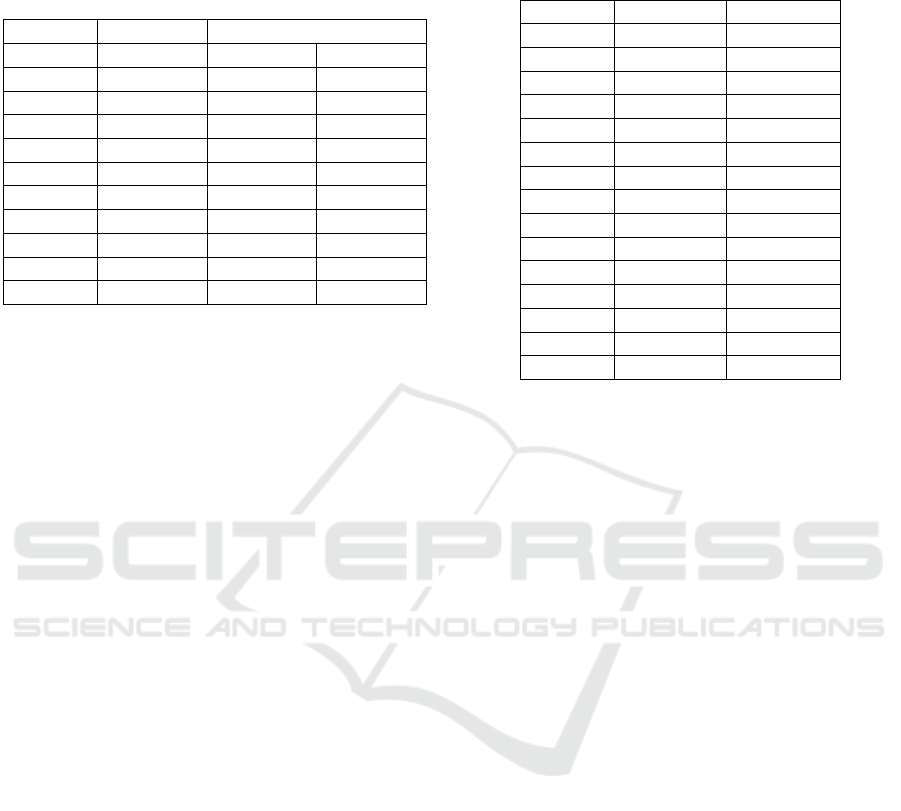
Table 1: Simulated production times for n products in

PlaSMA and Spin simulation, including the amount of

RAM required to compute the given result. (* indicates that

the whole state space was searched.)

PlaSMA Spin (Inﬂexible)

Products Sim. Time Sim. Time RAM

2 4:01 3:24 987 MB*

3 4:06 3:34 2154 MB*

4 4:46 3:56 557 MB

5 4:16 4:31 587 MB

6 5:29 4:31 611 MB

7 5:18 5:08 636 MB

8 5:57 5:43 670 MB

9 6:00 5:43 692 MB

10 6:08 5:43 715 MB

20 9:03 8:56 977 MB

Core(TM) i7-4710HQ CPU at 2.50 GHz, 16 GB of

RAM and Windows 10 (64 Bit). Second, a server

with an Intel(R) Xeon(R) CPU E5-4627 v2 at 3.30

GHz 128 GB of RAM and Windows Server 2012 R2

(64 Bit).

6.1 Inﬂexible Product Variants

For the ﬁrst series of experiments, we predeﬁned pro-

duction goals for each product: Products with even

IDs acquire clear bulbs, products with odd IDs ac-

quire colored ones.

Table 1 shows that in most cases the Spin model

checker proposes an optimal solution that is up to one

minute faster than the original MAS. While a certain

deviation between both simulations is unavoidable,

since the non-deterministic communication processes

between shuttles, products and stations are not con-

sidered in the Promela model, results clearly indicate

that the agents’ decision making leaves a lot of room

for improvement, especially, under consideration of

the agents’ ﬂexibility: The autonomous products in

the original MAS are able to decide, which product

variant they want to become to counter waiting times

at stations.

However, the Spin model checker also reveals

considerable limitations. While the state space of ex-

periments with n ∈ {2, 3} products can be searched

completely even on a standard notebook, experiments

with n > 3 shuttles easily exhaust 128 GB of RAM

on our server without ever completing the search of

the whole state space. Luckily, potentially good re-

sults can be found early on: Table 1 shows that even

in experiments that exhausted 128 GB of RAM, the

best results were found before the search space ﬁlled

2 GB of RAM. However, a valid solution for n > 30

shuttles could not be computed by the model checker

Table 2: Sequences of events for n = 2 products.

(Product ⇒ Station, where ⇒ indicates a ﬁnished produc-

tion step.)

PlaSMA Spin (Inﬂ.) Spin (ﬂex.)

0 ⇒ 4 0 ⇒ 4 0 ⇒ 4

1 ⇒ 2 1 ⇒ 4 1 ⇒ 4

0 ⇒ 3 2 ⇒ 4 2 ⇒ 4

2 ⇒ 1 0 ⇒ 3 0 ⇒ 3

0 ⇒ 2 2 ⇒ 3 1 ⇒ 3

1 ⇒ 4 1 ⇒ 2 0 ⇒ 2

0 ⇒ 0 1 ⇒ 1 2 ⇒ 2

2 ⇒ 4 2 ⇒ 2 1 ⇒ 2

0 ⇒ 5 1 ⇒ 0 0 ⇒ 0

1 ⇒ 1 0 ⇒ 2 2 ⇒ 1

2 ⇒ 2 2 ⇒ 0 1 ⇒ 0

1 ⇒ 0 0 ⇒ 0 2 ⇒ 0

2 ⇒ 0 1 ⇒ 5 1 ⇒ 5

1 ⇒ 5 2 ⇒ 5 0 ⇒ 5

2 ⇒ 5 0 ⇒ 5 2 ⇒ 5

before the RAM on our server was exhausted.

Regarding computation time, experiments in both

Spin and the PlaSMA system provided results within

few minutes. It is mentionable though, that Spin pro-

vides the above results in shorter computation time

than the corresponding PlaSMA simulation. How-

ever, exhausting the servers RAM takes about 20 min-

utes and slightly exceeds PlaSMAs computation time.

6.2 Flexible Product Variants

In a second series of experiments, we allowed the

model checker to decide, which products to provide

with a colored or clear bulb. In these experiments, a

desirable ﬁnal state is reached when all products have

returned to the storage station (station 5) and the dif-

ference d between the amount of both product vari-

ants is 0 ≤ d ≤ 1.

In these experiments, the model checker has even

more possibilities to branch its search space. There-

fore, it is hardly surprising that problems with n > 3

shuttles could not be computed on either of our test

machines. For n = 2 shuttles, the model checker pro-

poses a solution that takes 3:21 seconds and therefore

is 3 seconds faster than the inﬂexible solution. For

n = 3 shuttles, the difference is 10 seconds, as the

production takes 3:24 seconds of simulation time.

A closer look at the sequence of events reveals,

that a ﬂexible choice of product variants allows prod-

ucts to overtake stations more efﬁciently, as illustrated

in Table 2.

Branch-and-Bound Optimization of a Multiagent System for Flow Production using Model Checking

7 CONCLUSIONS

In this paper, we presented a novel approach for

model checking an industrial production line. The re-

search was motivated by our interest in ﬁnding and

comparing centralized and distributed solutions to the

optimization problems in autonomous production sys-

tems.

The formal model reﬂects the routing and schedul-

ing of shuttles in the multiagent system. Nodes of the

rail network were modeled as processes, the edges

between the nodes were modeled as communication

channels. Additional constraints to the order of pro-

duction steps enable to carry out a complex planning

task.

Our results clearly indicate a lot of room for im-

provement in the decentralized solution, since the

model checker found more efﬁcient ways to route and

schedule the shuttles on several occasions. Further-

more, the model checker could derive optimized plans

of several thousand steps.

In future work, we will consider a larger param-

eter space for the model checker. We are also think-

ing of applying an action planner or a general game

player for comparison. We do not expect a drastic im-

provement in state space size, as the model languages

(PDDL (Hoffmann and Edelkamp, 2005) and GDL

(Love et al., 2006)) are considerably different and do

not have native support for communication queues.

However as in directed model checking (Edelkamp

et al., 2001), the integration of informative heuristics

might help to guide the search process towards ﬁnd-

ing the goal.

ACKNOWLEDGEMENTS

This research was partly funded by the International

Graduate School for Dynamics in Logistics (IGS) of

the University of Bremen.

REFERENCES

Armando, A., Mantovani, J., and Platania, L. (2006).

Bounded model checking of software using SMT

solvers instead of SAT solvers. In SPIN, pages 146–

162. Springer.

Bhat, U. (1986). Finite capacity assembly-like queues.

Queueing Systems, 1:85–101.

Biere, A., Cimatti, A., Clarke, E., and Zhu, Y. (1999). Sym-

bolic model checking without BDDs. In Tools and

Algorithms for the Construction and Analysis of Sys-

tems.

sna

cki, D. and Dams, D. (1998). Integrating Real

Time Into Spin: A Prototype Implementation. In

Budkowski, S., Cavalli, A., and Najm, E., editors,

FORTE/PSTV, volume 6 of IFIP The International

Federation for Information Processing, pages 423–

438. Springer.

Bracht, U., Geckler, D., and Wenzel, S. (2011). Digi-

tale Fabrik: Methoden und Praxisbeispiele. Springer,

Berlin/Heidelberg.

Brinksma, E. and Mader, A. (2000). Veriﬁcation and opti-

mization of a PLC control schedule. In SPIN, volume

1885, pages 73–92.

urckert, H.-J., Fischer, K., and Vierke, G. (2000). Holonic

transport scheduling with teletruck. Applied Artiﬁcial

Intelligence, 14(7):697–725.

Burman, M. (1995). New results in ﬂow line analysis. PhD

thesis, Massachusetts Institute of Technology.

Cimatti, A., Giunchiglia, E., Giunchiglia, F., and Traverso,

P. (1997). Planning via model checking: A decision

procedure for AR. In ECP, pages 130–142. Springer.

Cimatti, A., Roveri, M., and Traverso, P. (1998). Auto-

matic OBDD-based generation of universal plans in

non-deterministic domains. In AAAI, pages 875–881.

Clarke, E., Grumberg, O., and Peled, D. (2000). Model

Checking. MIT Press.

Dorer, K. and Calisti, M. (2005). An adaptive solution to

dynamic transport optimization. In AAMAS, pages

45–51. ACM.

Edelkamp, S., Lluch-Lafuente, A., and Leue, S. (2001). Di-

rected model-checking in HSF-SPIN. In SPIN, pages

57–79.

Edelkamp, S. and Reffel, F. (1998). OBDDs in heuristic

search. In KI, pages 81–92.

Edelkamp, S. and Sulewski, D. (2008). Flash-efﬁcient LTL

model checking with minimal counterexamples. In

SEFM, pages 73–82.

Fischer, K., M

uller, J. R. P., and Pischel, M. (1996). Coop-

erative transportation scheduling: an application do-

main for dai. Applied Artiﬁcial Intelligence, 10(1):1–

34.

Fox, M. and Long, D. (1999). The detection and exploration

of symmetry in planning problems. In IJCAI, pages

956–961.

Fujimoto, R. (2000). Parallel and Distributed Simulation

Systems. Wiley & Sons.

Ganji, F., Morales Kluge, E., and Scholz-Reiter, B. (2010).

Bringing Agents into Application: Intelligent Prod-

ucts in Autonomous Logistics. In Schill, K., Scholz-

Reiter, B., and Frommberger, L., editors, Artiﬁcial in-

telligence and Logistics (AiLog) - Workshop at ECAI

2010, pages 37–42.

Gerth, R., Peled, D., Vardi, M., and Wolper, P. (1995). Sim-

ple on-the-ﬂy automatic veriﬁcation of linear temporal

logic. In PSTV, pages 3–18. Chapman & Hall.

Giunchiglia, F. and Traverso, P. (1999). Planning as model

checking. In ECP, pages 1–19.

Godefroid, P. (1991). Using partial orders to improve auto-

matic veriﬁcation methods. In CAV, pages 176–185.

Greulich, C., Edelkamp, S., and Eicke, N. (2015). Cyber-

Physical Multiagent-Simulation in Production Logis-

tics. In MATES, pages 119–136. Springer.

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

Harrison, J. (1973). Assembly-like queues. Journal of Ap-

plied Probability, 10:354–367.

Helias, A., Guerrin, F., and Steyer, J.-P. (2008). Using

timed automata and model-checking to simulate ma-

terial ﬂow in agricultural production systems – appli-

cation to animal waste management. Computers and

Electronics in Agriculture, 63(2):183–192.

Himoff, J., Rzevski, G., and Skobelev, P. (2006). Magenta

technology multi-agent logistics i-scheduler for road

transportation. In AAMAS, pages 1514–1521. ACM.

Hoffmann, J. and Edelkamp, S. (2005). The deterministic

part of IPC-4: An overview. Journal of Artiﬁcial In-

telligence Research, 24:519–579.

Hoffmann, J., Kissmann, P., and Torralba,

A. (2014). ”dis-

tance”? Who cares? Tailoring merge-and-shrink

heuristics to detect unsolvability. In ECAI, pages 441–

446.

Holzmann, G. J. (2004). The SPIN Model Checker - primer

and reference manual. Addison-Wesley.

Hopp, W. and Simon, J. (1989). Bounds and heuristics for

assembly-like queues. Queueing Systems, 4:137–156.

Jensen, R. M., Veloso, M. M., and Bowling, M. H. (2001).

Obdd-based optimistic and strong cyclic adversarial

planning. In ECP.

Kautz, H. and Selman, B. (1996). Pushing the envelope:

Planning propositional logic, and stochastic search. In

ECAI, pages 1194–1201.

Kupferschmid, S., Hoffmann, J., Dierks, H., and Behrmann,

G. (2006). Adapting an AI planning heuristic for di-

rected model checking. In SPIN, pages 35–52.

Lipper, E. and Sengupta, E. (1986). Assembly-like queues

with ﬁnite capacity: bounds, asymptotics and approx-

imations. Queueing Systems, pages 67–83.

Lluch-Lafuente, A. (2003). Symmetry reduction and

heuristic search for error detection in model checking.

In MOCHART, pages 77–86.

Love, N. C., Hinrichs, T. L., and Genesereth, M. R. (2006).

General Game Playing: Game Description Language

Speciﬁcation. Technical Report LG-2006-01, Stan-

ford Logic Group.

Manitz, M. (2008). Queueing-model based analysis of as-

sembly lines with ﬁnite buffers and general service

times. Computers & Operations Research, 35(8):2520

– 2536.

Morales Kluge, E., Ganji, F., and Scholz-Reiter, B. (2010).

Intelligent products - towards autonomous logistic

processes - a work in progress paper. In PLM, pages

348 – 357, Bremen.

Nau, D., Ghallab, M., and Traverso, P. (2004). Automated

Planning: Theory & Practice. Morgan Kaufmann

Publishers Inc., San Francisco, CA, USA.

Nissim, R. and Brafman, R. I. (2013). Cost-optimal plan-

ning by self-interested agents. In AAAI.

Parragh, S. N., Doerner, K. F., and Hartl, R. F. (2008).

A Survey on Pickup and Delivery Problems Part II:

Transportation between Pickup and Delivery Loca-

tions. Journal f

ur Betriebswirtschaft, 58(2):81–117.

Rekersbrink, H., Ludwig, B., and Scholz-Reiter, B. (2007).

Entscheidungen selbststeuernder logistischer Objekte.

Industrie Management, 23(4):25–30.

Russell, S. J. and Norvig, P. (2010). Artiﬁcial Intelligence -

A Modern Approach. Pearson Education, 3rd edition.

Ruys, T. C. (2003). Optimal scheduling using branch and

bound with SPIN 4.0. In SPIN, pages 1–17.

Ruys, T. C. and Brinksma, E. (1998). Experience with lit-

erate programming in the modelling and validation of

systems. In TACAS, pages 393–408.

Safﬁdine, A. (2014). Solving Games and All That. PhD

thesis, University Paris-Dauphine.

Valmari, A. (1991). A stubborn attack on state explosion.

Lecture Notes in Computer Science, 531:156–165.

Wooldridge, M. (2000). Reasoning about Rational Agents.

The MIT Press.

Wooldridge, M. (2002). An Introduction to Multi-Agent

Systems. Wiley and Sons, Chichester, UK.

Branch-and-Bound Optimization of a Multiagent System for Flow Production using Model Checking