
Police Officer Dynamic Positioning for Incident
Response and Community Presence
Using Maximum Demand Coverage and Kernel Density Estimation to Plan Patrols
Johanna Leigh, Lisa Jackson and Sarah Dunnett
Department of Aeronautical and Automotive Engineering, Loughoborugh University, Loughborough, U.K.
Keywords: Maximum Coverage Location Problem, Hotspots, Kernel Density Estimation, Tabu Search.
Abstract: Police Forces are under a constant struggle to provide the best service possible with limited and decreasing
resources. One area where service cannot be compromised is incident response. Resources which are
assigned to incident response must provide attendance to the scene of an incident in a timely manner to
protect the public. To ensure the possible demand is met maximum coverage location planning can be used
so response officers are located in the most effective position for incident response. This is not the only
concern of response officer positioning. Location planning must also consider targeting high crime areas,
hotspots, as an officer presence in these areas can reduce crime levels and hence reduce future demand on
the response officers. In this work hotspots are found using quadratic kernel density estimation with
historical crime data. These are then used to produce optimal dynamic patrol routes for response officers to
follow. Dynamic patrol routes result in reduced response times and reduced crime levels in hotspot areas
resulting in a lower demand on response officers.
1 INTRODUCTION
Police forces must operate to a high efficiency to
ensure the safety of the public and property with the
limited budget available. In many countries the
police are currently facing budget cuts and hence
this is of increasing importance. One area where the
public’s safety is very reliant on efficient use of
resources is incident response. This is where a
situation is brought to the attention of the police
dispatchers and it is determined that an officer
presence is required at the situation. An officer out
of those assigned to response is then allocated to the
situation. An example of this could be when a
burglary is reported to be currently taking place. In
this situation resources will be allocated to attend the
incident with the aim of apprehending the criminal.
The time taken to reach the scene of the incident can
affect the outcome of the situation. In the UK there
are target response times which are dependent on the
incident severity and whether it occurs in the city or
rural environment. To increase the chances of an
officer being able to respond to an incident within
these response times their positioning whilst not
attending an incident can be optimized. The key
factors to consider when positioning officers are:
predicted demand coverage
presence in areas where crime levels are
high
visibility.
The first key factor requires the officers, not
currently attending an incident, to be positioned to
give the highest possible demand coverage. Hence
this aspect of positioning is considered as a
maximum coverage location problem, using an
advancement of the double standard model used
previously for ambulance positioning (Gendreau et
al., 1997). The method varies from the original to
allow the response time restrictions for both city and
rural areas to be considered. Though demand
coverage is a major concern it is not the only
concern when positioning police officers. It has been
shown that a police presence in areas of high crime,
hotspots, can reduce crime in that area (Smallwood,
2015). The visible presence of a police officer also
increases the public’s feeling of safety. Due to the
need to visit hotspots and visibility requirements
police officers cannot be positioned by only
considering the ideal response location. Hence in
this work a method of dynamic patrol route planning
is developed, that takes into account demand
Leigh, J., Jackson, L. and Dunnett, S.
Police Officer Dynamic Positioning for Incident Response and Community Presence - Using Maximum Demand Coverage and Kernel Density Estimation to Plan Patrols.
DOI: 10.5220/0005705402610270
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 261-270
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
261

coverage, hotspots and visibility to determine the
most efficient route for officers to take when
patrolling. This model of patrol planning also
considers those response officers not presently
available to patrol by removing them from the
directed patrol routes whilst still considering them
with regards to demand coverage.
The current method of directing patrol routes in
the UK is through informing officers of waymarker
locations, which are areas of concern, during a
briefing before a shift. They are asked to visit these
and stay within the defined waymarker boundaries
for a set period of time, i.e. 15 minutes, when
possible. They are not advised when to do this,
where other officers are and hence are not
considering demand coverage. This research
demonstrates a method of advising officers on where
to travel in real time when not attending an incident.
This research address an issue experienced by
many police forces and has benefited from
collaboration with Leicestershire police in the UK.
Due to this collaboration Leicestershire has been
used as a case study. Processes may vary slightly
between forces but the tool will still be applicable.
The remainder of this paper is broken up as
follows. Section 2 gives background to the project
through looking at relevant research. Section 3
defines the problem to be addressed and aspects to
consider. Section 4 describes the maximum coverage
location problem to be solved. Section 5 shows how
crime analysis is performed using quadratic kernel
density estimation and how the crime data is
displayed using thematic mapping. Section 6 details
how the location problem is solved using a tabu
search heuristic. Section 7 describes the routing
process between hotspots. Section 8 contains the
results of solving the problem and finally section 9
concludes the paper.
2 LITERATURE REVIEW
Location planning has already been heavily
researched in many areas including ambulance
positioning. These applications are generally looking
at stationary locations. A maximal covering location
problem (MCLP) is used to find the optimal location
for ambulances (Daskin and Stern, 1981). This study
is relevant to the police demand coverage problem
but does not consider the two time restrictions
required in police coverage and does not consider
that repositioning is required. The MCLP problem is
advanced to consider two time standards and the
different levels of demand coverage required in the
double standard model (Gendreau et al., 1997). This
does not consider the two time restrictions required
by the police. Further studies also considers the
MCLP but considers repositioning when an
ambulance is sent to an incident (Mandell, 1998).
The study also considers the availability of the
servers and two different servers. This study is
relevant when considering the conditions of moving
officers but does not consider the different level of
coverage required and that police should not revisit
bases within a certain time.
Operation Savvy (Smallwood, 2015) is a police
operation carried out by West Midlands Police and
Cambridge University to investigate the effect of
directed patrols on crime hotspots. These directed
patrols consisted of police community support
officers (PCSOs) visiting the epicentre of a hotspot
for fifteen minutes, three times at prime time, which
is between 3pm and 10pm Wednesday to Saturday.
To form the hotspots demand data from two years
was used in a 150m radius. The hotspots focused on
in this study are anti-sociable behaviour (ASB),
burglary, criminal damage, theft and vehicle crime.
Patrols were stepped up in 40 hotspots and 40
hotspots were kept as controls. The results of this
study showed that in the high and medium crime
level experimental hotspots there was a noticeable
reduction in all crime types and anti-social
behaviour. Further results on the communities trust
and confidence in the police is to be examined by a
survey. This study proved the effectiveness of
directed patrol routes but only used this to direct
PCSO patrols at certain times of day and demand
coverage was not considered.
A tool, GAPatrol, to help police managers plan
patrol routes is proposed in (Reis et al., 2006). In
this study multiagent-based simulation assists in the
design of police patrol routes. The simulation finds
crime hotspots and plans routes with better coverage
in these hotspot areas. Hence the routes are planned
with the single aim of reducing crime levels and do
not consider demand coverage for incident response.
The patrol routes of state troopers concerned
with the prevention of traffic incidents has been
explored (Li and Keskin, 2013). The aim of the
study is to determine the best locations for
temporary stations and increase the effectiveness of
patrols by increasing visibility in time periods where
high levels of crime have been experienced whilst
minimizing associated costs which include price of
state troopers, travelling costs and station fees. The
problem to be solved is similar to a multi-depot,
dynamic location and routing problem.
A previous study on planning patrol routes based
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
262

patrol routes on giving each road a crime rating and
visiting those with the highest costs whilst also
keeping cost of travel low (Chawathe, 2007). This
study does not consider demand coverage for
incident response and also only considers one police
unit at a time which is not practical. In reality there
are many units and where each of these units are
patrolling effects the other units.
An alternative study on patrol routes uses ant
colony algorithms along with Bayesian decision tool
to plan patrol routes (Chen et al., 2015). The ant
colony aspect relates to the history of patrols being
tracked by the drop of virtual pheromone and its
decay. This is a good method of stopping repeat
hotspot visiting within short spaces of time whilst
also tracking when another visit is required. The
downfall of this study is that it doesn’t consider
coverage for incident response.
These previous studies help develop the idea of a
dynamic routing problem addressed in this research.
Once the problem is formulated a method of Tabu
search is considered to solve the problem using
MATLAB. Tabu search allows the search area to be
narrowed down to give a solution in a shorter
computational time, which is required in the fast
paced dispatch process.
Hotspot mapping is a means of analyzing historic
crime data to predict future crime patterns. This is
possible as crime is not random. Crime follows
patterns due to environmental influences effecting
criminal’s decisions (Kennedy et al., 2011). Crime
mapping is widely used within the police and law
enforcement agencies. There are many different
methods including point mapping, spatial ellipses,
thematic mapping and Kernel Density Estimation.
There have been many studies determining the best
method of hotspot mapping. A study by (Chainey et
al., 2008) identified Kernel Density Estimation as
the best method for predicting future crime
locations. Hence it is the method which will be used
in this study.
3 PROBLEM FORMULATION
A response officer’s main duty is to provide
emergency response to incidents of high severity.
Responding to incidents takes up the majority of
their time and there is limited time to patrol. When
there is time to patrol these patrols must be directed
efficiently. Those officers whom require patrol
direction are those which are not currently attending
an incident. The problem investigated is improving
the efficiency of these patrol routes by giving them
direction in real time. This direction is based on
keeping good demand coverage between all the
response officers and being visible in problem areas,
hotspots. This will keep response times low and in
the process deter crime from hotspots.
Response officers operate in units as some are
paired to create double crewed vehicles hence the
entities considered are response units. When a
response unit is free to patrol the location to patrol is
calculated using the processed formed in this
research. The chosen location is then conveyed to
the response unit as simple instructions. These
instructions include time to spend at the location and
what to look for, it assumed the unit will take the
quickest route to this incident hence directions are
not necessary. When they have attended the hotspot
for the appropriate length of time this hotspot is
marked as visited and if required a new hotspot
location is assigned to the response unit. As more
response units become free they are allocated
hotspots. If incidents arise within the patrolling time
the response to incident will take priority.
When solving the problem there are some
constraints to be considered regarding policing
standards and processes. Leicestershire Police
requires that in an emergency situation a unit should
attend the incident within fifteen minutes, which is
taken to be
, in heavily populated areas such as
cities and towns. In sparsely populated areas such as
rural areas the response time should be within
twenty minutes, which is taken to be
. The area
can then be divided into areas with a node at the
centre. Hence a node is considered covered if the
following conditions are met:
when considering a town/ city a unit must be
located within
of node
when considering a rural area a unit must be
located within
of node
Taking the distance which can be travelled within
to be
and within
to be
where
(Mandell, 1998).
This is a spatial problem which requires a region
to be used for modelling. Data from
OpenStreetMaps (© OpenStreetMap contributors,
2015) is used to form a directed graph of the roads in
Leicestershire within MATLAB. The road map
formed is shown in figure 1.
The problem formulated is now considered as a
MCLP using hotspots as possible nodes to locate
response units.
Police Officer Dynamic Positioning for Incident Response and Community Presence - Using Maximum Demand Coverage and Kernel
Density Estimation to Plan Patrols
263
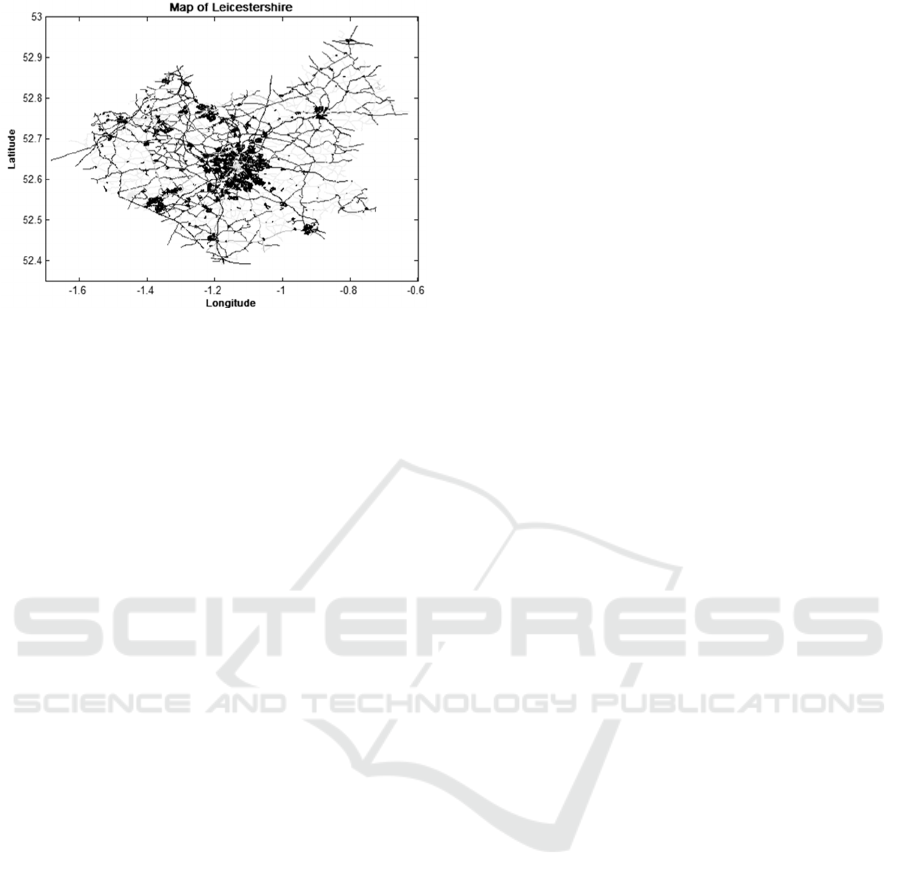
Figure 1: Road map of Leicestershire.
4 MAXIMUM COVERAGE
LOCATION PROBLEM
Demand coverage is a measure of how well response
units are able to cope with possible emergency
response demand. This can be determined by
predicting demand using historical incident data and
whether an officer can reach the demand location,
node , within the recommended response time.
Nodes are a point of reference to measure demand
from, they can be a point on a street or in reference
to an area.
A variation of the double standard model is used
to find maximum police coverage for a given
number of officers (Gendreau et al., 1997). This
method is suitable as it considers two time standards
and also allows different levels of coverage, , to be
considered. This is necessary because areas with
high levels of demand are not sufficiently covered
by one response unit. allows the level of response
units required to consider a region as covered to be
set. The objective function for this is equation (1)
which aims to maximize coverage. The demand
points are represented by the set
,
,…,
and the demand at these points is
.
is a binary
variable which equals 1 if
is covered a minimum
of k times within the radius
and 0 otherwise.
Where k is the number of units which are in range to
reach node .
Maximize
∑
∈
(1)
This objective function has been adapted here to
apply to the police positioning problem. The
adaption is necessary to account for the
recommended response times for city and rural
areas. Equation (2) accounts for city and rural
response guidelines. In this equation
is a binary
variable which equals 1 if
is covered a minimum
of k times within the radius
.
is a binary
variable which equals 1 if
is covered a minimum
of k times within the radius
. C and R are binary
variables which equal 1 if node
is in a city or rural
area.
Maximize
∑
∈
(2)
The objective function results in the total demand
covered at least k times within the required
emergency response distances,
or
depending on
its location. It is subject to the constraints:
1
∈
∈
(3)
,
,
∈
(4)
∈
(5)
,
∈
0,1
∈
(6)
,∈
0,1
(7)
1
(8)
When considering response unit positioning
,
,…,
represents the set of possible
locations, these are decided by the hotspots found
from incident analysis.
shows the number of
resources located at . The total number of units
available is taken to be and this is determined by
the number of officers on shift with an available
status at that time, whether they are single or double
crewed and their availability. These constraints also
differ from the original double standard model due
to the different priorities of the police (Gendreau et
al., 1997). The problem will still aim to cover all
demand within at least
which is taken into account
by constraint (3). Constraint (4) states that node
can only be covered +1 times if it is covered at
least times. Constraint (5) ensures that the sum of
all the officers at each point W is equal to .
Constraint (6) and (7) ensures
,
, and are
binary values. Finally constraint (8) states that either
or must equal 1, but never both at the same
time.
When solving the objective function above there
are rules on where each officer can be placed due to
their status and attached station. These are:
1. An officer can only move if its status is available
(they are not attending an incident, in custody, on
a break, etc.).
2. An officer only counts as covering an area if they
are free to attend an incident, this includes
officers who are available or attending an incident
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
264

more minor than an emergency incident.
3. The distance from their base police station must
be less than maximum displacement from their
station allowed
, where
is the distance
from the base police station to the possible
location where an officer is required and
is the
maximum distance an officer is allowed from
their base station determined by the police force.
Rule 1 is just the condition that a police officer must
be available before moving them. In rule 2 an officer
is counted as covering an area if attending a grade 2
incident because if necessary they can leave such an
incident to respond to an emergency incident but
they cannot be moved unnecessarily. Hence they are
not moved when solving for maximum coverage.
Rule 3 ensures that officers do not move too far
from their base police station. Each officer has an
attachment to a particular police station and even
though most police forces operate as boundaryless
within their area it is not efficient to move an officer
too far away from their associated station due to
their journey back at the end of a shift.
When applying this approach to the ambulance
location problem the possible nodes () where they
can be located are bases, such as car parks and
service stations. For the police it is more important
to be based in hotspot areas where they are a
deterrent to further crime.
5 INCIDENT MAPPING
Location is a very important factor when analyzing
crime as repeat area targeting is more common than
repeat offenders. Crime mapping is used to show
where crimes occur; this allows the movement of
crime over time to be analyzed. A study previously
discussed (Reis et al., 2006) showed that crime is not
evenly distributed but forms patterns due to the
habits of criminals. Figure 2 shows the crime spread
through Loughborough (a small town within
Leicestershire) by the numbers in grey circles. It
demonstrates the uneven distribution of crime, for
example the town centre has a high level of crime at
119 incidents (Police UK, 2015). Crime analysis
identifies these patterns which is the first step in
reducing crime levels. Crime analysis is vital in the
planning of patrol routes as routes should be directed
to visit areas of higher than average levels of crime,
called hotspots.
Finding hotspots, determining the causes and
responding to the results to reduce crime in the areas
identified is referred to as problem oriented policing.
Figure 2: Crime distribution.
Crime analysis has been in police forces for a long
time, beginning with a map with pins in to represent
crimes, developing to the same concept on a
computer. It has been proven that focused patrols
depending on these hotspots can assist with the
prevention of crime (Smallwood, 2015). Currently
police forces have a crime analysis team to look into
crime patterns and computer programs to determine
where high levels of crime occur.
Before crime can be analysed it requires filtering
to pick out the data which is relevant to the problem
and to discard bad data. This is described in section
5.1. Once it has been filter a means of analysing it is
required which is done using quadratic kernel
density estimation in section 5.2.
5.1 Incident Data Analysis
Data analysis is required to filter the
incidents/crimes down to those relevant to police
patrolling. The crimes and incidents considered are
those where the presence of an officer can help deter
them. These include:
anti-social behavior
theft
vehicle crime
burglary in dwelling and other
criminal damage.
Incidents in certain places should be excluded
from the analysis as they also cannot be prevented
by the presence of an officer patrolling on the
streets, these places include:
clubs or bars
shopping centers
hospitals.
There are some incidents on record which may
cause anomalies to the hotspot locations this is cases
such as incidents mapping to a default area when the
correct location has not been given. These are also
filtered out before analysis of crime data.
Crime levels change depending on day, time of
Police Officer Dynamic Positioning for Incident Response and Community Presence - Using Maximum Demand Coverage and Kernel
Density Estimation to Plan Patrols
265
day and season. Hence it is not accurate to find
general hotspots. Data is separated into Sunday-
Thursday and Friday – Saturday and also into day,
evening and night as well as seasonality. Hotspot
analysis is then carried out separately using only
data from the allocated time period. As hotspots
change with time the possible locations to position
officers (W) vary.
5.2 Kernel Density Estimation
Kernel Density Estimation is a method of spatial
analysis for crime mapping which allows complex
point patterns to be simplified to assist in the
identification of hotspots. This method is superior to
other crime mapping methods as it is not limited by
strict boundaries such as beat boundaries. Beat
boundaries are predefined areas, such as a town,
which an officer has to patrol. Using boundaries can
result in some hotspots which cross the boundary not
being identified. Kernel Density Estimation uses
grids however also considers the areas surrounding
the grid cell, by using kernels, to allow the
surrounding area to influence the intensity of crime
within the cell.
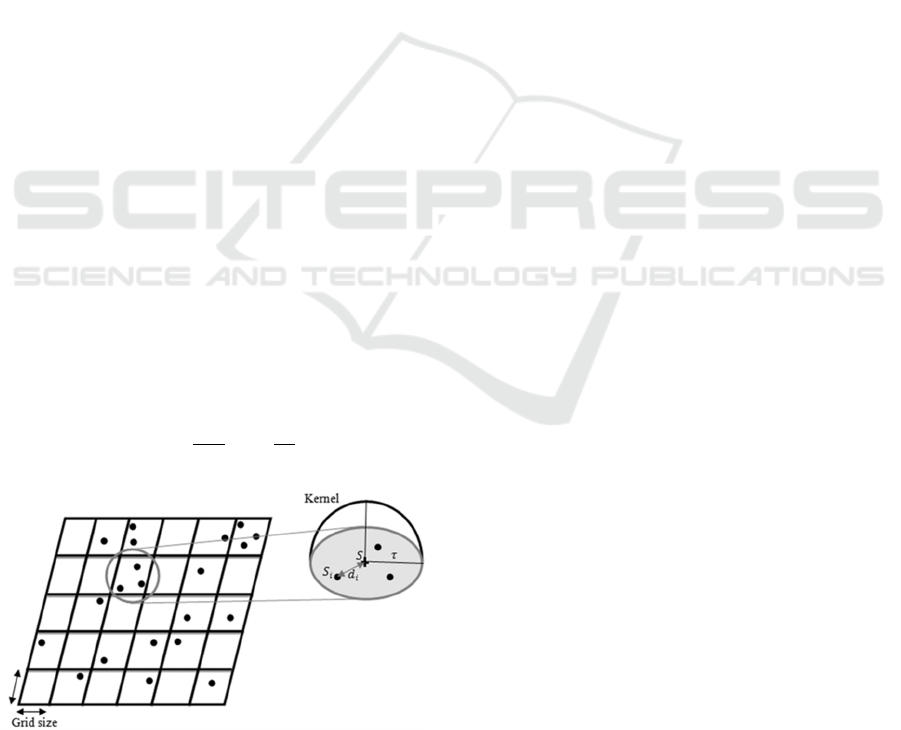
Quadratic kernel density estimation involves
overlaying a grid onto the map and visiting each grid
cell to preform kernel density estimation. Figure 3
shows how quadratic kernel density estimation is
performed and the process is then described below.
Kernel density estimation finds the points at
which crime incidents have occurred within the
predefined bandwidth boundary and determines the
influence each of these crimes has on the intensity of
crime in that area using equation 9 (Gatrell et al.,
1996).
3
1
(9)
Figure 3: Quadratic kernel estimation.
Where
is the intensity of crimes within the
bandwidth () as a function of the distance from the
center (s).
is the distance between the grid centre
and the point being investigated.
This intensity is inversely weighted, giving
crimes near the centre of the grid cell a greater
contribution to the intensity than those further from
the centre. As crimes move further from the centre
the intensity decreases until finally those on the
boundary have an intensity of zero.
To perform this successfully an appropriate
bandwidth and grid size must be determined. A
bandwidth too large causes excessive smoothing
which in turn leads to hotspots not being found. A
bandwidth which is too small leads to insufficient
smoothing causing a spikey graph, which leads to
incorrect identification of hotspots. In this work both
the bandwidth and grid cell size are determined
using testing where computational time is taken into
consideration. The resulting bandwidth for this
analysis is taken to be 0.001
ο
and grid cell size
0.001
ο
x 0.001
ο
, measured in the longitude and
latitude coordinate system.
Now the objective function is defined with
constraints and the hotspot locations have been
found the equation can be solved using tabu search.
6 TABU SEARCH
There are many possible solutions to the MCLP. The
ideal situation would be to find the optimal solution
to position officers in the optimal locations. To find
the optimal solution each solution must be
investigated, exhaustive search. Doing an exhaustive
search would take considerable computational time,
making it an impractical approach; hence a method
of narrowing the search is required. Tabu search is a
method of searching for a solution without
investigating every solution. It does not guaranty an
optimal solution but has been proven to be an
accurate method of solving similar problems
(Gendreau et al., 1997). Hence for this problem tabu
search is used to solve the MCLP for police officers.
Tabu search is a form of local search. Local
search has the disadvantage of getting stuck at local
optima, Tabu search stops the search getting stuck at
a local optima as it finds a solution and then moves
from this solution to its best neighbour even if this
causes the objective value to deteriorate which
allows solution to move on from local optima. A
neighbour is a solution one move away from the
previous solution and the best neighbour gives the
maximum value when calculating the objective
functions. Revisiting solutions is stopped by using a
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
266

tabu list, each solution which has been visited is
placed on the tabu list and the solutions on this list
can’t be revisited whilst they remain on the tabu list.
They will remain on the list for a selected number of
iterations.
Response units are advised to remain in the
hotspots they are allocated for a set period of time
determined by the police force, typically 15 minutes.
If a response unit completes the recommended
attendance period of a hotspot this hotspot is marked
as visited. Those hotspots recently completed are
placed on the tabu list to stop response units
revisiting hotspots which have recently been visited
and give preference to choosing those hotspots
which have not recently been visited. This tabu list
is kept through multiple searches. Revisits can be
performed only after a certain period of time which
is dependent on the strength of the hotspot.
6.1 Tabu Search Process
An initial solution is found randomly and solved
using equation (2) and constraints (3)-(8). The
neighbouring solutions are then found which are
found by moving one officer to a new location per
neighbouring solution and they are solved in the
same way. The hotspot locations available to
position officers will be decided depending on the
time of day, day of the week and season. Out of
these the best solution is taken and all others are
added to the tabu list. This stops the solution cycling
back to the same solution and getting stuck at a local
optima. This new solution is taken to be the solution
and the process is restarted. This process is repeated
until one of the stopping criteria is met.
When a stopping criterion is met the best
solution is used to position officers. Once the
appropriate time to visit a hotspot has passed, e.g. 15
minutes, the problem is solved again to re-determine
using the new response unit statuses and locations. A
new tabu list is started prohibiting revisiting hotspots
which have been visited.
6.2 Stopping Criteria
The maximum number of iterations has been
reached
The number of iterations since the last
improvement has exceeded a set value
Optimal solution obtained.
7 ROUTING BETWEEN
HOTSPOTS
The response units are allocated a hotspot to attend
but assumed to take the shortest route to this hotspot.
Which hotspot to allocate to each response unit is
determined by calculating the routes between the
response units and the hotspots which have been
chosen by the MCLP. The solution with the lowest
overall distance travelled whilst meeting all the
constraints is chosen and the response units are
allocated accordingly. The routes are calculated
using Dijkstra’s algorithm.
Figure 4: Patrol route.
Figure 4 represents a typical route between an
officer and a hotspot. The circle with no centre
represents a police officer. The filled circle
represents the centre of the hotspot. The thick black
line details the routes to the hotspots.
8 RESULTS
The resulting process to determine optimal officer
locations is detailed in figure 5. The flow chart
shows that the road map for the region of concern is
developed, the crime data is then filtered and used to
determine hotspots, before being solved as a
maximum coverage location problem. The results
are then conveyed to the response units. The MCLP
is solved each time response units require
positioning. The hotspots are reevaluated regularly,
using the new crime data available, to find new
hotspots.
The officer positioning process is tested by
simulation. The simulation runs through typical
situations which may occur within police response.
The officer positioning tool is used when necessary
Patrol route
Latitude
Longitude
Police Officer Dynamic Positioning for Incident Response and Community Presence - Using Maximum Demand Coverage and Kernel
Density Estimation to Plan Patrols
267
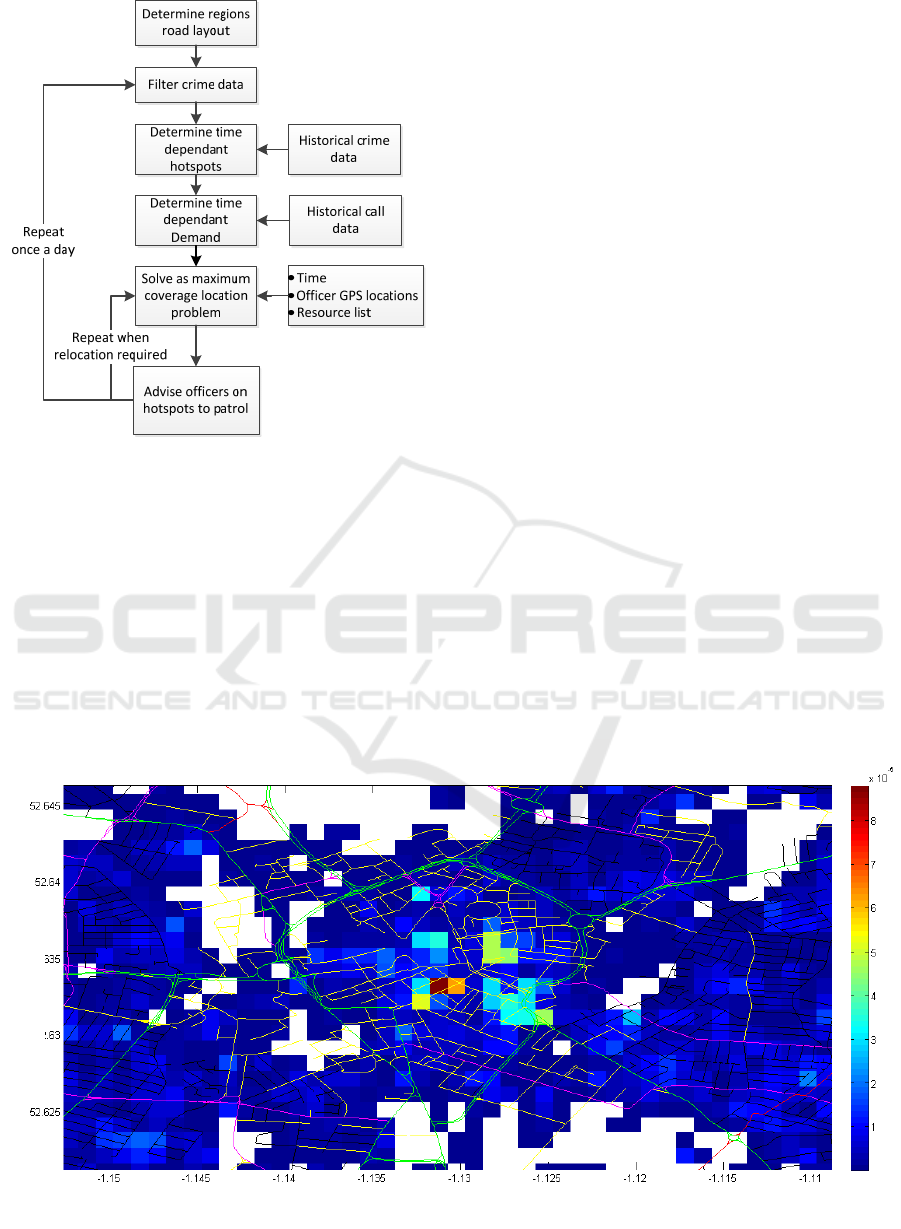
Figure 5: Automated positioning process.
to allocate officers to hotspots. The simulation
demonstrates the ability for the tool to determine
efficient positioning for the officers.
The first section of the processes is identifying
the hotspots. An example of a typical hotspot map
for anti-social behaviour, produced by Kernel
Density Estimation analysis, is shown in figure 6.
The figure shows the hotspots found in Leicester
center during the evenings of Friday and Saturday.
The red square indicates the area with the highest
crime intensity level, followed by orange and
yellow. The shades of blue represent a low crime
intensity level and no colour indicates that there is
no significant case of anti-social behaviour. Out of
all the hotspots identified through kernel density
estimation the top 3% are used as possible locations
to position officers. These hotpots are used to solve
for the objective function. Another grid is overlaid
onto the map which contains the predicted call
demand. This is used to determine what demand is
covered when positioning officers. The number of
officers is taken to be p which is based on the
number of officers on shift and typical availability of
these officers. The population in the area determines
whether the cell is considered rural or city.
The performance of the positioning processes is
currently measured using historical data to prove its
worthiness before testing within police forces. This
is done by running the simulation for a period of
time in history where crime data has been recorded
for. Only crime information recorded before this
period starts can be used in the analysis, to simulate
the fact that when using the positioning tool in real
time the crime data is not available as it hasn’t
happened. The difference is when using a historical
time period the crime data for this period can then be
used to determine how well the officers targeted the
areas which crimes did occur in within this time
period. Hence if the officers had targeted these areas
these are the crimes which the officers may have
prevented. Equation (10) is used to determine how
Figure 6: Thematic map of kernel density results.
Kernel Density Estimation Graph of Leicester Centre
Latitude
Longitude
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
268

accurately the positioning tool targeted crime. The
equation originates from a study by (Chainey et al.,
2008) to determine how efficiently different crime
mapping methods predicted where future crime
occurred. In this case n represents the number of
crimes which occur within the hotspots target by
officers, whilst N is the total number of crimes
which occur. a is the total area of all the hotspots
targeted, whist A is the total area of the region
studied.
100
100
(10)
Using this equation over a one month period
allowing for 5% of an officers shift time to be
allocated to patrolling resulted in the potential to
deter 22% of street crimes. Increasing the time
available to patrol would increase the ability to deter
crime. Decreasing the time available for officers to
patrol would decrease ability to deter crime.
Tabu search offered a search method with
lower computational costs than performing an
exhaustive search. It did not guarantee the optimal
solution though there wasn’t a significant difference
between the optimal result and the tabu result.
9 CONCLUSIONS
Dynamic directed patrol routes for response officers
are a way of ensuring officers are efficiently placed
for incident response whilst also visiting hotspot
areas. A program which advises officers on where to
patrol is unique and has a place in the current police
objective to work more efficiently using predictive
policing.
The variation of the double standard model
allows both city and rural response time
requirements to be considered. It also allows
different levels for coverage to be accounted for.
Whilst quadratic kernel density estimation
effectively predicts crime hotspots as it reduces
boundary effects by considering the surrounding
areas. This coupled with thematic mapping allows
clear graphical representation of crime hotspots.
Solving quickly is an important aspect of locating
police offices and tabu search gives a shorter
computational time than exhaustive search.
The effects of directing patrol routes include a
decrease in response times and an increased ability
to deter crime. The next stage for this method is to
include more methods of hotspot identification, as
well as testing in real time within a police force
response team. The performance of this method can
then be evaluated by testing within the police force.
Where the performance of hotspot targeting can be
measured by the overall level of crime and the
performance of demand coverage can be measured
by the change in response times.
ACKNOWLEDGEMENTS
The cooperation of the Leicestershire Police is
gratefully acknowledged as without their support
this project would not be possible. This work was
supported by the Economic and Social Research
Council [ES/K002392/1].
REFERENCES
Chainey, S., Tompson, L., Uhlig, S., (2008). The Utility of
Hotspot Mapping for Predicting Spatial Patterns of
Crime. Security Journal, palgrave. Vol. 21, p. 4-28.
Chawathe, S.S. (2007). Organizing Hot-Spot Police Patrol
Routes. Intelligence and Security Informatics, IEEE.
p.79-86.
Chen, H., Cheng, T., Wise, S., (2015) Designing Daily
Patrol Routes for Policing Based on Ant Colony
Algorithm. ISPRS Annals of the Photogrammetry
Spatial Informatics Sciences. Vol. II-4/W2. p. 103-
109.
Daskin, M. S., Stern, E. H., (1981). A Hierarchical
Objective Set Covering Model for Emergency Medical
Service Vehicle deployment. Transport Science,
Institute for Operations Research and the Management
Science. Vol. 15 (Issue 2). p. 137-152.
Gatrell, A. C., Bailey, T. C., Diggle, P. J., Rowlingson,
B.S. (1996). Spatial Point Pattern Analysis and its
Applications in Geographical Epidemiology.
Transactions of the Institute of British Geographers,
Royal Geographical Society. Vol. 21 (Issue 1). p. 256-
274.
Gendreau, M., Laporte, G., Semet, F., (1997). Solving an
Ambulance Location Model by Tabu Search. Location
Science, Elsevier Science Ltd. Vol. 5 (Issue 2). p. 75-
88.
Kennedy, L., Caplan, J., Piza, E., (2011). Risk Clusters,
Hotspots, and Spatial Intelligence Terrain Modeling as
an Algorithm for Police Response Allocation
Strategies. Journal of Quantitative Criminology,
Springer. Vol. 27, issue 3, p. 339-362.
Li, S. R., Keskin, B. B., (2013). Bi-criteria Dynamic
Location-Routing Problem for Patrol Coverage.
Journal of the Operational Research Society,
Operational Research Society. Vol. 65. p. 1711-1725.
Mandell, M., (1998). Covering Models for Two-Tiered
Emergency Medical Services Systems. Location
Police Officer Dynamic Positioning for Incident Response and Community Presence - Using Maximum Demand Coverage and Kernel
Density Estimation to Plan Patrols
269

Science, Elsevier Science Ltd. Vol. 6. p. 355-368.
© OpenStreetMap contributors. (2015). OpenStreetMaps
[Online]. Available at: http://
www.openstreetmap.org/#map=10/52.5964/-1.1838.
Police.UK (2015). Loughborough Central. Available at:
http://www.police.uk/leicestershire/L07/
Reis, D., Melo, A., Coelho, A., Furtado, V., (2006).
Towards Optimal Police Patrol Routes with Genetic
Algorithms. Mehrotra, Springer. Vol. 3975. p. 485-
491.
Smallwood, J. (2015) What Works Crime Reduction:
Operation SAVVY [Online]. College of Policing.
Available at: http://whatworks.college.police.uk/
Research-Map/Pages/ResearchProject.aspx?projectid=
306 [Accessed: 08/06/2015].
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
270
