Modeling of an Insect Proprioceptor System based on Different Neuron

Response Times

Daniel Rodrigues de Lima

, Michel Bessani

, Philip Newland

and Carlos Dias Maciel

Department of Electrical and Computational Engineering, University of S

ao Paulo, S

ao Carlos, S

ao Paulo, Brazil

Centre for Biological Science, University of Southampton, Highﬁeld Campus, S017 1BJ Southampton, U.K.

Keywords:

Neuronal Spike Signals, Neuronal Response, Desert Locust, FeCO, Transfer Entropy, Inter-Spike Interval,

Survival Analysis.

Abstract:

This paper analyzes neuronal spiking signals from the Desert Locust Femorotibial Chordotonal Organ (FeCO).

The data comes from records of the insect neuronal response due to external stimulation. We measured the

Inter-Spike Interval (ISI) and calculated Transfer Entropy for investigate different FeCO responses. ISI is a

technique that measures the time between two spikes; and transfer entropy is a theoretical information measure

used to ﬁnd dependencies and causal relationships. We also use survival functions to assemble FeCO models.

Furthermore, this work uses and compares results of two approaches, one with transfer entropy and other with

ISI measures. The results indicate evidence to support the existence of more than one type of FeCO neuron.

1 INTRODUCTION

The biologically inspired engineering studies biologi-

cal structures intending to ﬁnd solutions for engineer-

ing problems (Zhang et al., 2015). Examples include

the Particle Swarm Optimization Algorithm (Santos

and Maciel, 2014), the control of exoskeletons using

principles found in biomechanics (Jimnez-Fabin and

Verlinden, 2012) and neuronal circuits (Endo et al.,

2015). Recent works analyzed neural signals (Je-

gadeesan et al., 2015) trying to identify patterns and

connections inside the nervous system (Subramaniam

et al., 2015). They analyzed signals from neural ex-

periments which are records from the neuronal re-

sponses due to some speciﬁc stimulus or situations

(Birmingham et al., 2014).

This paper presents the analysis of signals col-

lected on experiments with desert locust neurons. The

experiments were made by stimulating the insect lag

with a forceps that was shaken by a Gaussian White

Noise (GWN). Figure 1 shows the signal analysis

schematic and presents a sample of the recorded sig-

nals. The data analyzed come from a large and multi-

variate neurobiological data set obtained from a neu-

ral insect network (Newland and Kondoh, 1997). This

network produces and controls the movements of the

desert locust hind leg (Angarita-Jaimes et al., 2012).

Speciﬁcally, the data analyzed here were collected on

the Femorotibial Chordotonal Organ (FeCO). FeCO

is a proprioceptor that detects movements from the

tibia relative to the femur of a desert locust hind leg

(Burrows et al., 1988), and its behavior is equivalent

to others found in more complex structures (Vidal-

Gadea et al., 2010).

Previous studies investigated neuronal structure

models in the FeCO data (Maciel et al., 2012).

They also investigated characteristics of the signal

transmission channel (Endo et al., 2015). While

doing these experiments, transfer entropy measure-

ments (Schreiber, 2000) suggested the existence of

different kinds of FeCO. Transfer entropy is an

information-theoretic measurement, which allows to

detect non-linearity (Nichols et al., 2005), establish

causal relationships (Barnett et al., 2009), and also

ﬁnd interaction delays between signals (Pampu et al.,

2013). Some curves obtained from these measure-

ments showed different FeCO responses and pointed

the possible existence of different groups of neurons.

Those curves motivated this investigation about how

many kinds of FeCO neurons exist.

In order to investigate different FeCO responses

we combined two analyzes: transfer entropy and the

Inter-Spike Interval (ISI) (Schwalger et al., 2015).

Classically, ISI measures the amount of time spent be-

tween spikes, trying to ﬁnd a probability distribution

for them (Chen et al., 2009). However, this study uses

ISI measurements to determine parameters to classify

the FeCO in different groups of neurons. The pa-

Lima, D., Bessani, M., Newland, P. and Maciel, C.

Modeling of an Insect Proprioceptor System based on Different Neuron Response Times.

DOI: 10.5220/0005706202190226

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 219-226

ISBN: 978-989-758-170-0

219

GWN

27HZ

GWN

200HZ

FeCO

Figure 1: Schematic of the signal analysis presenting the collected signals (bottom) and their interaction (top). In the ex-

periment, a Gaussian Withe Noise (GWN) with a bandwidth of 200Hz passed trough a low-pass ﬁlter with cutoff frequency

manually adjusted to 27Hz or 58Hz. The ﬁltered signal shook a forceps that moved the locust leg stimulating its nervous

system. The FeCO signal is the neuronal response to the excitation, and it is also a spiking signal. This diagram is the primary

assumption, which considers only one kind of FeCO.

rameters found are used in a statistical representation,

which uses survival functions (Lawless, 2011) to as-

semble FeCO models.

Survival Analysis aims to explore the behavior of

sets of individuals according to the time interval nec-

essary for an event to happen (Collett, 2003). Ex-

amples include a system failure (Achcar and Moala,

2015) or a patient longevity (MacKenzie et al., 2014).

The survival technique also analyzes data from remis-

sion time (Cabrero et al., 2015), which is the time

spent between two occurrences of an event (Bewick

et al., 2004). ISI is the time spent between two spikes

(two occurrences), and it is possible to use survival

functions to create FeCO models.

The study goal is to investigate whether the FeCO

response rates would change under the same stimula-

tion. For that, we analyzed FeCO signals recorded

during two different experiments: one applying a

GWN stimulation limited to 27Hz; and another lim-

ited to 58Hz. To perform the analysis, we used ISI

technique and statistical treatments as a criterion to

divide and classify the signals into different groups.

We also used transfer entropy to reinforce our as-

sumption about the existence of different kinds of

FeCO and investigate the differences between the

groups found. Finding different types of FeCO, the

diagram in Figure 1 will need to be changed. This

study will be useful then to check if the diagram from

Figure 1 is sufﬁcient to represent the FeCO neuronal

structure or if a more complex model is required.

Furthermore, using the two analyzes, ISI and

transfer entropy, it is possible to identify different

kinds of FeCO neurons. Additionally, next section

will present the survival analysis and transfer entropy

theories. They are followed by the methodology sec-

tion that describes the experiment. Also, the results

section will present the FeCO analysis, followed by

the conclusion and next steps.

2 THEORY

This section presents the theories used to analyze the

FeCO data, and assemble the models created, respec-

tively Transfer Entropy, and Survival Analysis.

2.1 Transfer Entropy

We used the property of transfer entropy detect time

delays (Pampu et al., 2013) as a reference measure

to check the algorithms consistency by calculating

the propagation time between the signals 200Hz and

27Hz. We also used it to look for dependencies be-

tween FeCO and 27Hz signals. Additionally, it will

be used to reinforce our assumption of different kinds

of FeCO.

Transfer entropy has signiﬁcant properties. The

ﬁrst one is that it indicates the shared information be-

tween two random variables, making possible to de-

termine connections and dependencies (Runge et al.,

2012). A second one is that transfer entropy uses

a time lag to introduce directional sense (Schreiber,

2000), causal sense (Wibral et al., 2012) and ﬁnd

time-delays (Ito et al., 2011). These properties make

it similar to time-delayed mutual information (Jin

et al., 2010). However, time-delayed mutual infor-

mation does not distinguish information exchanged

from shared information, while transfer entropy does

(Schreiber, 2000).

Transfer entropy (Vicente et al., 2011) is deﬁned

as follows by

T E(X;Y ) =

∑

p(y

t+u

, y

, x

)log

p(y

t+u

)

p(y

t+u

)

, (1)

where t represents the discrete time index, u the pre-

diction time, and x

and y

are the delay vectors.

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

220

2.2 Survival Analysis

A survival time variable (T) is a non-negative random

variable representing the time until an event occurs

(Klein and Moeschberger, 2003). If f(t) represents

T probability density function, and F(t) represents

its cumulative distribution function, then the survival

function (S(t)) is deﬁned as follows:

S(t) = Pr(T ≥ t) = 1 −F(t) =

∞

f (x)dx, (2)

which represents the probability of an event do not

occur during time t.

Another concept related to the survival variable T

is the hazard function h(t) deﬁned as:

h(t) = lim

∆t→0

P(t ≤ T < t + ∆t|T ≥ t)

∆t

. (3)

The function h(t) represents the instantaneous

rate of a given event occurs at time t (Klein and

Moeschberger, 2003). For ∆t → 0,

P(t ≤ T < t + ∆t) → f (t) (4)

and using the conditional probability rule (Walpole

et al., 2014) we can rewrite (3),

P(A|B) =

P(A ∩ B)

P(B)

⇒ h(t) =

f (t)

S(t)

. (5)

In the experiments, the excitation signals had a

constant bandwidth, hence we considered that the

spike rate is also constant. Consequently, the hazard

function is also constant, and in this case, it is possible

to use an exponential distribution,

f (t) = λe

−λt

= µe

−

, (6)

with survival function

S(t) = e

−λt

= e

−

, (7)

where λ is the spike rate (spikes/ms), and µ is the dis-

tribution mean (ms/spike) (Harrell, 2013).

To obtain the exponential models for the data sets,

we sampled the time between spikes (ISI), and calcu-

lated a mean time between spikes (MTBS - µ) on each

one of the signals.

3 MATERIALS AND METHODS

The experiments used thirty ﬁve adult desert locusts,

Schistocerca gregaria (Forsk

al), male and female, ar-

ranged ventral-side-uppermost in modeling clay. By

cutting a piece of cuticle in their anterior distal fe-

mur, the FeCO apodeme was exposed and gripped by

a forceps attached to a shaker (Ling Altec 101). A

small window opened in their ventral thorax exposed

the metathoracic ganglion that was immobilized on a

wax covered with a silver platform. The sheath was

treated with protease (Sigma type XIV) for 1 min be-

fore recording. After that, microelectrodes ﬁlled with

potassium acetate and with DC resistances of 50-80

MΩ were driven through the sheath. They entered

into the neuropilar processes of the nonspiking lo-

cal interneurons, the axons of sensory neurons, or

the somata of spiking local interneurons. Intracellular

recordings were made using an Axoclamp 2A ampli-

ﬁer (Axon Instruments, USA).

A GWN signal shook the forceps. The GWN

was produced by ﬁltering a pseudo random binary

sequence (CG-742, NF Circuit Design Block) band-

limited to 27Hz or 58Hz with low-pass ﬁlters (SR-

4BL, NF Circuit Design Block) with a decay of 24

dB/octave. This generated a signal with a Gaus-

sian probability density function in the bandwidth

of interest. The signal vibrated the forceps holding

the apodeme, stimulating and evoking the interneu-

rons responses, as shown in Figure 2. The signals

were stored on magnetic tape using a PCM-DAT data

recorder (RD-101 T, TEAC, Japan) and then sampled

at a rate of 10 kHz ofﬂine to a computer.

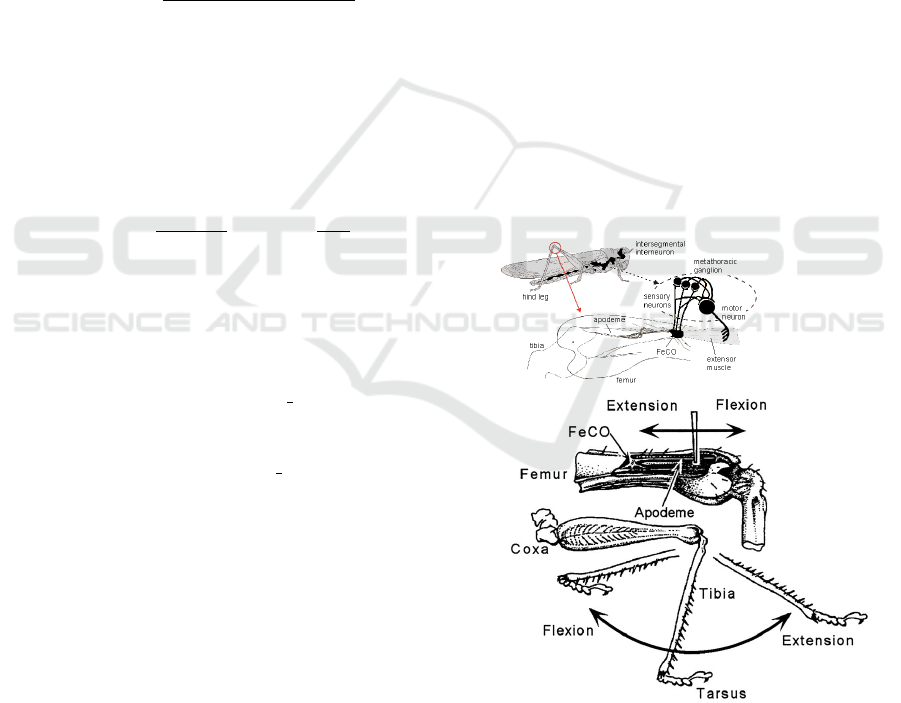
Figure 2: Desert Locust neuronal system (top) with the

neurons where the signals were collected, highlighting

the FeCO. Correspondent leg movement for the exten-

sion/ﬂexing caused by the forceps excitation (bottom).

Modeling of an Insect Proprioceptor System based on Different Neuron Response Times

221

4 RESULTS

This section presents the ISI Analysis on 27Hz, and

58Hz signals, and transfer entropy measurements in

the 27Hz signals.

4.1 ISI Analysis

Experiment with 27Hz Signals

The MTBS on each one of the 27Hz signals were

measured, and their conﬁdence intervals were calcu-

lated. Table 1 shows the results after processing the

27Hz data set, calculating the MTBS and conﬁdence

intervals considering an α = 5% for all 25 samples.

Table 1: MTBS and conﬁdence intervals for 27Hz signals.

Sample

CI Low MTBS CI Up

(ms/spike) (ms/spike) (ms/spike)

1 15.79 16.92 18.05

2 19.52 20.32 21.12

3 21.69 22.50 23.30

4 21.75 22.60 23.45

5 21.72 22.67 23.61

6 22.01 23.01 24.02

7 21.95 23.18 24.40

8 22.46 23.49 24.52

9 23.73 24.66 25.58

10 24.06 25.35 26.65

11 24.45 25.56 26.68

12 25.68 26.91 28.15

13 26.14 28.71 31.27

14 28.42 29.89 31.35

15 30.75 32.63 34.50

16 31.42 33.05 34.69

17 33.25 35.84 38.43

18 34.95 36.82 38.69

19 45.31 49.10 52.89

20 46.83 49.79 52.76

21 46.85 49.83 52.80

22 50.00 53.26 56.53

23 51.90 54.12 56.34

24 58.15 62.16 66.18

25 58.14 62.28 66.41

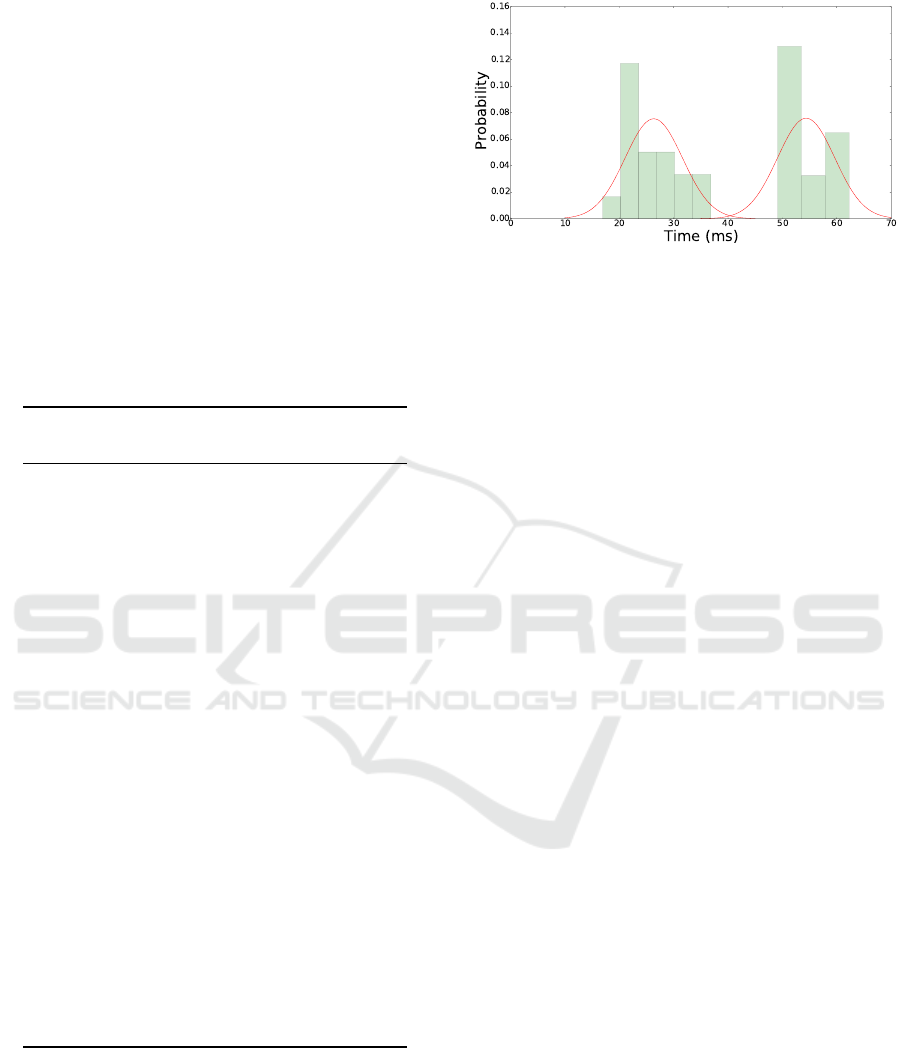
Table 1, presents a gap between samples 18 and

19 conﬁdence intervals. The same gap appears in the

MTBS histogram presented in Figure 3. These gaps

point to the existence of two groups, i.e., two different

neuronal responses rates.

Since samples 1 and 2 conﬁdence intervals are dis-

connected, we performed a hypothesis test comparing

the MTBS, testing if there are two or three groups of

Figure 3: Histogram of the MTBS (Table 1) calculated for

the 25 signals in the 27Hz data set. It is possible to note a

gap indicating the presence of two different groups.

neurons (Walpole et al., 2014). The tests assumed a t

statistic with an α = 5%, and followed the hypothesis



: µ = µ

: µ 6= µ

(8)

The hypothesis H

indicates that the MTBS mea-

sured (µ

) is equal to the group mean (µ), while the

hypothesis H

indicates the opposite. The hypothesis

was accepted with a signiﬁcance level α = 5% for

all MTBS inside each group.

Experiment with 58Hz Signals

The time between each spike on the 58Hz signals

was measured in order to calculate the MTBS and

their conﬁdence intervals. Table 2 shows the results

after processing all the 58Hz data set, calculating

the MTBS and conﬁdence intervals considering an

α = 5%.

From Table 2, it is possible to see that the sam-

ples conﬁdence intervals cannot be separated. This

suggests only one group of neurons in the 58Hz data.

This is reinforced by Figure 4 that shows the his-

togram of MTBS. To assure this assumption, a hy-

pothesis test (Equation 8) for the MTBS was made

with an α = 5%. As a result, the hypothesis H

was

accepted for all MTBS (µ

A consideration must be made for the 58Hz exper-

iment, since its results opposed to the ones presented

in Figure 3. The number of samples in the 58Hz ex-

periment is the same of the ﬁrst group found in the

27Hz experiment; thence it is possible that the 58Hz

experiment only recorded signals from the ﬁrst group.

However, it is known that there are nonlinear compo-

nents in the desert locust neuronal system (Dewhirst

et al., 2013). This implies that the output signal could

present an entirely different response once that the in-

put excitation is changed.

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

222

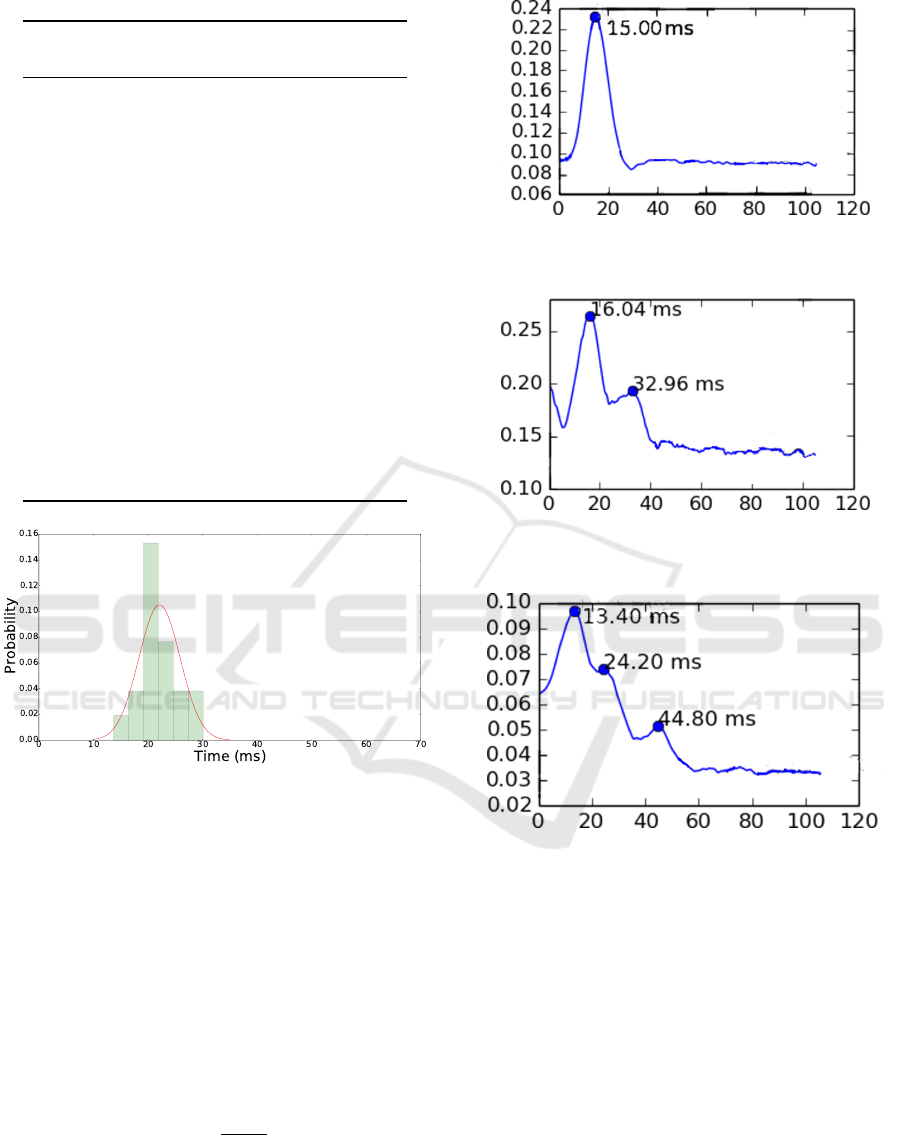
Table 2: MTBS and conﬁdence intervals for 58Hz signals.

Sample

CI Low MTBS CI Up

(ms/spike) (ms/spike) (ms/spike)

1 17.87 18.57 19.27

2 18.33 19.03 19.73

3 19.23 19.92 20.60

4 19.38 20.12 20.87

5 19.40 20.15 20.90

6 19.53 20.35 21.18

7 19.58 20.37 21.16

8 19.67 20.43 21.19

9 19.88 20.69 21.50

10 20.51 21.32 22.13

11 21.82 22.84 23.86

12 22.43 23.46 24.48

13 22.56 23.46 24.36

14 22.96 24.12 25.28

15 24.84 25.79 26.74

16 25.45 26.53 27.60

17 27.36 29.17 30.98

18 28.86 30.17 31.47

Figure 4: Histogram of MTBS (Table 2) calculated for the

18 signals in the 58Hz data set. It is possible to note only

one group of neurons.

4.2 Transfer Entropy

After making ISI analyzes and ﬁnd evidences of two

possible kinds of neuronal response in the 27Hz data

set, we made transfer entropy measurements for the

signals inside the 27Hz experiment.

The ﬁlter used adds a ﬁxed and well known time

delay for a given cutoff frequency f

(Manal and

Rose, 2007). The equation for the time delay is given

delay

0.416

, (9)

and since f

was 27Hz, it is expected that transfer en-

tropy presents a 15.41ms delay between 200Hz and

27Hz signals. Figure 5 shows that the time-delay

found is close to the expected.

Figure 5: Transfer entropy calculated between 200Hz and

27Hz signals for references purposes. The time delay found

is close to the expected with an error of 2.6%.

Figure 6: Transfer entropy calculated between 27Hz and

FeCO signals in the ﬁrst group of neurons, showing two

maximum points.

Figure 7: Transfer entropy calculated between 27Hz and

FeCO signals in the second group of neurons, showing three

maximum points.

We calculated transfer entropy between 27Hz and

FeCO signals in the ﬁrst group, which is presented in

Figure 6. It is important to note that the graph shows

two maximum points.

We also calculated transfer entropy between 27Hz

and FeCO signals in the second group. Figure 7

presents the results and points three time-delays.

Figure 6 differs from Figure 7 in the number of

time-delays found. The ﬁrst ﬁgure presents two max-

imum points: one at 16.04 ms, and another at 32.96

ms. The second presents three maximums: one at

13.40 ms, other at 24.20 ms, and another at 44.80 ms.

Modeling of an Insect Proprioceptor System based on Different Neuron Response Times

223

4.3 FeCO Survival Models

We found two groups of neurons in the 27Hz exper-

iment and one group in the 58Hz. Using MTBS it

is possible to construct models representing their re-

sponse due to a ﬁxed excitation. Thence, it is consid-

ered the Survival models for that construction.

Considering that the distribution mean is the mean

of the group, we calculated conﬁdence intervals with

an α = 5% for each group mean, as shown in Table 3.

Table 3: Parameters calculated for the 27Hz experiment.

Group

λ µ CI 95%

(spikes/ms) (ms/spike) Low Up

1st 0.04 26.34 23.64 29.04

2nd 0.02 54.36 51.55 57.12

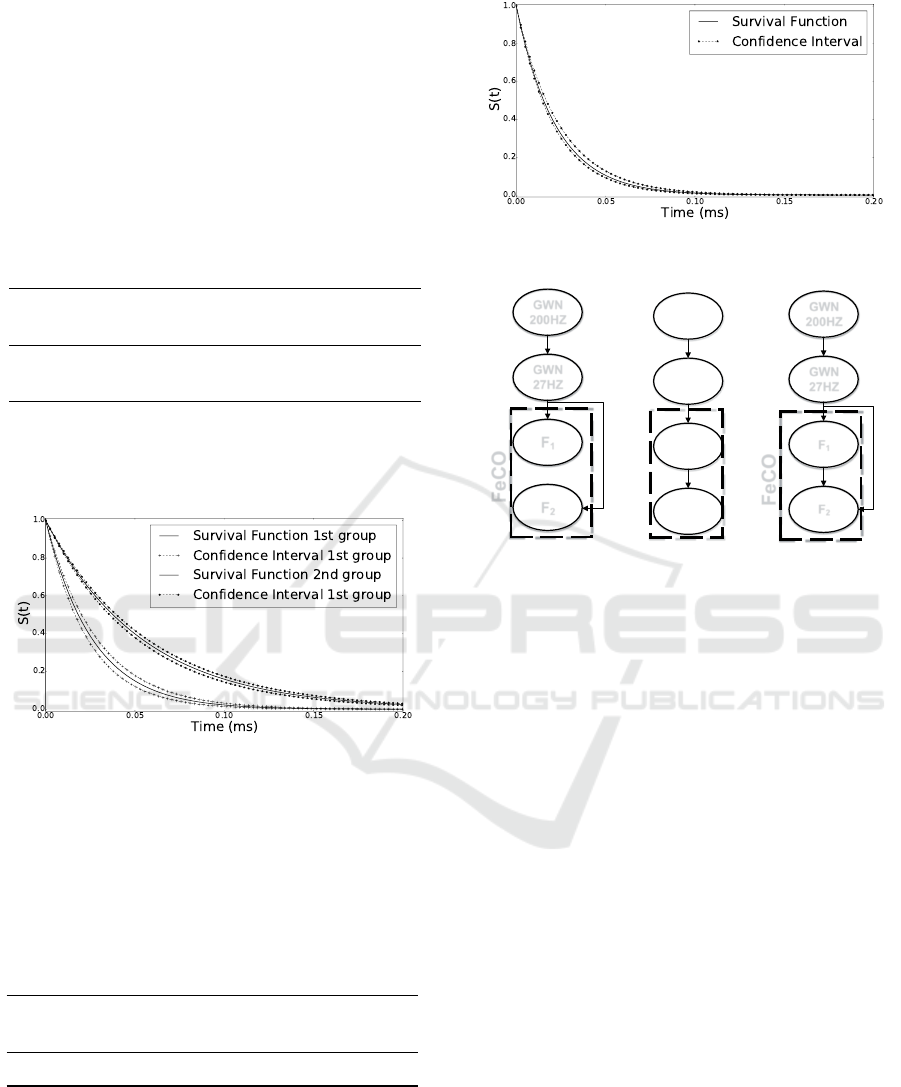
Figure 8 presents a graphic visualization, and it

is possible to notice that there is no common region

either for the functions or their conﬁdence intervals.

Figure 8: Survival probability functions for the two groups

of neurons. The conﬁdence intervals of those groups do not

touch, evidencing the existence of two groups of neurons.

In the 58Hz experiment we found only one neu-

ronal response rate. Considering that the distribution

mean is the group mean, we calculated a conﬁdence

interval with an α = 5% for the group, as shown in

Table 4.

Table 4: Parameters calculated for the 58Hz experiment.

Group

λ µ CI 95%

(spikes/ms) (ms/spike) Low Up

1st 0.05 22.11 20.89 24.27

4.4 FeCO Model

Results pointed two different neuronal responses,

which brings two possibilities. The ﬁrst one is that it

happens because there are two different FeCO struc-

tures. The second is that it happens because of the

Figure 9: Survival probability function for the group of neu-

rons found in the 58Hz data set with its conﬁdence intervals.

GWN

27HZ

GWN

200HZ

FeCO

GWN

27HZ

GWN

200HZ

FeCO

GWN

27HZ

GWN

200HZ

FeCO

Figure 10: Models suggested for the FeCO. A model with

two different neurons that are independent (left). Other

model where only the ﬁst kind of FeCO affects the second

type (middle). A model showing an inﬂuence of the ﬁrst

kind of FeCO, but it also presenting a direct inﬂuence of the

27Hz signal on the second kind of FeCO (right).

neuronal conﬁguration. Figure 10 presents three hy-

pothetical neuronal conﬁgurations.

The structures from Figure 10 are only sugges-

tions for the neuronal circuit conﬁguration, which

need deeper investigations to conﬁrm. The ﬁrst con-

ﬁguration assumes two different kinds of FeCO, and

they receive direct inﬂuence from the excitation sig-

nal. The second and the third conﬁgurations can as-

sume two distinct kinds of FeCO or only just two dif-

ferent response rates given by the same kind of FeCO

with different conﬁgurations. Both, third and second

conﬁgurations, suggest a model organized in layers

where there is a preprocessing process.

5 CONCLUSION

In this paper, we used two analyzes to investigate dif-

ferent neuronal responses due to the same excitation.

We analyzed signals from the desert locust metatho-

racic ganglion. Speciﬁcally we looked at the data

from the Desert Locust Femorotibial Chordotonal Or-

gan, which is a spiking neuron. The diagram shown in

Figure 1 was the simplest representation possible for

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

224

the FeCo experiment, ignoring the existence of any

other kind of FeCO neurons.

Figure 1 presented a diagram connecting the

200Hz signals to the 27Hz signals, and then 27Hz

to FeCO, and does not consider any other inﬂuences,

such as other neurons. However, here we pointed ev-

idence that suggest the existence of different kinds of

FeCO neurons. These ﬁndings show that it is possible

to obtain different response rates for FeCO neurons

even when they receive the same stimulation. There-

fore, it implies that there is a different connection than

the one presented in Figure 1.

Our assumption of a different connection than the

one showed in Figure 1 is supported by three differ-

ent analyses. The histograms of MTBS from Figure

3 pointed the existence of different neurons using the

ISI technique, and statistical hypothesis tests supports

these results. The survival models also showed two

different curves with non-overlapping conﬁdence in-

tervals. Additionally, Figure 6 and Figure 7 shows

two different responses for each group using the trans-

fer entropy technique.

All these measurements and tests point the exis-

tence of more than one kind of FeCO neuron. A con-

sideration must be made for the 58Hz signals since

they presented only one group, a result different than

the one showed for 27Hz signals. It is known that

there are nonlinear components inside the neuronal

system (Dewhirst et al., 2013), and this implies that

the output response could be entirely different once

the input excitation is changed.

We know that the algorithms for transfer entropy

are correct because of the reference measurement pre-

sented in Figure 5. A closer look at Figure 7 indicates

that it presents one more maximum point than Figure

6. By comparing the responses of Figure 6 and Figure

7 we made new assumptions about the connections in-

side the FeCO, they are presented in Figure 10.

The assumptions presented in Figure 10 suggest

two particular cases. The ﬁrst one with a structure

where there are no inﬂuence or iterations between the

two kinds of FeCO. The second case is that there is an

interaction between them. This case is supported by

Figure 7 that presents one more maximum point than

Figure 6, indicating a model organized in layers.

Those three possible structures shown in Figure

10 are not the only possible conﬁguration for the neu-

ronal system; the locust may have a complex struc-

ture. Future works are required to determine the best

connections and the best structure. Therefore, this is

our next steps when we intend to investigate the best

structure model using Dynamical Bayesian Networks

(Meyer-Baese and Schmid, 2014).

Moreover, this analysis indicates that the FeCO

neuronal connection structure is more complex than

the one presented in Figure 1. Additionally, we pre-

sented models based on survival functions for the

FeCO response. Those models can also be used to

perform simulations in future works.

ACKNOWLEDGEMENT

The authors would like to thank the Brazilian Federal

Agency for Support and Evaluation of Graduate Edu-

cation - CAPES; and also thank the National Counsel

of Technological and Scientiﬁc Development CNPq

for the Project number 475064/2013-5.

REFERENCES

Achcar, J. A. and Moala, F. A. (2015). Use of copula func-

tions for the reliability of series systems. Interna-

tional Journal of Quality & Reliability Management,

32(6):617–634.

Angarita-Jaimes, N., Dewhirst, O. P., Simpson, D. M., Kon-

doh, Y., Allen, R., and Newland, P. L. (2012). The dy-

namics of analogue signalling in local networks con-

trolling limb movement. European Journal of Neuro-

science, 36(9):3269–3282.

Barnett, L., Barrett, A. B., and Seth, A. K. (2009). Granger

causality and transfer entropy are equivalent for gaus-

sian variables. Phys. Rev. Lett., 103:238701.

Bewick, V., Cheek, L., and Ball, J. (2004). Statistics review

12: survival analysis. CRITICAL CARE-LONDON-,

8:389–394.

Birmingham, K., Gradinaru, V., Anikeeva, P., Grill, W. M.,

Pikov, V., McLaughlin, B., Pasricha, P., Weber, D.,

Ludwig, K., and Famm, K. (2014). Bioelectronic

medicines: a research roadmap. Nature Reviews Drug

Discovery, 13(6):399–400.

Burrows, M., Laurent, G., and Field, L. (1988). Propriocep-

tive inputs to nonspiking local interneurons contribute

to local reﬂexes of a locust hindleg. The Journal of

neuroscience, 8(8):3085–3093.

Cabrero, M., Jabbour, E., Ravandi, F., Bohannan, Z., Pierce,

S., Kantarjian, H. M., and Garcia-Manero, G. (2015).

Discontinuation of hypomethylating agent therapy in

patients with myelodysplastic syndromes or acute

myelogenous leukemia in complete remission or par-

tial response: Retrospective analysis of survival after

long-term follow-up. Leukemia Research, 39(5):520

– 524.

Chen, L., Deng, Y., Luo, W., Wang, Z., and Zeng, S. (2009).

Detection of bursts in neuronal spike trains by the

mean inter-spike interval method. Progress in Natural

Science, 19(2):229 – 235.

Collett, D. (2003). Modelling survival data in medical re-

search. Texts in statistical science. Chapman & Hall,

London, New York.

Modeling of an Insect Proprioceptor System based on Different Neuron Response Times

225

Dewhirst, O., Angarita-Jaimes, N., Simpson, D., Allen, R.,

and Newland, P. (2013). A system identiﬁcation anal-

ysis of neural adaptation dynamics and nonlinear re-

sponses in the local reﬂex control of locust hind limbs.

Journal of Computational Neuroscience, 34(1):39–58.

Endo, W., Santos, F., Simpson, D., Maciel, C., and New-

land, P. (2015). Delayed mutual information infers

patterns of synaptic connectivity in a proprioceptive

neural network. Journal of Computational Neuro-

science, 38(2):427–438.

Harrell, F. E. (2013). Regression modeling strategies: with

applications to linear models, logistic regression, and

survival analysis. Springer Science & Business Me-

dia.

Ito, S., Hansen, M. E., Heiland, R., Lumsdaine, A., Litke,

A. M., and Beggs, J. M. (2011). Extending transfer

entropy improves identiﬁcation of effective connectiv-

ity in a spiking cortical network model. PLoS ONE,

6(11):e27431.

Jegadeesan, R., Thakor, N., and Yen, S. C. (2015). Wire-

less for peripheral nerve prosthesis and safety. In

Neural Engineering (NER), 2015 7th International

IEEE/EMBS Conference on, pages 648–651.

Jimnez-Fabin, R. and Verlinden, O. (2012). Review of

control algorithms for robotic ankle systems in lower-

limb orthoses, prostheses, and exoskeletons. Medical

Engineering & Physics, 34(4):397 – 408.

Jin, S.-H., Lin, P., and Hallett, M. (2010). Linear and non-

linear information ﬂow based on time-delayed mu-

tual information method and its application to cor-

ticomuscular interaction. Clinical Neurophysiology,

121(3):392–401.

Klein, J. P. and Moeschberger, M. L. (2003). Survival

analysis: techniques for censored and truncated data.

Springer Science & Business Media.

Lawless, J. F. (2011). Statistical models and methods for

lifetime data, volume 362. John Wiley & Sons.

Maciel, C. D., Simpson, D. M., and Newland, P. L. (2012).

Inference about multiple pathways in motor control

limb in locust. In BIOSIGNALS, pages 69–75.

MacKenzie, T., Gifford, A. H., Sabadosa, K. A., Quinton,

H. B., Knapp, E. A., Goss, C. H., and Marshall, B. C.

(2014). Longevity of patients with cystic ﬁbrosis in

2000 to 2010 and beyond: survival analysis of the

cystic ﬁbrosis foundation patient registry. Annals of

internal medicine, 161(4):233–241.

Manal, K. and Rose, W. (2007). A general solution for the

time delay introduced by a low-pass butterworth digi-

tal ﬁlter: An application to musculoskeletal modeling.

Journal of Biomechanics, 40(3):678 – 681.

Meyer-Baese, A. and Schmid, V. J. (2014). Pattern Recog-

nition and Signal Analysis in Medical Imaging. Else-

vier.

Newland, P. L. and Kondoh, Y. (1997). Dynamics of neu-

rons controlling movements of a locust hind leg ii.

ﬂexor tibiae motor neurons. Journal of Neurophysi-

ology, 77(4):1731–1746.

Nichols, J., Seaver, M., Trickey, S., Todd, M., Olson, C.,

and Overbey, L. (2005). Detecting nonlinearity in

structural systems using the transfer entropy. Physi-

cal Review E, 72(4):046217.

Pampu, N., Vicente, R., Muresan, R., Priesemann, V.,

Siebenhuhner, F., and Wibral, M. (2013). Transfer

entropy as a tool for reconstructing interaction delays

in neural signals. In Signals, Circuits and Systems

(ISSCS), 2013 International Symposium on, pages 1–

Runge, J., Heitzig, J., Marwan, N., and Kurths, J. (2012).

Quantifying causal coupling strength: A lag-speciﬁc

measure for multivariate time series related to transfer

entropy. Phys. Rev. E, 86:061121.

Santos, F. P. and Maciel, C. D. (2014). A pso approach for

learning transition structures of higher-order dynamic

bayesian networks. In Biosignals and Biorobotics

Conference (2014): Biosignals and Robotics for Bet-

ter and Safer Living (BRC), 5th ISSNIP-IEEE, pages

1–6.

Schreiber, T. (2000). Measuring information transfer. Phys-

ical review letters, 85(2):461.

Schwalger, T., Droste, F., and Lindner, B. (2015). Statis-

tical structure of neural spiking under non-poissonian

or other non-white stimulation. Journal of Computa-

tional Neuroscience, 39(1):29–51.

Subramaniam, K., Hooker, C. I., Biagianti, B., Fisher,

M., Nagarajan, S., and Vinogradov, S. (2015). Neu-

ral signal during immediate reward anticipation in

schizophrenia: Relationship to real-world motivation

and function. NeuroImage: Clinical, 9:153 – 163.

Vicente, R., Wibral, M., Lindner, M., and Pipa, G. (2011).

Transfer entropya model-free measure of effective

connectivity for the neurosciences. Journal of Com-

putational Neuroscience, 30(1):45–67.

Vidal-Gadea, A. G., Jing, X., Simpson, D., Dewhirst, O. P.,

Kondoh, Y., Allen, R., and Newland, P. L. (2010).

Coding characteristics of spiking local interneurons

during imposed limb movements in the locust. Jour-

nal of neurophysiology, 103(2):603–615.

Walpole, R., Myers, R., Myers, S., and Ye, K. (2014). Prob-

ability and statistics for engineers and scientists.

Wibral, M., Wollstadt, P., Meyer, U., Pampu, N., Priese-

mann, V., and Vicente, R. (2012). Revisiting wiener’s

principle of causality #x2014; interaction-delay re-

construction using transfer entropy and multivariate

analysis on delay-weighted graphs. In Engineering in

Medicine and Biology Society (EMBC), 2012 Annual

International Conference of the IEEE, pages 3676–

3679.

Zhang, Q., Yang, X., Li, P., Huang, G., Feng, S., Shen, C.,

Han, B., Zhang, X., Jin, F., Xu, F., and Lu, T. J. (2015).

Bioinspired engineering of honeycomb structure us-

ing nature to inspire human innovation. Progress in

Materials Science, 74:332 – 400.

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

226