Post Flash Crash Recovery: An Agent-based Analysis

Iryna Veryzhenko

and Nathalie Oriol

LIRSA, Conservatoir National des Arts et M

etiers, 40 rue des Je

uneurs, 75002, Paris, France

GREDEG-CNRS, University of Nice Sophia-Antipolis, 250 rue Albert Einstein, 06560 Valbonne, France

Keywords:

Agent-based modeling, Limit order book, Technical trading, Flash crash.

Abstract:

In this paper we focus on the traders that purely rely on algorithms in their decision making and their impact

on market quality during moments of instability. We describe an agent-based framework that successfully

reproduces main aspects of ﬂash crash. We simulate the effect of a large liquidity shock generated by a

very aggressive market order. We show that, despite the absence of market makers, the electronic order-book

architecture favors market resiliency and recovery.

1 INTRODUCTION

Artiﬁcial intelligence-based applications for assets

trading has completely reshaped ﬁnancial markets de-

sign and end-users behaviors. The development of

information systems trading over the centuries stim-

ulated the emergence of ﬁnancial clusters and located

geographic proximity at the heart of recent trading

strategies. At a microscopic level, the development

of algorithms able to compute past charts set the ba-

sic tenets of automated trading systems. Human fun-

damentalists traders has been partly replaced by me-

chanical trading strategies based on various types of

indicators designated as technical analysis strategies.

At a macroscopic level, the 1970s saw the introduc-

tion of the ﬁrst exclusive electronic stock exchanges

(such as the NASDAQ in 1971), while the tradi-

tional open outcry call market’s organization began

to wane. Taking advantage of technological innova-

tion, the double auction system based on an electronic

order book (a dematerialized version of the open out-

cry blackboard hosted by an algorithm) started to be

widely adopted by ofﬁcial stock exchanges. The shift

from a physical artifact, such as a blackboard man-

aged by humans, to a digital artifact, such as an algo-

rithm managed by computers, led to a complete reor-

ganization of the price discovery process and the co-

ordination between traders. Interestingly, this recent

process of digital transformation of trading desks and

microstructure coincides with appearance of extreme

events initiating the so-called ”ﬂash crashes era” for

ﬁnancial markets (Giles, 2012). We propose to study

the role of agents’ behaviors and market microstruc-

ture derived from artiﬁcial-based applications on ﬂash

crash emergence.

Agent-based models, which provide the condi-

tions for a controlled experiment and allow to il-

lustrate cause and effect relationships between ini-

tial scenario settings and model behavior, is a proper

tool to study extreme events on the stock market,

like ﬂash crash phenomena. Moreover, the ﬂexible

character of simulation program allows to study sep-

arately the inﬂuence of electronic order book and au-

tomated chartists strategies, to test different regula-

tor policies in order to prevent such market dynam-

ics. To the best of our knowledge there is only few

papers that study ﬂash crash in an artiﬁcial market

framework. A wide variety of traders are designed

in the paper of (Vuorenmaa and Wang, 2014) to sim-

ulate the key aspects of the ﬂash crash of May 6,

2010. The authors deﬁne stylized traders (fundamen-

talists, noise and opportunistic traders), institutional

algorithmic trader and high-frequency traders (HFT).

It is reported that HFT agents provide higher liquidity

in normal trading conditions, but they become aggres-

sive liquidity takers during the crash. As the num-

ber of HFT agents increases, so does the probabil-

ity of ﬂash crash. (Paddrik et al., 2012b), propose

a similar agent-based model of the E-Mini S&P 500

futures market including fundamental traders, market

makers, HFT, small traders and opportunistic traders.

They conclude that a ”hot potato” effect was gen-

erated by HFT. Alternatively, (Lee et al., 2011) or

(Brewer et al., 2013) distinguish themselves from pre-

vious papers by their conclusions. (Lee et al., 2011)

claim that extreme event problem might be less about

190

Veryzhenko, I. and Oriol, N.

Post Flash Crash Recovery: An Agent-based Analysis.

DOI: 10.5220/0005707401900197

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 1, pages 190-197

ISBN: 978-989-758-172-4

 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

HFT but rather about a dominant population of traders

that are responding to a given set of market variables

in similar ways. They conclude that any regulatory at-

tempt to ”slow down” trading may cause more prob-

lems than it solves. (Brewer et al., 2013) focus on

the effect of large-volume order and change in funda-

mentals on the market quality. In this paper, market

is populated only by zero-intelligence agents. They

conclude that the nature and impact of liquidity ero-

sion is sensitive to the market structure and that the

exact nature of crash and book erosion depends on

the structure of the order ﬂow. Authors test differ-

ent mechanisms to reduce the negative effect of ﬂash

crashes: introducing minimum resting time; shutting

off trading for a certain period; switching to call auc-

tion market session, that is particularly effective.

Our paper is most closely related to those two lasts.

We study the impact of market participants relying

only on algorithm decision making on market qual-

ity during a liquidity shock. We argue that both mi-

crostructure and agents’ behavior are part of the crash

and the market recovery.

2 FLASH CRASH IN ARTIFICIAL

MULTI-AGENT MARKET

To study ﬂash crash phenomenon we use ArTifcial

Open Market (ATOM) (Brandouy et al., 2013), which

is highly ﬂexible simulations platform and allows dif-

ferent parametrization of microstructure and traders

behavior for different scenarios. This platform con-

tains three main modules. The ﬁrst one is market

microstructure, that provides a mechanism for or-

ders routing. ATOM clones the main features of

the Euronext-NYSE stock exchange microstructure.

Such market is ruled by a negotiation system be-

tween traders on a double auction machanism struc-

tured in an order book. The next system’s com-

ponent is economic world that provides exogenous

information about corporate development, dividends

and coupons changes. Finally, agents component en-

compasses multiple types of agents with different util-

ity functions, believes and strategies. Trading strate-

gies take into account exogenous information, func-

tionality and rules of market microstructure, and en-

dogenous information (post transaction information,

generated by agents interaction).

2.1 Continuous Double Auction Market

For current experiments, we choose to set a continu-

ous double auction (CDA) microstructure which is a

replication of the widely used electronic order book.

The CDA is a market protocol where agents place or-

ders on separate buying (bid) and selling (ask) books.

There are two main types of orders: limit and mar-

ket orders. Limit order is an order to buy or sell a

given quantity of stocks with a speciﬁc price or bet-

ter. These orders are stored in the order book until

their complete execution or end of validity. The high-

est bid is called best bid, the lowest ask is the best ask.

A transaction occurs when best bid is higher than best

ask. Market order is an order to immediately buy or

sell a given quantity at the best available prices. A

transaction occurs when market order hits the limit

orders stocked on the opposite side.

A major aspect of the quality of market place is its

liquidity. Liquidity is a possibility to realize immedi-

ately a big-size transaction without affecting a price in

signiﬁcant way. A market order for more shares than

the size of best bid (ask) will execute at worse price

until it is fully executed and will provoke signiﬁcant

price variations. This type of orders is considered as

an aggressive one. Liquidity is directly related to mar-

ket resilience, which is a speed of recovery of the mar-

ket after a large shock, like big-size aggressive market

order. We test these properties in the market popu-

lated by strategic agents and zero-intelligence traders.

2.2 Traders’ Strategies

One of the goals of our paper is to determine the

impact of strategic agents driven only by the techni-

cal signals on market quality (liquidity and volatility)

during a liquidity shock. We wish to keep our model

as simple as possible, to be able to catch such effects.

For this reason we focus only on two types of traders,

fundamentalists and chartists (technical traders).

Fundamentalists are driven by the true (funda-

mental) asset’s value. The fundamental value of

each stock evolves according to the jump process

= V

t−1

+ δ

, where δ

∼ N(0,σ). As the agents

are bounded rational (or noisily informed), the fun-

damental value is biased by ε

, which determines the

accuracy of the agent i to interpret the fundamen-

tal information W

= V

+ ε

, ε

∼ N(0, σ

). Agents

are heterogeneous with respect to their parameter ε

To make a buy/sell decision an agent compares the

stock’s current price P

with fundamental value W

The price ﬁxing mechanism is inspired from the pa-

per (Chan et al., 1999).

The fundamentalists submit their order according

to procedure described in Table 1. To summarize,

agents buy undervalued stocks and sell overvalued

stocks according to their beliefs. They stop trading

when they are out of cash or stocks, if short selling is

not allowed.

Post Flash Crash Recovery: An Agent-based Analysis

191

Table 1: The order-submission procedure. P

ask

denotes a best ask price, P

bid

best bid price, al ph

ask tick size, β

bid tick

size, Q

is a volume of the order issued at the moment t, S

t−1

is a number of stocks hold by an agent at moment t −1, C

t−1

available cash hold by an agent at moment t −1, U(x

) the uniform distribution in the interval [x

Conditions Order type

Existing bid, existing ask

> P

ask

bid market order

< P

bid

ask market order

bid

< W

< P

ask

bid/ask order with probability 50%/50% at price ∼ U (P

bid

ask

)

Order book is empty

with probability 1/2 limit ask order at W

+ α

, Q

∼ U (1,S

t−1

)

with probability 1/2 limit bid order at W

− β

, Q

∼ U (1,C

/(W

− β

))

Empty bid side, existing ask

> P

ask

bid market order, Q

∼ U (1,C

ask

)

≤ P

ask

limit bid order at W

− β

, Q

∼ U (1,C

/(W

− β

))

Existing bid side, empty ask side

< P

bid

ask market order, Q

∼ U (1,S

t−1

)

≥ P

bid

limit ask order at W

+ α

, Q

∼ U (1,S

t−1

)

Technical traders or chartists rely on algorithms

to generate trading signals using historical price series

or charts as a main source of information. The basic

hypothesis of technical trading are as follows:

• Market is not efﬁcient, price is impacted not only

by a fundamental information but also by past

trends.

• Price series follows the trends.

• History is repeating itself.

• Price reﬂects predictions and a common mood of

traders.

A graphic is considered as a synthesis of market be-

havior. There exist upward and downward trends. Up-

ward and downward conﬁrmed trends determine buy

and sell trades. Technical traders use the algorithms

to determine a trend and to estimate whether the stock

is underpriced of overprice compared to this trend. In

other terms, they identify tradings signals based on

past price movements (Murphy, 1999). Technical an-

alysts focus on generating trading signals that provide

a higher investment return. For these simulations we

use three strategies of technical analysis, widely used

by practicians and largely studied in theoretical and

empirical literature and quoted as proﬁtable on intra-

day data (Aldridge, 2013).

Momentum indicator compares the current price

with the price in the past D(t, n) =

t−n

× 100, where

n is a historical window length, which is uniformly

driven from an interval [50,500]. If D > 100, an agent

sends a bid order, and if D < 100 the agent sends an

ask order.

Simple Moving Average strategy determines a gen-

eral tendency on the market. A price series is replaced

by Y

∑

i=t−n

∀t =

n,N. They issue bid/ask

orders when price P

crosses either above or below

a long-period trend Y

. The lower the length of the

moving average n the more closely it tracks the price

moving and more often it generates buy/sell signals.

Longer moving average indicates overall direction of

the market and reacts slower to market ﬂuctuations.

Relative Strength Index strategy measures the

strength of a trend.

RSI =

U +D

× 100

U – an upward change, D – a downward change. The

RSI indicator is plotted on a scale of 0 to 100. 0 rep-

resents the most oversold conditions and 100 the most

overbought.

The population of chartist is heterogeneous with

respect with their trading signals and their individ-

ual periods of position recalculation. Then, at each

tick, you can have either trend followers or contrarian

traders.

To decide a volume of new bid limit order an agent

computes ﬁrst of all a potential quantity Q

potential

t−1

c, the order volume is determined as Q

∼

U(1,4 × Q

potential

), where 4 is borrowing rate. 4 >

1 if borrowing is allowed. The volume of ask order

is determined as follow Q

∼ U(1,4 × S

t−1

), where

4 is a short selling rate. 4 > 1 if short selling is

allowed. Q

is a volume of the order issued at the mo-

ment t, S

t−1

is a number of stocks hold by an agent at

moment t − 1, C

t−1

is available cash hold by an agent

at moment t − 1, U (x

) the uniform distribution in

the interval [x

]

However, we recognize the importance of quantity

as a choice variable and that our volume submission is

a simpliﬁcation of a real one, which depends on risk

aversion.

Another important issue is how the limit price of

chartists is determined, as it impacts market liquidity

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

192

and volatility. In each trading session, chartist agents

trade near best bid and best ask. For this type of

agents, we use the procedure inspired by price setting

rules described in (Jacobs et al., 2004).

1. Bid price

Bid

= P

Bid

t−1

+ β

where P

Bid

t−1

is the best bid price in the order

book in t − 1; β

is a random value in the range

[1; 5]: it means that best bid price at the moment t

will be increased by value from 1 to 5 cents. P

Bid

is equal to the previous day closing price. If agent

gets an intention to buy stocks, she should check

our the best bid order and increase it by a certain

value β

in order to set up her order on the top

of the order book, decrease bid-ask spread and in-

crease own chances to realize transaction. In other

words, bidder is ready to pay up to 5 cents more

than the rest of traders.

2. Ask price

Ask

= P

Ask

t−1

− α

where P

Ask

t−1

is the best ask price in the order

book in t − 1; α

is a random value with the range

[1; 5]: it means that best ask price at the time t will

be decreased by value from 1 to 5 cents. P

Ask

previous day closing price.

This rule provides liquidity and reduce the bid-ask

spread (difference between buy/sell prices).

In the condition of double auction market, a proﬁt-

oriented buyer sets up the price lower his limit price

because there would be a seller willing to accept this

low bid price. Similarly, a seller sets a price higher

his limit price, expecting that there would be a bidder

ready to accept a high ask price. In condition of com-

petitive market, the price comes closer to the market

equilibrium price. As long as the buyer can under-

cut a competitor and still make a proﬁt, he will add

some insigniﬁcant amount to the last best bid price,

similarly, seller will decrease the last best ask price

by insigniﬁcant value, if it does not exceed his limit

price.

2.3 Simulations and Results

Here we describe the model of market mechanism and

agents interaction parameters we use in our experi-

ments.

As in real market, trading occur asynchronously

at discrete-time interval t = 1,2...510, that represents

a trading day of 8.5 hours at a minute granularity. At

each round a trader is picked by the system to make

a decision. A trader can have only one open position

at the time and, therefore, before issuing a new or-

der he should cancel an old one pending in the order

book. The agents send limit, market and cancel or-

ders. They also have a possibility to send a null order.

In such a way we model different trading frequencies,

and hence model realistic patterns of activity through-

out the day.

According to study realized by (Paddrik et al.,

2012a) there are around 2500 fundamentalists (buy-

ers and sellers). Due to the large number of traders,

we scale our simulations to 1/10 of the market, and

populate our artiﬁcial market by 250 fundamentalists.

In the ﬁrst experiment we run two scenarios: i)

operation shock (without fundamental reasons) in the

market populated by 250 fundamentalists only (these

simulation results serve as a benchmark to study an

impact of technical traders) ii) operation shock in the

market populated by 100 fundamentalists, 50 momen-

tum agents, 50 RSI agents, and 50 SMA agents. Each

of these experiments we conduct consists of 100 runs,

where each run begins with the same initial condi-

tions (initial wealth, hold stocks, etc). In such a way,

all statistics are averaged by over 100 repetitions. The

main parameters of these experiments are detailed in

Table 2.

Flash crash can be initiated by events and prac-

tices destroying liquidity. In two scenarios we cause

a ﬂash crash by introducing an aggressive market or-

der like in the paper of (Brewer et al., 2013). In such a

way we get an immediate effect on the market dynam-

ics. Flash crash is produced by submitting a 20-time

higher volume market order compared to average or-

der size, that can be considered as operational error

produced by a trader. Liquidity measures take about

20 best limit updates to return to their initial level (De-

gryse et al., 2005). For this reason an agent submits

a 20-times higher volume market order in the expec-

tation of matching about 20 best limits. This error

is introduced in the middle of trading day, at 255th

round.

We study the impact of this operational shock on

the market liquidity and price dynamic. In both sce-

narios, ask market order destroys bid side liquidity

and price falls rapidly. Just after this crash, bid side

contains few orders, hence the market is at its most

vulnerable and sensitive stage. High volatility period

follows the crash. Figures 1(b) and 1(d) report an in-

creasing of bid/ask spread, and consequently, a high

volatility.

In the presence of intraday technical traders,

which ignore the true value of the stock, the market

crash is deeper (for the same shock, the speculative

market loses on average 26.5%, while fundamental-

ists market declines on 12.3%) because speculative

strategies bring down the prices. Downward trend

is quickly explored by chartist, which exacerbate the

Post Flash Crash Recovery: An Agent-based Analysis

193

Table 2: Parameters and their initialization used in simulations.

Parameter Value Description

f und

i) 250 ii) 100 Number of fundamentalists

tech

i) 0 ii) 150 Number of technical traders

0,i

[1 000 000; 2 000 000] Initial cash attributed at moment 0 to the agent i

0,i

[100; 10 000] Number of stocks attributed at moment 0 to the agent i

rounds

510 Number of rounds per day

4 2 Short selling and borrowing are allowed with respect to

the portfolio constraints: ϖ

∈ [−1,1] and ϖ

∈ [−1,1],

where ϖ

and ϖ

are respectively stock and cash weights

in total portfolio

already declining prices. As far as downward trend

is registered, some part of speculative traders cancel

their old bid orders to submit the new ones with lower

limit price, the other part takes short position on this

stock.

In the market of fundamentalists, the crash depth

is determined by the initial state of the order book.

The crash is ﬁnished as far as market order is over. If

a large majority of agents (60%) follows speculative

strategy bid side of order book is negatively impacted

by orders canceling and short sales. It provokes liq-

uidity problems and makes the correction more com-

plicated. As far as fundamentalists start actively buy-

ing the stocks (as it is undervalued) the stock price

goes back up but high volatility is registered due to

high bid/ask spread.

Next, we study the statistical properties of stock

market before and after ﬂash crash in the two sce-

narios. We particularly focus on volatility as risk

measure (Grouard et al., 2003). A price series is

divided in two subsequences before and after the

crash. The ﬁrst series is represented by P

,...,P

where k is a moment of big-volume ask order ar-

rival. We calculate returns based on this price series

,...,r

k−1

, where r

= ln(P

i+1

) − ln(P

). This se-

ries represents a period before the crash. The sec-

ond series is based on the prices P

k+m+1

,...,P

, where

k+1

> P

k+2

> ... > P

k+m

and P

k+m

< P

k+m+1

, m is

the time length of the ﬂash crash. Next we calculate

the series r

k+m+1

k+m+2

,...,r

n−1

which represents a

series after the ﬂash crash.

In table 3, we show the mean and standard devi-

ation of each subsets along with higher order statis-

tics such as skewness and kurtosis for historical intra-

day returns. We report increased volatility just after

the crash: in the market populated by fundamental-

ists increases on average by 20% (from 0.003777883

to 0.004609726), in the mixed market standard de-

viation jumps (from 0.003969339 to 0.005433639).

Next, we estimate skewness and kurtosis as well. In

the market populated by fundamentalists only, the co-

efﬁcient of asymmetry is negative (from -6.138734

to -2.496489, that indicates a high probability of ex-

treme loss, which decreases after crash), this coefﬁ-

cient is positive in the mixed market (it varies from

1.807211 to 3.125376, that means a high probability

for extreme loss, which increases after crash).

Table 3: Summary statistics of log returns before and after

ﬂash crash. All statistics are averaged by over 100 repeti-

tions.

Market of fundamentalists Mixed market

Before After Before After

Mean -0.0001 4.5420e-05 -1.9091e-06 0.0002

Sd 0.0038 0.0046 0.0039 0.0054

Skewness -6.1387 -2.4965 1.8072 3.1254

Kurtosis 131.1714 38.6699 38.76373 77.4977

The results provide the evidence that in presence

of chartists the operational shock affects a price dy-

namic in a more signiﬁcant manner. In addition, this

practice reduces resiliency properties of market and

makes the price rapid convergence towards its fair

value more difﬁcult. In the next section we focus on

the market microsctructure mechanisms and their ef-

fect on the price dynamic during an operational shock.

3 THE ROLE OF MARKET

MICROSTRUCTURE

The literature indicates that many stylized facts and

price patterns are due to the market microstructure

and not to some sophisticated traders strategies. Good

market performance should not be automatically at-

tributed to traders rationality and intelligence, it can

be also explained by market mechanisms (auction)

(Gode and Sunders, 1997). In this section, we fol-

low the spirit of Gode and Sunder’s (1993) ”zero-

intelligence” traders (ZIT) to study the role of market

micro-structure in market recovery after ﬂash crash.

To address this question formally, we use artiﬁcial

market populated only by zero-intelligence agents.

For traceability reasons, the market is populated

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

194

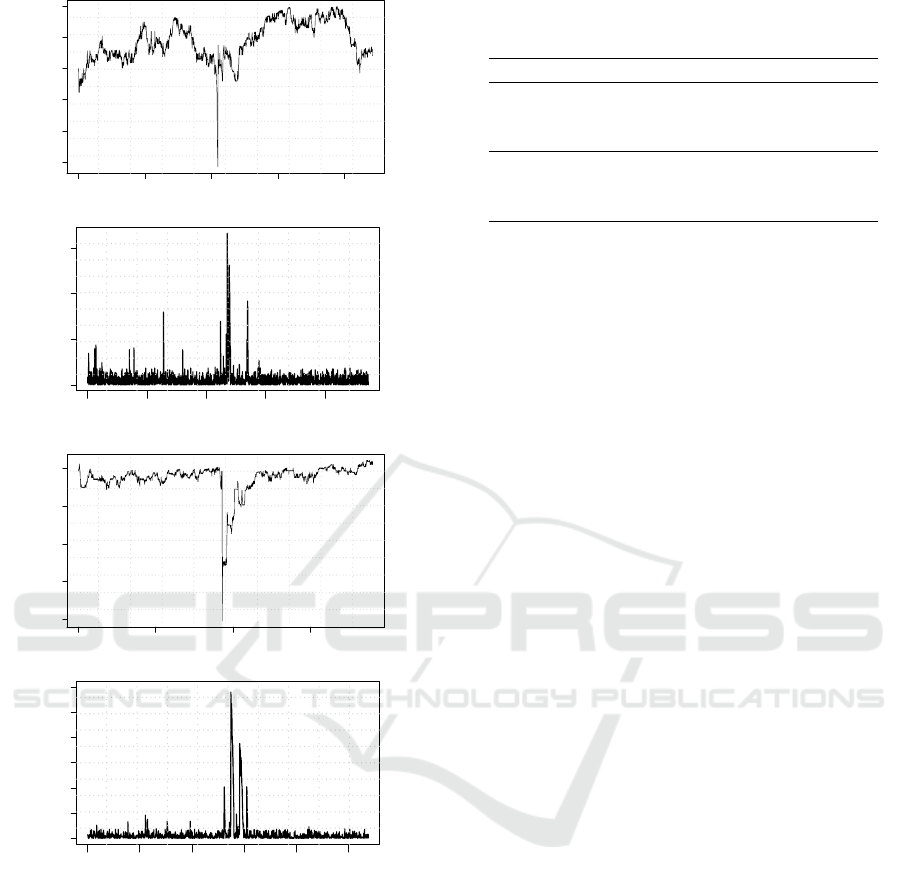
0 1000 2000 3000 4000

21 22 23 24 25 26

Times

Price

(a) Price. Market of fundamentalists.

0 1000 2000 3000 4000

0.0 0.5 1.0 1.5

Times

Price

(b) Bid/ask spread. Market of fundamentalists.

0 1000 2000 3000

22 24 26 28 30

Times

Price

0 500 1000 1500 2000 2500

0.0 1.0 2.0 3.0

Times

Bid/Ask Spread

(d) Bid/ask spread. Mixed market.

Figure 1: Simulations with 250 agents.

only by 15 zero-intelligence traders, who negotiate

only one asset. The ﬁxed price is a result of orders

submitted to the order book by traders. The price

of an order is randomly selected from the interval

min

max

]. That are settled to 43 and 46 respectively.

This interval initially communicated to all agents and

stay constant over simulations. We deﬁne two sub-

groups of agents which differ with respect to their

traded volume: ”Small ﬁshes” and ”Big ﬁshes” (send

10-times higher volume orders). Big ﬁshes ”feed”

Small ﬁshes. In other words, Small ﬁshes can eas-

ily buy or sell stocks with a price close to the cur-

rent market price, until a big order is completely exe-

Table 4: Zero intelligence trader’s decision making. P

min

max

, V

min

, V

max

minimum and maximum prices and vol-

umes, which are input parameters for algorithm.

Conditions Order type

with probability 1/2 limit ASK order at

price ∼ U(P

min

max

)

volume Q ∼ U(V

min

max

)

with probability 1/2 limit BID order at

price ∼ U(P

min

max

)

volume Q ∼ U(V

min

max

)

cuted. That generates patters of price stability. ”Small

ﬁshes” and ”big ﬁshes” represent 33% (1/3) and 67%

(2/3) of the total population respectively. This pro-

portion is explained in (Brandouy et al., 2012). Small

ﬁshes determine the trading volume arbitrary from the

interval [V

min

max

]. The order’s volume of big ﬁshes

is uniformly driven from the interval [V

max

,10×V

max

min

and V

max

are deﬁned as 5 and 50 respectively.

The ZIT decision making is presented in Table 4

There are two possible order types: limit, market.

Market order is used only once by an agent to generate

a market crash and to get an immediate effect on the

market dynamics. The rest of the agents submits only

limit orders, with no expiry.

Each agent can buy or sell the asset with the same

probability. The short selling is allowed, so the agents

can conclude the transaction even if they don’t have

enough cash to do so.

Figure 2(b) reports a typical picture of the

price series generated by the population of zero-

intelligence agents. The crash is followed by the high-

volatility regime over about 200 ticks. The upward

trend comes just after the high-volatility period. We

also report a signiﬁcant reduction of volatility. The

market mechanism explains this phenomenon. Over

ﬁrst 200 ticks big ﬁshes provide liquidity and permit

the market to stay quite stable. Due to operational

error a new big-size market order appears in the ask

side. This order immediately matches all Bid orders

pending in the order book as well as new incoming

orders. While the big-size ask order is not totally

fulﬁlled we observe the high-volatility regime. As

bid/ask orders arrive with the same probability and

only ”ex-market” order takes part in transaction, ask

side becomes deep and dense. As far as market order

is completed, other ask orders pending in the order

book can be proceed. According to the timestamps

priority, the concluded transaction price corresponds

to the ask order which generates a transaction. As a

result, market goes up that can be considered as the

market ”autocorrection”.

Figure 2(h) reports unusual behavior of slow de-

cay of autocorrelation in absolute returns |r

| over 174

lags that is followed by a cluster of negative corre-

Post Flash Crash Recovery: An Agent-based Analysis

195

0 200 400 600 800 1000

0 500 1500 2500

(a) Trading volume

0 200 400 600 800 1000

43.6 44.0 44.4

(b) Price

0 200 400 600 800 1000

−0.02 0.00 0.01 0.02

−0.02 −0.01 0.00 0.01 0.02

0 100 300 500

(d) Distribution of re-

turns

●

●●

●

●●

●

●●

●

●●

●

●●●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●●●●●

●

●●

●

●●●●

●●

●

●●●

●

●●

●●●●

●

●●

●●●●●●

●●●

●

●●

●●●

●●●●

●●

●

●●●●●●●●●●●●●●

●●●●●●

●●

●

●●

●●●●●●●●●●●●●●●●●●●●

●

●●

●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

●●●●●●

●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

●●●●●●●●●●●●●●●

●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

●

●●●●●●●●

●●

●●●●●

●●●

●●●●●●●●●

●●●●●●

●

●●●

●

●●

●

●●●

●●

●●●●●

●●

●

●●

●●●

●

●●●●●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

−3 −2 −1 0 1 2 3

−4 −2 0 2 4

(e) QQ plot

−10 −5 0 5 10

1e−08 1e−04 1e+00

●

(f) Normalized returns

0 200 400 600 800 1000

−1.0 −0.5 0.0 0.5 1.0

(g) Autocorrelation of

row returns

0 200 400 600 800 1000

−1.0 −0.5 0.0 0.5 1.0

(h) Autocorrelation of

abs returns

●

1 2 5 10 50 200

1e−05 1e−03 1e−01

(i) Slow decay in abs re-

turns, log scale

Figure 2: Simulations with 15 zero-intelligence agents.

lations. As one can see from the ﬁgure, the coefﬁ-

cients are signiﬁcant over long period which supports

the so called mean-reversion behavior of stock market

returns. These results are in agreement with observa-

tions reported in (Cont, 2007). This non trivial behav-

ior of autocorrelation is also reported in the absolute

returns of the real individual stocks during the ﬂash

crash on April 23, 2013. This observation is remark-

ably stable across S&P 500 stocks. This phenomenon

can be explained by the fact that positive effects of

past order ﬂows on current prices are reinforced dur-

ing periods of high stress (Cohen and Shin, 2002).

These results show that the electronic order book and

the market microstructure’s role is determinant in the

post-ﬂash crash recovery.

4 CONCLUSIONS

This paper aims at studying the ﬂash crash caused

by an operational shock with different market par-

ticipants. In particular, by including automated trad-

ing strategies and electronic order-book microstruc-

ture, simulations give some insights about artiﬁcial-

intelligence applications role in extreme disruptions.

We reproduce this shock in artiﬁcial market frame-

work to study market quality in different scenarios,

with or without strategic traders. Trading interactions

within a group of technical traders make a shock re-

ﬂected in the price dynamic deeper compared to the

similar shock in the market populated only by fun-

damentalists. We ﬁnd that ﬂash crash is much more

a feedback trading issue than a single population of

trader problem. Additionally, we study the role of

market microstructure on the prices collapse and re-

covery. We show that, despite the absence of market

makers, the order-driven market is resilient. The in-

traday continuous trading and the electronic double-

auction mechanism favor price recovery. Finally,

ﬂash crash anatomy is an outcome of complex interac-

tion between three key-ingredients: agents strategies,

liquidity withdrawal, and pre-existing microstructure

features.

REFERENCES

Aldridge, I. (2013). High-Frequency Trading: A Practical

Guide to Algorithmic Strategies and Trading Systems.

Wiley Trading Series.

Brandouy, O., Corelli, A., Veryzhenko, I., and Waldeck, R.

(2012). Why zero intelligence traders are not smart

enough for quantitative ﬁnance. Journal of Economic

Interaction and Coordination, 7:223–248.

Brandouy, O., Mathieu, P., and Veryzhenko, I. (2013).

On the design of agent-based artiﬁcial stock markets.

Communications in Computer and Information Sci-

ence, 271:350–364.

Brewer, P., Cvitanic, J., and Plott, C. (2013). Market mi-

crostructure design and ﬂash crashes : A simulation

approach. Journal of Applied Economics, 16(2):223–

250.

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

196

Chan, N. T., LeBaron, B., Lo, A. W., Poggio, T., Yy, A.

W. L., and Zz, T. P. (1999). Agent-based models of

ﬁnancial markets: A comparison with experimental

markets.

Cohen, B. and Shin, H. (2002). Positive feedback trading

under stress : Evidence from the us treasury securi-

ties market. In Risk Measurement and Systemic Risk

issued by Committee on the Global Financial System.

Basel: Bank for International Setlements.

Cont, R. (2007). Volatility clustering in ﬁnancial markets:

Empirical facts and agentbased modelsy. Long Mem-

ory in Economics, pages 289–309.

Degryse, H., Jong, F. D., Ravenswaaij, M. V., and Wuyts,

G. (2005). Aggressive orders and the resiliency of a

limit order market. Review of Finance, 9:201–242.

Giles, J. (2012). Flash crash forecast. New Scientist, 213:21.

Gode, D. and Sunders, S. (1997). What makes markets al-

locaationally efﬁcient? The Quarterly Journal of Eco-

nomics, 112(2):603–630.

Grouard, M., Levy, S., and Lubochinsky, C. (2003). La

volatilit boursire: des constats empiriques aux difﬁ-

cults d’interprtation. Revue de la Stabilit Financire,

pages 61–79.

Jacobs, B. I., Levy, K. N., and Markowitz, H. M. (2004).

Financial market simulation. The Journal of Portfolio

Management, 30th Anniversary Issue:142–151.

Lee, W. B., Cheng, S.-F., and Koh, A. (2011). Would price

limits have made any difference to the’ﬂash crash’on

may 6, 2010. The Review of Futures Markets, 19(Spe-

cial ifm issue):55–93.

Murphy, J. (1999). Technical analysis of ﬁnancial markets.

New York Institute of Finance, New York.

Paddrik, M., Hayes, R., Todd, A., Yand, S., Scherer, W.,

and Beling, P. (2012a). An agent basedmodel of the e-

mini s&p 500 and the ﬂash crash. Proceedings of the

2012 IEEE Computational Intelligence for Financial

Engineering and Finance, 1.

Paddrik, M., Hayes, R., Todd, A., Yang, S., Beling, P., and

Scherer, W. (2012b). An agent based model of the e-

mini s&p 500 applied to ﬂash crash analysis. In Com-

putational Intelligence for Financial Engineering &

Economics (CIFEr), 2012 IEEE Conference on, pages

1–8. IEEE.

Vuorenmaa, T. and Wang, L. (2014). An agent-based model

of the ﬂash crash of may 6, 2010 with policy implica-

tions. Working Paper.

Post Flash Crash Recovery: An Agent-based Analysis

197