Delineation of Rectangular Management Zones Under

Uncertainty Conditions

Jose L. Saez and Victor M. Albornoz

Universidad Tecnica Federico Santa Maria, Departamento de Industrias,

Campus Santiago Vitacura, Av. Santa Maria 6400, Santiago, Chile

Keywords:

OR in Agriculture, Stochastic Optimization, Management Zones, Precision Agriculture.

Abstract:

In this article we cover the problem of generating a partition of an agricultural ﬁeld into rectangular and

homogeneous management zones or quarters according to a given soil property, which has variability in time

that is presented as a number of possible scenarios. This problem combines aspects of precision agriculture

and optimization with the purpose of achieving a site and time speciﬁc management of the ﬁeld properties

that is consistent and effective in time for a medium term horizon. More speciﬁcally, we propose a two stage

integer stochastic linear programming model with recource that solves the problem of generating a partition

facing a ﬁnite number of future scenarios, with a solution that gives satisfactory results to any possible value of

the chosen soil property. We describe the proposed model, the adopted methodology and the results achieved

with this methodology.

1 INTRODUCTION

In agriculture, spatial variability of the soil properties

is a key aspect in yield and quality of crops. One of

the problems in precision agriculture consists in di-

viding the ﬁeld into site speciﬁc management zones

or quarters, which based on a soil property such as:

pH, organic matter, phosphorus, nitrogen, crop yield,

etc., deﬁnes zones with relative homogeneous charac-

teristics. Delineating rectangular zones allows better

agricultural machines performance and eases the de-

sign of irrigation systems, it is also important to con-

sider the zones size and the total amount of manage-

ment zones from ﬁeld partition.

The problem of deﬁning management zones in

presence of site speciﬁc variability has been stud-

ied in (Albornoz et al., 2013) and (Albornoz et al.,

2015), where a linear programming model for de-

termining rectangular zones is deﬁned, this problem

considers spatial variability of an speciﬁc soil prop-

erty and choose the best ﬁeld partition. The main idea

is to deﬁne homogeneous management zones to opti-

mize the use of inputs for crops. The model is solved

by the complete enumeration of the variables, but it

is possible only to solve small and medium size in-

stances due to the problem is np-hard. To deal with

this problem, a column generation algorithm was pro-

posed in (Albornoz and Nanco, 2015) which allows

to efﬁciently solve large instances of the problem.

Recently, this problem has been applied for irrigation

systems design, see (Haghverdi et al., 2015) where

linear programming is used as one of the methods for

delineating management zones among others as K-

means and Isodata, methods that are still being used.

These other methods are classiﬁed as clustering meth-

ods, see (Ortega et al.,2002), (Jaynes et al.,2005) and

(Jiang et al. (2011), but their major drawback is the

resulting fragmentation of the zones, because these

methods generate oval shaped and disjoint zones.

Although the problem of deﬁning management zones

in presence of site speciﬁc variability has been stud-

ied in previous works, to the best of our knowledge,

an important characteristic that has not been con-

sidered yet is variability in time of the chosen soil

property. Based on cited works we propose a two

stage stochastic linear programming model with re-

cource that solves ﬁeld partition problem considering

the chosen soil property as a random variable which

can be modeled by a ﬁnite number of scenarios.

Stochastic programming is chosen in these situ-

ations because deterministic models are not capable

of adding the effect of uncertainty to the solutions.

Stochastic programming is based on considering ran-

dom variables that are described by a number of pos-

sible scenarios; see e.g. (Birge and Loveaux, 2011),

(Ramos et al., 2008) and (Ruszczynski and Shapiro,

Saez, J. and Albornoz, V.

Delineation of Rectangular Management Zones Under Uncertainty Conditions.

DOI: 10.5220/0005708202710278

In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 271-278

ISBN: 978-989-758-171-7

271

2003).

In the last few years, stochastic programming is

being used more often in a wide variety of appli-

cations due to its capacity of solving problems in-

creasingly large, thus more realistic models, see e.g.

(Gassmann and Ziemba, 2012) and (Wallace and

Ziemba, 2005) for general applications.

In agriculture, Stochastic programming is being

used to solve many different problems related with

situations where uncertainty is a key aspect in the de-

cision making process. Besides delineation decision

there are other important decisions to make, as crop

planning, water planning, food supply chain and agri-

cultural raw materials supply planning, among others.

Crop planning is a decision where a crop pattern must

be chosen for each management zone, this pattern last

a speciﬁc number of crop cycles and thus must face

future weather scenarios and prices, see (Itoh et al.,

2003), (Zeng et al., 2010) and (Li et al., 2015). Wa-

ter planning is important because the need for more

agricultutal production requires large amounts of wa-

ter for irrigation purposes, making water resources

scarce, thus surface water resources must be allocated

among farmers and also plan for the use of this water,

see (Bravo and Gonzalez, 2009) and (Liu et al. 2014).

Stochastic programming is also applied in agricultural

supply chain problems, as food supply chain where

a growing and distribution plan must be made, and

raw materials supply where a raw material acquisi-

tion plan must be made considering that some raw

materials are seasonal, in these problems variability

appears in the form of weather conditions and product

demands, see (Ahumada et al., 2012) and (Wieden-

mann and Geldermann,2015).

Within stochastic programming models exists the

two stage models with recource. These models rec-

ognize two types of decisions that must be made se-

quentially. First stage decision or here-and-now must

be made previously to the performing of the random

variables. Then, second stage decision or wait-and-

see, which must compensate the effects of the ﬁrst

stage decisions once the performance of the random

variables are known, due to this, the variables in this

stage are denoted as recource variables. The goal of

these models consists in ﬁnding the optimal ﬁrst stage

decision that minimize total costs, deﬁned by the sum

of the ﬁrst stage decision costs and the expected costs

of the second stage decisions; see e.g. (Higle, 2005).

In this case, ﬁrst stage decision chooses a ﬁeld

partition that minimizes the number of quarters; these

zones must satisfy certain homogeneity level that de-

pends on the performance value of the sample points

which are the random variables in this case. On the

other hand, second stage decision uses looseness vari-

ables that relax homogeneity constraints in exchange

of a penalty. This penalty helps to achieve manage-

ment zones homogeneity goal while minimizes the

use of the looseness variables. In this problem, homo-

geneity is presented by relative variance concept; see

(Ortega and Santibanez, 2007), which helps to mea-

sure the quality of the chosen partition.

In this article, problem formulation needs the gen-

eration of the total number of potential quarters; in

other words, problem resolution considers the com-

plete enumeration of zones is known. This is feasible

for small and medium size instances as the ones used

in this work, which represents a good starting point to

approach to this problem. Although, proposed formu-

lation can be extended to large instances by the appli-

cation of a column generation algorithm, but its use

exceeds the purpose of this work, see (Albornoz and

Nanco, 2015).

In following sections, the article is organized as

follows. Next section details the proposed model to

solve this problem, from data collection to the solv-

ing process itself. After this, results obtained by the

application of proposed methodology are presented.

At last,future works and main conclusions from the

application of the model are presented.

2 MATERIALS AND METHODS

As we mentioned before, this work consists in gener-

ating a ﬁeld partition composed by a group of man-

agement zones or quarters based on a chosen soil

property which has variability in space and time. The

proposed methodology has three steps. First, the task

is to model the soil property space variability by tak-

ing samples on the ﬁeld, this process must be done

several times in different periods to measure variabil-

ity in time, with this data, instances are generated.

Second step consists on the application of the two

stage stochastic linear programming model that mini-

mizes the number of quarters in its ﬁrst stage and min-

imizes noncompliance of the homogeneity level in the

second stage. Then, in the third step we solve the pro-

posed model with appropriate software.

2.1 Instance Generation

In this step, we generate instances that will be solved

by the model. To achieve this is necessary to use

specialized software as MapInfo; this software cre-

ates thematic maps of the ﬁeld that summarizes and

shows spatial variability of the soil properties mea-

sured from the sample points. This includes sample

coordinates, pH level, organic matter index, phospho-

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

272

rus, base sum, crop yield, etc. As an example, Figure

1 shows two thematic maps from the same ﬁeld, one

with organic matter (MO) and the other with phos-

phorus (P). In MO case, green zones represent nor-

mal levels of MO, while red and yellow zones repre-

sent zones with 34.8% and 3.97% above normal val-

ues of MO, also sky blue and blue zones presents val-

ues with 6.06% and 30.68% under normal MO values.

On the other hand, in P case red and yellow zones

are 279.31% y 10.34% above normal, and sky blue

and blue zones are 13.79% y 48.27%, respectively.

Both maps show spatial variability of these indices in

a ﬁeld, this proves the importance of dividing the ﬁeld

into management zones with uniform characteristics,

to apply inputs needed in each zone through site spe-

ciﬁc farming.

Figure 1: Organic matter and phosphorus map.

Also, we need to include variability in time of the

measured indices. For that, we use thematic map data

sets from the same ﬁeld for several time periods; these

will be used either to generate the probability distribu-

tion function of the soil property or to create different

scenarios with each one of these instances. A possible

value of the random variable consist in assign a spe-

ciﬁc value to each of the sample points on the ﬁeld,

i.e., the random variable is represented by a vector

that includes each one of the sample points; this vec-

tor has a ﬁnite number of possible values. Scenario

probabilities are assigned depending on the number

of instances and the time between each sampling pro-

cess. It is important to notice that a ﬁeld partition is

a medium term decision, i.e. this partition will last

a speciﬁc number of years and after that horizon is

reached, another partition must be set, thus the model

must take into account possible changes in soil prop-

erties during this time. This article uses only histor-

ical data for scenario creation, but it is also valid to

consider forecasts for future periods in the scenario

creation step, but this exceeds the purpose of this ar-

ticle.

Finally, potential management zones are gener-

ated (Z set) through an algorithm that uses all sample

points (S set) as inputs. As an example, in Figure 2

there is an instance with 42 sample point ﬁeld (6 rows

and 7 columns) and three potential management zones

from a total of 588, each one of them has rectangular

form and includes at least one sample point.

Figure 2: Potential management zones example.

A relationship matrix C = (c

) is created from po-

tential zones generation, where c

= 1 means that po-

tential zone z includes sample point s, and c

= 0 oth-

erwise, for every z ∈ Z, s ∈ S. Besides, index variance

zω

is obtained for each potential quarter z and each

scenario ω ∈ Ω, where Ω is the set of possible scenar-

ios. Both parameters are used in the model presented

in the following section.

2.2 Optimization Model

Proposed model consist in a two stage integer

stochastic linear programming model with recource.

In the ﬁrst stage, the problem minimizes the number

of management zones or quarters that cover the entire

ﬁeld. In the second stage, the problem minimizes

noncompliance of the homogeneity level using

looseness variables for each scenario but with a

penalty cost for using them. This second stage is

necessary because ﬁeld partition must be chosen

before knowing random variables performance, and

it must satisfy the homogeneity constraint for any

scenario, this is achieved by minimizing the expected

value of the penalty for the noncompliance of the

homogeneity level.

Sets, parameters and variables used in the model

are described below:

Sets:

Z: set of potential quarters, with z ∈ Z.

S: set of sample points of the ﬁeld, with s ∈ S.

Ω: set of possible scenarios, with σ ∈ Ω.

Parameters:

: Coefﬁcient that represents if quarter z covers

sample point s or not.

M: Penalty cost per unit for noncompliance of the

required homogeneity level.

: Number of sample points in quarter or manage-

ment zone z.

: Probability of scenario ω.

zω

: Quarter variance z calculated from the soil

property in scenario ω.

T ω

: Total variance of the ﬁeld calculated from the

soil property data in scenario ω.

Delineation of Rectangular Management Zones Under Uncertainty Conditions

273

N: Total number of sample points.

UB: Upper bound for the number of quarters chosen.

α: Required homogeneity level.

Decision variables:







1, if quarter z is assigned to ﬁeld partition

0, otherwise

: Looseness for the homogeneity level in

scenario ω.

The two stage stochastic model with recource is

presented now:

Min

∑

z∈Z

∑

ω∈Ω

Q(q, h

) (1)

s.t.

∑

z∈Z

= 1 ∀s ∈ S (2)

∑

z∈Z

6 U B (3)

∈ 0, 1 ∀z ∈ Z (4)

W here Q(q, h

) = MinM

(5)

s.t.

∑

z∈Z

[(n

− k)σ

zω

(6)

+(1 − α)σ

T ω

− (1 − α)σ

T ω

> 0 (7)

Problem (1)-(4) correspond to the ﬁrst stage de-

cision, while (5)-(7) correspond to the second stage

decision. Objective function (1) minimizes the sum

of quarters chosen and minimizes the expected value

of the penalty cost for noncompliance of the required

homogeneity level, these are ﬁrst and second stage

objective functions respectively. Constraint (2) is typ-

ical for set partition models, guarantee that each sam-

ple point on the ﬁeld is assigned only to one quar-

ter. Constraint (3) establishes an upper bound to the

number of quarters chosen to divide the ﬁeld. Con-

straint (4) deﬁnes that quarter variables must be bi-

nary. Objective function (5) represents second stage

decision for each scenario. Constraint (6) states that

a required homogeneity level must be accomplished;

this constraint is made from the linear version of the

relative variance concept and a looseness variable for

each scenario. Finally, constraint (7) states nature of

second stage variables.

It is important to notice that this model, as in (Al-

bornoz et al., 2013), uses an equivalent linear version

of the constraint related to the relative variance con-

cept. However in this case, as we have different pos-

sible scenarios, we must meet homogeneity level in

each one of these scenarios, thus we will have a rela-

tive variance constraint for each scenario. As we have

to choose only one ﬁeld partition we need a way to

deal with uncertainty because otherwise we will have

to choose the best ﬁeld partition for worst possible

scenario in terms of relative variance. We propose

to add new variables named as looseness variables as

part of the second stage decision to get a solution that

considers all possible scenarios, meeting the required

homogeneity level in each one of these, and without

being forced to solve the problem for the worst sce-

nario.

Constraint (6) is created from the following non-

linear constraint used in (Albornoz et al., 2013) :

1 −

∑

z∈Z

− k)σ

[N −

∑

z∈Z

]

> α (8)

This constraint uses relative variance concept, pre-

sented in (Ortega and Santibanez, 2007), is a widely

used criteria to measure effectiveness of chosen man-

agement zones and it must be equal or higher to a

given value, which is the required homogeneity level,

that should be at least 0.5 to validate an ANOVA test

hypothesis assuming k degrees of freedom. To create

constraint (6) ﬁrst we need to linearize equation (8)

obtaining the following expression:

(1 − α)σ

[N −

∑

z∈Z

] >

∑

z∈Z

− k)σ

(9)

Then if we reorder equation (9) we obtain:

∑

z∈Z

[(n

− k)σ

+ (1 − α)σ

6 (1 − α)σ

N (10)

As we have a number of possible scenarios we

deﬁne a relative variance constraint for each one of

these, and also different parameters for each scenario

ω:

∑

z∈Z

[(n

− k)σ

zω

+ (1 − α)σ

T ω

6 (1 − α)σ

T ω

N (11)

Here is when we add the looseness variables h

the right side of equation (11):

∑

z∈Z

[(n

− k)σ

zω

+ (1 − α)σ

T ω

6 (1 − α)σ

T ω

N + h

(12)

These variables allow the problem to choose a

ﬁeld partition that considers all possible scenarios and

meet all relative variance constraints by relaxing the

right side of equation (11) for each scenario, thus ﬁ-

nally obtaining constraint (6). It is important to notice

that looseness variables are added to the linear version

of this constraint to have only linear constraints in the

model.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

274

3 RESULTS

To analyze the model behavior we used 10 instances

for the problem, each one of them with a different

number of sample points and using crop yield as soil

property because this index has strong variability

in time. In each instance, there are six possible

scenarios, all of them with similar probabilities,

where the two latest scenarios have are more likely to

occur. Chosen parameter values for problem (1)-(7)

are:

= 1.5 ∀ω ∈ Ω UB = 40

α = 0.9

= 0.15 ω ∈ 1..4

= 0.2 ω ∈ 5..6

The rest of the parameters are calculated

from crop yield data for each scenario. The number

of potential quarters is obtained by the formula

((n+1)n(m+1)m)

presented in (Albornoz and Nanco,

2015), where n is the number of sample points in

length and m is the number of sample points in width.

Instances used have a different number of potential

quarters, starting from 588 to 13915.

3.1 Instance Solving

Instances were solved with the parameter values de-

ﬁned in this section and using compact equivalent de-

terministic reformulation of the model (1)-(7) using

Cplex 12.4 as a solver in a Lenovo with Intel core i3-

2310M processor CPU 2.10 GHz and a 4 GB RAM

memory. Results are showed in Table 1.

First column indicates the instance number. Sec-

ond column shows total number of sample points on

the ﬁeld. Third column indicates the number of po-

tential quarters. Fourth column shows stochastic so-

lution of the model. Fifth column is related to the ex-

pected value of perfect information (EVPI), which is

the maximum willingness to pay for knowing all the

information related to random variables performance.

More precisely, this can be calculated using the fol-

lowing formula:

EV PI = RP − W S

Where RP is the optimum value of model (1)-(7)

and WS is the wait-and-see solution, which consid-

ers solving the model for each scenario separately and

then compute the expected value of this solution. At

last, sixth column shows the percentage that EVPI

represents from objective value function. It is im-

portant to notice that EVPI represents between 50%

and 60% of objective value function, this means that

willingness to pay for knowing random variables per-

formance is really high, all of this due to the differ-

ence between scenario solutions and stochastic solu-

tion. This is because stochastic solution must face

any possible scenario so it needs more quarters than

the individual solutions.

3.2 Sensitivity Analysis of Penalty Cost

Penalty cost is the coefﬁcient related to the loose-

ness variables in the objective function in the second

stage of the problem, thus if this cost is high or low,

looseness variables will have a lower o higher value,

and more or less quarters will be chosen respectively.

For sensitivity analysis we chose instance 9, using the

same parameters as we deﬁned at the beginning of

section 3. In this analysis we use the same value for

every penalty cost M

in each scenario. Table 2 sum-

marizes results achieved.

First column of Table 2 indicates the deﬁned

value of penalty cost. Second column shows total

number of quarters chosen for the optimal solution

(quarters are related to the ﬁrst stage decision). From

third to eighth column looseness variables from the

second stage for each scenario are showed. Finally

ninth column indicates the stochastic solution of the

model (1)-(7).

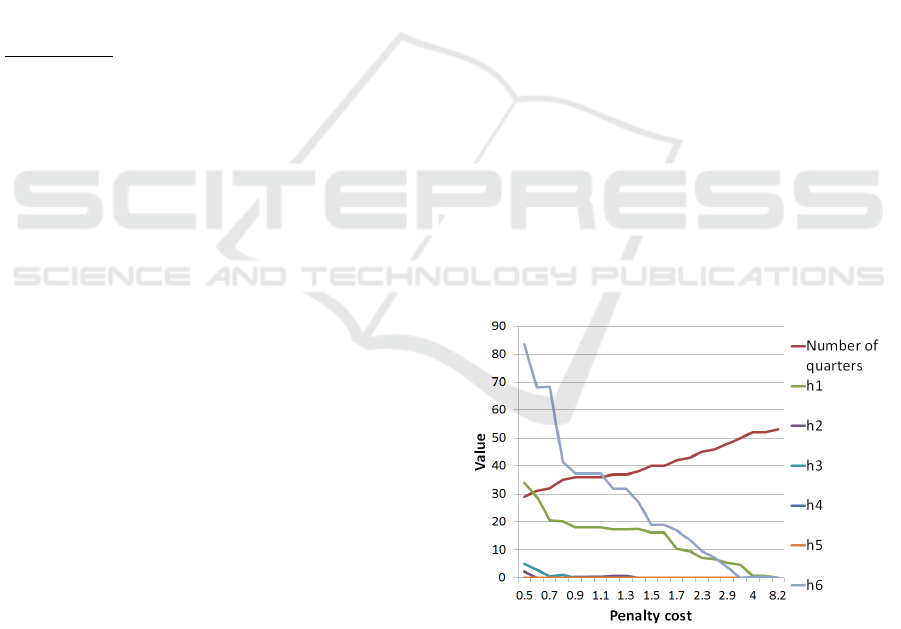
Figure 3 shows behavior of the number of quar-

ters chosen while penalty cost changes, it also shows

looseness variables behavior.

It is important to notice when penalty cost raises,

Figure 3: Solution behavior for different penalty costs M

looseness variables value decrease and at the same

time the number of quarters increases to satisfy homo-

geneity level constraints. Looseness variables value

decreases at a higher rate than number of quarters in-

crease, this is because when penalty cost is getting

higher it increases the impact of looseness variables

in the objective function. There is a breaking point

Delineation of Rectangular Management Zones Under Uncertainty Conditions

275

Table 1: Instance solution results.

Instance Sample Points Potential Quarters RP EVPI Percentage of O.F.

1 42 588 17.483 8.663 49.6 %

2 80 1980 29.952 15.991 53.4 %

3 100 3025 37.989 21.656 57.0 %

4 120 4290 45.531 27.307 60 %

5 140 5775 49.946 30.327 60.7 %

6 150 6600 52.586 33.125 63 %

7 160 7480 51.458 32.377 62.9 %

8 180 9405 50.817 31.974 62.9 %

9 200 11550 47.931 30.235 63.1 %

10 220 13915 43.999 27.49 62.5 %

Table 2: Sensitivity analysis for the penalty cost M

Number of quarters h

F.O.

0.5 29 34.050 2.172 4.951 0 0 83.679 38.363

0.6 31 28.834 0 2.832 0 0 68.119 39.980

0.7 32 20.531 0 0.627 0 0 68.374 41.400

0.8 35 20.292 0.033 1.150 0 0 41.425 42.548

0.9 36 17.924 0.321 0 0 0 37.280 43.496

1 36 17.924 0.321 0 0 0 37.280 44.329

1.1 36 17.924 0.321 0 0 0 37.280 45.162

1.2 37 17.244 0.704 0 0 0 31.714 45.939

1.3 37 17.244 0.704 0 0 0 31.714 46.684

1.4 38 17.430 0 0 0 0 27.182 47.368

1.5 40 16.245 0 0 0 0 19.005 47.931

1.6 40 16.245 0 0 0 0 19.005 48.460

1.7 42 10.198 0 0 0 0 16.861 48.900

2 43 9.590 0 0 0 0 13.567 49.947

2.3 45 7.1226 0 0 0 0 9.468 50.724

2.6 46 6.656 0 0 0 0 7.237 51.418

2.9 48 5.299 0 0 0 0 3.726 51.926

3 50 4.514 0 0 0 0 0 52.031

4 52 0.792 0 0 0 0 0.289 52.649

8 52 0.792 0 0 0 0 0.289 53.297

8.2 53 0 0 0 0 0 0 53

where penalty cost is 8.2, from this point it is not fea-

sible to use looseness variables in problem solution

because is more expensive than use more quarters,

when this occurs then the problem chooses a ﬁeld

partition based only on the worst scenario in terms

of space variability, this way, required homogeneity

level is reached in every scenario in exchange of a

ﬁeld partition with a higher number of quarters com-

pared to the other cases with lower penalty cost.

4 FUTURE WORKS

This article covers small and medium size instance

solving by the complete enumeration of all potential

quarters, this also needs computation of parameters

described in section 2.1 for each potential quarter.

This is not feasible for large instances due to the prob-

lem is np-hard and the number of variables increases

really fast when the problem gets bigger, thus we need

more computational effort to calculate all the param-

eters for each variable.

To deal with this issue, we propose to design a de-

composition method based in column generation to

solve large instances without using all the problem

variables. This will be developed based on the de-

composition of the deterministic version of the model

presented in this article, see (Albornoz and Nanco,

2015), because structure is similar, and quarters can

be added as columns in the algorithm as well. This

work is currently being done and it will be included

in a new article.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

276

5 CONCLUSIONS

This work presents a two stage stochastic linear

programming model with recource to approach the

ﬁeld partitioning problem facing uncertainty condi-

tions represented by a soil property, which presents

variability in time and is modeled by a set of possible

scenarios. Proposed model solution deﬁnes an

optimal ﬁeld partition that considers every possible

soil property value and as a recource it considers

looseness variables that help to achieve the required

homogeneity level. The model was applied to ten

different instances, and it showed that stochastic

solution is completely different from individual

scenario solutions; this is validated by the EVPI value

in each instance, concluding that a stochastic model

is a better choice than a deterministic one. Besides,

from sensitivity analysis we can conclude when

penalty cost raises, looseness variables use decrease

at a faster rate than the number of quarters increase.

Studied instances in this article were solved by the

complete enumeration of all the potential quarters,

but this is only feasible for small and medium size

instances because the number of potential quarters

grows exponentially as the number of sample points

increases. For this, problem size increases faster than

the sample points increase on the ﬁeld and a column

generation algorithm will be required to solve large

instances. Also there is another complex situation

when a greater number of scenarios are modeling the

random variables, these aspects will be considered in

future works.

ACKNOWLEDGEMENTS

This research was partially supported by Direccion

General de Investigacion y Postgrado (DGIP) from

Universidad Tecnica Federico Santa Maria, Grant

USM 28.15.20. Jose Luis Saez wishes to acknowl-

edge the Graduate Scholarship also from DGIP.

REFERENCES

Ahumada O., Villalobos J. R., Mason A. N. (2012), Tactical

planning of the production and distribution of fresh

agricultural products under uncertainty. Agricultural

Systems 112, 1726.

Albornoz V. M., Cid-Garcia N. M., Ortega R., Rios-Solis,

Y. A. (2013). Rectangular shape management zone de-

lineation using integer linear programming. Comput-

ers and Electronics in Agriculture 93, 1-9.

Albornoz, V.M., Cid-Garcia, N.M., Ortega, R. and Rios-

Solis, Y.A. (2015). A hierarchical planning scheme

based on precision agriculture. In Handbook of Oper-

ational Research in Agriculture and the Agri-Food In-

dustry, Pla-Aragones, L.M. (Ed.), 129-162, Springer.

Albornoz, V.M. and Nanco, L.J. (2015) An empirical design

of a column generation algorithm applied to a man-

agement zone delineation problem. Lecture Notes in

Economics and Mathematicasl Systems, to appear.

Birge, J. and Loveaux, F. (2011). Introduction to Stochastic

Programming. 2nd ed., New York: Springer.

Bravo M., Gonzalez I. (2009). Applying stochastic goal pro-

gramming: A case study on water use planning. Euro-

pean Journal of Operational Research 196, 11231129.

Gassmann, H.I and Ziemba, W.T. (2012). Stochastic Pro-

gramming. Applications in Finance, Energy, Planning

and Logistics. World Scientiﬁc Publishing Company.

Haghverdi A., Leib B.G., Washington-Allen R.A., Ayers

P.D., and Buschermohle M.J. (2015) Perspectives on

delineating management zones for variable rate irriga-

tion. Computers and Electronics in Agriculture 117,

154-167.

Higle, J.L. (2005). Stochastic Programming: Optimization

when uncertainty matters. Tutorials in Operations Re-

search. INFORMS, New Orleans.

Itoh T., Ishii H., Nanseki T. (2003), A model of crop plan-

ning under uncertainty in agricultural management.

Int. J. Production Economics 8182, 555558.

Jaynes D., Colvin T., Kaspar T., (2005). Identifying poten-

tial soybean management zones from multi-year yield

data. Computers and electronics in agriculture 46 (1),

309327.

Jiang Q., Fu Q., Wang Z. (2011). Study on delineation

of irrigation management zones based on manage-

ment zone analyst software. Computer and Comput-

ing Technologies in Agriculture IV, 419427.

Li M., Guo P., (2015), A coupled random fuzzy two-stage

programming model for crop area optimizationA case

study of the middle Heihe River basin, China. Agri-

cultural Water Management 155, 5366.

Liu J., Li Y.P., Huang G.H., Zeng X.T., (2014). A dual-

interval ﬁxed-mix stochastic programming method for

water resources management under uncertainty. Re-

sources, Conservation and Recycling 88, 5066.

Ortega J.A., Foster W. and Ortega R. (2002). Deﬁnition

of sub-stands for Precision Forestry: an application

of the fuzzy k-means method.Ciencia e Investigacin

Agraria 29 (1), 3544.

Ortega. R. & Santibanez, O. A. (2007). Determination of

management zones in corn (Zea mays L.) based on

soil fertility. Computers and Electronics in Agricul-

ture, 58, 49-59.

Ramos, A., Alonso-Ayuso, A. and Perez, G.(2008). Op-

timizacion bajo incertidumbre. Espaa, Biblioteca

Delineation of Rectangular Management Zones Under Uncertainty Conditions

277

Comillas. Publicaciones de la Universidad Pontiﬁcia

Comillas.

Ruszczynski A. and Shapiro A.(2003). Stochastic Program-

ming. Handbooks in Operations Research and Man-

agement Science, Vol. 10. New York, North-Holland.

Wallace S.W. and Ziemba W.T. (2005). Applications of

Stochastic Programming. MOS-SIAM Series on Op-

timization.

Wiedenmann S., Geldermann J. (2015). Supply planning

for processors of agricultural raw materials. European

Journal of Operational Research 242, 606619

Zeng X., Kang S., Li F., Zhang L., Guo P. (2010). Fuzzy

multi-objective linear programming applying to crop

area planning. Agricultural Water Management 98 ,

134142.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

278