
Detecting Colluding Attackers in Distributed Grid Systems
Jan Kantert
1
, Melanie Kauder
1
, Sarah Edenhofer
2
, Sven Tomforde
2
and Christian M
¨
uller-Schloer
1
1
Institute of Systems Engineering, Leibniz University Hanover, Appelstr. 4, 30167 Hanover, Germany
2
Organic Computing Group, University of Augsburg, Eichleitnerstr. 30, 86159 Augsburg, Germany
Keywords:
Colluding Attacks, Multi-Agent-Systems, Technical Trust, Normative Systems, Grid Computing Systems.
Abstract:
Distributed grid systems offer possible benefits in terms of fast computation of tasks. This is accompanied
by potential drawbacks due to their openness, the heterogeneity of participants, and the unpredictability of
agent behaviour, since agents have to be considered as black-boxes. The utilisation of technical trust within
adaptive collaboration strategies has been shown to counter negative effects caused by these characteristics. A
major challenge in this context is the presence of colluding attackers that try to exploit or damage the system
in a coordinated fashion. Therefore, this paper presents a novel approach to detect and isolate such colluding
attackers. The concept is based on observations of interaction patterns and derives a classification of agent
communities. Within the evaluation, we demonstrate the benefit of the approach and highlight the highly
reliable classification.
1 INTRODUCTION
Technical systems increasingly face cooperation and
interaction partners for which no valid estimation of
behaviour is available, cf. (Tomforde et al., 2014).
One particular instance of this problem class are dis-
tributed grid computing systems. In such a system,
agents can join and leave at any time, decide about
their resource sharing autonomously, and behave self-
ishly. Thereby, the goal of participation is to paral-
lelise computational load - while offering resources
during idle times. Consequently, the basic idea is a
kind of tit-for-tat strategy.
In order to allow for a stable system, malicious or
uncooperative agents have to be isolated. This is typ-
ically achieved by introducing technical trust – more
precisely, a modelling of expected behaviour in terms
of reliability and trustworthiness based on observed
behaviour in interactions (Kantert et al., 2014). This
has been shown to result in robust behaviour for cer-
tain stereo-type agent behaviour (Klejnowski, 2014).
A major issues that has been neglected so far is the
presence of colluding attackers. This refers to groups
of malicious agents that try to exploit or damage the
system by coordinated behaviour.
This paper introduces a novel concept to detect
colluding attackers by analysing the interaction and
trust patterns within the underlying community of
participating agents. Therefore, we discuss the con-
cept of a system-wide observation and control loop
that follows the adaptive control pattern from the Or-
ganic Computing domain (Tomforde et al., 2011). Af-
terwards, we demonstrate how the perceived informa-
tion can be utilised to detect and isolate such groups
of malicious agents efficiently.
The remainder of this paper is organised as fol-
lows: Section 2 describes the Trusted Computing
Grid as application scenario. This includes the
agents’ goals and classes, as well as details about
trust and normative control aspects. Afterwards, we
specify the particular challenge addressed in this pa-
per, which is then substantiated by the developed ap-
proach as presented in Section 3. Section 4 evaluates
the concepts and demonstrates the success. Section 5
compares the presented work with the state-of-the-art.
Finally, Section 6 summarises the paper and gives an
outlook to future work.
2 APPLICATION SCENARIO
As a possible application scenario, we investigate
open grid computing systems which can host numer-
ous distributable workloads, e.g., distributed render-
ing of films. The system is considered open since
there is no central controlling entity and all commu-
nication is performed peer-to-peer. Worker nodes be-
long to different administrative domains. Thus, good
198
Kantert, J., Kauder, M., Edenhofer, S., Tomforde, S. and Müller-Schloer, C.
Detecting Colluding Attackers in Distributed Grid Systems.
DOI: 10.5220/0005708301980206
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 1, pages 198-206
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

behaviour cannot be assumed. Nodes participate vol-
untarily to submit work into the system and, thereby,
increase the speedup of their jobs. However, they also
have to compute work units for other submitters.
2.1 Agent Goal
To analyse such systems, we model nodes as agents
and run a multi-agent system in simulation. Ev-
ery agent works for a user and periodically receives
a job, which contains multiple parallelisable work
units. It aims to accomplish all work units as fast
as possible by requesting other agents to work for it.
Since we consider an open system, agents behave au-
tonomously, and can join or leave at any time.
The system performance is measured by the
speedup σ. In Equation (1), t
self
is the time an agent
would require computing a job containing multiple
work units without any cooperation. t
distributed
repre-
sents the time to compute all work units of one job
with cooperation of other workers including all com-
munication times. As a consequence, the speedup can
only be determined after the results of the last work
unit have been returned.
σ
:
=
t
self
t
distributed
(1)
If no cooperation partners can be found, agents need
to compute their own work units and achieve a
speedup value of at most one (i.e., no speedup at all).
Especially when a worker fails to finish a job or de-
cides to cancel it, the speedup value will suffer and
be less than one. Communication overhead also de-
creases the speedup. However, we assume that jobs
require significantly more computing time than com-
munication time and this overhead to be negligible. In
general, agents behave selfishly and only cooperate if
they can expect an advantage. They have to decide
which agent they assign tasks to and for which agents
they perform jobs themselves. We do not control the
agent implementation, so they might behave uncoop-
eratively or even maliciously.
2.2 Worker and Submitter Component
Each agent consists of a worker and a submitter com-
ponent. The submitter component is responsible for
distributing work units. When an agent receives a
job containing multiple work units, it creates a list of
trusted workers. It then requests workers from this
list to cooperate and compute work units, until either
no more work units or no more workers are left. If
all workers were asked, but unprocessed work units
remain, the agent computes them on its own. The
worker component decides whether an agent wants to
work for a certain submitter. When the agent receives
an offer, it computes its rewards for accepting or re-
jecting the job. There are different strategies based
on reputation, workload, and environment. If the re-
ward of accepting the job prevails, the agent accepts
the job. It may cancel the job later on, but typically
it computes the job and returns the results to the sub-
mitter (Klejnowski, 2014).
2.3 Open Systems and Benevolence
In contrast to classical grid computing systems, we do
not assume the benevolence of the agents (Wang and
Vassileva, 2004). In such an open system, we cannot
control the implementation of agents and, therefore,
the system is vulnerable to different kinds of attacks.
For instance, a Freerider (see section 2.5) could sim-
ply refuse to work for other agents and gain an advan-
tage at the expense of cooperative agents. Another
attacker might just pretend to work and return wrong
results. Also, combinations of both or alternating be-
haviour are possible. Furthermore, attacker can col-
lude to exploit the system.
2.4 Trust and Norms
To overcome such problems of an open system where
no particular behaviour can be assumed, we introduce
a trust metric. Agents receive ratings for all their ac-
tions from their particular interaction partners. This
allows others to estimate the future behaviour of a cer-
tain agent based on its previous actions. To perform
this reasoning, a series of ratings for a certain agent
can be accumulated to a single reputation value using
the trust metric.
Autonomous agents need to become aware of the
expected behaviour in the system. Therefore, we in-
fluence the desired actions by norms. These norms are
valid for an Action in a certain Context and, thereby,
guide the agents. To enforce the behaviour, they im-
pose a Sanction if violated or offer an Incentive if ful-
filled.
In this scenario, good trust ratings are used as an
Incentive and, to the contrary, bad trust ratings impose
a Sanction. Based on the norms, agents receive a good
rating if they work for other agents and a bad rating
if they reject or cancel work requests. As a result,
the society isolates malevolent agents and maintains a
good system utility in most cases. Generally, agents
with higher reputation values have a higher chance to
get their work units computed. We call this system a
Trusted Desktop Grid (Klejnowski, 2014).
Since agents are considered as black boxes, they
cannot be controlled directly from the outside. Each
Detecting Colluding Attackers in Distributed Grid Systems
199

agent is autonomous and selfish. However, we want
to influence the system to optimise itself regarding
performance and robustness. Therefore, we introduce
norms to change the incentives and sanctions for all
agents.
2.5 Agent Types
We consider the following agent types in our system:
• Adaptive Agents - These agents behave coopera-
tively. They perform tasks for other agents who
earned good reputation in the system. The reputa-
tion value generally depends on the estimated cur-
rent system load and how much the input queue of
the agent is filled up.
• Freeriders - Such agents do not work for other
agents and reject all work requests. However, they
ask other agents to accomplish tasks for them.
This increases the overall system load and de-
creases the utility for well-behaving agents.
• Egoists - These agents only pretend to work for
other agents. They accept all work requests but
return faked results to other agents, blocking other
agents as they have to validate the results. On the
other hand, if results are not validated, this may
lead to wrong results. However, Egoists lower the
utility of the system.
• Cunning Agents - These agents behave well in the
beginning, but may change their behaviour later.
Periodically, randomly, or under certain condi-
tions, they behave like Freeriders or Egoists. Such
behaviour is hard to detect and may lower the
overall system utility.
• Altruistic Agents - Such agents will accept every
job. In general, this behaviour is not malicious
and increases the system performance. However,
it hinders isolation of bad-behaving agents and
impacts the system goals.
2.6 Challenge
Unfortunately, in an open distributed system attack-
ers can collude to gain advantages. In the Trusted
Desktop Grid (TDG) colluding attackers can pretend
to work for each other which results in good reputa-
tion. Other agents will happily work for those attack-
ers. Still, the attackers do not have to work for other
agents if they can generate enough fake ratings inside
their group.
In this paper, we focus on Freeriders which col-
lude as a group. They pretend to work for each others
all the time (at a normal work rate) and give out good
ratings for fake work to each other. Other stereotypes
could execute the same pattern but Freeriding is the
best exploitation strategy when an agent has a high
reputation.
3 APPROACH
Norm Manager
Agent A
Agent B
Agent C
Norm set
Agent E
Agent D
Observationmodel
Change norms
Distribute
norms
Collect data
on agents
Observer Controller
Situation
Description
Detect
situation
SuOC
Figure 1: System Overview of the Norm Manager consist-
ing of an Observer and a Controller which control the Sys-
tem under Observation and Control (SuOC) using norms.
To identify colluding attackers, we introduce a higher
level Norm Manager (NM) which consists of an ob-
server and a controller component. It monitors work
relations of all agents and collects reputation metrics.
Based on this information, it creates a work graph
with agents as nodes and edges between agents which
have cooperated in the monitored period. The inten-
sity of the cooperation between two agents determines
the weight of the edge connecting them. Addition-
ally, the controller creates a trust graph with agents
as nodes and trust relations as edges. Trust relations
between agents can be obtained from the reputation
system (Kantert et al., 2013).
Since we cannot see the internals or implementa-
tion of agents, we need to observe them from the out-
side. We could monitor interactions between agents,
but this may lead to a bottleneck in larger systems.
However, it is easy to monitor the actions indirectly:
We can observe the reputation system and use the rat-
ings which agents give their partners after every inter-
action. When we collect those ratings, we can build a
trust-graph. Multiple ratings will be merged using an
arithmetic mean.
Afterwards, we calculate some common graph
metrics for every node. Using statistics, the global
system state gets rated. Based on this metrics, we
form clusters and detect groups of similar agents. By
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
200
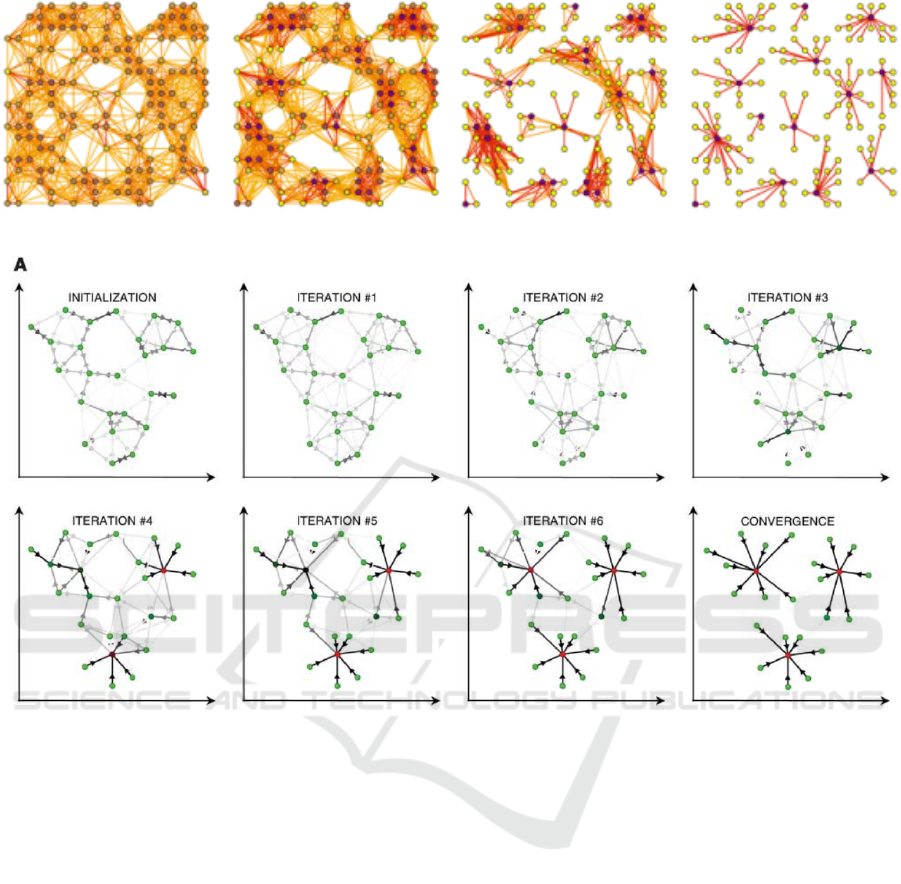
Figure 2: MCL running for four iterations (von Dogen, 2000).
Figure 3: Six iterations of Affinity Propagation Clustering (Frey and Dueck, 2007).
further classifying these groups, we achieve an even
better understanding about potentially occurring at-
tacks. In the end, the observer is able to tell when
the system is under attack, categorise the type of the
attacks, and rank how severe the attack is. There will
also be an estimation about the accuracy of this infor-
mation.
3.1 Requirements on Clustering
Algorithms
To find colluding groups of agents, we need a graph
clustering algorithm which fulfils the following re-
quirements:
1. Dynamic Cluster Count - Typically, we do not
know the total number of different agent groups
in advance. Therefore, we require an algorithm
which can find a dynamically changing number
of groups.
2. Weighted Cyclic Non-Symmetrical Graph - The
algorithms has to work directly on a weighted
graph where distances are not symmetrical
d(x, y) 6= d(y, x), cycles may exists and, espe-
cially, the triangle inequality d(x, z) ≤ d(x, y) +
d(y, z) does not hold (Khamsi and Kirk, 2011).
3. Semi-deterministic/Order-invariant - The cluster-
ing is performed periodically while the underly-
ing graph slightly changes. However, the resulting
clusters should not change fundamentally. Some
algorithms alternate between two different results
when the input changes only marginally. This of-
ten happened with our previous approach. There-
fore, we require a similar output when the input
changes only slightly (Jardine and Sibson, 1971).
4. Non-connected Components - The graph is not
necessarily always connected. Some agents or
even groups may be permanently disconnected
from the other groups. The algorithm has to be
able to cope with this requirement.
Starting with (Schaeffer, 2007) and based on this
analysis, we choose Markov Cluster Algorithm
(MCL) (Van Dongen, 2001) as a suitable algorithm
Detecting Colluding Attackers in Distributed Grid Systems
201

for graph clustering which uses flow simulation.
MCL is deterministic, can handle edge weights and
can find a dynamic amount of groups. Additionally,
we choose Affinity Propagation Clustering (AP) clus-
ters which is based on message passing and can find
variable numbers of clusters. Therefore, both meet
our requirements and can be used with directed or
undirected edges.
3.2 Markov Clustering
Markov Clustering Algorithm (MCL) (Van Dongen,
2001) is based on simulation of stochastic flow in net-
works. It runs iteratively on a matrix M which con-
tains all connections between nodes and performs two
steps:
In the expansion step the matrix gets coincided by
a normal matrix multiplication. This spreads out the
flow and makes the matrix more homogeneous:
M = M · M = M
2
Afterwards, the matrix is inflated which simulates the
contraction of flow. Mathematically is uses Hadamard
power followed by a diagonal scaling:
Γ
r
(M
i j
) =
M
i j
r
∑
r, j
(M)
=
M
i j
r
∑
N
k=1
M
k j
r
MCL has a runtime complexity ofv O(Nk
2
) with
nodes N and edges k which is sufficient for our appli-
cation. An exemplary run of MCL is shown in fig. 2.
3.3 Affinity Propagation Clustering
Another algorithm is Affinity Propagation Clustering
(AP) which works (like MCL) in two steps. It ini-
tialises two matrices responsibility R and availability
A which store probabilities and are initialised with 0.
s(i, j) describes is the edge weight in our graph. In
each step, AP updates responsibility and availability
(see fig. 4).
First, the responsibility matrix R is updated:
r(i, k) ← s(i, k) − max
k
0
s.t.k
0
6=k
{a(i,k
0
) + s(i, k
0
)}
Afterwards, the availability matrix A is updated:
a(i,k) ← min
n
0,r(k, k) +
∑
i
0
s.t.i
0
/∈{i,k}
max{0,r(i
0
,k)}
o
a(k, k) ←
∑
i
0
s.t.i
0
6=k
max{0,r(i
0
,k)}
The complexity of AP is O(n
2
) with n being the num-
ber of nodes which is sufficient for our application.
An example with six iterations is shown in fig. 3.
Figure 4: Illustration of Affinity Propagation Clustering
steps (Frey and Dueck, 2007).
3.4 Rating of Results
To rate the results of the clustering, we use metrics
which are similar to Precision and Recall used in in-
formation retrieval systems. Additionally, we want to
condense them to only one value. In an ideal cluster-
ing, every group (attackers, cooperating agents, etc)
has its own cluster which contains only agents of that
group.
First, we measure the share in a cluster i for group
t in ClusterShare
t,i
:
ClusterShare
t,i
:
=
|{a : a ∈ Cluster
i
∧ a ∈ Group
t
}|
|Cluster
i
|
Similarly, we calculate the share of the group t for
cluster i in GroupShare
t,i
:
GroupShare
t,i
:
=
|{a : a ∈ Group
t
∧ a ∈ Cluster
i
}|
|Group
t
|
To create a total measure, we weight the score of each
cluster based on the amount of clusters a group is in
using w
t,i
:
w
t,i
:
=
|Group
t
| − |{a : a ∈ Cluster
i
∧ a ∈ Group
t
}|
|Group
t
|
Based on that, we create the TotalShare
t
of ever
group t:
TotalShare
t
=
n
∑
i=1
ClusterShare
t,i
· GroupShare
t,i
·w
i,t
4 RELATED WORK
Our application scenario is a Trusted Desktop Grid
system. These systems are used to share resources
between multiple administrative authorities. The
ShareGrid Project in Northern Italy is an exam-
ple for a peer-to-peer-based system (Anglano et al.,
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
202

2008). A second approach is the Organic Grid, which
is peer-to-peer-based with decentralised schedul-
ing (Chakravarti et al., 2004). Compared to our sys-
tem, these approaches assume that there are no ma-
licious parties involved and each node behaves well.
Another implementation with a central tracker is the
Berkeley Open Infrastructure for Network Computing
project (BOINC) (Anderson and Fedak, 2006).
All those systems solve a distributed resource al-
location problem. Since work units can be com-
puted faster when agents cooperate, such systems re-
ward and, thus, maximise cooperation. Additionally,
a high fairness value ensures equal resource distribu-
tion (cf. (Jain et al., 1996; Demers et al., 1989; Ben-
nett and Zhang, 1996)).
We model our grid nodes as agents. Agents fol-
low a local goal which differs from the global system
goal (Rosenschein and Zlotkin, 1994). We consider
agents as black boxes which means that we cannot
observe their internal state. Thus, their actions and
behaviour cannot be predicted (Hewitt, 1991). Our
Trusted Desktop Grid supports Bag-of-Tasks applica-
tions (Anglano et al., 2006).
4.1 Normative Multi-Agent Systems
This work is part of wider research in the area of
norms in multi-agent systems. However, we fo-
cus more on improving system performance by us-
ing norms than researching the characteristics of
norms (Singh, 1999). Our scenario is similar to
management of common pool resources. Accord-
ing to game theory, this leads to a “tragedy of the
commons” (Hardin, 1968). However, Ostrom (Os-
trom, 1990) observed cases where this did not hap-
pen. She presented eight design principles for suc-
cessful self-management of decentralised institutions.
Pitt et al. (Pitt et al., 2011) adapted these to Norma-
tive Multi-Agent Systems (NMAS). NMAS are used
in multiple fields: e.g. (Governatori and Rotolo, 2008)
focuses on so-called policy-based intentions in the do-
main of business process design. Agents plan consec-
utive actions based on obligations, intentions, beliefs,
and desires. Based on DL, social agents reason about
norms and intentions.
In (Artikis and Pitt, 2009), the authors present a
generic approach to form organisations using norms.
They assign a role to agents in a normative system.
This system defines a goal, a process to reach the goal,
required skills, and policies constraining the process.
Agents directly or indirectly commit to certain actions
using a predefined protocol. Agents may join or form
an organisation with additional rules.
The normchange definition describes attributes,
which are required for Normative Multi-Agent Sys-
tems (Boella et al., 2009). Ten guidelines for imple-
mentation of norms to NMAS are given. We follow
those rules in our system. According to (Savarimuthu
and Cranefield, 2011), Normative Multi-Agent Sys-
tems can be divided into five categories: Norm cre-
ation, norm identification, norm spreading, norm en-
forcement, and network topology. We use a leader-
ship mechanism for norm creation and norm spread-
ing. For norm identification, we use data mining and
machine learning. For norm enforcement, we use
sanctioning and reputation. Our network topology is
static.
5 EVALUATION
Figure 5: Visualisation of clustering for MCL with 90
Adaptive Agents (ADA) and 10 Freerider Colluding (FRC).
Our approach was evaluated using our agent-based
Trusted Desktop Grid simulation. All experiments
were repeated fifty times using another random seed.
The system consists of 100 agents with 10 col-
luding Freeriders (FRC) as attacker and 90 well-
behaving adaptive agents (ADA). The simulation runs
for 160.000 ticks.
We rate our results according to the average
TotalShare
t
(see section 3.4) for every 50.000 ticks
as shown in table 1. Additionally, we present two
exemplary experiments for MCL and AP in figs. 5
and 6. We evaluated MCL in three variants: (i) using
the undirected trust graph; (ii) using the work graph;
Detecting Colluding Attackers in Distributed Grid Systems
203

Table 1: Results for adaptive Agents (ADA) and colluding Freerider (FRC) with MCL and AP.
AP MCL UD
Tick ADA FRC ADA FRC
5000 0,376±0,046 0,463±0,037 0,534±0,023 0,840±0,060
55000 0,760±0,106 0,562±0,163 0,672±0,061 0,936±0,038
105000 0,836±0,114 0,499±0,201 0,839±0,128 0,938±0,038
155000 0,842±0,109 0,475±0,176 0,847±0,136 0,938±0,038
MCL WORK MCL
Tick ADA FRC ADA FRC
5000 0,736±0,001 0,034±0,034 0,627±0,062 0,283±0,119
55000 0,857±0,071 0,233±0,014 0,745±0,155 0,267±0,122
105000 0,801±0,107 0,261±0,075 0,740±0,150 0,240±0,150
155000 0,797±0,102 0,240±0,095 0,662±0,072 0,295±0,096
and (iii) using the directed trust graph. AP was is only
shown for the undirected trust graph because it cannot
work on directed graphs.
As shown in fig. 5, MCL (undirected) performs
very well to find the group of colluding Freeriders.
Additionally, it finds a large cluster with adaptive
agents but some additional small clusters with adap-
tive agents exist. It converges quickly and already
shows good results after 5.000 ticks (see table 1; MCL
UD) and gradually improves until the end of the ex-
periment. Therefore, it perfectly fits our usecase.
Affinity Propagation Clustering (AP) performs
similar when clustering adaptive agents. However, it
fails to find a good cluster for colluding Freeriders as
shown in fig. 6. Results for ADA improve over time
but FRC stay at a low level (see table 1; AP).
Both MCL on the work graph and MCL directed
perform good to find adaptive agents (see table 1;
MCL Work and MCL). However, they archive very
bad results for colluding Freeriders.
6 CONCLUSION
This paper described the problem of colluding attack-
ers that try to exploit or damage distributed grid sys-
tems. We explained that utilising technical trust as
basis for cooperation decisions mitigates the nega-
tive effects of malicious elements but does not allow
for countering coordinated groups of malicious ele-
ments. Therefore, we introduced a system-wide de-
tection technique that is able to identify and isolate
such groups of agents. To demonstrate the potential
benefit and the success of the developed technique,
we analysed simulations of a trusted desktop comput-
ing grid. Therein, we considered different groups of
stereo-type agent behaviour and highlighted the suc-
cessful identification of even coordinated attacks.
Figure 6: Visualisation of clustering for AP with 90 Adap-
tive Agents (ADA) and 10 Freerider Colluding (FRC).
Using the Markov Clustering Algorithm on the
undirected trust graph performs well to solve the chal-
lenge of detecting colluding attackers in the Trusted
Desktop Grid. Affinity Propagation Clustering did
not fit for our needs. In future work, the group infor-
mation will be used to isolate agents by introducing
norms into the system.
Current and future work is concerned with a gen-
eralisation of the concept by shifting the focus to-
wards other application scenarios. We further develop
a generalised threat model to verify that all expected
meaningful attack types can be handled by the devel-
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
204

oped mechanisms. Finally, the approach is combined
with distributed accusation strategies that further im-
prove the efficiency of the isolation effects.
ACKNOWLEDGEMENTS
This research is funded by the research unit “OC-
Trust” (FOR 1085) of the German Research Founda-
tion (DFG).
REFERENCES
Anderson, D. P. and Fedak, G. (2006). The Computa-
tional and Storage Potential of Volunteer Computing.
In Proc. of CCGRID 2006, pages 73–80, Singapore.
IEEE.
Anglano, C., Brevik, J., Canonico, M., Nurmi, D., and Wol-
ski, R. (2006). Fault-aware Scheduling for Bag-of-
Tasks Applications on Desktop Grids. In Proc. of
GRID 2006, pages 56–63, Singapore. IEEE.
Anglano, C., Canonico, M., Guazzone, M., Botta, M., Ra-
bellino, S., Arena, S., and Girardi, G. (2008). Peer-to-
Peer Desktop Grids in the Real World: The ShareGrid
Project. Proc. of CCGrid 2008, 0:609–614.
Artikis, A. and Pitt, J. (2009). Specifying Open Agent
Systems: A Survey. In Artikis, A., Picard, G., and
Vercouter, L., editors, Engineering Societies in the
Agents World IX, volume 5485 of LNCS, pages 29–
45. Springer, Saint-Etienne, FR.
Bennett, J. C. and Zhang, H. (1996). WF2Q: Worst-case
Fair Weighted Fair Queueing. In INFOCOM ’96. Fif-
teenth Annual Joint Conference of the IEEE Computer
Societies. Networking the Next Generation. Proceed-
ings IEEE, volume 1, pages 120–128, San Francisco,
CA, USA. IEEE.
Boella, G., Pigozzi, G., and van der Torre, L. (2009). Nor-
mative Systems in Computer Science - Ten Guidelines
for Normative Multiagent Systems. In Boella, G.,
Noriega, P., Pigozzi, G., and Verhagen, H., editors,
Normative Multi-Agent Systems, number 09121 in
Dagstuhl Seminar Proceedings, pages 1–21, Dagstuhl,
Germany. Schloss Dagstuhl - Leibniz-Zentrum fuer
Informatik, Germany.
Chakravarti, A. J., Baumgartner, G., and Lauria, M. (2004).
Application-Specific Scheduling for the Organic Grid.
In Proc. of GRID 2004 Workshops, pages 146–155,
Washington, DC, USA. IEEE.
Demers, A., Keshav, S., and Shenker, S. (1989). Analy-
sis and Simulation of a Fair Queueing Algorithm. In
Symposium Proceedings on Communications Archi-
tectures & Protocols, SIGCOMM ’89, pages 1–12,
New York, NY, USA. ACM.
Frey, B. and Dueck, D. (2007). Clustering by passing mes-
sages between data points. Science, 315:972–976.
Governatori, G. and Rotolo, A. (2008). BIO Logical
Agents: Norms, Beliefs, Intentions in Defeasible
Logic. Autonomous Agents and Multi-Agent Systems,
17(1):36–69.
Hardin, G. (1968). The Tragedy of the Commons. Science,
162(3859):1243–1248.
Hewitt, C. (1991). Open Information Systems Semantics
for Distributed Artificial Intelligence. Artificial intel-
ligence, 47(1):79–106.
Jain, R., Babic, G., Nagendra, B., and Lam, C.-C. (1996).
Fairness, Call Establishment Latency and Other Per-
formance Metrics. ATM-Forum, 96(1173):1–6.
Jardine, N. and Sibson, R. (1971). Mathematical taxonomy.
John Wiley & Sons, Chichester, UK.
Kantert, J., Bernard, Y., Klejnowski, L., and M
¨
uller-
Schloer, C. (2013). Interactive Graph View of Ex-
plicit Trusted Communities in an Open Trusted Desk-
top Grid System. In Proc. of SASO Workshops, pages
13–14.
Kantert, J., B
¨
odelt, S., Edenhofer, S., Tomforde, S., H
¨
ahner,
J., and M
¨
uller-Schloer, C. (2014). Interactive Sim-
ulation of an Open Trusted Desktop Grid System
with Visualisation in 3D. In Self-Adaptive and Self-
Organizing Systems (SASO), 2014 IEEE Eighth Inter-
national Conference on, pages 191–192, London, UK.
IEEE.
Khamsi, M. A. and Kirk, W. A. (2011). An introduction to
metric spaces and fixed point theory, volume 53. John
Wiley & Sons, Chichester, UK.
Klejnowski, L. (2014). Trusted Community: A Novel Mul-
tiagent Organisation for Open Distributed Systems.
PhD thesis, Leibniz Universit
¨
at Hannover.
Ostrom, E. (1990). Governing the Commons: The Evolu-
tion of Institutions for Collective Action. Cambridge
university press, Cambridge, US.
Pitt, J., Schaumeier, J., and Artikis, A. (2011). The Ax-
iomatisation of Socio-Economic Principles for Self-
Organising Systems. In Self-Adaptive and Self-
Organizing Systems (SASO), 2011 Fifth IEEE Interna-
tional Conference on, pages 138–147, Michigan, US.
IEEE.
Rosenschein, J. S. and Zlotkin, G. (1994). Rules of En-
counter: Designing Conventions for Automated Ne-
gotiation Among Computers. MIT Press, Cambridge.
Savarimuthu, B. T. R. and Cranefield, S. (2011). Norm Cre-
ation, Spreading and Emergence: A Survey of Simula-
tion Models of Norms in Multi-Agent Systems. Mul-
tiagent and Grid Systems, 7(1):21–54.
Schaeffer, S. E. (2007). Graph clustering. Computer Sci-
ence Review, 1(1):27–64.
Singh, M. P. (1999). An Ontology for Commitments in
Multiagent Systems. Artificial Intelligence and Law,
7(1):97–113.
Tomforde, S., H
¨
ahner, J., Seebach, H., Reif, W., Sick, B.,
Wacker, A., and Scholtes, I. (2014). Engineering and
Mastering Interwoven Systems. In ARCS 2014 - 27th
International Conference on Architecture of Comput-
ing Systems, Workshop Proceedings, February 25-28,
2014, Luebeck, Germany, University of Luebeck, In-
stitute of Computer Engineering, pages 1–8.
Tomforde, S., Prothmann, H., Branke, J., H
¨
ahner, J., Mnif,
M., M
¨
uller-Schloer, C., Richter, U., and Schmeck, H.
(2011). Observation and Control of Organic Systems.
Detecting Colluding Attackers in Distributed Grid Systems
205

In Organic Computing - A Paradigm Shift for Complex
Systems, pages 325 – 338. Birkh
¨
auser Verlag.
Van Dongen, S. M. (2001). Graph clustering by flow simu-
lation. PhD thesis, Utrecht University.
von Dogen, S. M. (2000). An introduction to mcl. Ac-
cessed: March 30, 2015.
Wang, Y. and Vassileva, J. (2004). Trust-Based Community
Formation in Peer-to-Peer File Sharing Networks. In
Proc. on Web Intelligence, pages 341–348, Beijing,
China. IEEE.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
206
