
Physics-based and Retina-inspired Technique for Image
Enhancement
Mohamed Sedky, Ange A. Malek Aly
and Tomasz Bosakowski
School of Computing, Staffordshire University, Beaconside, Stafford, U.K.
Keywords: Retinex, Image Enhancement, Image Formation Models, Colour Constancy, Contrast Constancy.
Abstract: This paper develops a novel image/video enhancement technique that integrates a physics-based image
formation model, the dichromatic model, with a retina-inspired computational model, multiscale model of
adaptation. In particular, physics-based features (e.g. Power Spectral Distribution of the dominant illuminant
in the scene and the Surface Spectral Reflectance of the objects contained in the image are estimated and are
used as inputs to the multiscale model for adaptation. The results show that our technique can adapt itself to
scene variations such as a change in illumination, scene structure, camera position and shadowing and gives
superior performance over the original model.
1 INTRODUCTION
Image enhancement plays a fundamental role in
computer vision. Images and videos with good
lightness and contrast are a strong requirement in
several areas of applications, where human experts
make an important decision based on the imaging
information, such as medical, security, forensic and
remote sensing applications (Saichandana, 2014).
The objective of an image enhancement algorithm
is to improve the information perception in
images/videos for a human viewer and/or to support
an image/video processing algorithm with a better
input. The result, of such algorithms, is a processed
image that is more suitable than the original image for
a specific application (Maini and Aggarwal, 2010).
Typically, the enhancement is performed to
improve certain desired features e.g. image contrast,
lightness or grey-levels distribution. The choice of
these features and the way they are modified are
specific to a given task.
The well-known methods of image enhancement
include spatial and frequency enhancement
techniques such as linear transformation, gamma
correction, contrast stretching, histogram
equalisation, homomorphic filtering, etc. Those
conventional methods are easy to implement but
generally do not recover exact true colour of the
images hence they have limited application areas.
For example, one of the drawbacks of histogram
equalisation is generating colour distortion in images
during enhancement.
Conventional image enhancement methods have
been widely used with their different advantages and
drawbacks; since the last century, there has been
increased interest in retina-inspired techniques e.g.
Retinex and Cellular Neural Networks (CNN), as
they attempt to mimic the human retina.
Retinex, a compound word comprised of retina
and cortex, is a computational theory derived from
anatomy and neuroscience. Retinex is a very popular
and effective method to remove environmental light
interferences. The two main concepts behind the
theory are: (1) colours of objects are determined by
the capability to reflect rays of light, and (2) colours
are not influenced by uneven illumination. The main
advantages of Retinex are image sharpening and
colour constancy (Land, 1986).
Despite considerable advances in computer vision
techniques, the human eye and visual cortex by far
supersede the performance of state-of-the-art
algorithms.
Marr’s approach to studying computer vision
starts by following what is called representational
theories of minds (Marr and Vision, 1982). He argues
that in order to understand fully a particular machine
carrying out a particular information-processing task,
we have to study that machine as well as the
information-processing task. He saw the
computational study of vision as tightly linked to
psychophysics and neurophysiology. But the last
Sedky, M., Aly, A. and Bosakowski, T.
Physics-based and Retina-inspired Technique for Image Enhancement.
DOI: 10.5220/0005709902390247
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 239-247
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
239

three decades have seen some weakening of that
integration.
Georgeson and Sullivan (Georgeson and Sullivan,
1975) have studied apparent contrast at different
spatial frequencies, in foveal and peripheral vision,
under photopic and scotopic conditions, and at
various orientations in astigmatic subjects. In their
experiments, they found that despite extreme
differences in the contrast thresholds for two patterns,
they will match in apparent contrast when their
physical contrasts are equal. They have concluded
that in man, visual information is blurred by optical
and neural processes restored by an active process of
compensation; they have defined this ability as
‘contrast constancy’.
Similarly, humans have the ability to separate the
illumination power spectral distribution from the
surface spectral reflectance when judging object
appearance, ‘colour constancy’ (Ho et al., 1990).
Image enhancement approaches may be classified
depending on the image representation used as non-
physics-based or physics-based. Non-physics based
image enhancement methods use one of the known
colour spaces as a cue to model the scene. While the
word physics refers to the extraction of intrinsic
features about the materials contained in the scene
based on an understanding of the underlying physics
which govern the image formation. This process is
achieved by applying physics-based image formation
models that attempt to estimate or eliminate the
illumination and/or the geometric parameters to
extract information about the surface spectral
reflectance (SSR) (Sedky, 2014).
Recently, physics-based image formation models
e.g. Dichromatic model, have gained the attention of
the computer vision research community as they
describe mathematically how a digital image is
formed inside a camera, and they attempt to estimate
the Power Spectral Distribution (PSD) of the
dominant illuminant as well as the SSR of objects.
In this paper, we propose a novel physics-based
and retina-inspired image/video enhancement
technique that integrates a physics-based image
formation model, the dichromatic model, with a
retina-inspired computational model, a multiscale
model for adaptation proposed in (Pattanaik et al.,
1998). In particular, physics-based features (e.g. PSD
of the dominant illuminant and the SSR of the objects
contained in the image) are estimated and are used as
inputs to a retina-inspired algorithm to achieve both
colour and contrast constancy to overcome the
limitations of conventional image/video enhancement
methods.
The rest of the paper is organized as follows: the
following Section gives a background on Retina-
inspired models as well as image formation models,
Section 3 describes our computational model, Section
4 presents an illustrative visual comparison between
our proposed technique and the multiscale model for
adaptation, and finally Section 5 concludes the paper.
2 BACKGROUND
Retinex algorithms can be categorised into three
classes, which are: path-based, recursive and
centre/surround Retinex algorithms (Le, 2014).
A. Path-based algorithm: The original work of
Land (Land and McCann, 1971) (Land, 1986)
belongs to this category. In this algorithm, the
lightness of each pixel depends on the multiplication
of ratios along random walks. The drawbacks of this
algorithm are the dependency of the path geometry
and the computational complexity, which has a lot of
parameters.
B. Recursive algorithm: It was developed by
Frankly and McCann (Frankle and McCann, 1983).
This algorithm works on long distance iterations
between pixels, then moves to short distance
interactions. The spacing between pixels being
compared decreases at each step in clockwise order.
This algorithm is computationally more efficient than
the path-based one. The main drawback is that it
depends on the number of times a pixel’s neighbours
are to be visited. This parameter is named some
iterations. The optimal value for this parameter is not
clear and can negatively influence the final result
(Ciurea and Funt, 2004).
C. Centre/Surround algorithm (Morel, 2010): This
technique introduces a weight in the reciprocal
influence of two pixels (Finlayson, 1995), which is
inversely proportional to their square distance.
The lightness values are computed by subtracting
a blurred version of the input image from the original
image. This algorithm is faster than the path-based
one, with less parameter. The main drawback is the
“grey world” assumption, which was addressed
(Berns et al., 1993) by introducing the multi-scale
Retinex with colour restoration technique (Reddy,
2013).
2.1 Image Formation Models
Appearances of scenes depend on four fundamental
elements: an illuminant, a medium, a material and a
vision system. The illuminant represents the source of
visible electromagnetic energy and is characterised
by its PSD. The medium is the medium in which
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
240

electromagnetic waves travel. The surface of the
material modulates the incident electromagnetic
energy and is represented by the surface spectral
reflectance, the fraction of incident radiation reflected
by this surface. The vision system is identified by the
spectral sensitivities of its photosensitive sensors that
represent the response of such element to the received
reflected light.
Figure 1: Schematic diagram of image formation.
Another important parameter is the set of
geometrical features, which represent the scene
structure, the illuminant orientation, the surface
roughness and the viewing geometry. These features
combine non-linearly to form a digital image (Sedky,
2014).
Recovering these features from images is an
important problem in image processing; however, this
recovery is generally hard with the limited amount of
information provided by standard commercial
imaging devices.
The Dichromatic Model
The dichromatic model represents the light reflected
by an inhomogeneous dielectric material as a linear
combination of diffuse and specular reflections. Each
of these parts is further divided into two elements, one
accounting for the geometry and another purely
spectral. There are a great number of reflection
models, most of them developed in the field of
computer graphics. Among these methods, the
dichromatic reflection model is a usual choice for
those algorithms employing a physical model to
represent color images, as shown in Figure 1, and the
equation below:
c
=
d
∫ () ()
c
() +
s
∫ ()
c
()
(1)
Where Ω is the visible range from 400nm to
700nm, I
c
is the measured color intensity of the
reflected light, w
d
and w
s
are geometrical parameters
for diffuse and specular reflection respectively, E(λ)
is the spectral power distribution function of the
illumination, S(λ) is the SSR of the object, Q
c
(λ) is the
camera sensor spectral sensitivities characteristic, and
c represents the color channels (Red, Green and
Blue).
Assuming Lambertian surfaces, theoretically, an
image taken by a digital colour camera (for diffuse
only reflection) can be described as:
c
=
d
∫
Ω
() ()
c
()
(2)
Surface Spectral Reflectance Estimation
Linear Models
Several researchers (Bajcsy et al., 1990), (Maloney,
1986) and (Marimont and Wandell, 1992) show that
both illumination and surface spectral reflectance are
relatively smooth functions of the wavelength of light
in the visual spectrum and that they can be expressed
using finite-dimensional linear models.
The surface reflectances of a great variety of
materials have been studied. Parkkinnen et al.
(Parkkinen et al., 1989), Maloney (Maloney, 1986)
studied the reflectance properties of the Munsell
chips, which is a database of experimentally
measured surface spectral reflectance characteristics.
Parkkinen concludes that 8 basis functions can cover
almost all existing data in Munsell chips database.
However, it has been shown in the literature (Klinker
et al., 1990) that the spectral reflectance calculated
using the first three basis functions has average error
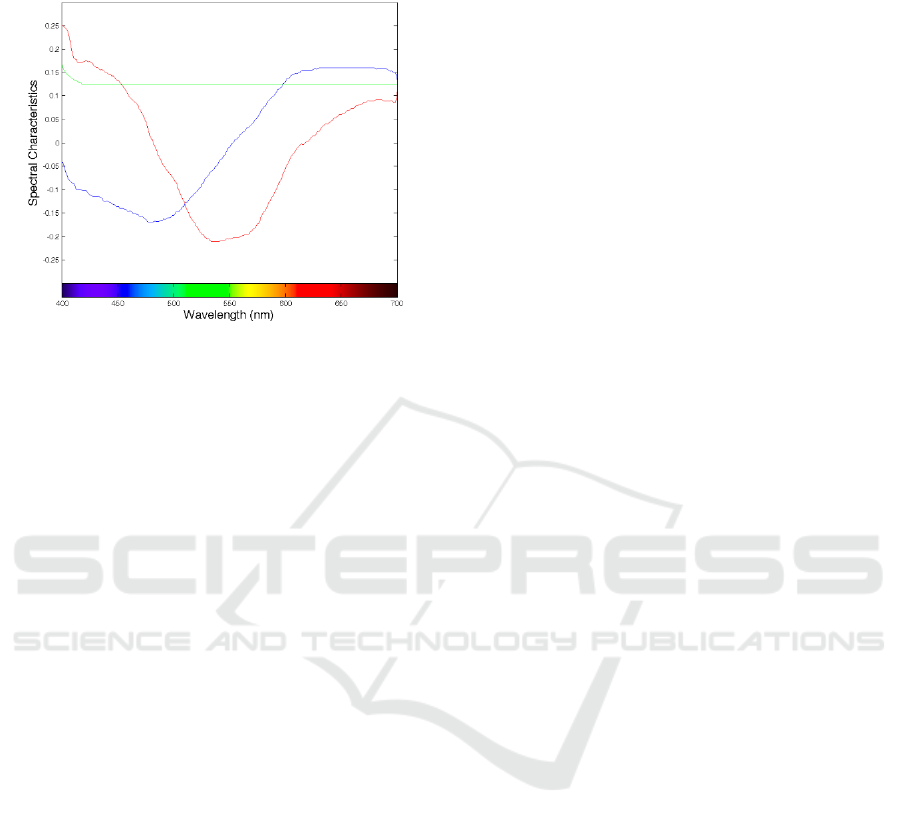
0.0055 and 0.01. Figure 2 shows the first 4 Parkkinen
basis functions. As it can be seen from the figure, a
significant characteristic of Parkkinen basis functions
is the flat distribution of his first basis function.
(
)
=
()
(3)
where
() is the i
th
reflectance linear basis
function, and
is its corresponding weight, is the
number of basis functions used.
Using finite-dimensional linear models to
represent the surface spectral reflectance provides a
compact description of data, with few basis functions
we can represent surface spectral reflectance for
general materials. The linear models have been
extensively used in some colour constancy algorithms
where the main aim was to recover either the
illumination or the reflectance functions, or both of
them.
The assumptions made by the dichromatic
reflection model are:
1. There is a single light source that can be a
point source or an area source;
2. The illumination has a constant PSD across
the scene;
Ω
Ω
Physics-based and Retina-inspired Technique for Image Enhancement
241
3. The amount of illumination can vary across
the scene.
Figure 2: Parkkinen’s first three basis functions.
For what concerns the surface properties, the
model assumes that:
1. The surface is opaque;
2. The surface is not optically active (no
fluorescence);
3. The colourant is uniformly distributed
The assumption of illumination being due to only
one source of illumination is limiting the application
of such models to scenes where there is a dominant
illuminant. The assumptions about the surface are
typical for reflection models and not too unrealistic.
Illuminant Estimation
The aim of the illuminant estimation is to imitate the
human ability to separate the illumination PSD from
the surface reflectance. Several approaches have been
proposed; this includes methods relying on linear
models (Ho et al., 1990), neural networks (Barnard et
al., 2002), reliance on highlights and mutual
reflection (Klinker et al., 1990), and Bayesian and
probabilistic approaches (Sapiro, 1999).
McCamy et al. (McCamy and Calvin, 1992)
derived a simple equation to compute correlated
colour temperature from CIE 1931 chromaticity
coordinates x and y, which is useful in designing
sources to simulate CIE illuminants.
Vision System
The light emitted by sources of illumination and
modulated by surfaces in the scene arrives at the
capturing sensors of the colour vision system that is
observing the scene. The vision system senses the
captured electromagnetic signal and then transforms
the information carried by light into a colour image of
the physical world.
Colour Charge Coupled Device (CCD) camera,
which is an example of a typical vision system,
contains a set of sensors that convert electromagnetic
energy into electric signals, which are, then sampled
and quantized. Conventional CCD cameras insert
colour filters, with different spectral sensitivity to the
various wavelengths, over each sensory element,
typically red, green, and blue filters to obtain colour
information. Figure 3 shows the spectral sensitivities
of the Sony ICX098BQ (Sony ICX098BQ) CCD
sensors, excluding lens characteristics and light
source characteristics, as an example of a typical
surveillance camera. Apart from the spectral
sensitivity of the colour filters, the formation of
digital image colour values includes other factors,
such as lens characteristics, and the electronics of the
camera.
Once a material surface is hit by a bundle of light
emitted by an illuminant, the electromagnetic waves
may be transmitted, absorbed, or reflected back into
the air. The quantities of transmitted absorbed and
reflected energy sum to the incident energy at each
wavelength. Those quantities are typically measured
in relative terms as a fraction of the incident energy.
Some materials may emit light, or fluorescence effect
may occur, where the material absorbs light at
specific wavelengths and then reflect light at different
wavelengths. The surface’s absorption, transmittance
and reflectance are obtained. In this report, materials
are assumed to be opaque, so light transmission
through the material is not considered. The materials
are assumed not to be fluorescence, and so the
emission is not considered to focus on reflection.
The surface spectral reflectance of a material
refers to the ability of the material to reflect different
spectral distributions when some light shines on it. A
reflectance model is a function that describes the
relationship between incident illumination PSD and
reflected light at a given point on a surface and at each
wavelength. S(λ) is defined as the ratio between the
reflected PSD to the incident PSD. Different
materials have different mechanisms of reflection,
optically; most materials can be divided into two
categories:
1. Homogeneous materials and,
2. Inhomogeneous materials
Homogeneous materials have a uniform refractive
index throughout their surface and bodies.
On the other hand, inhomogeneous materials have
varying refractive index throughout their surfaces and
bodies. If a light hits its surface, part of the light
reflects (specular reflection), while the other part
enters the object and then reflects back to the air
causing diffuse reflection. Such material’s surfaces
are known as diffuse (matte) surfaces or Lambertian
surfaces.
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
242
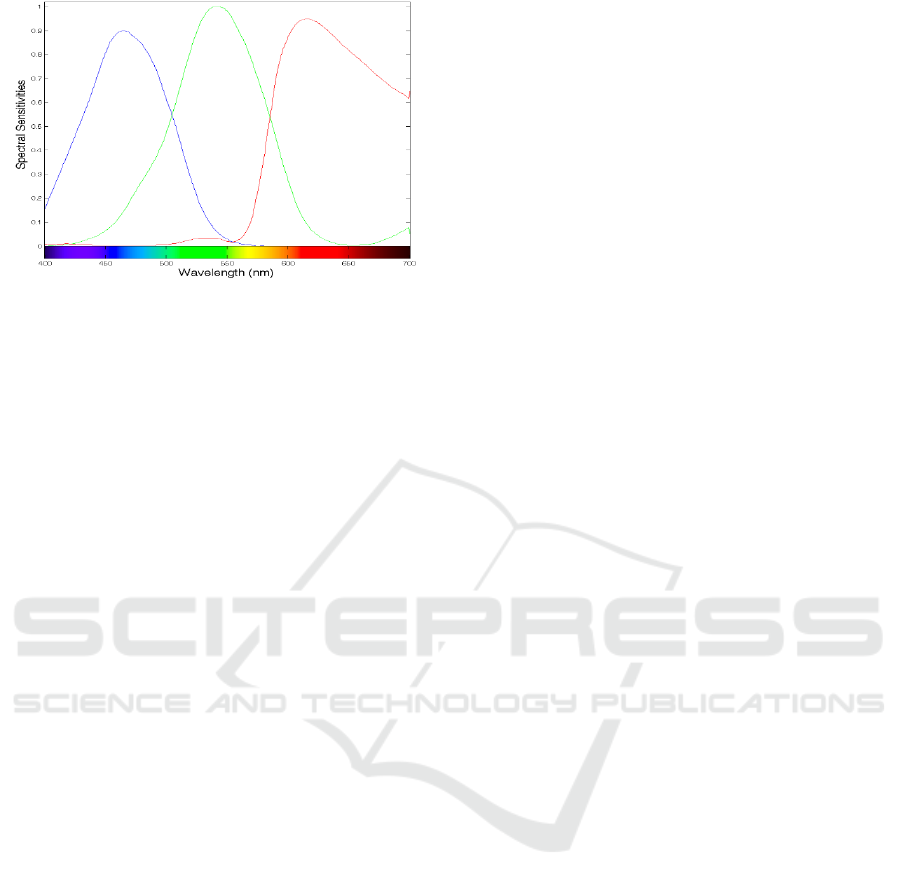
Figure 3: Spectral sensitivity characteristics of the Sony
ICX098BQ camera.
3 COMPUTATIONAL MODEL
Our method can be described in eight stages. The first
stage estimates the SSR based on the dichromatic
colour reflectance model. This approach uses image
formation models to computationally estimate, from
the camera output, a consistent physics-based color
descriptor of the spectral reflectance of surfaces
visible in the image, and then to convert the full-
spectrum reflectance to Long (L), Medium (M), Short
(S) Cone responses and Rod (R) response. This
method represents a new approach to image
enhancement, using explicit hypotheses about the
physics that create images. This step makes our
proposed different from the original model,
(Pattanaik et al., 1998), in that it relies on models,
which can represent wide classes of surface materials.
It makes use of the pre-trained linear SSR models,
shown in Figure 2, to represent the SSR of the objects
in the scene. For what concerns the surface properties,
this model assumes that: the surface is opaque; not
optically active (no fluorescence) and the colourant is
uniformly distributed.
The cones and rod spectral characteristics shown
in Figure 4 are multiplied by the SSR and the result is
integrated to obtain the cone and rod responses, four
images representing the calibrated photoreceptor
responses (L, M, S, R), where they represent, Long,
Medium, Short and rod signals respectively. Those
four signals will be subjected to spatial processing.
The second stage, is the spatial decomposition of
these four images, by applying the Laplacian pyramid
(difference-of-Gaussian pyramid) approach (Burt and
Adelson, 1983). We generate seven Gaussian
pyramid’s levels. Each level of the Gaussian pyramid
represents a low-pass image limited to spatial
frequencies half of those of the next higher level.
The third stage is the gain control stage, where the
difference-of-Gaussian images are then converted to
adapted contrast signals using a luminance gain
control. The gains are set using TVI-like functions
that represent the increment thresholds of the rod and
cone systems and the growth in response required to
allow perceived contrast to increase with luminance
level (sub Weber’s law behaviour). Performing the
gain control at this point in the model allows proper
prediction of chromatic adaptation effects. T
The fourth stage, is the opponent colour
processing, where the model uses the transform of
(Hunt, 1995) to transform the adapted contrast images
for the cones into opponent signals, that will result in
the transformation of the L, M, S-cone signals to A,
C
1
, C
2
, that represent luminance, red-green, and
yellow-blue opponent signals respectively.
The fifth stage is the adapted contrast transducers,
where the adapted contrast signals are then passed
through contrast transducer functions (Watson and
Solomon, 1997). Different transducer functions are
applied to each spatial frequency mechanism to
model psychophysically derived human spatial
contrast sensitivity functions. One of the key
functions of the transducers is to set the threshold
level (200) such that image content that is
imperceptible for a given set of viewing conditions
can be removed.
The sixth stage is the combination of rod and cone
signals, in previous stages it is important to keep the
rod signals separate from the cones to appropriately
integrate their unique adaptation and spatial vision
properties. After the contrast transducers, the rod and
cone signals can be combined to produce signals that
represent the three-dimensional colour appearances
of the input image. At this stage, the model has three
channels representing achromatic, red-green, and
yellow-blue apparent contrast for 6 band-pass
mechanisms.
The seventh stage is the treatment of the low-pass
image, where the lowest level (7
th
level) low-pass
image from the up-sampled Gaussian pyramid must
be retained in order to reconstruct an image from the
adapted contrast images that have been passed
through the model. The approach used, produces
maximum dynamic range compression, by
multiplying each pixel in the low-pass image by a
gain factor derived from the pixel value itself. This
treatment mimics the visual response assuming that
the observer fixated on each and every image location
and judged them completely independent of one
another.
The eighth and last stage, is the image
reconstruction stage, where the final outputs of the
Physics-based and Retina-inspired Technique for Image Enhancement
243
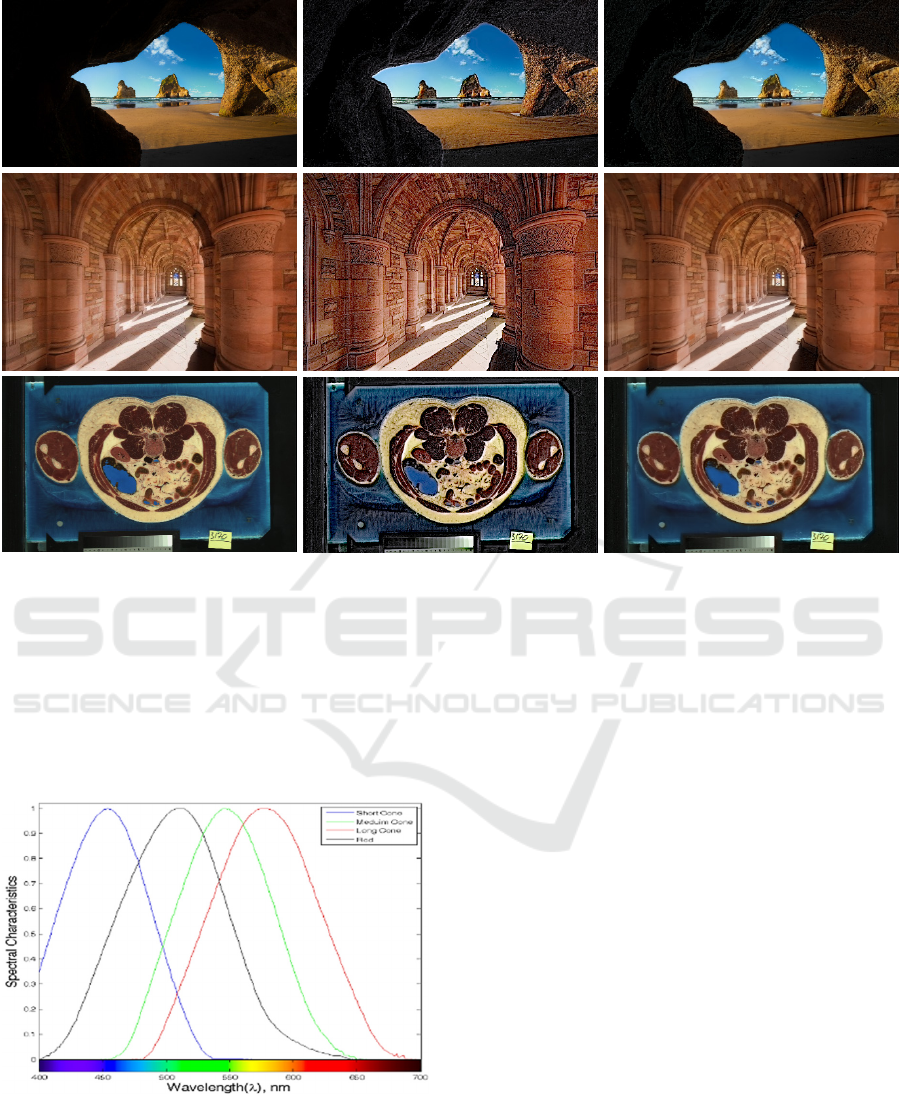
Figure 5: Illustrative visual comparison of the results obtained, the original image (left), the output of the multiscale model
of adaptation (middle) and physics-based retina-inspired model (right).
model are, signals in an achromatic and two
chromatic channels, six spatial band-pass
mechanisms and a low-pass image. In the last stage,
the model must be inverted, this procedure does not
“undo” the processes of the model since the threshold
and saturated ion procedures are accomplished.
Figure 4: Cones and Rod spectral characteristics.
4 ILLUSTRATIVE VISUAL
COMPARISON
We have implemented our computational model
using Matlab. The results of our implementation, are
evaluated by visually comparing the results of the
multiscale model of adaptation method (Pattanaik et
al., 1998) and our proposed model.
The subjective assessment method was selected to
initially evaluate results obtained by the proposed
physics-based retina-inspired model. This would
allow the authors to identify potential application
where image/video processing algorithms could be
improved by applying the proposed model.
The first image in the top section of Figure 5
shows a view taken from a sea cave looking across a
beach. In this image there is a shadow in the
foreground at the entrance to the cave. The wall of the
cave appears to be saturated almost black, and the
surface details are not defined. The middle image in
the top section is the output obtained by the
application of the multiscale model of adaptation. The
result shows that the model concentrated on
predominantly the darker areas highlighting, in
particular, the shadowed areas. This resulted in an
almost CGI rendition of the original image and
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
244

Figure 6: Illustrative visual comparison of the results obtained, the original image (left), the output of the multiscale model
of adaptation (middle) and physics-based retina-inspired model (right).
appeared unrealistic. When applying our proposed
model (right-hand image top section of Figure 5
however, the definition appears to be more precise
and clearer. On the other hand, the visual model used
in the middle image highlights the details of the sand
patterns within the cave shadow.
The first image of the second row (from the left-
hand side) is of a cloister in a monastic building
highlighting the shadows bouncing off sandstone
columns. The image also defines the details in the
carvings above the pillars. The second image of the
same row is less natural due to oversaturation of
detail. However, the intricate carvings are clearly
highlighted but to some extent exaggerated. The third
image in the same row on this occasion is visually
very similar to the first image.
The bottom left image in Figure 5 shows an
example of a medical image. The output of the
multiscale adaptation model is showing good
improvement by extracting details such as blood
vessels that could improve medical diagnosis.
Although, the results obtained by using our model
(right bottom of Figure 5 shows fewer details, it could
improve the segmentation quality of certain objects,
depending on the required application. The image on
the top of Figure 6 shows an image taken at night. The
gable ends, roofs and building facades are blurred.
The results obtained by the application of multiscale
adaptation model (the top middle image of Figure 6)
shows that too many artefacts were identified, make
it difficult to identify important features such as roof
tops or eaves. In comparison, the top left image of
Figure 6 shows the output of our proposed model.
This brings out the finer details with a reasonable
level of unwanted artefacts. Clear lines of the gable
end, roofs and building facades can be also observed.
The middle left image of Figure 6 represents a
bright image with glare from objects. The multiscale
adaptation model (the second image in the middle
row) although finds more features, it also detects
unwanted artefacts on a desk draw, and this can give
misleading results. It can be also noticed that some
book titles are distorted due to unwanted artefacts.
With the proposed model (middle right of Figure 6)
Physics-based and Retina-inspired Technique for Image Enhancement
245

the output of our algorithm detects less unwanted
data, yet still provides good sharpness of objects.
Finally, the bottom left the image in Figure 6
shows similar scenario as the middle image i.e. a desk
with a lamp and books on one side of the table.
However, this a darker image where the lamp was the
only source of light, and, therefore, the book titles are
not visible. Both models improved the image and
clear book edges are visible, and book titles can be
legible. However, the multiscale adaptation model
(the second image in the last row of Figure 6)
generates unwanted mist effect around the table lamp.
The computational complexity for the proposed
algorithms is evaluated regarding average processing
time for one frame. The presented results are obtained
using a personal computer (processor: Intel i7 3GHz,
Memory: 16GB RAM), an implementation in Matlab
(version: 8.3, release: R2014a). The multiscale model
of adaptation method requires 0.44 sec to process a
240x320 image while our proposed algorithm
requires 1.08 sec.
5 CONCLUSIONS
In this paper, we have developed a novel physics-
based and retina-inspired image/video enhancement
technique that integrates a physics-based image
formation model, the dichromatic model, with a
retina-inspired computational model, a multiscale
model for adaptation.
We have embedded both contrast and colour
constancy by extracting physical features from the
camera output; this approach is unlike other image
enhancement algorithms that use the camera output
directly without considering its physical meaning.
The estimation of the spectral characteristics of
the dominant illuminant allows the proposed
technique to adapt itself to different illumination
conditions; this means that it would be applicable for
a variety of scenes and not to be limited to certain
environments.
Our results have shown that the estimation and use
of physics-based spectral image representations,
deduced from the dichromatic model, represent a
more realistic input to the retina-inspired models and
would mimic the signal received by the human eye.
REFERENCES
Bajcsy R., Lee S., & Leonardis A., (1990). Colour image
segmentation with detection of highlights and local
illumination induced by inter-reflections In
Proceedings of ICPR, pp. 785-790.
Barnard, K., Cardei, V., & Funt, B. (2002). A comparison
of computational color constancy algorithms. I:
Methodology and experiments with synthesized data.
Image Processing, IEEE Transactions on, 11(9), 972-
984.
Berns, R. S., Motta, R. J., & Gorzynski, M. E. (1993). CRT
colorimetry. Part I: Theory and practice. Color Re-
search & Application, 18(5), 299-314.Burt, P.J., and
Adelson, E.H. (1983) The Laplacian Pyramid as a
Compact Image Code. IEEE Transaction on
Communication, 31(4), 532-540.
Ciurea, F., & Funt, B. (2004). Tuning retinex parameters.
Journal of Electronic Imaging, 13(1), 58-64.
Finlayson, G. D. (1995). Color constancy in diagonal
chromaticity space. In Computer Vision, 1995. Pro-
ceedings, Fifth International Conference on (pp. 218-
223). IEEE.
Frankle, J. and McCann, J., (1983). Method and apparatus
for lightness imaging, US Patent, May 1983, number
Patent 4384336.
Georgeson, M. A., and Sullivan, G. D. (1975). Contrast
constancy: deblurring in human vision by spatial
frequency channels. The Journal of Physiology, 252(3),
Ho, J., Funt, V., & Drew, M. S. (1990). Separating a color
signal into illumination and surface reflectance
components: Theory and applications. Pattern Analysis
and Machine Intelligence, IEEE Transactions on,
12(10), 966-977.
Hunt, R.W.G. (1995). The Reproduction of Color. 5th
edition, Kingstonupon-Thames, England: Fountain
Press.
Klinker, G. J., Shafer, S. A., & Kanade, T. (1990). A
physical approach to color image understanding.
International Journal of Computer Vision, 4(1), 7-38.
Land, E. H. (1986). Recent advances in Retinex theory.
Vision research, 26(1), 7-21.
Land, E. H., & McCann, J. (1971). Lightness and retinex
theory. JOSA, 61(1), 1-11.
Maini, R., & Aggarwal, H. (2010). A comprehensive
review of image enhancement techniques. arXiv
preprint arXiv:1003.4053.
Maloney L. T., (1986). Evaluation of linear models of
surface spectral reflectance with small numbers of
parameters. In: Journal of the Optical Society of
America A, vol. 3, pp. 1673-1683.
Marimont D. H., and Wandell B. A., (1992). Linear models
of surface and illuminant spectra. In: Journal of the
Optical Society of America A, vol. 3, pp. 1673-1683.
Marr, D., & Vision, A. (1982). A computational
investigation into the human representation and
processing of visual information. WH San Francisco:
Freeman and Company.
McCamy and Calvin S., (1992). Correlated colour
temperature as an explicit function of chromaticity
coordinates. In: Journal of Colour Research &
Application, vol. 17, no. 2, pp. 142-144.
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
246

Morel, J. M., Petro, A. B., & Sbert, C. (2010). A PDE
formalization of retinex theory. Image Processing,
IEEE Transactions on, 19(11), 2825-2837.
Parkkinen, J. P., Hallikainen, J., & Jaaskelainen, T. (1989).
Characteristic spectra of Munsell colors. JOSA A, 6(2),
318-322.
Pattanaik, S. N., Ferwerda, J. A., Fairchild, M. D., &
Greenberg, D. P. (1998, July). A multiscale model of
adaptation and spatial vision for realistic image display.
In Proceedings of the 25th annual conference on
Computer graphics and interactive techniques (pp. 287-
298). ACM.
Reddy, A. A., Jois, P. R., Deekshitha, J., Namratha, S., &
Hegde, R. (2013). Comparison of image enhancement
techniques using retinex models 1, 1–6.
Saichandana, B., Ramesh, S., Srinivas, K., & Kirankumar,
R. (2014). Image Fusion Technique for Remote Sensing
Image Enhancement. In ICT and Critical Infrastructure:
Sapiro G., (1999). Colour and illuminant voting. In: IEEE
Transaction on Pattern Analysis and Machine
Intelligence, vol. 21, no. 11, pp. 1210-1215.
Sedky, M., Moniri, M., & Chibelushi, C. C. (2014).
Spectral-360: A Physics-Based Technique for Change
Detection. In Computer Vision and Pattern Recognition
Workshops (CVPRW), 2014 IEEE Conference on (pp.
405-408). IEEE.
Watson, A.B. and Solomon, J.A. (1997) Model of Visual
Contrast Gain Control and Pattern Masking. J. Opt.
Soc. Am. A, 14(9), 2379-2391.
Physics-based and Retina-inspired Technique for Image Enhancement
247
