
Adaptive Two-stage Learning Algorithm for Repeated Games
Wataru Fujita
1
, Koichi Moriyama
2
, Ken-ichi Fukui
1,3
and Masayuki Numao
1,3
1
Graduate School of Information Science and Technology, Osaka University,
1-5, Yamadaoka, Suita, Osaka, 565-0871, Japan
2
Graduate School of Engineering, Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, 466-8555, Japan
3
The Institute of Scientific and Industrial Research, Osaka University, 8-1, Mihogaoka, Ibaraki, Osaka, 567-0047, Japan
Keywords:
Multi-agent, Reinforcement Learning, Game Theory.
Abstract:
In our society, people engage in a variety of interactions. To analyze such interactions, we consider these
interactions as a game and people as agents equipped with reinforcement learning algorithms. Reinforcement
learning algorithms are widely studied with a goal of identifying strategies of gaining large payoffs in games;
however, existing algorithms learn slowly because they require a large number of interactions. In this work,
we constructed an algorithm that both learns quickly and maximizes payoffs in various repeated games. Our
proposed algorithm combines two different algorithms that are used in the early and later stages of our algo-
rithm. We conducted experiments in which our proposed agents played ten kinds of games in self-play and
with other agents. Results showed that our proposed algorithm learned more quickly than existing algorithms
and gained sufficiently large payoffs in nine games.
1 INTRODUCTION
Humans make a variety of decisions in their daily
lives. In social situations in which a person’s deci-
sion depends on other people, there are complicated
mutual relations such as competition and cooperation
among people. Many researchers have widely stud-
ied game theory that models relations among people
as “games” and analyzed rational decision-making in
games.
Furthermore, humans have an instinctive desire
for survival; therefore, learning through trial-and-
error to avoid harmful and unpleasant states and ap-
proach beneficial and pleasant states. Such learn-
ing occurs given a learning mechanism in the human
brain. Many researchers study reinforcement learning
algorithms that model this learning mechanism.
Let us consider people who learn their behavior
from the result of interacting with others. As a model
of this, we discuss reinforcement learning agents that
play games. Many (multi-agent) reinforcement learn-
ing algorithms that perform well in various games
have already been proposed; however, such algo-
rithms typically require a large number of interactions
to learn appropriate behavior in the games. People in
the real world must quickly learn to make reasonable
decisions, because the world changes rapidly. Exist-
ing algorithms have various features, each with its ad-
vantages and disadvantages. These algorithms can be
complementary. Therefore, in this study, we construct
an algorithm that learns quickly and performs well in
any type of game by combining features from multi-
ple algorithms.
Aside from this introductory section, the structure
of this paper is as follows. In Section 2, we intro-
duce games and learning algorithms used in later sec-
tions. In Section 3, we construct a new learning algo-
rithm that learns quickly and performs well in various
games by combining two learning algorithms. Next,
we evaluate our proposed algorithm by conducting
experiments, as described in Section 4. In Section 5,
we introduce related works to show the relative posi-
tion of our algorithm. Finally, in Section 6, we con-
clude our paper and provide avenues for future work.
2 BACKGROUND
In this section, we introduce game theory that models
interactions among people and reinforcement learn-
ing algorithms that model trial-and-error learning for
adaptation to a given environment.
Fujita, W., Moriyama, K., Fukui, K-i. and Numao, M.
Adaptive Two-stage Learning Algorithm for Repeated Games.
DOI: 10.5220/0005711000470055
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 1, pages 47-55
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
47

2.1 Game Theory
We, as humans, are always making decisions as to
what to do next to achieve our desired purpose or
goals. In social environments, every decision is af-
fected by the decisions of other people. Game theory
(Okada, 2011) mathematically analyzes the relation-
ship among such decisions.
A game in game theory consists of the following
four elements (Okada, 2011):
1. Rules that govern the game;
2. Players who decide what to do;
3. Action strategies of the players; and
4. Payoffs given to the players as a result of their
decisions.
Game theory analyzes how players behave in an
environment in which their actions mutually influence
one another. We focus on two-person simultaneous
games in this study.
In a two-person simultaneous game, two players
simultaneously choose actions based on their given
strategies. After both players choose their respective
actions, each player is given a payoff determined by
the “joint actions” of both players. Since the payoff of
each player is determined by not only his or her action
but also the other player’s action, it is necessary to de-
liberate the other player’s action to maximize payoffs.
Note that all games used in this research are non-
cooperative game, and players choose their individual
strategies based on its own payoffs and all players’
actions. More specifically, after a player observes its
payoffs and the action of the other players, he or she
can then choose his or her own self-strategy.
A Nash equilibrium is defined as the combination
of actions in which no player is motivated to change
his or her strategy. Let us consider the ”prisoner’s
dilemma” game summarized in Table 1. Here, the row
and column correspond to the actions of Players 1 and
2, respectively; they gain the left and right payoffs,
respectively, corresponding to the joint action in the
matrix.
According to the payoff matrix, the player should
choose the Defection action regardless of the other
player’s action, because it always yields higher pay-
offs than the Cooperation action. Since the other
player considers the same, both players choose De-
fection, and finally, the combination of actions (i.e.,
Defection, Defection) becomes a Nash equilibrium.
Conversely, if both players select Cooperation,
both payoffs can be raised to 0.6 from 0.2; however,
it is very difficult for both players to choose Coopera-
tion, because the combination (i.e., Cooperation, Co-
operation) does not yield equilibrium and each player
is motivated to choose Defection. Moreover, even if a
player overcomes this motive for a certain reason, he
or she will yield a payoffof zero if the partner chooses
Defection. The prisoner’s dilemma game shows that
the individual’s rationality differs from that of social
rationality in a social situation.
Table 1: An example of payoffs in the prisoner’s dilemma
game.
Cooperation Defection
Cooperation 0.6,0.6 0.0,1.0
Defection 1.0,0.0 0.2,0.2
2.2 Reinforcement Learning
Reinforcement learning (Sutton and Barto, 1998) is a
learning method that learns strategies by interacting
with the given environment. An agent is defined as a
decision-making entity, while the environment is ev-
erything external to the agent that interacts with the
agent. Furthermore, the agent interacts with the en-
vironment at discrete time steps, i.e., t = 0,1,2,3,....
At each time step t, the agent recognizes current state
s
t
∈ S of the environment, where S is a set of possible
states, and decides action a
t
∈ A(s
t
) based on the cur-
rent state, where A(s
t
) is a set of actions selectable in
state s
t
.
At the next step, the agent receives reward r
t+1
∈
ℜ as a result of the action and transitions to new state
s
t+1
. The probability that the agent chooses possible
action a in state s is shown as strategy π
t
(s,a). Re-
inforcement learning algorithms update strategy π
t
or
the action values (not the strategy) at each time step,
choosing an action based on the strategy.
2.3 Three Foundational Learning
Algorithms
Here we introduce three learning algorithms that form
the basis for our proposal.
2.3.1 M-Qubed
M-Qubed (Crandall and Goodrich, 2011) is an excel-
lent state-of-the-art reinforcement learning algorithm
that consists of three strategies that can learn to coop-
erate with associates (i.e., other players) and avoid be-
ing exploited unilaterally in various games. M-Qubed
uses Sarsa (Rummery and Niranjan, 1994) to learn ac-
tion value function Q(s,a) (called the Q-value), which
means the value of action a in state s. Here, state is
defined as the latest joint action of the agent and its as-
sociates. Further, Q(s,a) is updated by the following
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
48

rule:
Q
t+1
(s
t
,a
t
)
= Q
t
(s
t
,a
t
) + α[r
t
+ γV
t
(s
t+1
) − Q
t
(s
t
,a
t
)],
(1)
V
t
(s) =
∑
a∈A(s)
π
t
(s,a)Q
t
(s,a), (2)
where r
t+1
∈ [0, 1], α is the learning rate, and γ is the
discount rate.
After M-Qubed updates the Q-value, it calculates
the strategy of the agent from three sub-strategies,
i.e., “Profit pursuit”, “Loss aversion”, or “Optimistic
search”. Each of these is described below. Further,
the maximin value is the secured payoff regardless
of the associates given by the maximin strategy that
maximizes the minimum payoff based on the payoff
definition of the game.
Profit Pursuit
This sub-strategy takes the action with the max-
imum Q-value if it is larger than the discounted
sum of the maximin value; otherwise, the max-
imin strategy is used.
Loss Aversion
This sub-strategy takes the action with the maxi-
mum Q-value if the accumulated loss is less than
a given threshold; otherwise, the maximin strat-
egy is used. Here, the accumulated loss is the dif-
ference between the accumulated payoffs and the
accumulated maximin value. The threshold is set
proportional to the number of possible states and
joint actions.
Optimistic Search
The “Profit pursuit” strategy can acquire high pay-
offs for the moment; however, it tends to produce
myopic actions as a result. The “Loss aversion”
strategy cannot lead cooperative strategies with
associates, which may yield higher payoffs. To
solve these problems, M-Qubed sets the initial Q-
values to their highest possible discounted reward
1/(1− γ), thereby learning wider strategies.
Next, the strategy is a weighted average of “Profit
pursuit” and “Loss aversion”, and Q-values are ini-
tialized by “Optimistic search”.
However, if all recently visited states have low Q-
values, the strategies of the agent and its associates
may remain at a local optimum. The agent must ex-
plore further to find a solution that may give a higher
payoff. Hence, in this case, the strategy is changed to
a weighted average of the above strategy and a com-
pletely random strategy.
2.3.2 Satisficing Algorithm
Satisficing algorithm (S-alg) (Stimpson and
Goodrich, 2003) is an algorithm that calculates
a value called the aspiration level of the agent. The
agent continues to take an action that gives payoffs
more than its aspiration level. The algorithm is shown
in Algorithm 1.
Algorithm 1: Satisficing algorithm.
Parameters:
t: time
α
t
: aspiration level at time t
a
t
: my action at time t
r
t
: payoff at time t
λ ∈ (0, 1): learning rate
Initialize:
t = 0
Set α
0
randomly between the maximum payoff
R
max
and 2R
max
repeat
Select a
t
if r
t−1
≥ α
t−1
then
a
t
← a
t−1
else if otherwise then
a
t
← Random
end if
Receive r
t
and update α
t
α
t+1
← λα
t
+ (1− λ)r
t
t ← t + 1
until Game Over
S-alg is an algorithm that enables an agent to learn
to take cooperative actions with its associates.
2.3.3 BM Algorithm
Fujita et al. (2016) proposed BM algorithm to maxi-
mize payoffs by combining M-Qubed and S-alg. BM
algorithm comprises the above two learning algo-
rithms and creates a new strategy that combines the
strategies derived from the two internal algorithms.
Both algorithms simultaneously update their func-
tions, i.e., the Q-value and aspiration level.
BM algorithm uses a Boltzmann multiplication
(Wiering and van Hasselt, 2008) as the method of
combination. Based on strategy π
t
j
of internal algo-
rithm j, Boltzmann multiplication multiplies strate-
gies of all internal algorithms for each available action
and determines the ensemble strategy by the Boltz-
mann distribution. The preference values of actions
are defined as
p
t
(s
t
,a[i]) =
∏
j
π
t
j
(s
t
,a[i]) (3)
Adaptive Two-stage Learning Algorithm for Repeated Games
49

and the resulting ensemble strategy is defined as
π
t
(s
t
,a[i]) =
p
t
(s
t
,a[i])
1
τ
∑
k
p
t
(s
t
,a[k])
1
τ
, (4)
where a[i] is a possible action and τ is a temperature
parameter. After calculating the ensemble strategy,
the agent selects an action, and then all internal algo-
rithms learn from the result of this selected action.
Since S-alg yields only pure strategies, all actions
except for the chosen one have zero probability. The
M-Qubed becomes meaningless when the Boltzmann
multiplication is used to combine M-Qubed and S-alg
without consideration. Therefore, the S-alg in BM
algorithm yields a mixed strategy in which the chosen
action is played with probability 0.99.
3 PROPOSED ALGORITHM
In this study, we consider reinforcement learning
agents that play games. M-Qubed, BM, and S-alg
agents perform well in some games, but have prob-
lems in other games, as summarized below:
• M-Qubed requires a long time to learn, because it
has multiple strategies and needs to decide which
one is used. Therefore, the average payoff be-
comes less than S-alg in the game having only one
suitable solution that is in cooperation with the as-
sociates.
• BM algorithm performs better than M-Qubed, but
it is still slow in search because the internal S-alg
cannot completely compensate for the slowness of
M-Qubed.
• If the associates are greedy, S-alg is exploited uni-
laterally, because it decreases the aspiration level,
and then S-alg is satisfied with low payoffs.
• Due to insufficient search, S-alg may be satisfied
with the second-best payoff.
These algorithms do not have sufficient perfor-
mance for a variety of reasons; however, their posi-
tive abilities are complementary. BM, which is not
exploited due to the “Loss aversion” strategy and ex-
plores the given environment thoroughly enough, can
compensate for the weakness of S-alg that tends to be
exploited. Conversely, S-alg, which quickly learns to
cooperate, can compensate for the weakness of BM,
i.e., its slowness of search. Search in an early stage
of interactions and the secured payoff are important
when the agent learns. Therefore, we combine BM
and S-alg to construct an algorithm that quickly learns
good strategies in various games.
We call our proposed algorithm J-algorithm (J-
alg). J-alg has an Exploration stage and a Static stage.
The Exploration stage is represented by our S’ algo-
rithm, which is a slightly modified version of S-alg.
Similarly, the Static stage is represented by BM algo-
rithm. In the following subsections, we introduce our
S’ algorithm (i.e., S’-alg) and our proposed two-stage
J-alg.
3.1 S’ Algorithm
We focused on S-alg to play a key role in the Ex-
ploration stage, because S-alg can learn to cooperate
quickly; however, S-alg tends to cover an insufficient
search space and falls prey to a myopic strategy. Sup-
pose that the S-alg agents play the Security game (SG)
shown in Table 2. If the aspiration level of the row
player is smaller than 0.84, the player loses his or her
motivation to change his or her action from x. Con-
sequently, both players are satisfied with a payoff that
is not the largest one. S-alg stops searching for other
actions and is therefore prone to a shortened search.
Table 2: Security game (SG).
z w
x 0.84, 0.33 0.84, 1.0
y 0.0, 1.0 1.0, 0.67
To solve this problem, we slightly modify S-alg
to add new action b; this new algorithm is called the
S’ algorithm (i.e., S’-alg). In short, in S’-alg, if the
agent receives the maximin value as the last payoff, it
selects action b. The modified algorithm is shown in
Algorithm 2.
This change stochastically forces the agent to take
other actions to escape from a local solution and po-
tentially find a better one.
3.2 Integrating the Two Stages
J-alg uses S’-alg for the Exploration stage and BM for
the Static stage. The J-alg agent starts in the Explo-
ration stage. After the joint action converges, the al-
gorithm switches to the Static stage and resets the Q-
values to choose the converged action more often. If
the joint action does not convergein the first t
c
rounds,
the algorithm simply changes to the Static stage with-
out changing the value. The algorithm is shown in
Algorithm 3.
Even though the J-alg agent is exploited in the
Exploration stage, it will recover in the Static stage
via BM algorithm that can evade a loss by using
“Loss aversion” strategy.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
50

Algorithm 2: S’ algorithm.
Parameters:
t: time
α
t
: aspiration level at time t
a
t
: my action at time t
r
t
: payoff at time t
λ ∈ (0, 1): learning rate
b: a random action other than a
t−1
with probabil-
ity p and a random action selected from all of the
actions with probability (1− p)
Initialize:
t = 0
Set α
0
randomly between the maximum payoff
R
max
and 2R
max
repeat
Select a
t
if r
t−1
≥ α
t−1
then
a
t
← a
t−1
else if r
t−1
= maximin value then
a
t
← b
else if otherwise then
a
t
← Random
end if
Receive r
t
and update α
t
α
t+1
← λα
t
+ (1− λ)r
t
t ← t + 1
until Game Over
4 EXPERIMENTS
To confirm sufficient performance of J-alg, we con-
ducted experiments using 10 two-person two-action
matrix games used in the M-Qubed paper (Crandall
and Goodrich, 2011). Here, the agent can observe
only the previous joint action and its own payoff. We
also set the M-Qubed parameters to be identical to the
original ones noted in Crandall and Goodrich (2011).
We set parameter τ of the BM algorithm to 0.2. Fur-
ther, we set learning rate λ = 0.99, probability p = 0.3
of S’-alg, reduction rate δ = 0.99 and time t
c
= 500
for the threshold at which a shift occurs from the Ex-
ploration stage to the Static stage. We considered that
a certain joint action converged when it had contin-
ued 30 rounds. Table 3 shows the games used in our
experiments. Here, we call the maximum joint action
a joint action by which the sum of both player’s pay-
offs becomes maximum (which is shown in bold italic
typeface in the table).
4.1 Experiment 1
Our first experiment was conducted in games
where both players are agents with the same algo-
Algorithm 3: J-alg.
Parameters:
s: state
a: action
a
c
: my action when joint action converges
r
c
: payoff when joint action converges
δ ∈ [0, 1]: reduction rate
Initialize:
t = 1
Start the Exploration stage
repeat
if in the Exploration stage and t < t
c
then
if joint action has not converged then
Continue the Exploration stage
else if otherwise then
if a = a
c
then
Q(s,a) ← r
c
/(1− γ)
else if otherwise then
Q(s,a) ← δ × r
c
/(1− γ)
for all s.
Start the Static stage
end if
end if
else if otherwise then
Start the Static stage
end if
t ← t + 1
until Game Over
rithm, i.e., in self-play. Agents played one of the 10
games for 50000 rounds, iterating 50 times for each
game. We then compared the normalized average
payoffs of M-Qubed, S-alg, BM, and J-alg. Note that
the earlier the actions of agents converge to the max-
imum joint action, the larger the normalized average
payoffs become. Table 4 shows the normalized aver-
age payoffs in the games, each of which is the average
payoff divided by that of the maximum joint action. If
the normalized averagepayoffis close to one, it shows
that the agent quickly learned the maximum joint ac-
tion in the game.
From our results, we observe that J-alg gained
high payoffs and quickly learned the maximum joint
action of nine games in self-play. It was able to learn
optimal strategies more quickly than M-Qubed and
BM due to the Exploration stage (i.e., S’-alg). M-
Qubed and BM particularly gained low payoffs in the
prisoner’s dilemma (PD) game, because of the mutual
defection (b,d) by performing many explorations to
learn the cooperative joint action (a,c). S-alg gained
high payoffs in eight games, not including the secu-
rity game (SG) and the offset game (OG). In these
games, the aspiration level of S-alg decreased be-
low the second-best payoff because of insufficient ex-
Adaptive Two-stage Learning Algorithm for Repeated Games
51
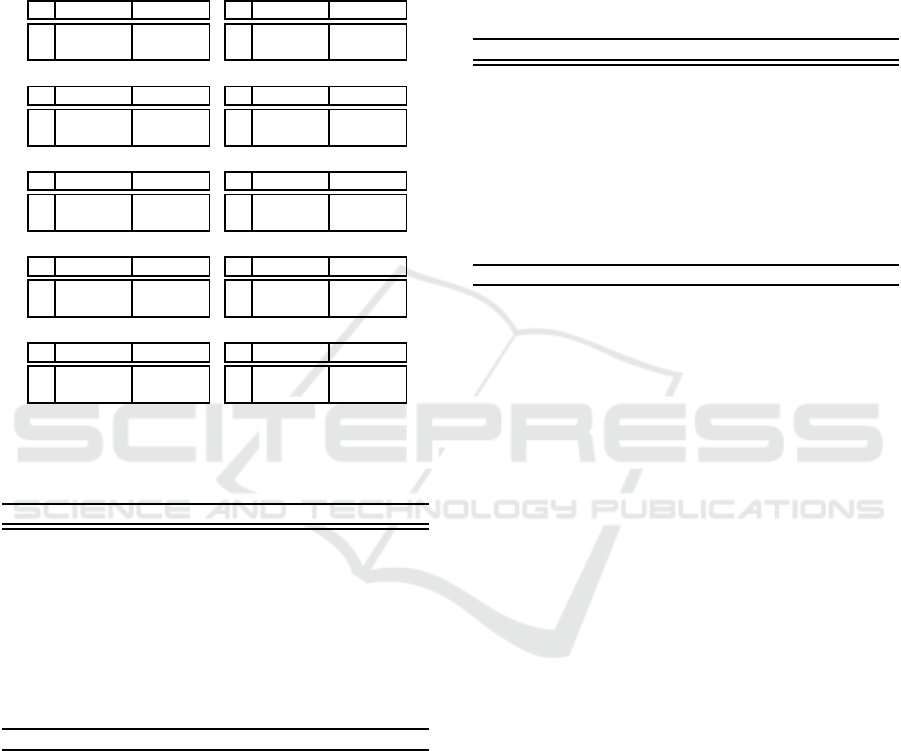
Table 3: Payoff matrices of the two-person two-action ma-
trix games used in our experiments. The row player has two
actions, a and b, and the column player has two actions, c
and d. The values in the cells show the payoffs the play-
ers are given when the joint action appears (i.e., left for the
row player and right for the column player). Payoffs in bold
italic typeface are those that maximize the sum of the two
payoffs.
(a) Common interest game (CIG)
c d
a 1.0, 1.0 0.0, 0.0
b 0.0, 0.0 0.5, 0.5
(b) Coordination game (CG)
c d
a 1.0, 0.5 0.0, 0.0
b 0.0, 0.0 0.5, 1.0
(c) Stag hunt (SH)
c d
a 1.0, 1.0 0.0, 0.75
b 0.75, 0.0 0.5, 0.5
(d) Tricky game (TG)
c d
a 0.0, 1.0 1.0, 0.67
b 0.33, 0.0 0.67, 0.33
(e) Prisoner’s dilemma (PD)
c d
a 0.6, 0.6 0.0, 1.0
b 1.0, 0.0 0.2, 0.2
(f) Battle of the sexes (BS)
c d
a 0.0, 0.0 0.67, 1.0
b 1.0, 0.67 0.33, 0.33
(g) Chicken (Ch)
c d
a 0.84, 0.84 0.33, 1.0
b 1.0, 0.33 0.0, 0.0
(h) Security game (SG)
c d
a 0.84, 0.33 0.84, 0.0
b 0.0, 1.0 1.0, 0.67
(i) Offset game (OG)
c d
a 0.0, 0.0 0.0, 1.0
b 1.0, 0.0 0.0, 0.0
(j) Matching pennies (MP)
c d
a 1.0, 0.0 0.0, 1.0
b 0.0, 1.0 1.0, 0.0
Table 4: Normalized average payoffs when agents played
games in self-play. The bold typeface indicates the best re-
sults among the four given methods.
J-alg M-Qubed S-alg BM
CIG 0.999080 0.993804 0.999039 0.999181
CG 0.951450 0.847301 0.997966 0.867965
SH 0.999182 0.995857 0.999149 0.998505
TG 0.998033 0.814068 0.998251 0.828770
PD 0.998569 0.711794 0.998626 0.723831
BS 0.998686 0.910656 0.998700 0.917655
Ch 0.998909 0.934089 0.998900 0.931541
SG 0.998612 0.902031 0.718236 0.907887
OG 0.466739 0.473539 0.499964 0.478196
MP 1.000000 1.000000 1.000000 1.000000
Avg. 0.940926 0.858314 0.920883 0.865353
ploration. For all algorithms, the offset game (OG)
proved difficult to learn the optimal strategy.
4.2 Experiment 2
In our second experiment, we compared J-alg with
M-Qubed, S-alg, and BM in round-robin tournaments
in which all combinations of agents were examined.
As with Experiment 1, the agents played one of the
10 games 50000 times, iterating 50 times for each
game. In asymmetric games, we replaced the posi-
tion of players and started our experiment again. The
normalized average payoffs of each game are shown
in Table 5. Values greater than one indicate that the
agent exploited other agents and gained high payoffs
as a result. If the average value of the normalized
average payoffs became larger, the agent gained high
payoffs across many rounds.
Table 5: Normalized average payoffs when agents play
games in round-robin tournaments. The bold typeface in-
dicates the best results from among the four given methods.
J-alg M-Qubed S-alg BM
CIG 0.998983 0.995743 0.998991 0.998603
CG 1.048619 0.915732 0.832476 0.905246
SH 0.999098 0.996896 0.999148 0.998226
TG 0.952595 0.863191 0.943683 0.868901
PD 0.900618 0.743598 0.871854 0.754596
BS 0.988460 1.002762 0.921269 0.951607
Ch 0.974938 0.933062 0.975377 0.926621
SG 0.935857 0.881564 0.810752 0.885159
OG 0.555748 0.497452 0.341784 0.538482
MP 1.041080 1.051359 0.858698 1.048864
Avg. 0.939600 0.888136 0.855403 0.887630
J-alg gained high average payoffs in many of the
games we used for our experiments. In the coordi-
nation game (CG), battle of the sexes (BS), the secu-
rity game (SG), the offset game (OG), and matching
pennies (MP), S-alg was exploited when the associate
took a greedy strategy, because its aspiration level de-
creased too much, and as a result, it was satisfied with
small payoffs. M-Qubed and BM were not able to
learn optimal strategies quickly and gain high aver-
age payoffs because they required a large number of
interactions. Note that M-Qubed did indeed gain high
average payoffs in battle of the sexes (BS) and match-
ing pennies (MP) by taking a greedy strategy.
The average payoffs shown in Table 4 and Ta-
ble 5 show that J-alg gained the highest average pay-
offs both in self-play and round-robin tournaments.
S-alg gained high payoffs in self-play, but it was ex-
ploited by greedy players and gained low payoffs in
round-robin tournaments. M-Qubed and BM gained
better payoffs by exploiting S-alg in round-robin tour-
naments than in self-play. However, they required a
large number of rounds to learn the maximum joint
action and therefore gained lower average payoffs
than that of J-alg.
4.3 Experiment 3
In our third experiment, we investigated whether S’-
alg actually contributed to the learning speed of J-alg.
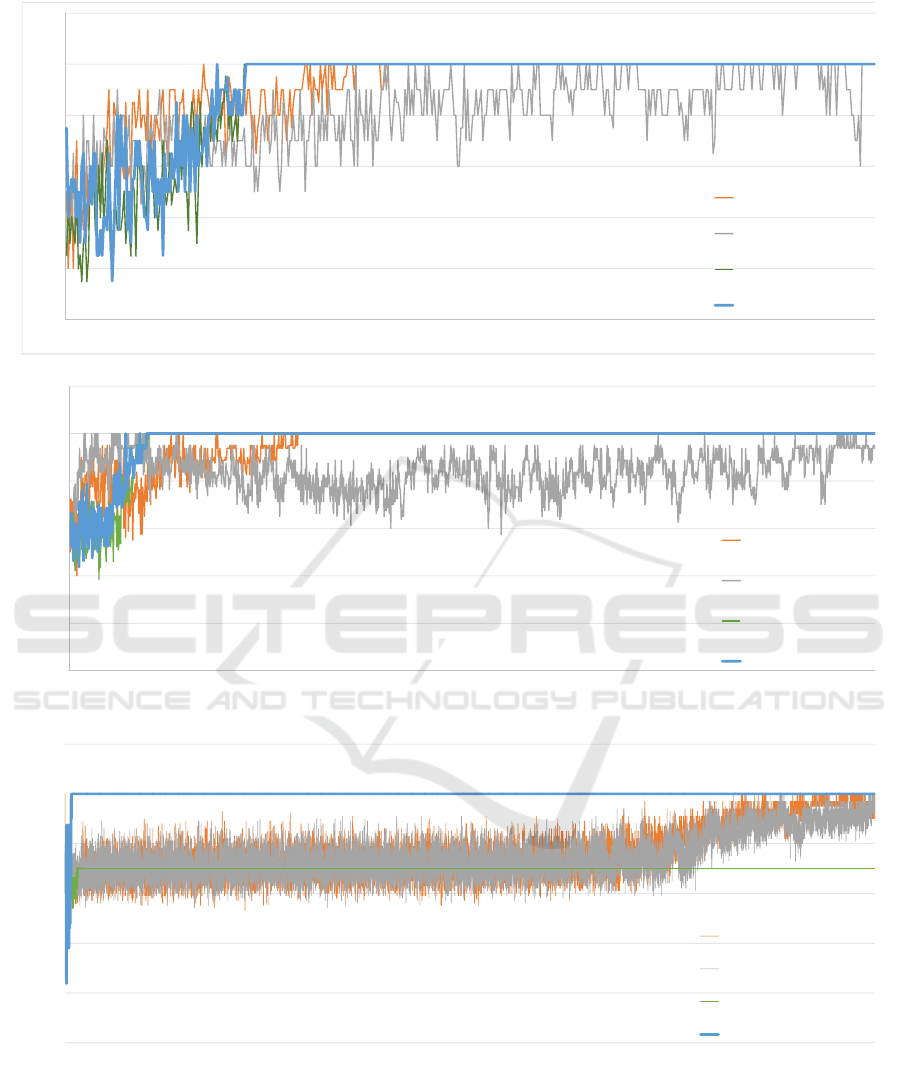
Figure 1 shows learning curves of J-alg, M-Qubed,
S-alg, and BM in the common interest game (CIG),
stag hunt (SH), and the security game (SG). Results
of these three games are good examples that show
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
52
(a) Common Interest Game (CIG)
(b) Stag Hunt (SH)
(c) Security Game (SG)
Figure 1: Learning curves of the four algorithms in self-play in three games. Blue lines show the curves of J-alg, gray show
those of M-Qubed, orange show those of BM, and green show those of S-alg. The x-axes show the rounds the agents played,
while the y-axes show normalized average payoffs.
how the algorithms comprised in J-alg complement
one another.
Figure 1(a), i.e., results of the common inter-
est game (CIG), shows that J-alg and S-alg quickly
Adaptive Two-stage Learning Algorithm for Repeated Games
53

learned the maximum joint action almost simultane-
ously. BM learned the maximum joint action by the
190th round, shortly after J-alg and S-alg. M-Qubed
was still learning at the 500th round. Results here
show that S’-alg contributed to the learning speed of
J-alg.
Results of the stag hunt (SH) game are shown in
Fig. 1(b), which shows that J-alg and S-alg finished
learning the maximum joint action the quickest. Next,
BM finished learning with the average payoff con-
verging to one by the 410th round. Finally, M-Qubed
finished learning by the 1500th round. Results here
show the same as Fig. 1(a), i.e., J-alg learned the max-
imum joint action fastest, whereas BM and M-Qubed
learned more slowly.
Turning to Fig. 1(c) reveals that BM compensated
for a flaw of S-alg by which it failed to learn the max-
imum joint action. In the figure, we observe that in
the security game (SG), S-alg finished learning first,
but did not obtain the optimal strategy because S-alg
was satisfied with the second-best payoff. As shown
in Table 4, S-alg gained smaller payoffs as compared
with the other three algorithms in this game. BM and
M-Qubed learned the maximum joint action, but they
required a large number of interactions and learned
slowly. Finally, J-alg successfully learned the quick-
est.
5 RELATED WORKS
Reinforcement learning is widely used as a learn-
ing method for agents. What defines reinforcement
learning as being different from other learning meth-
ods is the combination of trial-and-error searches and
delayed rewards. Temporal difference (TD) learn-
ing is arguably the most famous reinforcement learn-
ing method. TD learning compares the value of the
current state with the reward obtained by the cur-
rent action, updating the given value to decrease de-
viation. Q-learning (Watkins and Dayan, 1992) and
Sarsa (Rummery and Niranjan, 1994) are typical ex-
amples of TD learning.
While TD learning was originally proposed as a
learning method for a single agent, in a multi-agent
environment, Claus and Boutilier (1998) discussed
how to incorporate other agents in TD learning. They
showed that in payoff matrix games, a “joint action
learner” that updates Q-values based on actions of
the agent and others is better than an “independent
learner” that recognizes others as elements of the en-
vironment.
When designing a reinforcement learning agent in
a multi-agent environment, we often adopt the knowl-
edge of game theory. Hu and Wellman (2003) pro-
posed Nash Q-learning in which a Nash Q-learning
agent explores the game structure from the perspec-
tive of the actions and rewards of the agent and others,
updating its Q-values under the assumption that every
player selects a strategy that leads to Nash equilib-
rium.
There are also methods that do not update Q-
values from immediate joint actions, but instead as-
sign Q-values to a long (fixed-length) interaction his-
tory. Burkov and Chaib-draa (2009) proposed a learn-
ing approach for an agent when its associates learn its
strategies and adapt to its actions. Their agent, called
an Adaptive Dynamics Learner, can obtain higher
utility than that of an agent at an equilibrium by con-
sidering the associates’ strategies and assigning Q-
values to a long interaction history.
Further, there are reinforcement learning meth-
ods that do not use Q-values, instead they use a dy-
namic threshold called an aspiration level updated
by rewards. Masuda and Nakamura (2011) consid-
ered a model in which a reinforcement learning agent
learns from reinforcement signals calculated from
the reward and the aspiration level; they investigated
agent behavior when it played the iterated prisoner’s
dilemma games with other learning agents.
In summary, many researchers have proposed re-
inforcement learning algorithms for multi-agent en-
vironments; however, much of this work has focused
only on the convergence of player strategies and thus
requires an enormous number of interactions. In this
paper, we proposed an algorithm that learns appro-
priate strategies against the associate’s strategy faster
than these existing algorithms, because humans de-
cide very quickly in real situations.
6 CONCLUSIONS
Many researchers have studied and are studying re-
inforcement learning algorithms to acquire strategies
that maximize payoffs for agents that learn in games.
Existing reinforcement algorithms can gain high pay-
offs in various games, but typically require a large
number of interactions to learn an optimal strategy.
To overcome these limitations, we proposed an
algorithm called J-alg that learns quickly and gains
large payoffs in many games by combining two exist-
ing algorithms, namely, BM and S’-alg. S’-alg con-
tributes to learning speed, whereas BM contributes to
the prevention of exploitation by greedy opponents.
To evaluate our algorithm, we conducted two ex-
periments, i.e., self-play and round-robin, using 10
games. In both sets of experiments, J-alg gained suf-
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
54

ficiently large payoffs in nine games and the highest
average payoffs among four types of agents.
As future work, we plan to construct an algorithm
that can learn the maximum joint action in the offset
game (OG). In addition, we plan to extend our work
in two-person two-action games and construct an al-
gorithm that can quickly learn optimal strategies in
n-person n-action games.
ACKNOWLEDGEMENTS
This work was supported in part by the Management
Expenses Grants for National Universities Corpora-
tions from the Ministry of Education, Culture, Sports,
Science and Technology of Japan (MEXT).
REFERENCES
Burkov, A. and Chaib-draa, B. (2009). Effective learning
in the presence of adaptive counterparts. Journal of
Algorithms, 64:127–138.
Claus, C. and Boutilier, C. (1998). The Dynamics of Re-
inforcement Learning in Cooperative Multiagent Sys-
tems. In Proc. 15th National Conference on Artificial
Intelligence (AAAI), pages 746–752.
Crandall, J. W. and Goodrich, M. A. (2011). Learning
to compete, coordinate, and cooperate in repeated
games using reinforcement learning. Machine Learn-
ing, 82:281–314.
Fujita, W., Moriyama, K., Fukui, K., and Numao, M.
(2016). Learning better strategies with a combina-
tion of complementary reinforcement learning algo-
rithms. In Nishizaki, S., Numao, M., Caro, J. D. L.,
and Suarez, M. T. C., editors, Theory and Practice of
Computation, pages 43–54. World Scientific.
Hu, J. and Wellman, M. P. (2003). Nash Q-learning for
General-sum Stochastic Games. Journal of Machine
Learning Research, 4:1039–1069.
Masuda, N. and Nakamura, M. (2011). Numerical analysis
of a reinforcement learning model with the dynamic
aspiration level in the iterated Prisoner’s dilemma.
Journal of Theoretical Biology, 278:55–62.
Okada, A. (2011). Game Theory. Yuhikaku. (in Japanese).
Rummery, G. A. and Niranjan, M. (1994). On-line Q-
learning using connectionist systems. Technical Re-
port TR166, Cambridge University Engineering De-
partment.
Stimpson, J. L. and Goodrich, M. A. (2003). Learning To
Cooperate in a Social Dilemma: A Satisficing Ap-
proach to Bargaining. In Proc. 20th International
Conference on Machine Learning (ICML), pages 728–
735.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-
ing: An Introduction. MIT Press.
Watkins, C. J. C. H. and Dayan, P. (1992). Technical Note:
Q-Learning. Machine Learning, 8:279–292.
Wiering, M. A. and van Hasselt, H. (2008). Ensemble Algo-
rithms in Reinforcement Learning. IEEE Transactions
on Systems, Man, and Cybernetics, Part B, 38:930–
936.
Adaptive Two-stage Learning Algorithm for Repeated Games
55
