3D Human Poses Estimation from a Single 2D Silhouette

Fabrice Dieudonn

e Atrevi, Damien Vivet, Florent Duculty and Bruno Emile

Univ. Orl

eans, PRISME, EA 4229, F45072, Orl

eans, France

Keywords:

Pose Estimation, 3D Pose, 3D Modeling, Skeleton Extraction, Shape Descriptor, Geometric Moment,

Krawtchouk Moment.

Abstract:

This work focuses on the problem of automatically extracting human 3D poses from a single 2D image. By

pose we mean the conﬁguration of human bones in order to reconstruct a 3D skeleton representing the 3D

posture of the detected human. This problem is highly non-linear in nature and confounds standard regres-

sion techniques. Our approach combines prior learned correspondences between silhouettes and skeletons

extracted from 3D human models. In order to match detected silhouettes with simulated silhouettes, we used

Krawtchouk geometric moment as shape descriptor. We provide quantitative results for image retrieval across

different action and subjects, captured from differing viewpoints. We show that our approach gives promising

result for 3D pose extraction from a single silhouette.

1 INTRODUCTION

Recognizing human actions is really challenging for

computer vision scientists and researchers since the

last two decades (Wang et al., 2011). Nevertheless,

human action recognition systems have a lot of pos-

sible applications in surveillance, pedestrian tracking

and Human Machine Interaction (Aggarwal and Cai,

1999). Human pose estimation is a key step to action

recognition.

A human action is often represented as a succession

of human poses (Wang et al., 2013). As these poses

could be 2D or 3D, so estimating them have attracted

a lot of attention. A 2D pose is usually represented

by a set of joint locations (Yang and Ramanan, 2011)

whose estimation remains challenging because of the

human body shape variability, viewpoint change, etc.

Considering 3D pose, we usually represent it by a

skeleton model parameterized by joint locations (Tay-

lor, 2000) or by rotation angles (Lee and Nevatia,

2009). Such representation has the advantage to

be Viewpoint-invariant however, estimating 3D poses

from a single image still remains a difﬁcult problem.

The reasons are multiple. First, multiple 3D poses

may have the same 2D pose reprojection. Second,

3D pose is inferred from detected 2D joint locations

so 2D pose reliability is essential because it greatly

affects skeleton estimation performance. In camera

network used in a video-surveillance context, image

quality is often poor making 2D joint detection a dif-

ﬁcult task, moreover camera parameters are unknown

making the correspondence 2D/3D difﬁcult.

In this work we propose a new technique for the ex-

traction of 3D skeleton pose assumptions from a sin-

gle 2D image based on the silhouette shape recogni-

tion. This technique is based on the use of a 3D hu-

man pose and action simulator. A silhouette database

is constructed from this simulator and is used in order

to match nearest silhouette and as a results possible

3D human pose.

This article presents a silhouette shape description

and comparison between different subjects and action

steps and show that we can obtain 3D skeleton con-

ﬁguration by using only a single 2D silhouette detec-

tion. Section 2 presents related works in the human

skeleton and action recognition. Section 3 presents

the global framework of the method and the 3D sim-

ulation used. Section 4 deals with Krawtchouk shape

descriptors applied to human silhouettes. Finally, sec-

tion 3.1 and 5 present the databases and the obtained

results.

2 RELATED WORKS

There are many methods in the state-of-the-art that

deals with the human pose estimation and action

recognition. Nevertheless, these tasks are still chal-

lenging for computer vision community. Human

activity analyses started with O’Rourke and Badler

Atrevi, F., Vivet, D., Duculty, F. and Emile, B.

3D Human Poses Estimation from a Single 2D Silhouette.

DOI: 10.5220/0005711503610369

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 361-369

ISBN: 978-989-758-175-5

361

(O’Rourke et al., 1980) and Hogg (Hogg, 1983) in the

eighties. Since last decades scientists proposed many

approaches. We can categorize these approaches into

two main categories: on one hand the methods using

3D information and on the other hand technics using

only 2D data.

Most of the approaches use a 3D model or 3D detec-

tion for estimating the pose of a subject and for action

classiﬁcation. Rehg and Kanade (Rehg and Kanade,

1994) presented a 3D model-based hand tracking sys-

tem that can cover the state of a 27 DOF skeleton.

Gavrial and al.(Gavrila and Davis, 1996) used a 3D

model-based tracking of unconstrained human move-

ment. They used some sequence images acquired

from multiple views for recovering 3D body pose of

a human.

Bourdev and Malik (Bourdev and Malik, 2009) esti-

mated the human pose from key points. They used a

data set of annotations of human with 3D joins infor-

mations inferred using anthropometric constraints for

human action classiﬁcation (Maji et al., 2011). Hiyadi

and al. (Hiyadi et al., 2015) used the depht informa-

tion obtained from Kinect sensor and a tracking algo-

rithm for 3D human gestures recognition. Jian (Jiang,

2010) proposed an exemple-based method, based on

the kd-tree achieves real-time performance, to prune

the hypotheses. Ramakrishna and al. (Andriluka

et al., 2010) proposed a three-stage process for 3D

poses recovering in uncontrolled environment. Val-

madre and Lucey (Valmadre and Lucey, 2010) used

deterministic structure from multiple view of motion,

based on the related work of Wei and Chai (Wei and

Chai, 2009), for 3D pose estimation.

These approaches need multiple sensors or speciﬁc

devices such as time of ﬂight or active camera for

acquiring 3D information. These models also, need

good parametrization.

The second category of approaches, to which our pro-

posed method belongs, used 2D models trained from

various images. Baumberg and Hogg (Baumberg and

Hogg, 1994) used active shape model to track pedes-

trians in real world scenes. They used the B-spline

as a shape vector for training the model. Wren and

al. (Wren et al., 1997) tracked people and interpreted

their behaviour by using a multiclass statistical model

of colour and shape to obtain 2D representation of

head and hand. Gorelick and al. (Gorelick et al.,

2005) used the solution of Poisson’s equation to ex-

tract spatiotemporal features such as the saliancy, the

orientation of the shape for action recognition and

then human pose estimation. Guo and al. (Guo et al.,

2009) used a geometrical normalized vector of dimen-

sion 13 for describing the shape of a human. Mori

and Jitendra (Mori and Malik, 2002), or Agarwal and

Triggs (Agarwal and Triggs, 2006) used the shape

context in their research on human pose estimation.

Gorce and al. (de La Gorce et al., 2011) estimated

and tracked the human hand from monocular video

through minimization of an objective function. This

minimization is done using a quasi-Newton method,

for which they provide a rigorous derivation of the ob-

jective function gradient. Yang and Ramanan (Yang

and Ramanan, 2011) estimated the pose by capturing

the orientation of each part with a mixture of tem-

plates modeled by linear SVMs. All of these methods

focus on 2D image interpretation in order to detect

human pose or action. For this purpose, learning is

requiered and such algorithms need complex and ex-

pensive systems to get the training data set with the

ground truth.

Our method is based on a very simple silhou-

ette extraction and description. We use the robust

Krawtchouk geometric moment to shape analysis in

monocular image. For the database, we proposed to

use software applications from the open source com-

munity. These softwares makes realistic simulation

of various human poses and action possible. We

have shown in this work that using 3D simulations

for learning, without complex machine learning algo-

rithm and with a simple real time shape descriptor we

can achieve 3D pose estimation on real data with good

accuracy from a unique 2D image.

3 METHODOLOGY

The proposed approach for pose estimation is based

on shape analysis of human silhouette. The method

can be decomposed into four parts: (1) simulated

silhouette and skeleton database, (2) Human detec-

tion and 2D silhouette extraction, (3) silhouette shape

matching, (4) skeleton scaling and validation. The

workﬂow is presented Fig.1.

(1) First, Silhouette and Skeleton Database is built

thanks to opensource 3D software (see section 3.1).

Such database is composed of human silhouettes and

its corresponding 3D skeletons for different kind of

actions we want to recognize. So, for a requested sil-

houette, it’ll be possible to ﬁnd the matching silhou-

ette in the database and then the corresponding 3D

skeleton.

(2) 2D Silhouettte Detection is a well-studied ﬁeld in

machine learning and computer vision. For this pur-

pose we used classical real-time approach proposed

by Dollar et al. (P. Dollar and Perona, 2010) based on

multiscale HOG (Dalal and Triggs, 2005). Once the

human silhouette is detected, we converted it in a 128

x 48 pixels image for solving the translation and scale

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

362

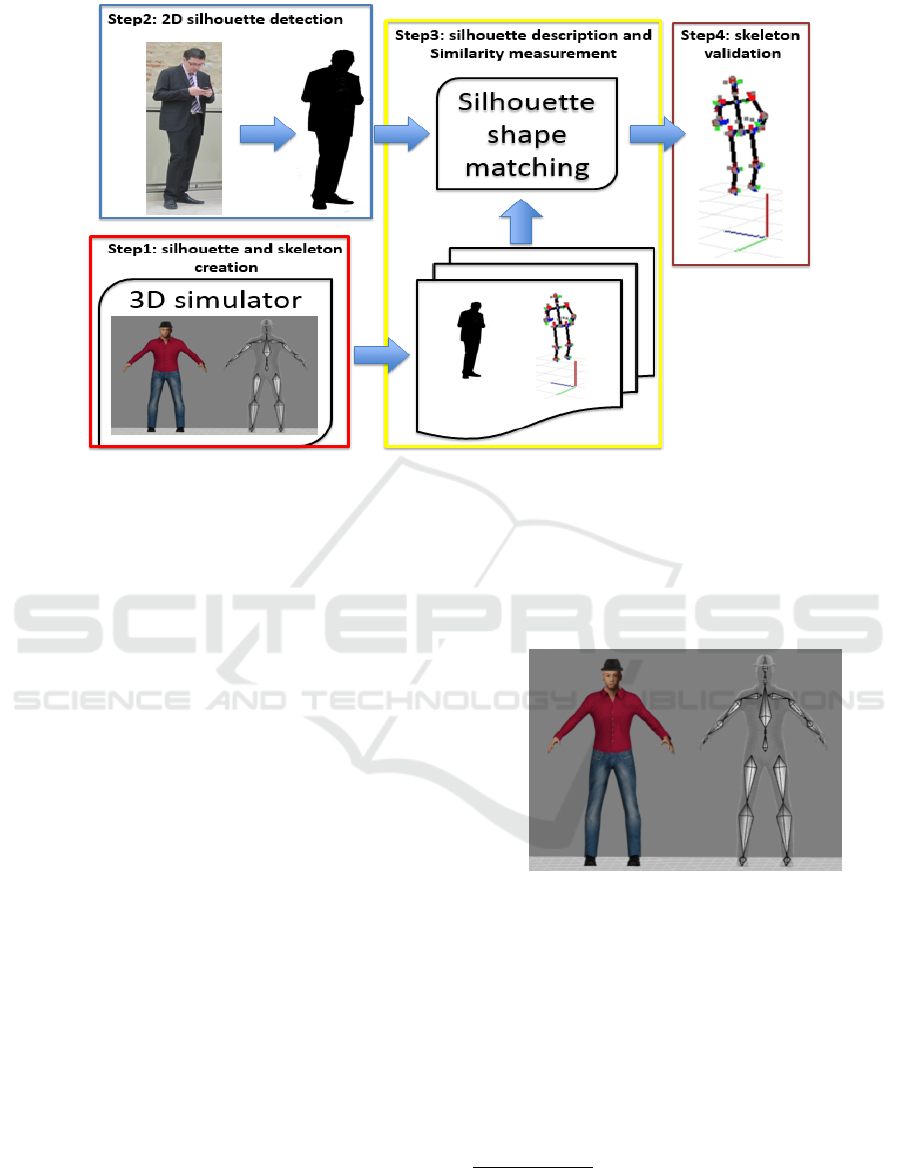
Figure 1: Human pose estimation methodology.

problem.

(3) Silhouette Description and Similarity Measure-

ment is the key point of our methodology. The main

objective is to describe accurately the shape of the sil-

houette. For this task, we used the geometric moment

of Krawtchouk because of its robustness compared to

Hu, Zernike or Shapecontext descriptors. (See sec-

tion 4) Based on this descriptor, a characteristic vector

is computed for each silhouette in the database. The

similarity between characteristic vector is measured

with the Euclidean distance given by :

d(z

, z

) =

∑

i=1



− z



(1)

where z

et z

is respectively the characteristic vec-

tor of request silhouette and the t th silhouette in the

database.

(4) Skeleton Scaling and Validation. For each sil-

houette we retrieve a 3D skeleton. This skeleton is

scaled to the current silhouette size. At this step we

use ground truth simulated database to valide the ap-

proach. The conﬁdence score is process by measuring

the reprojection error of predicted joints on the silhou-

ette.

3.1 Construction of the 2D/3D

Matching Database

3.1.1 3D Human Avatar and Action Simulation

In order to build our simulated humans, we choose to

use a professional free and open-source 3D computer

graphics software called Blender

associated with a

free software to create realistic 3d human makehu-

man

(see Fig. 2). These avatars can be animated

thanks to motion capture data in order to simulate

very realistic actions.

Figure 2: 3D simulated avatar and its associated skeleton.

In these softwares, we simulate different human

avatars with different morphologies and clothes and

animate them with different realistic motions taken

from the CMU motion capture database

3.1.2 Database Construction

In the 3D computer graphics software, we positioned

on an emisphere a virtual camera looking at the sub-

ject. For each movement of the avatar, we record

https://www.blender.org/

http://www.makehuman.org/

The data used in this project was obtained from mo-

cap.cs.cmu.edu.

3D Human Poses Estimation from a Single 2D Silhouette

363

both: 2D image and silhouette (see ﬁg 3), 3D cam-

era poses and 3D joints and bones poses. As a result

for each subject’s pose we can collect the detected sil-

houette related to its 3D skeleton which contains 19

bones. We recorded in 4 subjects with different phe-

notypes and for 4 differents animations: walk cycle,

basket action, jumb and climb. As a result, we ob-

tained 2925 couples silhouette / 3D skeleton.

For each silhouette, we calculated the feature vector

of the shape descriptors presented in section 4 and the

2D poses of reprojected joints for quantitative evalu-

ation of the method.

Figure 3: Human silhouette extracted.

4 KRAWTCHOUK POLYNOMIAL

AND MOMENTS

4.1 Krawtchouk Polynomial

The n-th order of Krawtchouk polynomial is based on

the hypergeometric function and is deﬁned as:

(x; p, N) =

∑

k=0



k,n,p





−n, −x; −N;



(2)

where x, n = 0, 1, 2, ..., N et N > 0, p ∈ (0, 1) and the

hypergeometric function deﬁned as:

(a, b; c; z) =

∞

∑

k=0



(a)

(b)

(c)



(3)

(a)

= a(a + 1)...(a + k − 1) =

Γ(a + k)

Γ(a)

(4)

Equation (4) is the Pochhammer symbol.

The set of (N+1) Krawtchouk polynomial forms the

complete set of discrete basis functions with weight

function

w(x; p, N) =





(1 − p)

N−x

(5)

and satisﬁes the orthogonality condition :

∑

k=0

w(x; p, N)K

(x; p, N)K

(x; p, N) = ρ(n; p, N)δ

(6)

where ρ(n; p, N) = (−1)



1−p



(−N)

and δ

the Kronecher function.

In order to eliminate the large variability in the

dynamic range, a normalization process is applied.

Then, the set of normalized (weighted) Krawtchouk

polynomials is deﬁned by (Yap et al., 2003) as:

(x; p, N) = K

(x; p, N)

w(x; p, N)

ρ(n; p, N)

(7)

4.2 Krawtchouk Moment

Krawtchouk moment is ﬁrstly used in image analysis

by P.T Yap and al.(Yap et al., 2003). Based on the

weighted Krawtchouk polynomials, the (n + m) order

of Krawtchouk moment for an N x M image with in-

tensity function f (x, y) is deﬁned as:

N−1

∑

x=0

M−1

∑

y=0

(x; p1, N − 1)

(y; p2, M − 1) f (x, y)

(8)

The parameter p1 and p2 can be viewed as a trans-

lation factor. Indeed, if p = 0.5 + ∆p, the weighted

Krawtchouk polynomials are shifted by about N∆p.

The direction of shifting relies on the sign of ∆p, with

the polynomials shifting along + x direction when ∆p

is positive and vice versa. This property allows to ex-

tract the local properties of an images. For software

like Matlab, there is a matrix form of the Krawtchouk

moment. In matrix form, it is deﬁned as:

Q = K

(9)

where Q = {Q

}

i, j=N−1

i, j=0

= {

( j; pv, N − 1)}

i, j=N−1

i, j=0

and

A = { f ( j, i)}

i, j=N−1

i, j=0

4.3 Feature Extraction

For a given image of human silhouette, we used

Krawtchouk moment to describe the shape of the

human belong to the image. That means to calcu-

late the characteristic vector of the image with dif-

ferent values of the moment. Thanks to the ability of

Krawtchouk moment to extract feature of speciﬁc re-

gions of the image, we divided each silhouette in two

parts (up and bottom) (ﬁg. 4) with the parameter p1 =

0.5, p2 = 0.1 (for the up) and p1 = 0.5, p2 = 0.95

(for the bottom). Then, we calculated two character-

istic vectors and combined them to get one vector de-

scriptor. Each human silhouette extracted is converted

to a common space 128 x 48 to get the invariance to

translation and scale. For rotation invariance, we sup-

posed that the vertical is preserved.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

364

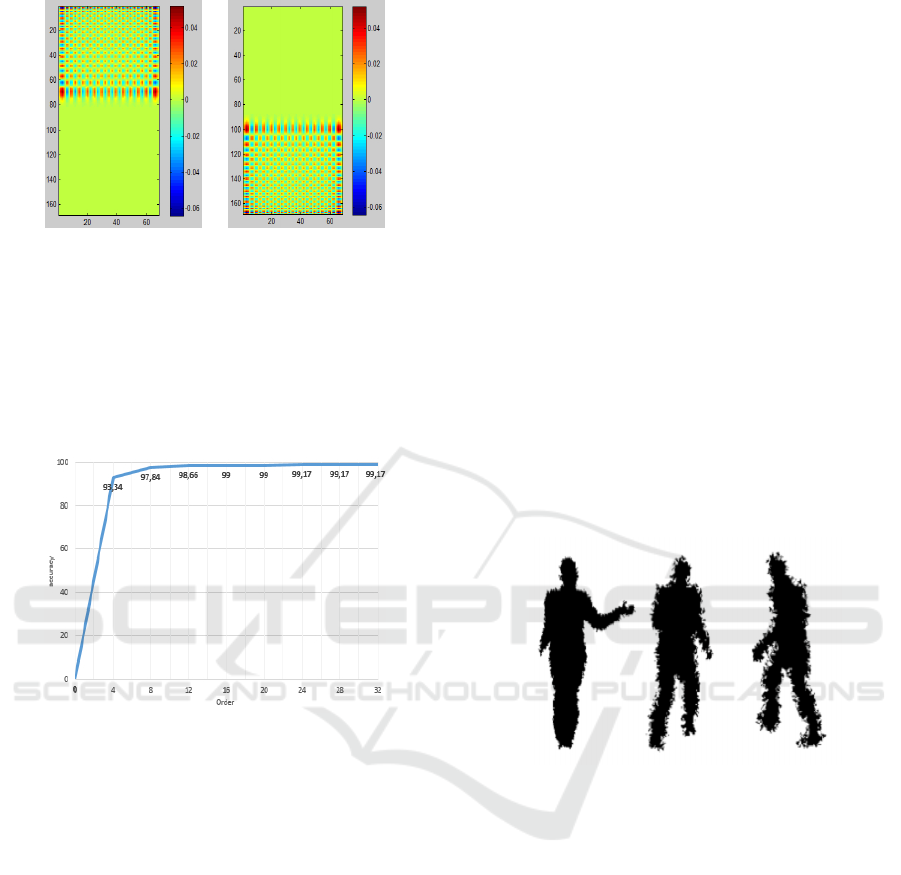
Figure 4: Krawtchouk polynomial for up and bottom.

According to some related works, we chose to calcu-

late Krawtchouk moment with parameter (m = n). In

order to ﬁnd the best value of n, we used a database

with 600 simulated silhouettes and done cross valida-

tion over all. The ﬁg 5 show that from order (n = m =

24), we got a stable and best accuracy for pose recog-

nition. So, the ﬁnal feature vector has 48 dimensions.

Figure 5: Accuracy of cross validation with differents value

of n.

5 EXPERIMENTS

In section 3.1 we have shown that for each 2D image

of silhouette of the database, we store both the silhou-

ette vector descriptors and the associated 3D skeleton

composed of 19 joints. Then, for a test image with

extracted silhouette, similarity is computed between

the processed vector of descriptors and database de-

scriptors using the Euclidian distance. As a result we

extract the corresponding silhouette in the database

and its joints 3D poses. Note that the approach does

not only give the more suitable silhouette but gives in

a classiﬁed way the N

most probable silhouettes. In

order to evaluate the given result, we used the simula-

tion. By knowing the real skeleton of the test image,

we can process the reprojection error of the estimated

3D joints. According to experimental result, when the

mean error is less than 5 pixels, the pose of the re-

sult is considered similar to the pose of the request

silhouette. For this empiric threshold, the difference

between two silhouettes is hardly visible for a human.

5.1 Representativity and Descriptor

Robustness to Noise

Silouette extraction is still an active reseach ﬁeld. It

is well known that extraction is subjected to noise.

First point was to check our descriptors robustness to

noise. For this, we conducted experiments with two

databases of simulated data for a human avatar with

different morphology and different actions. The ﬁrst

database contains 2925 training data with Gaussian

noise around the contour of the shape and the second

database contains 608 unlearning data. The aims of

this experience is to evaluate the capacity of shape de-

scriptors to encode various shapes with different value

of the standard deviation of Gaussian noise. Con-

sidering x

= [0, 0] the center of the silhouette, let

= [ρ

, θ

] the polar coordinates of a contour point.

The noise ∆σ is applied on ρ

. ∆σ → N (0, std) with

std = {0, 1, 2, 3}. Example of noised silhouettes are

presented on ﬁgure 6.

Figure 6: Noised silhouettes with ∆σ → N (0, std) and

std = {1, 2, 3}.

The aim of this experience is to see if the shape de-

scriptor can perfectly encode a silhouette and make

the difference between closed postures. The silhou-

ette in the database can be very similar because we

extracted it from a video of the motion, so two near

frames provide a very similar silhouette. For std = 0,

we have the original silhouette and for std > 0, the

Gaussian white noise is added on the silhouette. Fig-

ure 7 shows that the more the std increases, the more

the recognition accuracy decreases. For this test we

used a training data set composed of 2925 and a

testing test of 608 silouhettes. For a single neigh-

bour (N = 1), with std = {0, 1, 2, 3}, the recognition

rate is respectively RR = {98.81, 96.43, 74.6, 44.84}.

But, if we augment the number of N assumption re-

turned by the program, the recognition rate grows up

quickly. For N = 7 and std = {0, 1, 2, 3}, the RR are

{100, 100, 96.43, 73.41}. Considering that the silhou-

3D Human Poses Estimation from a Single 2D Silhouette

365

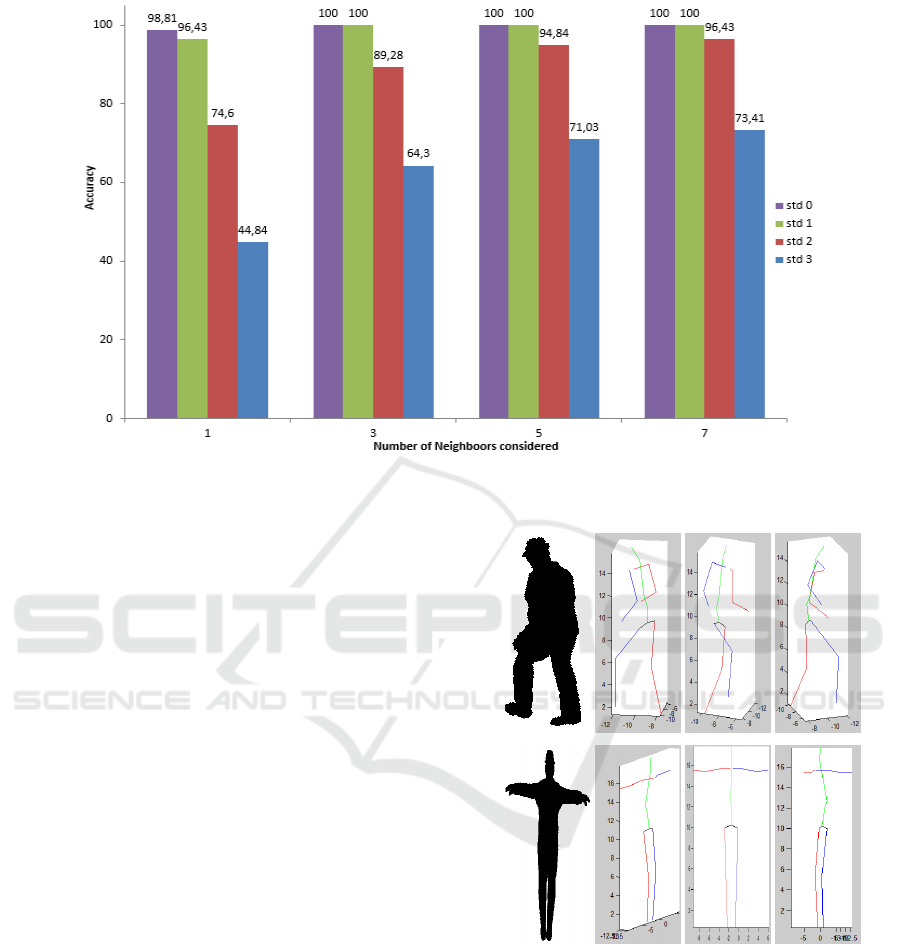
Figure 7: Histogramm of accuracy: colors represent the noise amplitude resp. {0, 1, 2, 3} pixels. The abscisses represent the

number N of neighboors considered {1, 3, 5, 7}.

ettes are very similar and the noise very strong, the

method gives very good results. For the rest of the ar-

ticle we will consider N = 7 ﬁrst silhouettes given by

the matcher.

In order to estimate the 3D extracted skeleton, we

use the same request silhouette as for previous exper-

iment. For each extracted silhouette, we process the

reprojection error and evaluate the accuracy for dif-

ferent value of N. The Figure 8 shows skeletons esti-

mations from a single monocular image. For this re-

sult, the reprojection error of the ﬁrst image (human

walking) is 2.4739 px and that of the second image

(human in cross position) is 1.2614 px. This means

error show that the retrieval pose is near to the origi-

nal pose. Note that, in the database, there a no avatar

with the similar appaerance, so this error is reason-

able.

The images that we used as request in ﬁg 8 are sim-

ulated and noised images not present in the learning

database. As expected, we got a very good result with

low reprojection error while comparing images from

the simulation. In order to test the approach on real

images we compute the pose recognition of real im-

ages but with simulated database.

The result of 3D skeleton extraction presented in ﬁg-

ure 9 shows a good association between simulated and

real data. In ﬁgure 10, we used an other real world im-

age extracted from a walking action video. The pose

that we process is similar but not exactly the same that

the one in the learning walks in the database. Consid-

ering the 3D pose estimated, the result shows a good

Figure 8: 3D pose estimation result: Left, the resquest sil-

houette and from left to right, the 3D estimated skeleton

from various viewpoints.

detection in term of the shape of the pose. As ex-

pected, confusion is made between right and left foot

and arm.

In order to evaluate the stability and the robustness

of our approach, we considered the successive detec-

tions during a complete movie of the movement. Note

that there is no use of the time line and each frame

is processed independently. Figure 11 (a) shows the

tracking results of four human’s joints during the ex-

ecution of the climbing motion. The red curve show

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

366

Figure 9: Real world data 1.

Figure 10: Real world data 2.

the real position over time and the green curve show

the estimate position over time. We can note that the

shape of different curves is the same. That means that

the successives detections are stable in time and that

our shape descriptor is reliable. We can note that there

is an offset due to shape scaling. The means error over

the motion execution is 1.9765 px. Figure 11 shows

that the shape of the curve changes as a fonction of

the motion. The means error obtained form the jump

motion is 1.9892 px. This discrimination factor con-

ﬁrmed that the 3D poses can be used for actions clas-

siﬁcation in a video.

(a) Climb motion.

(b) Jump motion.

Figure 11: Tracking result.

5.2 Application to Action Recognition

on Real Data

We used the same shape descriptor for human ac-

tion classiﬁcation in video, with the public Weizmann

database (see Figure 12). As we do not use tempo-

ral information, our method consists in matching each

frame to an action class and took the class with the

highest associated rate as the class action.

Figure 12: Some images of Weizmann database.

The database is a collection of 90 low-resolution (180

x 144, deinterlaced 50 fps) video sequences show-

ing 9 different people, each performing 10 natural ac-

tions: run, walk, skip, jumping-jack, jump, gallop-

sideways, wave-two-hands, waveone- hand, or bend.

On Weizmann data base, we made a cross validation

with the different movements and with the different

3D Human Poses Estimation from a Single 2D Silhouette

367

phenotypes. In each case and for each frame, we ap-

ply our shape matching method to each frame. As

the resulting silhouette from the database belongs to a

speciﬁc movement class we simply count the number

of occurencies. The more represented class is then

considered as the detected movement.

Based on this very simple workﬂow, we got 71.66%

of good action classiﬁcation. The confusion matrix

is shown on the ﬁg.13. Of course, this accuracy

rate is lower than the recent accuracy obtained on the

same database (Blank 99.64% (Blank et al., 2005) and

Gorelick 97.83% (Gorelick et al., 2007)). But both of

these approach used space-times cubes to analyse the

motion while we do not consider yet the temporal cor-

relation between successives frame.

According to Gorelick et al.: many successive frames

from the ﬁrst action (about run) may exhibit high spa-

tial similarity to the successive frames from the sec-

ond one. Ignoring the dynamics within the frames

might lead to confusion between the two actions. As

the approach does not take into account time dimen-

sion, frame to frame comparison leads to misclassiﬁ-

cation for these very similar frame to frame actions:

run, skip and jump.

Figure 13: Confusion matrix.

In future work, we will use our proposed approach

combined with the multi-hypothesis tracking tech-

niques (with N neighboors) to improve the accuracy

of action classiﬁcation. By this way, we will take into

account the temporal information and the dynamic of

the action.

6 CONCLUSIONS

In this paper, we presented a new approach for 3D

human pose estimation and action classiﬁcation in

video. The learning database is easily generated

thanks to open source softwares which allow any hu-

man pose simulaion. The proposed posture recogni-

tion method is based on the geometric Krawtchouck

moment and gives promising results. Both applica-

tion to 3D pose estimation and action classiﬁcation

have been presented. In our work, we tested different

moment order and selected the best suitable for our

approach. We compared our approach with some re-

lated work in action classiﬁcation and we concluded

that this approach can be improved by using multi-

hypothesis tracking during action identiﬁcation and

classiﬁcation. In future work, we will use a combina-

tion of local and global shape descriptor for improv-

ing the pose estimation, and use the estimated poses

to construct an action model for activity classiﬁcation.

REFERENCES

Agarwal, A. and Triggs, B. (2006). Recovering 3d hu-

man pose from monocular images. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

28(1):44–58.

Aggarwal, J. and Cai, Q. (1999). Human motion analysis:

A review. Computer Vision and Image Understanding,

73(3):428–440.

Andriluka, M., Roth, S., and Schiele, B. (2010). Monocular

3d pose estimation and tracking by detection. In Com-

puter Vision and Pattern Recognition (CVPR), 2010

IEEE Conference on, pages 623–630. IEEE.

Baumberg, A. and Hogg, D. (1994). Learning ﬂexible mod-

els from image sequences. Springer.

Blank, M., Gorelick, L., Shechtman, E., Irani, M., and

Basri, R. (2005). Actions as space-time shapes. In

The Tenth IEEE International Conference on Com-

puter Vision (ICCV’05), pages 1395–1402.

Bourdev, L. and Malik, J. (2009). Poselets: Body part de-

tectors trained using 3d human pose annotations. In

Computer Vision, 2009 IEEE 12th International Con-

ference on, pages 1365–1372. IEEE.

Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-

dients for human detection. In In: IEEE Conference

on Computer Vision and Pattern Recognition, pages

886–893.

de La Gorce, M., Fleet, D., and Paragios, N. (2011).

Model-based 3d hand pose estimation from monocu-

lar video. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 33(9):1793–1805.

Gavrila, D. M. and Davis, L. S. (1996). 3-d model-based

tracking of humans in action: a multi-view approach.

In Computer Vision and Pattern Recognition, 1996.

Proceedings CVPR’96, 1996 IEEE Computer Society

Conference on, pages 73–80. IEEE.

Gorelick, L., Blank, M., Shechtman, E., Irani, M., and

Basri, R. (2005). Actions as space-time shapes. In

In ICCV, pages 1395–1402.

Gorelick, L., Blank, M., Shechtman, E., Irani, M., and

Basri, R. (2007). Actions as space-time shapes. Trans-

actions on Pattern Analysis and Machine Intelligence,

29(12):2247–2253.

Guo, K., Ishwar, P., and Konrad, J. (2009). Action recogni-

tion in video by covariance matching of silhouette tun-

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

368

nels. In In: XXII Brazilian Symposium on Computer

Graphics and Image Processing, pages 299–306.

Hiyadi, H., Ababsa, F., Bouyakhf, E. H., Regragui, F., and

Montagne, C. (2015). Reconnaissance 3d des gestes

pour l’interaction naturelle homme robot. In Journ

ees

francophones des jeunes chercheurs en vision par or-

dinateur.

Hogg, D. (1983). Model-based vision: a program to see a

walking person. Image and Vision computing, 1(1):5–

20.

Jiang, H. (2010). 3d human pose reconstruction using mil-

lions of exemplars. In Pattern Recognition (ICPR),

2010 20th International Conference on, pages 1674–

1677.

Lee, M. W. and Nevatia, R. (2009). Human pose tracking in

monocular sequence using multilevel structured mod-

els. Pattern Analysis and Machine Intelligence, IEEE

Transactions on, 31(1):27–38.

Maji, S., Bourdev, L., and Malik, J. (2011). Action recog-

nition from a distributed representation of pose and

appearance. In Computer Vision and Pattern Recogni-

tion (CVPR), 2011 IEEE Conference on, pages 3177–

3184. IEEE.

Mori, G. and Malik, J. (2002). Estimating human body con-

ﬁgurations using shape context matching. In Com-

puter VisionECCV 2002, pages 666–680. Springer.

O’Rourke, J., Badler, N., et al. (1980). Model-based im-

age analysis of human motion using constraint prop-

agation. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, (6):522–536.

P. Dollar, S. B. and Perona, P. (2010). The fastest pedestrian

detector in the west. In In: Proceedings of the British

Machine Vision Conference, pages 1–11.

Rehg, J. M. and Kanade, T. (1994). Visual tracking of high

dof articulated structures: an application to human

hand tracking. In Computer VisionECCV’94, pages

35–46. Springer.

Taylor, C. (2000). Reconstruction of articulated objects

from point correspondences in a single uncalibrated

image. In Computer Vision and Pattern Recognition,

2000. Proceedings. IEEE Conference on, volume 1,

pages 677–684 vol.1.

Valmadre, J. and Lucey, S. (2010). Deterministic 3d hu-

man pose estimation using rigid structure. In Com-

puter Vision–ECCV 2010, pages 467–480. Springer.

Wang, C., Wang, Y., and Yuille, A. (2013). An approach

to pose-based action recognition. In Computer Vision

and Pattern Recognition (CVPR), 2013 IEEE Confer-

ence on, pages 915–922.

Wang, L., Wang, Y., and Gao, W. (2011). Mining layered

grammar rules for action recognition. International

Journal of Computer Vision, 93(2):162–182.

Wei, X. K. and Chai, J. (2009). Modeling 3d human poses

from uncalibrated monocular images. In Computer

Vision, 2009 IEEE 12th International Conference on,

pages 1873–1880. IEEE.

Wren, C. R., Azarbayejani, A., Darrell, T., and Pentland,

A. P. (1997). Pﬁnder: Real-time tracking of the hu-

man body. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 19(7):780–785.

Yang, Y. and Ramanan, D. (2011). Articulated pose esti-

mation with ﬂexible mixtures-of-parts. In Computer

Vision and Pattern Recognition (CVPR), 2011 IEEE

Conference on, pages 1385–1392. IEEE.

Yap, P.-T., Paramesran, R., and Ong, S.-H. (2003). Image

analysis by krawtchouk moments. Image Processing,

IEEE Transactions on, 12(11):1367–1377.

3D Human Poses Estimation from a Single 2D Silhouette

369