Optimization of Routes for Road Surface Inspection

An Application to the Portuguese National Road Network

Filipe F. Gomes

, Marta Castilho Gomes

and Alexandre B. Gonçalves

Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, Lisboa, Portugal

CERIS, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, Lisboa, Portugal

Keywords: Road Inspection Routing, Routing, Linear Programming, Geographical Information Systems (GIS).

Abstract: Infraestruturas de Portugal S.A. (IP) is responsible for managing the Portuguese rail network infrastructure

and a significant part of the road network. An annual inspection must be performed on every road segment

for which IP is responsible, which sums up around 14,000 km. This is a costly operation regarding time,

human and monetary resources. An optimization model that incorporates the problem technical constraints

was developed and a cost analysis performed to compare the distinct scenarios that IP may face in the

general layout of the inspection programme.

1 INTRODUCTION

Infraestruturas de Portugal, S.A. (IP) is a Portuguese

institution with the responsibility of managing the

rail network infrastructure and part of the road

network in Portugal. Every year, an inspection must

be conducted on the roads that IP manages, which

include national roads and some motorway

segments, in a total of ca. 14,000 km. The inspection

is done by directly registering a few parameters

related with pavement geometry and conditions, as

well as other relevant road events, by moving a

vehicle equipped with a device called Road Surface

Tester Laser (RST) and video registering travels

along the roads.

Additionally, there are technical constraints

related with the maintenance and calibration of the

RST device, which must be done every week in the

IP headquarters in the cities of Almada or Coimbra.

Another aspect concerns the inspection procedure

itself: for regular roads, i.e., with both directions and

at least two traffic lanes, it is assumed that road

surface conditions are equivalent in both sides, and a

single lane, the rightmost one, has to be travelled

along. In motorways, however, both directions must

be inspected. IP performs the operation usually in

summertime and has implemented a travel diary that

covers the entire Portuguese road network which IP

must inspect, based on empirical plans adopted in

previous years.

The implementation of the entire work plan is a

costly operation, in time, human and monetary

resources. A total of 65 working days is needed to

cover the road network, at an average speed of 55

km/h. Plans are supported by spatial data stored and

analysed in the institutional geographical

information system (GIS), which details the

geometry and attributes of the entire road network,

and not only that which must be inspected. The GIS

datasets have ca. 14,200 segments in total.

The goal of this work is to develop and apply a

model to define the inspection routes for the road

network managed by IP, which complies with the

inspection technical constraints and minimizes the

total cost.

2 METHODOLOGY

To achieve the expressed goals, a methodology

following the steps below was developed:

• Collection and processing of road network

data (namely, conversion to a format that the

optimization software can handle)

• Development of an optimization model

embedding the technical constraints

• Application of the model

• Critical analysis of model results.

362

Gomes, F., Gomes, M. and Gonçalves, A.

Optimization of Routes for Road Surface Inspection - An Application to the Portuguese National Road Network.

DOI: 10.5220/0005711803620365

In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 362-365

ISBN: 978-989-758-171-7

3 DATA COLLECTION AND

PROCESSING

This section describes the data collection and

processing stage, which was required to obtain and

transform data from the original datasets to a format

compatible with the optimization software.

IP maintains an exhaustive GIS database with the

road features stored in geodatabases, providing

topologically coherent datasets and at a detailed

positional and cartographic scale (for instance,

complex intersections such as roundabouts have

their segments broken into several features).

IP also maintains a record of previous inspection

routes and has established an empirical plan based

on travel diaries to direct the inspection procedure.

In it the travel directions are kept for future

reference.

It was necessary to process these data to enable

its representation as inputs to the optimization

software. The first task was to consider the required

level of detail for an accurate representation of road

inspection plans. This implied the edition of data

with a cartographic purpose to a simplified version

but maintaining the topological detail: for instance,

there is no need to consider all the small road

segments that constitute a roundabout since there is

enough detail in a description where the circular

intersection is replaced with a single node on which

the adjoining roads converge. Data was processed

and validated manually by overlaying the

geographic datasets over publicly available satellite

imagery as a layer in ArcGIS (ESRI, 2011) a

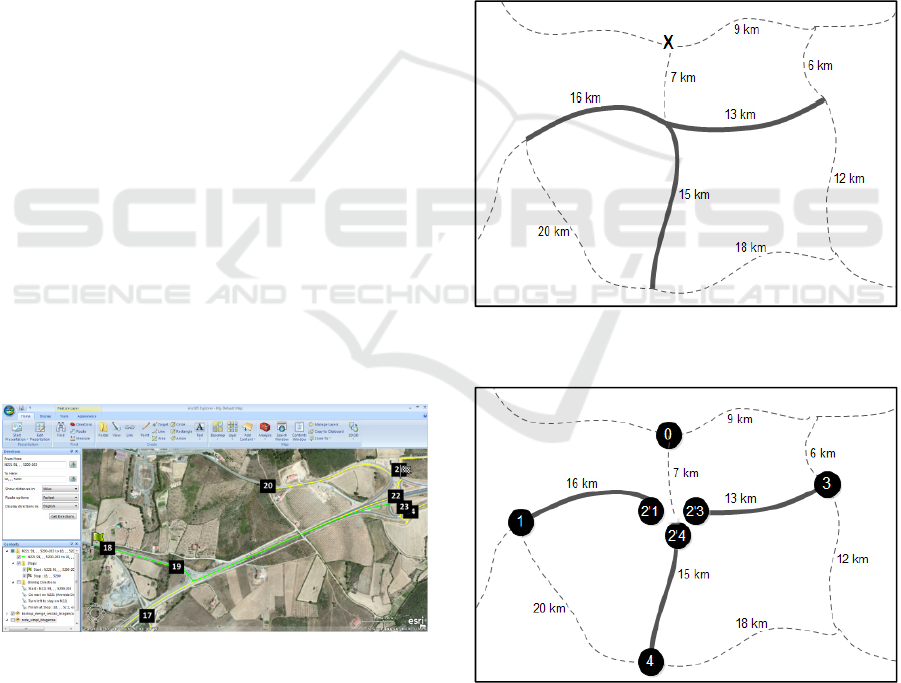
desktop GIS (Figure 1).

Figure 1: Processing of spatial data features: breaking

converging nodes into separated nodes.

After this edition, the next task was to assign to

each feature that represents a segment, which must

be inspected, and to each of its two endpoints,

unique identifiers. This action breaks the nodes

where two or more road segments converge into

several nodes. Figures 2 and 3 illustrate this

operation: Node 2, which was the intersection of

several road segments, of which three must be

inspected, is broken into three nodes, each

connecting to the respective segment.

Next, the shortest distance between each pair of

nodes is calculated with the GIS software, using a

network analysis function that produces an origin-

destination distance matrix by applying a shortest

path algorithm. The internal distances between the

duplicated node instances such as the case of Figure

1 are set to zero. Note that these shortest paths may

use the entire road system, i.e., they are not limited

to the road segments that must be inspected.

A complete list of pairs of nodes with the

corresponding shortest distance between them,

which is an input to the optimization model, is then

available.

Figure 2: Processing of spatial data features: breaking

converging nodes into separated nodes.

Figure 3: Processing of spatial data features: breaking

converging nodes into separated nodes (continued).

Optimization of Routes for Road Surface Inspection - An Application to the Portuguese National Road Network

363

4 MODEL FOR ROAD

INSPECTION ROUTING

The problem under study was characterized, among

routing problems, as an arc routing problem, and

corresponds, in particular, to the Rural Postman

Problem (RPP) were a sub-set of the arcs in a graph

has to be visited (inspected).

An original linear programming formulation for

the problem was developed, based on the one

presented by Monroy-Licht et al. (2014) – model on

the nodes. For sub-routes elimination, the Miller-

Tucker-Zemlin formulation (Miller et al., 1960, also

described in Pataki, 2003) for sub-route elimination

in the travelling salesman problem (TSP) was

adapted to the present problem.

Decision variables are binary and equal 1 if a

vertex j is visited immediately after vertex i and 0

otherwise. Auxiliary variables (integer) were

included in the model to enable sub-routes

elimination. Given the cost of inspecting each arc

(i,j) that has to be visited, the objective function is

the total inspection cost, to be minimized.

Formulations for the directed and undirected

variants of the problem under study (described in the

next section) were developed, as well as a mixed

formulation that combines the two.

5 MODEL APPLICATION AND

RESULTS

This section describes the model application to

obtain optimal routes for road inspection with the

existing technical constraints. The Bragança district,

in the northeast of Portugal, was selected as the case

study, as it presents a mixture of topological

combinations of road segments to be inspected and

other roads, and of short and long arcs, and thus was

also able to serve as a test dataset to verify if the

model constraints were able to represent feasible

inspection plans. Network size was also considered

adequate for a first model application.

As global parameters, values for the average

inspection speed, average speed for connections

(non-inspection), fuel consumption, gas price, daily

wage and overnight accommodation costs were set

to provide realistic values for the global operation

budget.

The model was implemented in GAMS

modelling system and solved with CPLEX version

12.6.1.

Table 1 presents the numeric characteristics of

the model (number of variables and equations), the

CPU time and the number of iterations of the

branch-and-bound search to reach a solution, as well

as the corresponding optimality gap.

Table 1: Summary of numeric characteristics and results

of the model.

Characteristic/re

sult

Value

# variables

70,225

# equations

71,148

# iterations

8,128 39,348 147,303 765,369

CPU time (s)

2 10 30 60

Relative gap (%)

27.39 7.88 6.00 1.11

Absolute gap (km)

530 123 92 16

Solutions were obtained for two scenarios: (i) a

model where the directions defined in the current

inspection plan were fixed; and (ii) a model where

road inspection directions were free. The reason to

consider scenario (i) was that it might be interesting

to the infrastructure manager to have an inspection

plan where each road stretch is examined following

the same direction of previous plans, as direct

comparisons are easier to made, while (ii) might

produce solutions that minimize the overall costs,

without necessarily respecting the directions of

previous inspection plans.

Best solutions of both scenarios were then

compared with the currently implemented IP

inspection plan, which was obtained empirically.

By including constraints that regulate the

location of the vehicle at the end of each working

day, it is possible to manage overnight stays in

specific locations. Options of overnight stays either

in the city of Coimbra (the closest IP headquarters)

or in the city of Bragança (the district capital) were

considered. Results with overnight stays are

presented in Table 2.

Table 2: Results (total length and cost) and savings of

solutions with overnight stays in Bragança, for both

scenarios.

Value Reduction %

km €

Current empirical

solution

3,281 1,308 -

Fixed directions

(i)

1,834 731 44

Non-fixed

directions (ii)

1,718 685 48

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

364

6 CONCLUSIONS

The developed optimization model for the route

inspection problem was able to produce solutions

that represent significant reductions of costs when

compared to the currently adopted solution.

By controlling the direction of inspection for

each road segment to match the current empirical

plan, savings of 44% were obtained. An additional

saving of 4% is obtainable when the inspection

direction is not fixed. A note should be made on

these preliminary results, as the model only

considered the district of Bragança while the current

inspection plans are designed for a national scale

where the administrative division is not taken into

account. As such, these preliminary results should

now be analysed by the experts in practice of

Infraestruturas de Portugal.

A future development of this work is its

extension to the entire country (divided by zones), to

produce full-scale inspection plans comparable with

the current empirical solution. Another development

is the integration of the solution generator with in-

vehicle systems to consider real-time unpredictable

changes to the plan, e.g. due to road blockage

(accidents, traffic congestion, etc.) and produce

alternative work plans.

REFERENCES

ESRI, 2011. ArcGIS Desktop: Release 10. Redlands, CA:

Environmental Systems Research Institute.

Miller, C.E., Tucker, A.W., Zemlin, R.A., 1960. Integer

Programming Formulations and Traveling Salesman

Problems, Journal of the Association for Computing

Machinery, 7, 326-329.

Monroy-Licht, M., Amaya, C.A., Langevin, A., 2014. The

Rural Postman Problem with Time Windows.

Networks, 64(3), 169-180.

Pataki, G., 2003. Teaching integer programming

formulations using the traveling salesman problem.

SIAM Review, 45(1), 116-123.

Optimization of Routes for Road Surface Inspection - An Application to the Portuguese National Road Network

365