Image Encryption using Improved Keystream Generator of

Achterbahn-128

Aissa Belmeguenai

1

, Oulaya Berrak

2

and Khaled Mansouri

2

1

Laboratoire de Recherche en Electronique de Skikda, Universit´e 20 Aoˆut 1955- Skikda,

BP 26 Route d’El-hadaeik Skikda, Algeria

2

Department of Electronics, Faculty of Science and Engineering, Badji Mokhtar University, LP 12 Annaba, Algeria

Keywords:

Boolean Function, Image Encryption, Keystream Generator, Stream Cipher, Security Analysis.

Abstract:

The images transmission become more and more widely used in everyday life and even have been known

to be vulnerable to interception and unauthorized access. The security of their transmission became neces-

sary. In this paper an improved version of the Achterbahn -128 for image encryption and decryption have

been proposed. The proposed design is based on seventeen binary primitive nonlinear feedback shift registers

(NLFSRs) whose polynomials are primitive and a nonlinear Boolean function. The outputs of seventeen regis-

ters are combined by the nonlinear Boolean function to produce keysteam sequence. The proposed scheme is

compared to a Achterbahn-128. The results of several experimental, statistical analysis and sensitivity analysis

show that the proposed image encryption scheme is better than Achterbahn-128 and provides an efﬁcient and

secure way for image encryption and transmission.

1 INTRODUCTION

The images are very largely used in our daily life;

with recent development of information and com-

munication technology, images transmission becomes

more critical day by day. Higher security for trans-

mitting data is highly required. Therefore, the stream

cipher is an important issue.

Stream cipher is secret key encryption system,

which combines plain text bits with a pseudo-random

bit sequence. Stream ciphers are widely used in many

domains (industrial, governmental, telecommunica-

tions and individuals), because they have the advan-

tage of no error propagation, and are particularly suit-

able for use in environments where no buffering is

available and /or plaintext elements need to be pro-

cessed individually.

The multiplied number of attacks concerning

the stream cipher systems based on linear feed-

back shift registers (combination model or ﬁltering

model) (Berlekamp, 1968), (Massey, 1969), (Siegen-

thaler, 1985), (Meier and Staffelbach, 1988), (Golic,

1994), (Courtois and Meier, 2003), and (Courtois,

2003) have led many researchers to be interested

to the design based on primitive nonlinear feedback

shift registers (NLFSRs), primarily motivated by eS-

TREAM, the ECRYPT stream cipher project (eS-

TREAM, 2002). Here we can mention the research

works (Gottfert and Knifﬂer, 2006) and (Johansson

and Meier, 2006).

In this paper a new version of Achterbahn-128

based on primitive NLFSRs oriented stream cipher

and also the implementation of this generator for im-

ages encryption is introduced. The new version is

based on seventeen binary primitive nonlinear feed-

back shift registers and a Boolean combining func-

tion. All feedback shift registers (NLFSRs) employed

are primitive and nonlinear. The combining function

achieves the best possible trade-offs between alge-

braic degree, resiliency order and nonlinearity (that

is, achieving Siegenthaler’s bound and Sarkar et al.’s

bound).

The proposed version is compared with the

Achterbahn-128. The comparison of the performance

of the two designs is investigated for different images.

The paper is organized as follows. In Section 2

we recall the Achterbahn-128. Section 3 gives the

speciﬁcation of the proposed design. In Section 4

we consider the software implementation of the pro-

posed design for image encryptionand decryption and

in section 5 we give the results of our visual testing.

In section 6 we give the security analysis. Section 7

concludes the paper.

Belmeguenai, A., Berrak, O. and Mansouri, K.

Image Encryption using Improved Keystream Generator of Achterbahn-128.

DOI: 10.5220/0005713503330339

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 335-341

ISBN: 978-989-758-175-5

Copyright

c

335

2 ACHTERBAHN-128 CIPHER

The Achterbahn-128 (Gottfert and Knifﬂer, 2006) is

a binary additive stream ciphers as candidates to eS-

TREAM. The Achterbahn-128 cipher is designed to

be small, simple and efﬁcient in hardware.

The Achterbahn-128 consists of thirteen bi-

nary nonlinear feedback shift registers (NLFSRs) of

lengths between 21 and 33 plus a Boolean function

F. We denote by x

k

for 1 ≤ k ≤ 13 the output se-

quence generated by the k-th constituent NLFSR. All

NLFSRs deployed in the Achterbahn-128 are primi-

tive and nonlinear; they can produce binary sequences

of period 2

L

k

− 1, where L

k

is the length of register

R

k

. The output sequences of the thirteen NLFSR’s x

k

are combined by a Boolean combining function F of

thirteen variables. The combining function F has re-

siliency 8, nonlinearity 3584, algebraic degree 4 and

algebraic immunity 4.

The output of the keystream generator of

Achterbahn-128 at time i, denoted by Z(i), is gener-

ated as:

Z(i) = F(x

1

(i), ..., x

13

(i)). (1)

3 IMPROVED VERSION

In this section we give an improved version of the

keystream generator of Achterbahn-128. The pro-

posed design consists of seventeen binary primitive

NLFSRs denoted R

j

of lengths L

j

, where 1 ≤ j ≤ 17

and a nonlinear Boolean function G : F

17

2

→ F

2

. All

feedback shift registers employed in the proposed ver-

sion are primitive and nonlinear. The NLFSR’s are

such that they can produce binary sequences of pe-

riod 2

L

j

− 1. Each shift register is described by its

feedback function g

j

. For the eleven NLFSR’s whose

lengths 25 ≤ L

j

≤ 33 , we us the feedback shift reg-

isters used in the keystream generator of Achterbahn-

128/80 (Gottfert and Knifﬂer, 2006).

For the others NLFSR’s the algebraic normal

forms of the feedbackfunctions are givenin appendix.

The nonzero output sequences of the seventeen binary

primitive NLFSRs are taken as input to a combining

function, G. It is deﬁned as:

G = (1 ⊕ P) f ⊕ Pf

∗

⊕ Q = f ⊕ ( f ⊕ f

∗

)P⊕ Q. (2)

Where f, f ⊕ f

∗

, P and Q are given in appendix.

For more detaill on G refer to construction 1 page 49

presented in (Dalai, 2006). The combining function

G is balanced, has algebraic degree 7, correlation im-

mune of order 9 and has nonlinearity 2

16

− 2

10

.

The keystream sequence (Y

i

)

i≥0

is computed as:

Y(i) = G(x

1

(i), x

2

(i), · · · , x

17

(i)), ∀i ≥ 0, (3)

where (x

j

(i))

i≥0

denotes the output sequence gener-

ated by the j-th constituent NLFSR. The variables

x

1

(i), x

2

(i), ..., x

17

(i) corresponds to the tap positions

19, 39, 34, 23, 25, 36, 26, 29, 27, 28, 30, 40, 31, 44, 45, 32

and 33 respectively.

4 IMPLEMENTATION

In this section we present the implementation of pro-

posed design for image encryption and decryption.

The implementation of the scheme is written by MAT-

LAB.7.5. By M(i), Y(i) and C(i) we denote respec-

tively original image digits, keystream digits and en-

crypted image digits at time i. The ﬂow chart of the

encryption and decryption process are depicted in ﬁg-

ures 1 and 2. Figure 3 illustrates the ﬂow chart dia-

gram for keystream generator.

Figure 1: Flow chart of the encryption process.

5 VISUAL TESTING RESULTS

AND SECURITY ANALYSIS

In this section we discuss the obtained results from

implementing the proposed scheme system and the

Achterbahn-128. Two images Baboon and House in-

dicated in ﬁgures 4 and 5 are used. After loading

and processing the original image, it is converted into

original image digit then encrypted by the proposed

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

336

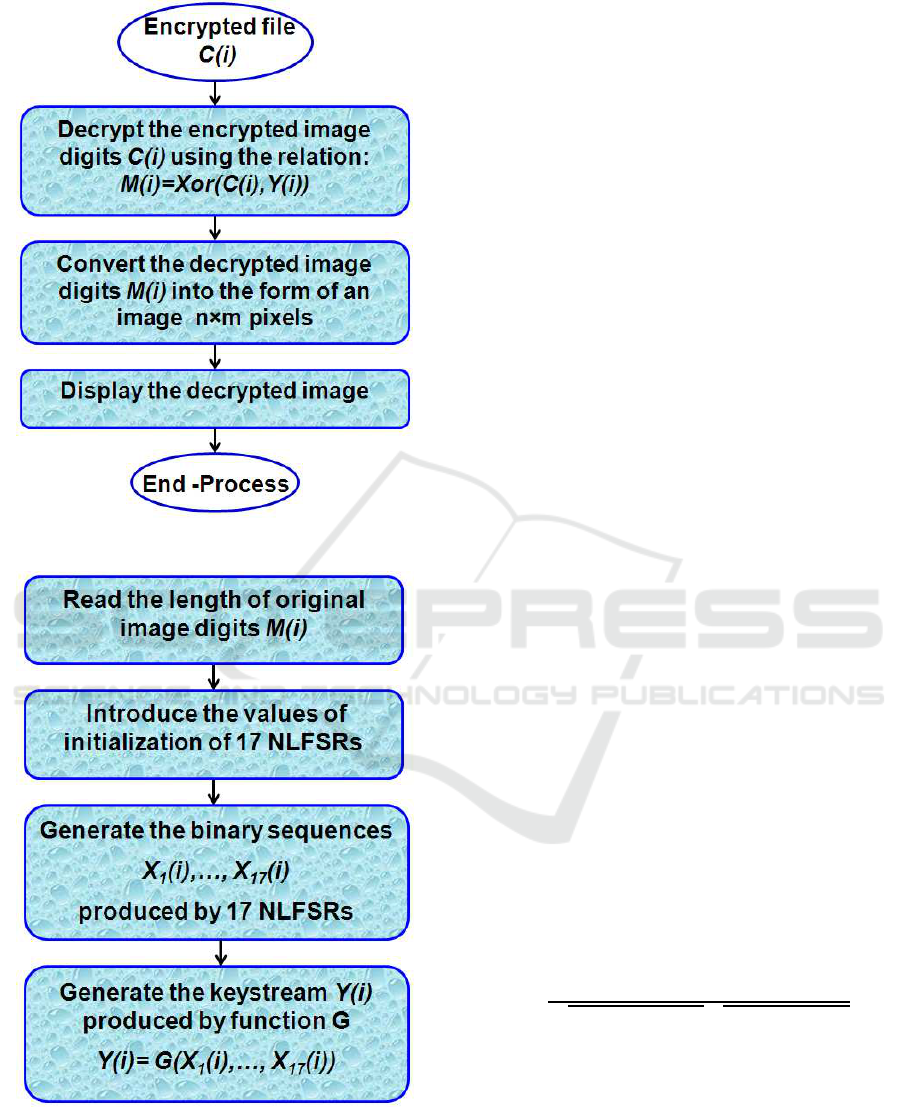
Figure 2: Flow chart of the decryption process.

Figure 3: Flow chart of the keystream generator.

keystream generator and sent to the receiver. The

function of the receiver is to decrypt the encrypted

image with the same keystream in order to obtain the

original image.

As a general requirement for all the image encryp-

tion schemes, the encrypted image should be greatly

different from its original form.

From the original images shown in ﬁgures 4 and 5,

we applied the proposed encryption algorithm in or-

der to obtain the encrypted images illustrated by ﬁg-

ures 4 and 5.

By comparing the original images and their en-

crypted images in ﬁgures 4 and 5, there is no vi-

sual information observed in the encrypted images,

and the encrypted images are visual indistinguishable

even with a big difference found in the original im-

ages.

From the encrypted images illustrated by the ﬁg-

ures 4 and 5, we apply the decryption algorithm with

the same key in order to obtain the decrypted images

shown in ﬁgures 4 and 5.

An image histogram illustrates how pixels in an

image are distributed by graphing the number of pix-

els at each gray intensity level. The histograms of the

original images and the encrypted images are com-

pared in ﬁgures 4 and 5. Our ideal goal is the en-

crypted image has histogram with random behavior.

It is clear that the histograms of the encrypted im-

ages are almost uniformly distributed in gray scale

[0-255] and signiﬁcantly different from the original

images histograms. Thus, our approach is more ro-

bust against statistical analysis.

Difference between original images and their cor-

responding decrypted images and their histograms are

prove that, there is no loss of information, the differ-

ence is always 0.

Figures 6 and 7. show the experimental results

of encryption and decryption for Baboon and House

using the Achterbahn-128.

5.1 Correlation Coefﬁcient

As an example we take the original image M and the

encrypted image C. For gray scale image, the Pearson

correlation coefﬁcient between the original image M

and encrypted image C is deﬁned as:

Cor =

Σ

j

(M

j

− E(M))(C

j

− E(C))

p

Σ

j

(M

j

− E(M))

2

p

Σ

j

(C

j

− E(C))

2

. (4)

Where M

j

is the intensity of the j-th pixel in im-

age M, E(M) is the mean intensity of the image M.

Table 1 gives the correlation coefﬁcient results. It

is observed that the values shown in the table 1 are

quite close to the value of zero, which implies that

the original images and its corresponding encrypted

images are totally different i.e. the encrypted image

has no features and highly independent on the original

image.

Image Encryption using Improved Keystream Generator of Achterbahn-128

337

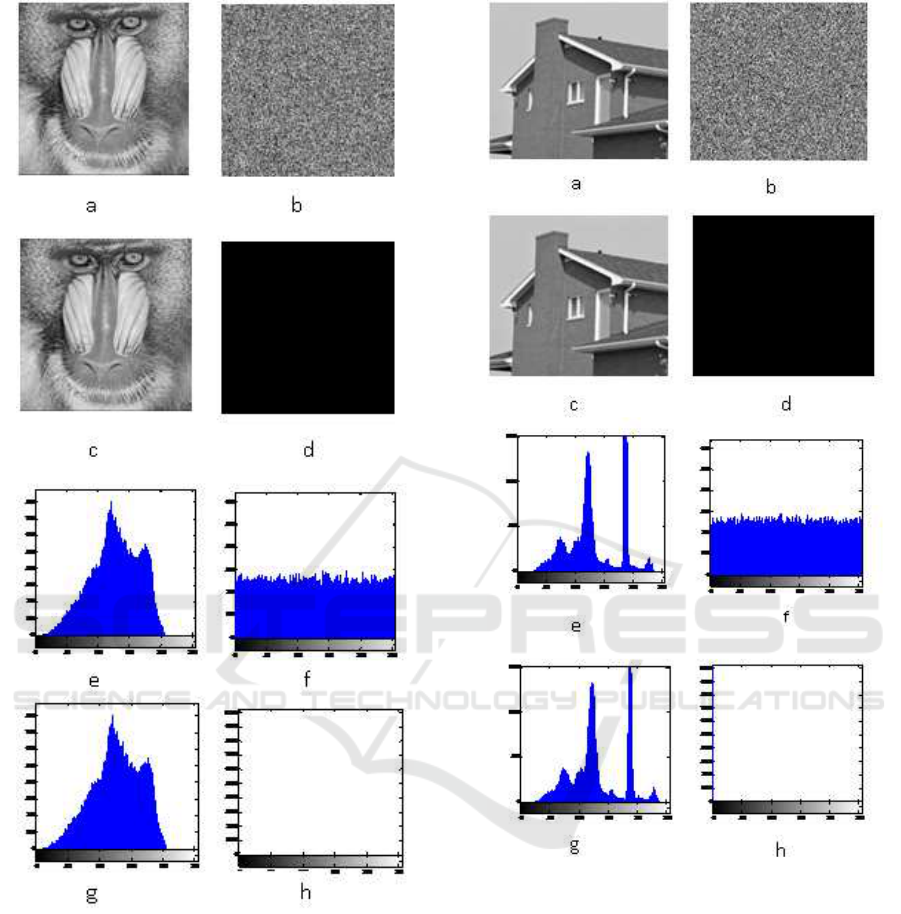
Figure 4: Experimental results using proposed scheme:

Frame (a) show image Baboon, frame (b) show encrypted

image, frame (c) show decrypted image, frame (d) show the

difference between Baboon image and the corresponding

decrypted image, frames (e), (f), (g) and (h) respectively;

show the histograms of images shown in ﬁgures 4(a), 4(b),

4(c) and 4(d).

5.2 Information Entropy

The entropy of a message can be computed by the

formula:

E(m) = −Σ

255

i=0

Pr(m

i

)log

2

Pr(m

i

). (5)

Where Pr(m

i

) represents the probability of sym-

bol m

i

. The entropy is expressed in bits.

Figure 5: Experimental results using proposed scheme:

Frame (a) show image House, frame (b) show encrypted

image, frame (c) show decrypted image, frame (d) show

the difference between House image and the corresponding

decrypted image, frames (e), (f), (g) and (h) respectively;

show the histograms of images shown in ﬁgures 5(a), 5(b),

5(c) and 5(d).

Table 2 gives the entropy results. The values pre-

sented in the table 2 are very close to the theoretical

value of 8. This means that information leakage in

the encryption process is negligible and the encryp-

tion system is secure upon the entropy attack.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

338

Figure 6: Experimental results using Achterbahn-128:

Frame (a) show image Baboon, frame (b) show encrypted

image, frame (c) show decrypted image, frame (d) show the

difference between Baboon image and the corresponding

decrypted image, frames (e), (f), (g) and (h) respectively;

show the histograms of images shown in ﬁgures 4(a), 4(b),

4(c) and 4(d).

5.3 Sensitivity Analysis

To test the inﬂuence of one-pixel change on the over-

all image encrypted by the proposed algorithm, three

common measures were used: the Mean Absolute Er-

ror (MAE), number of pixels change rate (NPCR) and

uniﬁed average changing intensity (UACI).

The MAE, NPCR and UACI are deﬁned respec-

tively by:

Figure 7: Experimental results using Achterbahn-128:

Frame (a) show image House, frame (b) show encrypted

image, frame (c) show decrypted image, frame (d) show

the difference between House image and the corresponding

decrypted image, frames (e), (f), (g) and (h) respectively;

show the histograms of images shown in ﬁgures 5(a), 5(b),

5(c) and 5(d).

MAE =

1

h× w

Σ

h−1

i=0

Σ

w−1

j=0

|C(i, j) − M(i, j)|. (6)

Where M(i, j) and C(i, j) be the gray level of the

pixels at the i-th row and j-th column of a h× w orig-

inal image and encrypted image, respectively. |.| de-

notes absolute value function. The NPCR of these

two images is deﬁned by:

NPCR(M, C) =

1

h× w

Σ

ij

D(i, j) × 100%. (7)

Image Encryption using Improved Keystream Generator of Achterbahn-128

339

Table 1: Correlation Coefﬁcients Analysis.

Images Proposed scheme Achterbahn-128

Baboon 0.0007805 0.0014

House 0.000070905 0.0066

Table 2: Entropy.

Cases Proposed scheme Achterbahn-128

Baboon 7.9985 7.9971

House 7.9992 7.9973

Table 3: MAE, NPCR and UACI between original image

and encrypted image using proposed scheme.

Image MAE NPCR (%) UACI(%)

Baboon 34.89 27,38 99,60

House 30.99 28,45 99,60

Table 4: MAE, NPCR and UACI between original image

and encrypted image using Achterbahn-128.

Image MAE NPCR (%) UACI(%)

Baboon 35.03 27,34 99,58

House 30.95 28,39 99,58

Where D(i, j) = 0, if C

1

(i, j) = C

2

(i, j) and

D(i, j) = 1, if C

1

(i, j) 6= C

2

(i, j), C

1

(i, j) and C

2

(i, j)

, whose corresponding original image have only one

pixel difference.

UACI(M, C) =

1

h× w

Σ

ij

D(i, j)

255

× 100%. (8)

A sufﬁciently high NPCR/UACI score is usually con-

sidered to be a strong resistance against attacks.

The MAE,NPCR and UACI test results are shown

in table 3 and table 4. Higher NPCR values are de-

sired for ideal encryption schemes. The UACI values

must be in the range of 33%. The results demonstrate

that the proposed scheme can resist to differential at-

tack.

5.4 Peak Signal to Noise Ratio (PSNR

(dB)) Test

Peak signal to noise ratio can be used to evaluate

an encryption scheme. PSNR reﬂects the encryption

quality. This is a measurement which indicates the

changes in pixel values between the original image

and the encrypted image. The formula to calculate

PSNR is:

PSNR = 10× log

10

"

n× m×255

2

Σ

n−1

i=0

Σ

m−1

j=0

(C(i, j) − M(i, j))

2

#

.

(9)

Where n and m are the width and height of the

original image. The lower value of PSNR represents

better encryption quality. The PSNR value of the pro-

posed scheme are 9.31 (dB) for image House and 9.74

(dB) for Baboon. The PSNR value of the Achterbahn-

128 are 9.33 (dB) for image House and 9.75 (dB) for

Baboon.

6 CONCLUSION

In this Work, a new version of Achterbahn-128 for

images encryption was introduced. Simulations were

carried out with two different images. The visual test

indicates that the encrypted image was very different

and no visual information can be deduced about the

original image for all images. The design is very sim-

ple, fast and easy to implement for the encryption and

decryption of image.

Several tests have been performed to compare the

proposed scheme with Achterbahn-128; likely, sta-

tistical analysis, which includes information entropy

analysis, correlation analysis and Histogram analysis;

and MAE, NPCR, UACI and PSNR analysis. The

experimental values show that the proposed scheme

yield a very good performance over the Achterbahn-

128.

REFERENCES

Berlekamp, E. R. (1968). Algebraic Coding Theory. Mc

Grow-Hil, New- York.

Courtois, N. (2003). Fast algebraic attacks on stream ci-

phers with linear feedback. In Advances in cryptology

CRYPTO 2003. Lecture Notes in Computer Science,

2729, p 177–194. Springer.

Courtois, N. and Meier, W. (2003). Algebraic attacks on

stream ciphers with linear feedback. In Advances

in cryptology EUROCRYPT 2003. Lecture Notes in

Computer Science, 2656, p 345–359. Springer.

Dalai, D. K. (2006). On some necessary conditions of

boolean functions to resist algebraic attacks. The-

sis, Applied Statistics Unit Indian Statistical Institute

Kolkata, India.

eSTREAM (2002). Ecrypt stream cipher

project. In IST-2002-507932. Available at.

http://www.ecrypt.eu.org/stream/.

Golic, J. D. (1994). Linear cryptanalysis of stream ciphers.

In Fast Software Encryption 1994. Lecture Notes in

Computer Science, 1008, p 154–169, Springer-Verlag.

Gottfert, B. G. R. and Knifﬂer, O. (2006).

Achterbahn-128/80. eSTREAM, ECRYPT

Stream Cipher Project, Report 2006/001,

http://www.ecrypt.eu.org/stream/p2ciphers/achterbahn/

achterbahn-p2.pdf.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

340

Johansson, M. H. T. and Meier, W. (2006). A stream cipher

proposal: Grain-128. In IEEE International Sympo-

sium on Information Theory. ISIT 2006.

Massey, J. L. (1969). Shift-register synthesis and bch de-

coding. In IEEE Transactions on information Theory.

vol IT–15, p 122–127,1969.

Meier, W. and Staffelbach, O. (1988). Fast correlation at-

tacks on stream chiper. In Advances in cryptology-

EUROCRYPT’88. Lectures Notes in Computer sci-

ence, 430, p 301–314, Springer Verlag, 1988.

Siegenthaler, T. (1985). Decrypting a class of stream ci-

phers using cipher text only. In IEEE Transactions on

Computers. C–34, N 1, P 81–85, 1985.

APPENDIX

The algebraic normal form of the function f

0

is:

f

0

= (x

5

⊕ x

8

x

5

⊕ x

8

x

6

⊕ x

8

x

7

)(x

1

x

4

⊕ x

3

x

4

⊕ x

2

x

3

) ⊕

x

6

⊕ x

7

x

8

x

5

⊕ x

8

x

6

⊕ x

1

x

4

⊕ x

3

x

4

⊕ x

2

⊕ x

1

.

f

0

is balanced and is correlation immune of order

3,it has algebraic degree 4 and nonlinearity 112.

The algebraic normal form of the polynomial f

0

⊕

f

∗

0

is:

f

0

⊕ f

∗

0

= x

5

x

8

⊕ x

5

x

9

⊕ x

5

x

10

⊕ x

6

x

8

⊕ x

6

x

9

⊕

x

6

x

10

⊕ x

1

x

4

x

5

x

8

⊕ x

1

x

4

x

5

x

9

⊕ x

1

x

4

x

5

x

10

⊕ x

3

x

4

x

5

x

8

⊕

x

3

x

4

x

5

x

9

⊕ x

3

x

4

x

5

x

10

⊕ x

2

x

3

x

5

x

8

⊕ x

2

x

3

x

5

x

9

⊕

x

2

x

3

x

5

x

10

⊕ x

1

x

4

x

6

x

8

⊕ x

1

x

4

x

6

x

9

⊕ x

1

x

4

x

6

x

10

⊕

x

3

x

4

x

6

x

8

⊕ x

3

x

4

x

6

x

9

⊕ x

3

x

4

x

6

x

10

⊕ x

2

x

3

x

6

x

8

⊕

x

2

x

3

x

6

x

9

⊕ x

2

x

3

x

6

x

10

⊕ x

1

x

4

x

7

x

8

⊕ x

1

x

4

x

7

x

9

⊕

x

1

x

4

x

7

x

10

⊕ x

3

x

4

x

7

x

8

⊕ x

3

x

4

x

7

x

9

⊕ x

3

x

4

x

7

x

10

⊕

x

2

x

3

x

7

x

8

⊕ x

2

x

3

x

7

x

9

⊕ x

2

x

3

x

7

x

10

.

Where f

∗

0

is Boolean function generated from f

0

by replacing the variable x

8

by (x

9

⊕ x

10

).

The algebraic normal form of the polynomial P is:

P = x

11

⊕ x

11

x

14

⊕ x

12

x

14

⊕ x

13

x

14

⊕ x

11

x

14

x

17

⊕

x

12

x

14

x

17

⊕ x

13

x

14

x

17

⊕ x

11

x

15

x

17

⊕ x

12

x

15

x

17

⊕

x

13

x

15

x

17

⊕ x

11

x

16

x

17

⊕ x

12

x

16

x

17

⊕ x

13

x

16

x

17

.

The algebraic normal form of the polynomial Q is:

Q = x

9

⊕ x

10

⊕ x

12

⊕ x

13

⊕ x

8

x

11

⊕ x

9

x

11

⊕

x

11

x

14

⊕ x

12

x

14

⊕ x

14

x

17

⊕ x

15

x

17

⊕x

8

x

11

x

14

⊕

x

8

x

12

x

14

⊕x

8

x

13

x

14

⊕x

9

x

11

x

14

⊕x

9

x

12

x

14

⊕x

9

x

13

x

14

⊕

x

11

x

14

x

17

⊕ x

12

x

14

x

17

⊕ x

11

x

15

x

17

⊕ x

12

x

15

x

17

⊕

x

11

x

16

x

17

⊕ x

12

x

16

x

17

⊕ x

8

x

11

x

14

x

17

⊕ x

9

x

11

x

14

x

17

⊕

x

8

x

12

x

14

x

17

⊕ x

9

x

12

x

14

x

17

⊕ x

8

x

13

x

14

x

17

⊕ x

9

x

13

x

14

x

17

⊕x

8

x

11

x

15

x

17

⊕ x

9

x

11

x

15

x

17

⊕ x

8

x

12

x

15

x

17

⊕

x

9

x

12

x

15

x

17

⊕ x

8

x

13

x

15

x

17

⊕ x

9

x

13

x

15

x

17

⊕

x

8

x

11

x

16

x

17

⊕ x

9

x

11

x

16

x

17

⊕ x

8

x

12

x

16

x

17

⊕ x

9

x

12

x

16

x

17

⊕x

8

x

13

x

16

x

17

⊕ x

9

x

13

x

16

x

17

.

Agebraic normal forms of the feedback functions

used in proposed version

g

1

(u

0

, u

1

, ··· , u

18

) = u

0

⊕u

2

⊕u

3

⊕u

5

⊕u

8

⊕u

12

⊕

u

1

u

6

⊕ u

2

s

6

⊕ u

2

u

9

⊕ u

4

u

7

⊕ u

5

u

6

⊕ u

9

u

10

⊕ u

9

u

11

⊕

u

2

u

4

u

6

⊕ u

2

u

4

u

10

⊕ u

2

u

6

u

9

⊕ u

4

u

9

u

10

⊕ u

6

u

9

u

10

⊕

u

9

u

10

u

11

⊕ u

2

u

4

u

6

u

9

⊕ u

2

u

4

u

9

u

10

⊕ u

4

u

6

u

9

u

10

.

g

2

(u

0

, u

1

, ··· , u

38

) = u

0

⊕ u

1

⊕ u

3

⊕ u

5

⊕ u

12

⊕

u

16

⊕ u

37

⊕ u

38

⊕ u

1

u

5

⊕ u

5

u

8

⊕ u

6

u

10

⊕ u

11

u

37

⊕

u

4

u

6

u

16

⊕ u

4

u

9

u

14

⊕ u

6

u

15

u

16

⊕ u

1

u

9

u

14

u

36

.

g

3

(u

0

, u

1

, ··· , u

33

) = u

0

⊕ u

3

⊕ u

6

⊕ u

9

⊕

u

33

⊕ u

3

u

4

⊕ u

4

u

8

⊕ u

4

u

9

⊕ u

7

u

9

⊕ u

1

u

3

u

4

⊕

u

2

u

4

u

5

⊕ u

5

u

3

u

9

⊕ u

1

u

4

u

9

⊕ u

2

u

3

u

4

u

5

⊕ u

2

u

4

u

5

u

9

⊕

u

2

u

3

u

4

u

5

u

9

.

g

6

(u

0

, u

1

, ··· , u

35

) = u

0

⊕u

2

⊕u

3

⊕u

5

⊕u

8

⊕u

35

⊕

u

1

u

6

⊕ u

2

u

6

⊕ u

2

u

9

⊕ u

4

u

7

⊕ u

5

u

6

⊕ u

9

u

10

⊕ u

9

u

11

⊕

u

2

u

4

u

6

⊕ u

2

u

4

u

10

⊕ u

2

u

6

u

9

⊕ u

4

u

9

u

10

⊕ u

6

s

9

u

10

⊕

u

9

u

10

u

11

⊕ u

2

u

4

u

6

u

9

⊕ u

2

u

6

u

9

u

10

⊕ u

4

u

6

u

9

u

10

.

g

12

(u

0

, u

1

, ··· , u

39

) = u

0

⊕u

2

⊕u

3

⊕u

4

⊕u

5

⊕u

6

⊕

u

8

⊕u

11

⊕u

37

⊕u

1

u

11

⊕u

2

u

11

⊕u

3

u

12

⊕u

4

u

6

⊕u

4

u

7

⊕

u

5

u

6

⊕ u

1

u

2

u

11

⊕ u

1

u

2

u

12

⊕ u

1

u

9

u

11

⊕ u

9

u

10

u

11

⊕

u

1

u

2

u

6

u

13

⊕ u

1

u

2

u

9

u

11

⊕ u

1

u

2

u

9

u

12

⊕ u

2

u

9

u

10

u

11

⊕

u

2

u

9

u

10

u

12

⊕ u

1

u

2

u

6

u

9

u

13

⊕ u

2

u

6

u

9

u

10

u

13

.

g

14

(u

0

, u

1

, ··· , u

43

) = u

0

⊕ u

1

⊕ u

5

⊕ u

6

⊕ u

8

⊕

u

35

⊕ u

41

⊕ u

1

u

3

⊕ u

1

u

7

⊕ u

1

u

35

⊕ u

4

u

12

⊕ u

5

u

11

⊕

u

6

u

12

⊕ u

7

u

9

⊕ u

1

u

11

u

38

⊕ u

1

u

4

u

11

u

38

⊕ u

1

u

7

u

11

u

38

⊕

u

1

u

4

u

10

u

11

u

38

⊕ u

1

u

7

u

9

u

11

u

38

⊕ u

1

u

10

u

11

u

12

u

38

.

g

15

(u

0

, u

1

, ··· , u

44

) = u

0

⊕ u

1

⊕ u

6

⊕ u

7

⊕ u

9

⊕

u

10

⊕u

11

⊕u

15

⊕u

16

⊕u

18

⊕u

22

⊕u

26

⊕u

1

u

8

⊕u

6

u

9

⊕

u

16

u

18

⊕u

17

u

19

⊕u

6

u

17

u

19

⊕u

9

u

11

u

12

⊕u

1

u

5

u

16

u

18

⊕

u

10

u

13

u

16

u

19

.

Image Encryption using Improved Keystream Generator of Achterbahn-128

341