
3D Geometric Primitive Alignment Revisited
Trung-Thien Tran, Van-Toan Cao and Denis Laurendeau
Computer Vision and Systems Laboratory, Laval University, 1065, avenue de la Medecine, Quebec, G1V 0A6, Canada
Keywords:
Plane, Cylinder, Sphere, Primitive-based Alignment, Rigid Registration, Coarse Registration.
Abstract:
Rigid registration is an important step in 3D scanning and modeling of manufactured objects that are gener-
ally composed of a combination of basic geometric primitives such as planes, spheres, cylinders, etc. In this
paper, an efficient and robust method is proposed to align two basic geometric primitives. The transformation
between two primitives is found by minimizing the parameter error between primitive correspondences. The
approach applies an interior-point method and a new objective function to achieve good results. Compared
to previous primitive-based alignment approach proposed by Rabbani et al. (Rabbani et al., 2007), the pre-
sented approach achieves better results in terms of convergence and accuracy. Finally, the proposed method is
used in various applications such as data completion and primitive-based registration for quality control and
inspection.
1 INTRODUCTION
3D sensors are being used more and more widely in
several applications, especially in industrial manufac-
turing. Since the field of view of these sensors is
limited, it is necessary to scan an object from dif-
ferent viewpoints in order to cover its complete sur-
face. These local scans are then used in the mod-
eling and reconstruction process. Among common
problems, a registration step is inevitable to transform
all of the scans into a common coordinate reference
frame. Registration is also referred to as alignment
or matching, so these terms are used interchangeably
throughout the paper.
The 3D registration problem can be classified in
several ways. On one hand, according to the rigidity
of the objects, registration is categorized as rigid and
non-rigid as summarized in (Tam et al., 2013). On the
other hand, following the quality of the result, regis-
tration methods can also be classified as coarse regis-
tration (Planitz et al., 2005; D
´
ıez et al., 2015) and fine
registration (Besl and McKay, 1992; Rusinkiewicz
and Levoy, 2001; Salvi et al., 2007). In this paper,
we investigate the problem of coarse registration in
which the parts are aligned roughly with each other.
From now on, the word registration will refer to the
coarse registration problem.
Currently, registration methods often address the
problem of aligning meshes or point clouds having
similar densities of data points. 3D descriptors (D
´
ıez
et al., 2015) are proposed and keypoints (Tombari
et al., 2013) are extracted from 3D data for correspon-
dence and shape matching. However, most existing
descriptors and keypoints fail to register two scans of
man-made objects, because the main challenge is to
propose a descriptor that is able to deal with symmet-
rical and similar geometries from the primitive sur-
faces.
Some research has been conducted to align
datasets using primitives as descriptors. The primi-
tives could be linear and circular features as in (Sta-
mos et al., 2008) or planes in (Bosch
´
e, 2012). Lin-
ear features (Chao and Stamos, 2005) between two
planes and circular features (Stamos et al., 2008)
from 2D and range images of buildings and urban
scenes are used. Bosche’s approach (Bosch
´
e, 2012)
use planes that are extracted at a single point se-
lected by the user. Iterative Closest Point (ICP) is
then used to compute the transformation using three
pairs of plane correspondences. Rabbani et al. (Rab-
bani et al., 2007) have also used geometric primi-
tives such as planes, cylinders and spheres for regis-
tration and modeling. The method minimizes the sum
of squares of the differences of parameters by using
the Levenberg-Marquardt optimization (LM) (Mar-
quardt, 1963). The proposed approach exploits this
idea and brings many improvements in terms of con-
vergence and accuracy.
The contributions of the paper are summarized as
follows.
Tran, T-T., Cao, V-T. and Laurendeau, D.
3D Geometric Primitive Alignment Revisited.
DOI: 10.5220/0005715800890096
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 91-98
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
91

• A robust approach is proposed to align geometric
primitives. Each type of primitive (plane, sphere,
cylinder) is described in detail in Sec. 2.3.
• A new minimization technique is exploited to
achieve better results than other techniques with
respect to convergence and error of descriptive pa-
rameters.
• The proposed method is used in primitive-based
alignment and quality control applications, which
registers two scans to create an error map or com-
plete model of the object of interest.
2 PRIMITIVE ALIGNMENT
2.1 Quaternion Representation
Rigid registration consists of finding a unique trans-
formation T : R
3
7→ R
3
, which brings two datasets as
close as possible. This transformation is expressed
as a 3x3 rotation matrix R and a translation vector
t = {t
x
,t
y
,t
z
}. Horn (Horn, 1987) has proposed a
closed-form solution for determining a rotation ma-
trix using a quaternion representation. With a given
quaternion q = {q
0
,q
1
,q
2
,q
3
}, the rotation matrix R
is computed as
R =
2q
2
0
+ 2q
2
1
− 1 2(q
1
q
2
− q
0
q
3
) 2(q
1
q
3
+ q
0
q
2
)
2(q
1
q
2
+ q
0
q
3
) 2q
2
0
+ 2q
2
2
− 1 2(q
2
q
3
− q
0
q
1
)
2(q
1
q
3
− q
0
q
2
) 2(q
2
q
3
+ q
0
q
1
) 2q
2
0
+ 2q
2
3
− 1
with the constraint kqk =
q
q
2
0
+ q
2
1
+ q
2
2
+ q
2
3
=
1 which guarantees a rotation operator in R
3
having
only three degrees of freedom.
2.2 Rabbani’s Approach and Associated
Drawbacks
Rabbani et al. (Rabbani et al., 2007) have proposed
an approach that combines registration and modeling
in one framework. At the registration step, quater-
nion and geometric primitives are used to align two
scans called S
1
and S
2
, respectively. The transforma-
tion T is calculated using a least-squares algorithm in
the parameter space of the primitives. In other words,
this step minimizes the sum of the square of errors of
primitive parameters as follows:
min
{R(q),t}
|C|
∑
i
M
i
∑
j
∆
2
u
i j
(1)
where ∆
u
i j
= u
S
1
i j
−T(u
S
2
i j
) and u
i j
is the j-th parameter
of the i-th correspondence that has |M
i
| criteria of pa-
rameter convergence. C is the set of correspondences.
For example, when the first correspondence pair is
plane-plane, |M
1
| is equal to 2 since there is a cri-
terion for the error on the normal vector and another
criterion for the error on the distance to the origin.
The mathematical equations for each single primitive
are expressed later in Sec. 2.3.
The Levenberg-Marquardt optimization (Mar-
quardt, 1963) is used to solve the non-linear least-
squares problem in Eq. 1. Partial derivatives of ∆
w.r.t of rotation R and translation t are required and
computed as
n
∂∆
∂q
0
,
∂∆
∂q
1
,
∂∆
∂q
2
,
∂∆
∂q
3
,
∂∆
∂t
x
,
∂∆
∂t
y
,
∂∆
∂t
z
o
These derivatives are used to compute the Jaco-
bian matrix J and update the transformation parame-
ter Γ = {q, t} as follows:
X
Y
Z
݊
(a) Plane represented by normal vector~n
and the distance to the origin ρ.
ݎ
X
Y
Z
ܽ
Ԧ
(b) Cylinder described by axis vector
~a, radius r and a closest point to the ori-
gin in axis p.
X
Y
Z
ݎ
ܿ
(c) Sphere represented by center c and
radius r
Figure 1: Representative parameter of primitives: plane, cylinder and sphere.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
92

Γ = {q, t} = {q
0
,q
1
,q
2
,q
3
,t
x
,t
y
,t
z
} (2)
Γ
t+1
= Γ
t
− (J
T
J + λI)
−1
J∆ (3)
J =
∂∆
∂Γ
; (4)
where t is the iteration step, and J is the Jacobian
matrix. Observing Eq.3, the Levenberg-Marquardt
optimization consists of Gauss-Newton and Steep-
est descent methods by using a non-negative scalar
λ, which is called the Levenberg-Marquardt param-
eter. The selection of λ and its impact on conver-
gence are discussed in (Press et al., 2007). Gen-
erally, Levenberg-Marquardt optimization achieves
better convergence compared to Gauss-Newton and
Steepest descent methods taken separately.
Rabbani’s approach faces many problems that
have an impact on the convergence of the result.
• First, the LM optimization generally provides a
solution to an unconstrained problem. Therefore,
the method does not guarantee that the solution
provides a unit quaternion kqk = 1 for each iter-
ation of the optimization loop. This leads to poor
results for the rotation matrix R. This behavior
has been tested in the experiments reported in Sec.
3. The method proposed in this paper uses an inte-
rior point technique with constraints to guarantee
that condition (kqk = 1) is satisfied.
• Second, the objective function for cylinders lacks
a robust criterion for alignment, which has an ad-
verse effect on convergence. The proposed ap-
proach complements the objective function with
a new criterion that guarantees good convergence
(Eq. 8).
2.3 Proposed Approach for Primitive
Alignment
In this section, the detailed framework for registering
two primitives is presented. These primitives can be
planes, cylinders and spheres. We assume the corre-
spondence pairs C = {S
1
,S
2
} between primitives are
already determined. The transformation T = {R, t} is
computed by minimizing the following cost function.
min
{R(q),t}
|C|
∑
i
M
i
∑
j
∆
2
u
i j
subject to:kqk =
q
q
2
0
+ q
2
1
+ q
2
2
+ q
2
3
= 1
(5)
where the error is defined as ∆
u
i j
= u
S
1
i j
− T(u
S
2
i j
).
To solve the non-linear least-squares problem in
Eq. 5, the interior-point method (Forsgren et al.,
2002) is used. The interior point method guarantees
that the constraint kqk = 1 is always satisfied at each
iteration of the optimization loop. The mathematical
equations for aligning each type of primitive are de-
scribed in the following.
2.3.1 Plane
Planes are geometric primitives frequently found on
manufactured objects. A plane is represented by a
normal vector
~
n and a distance from the closest point
to the origin ρ, as shown in Fig. 1(a). Assume that
there are two planes with parameters {
~
n
1
,ρ
1
} and
{
~
n
2
,ρ
2
}, respectively.
To align plane 2 to plane 1, the error on the normal
vector and the error on the distance to the origin are
minimized as follows:
~
n
δ
=
~
n
1
− R
~
n
2
(6)
ρ
δ
= ρ
2
− ρ
1
+ (R
~
n
2
)
T
t (7)
Eq. 6-7 are fed to Eq. 5 for the minimization step.
2.3.2 Cylinder
A cylinder is described by three parameters: its axis
vector
−→
a , its radius r and a closest point to the origin
on the cylinder axis p, as shown in Fig. 1(b). To bring
a cylinder C
2
= {
−→
a
2
;p
2
;r} as close as possible to a
cylinder C
1
= {
−→
a
1
;p
1
;r}, two points p
1
and p
2
and
two vectors
−→
a
1
and
−→
a
2
need to coincide.
~
a
δ
=
~
a
1
− R
~
a
2
(8)
~
p
δ
= R
~
p
2
+ t − (
~
a
R
∗ t
T
)
~
a
R
−
~
p
1
(9)
where
~
a
R
= R
~
a
2
Eq. 8-9 are fed to Eq. 5 for the minimization step.
2.3.3 Sphere
A sphere is simply represented by its center c and ra-
dius r, as shown in Fig. 1(c). To align a sphere 2
{c
2
,r} to sphere 1 {c
1
,r}, the two centers need to co-
incide (c
δ
= 0).
c
δ
= Rc
2
+ t − c
1
(10)
Eq. 10 is fed to Eq. 5 for the minimization step.
The framework is applied to align a set of sev-
eral multiple primitives simultaneously. The objec-
tive functions of each primitive pair are combined and
minimized in Eq. 5. When the minimization ends, the
transformation between the datasets is available.
3 RESULTS AND DISCUSSION
In this section, the results of the proposed approach
are compared to the ones reported by Rabbani’s in
3D Geometric Primitive Alignment Revisited
93
(Rabbani et al., 2007). Both methods use geomet-
ric primitives for alignment. The sets of primitives
Ψ
1
= {P
1
,C
1
,S
1
} and their parameters are known a
priori. Dataset Ψ
1
is transformed by 100 sets of trans-
formation T randomly generated to create new sets of
primitives Ψ
2
= {P
2
,C
2
,S
2
}. Then four experiments
are conducted.
• Experiment 1: The transformation T
0
needed to
transform plane P
2
to plane P
1
is estimated. The
convergence is evaluated by
cos(∠(T
0
(n
P
2
),n
P
1
)) == 1 (11)
• Experiment 2: The transformation T
0
needed to
align cylinder C
2
to cylinder C
1
is estimated. The
convergence is evaluated by
cos(∠(T
0
(a
C
2
),a
C
1
)) == 1 (12)
• Experiment 3: The transformation T
0
to align a
sphere S
2
to sphere S
1
is also computed. The con-
vergence is then evaluated by
kc
S
1
− T
0
(c
S
2
)k
2
== 0 (13)
• Experiment 4: All types of primitives are com-
bined simultaneously into the framework. The
convergence is reached if Eq. 11-13 are satisfied
simultaneously.
The proposed framework is implemented on
MATLAB on a 3.2 GHz Intel Core i7 platform.
In the implementation of primitive alignment, Rab-
bani et al. (Rabbani et al., 2007) use Levenberg-
Maquardt non-linear optimization which is imple-
mented in the lsqnonlin function in MATLAB. The
proposed framework rather uses the fmincon function
which is implemented for the interior-point method.
The percentage of success and the error on the pa-
rameters are investigated for both methods.
3.1 Success Rate of the Proposed
Method
With 100 randomly generated sets of transformations,
four alignment experiments are carried out and the
conditions in Eq. 11-13 are checked sequentially or
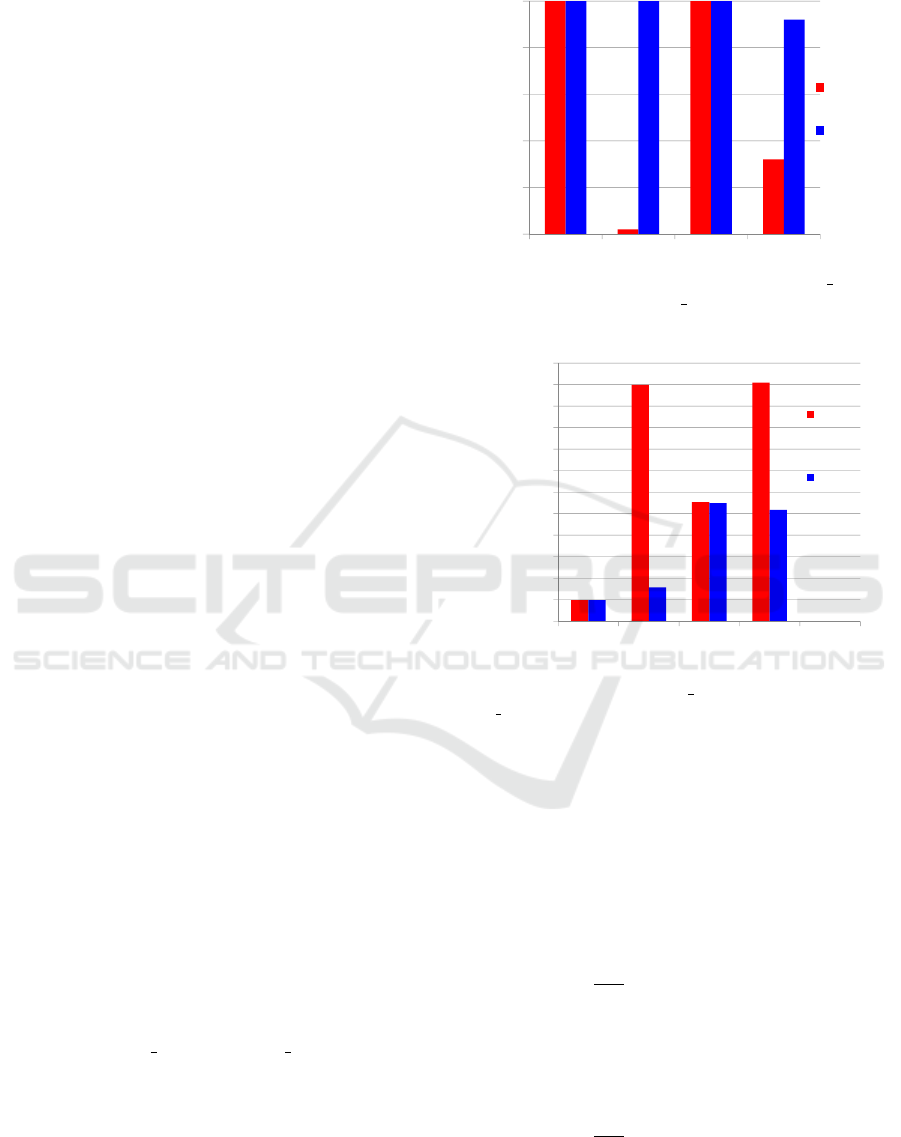
simultaneously. Fig. 2 illustrates the success rate of
both methods LM Rabbani and IP OUR in the four
experiments.
Rabbani’s method is able to align planar and
sphere primitives, but fails with cylinder primitives,
as shown in Fig. 2. Therefore, in general, Rabbani’s
method cannot align a set of multiple primitives. The
approach proposed in this paper achieves high success
rates for all cases (> 90%).
0
20
40
60
80
100
Plane Cylinder Sphere Primitives
LM_Rabbani
IP_OUR
Success Rate
Figure 2: Success rate for Rabbani’s method (LM Rabbani)
and the proposed method (IP OUR).
1.00E-11
1.00E-10
1.00E-09
1.00E-08
1.00E-07
1.00E-06
1.00E-05
1.00E-04
1.00E-03
1.00E-02
1.00E-01
1.00E+00
1.00E+01
Plane Cylinder Sphere Primitives
LM_Rabbani
IP_OUR
Mean Absolute Error
Figure 3: Logarithmic graph of mean absolute errors
for Rabbani’s method (LM Rabbani) and our method
(IP OUR).
3.2 Errors on Primitive Parameters
The mean absolute error (MAE) values in Eq. 11-
13 are computed for each of the 100 random sets of
transformation.
• Experiment 1: The error on the plane normal after
transformation is computed as follows:
MAE
P
=
1
100
100
∑
i=1
1 − |cos(∠(T
i
0
(n
P
2
),n
P
1
))|
(14)
• Experiment 2: The error on axis directions of the
cylinders after transformation is computed as:
MAE
C
=
1
100
100
∑
i=1
1 − |cos(∠(T
i
0
(a
C
2
),a
C
1
))|
(15)
• Experiment 3: The error of the sphere centers af-
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
94

(a) CAD model designed
with 3DS Max.
(b) The plastic object
printed with a Stratasys
Dimension 1200es printer.
(c) A partial scan of the plas-
tic model scanned with the
GO!SCAN 3D sensor.
(d) Complete scan of the
plastic model.
Figure 4: The plastic object is printed and scanned to create partial and complete scan datasets.
ter transformation is computed:
MAE
S
=
1
100
100
∑
i=1
kc
S
1
− T
i
0
(c
S
2
)k
2
(16)
• Experiment 4: The error on combined primitives
taken altogether is computed as:
MAE
∑
= MAE
P
+ MAE
C
+ MAE
S
(17)
A logarithm plot of the MAE for the four exper-
iments is shown in Fig. 3. The proposed method
clearly outperforms Rabbani’s method in aligning
primitives.
From the results of the experiments, it is con-
cluded that the proposed method, which combines a
new optimization technique and a new objective func-
tion, solves the problem of primitive-based alignment
with better results with respect to convergence and er-
ror of descriptive parameters.
One more experiment has been conducted to show
the performance of the proposed method. The esti-
mated transformation T
0
in the 4th experiment is com-
pared to the ground-truth transformation T as follows:
• The error of rotation matrix is defined as:
E
R
=
1
100
100
∑
i=1
kR − R
0
k
2
= 6.85e
−7
(18)
• Translation vector is commutative, so the error of
translation is computed by:
E
t
=
1
100
100
∑
i=1
ktk − kt
0
k
= 2.68e
−6
(19)
The values of E
R
and E
t
prove that the proposed
method estimates the transformation between datasets
accurately.
3.3 Application of the Proposed
Approach on Real 3D Scans
The first application is to register the scanned data of
a printed 3D object with its CAD model. The object
is printed with a Stratasys Dimension 1200es printer
(Fig. 4(b)) and scanned by the Creaform GO!SCAN
3D scanner. Markers are used by the scanner for self
positioning. This part-to-CAD problem is frequently
used in quality control and inspection applications.
The proposed framework for primitive alignment is
applied as follows in this case. First, primitives from
the point cloud are extracted using the method in
(Tran et al., 2015b), and primitives from the CAD
model are extracted by the approached proposed in
(Attene et al., 2006). The correspondence pairs of
primitives are defined manually. After being aligned,
the distances between points and the CAD model are
computed to generate an error map, as shown in Fig.
5. In this experiment, the scanned object’s pose is
close to the one of the CAD model.
Observing the results in Fig. 5, it is observed
that our method outperforms Rabbani’s approach in
terms of alignment errors (Fig. 5(b)-5(c)). On the his-
tograms of the error maps, the error of our method is
smaller than the one of Rabbani’s approach. The rea-
son is that Rabbani’s approach does not guarantee the
condition (kqk = 1) when LM optimization updates
the parameters in the minimization process. More-
over, the lack of objective function for cylinders has
a significant influence on convergence. The proposed
method solves these two problems and achieves better
alignment result.
A more challenging experiment has been con-
ducted in which the pose of the scanned object is in
the opposite direction of the one of the CAD model
(Fig 6). Rabbani’s method fails to align the datasets
while the proposed method achieves a good alignment
result with an error map similar to the one in Fig 5(c).
The second application of the proposed approach
is data completion. The complete model of an object
is often built from multiple partial scans. Separate
scans are needed and must be expressed in a common
coordinate frame using registration. In this section,
the proposed method is used to register two real scans.
In Fig. 7, two scans of the object in Fig. 7(a) are
3D Geometric Primitive Alignment Revisited
95
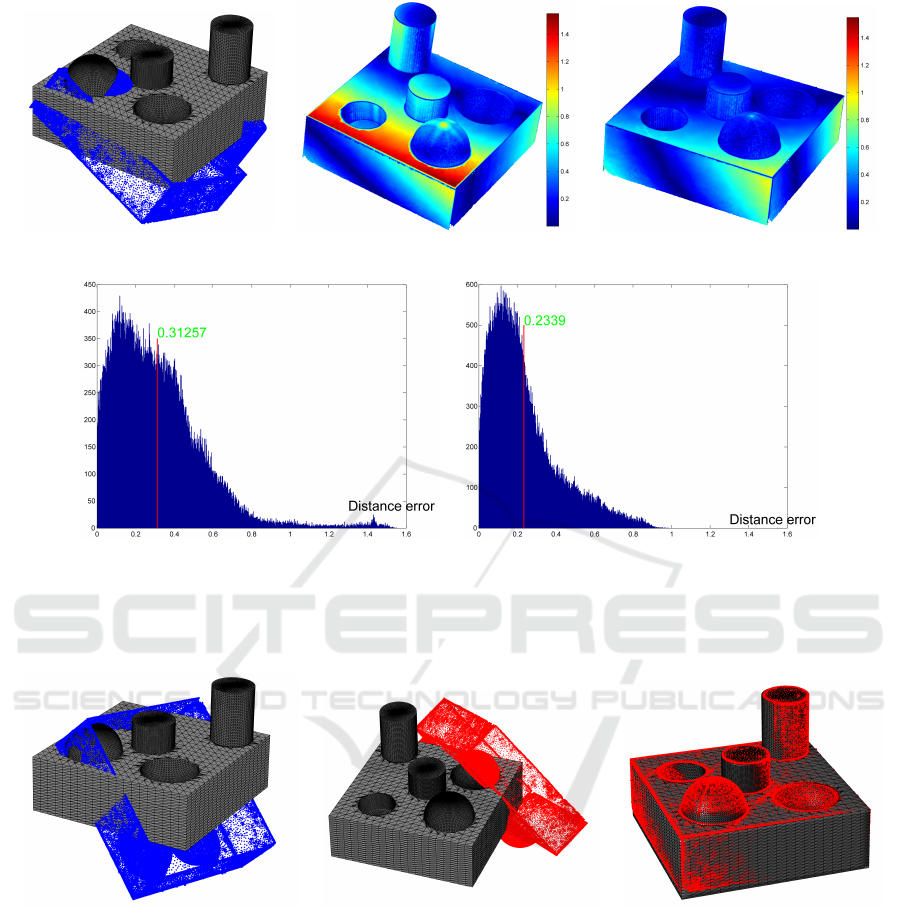
(a) Scanned data and CAD model. (b) Error map of the result for Rabbani’s
approach.
(c) Error map of the result for the pro-
posed approach.
(d) Histogram of the error map created from Rab-
bani’s approach, largest value (1.55) mean error
value (0.31).
(e) Histogram of the error map generated from our
proposed method, largest value (0.98) and mean er-
ror value (0.23).
Figure 5: Alignment of scanned data with its CAD model. Error maps of both methods are created and analyzed. The distance
error of our method is smaller than the one of Rabbani’s approach.
(a) (b) (c)
Figure 6: Comparison between two methods in the case where the pose of the scanned object is in the opposite direction of
that of the CAD model. (a) Datasets with opposite pose between the scan and its CAD model. (b) Rabbani’s method fails to
align the datasets. (c) Good alignment result is still achieved by the proposed method.
shown. First, planar, cylindrical and spherical prim-
itives are extracted from the scans using the method
reported in (Tran et al., 2015a; Tran et al., 2016; Tran
et al., 2015b). These primitives are then fed to the
alignment approach presented in Sec. 2.3 to build a
complete model of the object. The resulting model is
shown in Fig. 7(b). The same strategy is used for the
planes on two point clouds of the church in Fig. 7(c)
with the resulting model in Fig. 7(d) after alignment
using planar primitives.
Although primitive correspondences are selected
manually by the user, this operation is not difficult
even for a novice. In addition, this operation is easier
than choosing the points used in manual ICP (Besl
and McKay, 1992) and the other approach proposed
in Bosche et al. (Bosch
´
e, 2012).
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
96

(a) Two partial scans of the plastic model. (b) Complete model created using the extracted primitives
for alignment.
(c) Two partial point clouds of the church in the town of
LansleVillard (France). The church is scanned with a LE-
ICA Cyrax scanner.
(d) The church model is built by aligning the extracted
planes from partial data.
Figure 7: Complete models are created from partial data using the proposed method of primitive alignment.
4 CONCLUSION
An efficient and robust method for registering two
basic primitives is proposed in this paper. Using a
new optimization technique and with the addition of
a complementary objective function, the convergence
is guaranteed to achieve accurate results. The pro-
posed method can benefit other applications such as
scan alignment, quality control and inspection.
Currently, the framework of primitive-based regis-
tration manually assigns the correspondence pairs of
primitives between datasets. An automatic detection
of the correspondence between primitives will be the
object of future work.
ACKNOWLEDGEMENT
This research project was supported by the
NSERC/Creaform Industrial Research Chair on
3-D Scanning. The authors thank to AIM@SHAPE
for providing the scanned data of the church in Fig.
7. We are grateful to Annette Schwerdtfeger for
proofreading the manuscript.
REFERENCES
Attene, M., Falcidieno, B., and Spagnuolo, M. (2006). Hi-
erarchical mesh segmentation based on fitting primi-
tives. The Visual Computer, 22(3):181–193.
3D Geometric Primitive Alignment Revisited
97

Besl, P. and McKay, N. D. (1992). A method for registration
of 3-D shapes. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 14(2):239–256.
Bosch
´
e, F. (2012). Plane-based registration of construction
laser scans with 3D/4D building models. Advanced
Engineering Informatics, 26(1):90–102.
Chao, C. and Stamos, I. (2005). Semi-automatic range to
range registration: a feature-based method. In Pro-
ceedings of the Fifth International Conference on 3-D
Digital Imaging and Modeling, pages 254–261. IEEE.
D
´
ıez, Y., Roure, F., Llad
´
o, X., and Salvi, J. (2015). A quali-
tative review on 3D coarse registration methods. ACM
Computing Surveys, 47(3):45.
Forsgren, A., Gill, P. E., and Wright, M. H. (2002). Inte-
rior methods for nonlinear optimization. SIAM review,
44(4):525–597.
Horn, B. K. (1987). Closed-form solution of absolute orien-
tation using unit quaternions. Journal of the Optical
Society of America A, 4(4):629–642.
Marquardt, D. W. (1963). An algorithm for least-squares es-
timation of nonlinear parameters. Journal of the Soci-
ety for Industrial & Applied Mathematics, 11(2):431–
441.
Planitz, B. M., Maeder, A. J., and Williams, J. (2005). The
correspondence framework for 3D surface matching
algorithms. Computer Vision and Image Understand-
ing, 97(3):347–383.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-
nery, B. P. (2007). Numerical Recipes 3rd Edition:
The Art of Scientific Computing. Cambridge Univer-
sity Press, New York, NY, USA, 3 edition.
Rabbani, T., Dijkman, S., van den Heuvel, F., and Vossel-
man, G. (2007). An integrated approach for mod-
elling and global registration of point clouds. {ISPRS}
Journal of Photogrammetry and Remote Sensing,
61(6):355 – 370.
Rusinkiewicz, S. and Levoy, M. (2001). Efficient variants
of the ICP algorithm. In Proceedings Third Interna-
tional Conference on 3-D Digital Imaging and Mod-
eling, pages 145–152. IEEE.
Salvi, J., Matabosch, C., Fofi, D., and Forest, J. (2007).
A review of recent range image registration methods
with accuracy evaluation. Image and Vision Comput-
ing, 25(5):578–596.
Stamos, I., Liu, L., Chen, C., Wolberg, G., Yu, G., and
Zokai, S. (2008). Integrating automated range regis-
tration with multiview geometry for the photorealistic
modeling of large-scale scenes. International Journal
of Computer Vision, 78(2-3):237–260.
Tam, G. K., Cheng, Z.-Q., Lai, Y.-K., Langbein, F. C.,
Liu, Y., Marshall, D., Martin, R. R., Sun, X.-F., and
Rosin, P. L. (2013). Registration of 3D point clouds
and meshes: a survey from rigid to nonrigid. IEEE
Transactions on Visualization and Computer Graph-
ics, 19(7):1199–1217.
Tombari, F., Salti, S., and Di Stefano, L. (2013). Perfor-
mance evaluation of 3D keypoint detectors. Interna-
tional Journal of Computer Vision, 102(1-3):198–220.
Tran, T.-T., Cao, V.-T., and Laurendeau, D. (2015a). Extrac-
tion of cylinders and estimation of their parameters
from point clouds. Computers & Graphics, 46:345 –
357.
Tran, T.-T., Cao, V.-T., and Laurendeau, D. (2015b). Ex-
traction of reliable primitives from unorganized point
clouds. 3D Research, 6(4).
Tran, T.-T., Cao, V.-T., and Laurendeau, D. (2016). esphere:
extracting spheres from unorganized point clouds. The
Visual Computer, pages 1–18.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
98
