Multiple People Tracking in Smart Camera Networks by Greedy

Joint-Likelihood Maximization

Nyan Bo Bo, Francis Deboeverie, Peter Veelaert and Wilfried Philips

Ghent University/iMinds, TELIN, Image Processing and Interpretation

Sint-Pietersnieuwstraat 41, Ghent 9000, Belgium

Keywords:

Multi-camera Tracking, Decentralized System, Joint-likelihood Maximization.

Abstract:

This paper presents a new method to track multiple people reliably using a network of calibrated smart cam-

eras. The task of tracking multiple persons is very difﬁcult due to non-rigid nature of the human body, oc-

clusions and environmental changes. Our proposed method recursively updates the positions of all persons

based on the observed foreground images from all smart cameras and the previously known location of each

person. The performance of our proposed method is evaluated on indoor video sequences containing person–

person/object–person occlusions and sudden illumination changes. The results show that our method performs

well with Multiple Object Tracking Accuracy as high as 100% and Multiple Object Tracking Precision as high

as 86%. Performance comparison to a state of the art tracking system shows that our method outperforms.

1 INTRODUCTION

Nowadays, many computer vision-based applica-

tions, such as automatic surveillance, smart meeting

rooms/homes and human behavior/activity analysis,

require robust tracking of multiple people in indoor

or outdoor environment. However, the task of reliably

tacking multiple non-rigid targets such as humans is

in fact very challenging because the appearance of a

person easily changes by body movement, pose and

orientation changes with respect to the camera view.

Moreover, the appearance of the target may also be al-

tered by changes in the environment, such as lighting,

which makes the tracking even more difﬁcult.

Since multiple people may be moving about in the

scene, a person can be fully/partially occluded by an-

other person(s) or other object(s) in the scene. This

occlusion problem makes the tracking task even more

challenging and is very difﬁcult to address in single

camera methods. Over the past ﬁfteen years, many

trackers for camera networks with overlapping views

have been introduced. These trackers use informa-

tion from different view points to handle the occlusion

problem. Additionally, joint estimation of a person’s

position from multiple views is usually more precise

than estimation from a single view point.

In this paper, we propose a new method to track

multiple people in real time using a network of smart

cameras. Our proposed method follows a decen-

tralized architecture, i.e., all image processing tasks

can be executed on smart cameras and only num-

bers are exchanged between nodes rather than im-

ages/frames.

Our tracker recursively estimates the

current positions of all persons by maximizing the

likelihood of the current observations of all cameras.

The estimate is recursive because the aforementioned

likelihood is determined by the previous positions.

In our method, the observations are binary images

obtained by foreground/background estimation on all

camera views. Moreover in our method these images

remain in private memory within each smart camera

and are never transmitted; this is one of the contribu-

tions of our method. In practice, observations clearly

depend on the positions of all persons in the scene.

Therefore in this paper observations are not tied to in-

dividual persons, but to camera views. Since the like-

lihood maximization takes into account the positions

of all persons, our tracker does not need to perform an

explicit occlusion detection and handling.

Another contribution of this paper is the real-time

maximization of the likelihood of an observations

from all cameras, given the positions of all persons,

using a greedy search. The search space is deﬁned

by the known positions of all persons at previous time

instance and the physical limitation that a person can-

not move very far between two consecutive frames.

In this paper, the smart cameras are simulated on a

computer.

604

Bo, N., Deboeverie, F., Veelaert, P. and Philips, W.

Multiple People Tracking in Smart Camera Networks by Greedy Joint-Likelihood Maximization.

DOI: 10.5220/0005716206020609

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 604-611

ISBN: 978-989-758-175-5

These known positions at earlier time instance comes

from a person detector or from the previous estima-

tions of the tracker itself. We use the integral image in

the algorithm’s implementation to achieve high com-

putational efﬁciency.

We evaluate our method on three multi-camera

video sequences, each of which contains different

scenarios such as people having meeting, walking a

round under steady and varying lighting, captured

in an indoor meeting room environment. The re-

sults conﬁrm that our method achieves high accuracy

and precision on video sequences containing frequent

person–person and object–person occlusions. The

performance comparison to a publicly available state

of the art tracker shows that our method outperforms.

2 RELATED WORK

Over the last decade, many techniques have been pro-

posed for robust tracking of multiple people using a

single-camera as well as networks of cameras. Many

trackers (Yang et al., 2009), (Henriques et al., 2011),

(Yun et al., 2012) (single-camera trackers) (Bredereck

et al., 2012), (Gruenwedel et al., 2014), (Bo Bo et al.,

2014) (multi-camera trackers) recursively update the

position of each person based on priors from previ-

ous frames and the observations in the current frame,

such as appearance models based on color/texture,

foreground blobs, person detector responses, and so

on. These trackers are usually relying on extracting

observations of individual persons from all the input

images. Most of these methods then process the “per-

son observations” independently, e.g. feeding them to

a recursive state estimator (Kalman ﬁlter, Particle ﬁl-

ter, . . . ) for that person. As such, persons are tracked

independently after their observations have been sep-

arated.

Some trackers (Zhang et al., 2008), (Bredereck

et al., 2012), (Andriyenko and Schindler, 2010)

(Berclaz et al., 2011) adopt a tracking-by-detection

strategy, i.e., people are ﬁrstly detected in multiple

video frames and then detections are linked across

time. These systems usually need input of the en-

tire video or a batch of frames. Additionally, to our

knowledge the computation of occupancy maps or

detection of humans takes a relatively large potion

of allowed computation time for real-time tracking.

These factors limit the feasibility for real-time track-

ing. However, these methods have the advantage of

having information from future video frames, while

estimating the person’s positions. Therefore, by ex-

ploiting information from future video frames, these

methods can potentially perform better in terms of ac-

curacy.

Recently, several methods (Andriyenko and

Schindler, 2011), (Milan et al., 2013) have been intro-

duced to improve the trajectories produced by base-

line trackers (Wojek et al., 2010), (Pirsiavash et al.,

2011). The approach of Andriyenko et al. (An-

driyenko and Schindler, 2011) formulates an energy

function from human detector’s detections, object dy-

namics, collision avoidance and object persistence

together with a regularization term for each trajec-

tory produced by a baseline tracker. Then the energy

is minimized by growing/shrinking, splitting/merging

or adding/removing the trajectories. The work of Mi-

lan et al. follows a similar approach but using a dif-

ferent energy formulation and optimization. The re-

ported optimization time for these approaches is 1 to

2 second per frames excluding the time for generat-

ing baseline trajectories and person detections. There-

fore, they are not feasible for real-time applications.

3 PROPOSED TRACKER

Our tracking system uses a decentralized architec-

ture, i.e., the computational load is distributed over

C calibrated cameras and a greedy likelihood maxi-

mization node. Each smart camera captures and pro-

cesses its video on board. Thus, only meta-data, such

as positions and likelihoods, are exchanged between

nodes rather than images. This reduces network band-

width requirements, thus increasing scalability, i.e.,

additional smart cameras may be added to the system

without concerning too much about the communica-

tion bottleneck. Fig. 1 shows the building blocks of

the proposed tracker and the data exchange between

nodes.

One analysis cycle of processing a single video

frame from all cameras is as follows. At time t, each

smart camera c captures image and computes a fore-

ground image from it. In our tracker, we use the same

texture-based foreground detection method as in our

previous work (Bo Bo et al., 2015). The likelihood

maximizer node then requests the likelihood of ob-

serving foreground image in each camera view given

the hypothesized positions of all persons. All smart

cameras compute the requested likelihood and send

back to the likelihood maximizer. This likelihood re-

quest and response process is repeated until the like-

lihood maximizer ﬁnds the positions of all persons

which give the highest likelihood. Finally, the like-

lihood maximizer then outputs the jointly estimated

positions of all persons and begins a new cycle to esti-

mate the positions of all persons at next time instance

t + 1. The following subsections describe the details

Multiple People Tracking in Smart Camera Networks by Greedy Joint-Likelihood Maximization

605

of each component of our tracker.

3.1 The Proposed Likelihood Model

We extend the single camera likelihood model that we

have previously proposed in (Bo Bo et al., 2015) to a

multi-camera likelihood model. We model a person

m at position s

as a ﬁxed size cuboid placed at s

Thus, the observation model of a person m at s

from

a smart camera c is in fact the projection of the cuboid

at s

. A more accurate model would be to represent

persons by detailed 3D shapes, better approximating

to the shape of the human body. However, projecting

a cuboid on the image plane is computationally more

efﬁcient than projecting more complex 3D shapes and

allows speedups using integral images. Also, com-

plex 3D shapes with more parameters, require these

parameters to be optimized as part of tracking. Fi-

nally, the foreground observations are imperfect any-

way and the there is little beneﬁt in employing an

“perfect model.” For this reason, we also further ap-

proximate the projected cuboid by its bounding box

Consider a particular smart camera c, we have

a foreground image F

t,c

as an observation at time t.

Given the positions of M persons s

,. ..s

, we would

like to compute the likelihood

t,c

,. ..s

) = l

,. ..s

). (1)

of the observed image F

t,c

. Since there are M per-

sons in the scene, there will be M rectangles on the

image plane, some of which may be intersecting each

other. For simplicity, let S

= [s

,. ..s

] be the ma-

trix whose columns are the M person positions and

let Ω

)

m=1

) be the union of all rectan-

gles in the image. Ideally, when S

is equal to the true

positions of all M persons, Ω

) must contain all

foreground pixels, and all background pixels must be

outside of Ω

). However, this ideal situation can

never be reached since the cuboid model is far from

the actual 3D shape of the human body. Moreover, a

true foreground pixel can accidentally be detected as a

background pixel and vice versa due to noise. There-

fore, we formulate a likelihood function based on a

noisy binary channel model.

Let us denote the probability that a true fore-

ground pixel is wrongly detected as background as

and the probability that a true background pixel

is wrongly detected as foreground as ε

. Obviously,

the values of ε

and ε

highly depend on the perfor-

mance of the foreground detection method. Here, we

make an assumption that conditioned on S

, all pixels

of F

t,c

are statistically independent. Then the condi-

tional probability p

) becomes a binomial dis-

tribution and the likelihood l

of M person(s) at S

given the observation F

t,c

from a smart camera c can

be computed as:

) =

∏

r∈Ω

)

(1 − ε

)

t,c

(r)

1−F

t,c

(r)

∏

r/∈Ω

)

(1 − ε

)

1−F

t,c

(r)

t,c

(r)

(2)

The ﬁrst factor of Eq. (2) evaluates how well the

pixels inside Ω

) agree with the hypothesis that

is correct, while the second factor evaluates how

well the pixels outside of Ω

) agree with the same

hypothesis. In many heuristic methods for “template

matching” in literature, the second factor is not taken

into account, but it is required according to the pro-

posed likelihood model and plays an important role.

To simplify the computation, taking the logarithm of

Eq. (2) gives

) =k + λ|Ω

)| + λ

∑

r∈Ω

)

t,c

(r)

+ λ

∑

r/∈Ω

)

(1 − F

t,c

(r)),

(3)

where |R| is the area of an image region R, λ



1−ε



, λ

= ln



1−ε



, λ

= ln





, and k

|ln(ε

) is a constant independent of S

The interpretation of Eq. (3) is simplest when

= ε

, i.e., the chance of a true foreground pixel

accidentally detected as background and the change

of a true background pixel accidentally detected as

foreground are equally likely. This simpliﬁcation is

reasonable in practice since parameters of foreground

detection can be tuned to meet this condition. Thus

λ = 0 and Eq. (4) becomes

) =k + λ

∑

r∈Ω

)

t,c

(r)

+ λ

∑

r/∈Ω

)

(1 − F

t,c

(r)).

(4)

This shows that log-likelihood increases when more

foreground pixels are in Ω(S

) and fewer foreground

pixels are outside of Ω(S

To compute the likelihood of jointly observ-

ing F

t,1

t,2

,. ..F

t,C

in camera 1,2,...C respectively,

given the positions of all persons S

, we assume that

the observations F

t,c

of different cameras are statisti-

cally independent, when conditioned on S

. the joint

likelihood l of all camera observations is then

p(F

t,1

t,2

,. ..F

t,C

) =

∏

c=1

)

(5)

and

ll(S

) =

∑

c=1

). (6)

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

606

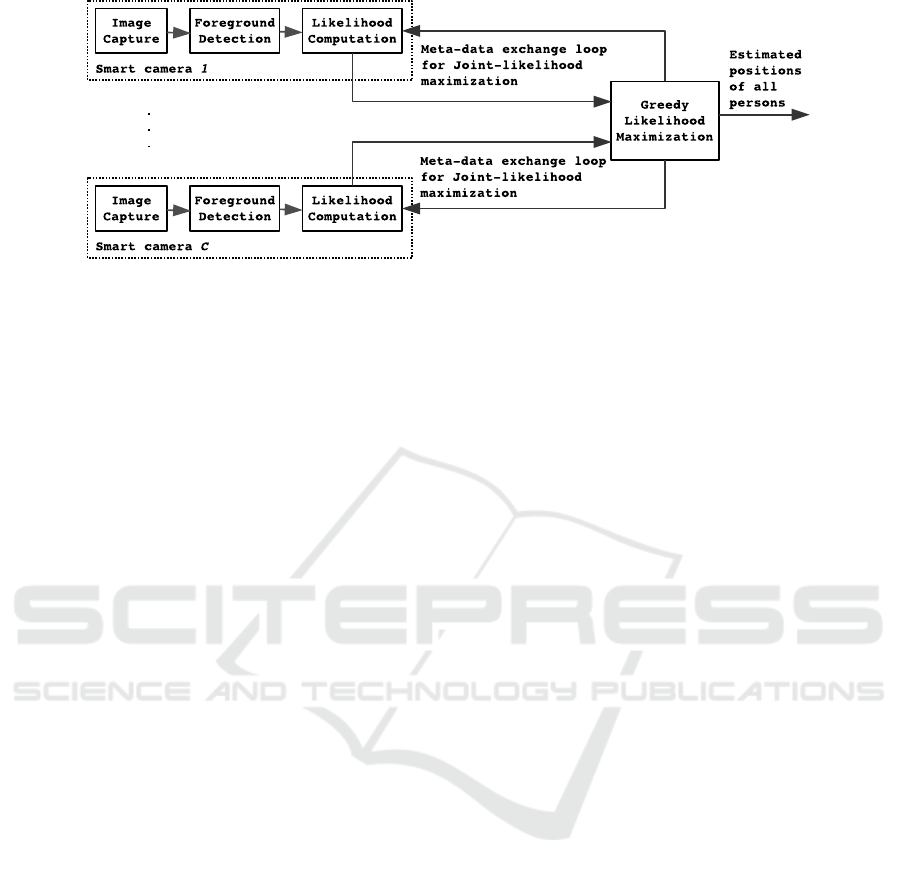
Figure 1: Block diagram showing the essential components and information ﬂow of proposed decentralized multi-camera

tracker.

3.2 Real-time Likelihood Maximization

Our tracker maximizes the product of the likeli-

hood p(F

t,1

t,2

,. ..F

t,C

) and the motion model

p(S

t−1

). The motion model expresses the probabil-

ity of persons moving from one position to the another

over the course of one time unit. We assume that all

persons move independently of each other. This as-

sumption is reasonable when people are far apart, but

not when they get closer together. In the latter case,

our assumption e.g., allows that people move to ex-

actly the same position, which is physically impossi-

ble. However, this assumption makes the likelihood

computation computationally tractable and some of

the possible inconsistencies can be detected and cor-

rected using post-processing.

Because of the assumption, the motion model be-

comes:

p(S

t−1

) = p(s

t−1

),. .. p(s

t−1

(7)

Due to physical limitation, a person can move up to

a particular distance limit d

max

over the course of one

time unit. For our tracker, we assume that all motion

within a distance less than d

max

is equally likely, i.e.,

we adopt a uniform motion model. We believe that

this model is more robust to sudden motion changes

than more traditional Gaussian models. The latter fa-

vors slow motion over fast motion, but the uniform

model allows sudden motion changes. In the motion

model, we also do not take into account people’s ve-

locities and motion directions at time t − 1, as would

be done in popular Kalman models. Many Kalman

models in literature employ unrealistic assumptions,

i.e., they favor continuous or even constant velocity or

acceleration, which increases the probability of track-

ing loss. On the other hand, modeling discontinu-

ous motion is quite difﬁcult. Therefore, we prefer the

“non-informative” uniform motion model.

A brute force search for S

= {s

,..., s

} that gives

the highest likelihood ll(S

) in a discretized search

space is a very time consuming task because it re-

quires the computation of likelihood using Eq. (6) for

all possible combinations of discretized people’s posi-

tions on the ground plane. Fortunately, because of the

constrained uniform motion model, the search space

is already greatly reduced: each person position can

only be in a circular region with radius d

max

around

the last known position of each person. Even in this

constrained search space, the computation time for

brute force likelihood maximization increases expo-

nentially with the number of persons M and with the

discretization accuracy.

However, by using the greedy likelihood maxi-

mization as shown in the pseudo code in Algorithm

1, we can make the computation time increases lin-

early with the number of persons M. The inputs of

the algorithm are the positions of all persons at time

t −1 sorted in descending order of

∑

c=1

Ω

t−1

), i.e.,

the sum of the area of projected cuboids in all views

for a person at position s

t−1

. The reason behind this

sorting is that a larger projected cuboid contributes

more in likelihood computation. Thus it is desirable

to start the greedy maximization from a person’s posi-

tion which contributes the most to the joint likelihood

computation.

In Algorithm 1, we initialize S

with all previously

known positions in S

t−1

. Then, each position in S

optimized one at a time. The following steps are re-

peated until all positions in S

are updated. At each

iteration, a previously known location at the m

col-

umn is selected as s

t−1

. We deﬁne H as a set of all

discretized positions that fall within the circle with ra-

dius d

max

, which center is at s

t−1

. Then, an exhaustive

search is performed for each position in H as s

which gives the highest likelihood while keeping the

positions of the remaining person(s) ﬁxed. The pre-

viously known position at the m

column in S

is re-

placed by s

. The iteration in Algorithm 1 can be

repeated until a stable solution is reached. However,

we experimentally found that terminating the iteration

when all the positions in S

are updated gives the op-

Multiple People Tracking in Smart Camera Networks by Greedy Joint-Likelihood Maximization

607

Algorithm 1: Greedy likelihood maximization.

1: Initialize S

= [s

,. ..s

] with [s

t−1

,. ..s

t−1

]

2: for m = 1 to M step 1 do

3: s

= the m

column of S

4: H

= the set of points s with ks − s

k ≤

max

= max

s∈H

ll([s

,. ..s

,s, s

m+1

,. ..s

])

6: Update S

by replacing its m

column by

7: end for

timal trade-off between the accuracy and the compu-

tational time.

3.3 Decentralized Processing

This subsection describes how decentralized process-

ing is done in Algorithm 1 as well as the meta-data

exchanges between nodes. At each iteration of the

loop in the algorithm, all smart cameras compute

([s

,. ..s

,s, s

m+1

,. ..s

]) : ∀s ∈ H

using Eq. 4 lo-

cally and send computed likelihoods (a set of num-

bers) to the likelihood maximizer. This meta-data

exchange is the most signiﬁcant amount of data ex-

change between smart cameras and the likelihood

maximizer. The numbers of likelihoods to be sent

depends on the grid size of the discretized ground

plane and d

max

. The detailed analysis on commu-

nication bandwidth between nodes will be discussed

in Section 5. Once required likelihoods are received

from all cameras, the likelihood maximizer computes

ll([s

,. ..s

,s, s

m+1

,. ..s

]) using Eq. 6 and proceeds

to the remaining steps in the algorithm.

4 EVALUATION

4.1 Test Videos

To evaluate the performance of our tracker, we use

video sequences captured in a room of 8.8×9.2 m

Each sequence has a total duration of approximately

six minutes and is captured using four calibrated cam-

eras with overlapping views. There are a table and

chairs at the center of the meeting room. All videos

are captured at 20 fps with a resolution of 780×580

pixels. Up to four people are walking in the scene

and they are often occluded by other persons or furni-

ture. During the video capturing of the last sequences,

lights are switched on and off a couple of times to cre-

ate a scenario of rapid illumination changes. Ground

plane positions for each person are manually anno-

tated every 20 frames.

Walking Sequence: The purpose of this sequence

is to measure the performance of the tracker when

people are just walking around in the scene. In this

sequence, four people come into the meeting room

one after another, greet each other, walk around in the

room and ﬁnally leave the room. Most of the existing

publicly available datasets focus on tracking people

over a short period of time. For example, tracking a

person passing through the scene which may last for

a minute or two. In contrast, the same people walk

around in the room for about ﬁve minutes in this se-

quence.

Meeting Sequence: The majority of publicly

available dataset for people tracking are made in a

scenario in which people are moving around in the

scene. We are interested in evaluating our tracker in

a scenario in which people walk, sit down and walk

again. Thus, we capture this video sequence in a

meeting room scenario. In this video, four people

come into the room, greet each other and sit around

the table. During the meeting, a person sometimes

leave the chair to give a presentation.

Unsteady Lighting Sequence: To evaluate the

performance of our tracker when there are rapid il-

lumination changes, we capture the video sequence

of people walking while the illumination of the scene

is deliberately changed suddenly several times. The

scenario of this sequence is the same as Walking se-

quence except for the lighting in the room which is de-

liberately reduced to half and then completely turned

off several times. Note that although the lights are

switched off in the room, there is still dimmed light

coming from outside of the room.

4.2 Evaluation and Comparison

The performance of our tracker is evaluated on three

aforementioned video sequences. The same set of pa-

rameters is used for processing all sequences. We

experimentally select the parameters, i.e., brute force

search for a parameters combination, which gives the

optimal performance on all video sequences. The pa-

rameters of foreground extraction are set as follows:

the sliding window size k = 9, the correlation coefﬁ-

cient threshold ρ

min

= 0.98. For likelihood maximiza-

tion, the ground plane is discretized with 10 cm × 10

cm grid. The other parameters are set ε

= ε

= 0.001

and the maximum distance that a person can move be-

tween two consecutive frames d

max

= 50 cm. Using

aforementioned ground truth, we compute the most

widely used systematic evaluation metrics (Bernardin

and Stiefelhagen, 2008); the Multiple Object Track-

ing Accuracy (MOTA) and the Multiple Object Track-

ing Precision (MOTP) of the resulting trajectories.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

608

We use the same hit/miss threshold 100 cm as in

(Bredereck et al., 2012), (Andriyenko and Schindler,

2011), (Milan et al., 2013). For both metrics, higher

value indicates better performance.

Moreover, we compare the performance of our

tracker to the publicly available state of the art tracker

of Berclaz et al. (Berclaz et al., 2011) in terms of

both MOTA and MOTP. Their approach computes the

Probabilistic Occupancy Map (POM) on the ground

plane using the results of foreground detection from

all camera views. Their POM computation only con-

siders information from the current frames of all cam-

eras, but not the positions estimated in the previous

frame. However, in the data association step, K-

Shortest Path (KSP) optimization is used to ﬁnd the

optimal trajectory of a person by enforcing tempo-

ral continuity constraints over POMs computed from

both past and future frames. In this paper, we will

refer to their tracker as POM-KSP.

For fair comparison, we use the same foreground

detection method as well as the same set of param-

eters for the POM-KSP tracker. As in our tracker,

we also set 10 cm ×10 cm grids for the POM-KSP

tracker. Since we set d

max

= 50 cm for our tracker, we

also set maximum distance traveled between consec-

utive frames for POM-KSP to be 5 grid locations.

5 RESULTS AND DISCUSSION

Our tracker achieves a MOTA value of 100% for

Walking sequence with a MOTP value as high as

86%. In the Meeting sequence, the MOTA value

drops slightly to 98% with MOTP of 77%, which is

still showing quite good performance for such chal-

lenging sequence. Performance comparison to pub-

licly available state of the art tracker shows that our

tracker outperforms.

In our tracker, we just approximate the volumet-

ric model of an upright standing human as a cuboid

with ﬁxed width and height. The model ﬁts well to

the observation as long as a person is standing. How-

ever, when a person sits down, the height of a person

is just a bit over an half of the standing height and

the actual observed foreground shape is far from the

shape of the projected model. Moreover, lower body

parts are occluded by both table and chair when a per-

son sits down and foreground detection fails to detect

occluded body parts. These are the main reasons for

small drop in MOTA and relatively high decrement in

MOTP. The example tracking results from our tracker

for both the Walking and the Meeting sequences are

shown in Fig. 2. The bounding box around each per-

son is in fact the Ω

) and a different box color

shows different identity. The tailing dots of the bound

box, which has the same color as the box, is the pro-

jection of the positions estimates from the past 80

frames.

The evaluation of the Unsteady Lighting sequence

shows that our tracker is robust to sudden illumination

changes. Even in such difﬁcult scenario, our tracker

achieves a MOTA value of 97% and a MOTP value

of 84%. The drop in MOTA is mainly caused by

false positive trajectories due to the presence of false

positive foreground blobs. These false positive fore-

ground blobs appear every time the light of the room

is completely off, i.e., the captured image tends to be

very noisy when illumination in the scene is very low.

The example frames for all four views of the Unsteady

Lighting sequence is shown in Fig. 3.

The projected cuboid to all views Ω

) and the

projected points of 80 previously estimated positions

are shown as in Fig. 2. The ﬁrst row of Fig.3 shows

the scene under under usual illumination. The second

row shows the frame after ﬁve seconds (100 frames),

where the lighting in the room is completely off.

Within a ﬁve seconds interval, the lighting in the room

is ﬁrstly reduced to half and then fully off. Despite the

presence of sudden illumination changes, we can see

that our tracker is still able to track all persons cor-

rectly.

As aforementioned, we compare the performance

of our tracker to the state of the art tracker of Berclaz

et al. (POM-KSP) as shown in Table 1. The compari-

son shows that our tracker outperforms in all three se-

quences. The POM-KSP performs well in sequences

containing only upright walking persons, i.e., the

Walking and the Meeting sequences. However, the

POM-KSP performs poorly in the Meeting sequence.

The reason could be that their tracker is not designed

to track sitting persons as there is reported results in

their paper (Berclaz et al., 2011) are only for upright

moving people. Moreover, Berclaz et al. (Berclaz

et al., 2011) reported that their POM-KSP tracker is

sensitive to false detections and missing ones. In the

Unsteady Lighting sequence, the sudden illumination

changes cause foreground detection to produce false

positive blobs which leads to false detection in POM

thus lower accuracy in tracking. However, for our

tracker, these false positive blobs cause only 3% drop

in MOTA. This shows that our tracker is less sensitive

to false positive detections.

In each iteration of greedy likelihood algorithm

(Algorithm 1), each smart camera sends 81 likelihood

values (numbers) to the likelihood maximizer when

using 10 cm ×10 cm grids and d

max

= 50 cm. Since

the number of iteration is the number of person being

tracked, each smart camera sends 81 ×m numbers per

Multiple People Tracking in Smart Camera Networks by Greedy Joint-Likelihood Maximization

609

Cam 1 Cam 2 Cam 3 Cam 4

Figure 2: Example tracking results obtained by our tracker. The ﬁrst row shows the example trajectories in four views of

the Walking Sequence and the second row shows the Metting Sequence. Different bounding box colors indicates different

identities.

Cam 1 Cam 2 Cam 3 Cam 4

Figure 3: Example tracking results obtained by our proposed tracker in the Unsteady Lighting sequence. Different bounding

box colors indicates different identities.

frame, i.e., the amount of data exchange increases lin-

early with the number of person being tracked. This

shows that our tracker is more communication efﬁ-

cient than those follows centralized architecture.

6 CONCLUSION

In this paper, we present a novel method for tracking

multiple people simultaneously within a smart camera

network by maximizing the likelihood of observed

foreground image in all camera views given the posi-

tions of all persons. The evaluation results show that

our tracker achieves MOTA value as high as 100%

and MOTP value as high as 86%. We also show that

our tracker is able to track people reliably even when

they are sitting down. This is a desirable advantage

in several applications, such as smart meeting room,

since people are sitting in the scene most of the time.

Moreover, our tracker is robust to sudden illumination

changes.

When we compare to publicly available state of

the art tracker (POM-KSP), our tracker outperforms.

Currently, our prototype tracker is implemented on

an ordinary computer as a single thread C++ pro-

gram, which processes all four camera views sequen-

tially. Without code optimization, the average pro-

cessing time of our tracker is 200 milliseconds per

frame, approximately 50 milliseconds per frame per

camera view, on a single core of Intel Core2Quad @

2.66 GHz with 8 GB of memory. Therefore, we be-

lieve that our tracker can reach the processing speed

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

610

Table 1: MOTA and MOTP comparison.

MOTA MOTP

Sequence Proposed POM-KSP Proposed POM-KSP

Walking 100% 93% 86% 83%

Meeting 98% 54% 77% 75%

Unsteady Lighting 97% 83% 86% 84%

of 20 frames per second if the processing is paral-

lelized in a distributed architecture, i.e., processing

for each camera is implemented as a separate thread

or on a smart camera.

ACKNOWLEDGEMENT

The work was ﬁnancially supported by FWO through

the project G.0.398.11.N.10 “Multi-camera human

behavior monitoring and unusual event detection”.

REFERENCES

Andriyenko, A. and Schindler, K. (2010). Globally optimal

multi-target tracking on a hexagonal lattice. In Pro-

ceedings of the 11th European Conference on Com-

puter Vision: Part I, ECCV’10, pages 466–479.

Andriyenko, A. and Schindler, K. (2011). Multi-target

tracking by continuous energy minimization. In Com-

puter Vision and Pattern Recognition (CVPR), 2011

IEEE Conference on, pages 1265–1272.

Berclaz, J., Fleuret, F., Turetken, E., and Fua, P. (2011).

Multiple object tracking using k-shortest paths opti-

mization. IEEE Trans. on Pattern Analysis and Ma-

chine Intelligence, 33(9):1806–1819.

Bernardin, K. and Stiefelhagen, R. (2008). Evaluating mul-

tiple object tracking performance: The clear mot met-

rics. J. Image Video Process., 2008:1–10.

Bo Bo, N., Deboeverie, F., Eldib, M., Guan, J., Xie, X.,

Nio, J., Van Haerenborgh, D., Slembrouck, M., Van de

Velde, S., Steendam, H., Veelaert, P., Kleihorst, R.,

Aghajan, H., and Philips, W. (2014). Human mobility

monitoring in very low resolution visual sensor net-

work. Sensors, 14(11):20800–20824.

Bo Bo, N., Deboeverie, F., Veelaert, P., and Philips, W.

(2015). Real-time multi-people tracking by greedy

likelihood maximization. In International Conference

on Distributed Smart Cameras (ICDSC2015), Seville,

Spain.

Bredereck, M., Jiang, X., Korner, M., and Denzler, J.

(2012). Data association for multi-object tracking-by-

detection in multi-camera networks. In Distributed

Smart Cameras (ICDSC), 2012 Sixth International

Conference on, pages 1–6.

Gruenwedel, S., Jela

ca, V., Ni

no Casta

neda, J., Van Hese,

P., Van Cauwelaert, D., Van Haerenborgh, D., Vee-

laert, P., and Philips, W. (2014). Low-complexity

scalable distributed multi-camera tracking of humans.

ACM Transactions on Sensor Networks, 10(2).

Henriques, J. F., Caseiro, R., and Batista, J. (2011). Glob-

ally optimal solution to multi-object tracking with

merged measurements. In IEEE International Con-

ference on Computer Vision, ICCV 2011, Barcelona,

Spain, November 6-13, 2011, pages 2470–2477.

Milan, A., Schindler, K., and Roth, S. (2013). Detection-

and trajectory-level exclusion in multiple object track-

ing. In Computer Vision and Pattern Recognition

(CVPR), 2013 IEEE Conference on, pages 3682–

3689.

Pirsiavash, H., Ramanan, D., and Fowlkes, C. C. (2011).

Globally-optimal greedy algorithms for tracking a

variable number of objects. In Proceedings of the

2011 IEEE Conference on Computer Vision and Pat-

tern Recognition, CVPR ’11, pages 1201–1208.

Wojek, C., Roth, S., Schindler, K., and Schiele, B. (2010).

Monocular 3d scene modeling and inference: Under-

standing multi-object trafﬁc scenes. In Proceedings of

the 11th European Conference on Computer Vision:

Part IV, ECCV’10, pages 467–481.

Yang, J., Vela, P. A., Shi, Z., and Teizer, J. (2009). Proba-

bilistic multiple people tracking through complex sit-

uations. In 11th IEEE International Workshop on

PETS, pages 79–86.

Yun, Y., Gu, I.-H., and Aghajan, H. (2012). Maximum-

likelihood object tracking from multi-view video by

combining homography and epipolar constraints. In

The 2012 Sixth International Conference on Dis-

tributed Smart Cameras (ICDSC).

Zhang, L., Li, Y., and Nevatia, R. (2008). Global data asso-

ciation for multi-object tracking using network ﬂows.

In Computer Vision and Pattern Recognition, 2008.

CVPR 2008. IEEE Conference on.

Multiple People Tracking in Smart Camera Networks by Greedy Joint-Likelihood Maximization

611