Improved Identiﬁcation of Data Correlations

through Correlation Coordinate Plots

Hoa Nguyen

and Paul Rosen

Scientiﬁc Computing and Imaging Institute, University of Utah, Salt Lake City, U.S.A.

Department of Computer Science and Engineering, University of South Florida, Tampa, U.S.A.

Keywords:

Correlation, Correlation Visualization, Statistical Visualization.

Abstract:

Correlation is a powerful relationship measure used in science, engineering, and business to estimate trends

and make forecasts. Visualization methods, such as scatterplots and parallel coordinates, are designed to be

general, supporting many visualization tasks, including identifying correlation. However, due to their gener-

ality, they do not provide the most efﬁcient interface, in terms of speed and accuracy. This can be problematic

when a task needs to be repeated frequently. To address this shortcoming, we propose a new correlation

task-speciﬁc visualization method called Correlation Coordinate Plots (CCPs). CCPs transform data into a

powerful coordinate system for estimating the direction and strength of correlation. To support multiple at-

tributes, we propose 2 additional interfaces. The ﬁrst is the Snowﬂake Visualization, a focus+context layout

for exploring all pairwise correlations. The second enhances the basic CCP by using principal component

analysis to project multiple attributes. We validate CCP performance in correlation-speciﬁc tasks through an

extensive user study that shows improvement in both accuracy and speed.

1 INTRODUCTION

Correlation is a powerful metric that provides a pre-

dictive relationship between variables used in science,

engineering, and business (Hong et al., 2010; Sharma

and Wallace, 2011; Yu et al., 2012). A correlation co-

efﬁcient is a measure of the strength and direction of

such a relationship. While correlation is a powerful

metric, visual examination is also critical. The many-

to-one relationship between data and a correlation co-

efﬁcient may obscure important features of the data.

In Anscombe’s Quartet (see Figure 1) (Anscombe,

1973), 4 distributions (i.e. the many relationship) have

identical correlation coefﬁcients (i.e. the one relation-

ship). Visual examination can disambiguate the varia-

tions to outliers (case 1), noise (case 2), non-linearity

(case 3), and non-relationship (case 4).

Both scatterplots (SCP) (Jarrell, 1994) and paral-

lel coordinates plots (PCP) (Inselberg, 1985) are ca-

pable of being used to investigate correlation. How-

ever, that does not mean one should not infer that

these are the ideal tools for performing such a task. In

analytic scenarios where correlation is the most im-

portant task, these encodings are non-optimal. This

challenge is exacerbated by the increasing desire to

analyze multi-attribute data. A number of multi-

attribute visualization techniques exist for this anal-

ysis (Aris and Shneiderman, 2007; Bezerianos et al.,

2010; Wattenberg, 2006), with Scatterplot Matrices

(SPLOMs) and PCPs remaining the most popular.

SPLOMs simultaneously show all possible combina-

tions of attribute, but the plots become small as the

number of combinations grows quadratically. For

PCPs, the series of axes grow linearly, but the inter-

face relies heavily upon interaction.

The critical shortcoming to these methods is in

their design goal—they are designed as general-

purpose tools for performing a wide variety of ana-

lytic tasks. No special consideration has been made

to any single task, meaning that while they can be

used to identify correlation, they are not designed op-

timally for it.

With these limitations in mind, we have devel-

oped a new, correlation task-speciﬁc visual design

called Correlation Coordinate Plots, or CCPs (see

Figure 1: Anscombe’s Quartet (Anscombe, 1973) shows 4

distributions that all have correlation coefﬁcients of 0.816.

Nguyen, H. and Rosen, P.

Improved Identiﬁcation of Data Correlations through Correlation Coordinate Plots.

DOI: 10.5220/0005717500600071

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 2: IVAPP, pages 62-73

ISBN: 978-989-758-175-5

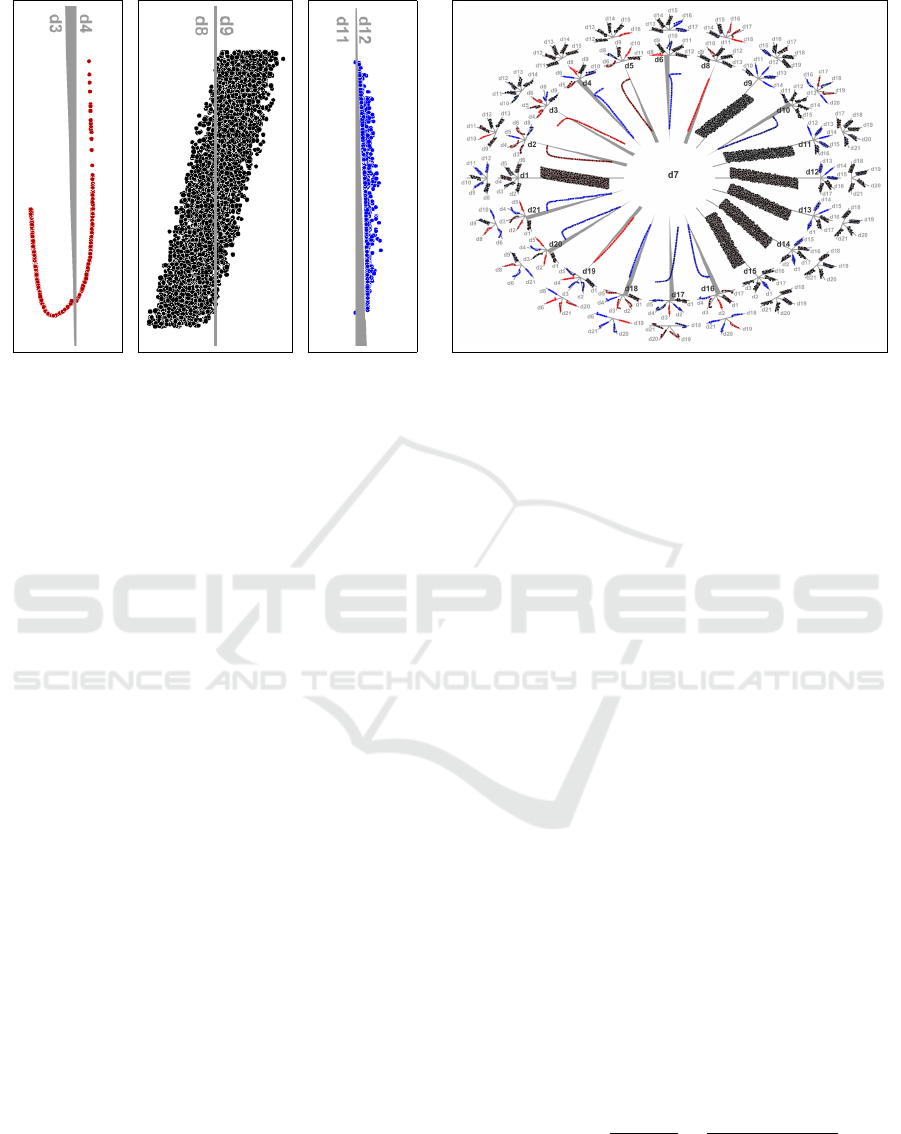
(a) Positive (b) No Corr (c) Negative (d) Snowﬂake Visualization

Figure 2: Correlation Coordinate Plots (CCPs) transform data into a coordinate system better suited to investigating correlation

between 2 attributes. (a-c): Example CCPs show positive, no, and negative (or anti-) correlation, respectively. (d): The

Snowﬂake Visualization is a focus+context interface that combines CCPs for 1 attribute to all others in the middle (i.e. the

focus) and CCPs for all other attribute pairings on the perimeter (i.e. the context).

Figure 2(a-c)). CCPs use design attributes, such as

axis shape and a simple, yet effective, point transform

to enable quick and accurate determination of corre-

lation direction and strength.

To support multi-attribute analysis we developed

a focus+context style circular layout for CCPs, called

the Snowﬂake Visualization (see Figure 2(d)). This

visualization represents a compromise where the

screen space needed to represent additional attributes

in the focus region grows linearly, and it grows

quadratically for the context region. There remains

some reliance on interaction for full investigation.

We have also extended the visual metaphors of the

CCP to support a single visual interface for multi-

attribute analysis by using principal component anal-

ysis (PCA) of the data.

To validate the efﬁcacy of our new approaches,

use case examples and a user study are used. Our

user study had novice and expert subjects perform

correlation-related tasks in SCP, PCP, and CCP en-

vironments. Our results conﬁrmed that CCP methods

outperform SCP and PCP in accuracy and timing.

In summary, the contributions of this paper are:

• a task-speciﬁc visualization, the Correlation Co-

ordinate Plot, designed to efﬁciently identify cor-

relations;

• a circular layout, the Snowﬂake Visualization,

that provides an efﬁcient focus+content style vi-

sualization of all pairwise relationships in multi-

attribute data;

• a single plot visualization for exploring multi-

attribute correlations using PCA; and

• a use case analysis and user study conﬁrming the

superior performance of CCP with correlation-

related tasks when compared to SCP and PCP.

2 RELATED WORK

2.1 Correlation

Correlation is a metric calculated between data and

can be used to model and predict relationships (Hong

et al., 2010; Yu et al., 2012). The ”quality of rela-

tionship” is often measured using a correlation co-

efﬁcient (Chen et al., 2010; Xu et al., 2008), with

positive correlation indicating 2 attributes are increas-

ing together, while negative or anti-correlation indi-

cates that 1 attribute increases and the other decreases.

There are several correlation coefﬁcient measures,

the most common of which is the Pearson Correla-

tion Coefﬁcient (PCC) (Magnello and Vanloon, 2009;

Wang and Zheng, 2013). PCC, ρ(x,y), measures the

linear relationship between 2 attributes x and y with

means ¯x and ¯y and standard deviations σ

and σ

. It is

deﬁned as:

ρ(x,y) =

cov(x,y)

Σ(x

− ¯x)(y

− ¯y)

(1)

As far as correlation in visualization is concerned,

there are 2 schools of thought. The ﬁrst is to show

metrics on data, not the data themselves. Examples

Improved Identiﬁcation of Data Correlations through Correlation Coordinate Plots

include Corrgrams (Friendly, 2002a) and Scagnos-

tics (Wilkinson et al., 2005; Dang and Wilkin-

son, 2014). These approaches have the advantages

of visual scalability but the potential disadvantages

demonstrated by Anscombe’s Quartet (Anscombe,

1973). An overview of the metrics used in these ap-

proaches can be found in (Bertini et al., 2011).

The alternative approach shows all data points.

In this category, scatterplots and parallel coordinates

have been shown most effective (Harrison et al.,

2014). Since our approach follows this paradigm, we

compare against these techniques.

2.2 Scatterplot

A Scatterplot (SCP) (Buering et al., 2006; Jarrell,

1994) is a simple plot of points used to investigate

the linear and nonlinear relationships between 2 at-

tributes (Hartigan, 1975). The patterns of importance

in this context are when the data points slope from

lower left to upper right, suggesting positive correla-

tion, and sloping from upper left to lower right sug-

gests negative correlation. The direction of correla-

tion (positive or negative) can be confusing to novice

users. More importantly, the strength of correlation

(high versus low) can at times be difﬁcult to interpret.

For multi-attribute data, a Scatterplot Matrix

(SPLOM) (Hartigan, 1975; Huang et al., 2012) shows

the relationships of all pairs of attributes by organiz-

ing a grid of SCPs with each attribute occupying 1

row and 1 column. As the number of attributes in-

creases, the number of plots grows quadratically mak-

ing it difﬁcult to present all of the data. This prob-

lem can be mitigated by approaches such as Cor-

rgrams (Friendly, 2002b), which display a matrix of

correlation glyphs. These glyphs scale well and give

the user quick access to summary statistics, but they

may hide important data features (e.g. Anscombe’s

Quartet). In other cases, navigation can be used to

search larger spaces (Elmqvist et al., 2008).

2.3 Parallel Coordinates Plot

Parallel Coordinates Plots (PCPs) (Fanea et al., 2005;

Inselberg, 1985) are another well-known visualiza-

tion technique for exploring multi-attribute datasets,

which display n parallel axes, 1 for each attribute.

Data points map to vertices on each parallel axis and

connect with line segments. For PCPs, in simple

cases, the direction of correlation, though not intu-

itive, is easy to identify. Positive correlation appears

as a series of parallel lines, while negative correlation

appears as crossing lines.

In noisy cases, the ambiguity created by the cross-

ing lines hides patterns but retains outlier visibil-

ity (Zhou et al., 2009; Zhou et al., 2008). This makes

correlation direction and strength difﬁcult to interpret.

Modiﬁcations to PCPs have been proposed by using

color, opacity, smooth curves, frequency, density or

animation (Heinrich and Weiskopf, 2013; Geng et al.,

2011; Holten and van Wijk, 2010) to partially address

this. However, previous studies have shown that PCPs

are slower and less accurate than SCPs for correlation

tasks (Li et al., 2010).

The advantage of a PCP is that it provides a con-

tinuous and comparative view across the axes, and

the screen space needed for the visualization scales

linearly with the number of attributes. At the same

time, PCPs do not show all possible combinations of

attribute pairs, requiring signiﬁcant user interaction

for exhaustive exploration. Using 3D parallel coor-

dinates can enable exploration of the many-to-one re-

lationship (Johansson et al., 2006) with the traditional

downsides of 3D: perspective effects and occlusion in

large data. A PCP matrix (Heinrich et al., 2012) is

another method that may help overcome this limita-

tion.

3 CORRELATION

COORDINATES PLOT

The task generality (i.e. the support for many tasks)

plays as both an advantage and disadvantage for the

SCP and PCP. Either method is capable of being used

for correlation tasks, but they are not necessarily the

most efﬁcient methods available. This has led us to

develop a new visual encoding focused speciﬁcally on

correlation tasks, called Correlation Coordinate Plots

(CCPs). The proposed method is centered on help-

ing users quickly identify the existence, direction, and

strength of pairwise correlations. The visual design is

motivated by our desire to make the correlation task

one of comparison using position along a common

baseline.

For clarity in notation, we assume a dataset X con-

tains n attributes and m data points, with X

indicating

a single data attribute of m values and X

i j

indicating

data point j of attribute i.

3.1 Coordinate System

We propose using a correlation coordinate system that

differs from the Cartesian coordinate system, so as

to highlight how well points adhere to the correla-

tion. The coordinate system can be seen as a 1D

parametrization of the data to an underlying model, in

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

this case a line. The vertical position of a data point

is the parameterization of the data. The position hori-

zontally is more important, demonstrating the quality

of the ﬁt. Therefore, identifying correlation primarily

relies on visibility of points to the left and right of the

axis.

Transforming the data from a Cartesian domain

into the correlation coordinate system is a two step

process laid out in Figure 3, with the top panel show-

ing the positive relationships and the bottom panel

demonstrating the negative relationships.

The ﬁrst step is a scaling operation (Scl) that

forces the data into a square region (see Figure 3 pan-

els 1 & 2). The second step is the projection (P

ma jor

and P

minor

) operation, which measures the location of

the point relative to the positive correlation diagonal

(lower left to upper right) or negative correlation diag-

onal (upper left to lower right). That measure is used

to place the points into the CCP (see panels 3 & 4).

The process begins by normalizing the data to [−1,1].

Scl(X

) =

− argmin

i j

argmax

i j

− argmin

i j

(2)

Once normalized, the location of a point i from at-

tributes j and k can be determined. The location on

the major (vertical) axis is:

ma jor

) = X

(3)

The position on the minor axis is:

minor

) =



α · (X

− X

) pos. or no corr.

α · (X

+ X

) neg. corr.

(4)

The variable α is a scalar that effects the spread of

data points when plotting. We selected a constant

value based upon the width of the CCP.

The plot orientation was initially chosen to be ver-

tical in order to pack many plots side by side on the

(0,0)

(3,10)

(-1,-1)

(1,1)

𝑷

𝒎𝒊𝒏𝒐𝒓

𝑷

𝒎𝒂𝒋𝒐𝒓

𝑿

𝒌𝒊

𝑿

𝒋𝒊

𝑷

𝒎𝒊𝒏𝒐𝒓

𝑷

𝒎𝒂𝒋𝒐𝒓

Figure 3: Conversion to correlation coordinate system for

positive (top) and negative (bottom) cases.

display. Ultimately, the choice of a vertical plot is

somewhat arbitrary and will be relaxed in forthcom-

ing sections. Nevertheless, we present and evaluate

our approach based upon the vertical orientation.

3.2 Coordinate Axis

We designed the coordinate axis to serves as a visual

indicator of the existence and direction of correlation.

For 2 attributes of a dataset, X

and X

, PCC is used to

indicate positive correlation by ρ(X

) > ε, negative

correlation by ρ(X

) < −ε, and uncorrelated by all

other values. The major coordinate axis is laid out

vertically and represented by a triangle whose base is

at the top for positive correlation (Figure 2a), the bot-

tom for negative correlation (Figure 2c), and a straight

line for uncorrelated (Figure 2b) data.

We have also considered mapping PCC to the

width of the axis, where higher values are wider and

lower values thinner. Due to the relatively small width

of the axis, we decided this mapping was not particu-

larly informative. Instead, to identify the strength of

correlation, users should investigate the distribution

of data in the correlation coordinate system, presented

in the following sections.

3.3 Coloring Data Points

A number of ﬁgures have had their data points col-

ored based upon their PCC value [{−1 : blue},{0 :

black},{1 : red}]. Strictly speaking, this encoding is

redundant and not required. However, if colors are in-

terpolated based upon PCC value, they do carry some

additional information, and in general, we ﬁnd them

more aesthetically pleasing. Because our focus is on

the use of the coordinate axis and coordinate system,

our method does not rely on color, and color was not

used in the user study to be described in Section 7.

3.4 Correlation Identiﬁcation

Using CCPs for correlation tasks is fairly simple. De-

pending upon your goal, we suggest:

• First, use the axis to determine if the data is posi-

tive, negative, or uncorrelated.

• Next, use the shape of the data points to determine

the basic relationship between the attributes (i.e.

linear, nonlinear, etc.).

• Finally, the distance of the points from the axis

can be used to estimate the strength of correlation,

with small distances indicating high correlation,

and other conditions such as outliers, noise, etc.

Improved Identiﬁcation of Data Correlations through Correlation Coordinate Plots

For example, in Figure 2c, by checking the axis, a

negative correlation can be seen. By observing the

closeness of the data points to the axis, a strong linear

relationship with small amount of noise. On the other

hand in Figure 2a, the axis indicates positive correla-

tion. From the shape of the data, it is apparent that a

nonlinear relationship exists with weak linear correla-

tion properties.

4 SNOWFLAKE VISUALIZATION

Thus far, our approach can be used to investigate pair-

wise correlation. Our next goal was to develop an

approach for investigating multi-attribute data. We

focused on a radial based design due to their efﬁ-

cient use of space for multiple attribute visualiza-

tions (Tominski et al., 2004). As such, we have de-

veloped the Snowﬂake Visualization, which is con-

structed of a focus+context views.

4.1 Focus View

The focus view (Figure 4a) enables investigating the

correlation of 1 attribute to all other attributes. Given

n attributes, there are (n −1) pairs laid out around the

center of the circle with equal angular spacing. By

default, the ﬁnal attribute of data is the initial focus

attribute. Attributes are sorted by ID but can be re-

ordered with other sorting methods. The inner radius

(the start of the CCP axes) is chosen such that none of

the data points between CCPs will overlap. The outer

radius (the end of the CCP axes) is adjustable as to

give more or less space to the context views.

4.2 Context View

Given the attributes covered by the focus view, we

designed the context view to give complete coverage

(a) Focus view

(b) Upper branch of

context view

of context view

Figure 4: A focus view (a) and multiple context views (b-c)

for Snowﬂake Visualization.

of the remaining attribute pairs. These context views

(Figures 4b and 4c) are attached to the branches of

the focus view. The objective is to prevent pairs of

attributes from being repeated. This is done by orga-

nizing the pairings based on parity of n.

When the number of attributes n is odd, m = (n −

1)/2. In this case, two types of context groups appear.

The ﬁrst type contains the ﬁrst m attributes, excluding

the focus attribute. Each attribute i is paired with the

following m attributes (with wrap around back to the

ﬁrst attribute), again excluding the focus attribute. For

the second type, the attribute i is paired with the fol-

lowing m − 1 attributes. Each pairing represents one

CCP on the context branch. Figure 4b shows a view

from the ﬁrst type where n = 9, m = 4, and i = 3. In

this case, the 4 attributes following (4, 5, 6, and 7)

are paired with attribute 3. Figure 4c shows a view

of the second type. Here, since i = 7, 3 attributes are

selected (8, 1, and 2), skipping the focus attribute 9.

When the number of attributes n is even, m = n/2.

Here, only a single type appears with each attribute

receiving m − 1 pairings.

4.3 Detail View & Interaction

Typically a single large CCP detail view is also in-

cluded with the Snowﬂake Visualization (a similar

practice to SPLOMs). A few interactions are included

with the Snowﬂake Visualization. These include:

• Click-to-swap: When the user clicks an attribute,

it becomes the focus attribute. After swapping,

outer attributes are reordered based upon a sorting

criteria (by attribute ID).

• Over-to-detail: As the mouse moves over a plot,

the detail view is updated to that pairing.

5 MANY-ATTRIBUTE

CORRELATIONS

Pairwise correlations are frequently important to un-

derstanding data. However, as the number of at-

tributes increases, the desire to explore relationships

of multiple attributes simultaneously increases as

well. The Snowﬂake Visualization partially addressed

the need by presenting many pairwise relationships

simultaneously. Comparing 3 or more attributes re-

quires looking at an exponentially increasing number

of plots and mentally fusing the distributions. We

can extend CCP design for presenting certain types

of multi-attribute relationships.

To do this, we slightly modify visual metaphors of

the CCP. First of all, we remove the positive/negative

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

(a) SPLOM

(b) CCP of linear feature (c) CCP of nonlinear feature

Figure 5: CCP for multiple attributes using PCA. (b) The at-

tributes in red are a linear feature. (c) The nonlinear feature

in blue is 2D, with the residual visible in the red haze.

metaphor encoded via the axis. This is because multi-

attribute relationships tend to not have a directional

measure, only magnitude. Now, the parameteriza-

tion model can be relaxed to any invertible function,

[s,t] = g(¯x). The vertical axis still represents a 1D pa-

rameterization of the data, s. The horizontal axis can

now represent a secondary model parameterization, t.

Finally, we represent information lost in this encod-

ing via a series of partially transparent boxes, one per

data point, that form a “haze” surrounding the data

points. The size of the boxes found using the resid-

ual, r = || ¯x − g

−1

(s,t)||.

For our experiments we have used Principal Com-

ponent Analysis (PCA) to parameterize the data. This

could be replaced with any other model that ﬁts our

functional deﬁnition. Using PCA, we set g( ¯x) equal

to the magnitude of the ﬁrst two principal components

of the data, and the size of the box is set to the resid-

ual. Figure 5 shows 2 examples. The SPLOM on

the left (Figure 5a) shows all of the attributes of the

dataset. Two subsets have been selected in red and

blue. The red subset are attributes that all appear pair-

wise linear. When we use the many-attribute CCP

(Figure 5b), we can see that all of the attributes are

linear with respect to one another. On the other hand,

the blue attributes appear nonlinear. When visualized

with the many-attribute CCP (Figure 5c), we can see a

relatively simple nonlinear 2D pattern within the data.

6 USAGE EXAMPLES

We applied three visualization methods, including

Snowﬂake Visualization, SPLOM, and PCP, to two

publicly available datasets including Boston house

price data

and Hurricane Isabel data

6.1 Boston House Price

Boston housing data (see Figure 6) is multivariate

dataset containing 506 items across 14 attributes.

When comparing this dataset in a Snowﬂake Vi-

sualization and SPLOM, there are a number of fea-

tures observable in both visualizations. For example,

in both visualizations the Age/Rad pairing is fairly

clearly a case for segmentation into two data groups.

However, in the SPLOM, it likely takes longer.

A big advantage in Snowﬂake Visualization is that

it makes way for exploiting additional visual chan-

nels. Take the Age/Ind pairing. In all visualization

approaches, coloring scheme we have used makes it

fairly easy to see that there is a strong positive corre-

lation. However, without the coloring that might not

be the case. If color had been used for some other

purpose, classiﬁcation for example, suddenly we lose

the ability in SPLOMs to quickly determine correla-

tion, while observing classiﬁcation. Since CCPs do

not rely on color to communicate correlation, we can

encode other information in the color channel without

signiﬁcant loss of correlation information.

6.2 Hurricane Data

Hurricane Isabel (Figures 7) data is provided as part

of the IEEE Visualization 2004 contest. Hurricane Is-

abel data set consists of 48 timesteps, each containing

measurements of 11 attributes with a spatial resolu-

tion of 500 × 500 × 100. We also only show 7 of the

more “interesting” attributes due to space considera-

tions. Of the original data 25 million data items, we

only use 10 million because approximately 15 million

data items contain at least 1 invalid NaN ﬁeld.

With 10 million data items in Hurricane data, the

overdraw problem in PCP makes it hard to understand

http://lib.stat.cmu.edu/datasets/boston

http://vis.computer.org/vis2004contest/

Improved Identiﬁcation of Data Correlations through Correlation Coordinate Plots

(a) Snowﬂake Visualization

(b) Scatterplot Matrix

Figure 6: Visualizations for Boston House data.

relationships in the data. For example, the relation-

ship Temp/Pres shows only the bowtie shape, losing

the individual data patterns. In many ways, SCPs do

a better job than PCPs. The Temp/Press relationship

is visible with the SCP. However, clear interpretation

is difﬁcult, since as Temp increases, Press ﬁrst de-

creases, then increases, and ﬁnally decreases.

Our approach presents these relationships more

clearly. The direction and strength of relationship be-

tween Temp and Pres can be identiﬁed in Snowﬂake

Visualization. The lower triangle shape of axis iden-

tiﬁes the negative relationship. Additionally, the data

points distribution, mostly being of similar distance

to the axis with a few spread out, enables identifying

that this relationship is not too strongly negative and

nonlinear.

(a) Snowﬂake Visualization

(b) Scatterplot Matrix

Figure 7: Visualization techniques for Hurricane data.

7 USER STUDY ON

IDENTIFYING CORRELATION

To further evaluate our visualization methods, we

conducted a user study comparing CCP with SCP and

PCP. In this study, we performed 3 experiments that

ask subjects to perform correlation related tasks.

We invited 25 participants to take part in our study,

9 female and 16 male, all graduate students from a

variety of science and engineering ﬁelds. Their ages

range from 23 to 35 years old.

In each experiment, subjects started with a short

set of slides and/or video to introduce the neces-

sary background. Subjects were then given practice

questions where, after answering, the correct answers

were provided. They would then perform the experi-

mental tasks. For each test, the subjects’ answers and

response times were recorded. Following the experi-

ment, subjects completed a short survey. In total, the

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

study lasted less than one hour, including training and

testing. For all visualizations, gray color was used for

axes and labels, black color was used to present data

items.

The software for the user study was built using

C++ and Qt, and run on a MacBook pro with a 2.5

GHz Intel Core i5, 4 GB RAM, and 512 MB Intel

HD Graphics 4000. The study used a particle physics

dataset containing 41 output attributes and 4000 data

items per attribute. The data represents a parame-

ter space search of 25 input attributes generated by

a series of tools that simulate the theoretical physi-

cal properties of subatomic particles under the Super-

symmetic extension of the Standard Model of particle

physics.

The independent and dependent variables used in

each experiment can be found in Table 1. We used

a mixed experimental design using t-testing to calcu-

late t-value, p-value, mean difference, and 95% conﬁ-

dence interval to conﬁrm our hypotheses. Only mean

value and p-value are reported, but other data can be

provided upon request.

7.1 Exp. 1: Speed/Accuracy in Pairwise

Correlation

When looking at SCP & PCP, 2 challenges persist.

First, it can be confusing to determine positive ver-

Table 1: Variables used to test hypotheses.

Independent Variables Potential Values

Data [ H1 | H2 | H3 | H4 ] 2 random attributes from 41 attribute data

Data [ H5 | H6 | H7 ] 10 or 21 attributes from 41 attribute data

Plot [ H1 | H2 | H3 | H4 ] SCP/PCP/CCP

Plot [ H5 | H6 | H7 ] SPLOM/PCP/Snowﬂake Visualization

Question [ H1 | H2 ] How are the 2 attributes correlated?

Question [ H3 | H4 ] What is the type of correlation?

Question [ H5 ] How are the 2 attributes correlated?

Question [ H6 ] How many attributes are correlated to i?

Question [ H7 ] Which attributes are correlated to i?

Dependent Variables Potential Values

Answer [ H1 | H2 | H5 ]

High Positive Correlation

Low Positive Correlation

No Correlation

Low Negative Correlation

High Negative Correlation

Answer [ H3 | H4 ]

Nonlinear Correlation

Linear Correlation

No Correlation

Answer [ H6 ] Number of attribute

Answer [ H7 ] List of attribute

Response Time [ all H ] Time recorded automatically

sus negative correlations. Granted, for experts this

is a trivial task, but for others, it can be confusing.

In many ways the identiﬁcation of correlation direc-

tion is easier with PCP than SCP—parallel lines pos-

itive and crossing lines negative. Second, there is

some ambiguity when trying to identify the strength

of correlation between 2 attributes. Ambiguity is a

much larger problem for PCP. When the relationship

is noisy or nonlinear, overlapping lines quickly ob-

scure detail.

When comparing CCP with these other methods,

CCP: (1) provides simple visual cues making identiﬁ-

cation of the direction of correlation fairly trivial; (2)

and reduces (not eliminates) the ambiguity by con-

centrating on correlation in the formulation of the co-

ordinate system. Given these factors, we developed 2

hypotheses as follows:

H1 | H2: Using a Correlation Coordinates Plot will

enable more accurate and faster identiﬁcation in di-

rection and strength of correlation between 2 at-

tributes than a [ H1: Scatterplot | H2: Parallel Coor-

dinates Plot ].

7.1.1 Method

The experiment is summarized in Table 1 (H1 & H2).

For a block of trials, we showed a participant a plot

between 2 random attributes using either the SCP,

PCP, or CCP method and asked a forced choice ques-

tion. Subject accuracy and time were measured.

At the start of the experiment, participants were

given an introduction to correlation, instructions on

ﬁnding correlation in SCP, PCP, and CCP, and 6 train-

ing questions. Participants were then given 21 exper-

imental questions (7 for each plot type, interleaved

order).

7.1.2 Results & Discussion

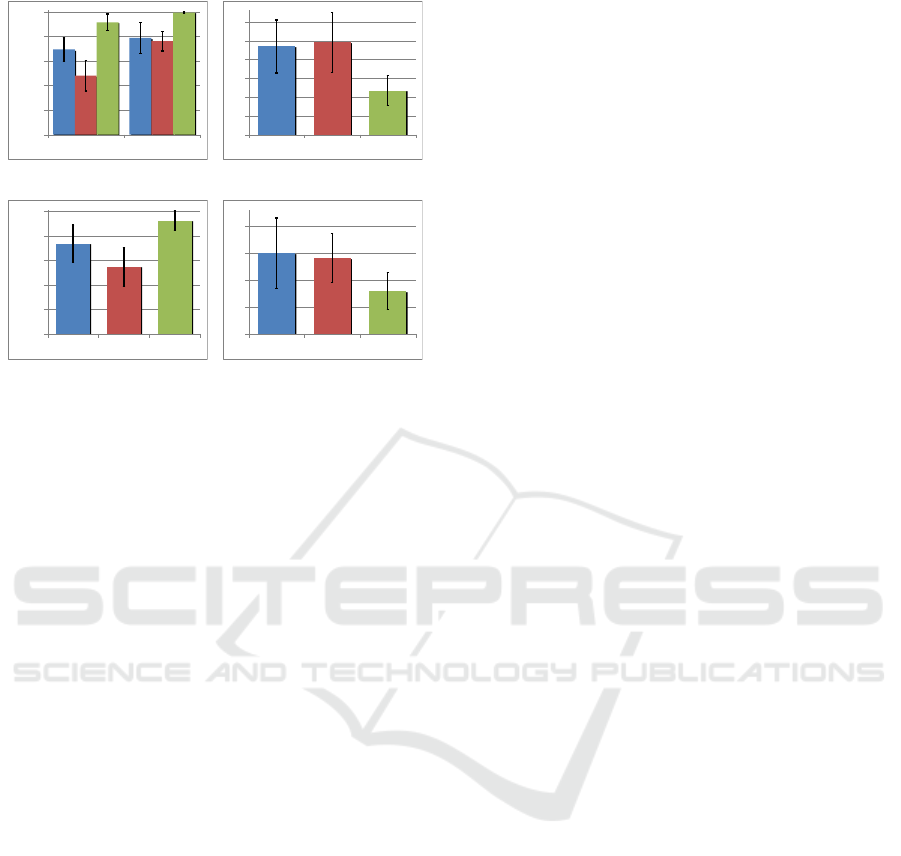
The results of both the measured speed and accuracy

of our experiments are shown in Figure 8a and 8b.

The results from Figure 8a shows that when com-

paring accuracy, CCP showed improvement over SCP

on average 91% compared to 69%, with statistical sig-

niﬁcance (p = 0.001). We also looked at subjects per-

formance in just identifying the direction of correla-

tion, where CCP had an accuracy of 99% compared

to 79% for SCP, though not quite with statistical sig-

niﬁcance (p = 0.06). The response times (Figure 8b)

showed similar results with CCP responses averaging

11.71s compared to 23.4s for SCP (p = 0.001). Given

that in our experiments CCP outperformed SCP in

both speed and accuracy, we consider H1 conﬁrmed.

A similar analysis shows that the accuracy CCP

was 91% compared to 48% for PCP (p = 0.001). The

Improved Identiﬁcation of Data Correlations through Correlation Coordinate Plots

20%

40%

60%

80%

100%

Strength & Dir. Direction

SCP PCP CCP

(a) Accuracy in exp. 1

20%

40%

60%

80%

100%

Strength & Dir. Direction

SCP PCP CCP

(b) Speed in exp. 1

20%

40%

60%

80%

100%

SCP PCP CCP

20%

40%

60%

80%

100%

SCP PCP CCP

(d) Speed in exp. 2

Figure 8: Results of exp. 1 and exp. 2 show CCP (green,

col. 3) outperforming SCP (blue, col. 1) and PCP (red, col.

2) in speed (sec) and accuracy (%). In all ﬁgures, error bars

indicate standard deviation.

response times (Figure 8b) showed a similar result

with CCP coming in on average 11.71s compared to

24.5s for PCP (p < 0.001). Given that CCP outper-

formed PCP in speed and accuracy, we consider hy-

pothesis H2 conﬁrmed.

The results of Exp. 1 conﬁrmed the hypotheses

H1 and H2, indicating that using CCP subjects can

identify correlation in less time and with higher ac-

curacy compared to SCP and PCP. In our informal

discussions with subjects after the experiment, they

indicated that the shape of the axis and the distribu-

tion of points in CCP greatly assisted their compre-

hension of the correlation. Subjects complained that

both SCP and, in particular, PCP were more difﬁcult

to distinguish positive and negative correlation in sce-

narios with low correlation. However, they found us-

ing CCP enabled them to easily recognize both the

direction and strength.

7.2 Exp. 2: Differentiating Linear,

Nonlinear, and Uncorrelated

Identifying nonlinear relationships between attributes

can also be an important task. When comparing CCP

with other methods, CCP provides simple visual cues

making identiﬁcation of correlation direction easier.

Beyond that, CCP and SCP give similar visual cues

(i.e. the tasks performed are basically the same) for

the shape of the relationship, linear or nonlinear. This

motivates our next hypothesis:

H3: Using a Correlation Coordinates Plot and a

Scatterplot will result in similar accuracy and speed

for identiﬁcation of linear, nonlinear, and uncorre-

lated relationships in 2 attributes.

For PCP, identifying these relationships is far

more challenging. The overdraw ambiguity that

plagues linear correlations becomes signiﬁcantly

worse as even more lines overlap each other in non-

linear cases. This will slow and confuse users. This

leads to our next hypothesis:

H4: Using a Correlation Coordinates Plot will result

in more accurate and faster identiﬁcation of linear,

nonlinear, uncorrelated relationships in 2 attributes

than a Parallel Coordinates Plot.

7.2.1 Method

The experiment is summarized in Table 1 (H3 & H4).

At the start of the experiment, participants were given

instructions on linear and nonlinear correlation. Par-

ticipants were then given 3 training questions fol-

lowed by 9 experimental questions (3 for each plot

type, interleaving order). For each question, partici-

pants saw a plot from 2 random attributes and were

asked a forced choice question. Subject accuracy and

time were measured.

7.2.2 Results & Discussion

The results of the measured speed and accuracy of

our experiments are shown in Figure 8c and 8d, with

all differences showing statistical signiﬁcance (p <

0.005). The results of our experiment showed that

CCP outperformed SCP. Our hypothesis H3 however

had predicted that the performance of CCP and SCP

would be identical. This leads us to reject H3. In our

discussions with subjects after the experiment, they

indicated that the shape of axis and the distribution

of points in SCP was more difﬁcult to distinguish and

that CCP assisted their comprehension of these spe-

ciﬁc types of correlation.

Due to CCP substantially outperforming PCP in

both speed and accuracy, we consider hypothesis H4

conﬁrmed. As anticipated, participants complained

that the overdraw problems made it difﬁcult differen-

tiate linear vs. nonlinear correlations in PCP.

7.3 Exp. 3: Accuracy/Speed in

Multi-Attribute Datasets

The Snowﬂake Visualization was designed speciﬁ-

cally for the task of quickly and accurately explor-

ing pairwise correlations in multi-attribute data as

compared with SPLOMs and PCP. As the number of

attributes increases each SCP within a SPLOM be-

comes quite small and the number of plots becomes

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

overwhelming. For PCP, as the number of attributes

increases, the interaction required for many tasks puts

increased pressure on the user to explore for features

of interest. With these factors in mind, we developed

3 hypotheses:

H5: Using a Snowﬂake Visualization will enable more

accurate and faster identiﬁcation of correlation be-

tween 2 attributes in multi-attribute data than a Scat-

terplot Matrix or Parallel Coordinates Plot.

H6: Using a Snowﬂake Visualization will enable

more accurate and faster identiﬁcation of how many

attributes are correlated with a chosen attribute in

multi-attribute data than a Scatterplot Matrix or Par-

allel Coordinates Plot.

H7: Using a Snowﬂake Visualization will enable

more accurate and faster identiﬁcation of which at-

tributes are correlated with a chosen attribute in

multi-attribute data than a Scatterplot Matrix or Par-

allel Coordinates Plot.

7.3.1 Method

The experiment is outlined in Table 1 (H5-H7). Each

participant was given an introduction and demo video

for each visualization method and completed 12 sam-

ple questions using data unrelated to experimental

trials. Then, each performed 21 experimental ques-

tions interleaving ﬁrst between visualization types,

then question types.

7.3.2 Results & Discussion

Identiﬁcation of a Pairwise Correlation in Multi-

attribute Data. The results of measured speed and

accuracy in Figure 9 (Type 1) show the Snowﬂake

Visualization improved accuracy and speed over

SPLOMs and PCPs with statistical signiﬁcance (all

p < 0.05). We consider hypothesis H5 conﬁrmed.

Finding the Number of Correlated Attributes

in Data. Again, the results of the experiments

showed that the Snowﬂake Visualization improved

accuracy and speed over SPLOMs and PCPs (see Fig-

20%

40%

60%

80%

100%

Type 1 Type 2 Type 3

120

160

200

Type 1 Type 2 Type 3

(a) Accuracy (%)

20%

40%

60%

80%

100%

Type 1 Type 2 Type 3

120

160

200

Type 1 Type 2 Type 3

(b) Response Time (sec.)

Figure 9: Exp. 3 results show CCP (green, col. 3) outper-

formed SCP (blue, col. 1) and PCP (red, col. 2).

ure 9, Type 2) with statistical signiﬁcance (p < 0.05).

Therefore, we consider hypothesis H6 conﬁrmed.

Finding which Attributes are correlated in

Multi-attribute Data. The results of this ﬁnal

test also showed improved accuracy and speed over

SPLOMs and PCPs (see Figure 9, Type 3) with statis-

tical signiﬁcance (p < 0.05), leading us to also con-

sider hypothesis H7 conﬁrmed.

The Snowﬂake Visualization’s focus+context

style greatly assisted subjects interactions and com-

prehension when working through multiple pairwise

correlation questions. The participants complained

that small SCPs made the SPLOM difﬁcult to use, due

to inability to see individual plots and difﬁculty track-

ing rows or columns of plots. Using PCP, participants

complained that the number of dragging operations

required to explore multiple correlations made it very

difﬁcult for them.

8 DISCUSSION

User Study Task Selection: Selecting realistic tasks

for a user study is a challenging problem when users

are unfamiliar with the data and potentially visualiza-

tion altogether. We have selected a number of sim-

ple tasks, which are building blocks for more com-

plicated data analysis tasks that are commonly per-

formed. The overall out performance of the CCP over

SCP and PCP stands as evidence of its superiority,

which should translate to more complex tasks.

Abstraction Selection: SCP and PCP have served a

straw man role in our evaluation. There are any num-

ber of modiﬁcations that could be applied to either

technique to better inform the user about correlation.

However, since there is no single de facto standard,

we did not want our evaluation to be clouded by ques-

tions of abstraction selection in SCP or PCP. There-

fore, we stuck to the basic formulations of each ap-

proach. We hope this paper spurs the community to

dig deeper into this subject and generate a more ex-

tensive evaluation of approaches.

Very High Attribute Count Data: For data with

large numbers of attributes, we believe that ap-

proaches to extract the natural dimensionality of data,

such as PCA, in combination with techniques such as

CCP, will be critical in analysis. For all practical pur-

poses, beyond 30 or 40 attributes, our approach is no

longer viable. However, this is a similar limitation to

SPLOMs and PCPs. We consider higher-dimensional

cases to still be an open problem.

Improved Identiﬁcation of Data Correlations through Correlation Coordinate Plots

9 CONCLUSION

Correlation Coordinate Plots have been developed

with the speciﬁc task of correlation identiﬁcation in

mind. They have distinct advantages when compared

to general task visualizations such as SCP and PCP.

The advantages, as conﬁrmed by our user study, in-

clude:

• providing simple visual cues that make identiﬁca-

tion of the existence and direction of correlation

fairly trivial;

• improving estimation of correlation strength by

focusing the coordinate system on model ﬁt; and

• improving identiﬁcation of linear, nonlinear, and

uncorrelated data by reducing ambiguity in the vi-

sualization.

In addition, the Snowﬂake Visualization showed

signiﬁcant performance improvements over SPLOMs

and PCPs. The Snowﬂake Visualization is an efﬁcient

focus+context style layout representing a fair compro-

mise between space efﬁcient design, comprehensive

visualization, and reduced user interaction for show-

ing all pairwise correlations in multi-attribute data.

In conclusion, we believe that the CCP and

Snowﬂake Visualization represent complementary

approaches to existing techniques, replacing existing

approaches only where correlation is the major fea-

ture of focus in data. We believe that more of these

task speciﬁc approaches are on the horizon and will

provide data analysts better, faster access to relevant

information in their data.

ACKNOWLEDGEMENTS

We would like to thank our reviewers and colleagues

who gave us valuable feedback on our approach. We

would also like to thank our funding agents, NSF

CIF21 DIBBs (ACI-1443046), Lawrence Livermore

National Laboratory, and Paciﬁc Northwest National

Laboratory Analysis in Motion (AIM) Initiative.

REFERENCES

Anscombe, F. J. (1973). Graphs in statistical analysis. In

American Statistical Association, pages 17–21.

Aris, A. and Shneiderman, B. (2007). Designing semantic

substrates for visual network exploration. In InfoVis,

pages 281–300.

Bertini, E., Tatu, A., and Keim, D. (2011). Quality metrics

in high-dimensional data visualization: An overview

and systematization. IEEE Trans. on Visualization and

Comp. Graphics, 17(12):2203–2212.

Bezerianos, A., Chevalier, F., Dragicevic, P., Elmqvist,

N., and Fekete, J.-D. (2010). Graphdice: A system

for exploring multivariate social networks. Computer

Graphics Forum, 29(3):863–872.

Buering, T., Gerken, J., and Reiterer, H. (2006). User in-

teraction with scatterplots on small screens - a com-

parative evaluation of geometric-semantic zoom and

ﬁsheye distortion. IEEE Trans. on Visualization and

Comp. Graphics, 12(5):829–836.

Chen, Y. A., Almeida, J. S., Richards, A. J., Muller, P., Car-

roll, R. J., and Rohrer, B. (2010). A nonparametric

approach to detect nonlinear correlation in gene ex-

pression. Journal of Computational and Statistical

Graphics, 19(3):552–568.

Dang, T. N. and Wilkinson, L. (2014). Transforming

scagnostics to reveal hidden features. IEEE Trans.

on Visualization and Comp. Graphics, 20(12):1624–

1632.

Elmqvist, N., Dragicevic, P., and Fekete, J.-D. (2008).

Rolling the dice: Multidimensional visual exploration

using scatterplot matrix navigation. IEEE Trans. on

Visualization and Comp. Graphics, 14(6):1539–1148.

Fanea, E., Carpendale, M. S. T., and Isenberg, T. (2005).

An interactive 3d integration of parallel coordinates

and star glyphs. In InfoVis, pages 149–156.

Friendly, M. (2002a). Corrgrams: Exploratory displays

for correlation matrices. The American Statistician,

56(4):316–324.

Friendly, M. (2002b). Corrgrams: Exploratory displays for

correlation matrices. Ame. Stats, 1.

Geng, Z., Peng, Z., S.Laramee, R., Roberts, J. C., and

Walker, R. (2011). Angular histograms: Frequency-

based visualizations for large, high dimensional data.

IEEE Trans. on Visualization and Comp. Graphics,

17(12):2572–2580.

Harrison, L., Yang, F., Franconeri, S., and Chang, R.

(2014). Ranking visualizations of correlation using

weber’s law. IEEE Trans. on Visualization and Comp.

Graphics, 20(12):1943–1952.

Hartigan, J. A. (1975). Printer graphics for clustering.

JSCS, 4(3).

Heinrich, J., Stasko, J., and Weiskopf, D. (2012). The par-

allel coordinates matrix. In EuroVis - Short Papers,

pages 37–41.

Heinrich, J. and Weiskopf, D. (2013). State of the art of par-

allel coordinates. In Eurographics STAR, pages 95–

116.

Holten, D. and van Wijk, J. J. (2010). Evaluation of cluster

identiﬁcation performance for different pcp variants.

EuroVis, 29(3).

Hong, X., Wang, C.-X., Thompson, J. S., Allen, B., Malik,

W. Q., and Ge, X. (2010). On space-frequency cor-

relation of uwb mimo channels. IEEE Trans. on Veh.

Tech., 59(9):4201–4213.

Huang, T.-H., Huang, M. L., and Zhang, K. (2012). An

interactive scatter plot metrics visualization for deci-

sion trend analysis. In Conf. on Machine Learning,

Applications, pages 258–264.

Inselberg, A. (1985). The plane with parallel coordinates.

The Visual Computer, 1(2):69–91.

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

Jarrell, S. B. (1994). Basic Statistics. W. C. Brow Comm.

Johansson, J., Ljung, P., Jern, M., and Cooper, M. (2006).

Revealing structure in visualizations of dense 2d and

3d parallel coordinates. Information Visualization,

5(2):125–136.

Li, J., Martens, J.-B., and van Wijk, J. J. (2010). Judging

correlation from scatterplots and parallel coordinate

plots. InfoVis, 9:13–30.

Magnello, E. and Vanloon, B. (2009). Introducing Statis-

tics: A Graphic Guide. Icon Books.

Sharma, R. K. and Wallace, J. W. (2011). Correlation-based

sensing for cognitive radio networks: Bounds and ex-

perimental assessment. IEEE Sensors Journal, 11(3).

Tominski, C., Abello, J., and Schumann, H. (2004). Axes-

based visualizations with radial layouts. In ACM

symposium on Applied computing, pages 1242–1247.

ACM.

Wang, J. and Zheng, N. (2013). A novel fractal image com-

pression scheme with block classiﬁcation and sort-

ing based on pearsons correlation coefﬁcient. IEEE

Transactions on Image Processing, 22(9).

Wattenberg, M. (2006). Visual exploration of multivariate

graphs. In SIGCHI, CHI ’06, pages 811–819.

Wilkinson, L., Anand, A., and Grossman, R. L. (2005).

Graph-theoretic scagnostics. In InfoVis, volume 5,

page 21.

Xu, W., Chang, C., Hung, Y. S., and Fung, P. C. W. (2008).

Asymptotic properties of order statistics correlation

coefﬁcient in the normal cases. IEEE Trans. on Signal

Pro., 56(6):2239–2248.

Yu, S., Zhou, W., Jia, W., Guo, S., Xiang, Y., and Tang, F.

(2012). Discriminating ddos attacks from ﬂash crowds

using ﬂow correlation coefﬁcient. IEEE Trans. on

PDS, 23(6):1073–1080.

Zhou, H., Cui, W., Qu, H., Wu, Y., Yuan, X., and Zhuo, W.

(2009). Splatting lines in parallel coordinates. Com-

puter Graphics Forum, 28(3):759–766.

Zhou, H., Yuan, X., Qu, H., Cui, W., and Chen, B. (2008).

Visual clustering in parallel coordinates. Computer

Graphics Forum.

Improved Identiﬁcation of Data Correlations through Correlation Coordinate Plots