Flattening of the Lung Surface with Temporal Consistency for the

Follow-Up Assessment of Pleural Mesothelioma

Peter Faltin

, Thomas Kraus

, Marcin Kopaczka

and Dorit Merhof

Institute of Imaging and Computer Vision, RWTH Aachen University, Aachen, Germany

Institute and Out-patient Clinic of Occupational Medicine, Uniklinik RWTH Aachen, Aachen, Germany

Keywords:

Surface Representation, Planar Visualization, Multidimensional Scaling, Flattening, Temporal Consistency.

Abstract:

Malignant pleural mesothelioma is an aggressive tumor of the lung surrounding membrane. The standardized

workﬂow for the assessment comprises an inspection of 3D CT images to detect pleural thickenings which

act as indicators for this tumor. Up to now, the visualization of relevant information from the pleura has only

been superﬁcially addressed. Current approaches still utilize a slice-wise visualization which does not allow

a global assessment of the lung surface. In this publication, we present an approach which enables a planar

2D visualization of the pleura by ﬂattening its surface. A distortion free mapping to a planar representation

is generally not possible. The present method determines a planar representation with low distortions directly

from a voxel-based surface. For a meaningful follow-up assessment, the consistent representation of a lung

from different points in time is highly important. Therefore, the main focus in this publication is to guarantee

a consistent representation of the pleura from the same patient extracted from images taken at two different

points in time. This temporal consistency is achieved by our newly proposed link of both surfaces during the

ﬂattening process. Additionally, a new initialization method which utilizes a ﬂattened lung prototype speeds

up the ﬂattening process.

1 INTRODUCTION

Asbestos is a silicate mineral which was commonly

used in many countries because of its advantageous

properties, e.g. resistance to acid and heat. During

mechanical processing, asbestos ﬁbers can get into

the lung by inhalation. A deposition of these ﬁbers in

the tissue can cause different kinds of cancer such as

the malignant pleural mesothelioma (MPM) which is

an aggressive tumor of the pleura. The pleura is a lung

surrounding membrane consisting of two layers. Be-

cause of the long latency of about 38 years and a peak

usage of asbestos in the 1980s, an increasing number

of MPM cases is expected in Europe till 2018 (Pis-

tolesi and Rusthoven, 2004). In some other countries,

especially in Asia, the asbestos consumption is still

rising (Virta, 2012). Therefore, an increasing number

of MPM cases is expected in these countries. Because

of the aggressive tumor growth, early stage detection

is absolutely essential. For this purpose, high risk

patients undergo a regular medical check-up. These

checks also include CT image acquisition to identify

pleural thickenings which are indicators for the MPM.

Especially the identiﬁcation of their growth is an im-

Figure 1: CT slice with thickenings indicated by orange cir-

cles.

portant aspect in the diagnosis. The growth can be es-

timated by a follow-up assessment, based on images

from two different points in time.

As shown in Figure 1, pleural thickenings are

difﬁcult to spot because of the low image con-

trast between their tissue and the surrounding tis-

sue. At an early stage, they have a small thick-

Faltin, P., Kraus, T., Kopaczka, M. and Merhof, D.

Flattening of the Lung Surface with Temporal Consistency for the Follow-Up Assessment of Pleural Mesothelioma.

DOI: 10.5220/0005718702330243

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 2: IVAPP, pages 235-245

ISBN: 978-989-758-175-5

235

ness in terms of the image resolution of typically

1-3 voxels. Therefore, a manual analysis of the im-

ages is time consuming and subject to strong inter-

and intra-reader variability (Ochsmann et al., 2010).

Several (semi-)automated methods (Rudrapatna et al.,

2005; Chen et al., 2011; Frauenfelder et al., 2011;

Sensakovic et al., 2011; Faltin et al., 2013; Kengne

Nzegne et al., 2013) have been developed to sup-

port the physician in the decision process. Never-

theless, the ﬁnal decision is made by the physician.

For this purpose, a visualization of the relevant data

is highly important. Two publications (Faltin et al.,

2013; Kengne Nzegne et al., 2013) propose a global

3D visualization of the thickening locations, while

other publications only consider 2D slice-wise visual-

ization. With the 3D visualization a global overview

is possible. However, due to the 3D shaped surface,

thickenings might be occluded and the affected areas

on the surface can only be qualitatively recognized. A

slice-wise view facilitates a more precise assessment

of the affected surface, but it is time consuming, does

not visualize the complex thickening morphologies,

and does not give an overview. To address these is-

sues, a planar visualization of the lung surface is sug-

gested in this publication. An exemplary mapping of a

3D lung surface into a planar visualization is shown in

Figure 2. This kind of visualization enables a global

overview and a precise recognition of the affected ar-

eas on the surface. Different features, e.g. tissue at-

tenuation or surface roughness are utilized in a man-

ual or automated thickening identiﬁcation. These fea-

tures can be visualized for the whole lung at once by

utilizing the planar representation. Beside the detec-

tion of thickenings, it is important to compare the dif-

ferent points in time for a growth assessment. For this

purpose the planar representations of the lung at both

points in time need to be consistent regarding their

spatial arrangement.

The concept of mapping a 2D surface from a 3D

space to a planar 2D space is often referred to as

ﬂattening. To provide a meaningful interpretation of

the ﬂattened surface, the mapping should preserve an-

gles and be equiareal, as far as possible. If both an-

gle and area are preserved the mapping is called iso-

metric or distance-preserving. However, an isomet-

ric mapping of arbitrary shaped surfaces is not gen-

erally possible (Floater and Hormann, 2005). The

aim of ﬂattening methods is to approximate this iso-

metric mapping. Most of these methods (Zigelman

et al., 2002; Bronstein et al., 2003; Tosun et al., 2004;

Zhao et al., 2013; Hurdal and Stephenson, 2009) are

based on triangular meshes. In our case, the rele-

vant feature information is available for each of the

350 000 lung surface voxels. For a mesh-based ﬂat-

(a) 3D lung surface. (b) 2D planar visualization of

lung surface from Figure 2a.

Figure 2: Exemplary mapping of the 3D surface to a planar

2D visualization. The 3D coordinates of each surface point

are taken as color components for a RGB coding.

tening a very highly resolved mesh needs to be pro-

cessed or resampled. This results either in high com-

putational demands or the need of additional mesh

simpliﬁcation methods which might induce inaccu-

racies. An efﬁcient alternative is the method from

Saroul et al. (Saroul et al., 2006) which can be di-

rectly applied on discrete voxel data and focuses on an

interactive visualization with adjustable planes and a

center of low distortion. However, it does not include

a global optimization of the chosen plane. There-

fore, our approach utilizes multidimensional scaling

(MDS) which has been applied for the ﬂattening of

discrete surfaces (Grossmann et al., 2002) and pro-

vides a global optimization on a discrete voxel sur-

face. With this approach, the preserved surface dis-

tances are directly calculated on the high resolution

data set and the computation can still be performed on

a down-sampled set of surface points. In this publica-

tion, we suggest a new method to link both points in

time globally to achieve consistent representations of

the surfaces. Existing approaches to compare similar

shaped surface (Tosun et al., 2004; Zhao et al., 2013;

Hurdal and Stephenson, 2009) often use a standard-

ized mapping target. The approach from Bronstein

et al. (Bronstein et al., 2003) was especially designed

for an inter- and intra-subject comparison. However,

none of these approaches uses a mapping target which

is individually optimized for each subject. In con-

trast to these methods, our method results in subject

adapted representations and facilitates the comparison

between different points in time. Additionally, we de-

duce a method to efﬁciently initialize the MDS pro-

cess to speed up the processing of a similar shaped

surface. For this purpose, the results of a ﬂattening

from a prototype lung are utilized. A closed-form so-

lution to directly compute the initial points from this

prototype is derived.

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

236

adjacency matrix

dissimilarity matrices

2D points after MDS

considered interpolated planar representation

MDS

t = t

BFS

NMS

t = p:

BFS

t = t

BFS

lung surface I

of set I

sub,r

of set I

sub,r

of set I

Figure 3: Overview of the presented method: First, an adjacency matrix is extracted from the lung surface of the two points in

time t

and t

and the prototype surface t = p. By a non-maxima suppression (NMS) the set I

I of all surface points is reduced to

the set I

sub,r

⊂ I

I. From the full adjacency matrices and the reduced point set, the dissimilarities are extracted by a breadth ﬁrst

search (BFS). Then, the multidimensional scaling (MDS) extracts a subsampled 2D representation. Finally, an interpolation

by radial basis functions (RBF) is used to determine a full planar visualization. The prototype t = p can be used to initialize

the MDS. To connect the different lung surfaces, the transformations Tr and Tr

are required.

2 METHODS

In the ﬁrst part of this section, the extraction of the

discrete lung surface is shortly described. This is fol-

lowed by a general introduction to MDS. The idea

of mapping a discrete 3D surface to a 2D plane by

MDS was introduced by Grossmann et al. (Gross-

mann et al., 2002) and is described in Section 2.3, 2.4

and 2.6. We embed this method into a follow-up as-

sessment which requires a temporal consistent ﬂatten-

ing at both points in time. This methodical extension

is described in Section 2.5. To speed up the ﬂattening

processing, we also derive an initialization approach

to map the data from a ﬂattened prototype lung to an

actual lung, described in Section 2.7. An overview of

the complete work ﬂow is shown in Figure 3.

2.1 Discrete Lung Surface

The extraction of the discrete lung surface ∂R

R from

the chest CT image data g is performed in multiple

steps, as shown in Figure 4. Firstly, the body is seg-

mented by a simple thresholding, keeping the largest

connected component, followed by a morphological

ﬁlling. The chosen threshold of -250 HU is not critical

regarding the exact value. Within this body segment,

the lungs are identiﬁed. In this case the exact thresh-

old of -250 HU is relevant and conforms to the lower

boundary of the standard thickening window. This

window is used to visualize the CT data g in a stan-

dardized manual assessment of pleural thickenings.

Additionally, the mediastinal region R

medias

in be-

tween left and right lung is identiﬁed. It is the largest

concave region of the lung surfaces in each slice. Fi-

nally, a discrete surface which guarantees connectiv-

ity within a 26-connected neighborhood N

is ex-

tracted. For this purpose, a lung mask with removed

6-neighborhood N

is subtracted from the segmented

lung R

R itself

∂R

full

= R

R \ (R

R  N

), (1)

with the morphological erosion . The surface part

surrounded from the mediastinal region R

medias

is ex-

cluded, because it is not relevant for the thickening

assessment. The resulting lung surface is given by

∂R

R = ∂R

full

\ (R

medias

⊕ N

), (2)

with the morphological dilation ⊕.

2.2 Multidimensional Scaling

MDS is an approach to map a set of N points into

a space of any dimension M, by considering only

Flattening of the Lung Surface with Temporal Consistency for the Follow-Up Assessment of Pleural Mesothelioma

237

Figure 4: 2D visualization of the lung surface segmentation for an exemplary slice. First, the body (green) is detected, then

lungs (yellow and orange) and mediastinum (blue) are segmented. Finally, the pleura surface is extracted (yellow and orange).

the dissimilarities δ

i, j

of the data points, with i, j ∈

I =

{

1. . . N

}

. This section gives a short idea of the

method. Details can be found in the relevant litera-

ture (Cox and Cox, 2001). The results are only mean-

ingful if the dissimilarities can be, at least approxi-

mately, described in the target space of dimension M.

In the target space, the positions p

MD,i

are estimated

depending on their distances d

i, j



MD,i

− p

MD, j



These distances should be as close as possible to the

associated dissimilarities in the original space. This is

achieved by solving

∂R

= arg min

MD,1

...p

MD,N

loss

∆

MD,1

, . . . , p

MD,N

(3)

with a certain loss measure and the matrix ∆

∆

∆ contain-

ing the dissimilarities δ

i, j

. The MDS methods in lit-

erature are differentiated into

• classical vs. non-classical and

• metric vs. non-metric

approaches. These terms and the resulting loss crite-

ria named stress or strain are sometimes ambiguously

used. In this publication the terminology from Buja

et al. (Buja et al., 2008) is chosen and non-classical

MDS with the loss criterion

loss

∆

MD,1

, . . . , p

MD,N

)

=Sstress

∆

MD,1

, . . . , p

MD,N

)

∑

i, j=1...N

i6= j



i, j

− δ

i, j



∑

i, j=1...N

i6= j



i, j



(4)

is utilized. This criterion is differentiable even if two

points are coincident. The solution is found by a

gradient-based minimization, utilizing the conjugate-

gradient method (Navon and Legler, 1987). Weight-

ing terms w

i, j

for each pair of points can be chosen

individually, resulting in the new criterion

Sstress

∆

∆,W

MD,1

, . . . , p

MD,N

)

∑

i, j=1...N

i6= j

i, j



i, j

− δ

i, j



∑

i, j=1...N

i6= j



i, j



, (5)

with the weights denoted by the matrix W

W of same

size as ∆

∆

∆. In the case of a planar visualization, the

target dimension is chosen as M = 2.

2.3 Distances on Discrete Surface

As described in the last section, the optimization for

the 2D representation aims for distances d

i, j

identical

to the dissimilarities δ

i, j

. For a surface ﬂattening, the

dissimilarities are chosen as the distances on the lung

surface between all surface points p

∈ ∂R

R (Gross-

mann et al., 2002). To calculate the distances between

the discrete points on the surface, ﬁrst a weighted ad-

jacency matrix with distances between the connected

surface points p

3D,i

with i ∈ I

I, I

I =

{

1. . .

∂R

of a

26-connected neighborhood is extracted. Based on

this information, a breadth ﬁrst search (BFS), based

on the Boost C++ Library (Gleich, 2009), is used to

determine the distances on the surface. A lung sur-

face has approximately

∂R

= 350 000 surface points.

Just to store all pair distances, approximately 450 GB

of memory would be necessary. So, the distances

are only extracted for a subsampled number of sur-

face points. A regular subsampling of the unparam-

eterized 3D surface is not easily possible. There-

fore, non-maxima suppression (Neubeck and Gool,

2006) (NMS) with a suppression radius r is applied to

the binary surface ∂R

R. The free parameter r represents

a compromise between exact surface description and

computational complexity. In this case, the NMS on a

binary image is only utilized to generate a uniformly

distributed subset of points ∂R

sub,r

⊂ ∂R

R, with



3D,i

− p

3D, j



≥ r, ∀i, j ∈ I

I, i 6= j. (6)

The indices of the subsampled surface points are con-

tained in the set I

sub,r

⊂ I

I. Also other point distribu-

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

238

tion algorithms could be applied. The NMS was cho-

sen to be conforming to the procedure in a subsequent

step.

2.4 Surface Mapping for a Single Point

in Time

The sample points describe a 2D surface embed-

ded in a 3D space, therefore a meaningful 2D rep-

resentation can be obtained, but of course a perfect

isometric mapping cannot be achieved. All sample

points are mapped depending on their dissimilari-

ties δ

i, j

= δ(p

3D,i

, p

3D, j

), ∀i, j ∈ I

sub,r

and indepen-

dent on their actual 3D position p

3D,i

. These dis-

similarity measures δ

i, j

are given by the surface dis-

tances from Section 2.3. Solving the minimization

problem in Equation 3 leads to the 2D representa-

tion ∂R

. This representation is not unique regard-

ing the degrees of freedom (DOF) rotation, transla-

tion and reﬂection, as these properties are not observ-

able from the dissimilarities. For a single surface all

weights w

i, j

are kept equal to one, if all regions are

of similar importance. Focusing on some important

regions which are, e.g. subject to thickenings can be

achieved by increasing the weights in these regions.

2.5 Consistent Mapping for Two Points

in Time

The process described in the previous section, could

be independently applied to the lungs’ surfaces of

the same patient from images, taken at two different

points in time. In most cases, this leads, beside the

DOFs, to a similar spatial arrangement of the points

in 2D which is however not guaranteed. The problem

described in Equation 3 might have multiple solutions

and also local minima. To avoid different solutions at

both points in time, we propose to join both indepen-

dent problems into a single problem. For this pur-

pose, identical points on the lung surfaces ∂R

and

∂R

from both points in time t

and t

are linked by

enforcing identical target positions in the 2D visual-

ization.

Firstly, suitable points to establish a link are se-

lected. They should be located at the same 3D sur-

face position for both points in time, after a registra-

tion Tr : p

3D,t

7→ p

3D,t

. This registration is usu-

ally not perfect and afterwards the points Tr



3D,t



and p

3D,t

are not identical. For each surface

point p

3D,t

, i ∈ I

I the closest point at the other point

in time and their temporal distance is extracted by uti-

lizing the k-d tree algorithm (Bentley, 1975).

conn(i) = arg min

=1...

∂R





3D,t



− p

3D,t



(7)

(i) = p

3D,t

− p

3D,t

,conn(i)

, (8)

In the subsampling process, point pairs which can be

well aligned by the registration should be locally pre-

ferred to pairs which can only be poorly aligned by the

registration. This quality can be measured by the tem-

poral distance d

(i). Therefore, the NMS (Neubeck

and Gool, 2006) with radius of r is now applied to

the inverse distances

(i)

to obtain the subsampled

set I

sub,r

for the linking process. The ﬂattening in re-

gions of high importance could be improved by keep-

ing additional points in these regions. Points within

growing thickening regions will result in inconsistent

surface distances at both points in time and should be

avoided. Strong growth also results in large temporal

distances. Hence, thickening points which are critical

for the ﬂattening are suppressed automatically.

In the second step, the minimization problems are

independently formulated as in the previous section

and then connected. The set of linked points does not

have to be identical with the set of subsampled points

in Section 2.3. However, the problem statement is

given by the matrices W

W and ∆

∆

∆, whose size depends

on the number of involved points. Therefore, the point

sets are chosen to be identical to reduce the number

of variables in the optimization problem. The matri-

ces ∆

∆

and ∆

∆

are the dissimilarities for the different

points with identical order of the points at both points

in time. So, the entries δ

,i, j

, δ

,conn(i),conn( j)

corre-

spond to the same point combination at both points

in time, because point i corresponds to point i

and j

corresponds to j

. Then, the matrices describing the

linked problem are

∆

conn



∆

0 ∆

∆



, (9)

conn



1 κ diag(1, ..., 1)

κ diag(1, ..., 1) 1



,(10)

with 1

1 being matrices of size

sub,r

with

ones in each entry, diag(1, ..., 1) being matrices of

same size with ones on the diagonal and zeros at each

other entry, and 0

0 being a matrix of same size with

zeros at each entry. The parameter κ is a free weight-

ing parameter to balance the inﬂuence of inter- and

intra-temporal distances given in ∆

∆

conn

. Only the di-

agonal entries of the matrices 0

0 are relevant to set the

temporal distances of connected points. The other en-

tries are of no importance and are ignored because of

their zero weights in W

conn

. Finally, the connected

problem can be solved as described in Equation 3.

Flattening of the Lung Surface with Temporal Consistency for the Follow-Up Assessment of Pleural Mesothelioma

239

2.6 Interpolation

Only the subset of points I

sub,r

is mapped to

points p

2D,c

, c ∈ I

sub,r

on the 2D plane by MDS. For

all other discrete image points p

3D,i

, i ∈ (I

I \ I

sub,r

)

their matching 2D positions p

2D,i

are estimated

by an interpolation based on radial basis functions

(RBF) (Morse et al., 2005). RBF approximate a func-

tion f by a sum of radially symmetric functions Φ,

around the subsampled points p

3D,c

with c ∈ I

sub,r

3D,i

) =poly

3D,i

∑

c∈I

sub,r

(c)Φ





− p

3D,c





, (11)

for any point p

3D,i

, where λ

ual weighting terms for each center point p

3D,c

poly

3D,i

) represents the polynomial part of the

function, and ζ allows the separate interpolation for

both planar dimensions ζ ∈ {x, y}. A resulting planar

point p

2D,i

is given by p

2D,i

= ( f

3D,i

), f

3D,i

))

The weights λ

mial part poly

are determined by a least squares ap-

proach (Morse et al., 2005), considering all mapped

points I

sub,r

. This method has been successfully ap-

plied to various medical interpolation problems (Carr

et al., 1997; Morse et al., 2005). Different RBFs with

similar interpolation results have been applied in pre-

liminary experiments. In this publication, only radi-

ally symmetric function Φ(ρ) = ρ is regarded in detail

which showed a slightly superior performance.

2.7 Initialization

MDS is an optimization process, thus its calculation

time depends on the initialization with the 2D point

positions. To reduce the calculation time a prototype

lung can be utilized. For this prototype, a planar rep-

resentation must be calculated once. Then, it can be

utilized for all future ﬂattening processes. A registra-

tion Tr

: p

3D,i

7→ p

3D,p,i

between points p

3D,p,i

∈ ∂R

of the prototype lung surface and the correspond-

ing points p

∈ ∂R

R of the actual lung surface ∂R

is required. For the subsampled points with in-

dices i ∈ I

sub,r

, the initial 2D positions can be approx-

imated from the prototype positions p

2D,p,i

Different physical dimensions of the actual and

prototype lung in 3D cannot be directly transferred to

the planar 2D representation. The 2D offset between

two points is a mixture of the 3D offset, obtained from

the optimization process. However, we deduce an ap-

proximation for a deformation of the ﬂattened proto-

type which considers different 3D dimensions of the

lung. As a result of Section 2.3, the surface distance

between two points p

and p

is calculated by a sum

of distances between neighboring surface points, on

the shortest path E

E between those points. This path is

described by the edges (µ, ν)

∈ E

E and results in the

surface distance

i, j

∑

(µ,ν)

∈E



3D,µ

− p

3D,ν



. (12)

An isometric mapping to 2D is not possible for lung

surfaces and therefore, the distances between the

points p

2D,µ

and p

2D,ν

of each edge (µ, ν)

are sub-

ject to an error caused by the mapping. The planar

distances can therefore be described by

i, j

∑

(µ,ν)

∈E

µ,ν



3D,µ

− p

3D,ν



| {z }

µ,ν

, (13)

with the mapping error e

µ,ν

. The prototype and ac-

tual lungs have similar shapes and the aim is a sim-

ilar 2D mapping. Therefore, it is assumed that the

distance d

p,i, j

, of the corresponding points p

2D,p,i

and

2D,p, j

on the prototype surface, is subject to the same

mapping errors e

µ,ν

and given by the same shortest

path E

E. Then, the prototype distance of two neighbor

points is given by

p,µ,ν

= e

µ,ν





3D,µ

) − Tr

3D,ν

)





| {z }

µ,ν

. (14)

As a result of Equation 13 and 14, the planar distances

of the actual lung can be approximated by

i, j

∑

(µ,ν)

∈E

µ,ν

p,µ,ν

, (15)

with the planar distances d

p,µ,ν

known from the proto-

type and the shortest path E

E, which can be efﬁciently

calculated during the BFS (Gleich, 2009), discussed

in Section 2.3.

By choosing a ﬁxed point p

2D, f

, with f ∈ I

sub

, the

distances d

f ,i

from Equation 15 to this point can be

used for an initialization. The position p

2D,i

of all

other points i ∈ I

sub

\ { f } can be described in polar

coordinates, as shown in Figure 5, by

2D,i

= p

2D, f

+ d

f ,i



cos(φ

f ,i

)

sin(φ

f ,i

)



, (16)

and for the prototype by

2D,p,i

= p

2D,p, f

+ d

p, f ,i



cos(φ

p, f ,i

)

sin(φ

p, f ,i

)



, (17)

with the unknown angles φ

f ,i

and φ

p, f ,i

. Without loss

of generality these angles and also the ﬁxed point can

be chosen identically

• p

2D, f

= p

2D,p, f

results in identical translation, and

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

240

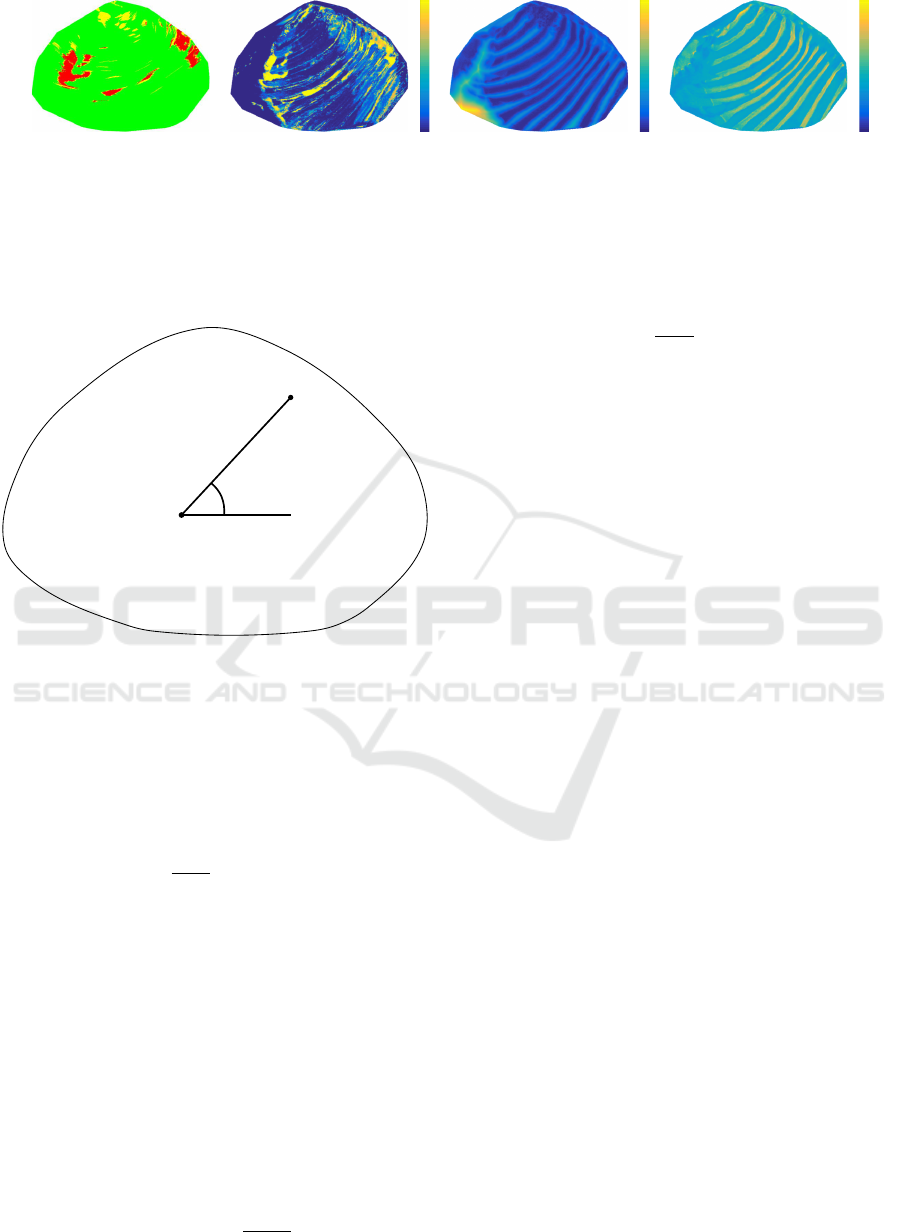
(a) Ground truth. Red

indicates thickenings, yel-

low uncertain ﬁndings and

green the healthy pleura

surface.

(b) Predicted thickening con-

ﬁdence in an exemplary clas-

siﬁcation.

0 mm

41 mm

bone. The ribs are located in

between the line-shaped re-

gions with high distances.

-760 HU

1300 HU

(d) Average attenuation val-

ues of tissue surrounding the

lung. The ribs are located in

the line-shaped regions with

high attenuation.

Figure 6: Planar visualization of lung surface with ground truth of thickening locations, automatic prediction, and exemplary

features considered for the prediction.

f ,i

2D, f

2D,i

Figure 5: Sketch of the planar lung surface, with description

of the point p

2D,i

, relative to the ﬁxed point p

2D, f

in polar

coordinates d

f ,i

and φ

p, f ,i

• φ

f ,i

= φ

p, f ,i

results in identical rotation and reﬂec-

tion

of prototype and actual lung. Finally, the initial point

position is approximated by

2D,i

= p

2D,p, f

f ,i

p, f ,i



2D,p,i

− p

2D,p, f



. (18)

The derived initialization does not compensate po-

tential changes in the angle φ

f ,i

, caused by the differ-

ent spacings. Therefore, they are subject to a mapping

error φ

err, f ,i

and the correct condition is

f ,i

= φ

p, f ,i

+ φ

err, f ,i

, (19)

resulting in the point positions

2D,i

. So the error

caused by incorrect angles is



2D,i

−

2D,i



. (20)

With the help of trigonometric functions and Equa-

tions 16 and 20 it can be shown, that the error is

= 2d

f ,i

sin



err, f ,i



. (21)

Since the term sin



err, f ,i



cannot be determined

without the solution, it is replaced by an unknown ex-

pected value which is assumed to be identical for all

combinations of f and i. Under this condition, the

ﬁxed point, which minimizes the overall error

∑

, is

given by the mean value of all points

2D,opt, f

= |I

sub

−1

sub

∑

i=1

2D,i

. (22)

A prototype lung should have a similar shape to

the processed lung so the surfaces can be well aligned

by the registration Tr

. That is why creating a mean

shape as a prototype could improve the initialization.

If the prototype and actual lung are too different, the

assumptions in this section might not hold. However,

the resulting imperfect initialization would not have

a negative inﬂuence on the mapping quality, but only

on the computation time.

3 RESULTS

To assess potential thickenings at an early stage,

high resolution chest CT data with a resolution

of 512 × 512 × 600 to 512 × 512 × 700 voxels is uti-

lized. The anisotropic image resolution varies be-

tween 0.63 mm and 1 mm in the transverse plane and

between 0.5 mm and 0.8 mm orthogonal to this plane.

Altogether, twenty data sets from ten different pa-

tients at two different points in time have been evalu-

ated. All calculations have been performed on an Intel

Core i5 with 16 GB of memory.

Some visual results for an exemplary patient are

given in Figure 6. The ground truth, extracted on the

volumetric data from a physician by labeling approx-

imately 550 2D slices, is shown in the ﬁrst image 6a.

The following images 6c–6d show relevant scalar fea-

tures which have been extracted on the lung surface

for each surface point and Figure 6b shows the con-

ﬁdence of an exemplary thickening classiﬁcation, not

Flattening of the Lung Surface with Temporal Consistency for the Follow-Up Assessment of Pleural Mesothelioma

241

100

120

140

160

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

16 32 48 64 80 96 112 128

duration/s

STRESS

STRESS1 STRESS2 duration

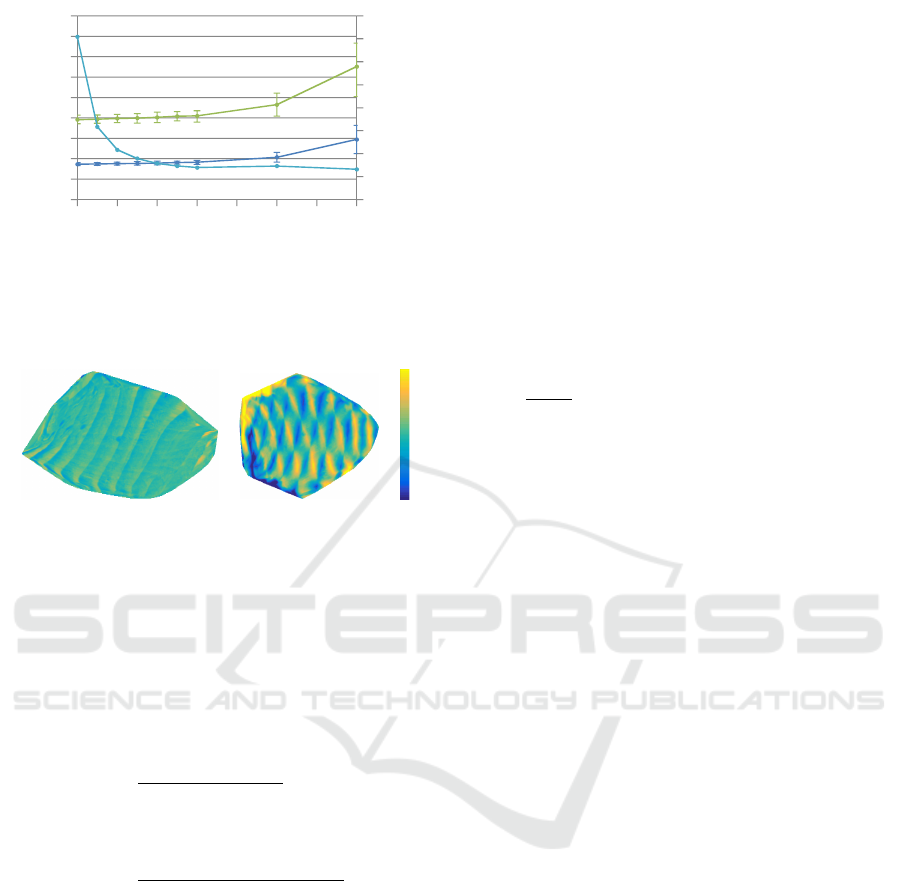
Figure 7: Distortion and computation time, depending on

radius r for the non-maxima suppression. The results are

given as mean values for all patients of left and right lung.

The error bars indicate the standard deviation.

(a) Differences with align-

ment (κ = 500).

-10 mm

10 mm

(b) Differences without

alignment (κ = 0).

Figure 8: Planar visualization of a lung at two points in time

from the same patient. The colors represent the differences

of the rib distances clipped to the interval [-10, 10] mm.

discussed in this publication. For a quantitative as-

sessment, the duration and the error of the ﬂattening

as stress (Kruskal, 1964)

STRESS1 =







∑

i> j

i, j∈I

i, j

− δ

i, j

)

∑

i> j

i, j∈I

i, j







0.5

, (23)

STRESS2 =







∑

i> j

i, j∈I

i, j

− δ

i, j

)

∑

i> j

i, j∈I

i, j

− mean (d

i, j

))







0.5

(24)

is plotted against the radius r of the NMS. The stress

measures indicate if the distances δ

i, j

on the 3D sur-

face are similar to the distances d

i, j

in the planar rep-

resentation. Low stress indicates similar distances

and high stress different distances. A vague verbal

scale of the STRESS1 measures was published by

Kruskal (Kruskal, 1964): starting with a values of 0

for perfect matching and ending with a value of 0.2

for poor matching. The average results for the left

and right lung of 10 patients at one point in time are

given in Figure 7.

For the temporal consistent ﬂattening, a non-

rigid registration, based on B-splines (Rueckert et al.,

1999), was applied. This registration has already been

utilized for the automated assessment of the thicken-

ings and is available at no extra computational cost.

An exemplary visual comparison of two points in time

showing the effect of temporal consistency is shown

in Figure 8. The relation of slice-wise visualization

and planar visualization for a growing thickening is

shown in Figure 11. Quantitative results for the con-

sistent planar visualization are given in Figure 9. The

radii values (visualized by the different colors), lead-

ing to stable results for the planar visualization of a

single point in time, are investigated for the prob-

lem with two points in time with different connec-

tion strengths κ ∈

{

0, 1, 500, 1000

}

(indicated by the

grouping). Additionally to the average STRESS1 cri-

terion, shown in Figure 9a, the average temporal dis-

tance between both data sets on the 2D plane

∂R

∑

i=1...

∂R

min

=1...

∂R

2D,t

, p

2D,t

)

(25)

with

, p

) =



2D,t

− p

2D,t

, j



(26)

is given in Figure 9b to evaluate the consistency.

For the MDS initialization, a rough mapping to the

prototype is sufﬁcient. Therefore, only a simple rigid

registration was applied which can be calculated in a

couple of seconds, while a non-rigid registration takes

typically a couple of minutes (Glocker et al., 2010).

An additional lung, not utilized in the evaluation, has

been chosen as the prototype. The calculation time

for the different components: adjacency matrix, dis-

similarity calculation by BFS and the MDS (with and

without initialization) are given in Figure 10. The

duration of the initialized MDS covers all additional

computations required, namely, the mapping of the

points Tr : p

3D,i

7→ p

3D,p,i

and the initialization itself.

4 DISCUSSION

Comparing the resulting computation time and the

quality of the ﬂattening process depending on the ra-

dius, as shown in Figure 7, reveals a good compro-

mise of calculation time and error for r = 40. On aver-

age, the smallest evaluated radius of r = 16 results in

approximately 2350 surface points, the radius r = 40

results in approx. 410 surface points and a radius of

r = 128 results in only 14 surface points. For smaller

radii the computation time is signiﬁcantly larger and

for larger radii the computation time is only slightly

decreasing, while the error is strongly increasing. The

stress stays relatively low even for large radii, which

indicates a good performance of the RBFs in interpo-

lating the lung shape. The relatively large acceptable

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

242

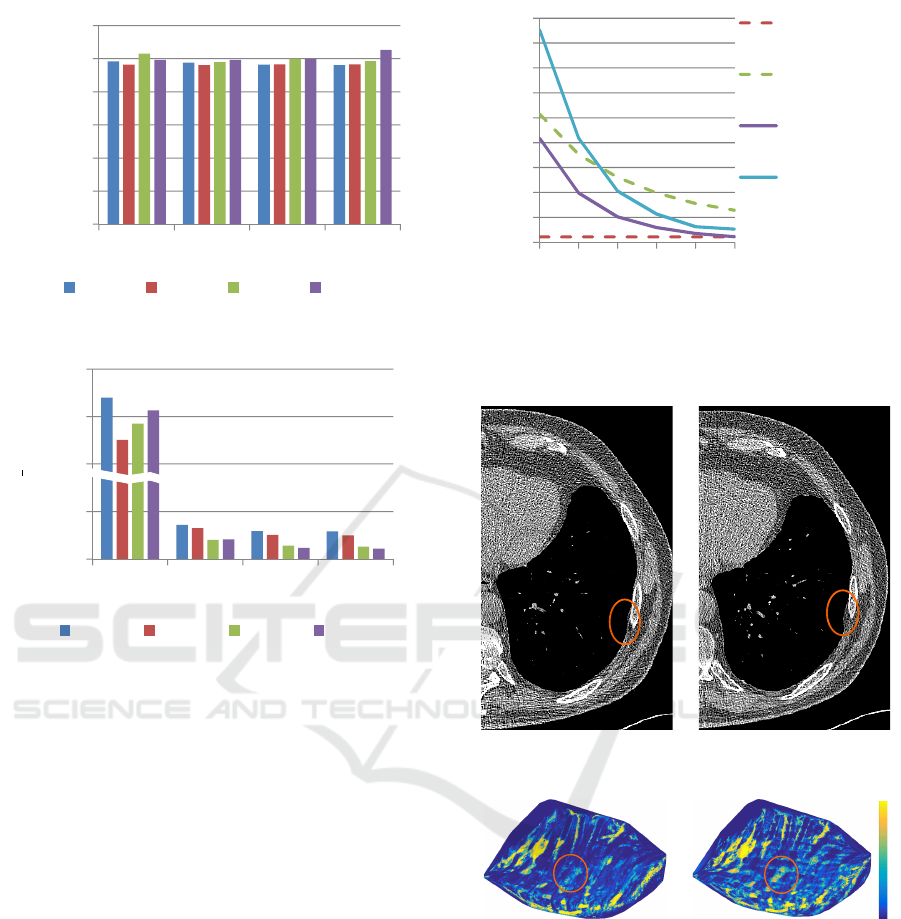
0,02

0,04

0,06

0,08

0,1

0,12

0 1 500 1000

average STRESS1

r=16 r=24 r=32 r=40

(a) The average STRESS1 results.

0 1 500 1000

r=16 r=24 r=32 r=40

avgerage

/pixel

130

110

(b) The average distances between the 2D representations

of both points in time.

Figure 9: Results for consistent mapping for various radii r

and various weightings κ.

radius of r = 40 might be surprising at ﬁrst glance.

However the experiments showed that it is important

to map a few point optimally to the planar plane, and

all points in between can be interpolated with a simi-

lar quality as the mapping itself. An analogy would

be to thinly cover a 3D surface with liquid rubber.

After cooling down, the resulting rubber sheet can be

pinned to a planar surface at a few ﬁxed points. If

the ﬁxed points are chosen properly, the rubber sheet

arranges the surface in between these points auto-

matically with low stress. The stress asymptotically

approaches a minimum value larger zero, which is

caused by the shape of the lung itself which does not

allow a perfect isometric mapping.

As shown in Figure 9b, the temporal distance

between two points in time is signiﬁcantly reduced

for κ = 1, but decreases only slightly for larger val-

ues κ ∈ {500, 1000}. As expected, both points in

time can be represented by a similar planar represen-

tation. Therefore, the problem deﬁned by the matrices

in Equations 9 and 10 need only a small connection

16 20 24 28 32 36

duration/s

adjacency

matrix

dissimilarities

by BFS

MDS with

initialization

MDS without

initialization

Figure 10: Computation time for the different parts of the

algorithm, depending on the non-maxima suppression ra-

dius r.

(a) Slice view at point in

time t

(b) Slice view at point in

time t

of thickening probability

at point in time t

(d) Planar representation

of thickening probability at

point in time t

Figure 11: Exemplary comparison of grown thickening (in-

dicated by orange circle) between two points in time t

and

utilizing the result of a pleura classiﬁcation.

weight κ to reach a similar solution at both points in

time. The stable stress values for increasing connec-

tion strength κ, shown in Figure 9a, indicate that tem-

poral consistency has only a minor inﬂuence on the

individual ﬂattening quality. The suggested method

results in planar representations of both points in time

which are much better comparable then before, with

minimal inﬂuence on the individual ﬂattening. In

Flattening of the Lung Surface with Temporal Consistency for the Follow-Up Assessment of Pleural Mesothelioma

243

cases of κ > 0, the stress slightly increases with in-

creasing radius r and at the same time, the temporal

distance is decreasing. An increasing radius r results

in a reduced number of constrains and therefore a less

accurate but more consistent ﬂattening at both points

in time.

In the visualization of the non-aligned (κ = 0) sur-

faces in Figure 8b, a rotation between the rib struc-

tures is visible whereas the aligned (κ = 500) vi-

sualization reveals only minor differences between

the surfaces. The different alignment for the non-

connected MDS is mainly caused by the rotational

DOF. An exemplary comparison of a single thicken-

ing at two points in time is shown in Figure 11.

The initialization with the prototype reduces the

calculation time for the MDS approximately by a fac-

tor of 2, as shown by the blue and purple curve in Fig-

ure 10. For larger radii, the duration to calculate the

dissimilarities by BFS is getting more dominant. The

calculation of the adjacency matrix is independent of

the chosen radius and therefore its computation time

is constant.

5 CONCLUSIONS AND

OUTLOOK

The presented approach results in a planar visual-

ization of the lung surface, which enables a global

assessment of the pleura. Potential ﬁndings can be

exactly located and assessed regarding their extent.

With the newly introduced temporal link, which im-

proves the consistency of the visualizations from dif-

ferent points in time, the planar representation can

also be utilized for a follow-up assessment. An im-

portant result is that this consistency does not have a

considerable negative inﬂuence on the ﬂattening qual-

ity. Additionally, with a closed-form initialization by

a prototype lung, the MDS can be sped up. The new

visualization can present simple scalar features. For a

correct judgment of pleural thickenings, the 3D view

is still required. However, the one-to-one mapping

of 2D points and 3D points enables an synchronized

3D volume and planar visualization. With this syn-

chronization, the user can beneﬁt from both visual-

ization types, as motivated in Figure 11. For docu-

mentation purposes, the planar representation itself is

highly useful to record the ﬁnal decision of the physi-

cian about the thickening locations.

Because of the rigid registration, only a rough

mapping of surface points to the prototype is possi-

ble. This limits the use of the prototype lung to the

initialization. With the presented approach, a perma-

nent link of all prototype points during optimization,

similar to the temporal link, would have a negative

impact on the ﬂattening quality. However, a perma-

nent link without negative inﬂuence on the ﬂattening

is desirable for inter-patient consistency and might be

an interesting topic for future research.

REFERENCES

Bentley, J. L. (1975). Multidimensional binary search

trees used for associative searching. Commun. ACM,

18(9):509–517.

Bronstein, A. M., Bronstein, M. M., and Kimmel, R.

(2003). Expression-invariant 3D face recognition. In

Audio-and Video-Based Biometric Person Authentica-

tion, pages 62–70. Springer.

Buja, A., Swayne, D. F., Littman, M. L., Dean, N., Hof-

mann, H., and Chen, L. (2008). Data visualization

with multidimensional scaling. Journal of Computa-

tional and Graphical Statistics, 17(2):444–472.

Carr, J. C., Fright, W. R., and Beatson, R. K. (1997). Sur-

face interpolation with radial basis functions for med-

ical imaging. IEEE Transactions on Medical Imaging,

16(1):96–107.

Chen, M., Helm, E., Joshi, N., and Brady, M. (2011).

Random walk-based automated segmentation for the

prognosis of malignant pleural mesothelioma. In

IEEE International Symposium on Biomedical Imag-

ing: From Nano to Macro, pages 1978–1981. IEEE.

Cox, T. F. and Cox, M. A. A. (2001). Multidimensional

Scaling. CRC Press.

Faltin, P., Chaisaowong, K., Ochsmann, E., and Kraus,

T. (2013). Vollautomatische Detektion und Ver-

laufskontrolle der pleuralen Verdickungen. In

53. Wissenschaftliche Jahrestagung der Deutschen

Gesellschaft f

ur Arbeitsmedizin und Umweltmedizin

e.V. (DGAUM), Arbeitsmedizin in Europa, Muskel-

Skelett-Erkrankungen und Beruf, page 144, Bregenz

(Austria).

Floater, M. S. and Hormann, K. (2005). Surface parame-

terization: a tutorial and survey. In Advances in mul-

tiresolution for geometric modelling, pages 157–186.

Springer.

Frauenfelder, T., Tutic, M., Weder, W., G

otti, R., Stahel,

R., Seifert, B., and Opitz, I. (2011). Volumetry: an

alternative to assess therapy response for malignant

pleural mesothelioma? European Respiratory Jour-

nal, 38(1):162–168.

Gleich, D. F. (2009). Models and Algorithms for PageRank

Sensitivity. PhD thesis, Stanford University. Chapter

7 on MatlabBGL.

Glocker, B., Komodakis, N., Paragios, N., and Navab, N.

(2010). Non-rigid registration using discrete mrfs:

Application to thoracic ct images. In Workshop Eval-

uation of Methods for Pulmonary Image Registration,

MICCAI 2010.

Grossmann, R., Kiryati, N., and Kimmel, R. (2002). Com-

putational surface ﬂattening: a voxel-based approach.

IVAPP 2016 - International Conference on Information Visualization Theory and Applications

244

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 24(4):433–441.

Hurdal, M. K. and Stephenson, K. (2009). Discrete confor-

mal methods for cortical brain ﬂattening. Neuroimage,

45(1):S86–S98.

Kengne Nzegne, P., Faltin, P., Kraus, T., and Chaisaowong,

K. (2013). 3D lung surface analysis towards segmen-

tation of pleural thickenings. In Bildverarbeitung f

die Medizin 2013, pages 253–258. Springer.

Kruskal, J. B. (1964). Multidimensional scaling by opti-

mizing goodness of ﬁt to a nonmetric hypothesis. Psy-

chometrika, 29(1):1–27.

Morse, B. S., Yoo, T. S., Rheingans, P., Chen, D. T., and

Subramanian, K. R. (2005). Interpolating implicit

surfaces from scattered surface data using compactly

supported radial basis functions. In Proc. ACM SIG-

GRAPH, pages 78–87. ACM.

Navon, I. and Legler, D. M. (1987). Conjugate-gradient

methods for large-scale minimization in meteorology.

Monthly Weather Review, 115(8):1479–1502.

Neubeck, A. and Gool, L. J. V. (2006). Efﬁcient non-

maximum suppression. In Proc. of International Con-

ference on Pattern Recognition, pages 850–855.

Ochsmann, E., Carl, T., Brand, P., Raithel, H., and Kraus,

T. (2010). Inter-reader variability in chest radiogra-

phy and HRCT for the early detection of asbestos-

related lung and pleural abnormalities in a cohort of

636 asbestos-exposed subjects. INT ARCH OCC ENV

HEA, 83:39–46.

Pistolesi, M. and Rusthoven, J. (2004). Malignant pleu-

ral mesothelioma: Update, current management, and

newer therapeutic strategies. Chest, 126(4):1318–

1329.

Rudrapatna, M., Mai, V., Sowmya, A., and Wilson, P.

(2005). Knowledge-driven automated detection of

pleural plaques and thickening in high resolution CT

of the lung. In Information Processing in Medical

Imaging, pages 147–167. Springer.

Rueckert, D., Sonoda, L. I., Hayes, C., Hill, D. L. G., Leach,

M. O., and Hawkes, D. J. (1999). Nonrigid regis-

tration using free-form deformations: Application to

breast MR images. IEEE Transactions on Medical

Imaging, 18:712–721.

Saroul, L., Figueiredo, O., and Hersch, R. D. (2006). Dis-

tance preserving ﬂattening of surface sections. IEEE

Transactions on Visualization and Computer Graph-

ics, 12(1):26–35.

Sensakovic, W. F., Armato III, S. G., Straus, C., Roberts,

R. Y., Caligiuri, P., Starkey, A., and Kindler, H. L.

(2011). Computerized segmentation and measurement

of malignant pleural mesothelioma. Medical physics,

38(1):238–244.

Tosun, D., Rettmann, M. E., and Prince, J. L. (2004).

Mapping techniques for aligning sulci across multiple

brains. Medical image analysis, 8(3):295–309.

Virta, R. L. (2012). 2012 Minerals Yearbook. U.S. Depart-

ment of the Interior, U.S. Geological Survey.

Zhao, X., Su, Z., Gu, X. D., Kaufman, A., Sun, J., Gao, J.,

and Luo, F. (2013). Area-preservation mapping using

optimal mass transport. Visualization and Computer

Graphics, IEEE Transactions on, 19(12):2838–2847.

Zigelman, G., Kimmel, R., and Kiryati, N. (2002). Tex-

ture mapping using surface ﬂattening via multidimen-

sional scaling. Visualization and Computer Graphics,

IEEE Transactions on, 8(2):198–207.

Flattening of the Lung Surface with Temporal Consistency for the Follow-Up Assessment of Pleural Mesothelioma

245