
Global Hybrid Registration for 3D Constructed Surfaces using
Ray-casting and Improved Self Adaptive Differential Evolution
Algorithm
Tao Ngoc Linh
1
, Tam Bui
1
and Hasegawa Hiroshi
2
1
Deparment of Functional Control Systems, Graduate School of Engineering and Science,
Shibaura Institute of Technology, Saitama 337-8570, Japan
2
Department of Machinery and Control System, College of Systems Engineering and Science,
Shibaura Institute of Technology, Saitama 337-8570, Japan
Keywords:
3D Registration, ISADE, Global Registration, Ray-casting.
Abstract:
As a fundamental task in computer vision, registration has been a solution for many application such as:
world modeling, part inspection and manufacturing, object recognition, pose estimation, robotic navigation,
and reverse engineering. Given two images, the aim is to find the best possible homogenous transformation
movement resulting in a more completed view of objects or scenarios. The paper presents a novel algorithm
of registering structured pointcloud surfaces by using a fast ray-casting based closest point method intergrated
with a new developed global optimization method Improve Self Adaptive Differential Evolution (ISADE).
Ray-casting based L
2
error calculation method enables the algorithm to find the local minima error effectively
while ISADE exploits the searching boundary to find the global minima. The new algorithm is evaluated on
structured images captured by a Kinect camera to show the superior in quality and robustness of ISADE over
state-of-the-art searching method and accuracy of the new method over a well known registration algorithm,
KinectFusion.
1 INTRODUCTION
The introduction of commercial depth sensing devices
such as Microsoft Kinect, Asus Xtion, etc has shifted
robotics, computer vision research areas from 2D
based imaging and laser scanning toward 3D based
depth scenes of environment processing. As a physi-
cal object or scenario can not be completely captured
with a single image, different images from different
time and positions need to be aligned into a more
completed view of the senario, the process of align-
ment is called registration. Registration algorithms
estimate the movement of the camera through cal-
culating the transformation that optimally maps two
point clouds. Various applications such as 3D ob-
ject scanning, 3D mapping, 3D localization use reg-
istration algorithms as backbone algorithms. Accord-
ing to how many views or images of the objects are
processed at the same time, registration strategies
are divided into multi-view registration (for all views
case) and pair-wise registration (for two views case).
Our paper focus on the pair-wise registration of con-
structed range images taken by 3D cameras. As a con-
sequence, starting from two views, i.e., the model and
the data, the objective of our registration process is to
find the best homogeneous transformation that, when
applied to the data, aligns it with the model in a com-
mon coordinate system.
Iterative Closest Point (ICP)(1) and its variants
such as non-linear ICP, generalized ICP and non-rigid
ICP have been always indispensable tools in registra-
tion tasks. ICP’s concept and implementationare easy
to understand. ICP uses L
2
error estimated from pair-
wise point-clouds to derive a transformation which
draws them closer to each other. Registration process
finishes after many iterations of minimizing error and
results in a homogeneous transformation.
However, ICP-class algorithms alone cannot solve
problems for general registration tasks since they re-
quire a further assumption in which a initial near-
optimal pose transformation is necessary for right
convergences. Otherwise, the registration process
would likely converge to local optimal solutions in-
stead of the global optimal or near global optimal
one. This result cannot be overcome merely by it-
eration procedure. In some mesh and point-cloud edi-
Linh, T., Hiroshi, H. and Bui, T.
Global Hybrid Registration for 3D Constructed Surfaces using Ray-casting and Improved Self Adaptive Differential Evolution Algorithm.
DOI: 10.5220/0005718901670174
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 167-174
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
167

tor softwares such as Meshlab (2), registering tool for
range data is available. It requires manually data pre-
alignment from users before ICP comes into use.
To overcome the shortage of ICP-class methods,
in general, registration processes are generally di-
vided into two steps: coarse transformation or initial-
ization and fine transformation. If two point-clouds
are close enough, the first step could be omitted. Oth-
erwise, the problem remains a big challenge for re-
searchers. Coarse transformation, pre-alignment es-
timation or initialization solving has two approaches:
local and global. Local methods use local descriptors
(or signatures) such as PFH(3) and SIFT(4) which en-
code local shape variation in neighborhood points. If
points with those descriptors appear in both register-
ing point-clouds, initialization movement could be es-
timated by using sample consensus algorithms such
as RANSAC (5). The problem of local approaches is
that those signatures are not always guarantied to ap-
pear on both registering point-clouds. On the other
hand, global approaches take every points into ac-
count such as Go-ICP (6) and SAICP(7). The biggest
problem of those methods is computation cost in find-
ing the corresponding points in point-clouds. If there
are big number of point in point-clouds, the compu-
tation cost is going large. However, thanks to new al-
gorithms especially heuristic optimal searching meth-
ods as well as the increasing in computer speed espe-
cially with parallel computing with multi-core CPU
processor and Graphic Computation Unit (GPU)(8) it
is possible to find solutions of global approaches of
registration problem. After estimating coarse trans-
formation, ICP algorithm is an efficient tool to find
the fine transformation.
This paper proposes a new global registration
method for 3D constructed images without need of
good initializing. It is called Global Hybrid Registra-
tion for 3D Constructed Surface Using Ray-casting
and ISADE (12). As other global registration meth-
ods, our method requires no local descriptors on
works directly on raw scan surfaces. The method uses
ray-casting based method for local minima searching
together with ISADE as a search engine to find the
global minima without using fine registration. Our
method rapidly produces results at high rate conver-
gence of the global optimization solution.
2 THREE DIMENSION
REGISTRATION
This part summaries some approaches for global
range image registration task up to date. SVD, PCA
(13) are integrated together with ICP as classical
methods and global searching algorithms are inte-
grated with ICP as in the most current methods.
2.1 ICP Algorithm
SVD and PCA have been used to find coarse trans-
formation together with ICP as the fine transforma-
tion estimating tool. Original version of ICP algo-
rithm relies on L
2
error to derive the transforma-
tion including rotation and translation. To register
two point-clouds X = {x
i
},{i = 1, 2,3,...,m} (model
point-cloud) and Y = {y
j
},{ j = 1,2,3,..., n} (data
point-clouds), where x
i
and y
j
∈ R
3
are point coor-
dinates of points in point-cloud. ICP algorithm arms
to find rotation R ∈ SO
3
and translation t ∈ R
3
, which
minimize L
2
type error as in Equation 1:
E(R,t) =
n
∑
i=1
e
i
(R,t) =
n
∑
i=1
|Rx
i
+ t− y
j
∗
| (1)
where R and t are rotation and translation matrix, y
j
∗
is the corresponding point of x
i
denoted for its clos-
est point in data point-cloud Y. There are some ICP
variants which rely on different categories to define
closest points. Point-to-point and Point-to-plane are
two popular examples. Equation 2 is used to search
for closest point by Point-to-point category.
j
∗
= argmin
j∈{1,...,n}
||Rx
i
+ t− y
j
|| (2)
The iteration process is as following to archives the
final transformation:
1. Compute the closest model points for each data
point as (2).
2. Compute the transformation R and t based on
the error from (1).
3. Apply R and t to the data point-clouds.
4. Repeat step 1, 2, 3 until error as (1) smaller
then a set tolerant or the procedure reaches its max
iteration.
Step by step, ICP draws the data point-cloud
closer to model point-cloud and the process stops
at local minima. There are some variants of ICP
algorithm based on different methods to calculate the
transformation from error E(R,t) and error itself as
in LMICP (14) and SICP (15).
2.2 Global Hybrid Searching Algorithm
ICP algorithms are superior for registering close or
pre-aligned point-cloud data, otherwise, it often con-
verges wrongly. Global searching algorithms are so-
lution to solve this problem since they are able to find
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
168

ICP step
ICP to local best
Begin p osition
Local best
Local best
NA search jump
Global best
Figure 1: global searching algorithm with ICP integrated.
f(x)
x
Figure 2: Example of flatten objective function after icp in
red color where original function is in black.
the global minima instead of local one. To make the
task of global searching algorithm less difficult, ICP
are often applied to flatten the searching space. Fig-
ure 1 and Figure 2 show how ICP works as a objec-
tive function flattening tool. By using ICP, a complex
fitness function in black turns into simpler one in red
color. And with such a much more flatten fitness func-
tion, global searching method find a global minima
more effectively.
The integration work well in case of point-cloud
data with small point number. For large data case,
ICP becomes slow and impossible for applying into
real time applications. Our method integrates new
global searching algorithm ISADE which works well
in complicated fitness function without flattening pro-
cess and fast error calculation method based on ray-
casting corresponding searching algorithm which ac-
celerates registration procedure to high speed.
3 METHOD OVERVIEW
3.1 Methodology Approach
The biggest disadvantage of ICP based registration
methods in calculating cost function is runtime. In
KinectFusion (16), a real-time scene reconstruction
algorithm, ICP is used as a only method for regis-
tering two continuous frames. The method requires
a powerful Graphic Card to fasten calculations and
reduce runtime. However, in global registration algo-
rithms with thousand times of error function calcula-
tion more than ICP through many iterations and pop-
ulations, to make the algorithm can run real-time, we
need a faster error calculation method. The proposed
algorithm takes the advantage of fast error calculat-
ing by using ray-casting based corresponding point
searching to applied for a new optimization algorithm
ISADE with a purpose of getting a faster and global
optimal convergence guaranty.
3.2 Ray-casting Closest Point
ICP-class algorithms often uses kd-tree(17) structure
to speed up the process of finding j
∗
in Equation 2.
The order of kd-tree searching closest algorithm is
O(log(n)) where n is number of searching point set.
Figure 3 shows an example of corresponding points
of the data point-cloud in the model one.
Figure 3: closest corresponding point defined in original
ICP algorithm.
Since depth image or point cloud data are often
obtained from 3D range camera in which the data
could be consider as an 2D gray image G where value
of each pixel show the depth of the point.
z
i,j
= G
i,j
(3)
where z
i, j
is depth of image at pixel i,j.
Equations 4 is to convert from depth image and real
3D depth data {x,y,z}.
x
i,j
= (i− cx)G
i,j
/fx (4a)
y
i,j
= (j− cy)G
i,j
/fy (4b)
z
i,j
= G
i,j
(4c)
where fx, fy, cx, cy are intrinsics of the depth camera.
In conversion, pixel position and structured expres-
sion of a point x,y,z can be calculated as equation 5.
G
i,j
= z
i,j
(5a)
i = round(cx+ x
i,j
∗ fx/G
i,j
) (5b)
Global Hybrid Registration for 3D Constructed Surfaces using Ray-casting and Improved Self Adaptive Differential Evolution Algorithm
169

j = round(cy+ y
i,j
∗ fy/G
i,j
) (5c)
Equations 5 is to calculate i,j of data points which are
also i,j of corresponding point in model point-clouds.
The idea of the method is showed as Figure 4 which
reminds the ray-casting process in computer vision.
j
i
datamodel
camera origin
Figure 4: Ray-casting method for searching corresponding
point.
3.3 Objective Function
The fitness function need to provide an error score
that is minimized when the best transformation ma-
trix are applied. The paper uses fitness function as
Equation 6.
F(R,t) = f(n)
1
n
2
n
∑
i=1
(Rx
i
+ t− y
j
∗
)
2
(6)
where f(n) is a function of inlier point number, n,
dependence. n is the number of inlier points in the
data point-cloud.
The error function should be smaller in bigger number
of inlier point. Since that, searching algorithm would
get rid of the case in which cost function is small for
only small inlier points. Function f(n) is calculated
as in Equation 7.
f(n) =
∞
1− n/N
if
n < N/10
n > N/10
(7)
where N is number of points in the data point-cloud.
3.4 ISADE
Differential evolution (DE) is an optimization tech-
nique originally proposed by Storn and Price (18). It
is categorized into evolution algorithm group which is
characterized by operators of mutation and crossover.
In DE, two important coefficients which play key rolls
to decide the correction and speed of convergence are
scaling factor F and crossover rate C
r
. Another im-
portant parameter in DE, population size NP remains
a user-assigned value to cope with problem com-
plexity. ISADE not only adaptively changes those
three coefficients but also integrates different muta-
tion schemes to take advantages of them.
3.4.1 Adaptive Learning Strategies Selection
In their paper of ISADE, Tam Bui et al. ran-
domly chose three mutation schemes which
are DE/best/1/bin, DE/best/2/bin and
DE/randtobest/1/bin. Among DE’s schemes,
DE/best/1/bin and DE/best/2/bin are known
for good convergence property and ”DE/rand to
best/1/bin” is known for good diversity. The
probability of applying those strategies are equal
equally assigned at with values p
1
= p
2
= p
3
= 1/3.
Equations 8 show the formula of chosen schemes.
DE/best/1 : V
G
i, j
= X
G
best, j
+ F(X
G
r1, j
− X
G
r2, j
) (8a)
DE/best/2 : V
G
i, j
= X
G
best, j
+ F(X
G
r1, j
− X
G
r2, j
)
+ F(X
G
r3, j
− X
G
r4, j
) (8b)
DE/randtobest/1 :V
G
i, j
= X
G
best, j
+F(X
G
best, j
−X
G
r2, j
)
+ F(X
G
r2, j
− X
G
r3, j
) (8c)
3.4.2 Adaptive Scaling Factor
In APGA/VNC appoach proposed by S.Tooyama and
H.Hasegawa (19), scaling factor changes according to
iteration as sigmoid function as in Equation 9.
F
i
=
1
1+ exp(α∗
i−NP/2
NP
)
(9)
ISADE give addition scaling F
mean
i
as in Equation 10.
F
mean
i
= F
min
+ (F
max
− F
min
)(
i
max
− i
i
max
)
n
iter
(10)
where
n
iter
= n
min
+ (n
max
− n
min
)(
i
i
max
) (11)
F
i
in Equation 9 is modified as in Equation 12.
F
i
=
F
i
+ F
mean
i
2
(12)
Now scaling factor is set to be high in first iterations
and after certain generations it become smaller for
proper exploitation.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
170
3.4.3 Crossver Control Parameter
ISADE algorithm is able to detect whether hight val-
ues of C
r
are useful and if a rotationally invariant
crossover is required. A minimum base for C
r
around
its median value is incorporated to avoid stagnation
around a single value. The control parameter C
r
is
assigned as Equation 13.
C
i+1
r
=
rand
2
ifrand
1
6 τ
C
i
r
otherwise
(13)
where rand
1
and rand
2
are random values ∈ [0,1], τ
presents probability to adjust C
r
. C
r
is adjusted as in
Equation 14.
C
i
r
=
C
r
min
C
r
min
6 C
i+1
r
6 C
r
medium
C
r
max
C
r
medium
6 C
i+1
r
6 C
r
max
(14)
where C
r
min
, C
r
medium
, C
r
max
denote low value, median
value and high value of crossover parameter respec-
tively. As in (12), we take τ = 0.1, C
r
min
= 0.05,
C
r
medium
= 0.50, C
r
max
= 0.95.
All above ideas and theories are implemented as in
flowchart in Figure 5.
Population Initialization
Start
Population rank evaluation
Adaptive scaling factor F
i
parameter C
r
Adaptive crossover control
Mutation with learning with
different strategies
Crossover
Selection
Ranking find best so far
maxgen?
Stop
No
Yes
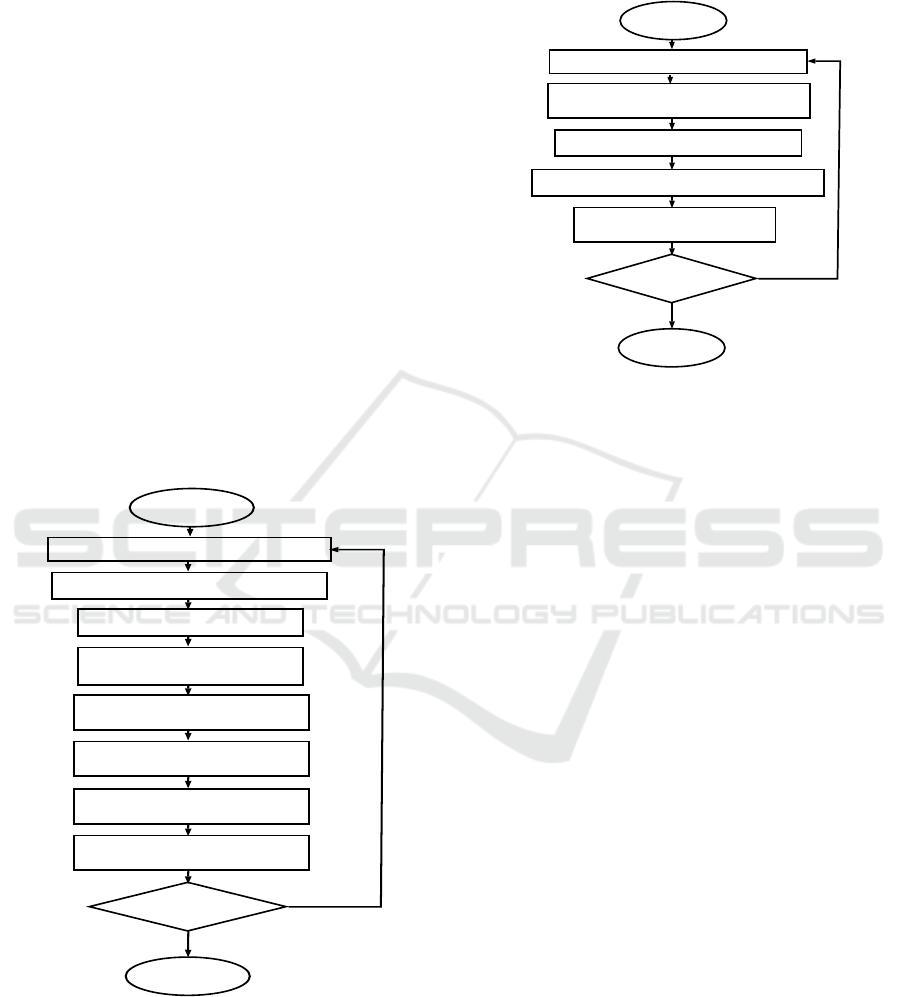
Figure 5: ISADE implementation process.
3.5 A New Combination Method
From initial position matrix, using ICP with one it-
eration to gain a slightly better rotation and transla-
tion matrix. The algorithm recalculates the error as in
Equation 6 and uses it in ISADE searching algorithm.
Flowchart in Figure 6 shows implementation of the
whole algorithm.
Generate new set of movement
Start
Calculate optimized Rotation a nd
Calculate cost function for each
Mutation, crossover, selectio n from ISADE
Ranking find best so far
maxgen?
Stop
No
Yes
Translation matrix for each position
new rotation and translation matrix
Figure 6: Registration with ISADE and Ray-casting.
4 EXPERIMENT AND RESULTS
This section arms at presenting a number of exper-
imental results to study how robust and accurate of
ISADE results in comparison to other Global search-
ing algorithm in using the same ray-casting based
error function as well as comparison of result from
new algorithm to KinecFusion in term of accuracy.
1) De Falco et al’s proposal (DE), Differential
Evolution as a viable tool for satellite image registra-
tion (20).
2) Valsecchi et al.’s proposal (GA), An Image
Registration Approach using Genetic Algorithms
(11).
3) Talbi et al.’s proposal (PSO), Particle Swarm
Optimization for Image Processing (10).
4) Luck et al.’s proposal (SA), registration of
range data using a hybrid simulated annealing and
iterative closest point algorithm (7).
The proposed algorithm is implemented in C++ and
compiled with GNU/g++ tool.
In order to perform a fair comparison between dif-
ferent optimization tools, in all methods, maximum
iteration is set to 100 with population of 25 for each
iteration. As SAICP is not a multi agent methods, its
maximum iteration is set to 2500.
4.1 Range Image Dataset
Our experiments carry out number of pair-wise
Global Hybrid Registration for 3D Constructed Surfaces using Ray-casting and Improved Self Adaptive Differential Evolution Algorithm
171

Figure 7: RGB-D 7 scenes Dataset for experiments.
registration task using well-known Depth data
taken from Kinect Microsoft Camera down-
loaded from website of Microsoft Research
http://research.microsoft.com/en-us/projects/7-
scenes/. Specifically, Figure 7 shows all scenes:
Chess, Fire, Heads, Office, Pumpkin, RedKitchen,
Stairs.
Those png format depth images are sub-sampled
into smaller solution of 128 × 96 which is 5 times
smaller than original solution of 640 × 480 in each
dimension. The reason for using smaller number of
points dataset is to archive considerable suitable run-
time while accuracy remains unchanged.
4.2 KinectFusion Error from Camera
Transpose
Accompany with depth datasets, 7 scenes database
gives us camera homogeneous transposes at each
frame calculated from Kinect-Fusion algorithm. Us-
ing those transpose, we could calculate transforma-
tion matrix between two scene as Equations 15.
T
j
i
= T
−1
i
∗ T
j
(15a)
T
j
i
=
R
j
i
t
j
i
0 0 0 1
(15b)
where T
j
i
is transformation matrix to move frame j to
align with frame i, T
i
and T
j
are homogeneous trans-
pose matrix for camera at frame i and j respectively,
R
j
i
,t
j
i
are rotation and translation matrix of T
j
i
.
R
j
i
,t
j
i
are applied into ray-casting error calculation
methods for two frames as in Equation 6 to draw er-
rors of KinectFusion algorithm for the next compari-
son step.
4.3 Parameter Settings
In each methods 30 runs were executed with two reg-
istration depth images are at distance of 20 frames
in the sequence. The searching space is set so rota-
tion and translation limitation at [−2π/10,2π/10] and
[−0.3, 0.3] separately. All methods are run on a PC of
Intel core I7-4790 CPU 3.60 GHz × 8 processor and
8 GB of RAM memory.
4.4 Comparision between Different
Algorithms
ISADE searching algorithm results are compared
with other algorithms’ results in three categories in-
cluding convergent rate, mean and standard deviation
which are shown in Table 1.
Table 1: Results of different algorithms for 7 scenes.
Scene name Algorithm CvR (%) Mean St. dev.
Chess ISADE 100 0.0695 0.0107
ref: 0.2483 DE 100 0.0752 0.0144
GA 0 1.8018 0.6643
PSO 10 0.6753 0.4502
SA 6.6667 0.9413 0.7171
Fire ISADE 100 0.0230 8.8565e-04
ref: 0.2431 DE 100 0.0290 2.5576e-04
GA 0 0.7740 0.2300
PSO 20 0.3497 0.2826
SA 6.6667 0.3306 0.2679
Heads ISADE 100 0.0024 3.5903e-05
ref: 2.9907 DE 100 0.0027 0.0048
GA 100 0.3080 0.1349
PSO 100 0.0824 0.0836
SA 73.3333 0.4494 0.3385
Office ISADE 100 0.0358 8.4689e-05
ref: 0.6294 DE 100 0.0371 8.2449e-04
GA 100 0.8577 0.3445
PSO 100 0.2819 0.3702
SA 33.3333 0.5526 0.5851
Pumpkin ISADE 100 0.0407 0.0071
ref: 0.111361 DE 100 0.0489 0.0127
GA 0 1.1097 0.4057
PSO 6.6667 0.3779 0.3330
SA 0 6.6667 0.6984
RedKitchen ISADE 100 0.0315 0.0049
ref: 0.0984 DE 93.3333 0.0473 0.0239
GA 0 1.4215 0.6508
PSO 0 0.4863 0.3829
SA 10 0.3021 0.2898
Stairs ISADE 100 0.0056 5.6268e-06
ref: 0.0156 DE 100 0.0062 0.0014
GA 0 0.9413 0.3373
PSO 0 0.2441 0.2435
SA 3.3333 0.4808 0.6281
KinectFusion error or reference value is considered
as correct convergence. In Table 1, convergence rate
(CvR) means percentage of algorithms results smaller
than reference value.
Proposed algorithm and DE are superior than
other methods in every categories. ISADE are bet-
ter than DE in almost cases only in the Fire scene
standard deviation of ISADE method larger than DE
method’s.
The proposed method are qualified in all tested
scenes with convergence value are always smaller
than reference value. This can be explained by ac-
cumulating error by using ICP algorithm from frame
to frame. As using ICP continuously from frame to
frame in Kinect Fusion algorithm error would be ac-
cumulated and become large. The final transforma-
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
172

tion matrix becomes less accurate than which gained
from direct registration method using only two frame.
Figure 8 shows four scenes registration results
using ISADE integrated algorithms including: Fire,
Head, Office, Stairs. Model pointsets are in red and
data pointsets are in grey color.
4.5 Runtime
For the data of 128× 96 resolution, average running
time for the proposed method are shown in Table 2.
The results show the average time for registration at
Table 2: Average runtime (in second) on different scenes.
Chess Fire Heads Office Pumpkin RedKitchen Stairs
7.5053 5.8596 8.0114 7.4527 5.9005 6.0466 7.8627
around 8 second. Two registering frames are at dis-
tance of 20 frames. That means the rate of register-
ing equivalence at rate of 2.5 fps (frames per second).
To make algorithm run at real-time rate of 20fps, the
speed need to be increased by 8 times. This is pos-
sible if we exploit all core of 8-core-processors not
mention using GPU.
Figure 8: Registration output example.
5 DISCUSSION AND
CONCLUSION
Image registration has been a very active research
area. Recently, the approach of using evolutionary
algorithms (EAs), especially new methods, proved
their potential of tackling image registration problem
based on their robustness and accuracy on searching
for global optimal. With EAs algorithm as search-
ing tools, it is not necessary to have good initials to
avoid local minima and converge to near-global min-
ima solutions. To do that, EAs algorithms need tuning
carefully to gain best results.
We proposed the new registration algorithm by in-
tegrating a new self-adaptive optimization algorithm
(ISADE) into a fast closest point searching method to
tackle well-known challenging task of computer vi-
sion area. In the experiments, the results show that
ISADE is able to find a robust and accurate transfor-
mation matrix of camera movement.
What is more important, accuracy and robustness
results has been obtained in comparison with other
state-of-the-art evolution based algorithms. ISADE
shows its superior than GA, PSO, SA in searching
for global minima solution. In comparision with
DE, ISADE also show its much better in almost
tested scenes. The robustness and accuracy is tested
and proved in real 3D scenes captured by Microsoft
Kinect camera.
In term of running time, by using fast searching
closest point methods, proposed algorithms are con-
sidered fast in our sense. It shows potential of apply-
ing in real-time application if using parallel program-
ing technique with multi-core processors.
In future work, ISADE algorithm can be imple-
mented in parallel in GPU (Graphic Processor Unit)
which can help algorithm reduces runtime to prove
real-time implement possibility in 3D reconstruction,
3D mapping and 3D localization.
REFERENCES
Besl, P.J.; McKay, Neil D., A method for registration of 3-
D shapes. Pattern Analysis and Machine Intelligence,
IEEE Transactions on , vol.14, no.2, pp.239,256, Feb
1992
”Meshlab opensource software”. http://meshlab.
sourceforge.net/
Radu Bogdan Rusu and Zoltan Csaba Marton and Nico
Blodow and Michael Beetz, Persistent Point Feature
Histograms for 3D Point Clouds. In Proceedings of
the 10th International Conference on Intelligent Au-
tonomous Systems (IAS-10), 2008
Anuj Sehgal, Daniel Cernea, and Milena Makaveeva. Real-
Time Scale Invariant 3D Range Point Cloud Registra-
tion. author = Wu, Fuli and Fang, Xianyong,
Wu, Fuli and Fang, Xianyong. An Improved RANSAC Ho-
mography Algorithm for Feature Based Image Mo-
saic. Proceedings of the 7th WSEAS International
Conference on Signal Processing, Computational Ge-
ometry & Artificial Vision, ISCGAV’07, 2007.
Jiaolong Yang, Hongdong Li, Yunde Jia. Go-ICP: Solving
3D Registration Efficiently and Globally Optimally.
Computer Vision (ICCV), 2013 IEEE International
Conference on , vol., no., pp.1457,1464, 1-8 Dec.
2013.
Luck J., Little C., Hoff, W.. Registration of range data us-
ing a hybrid simulated annealing and iterative closest
point algorithm. Robotics and Automation, 2000. Pro-
ceedings. ICRA ’00. IEEE International Conference
on , vol.4, no., pp.3739,3744 vol.4, 2000.
Global Hybrid Registration for 3D Constructed Surfaces using Ray-casting and Improved Self Adaptive Differential Evolution Algorithm
173

Neumann, D.; Lugauer, F.; Bauer, S.; Wasza, J.; Horneg-
ger, J.. Real-time RGB-D mapping and 3-D model-
ing on the GPU using the random ball cover data
structure. Computer Vision Workshops (ICCV Work-
shops), 2011 IEEE International Conference on , vol.,
no., pp.1161,1167, 6-13 Nov. 2011.
Ingber, L. . Simulated Annealing: Practice Versus Theory.
Math. Comput. Modelling 18, 29-57, 1993.
Talbi, H.; Batouche, M.C., ”Particle swam optimization
for image registration,” in Information and Commu-
nication Technologies: From Theory to Applications,
2004. Proceedings. 2004 International Conference on
, vol., no., pp.397-398, 19-23 April 2004
Valsecchi, A.; Damas, S.; Santamaria, J., ”An image reg-
istration approach using genetic algorithms,” in Evo-
lutionary Computation (CEC), 2012 IEEE Congress
on , vol., no., pp.1-8, 10-15 June 2012. doi:
”http://dx.doi.org/10.1016/j.asoc.2007.10.013”,
Tam Bui, Hieu Pham, Hiroshi Hasegawa, Improve Self-
Adaptive Control Parameters in Differential Evo-
lution for Solving Constrained Engineering Opti-
mization Problems. Journal of Computational Sci-
ence and Technology 01/2013; 7(1):59-74. DOI:
10.1299/jcst.7.59
S. Marden and J. Guivant, Improving the Performance of
ICP for Real-Time Applications using an Approxi-
mate Nearest Neighbour Search, Proceedings of Aus-
tralasian Conference on Robotics and Automation, 3-
5 Dec 2012, Victoria University of Wellington, New
Zealand.
Kok-lim Low, Linear least-squares optimization for point-
toplane ICP surface registration, Technical Report
TR04-004, Department of Computer Science, Univer-
sity of North Carolina at Chapel Hill, February 2004
Sofien Bouaziz and Andrea Tagliasacchi and Mark Pauly,
Sparse Iterative Closest Point, Journal Computer
Graphics Forum (Symposium on Geometry Process-
ing), volume 32, number 5, 2013, pages 1–11
Shahram Izadi and David Kim and Otmar Hilliges and
David Molyneaux and Richard Newcombe and Push-
meet Kohli and Jamie Shotton and Steve Hodges and
Dustin Freeman and Andrew Davison and Andrew
Fitzgibbon, KinectFusion: Real-time 3D Reconstruc-
tion and Interaction Using a Moving Depth Camera.
ACM Symposium on User Interface Software and
Technology, October 2011.
Chandran, Sharat. Introduction to kd-trees. University of
Maryland Department of Computer Science.
Storn, Rainer and Price, Kenneth, Differential Evolution A
Simple and Efficient Heuristic for global Optimization
over Continuous Spaces. Journal of Global Optimiza-
tion, volume 11, number 4, 1997 pages 341-359 doi:
10.1023/A:1008202821328.
Tooyama, S.; Hasegawa, H., Adaptive Plan system with
Genetic Algorithm using the Variable Neighborhood
range Control, in Evolutionary Computation, 2009.
CEC ’09. IEEE Congress on , vol., no., pp.846-853,
18-21 May 2009.
I. De Falco and A. Della Cioppa and D. Maisto and E.
Tarantino. ”Differential Evolution as a viable tool for
satellite image registration ”. Applied Soft Comput-
ing, volume 8, number 4, pages 1453 - 1462. 2008.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
174
