A Turntable-based Approach for Ground Truth Tracking Data

Generation

Zolt

an Pusztai

1,2

and Levente Hajder

Distributed Events Analysis Laboratory, MTA SZTAKI, Kende utca 13-17. H-1111, Budapest, Hungary

otv

os Lor

and University, Budapest, Hungary

Keywords:

Ground Truth Dataset, Ground Truth Dataset, 3D Scanner, 3D Reconstruction.

Abstract:

Quantitative evaluation of feature trackers can lead signiﬁcant improvements in accuracy. There are widely

used ground truth databases in the ﬁeld. One of the most popular datasets is the Middlebury database to

compare optical ﬂow algorithms. However, the database does not contain rotating 3D objects. This paper

proposes a turntable-based approach that ﬁlls this gap. The key challenge here is to calibrate very accurately

the applied camera, projector, and turntable. We show here that this is possible, even if just a simple chessboard

plane is used for the calibration. The proposed approach is validated on 3D reconstruction and ground truth

tracking data generation of real-world objects.

1 INTRODUCTION

Developing a realistic 3D approach for feature tracker

evaluation is very challenging since realistic moving

3D objects can simultaneously rotate and translate,

moreover, occlusion can also appear in the images.

It is not easy to implement a system that can generate

ground truth (GT) data for real-world 3D objects. The

aim of this paper is to present a novel structured-light

reconstruction system that can produce extremely ac-

curate feature points of rotating spatial objects.

The Middlebury database

is considered as the

state-of-the-art GT feature point generator. The

database itself consists of several datasets that had

been continuously developed since 2002. In the

ﬁrst period, they generated corresponding feature

points of real-world objects (Scharstein and Szeliski,

2002). The ﬁrst Middlebury dataset can be used for

the comparison of feature matchers. Later on, this

stereo database was extended with novel datasets us-

ing structured-light (Scharstein and Szeliski, 2003) or

conditional random ﬁelds (Pal et al., 2012). Even sub-

pixel accuracy can be achieved in this way as it is dis-

cussed in (Scharstein et al., 2014).

However, our goal is to generate tracking data via

multiple frames, the stereo setup is too strict limita-

tion for us.

http://vision.middlebury.edu/

The description of the optical ﬂow datasets of

Middlebury database was published in (Baker et al.,

2011). It was developed in order to make the optical

ﬂow methods comparable. The latest version contains

four kinds of video sequences:

1. Fluorescent Images: Nonrigid motion is taken by

a color and a UV-camera. Dense ground truth

ﬂow is obtained using hidden ﬂuorescent texture

painted on the scene. The scenes are moved

slowly, at each point capturing separate test im-

ages in visible light, and ground truth images with

trackable texture in UV light.

2. Synthesized Database: Realistic images are gen-

erated by an image syntheses method. The tracked

data can be computed by this system as every

parameters of the cameras and the 3D scene are

known.

3. Imagery for Frame Interpolation: GT data is com-

puted by interpolating the frames. Therefore the

data is computed by a prediction from the mea-

sured frames.

4. Stereo Images of Rigid Scenes: Structured light

scanning is applied ﬁrst to obtain stereo recon-

struction. (Scharstein and Szeliski 2003). The

optical ﬂow is computed from ground truth stereo

data.

The main limitation of the Middlebury optical

ﬂow database is that the objects move approximately

500

Pusztai, Z. and Hajder, L.

A Turntable-based Approach for Ground Truth Tracking Data Generation.

DOI: 10.5220/0005719404980509

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 500-511

ISBN: 978-989-758-175-5

linearly, there is no rotating object in the datasets.

This is a very strict limitation as tracking is a chal-

lenging task mainly when the same texture is seen

from different viewpoint.

It is interesting that the Middlebury multi-view

database (Seitz et al., 2006) contains ground truth 3D

reconstruction of two objects, however, the ground

truth tracking data were not generated for these se-

quences. Another limitation of the dataset is that only

two low-textured objects are used.

It is obvious that tracking data can also be gen-

erated by a depth camera (Sturm et al., 2012) such

as Microsoft Kinect, but its accuracy is very limited.

There are other interesting GT generators for planar

objects such as the work proposed in (Gauglitz et al.,

2011), however, we would like to obtain the tracked

feature points of real spatial objects.

Due to these limitations, we decided to build a

special hardware in order to generate ground truth

data. Our approach is based on a turntable, a cam-

era, and a projector. They are not too costly, however,

the whole setup is extremely accurate as it is shown

here.

Accurate Calibration of Turntable-based 3D Scan-

ners. The application of structured-light scanner is

a relatively cheap and accurate possibility to build a

real 3D scanner as it is discussed in the latest work

of (Moreno and Taubin, 2012). Another possibility

for a very accurate 3D reconstruction is laser scan-

ning (Bradley et al., 1991), however, the accurate cal-

ibration of the turntable is not possible using a laser

stripe since it can only reconstruct a 2D curve at a mo-

ment. For turntable calibration, the reconstruction of

2D objects is a requirement since the axis of the rota-

tion can be computed by registrating the point clouds

of the same rotating object.

Moreover, the calibration of the camera and pro-

jector intrinsic and extrinsic parameters is also cru-

cial. While the camera calibration can be accurately

carried out by the well-known calibration method

of (Zhang, 2000), the projector calibration is a more

challenging task. The projector itself can be consid-

ered as an inverse camera: while the camera projects

the 3D world to the 2D image, the projector projects

the planar image onto the 3D world. For this rea-

son, the corresponding points of the 3D world and

the projector image cannot be matched. Therefore,

ﬁrstly the pixel-pixel correspondences have to be de-

tected between the camera and the projector. The

application of structured light was developed in or-

der to efﬁciently realize this correspondence detec-

tion (Scharstein and Szeliski, 2003).

Many projector calibration methods exist in the

ﬁeld. The ﬁrst popular class of existing solu-

tions (Sadlo et al., 2005; Liao and Cai, 2008; Ya-

mauchi et al., 2008) is to (i) use a calibrated camera

to determine the world coordinate, (ii) then a pattern

is projected onto the calibration plane, the corners are

detected and locations are estimated in 3D, (iii) then

the 3D → 2D correspondences are given by running

the (Zhang, 2000) calibration. The drawback of this

kind of approaches is that its accuracy is relatively

low since the projected 3D corner locations are esti-

mated, and these estimated data are used for the ﬁnal

calculation.

Another possible solution is to ask the user to

move the projector at different positions (Anwar et al.,

2012; Jamil Drar

eni, 2009). It is not possible for our

approach as the projector is ﬁxed. Moreover, the ac-

curacy of these kind of approaches is also very low.

There are algorithms where both projected and

printed pattern are used (Audet, 2009; Martynov

et al., 2011). The main idea here is that if the pro-

jected pattern is iteratively adjusted until it fully over-

laps the printed pattern, then the projector parameters

can be estimated. Color patterns can also be applied

for this purpose (Park and Park, 2010). However, we

found that this quite complicated method is not re-

quired to calibrate the camera-projector system.

Our calibration methods for both the camera and

projector use a simply chessboard plane. Our al-

gorithms are very similar to those of (Moreno and

Taubin, 2012). As it is shown here later, we cali-

brate the camera ﬁrst by the method of (Zhang, 2000).

Then the point correspondences between camera and

projector pixels are determined by robustly estimating

the local homography close to the chessboard corners.

Then the intrinsic projector parameters can be com-

puted by (Zhang, 2000) as well. The extrinsic param-

eters (relative translation and orientation between the

camera and the projector) can given by a stereo cal-

ibration problem. For this purpose, there are several

solutions as it is discussed in (Hartley and Zisserman,

2003) in detail. However, we found that the accuracy

of stereo calibration is not accurate, therefore we pro-

poses a more sophisticated estimation here.

Contribution of this Study. The main novelty of

this paper is that we show here that very accurate GT

feature data can be generated for rotating object if a

camera-projector system is applied with turntable. To

the best of our knowledge, our approach is the ﬁrst

system that can yield such accurate GT tracking data.

The usage of a turntable for 3D reconstruction itself is

not a novel idea, but its application for GT data gen-

eration it is.

The calibration algorithms within the system have

a minor and a major improvements:

• The camera-projector correspondence estimation

A Turntable-based Approach for Ground Truth Tracking Data Generation

501

Turntable

Projector

Object

Camera

Figure 1: Hardware components of structured light scanner. Left: schematic ﬁgure. Right: Realized scanner.

is based on a robust (RANSAC-based) homogra-

phy estimation.

• The turntable calibration is totally new: while

usual turntable calibrators (Kazo and Hajder,

2012) compute the axis by performing a usual

chessboard-based calibration method (Zhang,

2000) for the rotating chessboard plane, and the

axis of the rotation is computed from the extrin-

sic camera parameters, we propose a novel opti-

mization problem that minimizes the reprojection

for the corners of the rotating chessboard. We

found the accuracy of this novel algorithm is sig-

niﬁcantly better. During the turnable calibration,

the extrinsic parameters of the camera and projec-

tor are also obtained.

2 PROPOSED EQUIPMENT AND

ALGORITHMS

Our 3D scanner consists of 3 main parts. It is visu-

alized in Fig. 1. The left plot is the schematic setup,

while the right one shows the realization of the scan-

ner. The main components of the equipment are the

camera, the projector, and the turntable. Each of the

above needs to be calibrated correctly to reach high

accuracy in 3D scanning. The camera and the pro-

jector are ﬁxed to their arms, but the turntable can

move

: it is able to rotate the object to be recon-

structed.

The bottleneck of the proposed approach is the

calibration of the components. In this section, it is

overviewed how the camera, the projector, and the

axis of the rotating table can be accurately calibrated.

These arms are also moving, but their calibration is not

considered here, it is a possible future work.

The paper is organized as follows. The software

components are overviewed in Figure 2. The cam-

era, projector and turntable calibration is described in

Section 2.1, 2.1, and 2.3, respectively. Sec. 3 shows

how accurate GT data can be generated by the devel-

oped equipment. Finally, Sec. 6 concludes the work

and discusses the limitations. calibration,

2.1 Camera Calibration

For describing the camera we choose the pinhole

model with radial distortion. Assuming that the coor-

dinate system is aligned to the camera, the projection

of the point X ∈ R

to the camera plane is u ∈ R

which can be described by the equation:

u = K

˜u,





γ p

0 f

0 0 1





˜u =



[1 + k

+ k

]

[1 + k

+ k

]



= u

+ u

where K

stands for the camera matrix, f

and f

are

the focal length, (p

, p

) is the principal point, and γ is

the shear. In our case we only used radial distortion,

which can be described by two parameters: (k

The camera matrix and the distortion parameters are

together called the intrinsic parameters of the camera.

A black and white chessboard is held in sight of

the camera at arbitrary positions. Images were taken

and the chessboard corners were found on the images,

and they reﬁned to reach sub-pixel precision. Then we

can compute the intrinsic parameters of the camera by

the method of (Zhang, 2000).

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

502

parameters

calibration

Camera

calibration

Projector

Basic Calibration

calibration images

illuminated by projector

Turntable Calibration

in Chessboard Plane

Axis Point Estimation

camera extrinsic

parameters

projector extrinsic

parameters

camera intrinsic

projector intrinsic

turntable axis

using PnP Method

with/without illumination of projector

Images of rotating chessboard

Axis Direction Estimation

Figure 2: Software components of the whole calibration pipeline.

2.2 Projector Calibration

Since the projector can be viewed as an inverse cam-

era, it can be described by the same model applied for

the camera before. However, ﬁnding the right pro-

jector pixels, which through the chessboard corners

are seen from the viewpoint of the projector is not

so obvious. To overcome this problem, a structured

light sequence is projected to the scene. It precisely

encodes the pixel coordinates in the projector image.

For each scene point, the projected codes has to be

decoded. From this point, the chessboard must be

placed in a position that can be viewed from both the

camera and projector.

The structured light we used for the calibration is

based on the binary Gray code since it is the most

accurate coding for structured light scanning as it is

discussed in (Scharstein and Szeliski, 2003). In addi-

tion, we project inverse images after every single one,

meaning that every pixel on the images is reversed.

But before structured light utilized, full black and

white images are projected for easier object recogni-

tion, and for easier decoding of the structured light.

Since the resolution of our projector is 1024×768,

the number of the projected images are 42 for each

chessboard orientation. The projected sequence con-

sists of 2 pure black and white images, 10 images for

encoding the horizontal, and 10 for encoding the ver-

tical coordinates of each projector pixel. Addition-

ally, the inverse images have to be inserted into the

sequence as well. These images are taken from one

viewpoint, and they are called as the image set.

After all the images are taken, one can begin

the decoding of the structured light. First of all, we

calculate the direct and indirect intensity of the light,

pixel by pixel for each image set. The full method is

described in (Nayar et al., 2006). Then the minimum

and maximum intensities are determined per pixel

and then the direct and indirect values are given by

the equations as follows:

max

− L

min

1 − B

2(L

min

− B ∗ L

max

)

1 − B

Where B is the amount of light emitted by a

turned-off projector pixel. We needed to separate

these 2 components from each other, because we are

only interested in the direct intensities lit by the pro-

jector.

Then we need to classify the pixels on each image

pair, consisting the image given by the structured light

and its inverse. There are 3 clusters to classify into:

1. The pixel is lit on the ﬁrst image.

2. The pixel is not lit on the ﬁrst image.

3. Cannot be determined.

The classiﬁcation rules are as follows:

• L

< M =⇒ the pixel is in the 3. class,

• L

> L

∧ P

> P

=⇒ the pixel is lit,

• L

> L

∧ P

< P

=⇒ the pixel is not lit,

• P

< L

∧ P

> L

=⇒ the pixel is not lit,

• P

> L

∧ P

< L

=⇒ the pixel is lit,

• otherwise it cannot be determined.

The pixel intensity in the ﬁrst and inverse images are

denoted by P

, and P

, respectively, while M is a user-

deﬁned threshold: M = 5 is set in our approach. If the

difference between P

and P

is greater than M, then

the pixel is discarded.

For further reading about the classiﬁcation, we

recommend to read the study of (Xu and Aliaga,

2007).

Since the chessboard consists of alternating black

and white squares, decoding near the chessboard cor-

ners can resolve errors. To avoid these errors, we cal-

culate local homographies around the corners. We use

A Turntable-based Approach for Ground Truth Tracking Data Generation

503

11 pixel-wide kernel window and every successfully

decoded projector pixel is in consideration. For the

homography estimation, a RANSAC-based (Fischler

and Bolles, 1981) DLT homography estimator is ap-

plied in contrast to the work of (Moreno and Taubin,

2012) where robustiﬁcation is not dealt with. We

found that the accuracy is increased when RANSAC-

scheme is applied. After the homography is com-

puted among the camera and projector pixels, we use

this homography to transform the camera pixels to the

projector image. In this way we get the exact projec-

tor pixels we needed, so we can use the method of

(Zhang, 2000) to calibrate the projector. Remark that

the extrinsic projector calibration will be reﬁned later,

but the intrinsic parameters will not.

2.3 Turntable Calibration

The aim of the turntable calibration is to compute the

axis of the turntable. It is represented by a point and

a direction. Therefore, the degree of freedom of a

general axis estimation is four (2 DoFs: position of a

plane; other 2 DoFs: direction) .

Fortunately, the current problem is constrained.

We know that the axis is perpendicular to the plane

of the turntable. Thus, the direction is given, only

the position should be calculated within the turntable

plane.

The turntable is calibrated if we know the center-

line which the table is turning around. Two methods

was used to calculate this 3D line. First we place the

chessboard on the turntable, and start rotating it. Im-

ages are taken between the rotations, and the extrinsic

parameters can be computed for each image since the

camera is already calibrated. This motion is equiv-

alent with the motion of a steady chessboard and a

moving camera. The circle that the camera follows

has the same centerline as the turntable. Thus ﬁtting a

circle to the camera points estimates the centerline of

the turntable (Kazo and Hajder, 2012).

However, we found that this method is not accu-

rate enough. Therefore, we developed a novel algo-

rithm that is overviewed in the rest of this section.

2.3.1 Problem Statement of Turntable Axis

Calibration

Given a chessboard with known size, for which the

corners can be easily detected by widely used pat-

tern recognition algorithms, the goal is to estimate

the axis of the turntable. This is part of the calibra-

tion of a complex structured-light 3D reconstruction

system that consists of one camera, one projector, and

one turntable. The latter one is driven by a stepping

motor, the angle of the rotation can be very accurately

set. The camera and projector intrinsic parameters are

also known, in other words, they are calibrated.

The input data for axis calibration comes from de-

tected chessboard corners. The chessboard are placed

on the turntable. Then it is rotated and images are

taken with different rotational axis. The corners are

detected on all of these images. Then the chessboard

is placed in a higher position on the turntable, but the

new plane orientation is also parallel to the turntable.

Then the chessboard are rotated, and the corners are

detected as well. (The chessboard can be placed in

arbitrary altitudes. We only use two different values,

but the proposed calibration method can work with

arbitrary number of positions.)

If we consider the case when the planes of the

chessboard and the turntable are parallel, the distance

between them is h, then the chessboard corners can be

written as





= (1)



cosα − sin α

sinα cosα



x − o

y − o









cosαx − sin αy + o

(1 − cos α) + o

sinα

sinαx + cos αy − o

cosα + o

(1 − cos α)



where α denotes the current angle of the rotation.

Note that altitude h does not inﬂuence the relation-

ship. Also remark that capital X and Y denote spatial

coordinates, while their lowercase letters (x and y) are

2D coordinates in image space.

2.3.2 Proposed Algorithm

The proposed axis calibration consists of two main

steps:

1. Determination of the axis center [o

]

chessboard plane, and

2. computation of the camera and projector extrinsic

parameters.

Axis Center [o

]

Estimation on Chessboard

Plane. The goal of the axis center estimation is

to calculate the location [o

]

. We propose an

alternation-type method with two substeps:

Homography-step. The plane-plane homography

is estimated for each image. The 2D locations

of the corners in the images are known. The 2D

coordinates can be determined in the chessboard

plane by Eq. 1. If the homogenous coordinates are

used, the relationship becomes

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

504









∼





cosαx − sin αy + o

(1 − cos α) + o

sinα

sinαx + cos αy − o

cosα + o

(1 − cos α)





(2)

We apply the standard normalized direct linear

transformation (normalized DLT) with a numerical

reﬁnement step (Hartley and Zisserman, 2003) in or-

der to estimate the homography. It solves the lin-

earized version of Eq. 2:

E (α,x,y,o

) = E

(α,x,y,o

)+E

(α,x,y,o

)

where

(α,x,y,o

) =

(cosαx − sin αy + o

(1 − cos α) + o

sinα) +

(sinαx + cos αy + −o

cosα + o

(1 − cos α)) +

−

(cosαx − sin αy + o

(1 − cos α) + o

sinα) −

(sinαx + cos αy + −o

cosα + o

(1 − cos α)) −

and

(α,x,y,o

) =

(cosαx − sin αy + o

(1 − cos α) + o

sinα) +

(sinαx + cos αy + −o

cosα + o

(1 − cos α)) +

−

(cosαx − sin αy + o

(1 − cos α) + o

sinα) −

(sinαx + cos αy + −o

cosα + o

(1 − cos α)) −

This is a linear problem. The center and the scale of

the applied coordinate system can be arbitrary chosen.

As it is discussed in (Hartley and Zisserman, 2003),

the mass center and quasi-uniform scale is the most

accurate choice. The error function E (α,x,y, o

)

can be written for every chessboard corner point for

every rotational angle. Therefore, the minimization

problem is formulated as

argmin

∑

i=1

∑

j=1

∑

k=1

E (α

i,α

j,α

x,α

y,α

where a

∈ [0,2π], x

∈ [0,G

], and y

∈ [0,G

and G

are the dimensions of chessboard cor-

ners, respectively. (Possible values for (x

) are

(1,1),(1,2),(2,1),...etc. ) This problem remains an

over-constrained homogeneous linear one that can be

optimally solved.

Axis-step. Its goal is to estimate the axis location

]

. The above two equations are linear with re-

spect to the center coordinates. Therefore, the equa-

tions form a homogeneous linear system of equations

A[o

]

= b, where

A =





where

= h

− h

cosα − h

sinα −

u(h

− h

cosα − h

sinα),

= h

sinα + h

− h

cosα −

u(h

sinα + h

− h

cosα),

= h

− h

cosα − h

sinα −

v(h

− h

cosα − h

sinα),

= h

sinα + h

− h

cosα −

v(h

sinα + h

− h

cosα),

and

b =



− b



where

= h

(x cosα − y sin α) + h

(ycosα + x sin α),

= h

) +

u(h

(x cosα − y sin α) + h

(ycosα + x sin α),

= h

(x cosα − y sin α) + h

(ycosα + x sin α),

= h

v(h

(x cosα − y sin α) + h

(ycosα + x sin α)).

The above equations can be written for all corners

of the chessboard for all rotated positions. There-

fore, both the homography- and the axis-steps are ex-

tremely over-constrained. Thus, the parameters can

be very accurately estimated. It is interesting that

the homography and the axis location estimations

are homogeneous, and inhomogeneous linear prob-

lems, respectively. They can also solved for the over-

determined case as it is well-known (Bj

orck, 1996).

The two substeps have to be run one after the

other. Both steps minimize the same algebraic error,

therefore the method converges to the closest (local)

minimum. Unfortunately, global optimum cannot be

theoretically guaranteed. But we found that the algo-

rithm converges to the correct solution. The speed of

A Turntable-based Approach for Ground Truth Tracking Data Generation

505

the convergence is relatively fast, to our experiments,

20 − 30 iterations are required to reach the minimum.

Parameter Initialization. The proposed alternation

method requires initial values for o

and o

. It has

been found that the algorithm is not too sensitive to

the locations of the initial values. The center of the

chessboard is an appropriate solution for o

and o

Moreover, we have tried more sophisticated methods.

If the camera centers are estimated by a Perspective

n Point (PnP) algorithm such as (Lepetit et al., 2009),

then the camera centers for the rotating sequence form

a circle (Kazo and Hajder, 2012) as it is mentioned in

the ﬁrst part of this section. The center of this circle is

also a good initial value. However, we found that the

correct solution is reached as well if the initial center

is an arbitrary point within the chessboard region.

2.3.3 Axis Center Estimation in the Global

System

The ﬁrst algorithm estimates the center of the axis

in the coordinate system of the chessboard. But the

chessboard are placed in different positions with dif-

ferent altitudes. The purpose of the algorithm dis-

cussed in this section is to place the rotated chess-

board in the global coordinate system and to deter-

mine the extrinsic parameters (location and orienta-

tion) of the projector. The global system is ﬁxed to

the camera, therefore, the camera extrinsic parame-

ters have not to be estimated.

In our calibration setup, only two chessboard se-

quences are taken. The extrinsic position can be eas-

ily determined. If the 3D coordinates of the plane are

known, the 2D locations are detected, then the esti-

mation of the projective parameters is called the PnP

problem. Mathematically, the PnP optimization can

be written as

argmin

R,t

∑

i=1

∑

j=1

∑

k=1

Rep



R,t,



i,α

j,α





i,α



where the deﬁnition of the function Rep is as fol-

lows:

Rep





R,t,



















DeHom

















−







The applied comma (’) means that the origin

of the coordinate system for chessboard corners

are placed at [o

]

.Function DeHom gives

the dehomogeneous 2D vector of a spatial vector

as DeHom([X,Y, Z]

) = [X/Z,Y /Z]

There are solutions that can cope with planar

points. We used the EPnP (Lepetit et al., 2009) al-

gorithm for our approach. At this point, the rel-

ative transformation between the chessboard planes

and the camera can be calculated. They are denoted

by [R

], and [R

]. The altitude of the chessboard

can be measured. Without loss of generalization, al-

titude of the ﬁrst plane can be set to zero: h

= 0.

(The simplest way is to set the ﬁrst chessboard to the

turntable. Then the altitude of the second chessboard

can be easily measured with respect to the turntable.)

The estimation of one parameter is relatively sim-

ple. We solve it by exhaustive search. The best value

is given by the rotation for which the reprojection er-

ror of the PnP problem is minimal:

argmin

R,t

∑

i=1

∑

j=1

∑

k=1



Rep

+ Rep



where

Rep

= Rep







i,α

j,α







i,α

j,α









Rep

= Rep







i,k







i,α+α

j,α+α









where the upper index denotes the number of the

chessboard. The relationship between the left and

right terms are that the spatial points have to rotated

with the same angle, but a ﬁx angular offset ∆α has to

be added to each rotation for the second chessboard

plane with respect to the ﬁrst one. (The setup is vi-

sualized in Fig. 3.) The impact of ∆α for the second

rotation matrix is written as follows:





cos∆α − sin ∆α 0

sin∆α cos∆α 0

0 0 1





(3)

The minimization problem is also a PnP one,

therefore it can be efﬁciently solved by (Lepetit et al.,

2009). The estimation of ∆α is obtained by an ex-

haustive search.

Finally, the extrinsic parameters of the projector

are computed by running the PnP algorithm again for

the corners detected in the projector images. The ob-

tained projector parameters have to be transformed by

the inverse of the camera extrinsic parameters since

our global coordinate system is ﬁxed to the camera.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

506

Figure 3: Visualized chessboard planed in the ﬁrst position.

The edged are not parallel, therefore the relative angle ∆α

has to be estimated.

2.4 Object Reconstruction

The object reconstruction looks very similar to the

projector calibration. In this case, an object is placed

on the turntable instead of the chessboard. Structured

light is projected onto it, images are taken, then the

object is rotated. This procedure is repeated until

the object returns to the starting position. Then we

decode the projector pixels back from the structured

light projected in each image set. After it is done,

we use the Hartley-Strum triangulation (Hartley and

Sturm, 1997) for corresponding camera-projector pix-

els due to its accuracy to determine the object points

from one viewpoint. We calculate these for each

viewpoint, and then we can combine the point sets

together, which results a 3D points et of the full ob-

ject.

3 RESULTS

The main advantage of our method is that the whole

GT data generation is totally automatic. Therefore,

arbitrary number of objects can be reconstructed. We

show here four typical objects that have well trackable

feature points. They are as follows:

• Dinosaur. A typical researcher enjoys the recon-

struction of dinosaurs as it is shown in several sci-

entiﬁc papers, e.g (”Fitzgibbon et al., 1998). For-

tunately, kids also like it, and one of the authors’

sons has a plastic dinosaurs that could be recon-

structed. Therefore, we inserted a dino to our test-

ing dataset.

• Flacon. The Plastic holder is a good test case

since at least one well-textured label is ﬁxed on

the surface of a usual ﬂacon.

• Plush Dog. The tracking of the feature point of a

soft toy is a challenging task as it does not have a

ﬂat surface. For this reason, we include a plush

dog into the testing database.

• Poster. The last sequence of our dataset is a rotat-

ing newspaper page. It is useful since it is a simple

textured plane. The efﬁciency of the trackers can

be checked in this example due to two reasons: (i)

there is no occlusion, and (ii) the feature tracking

is the determination of a plane-plane homography.

During the test, the objects were rotated by the

turntable, the difference of the degree of two subse-

quent was set to 3

◦

. Our GT tracking data generator

has two modes. (i) The ﬁrst version regularly gener-

ates the feature points in the ﬁrst image. The feature

points are located across a regular grid in the valid re-

gion of the camera image. (ii) The points in the ﬁrst

image is determined by a feature generator. We use

the SIFT features (Lowe, 1999) in our testing exam-

ples, but arbitrary feature generators can be included.

Then the generated feature points were recon-

structed in the ﬁrst image using the structured light.

Then these 3D reconstructed point coordinates were

rotated around the turntable axis with the known ro-

tating axis, and projected to the next image. This pro-

cedure was repeated for all the images of the test se-

quence. The 2D feature coordinates after projection

give the ﬁnal GT for quantitative feature tracker com-

parison.

The input images of the sequences are visualized

in Figs. 4– 7. The 3D model of the reconstructed ob-

jects are also visualized in these Figures except the

Poster as it is a planar paper and its 3D model is not

interesting. The 3D models are represented by col-

ored point clouds, however, the color itself does not

inﬂuence the reconstruction. It is only painted due to

its spectacularity.

The computed ground truth data for the four ex-

amined sequences are pictured in Figs. 8– 11. The

ﬁrst row shows the tracked points when the points are

selected across a grid. The second rows of Figs. 8– 7

consist of images with the tracked GT SIFT feature

points (yellow dots). We also applied an automatic

feature tracker (BruteForceMatcher of OpenCV) and

the estimated feature points are drawn in the images

with red color. However, the comparison of feature

vectors is out of the scope of this paper, we only want

to demonstrate that this comparison can be easily car-

ried out.

The obtained ground truth data were visually

checked by us and we have not found any inaccu-

racy on it. We think that the accuracy is below

pixel, in other word, subpixel accuracy was reached.

This is extremely low as the camera resolution is

2592 × 1936 (5 Mpixel).

A Turntable-based Approach for Ground Truth Tracking Data Generation

507

Figure 4: Two images of the ’Dino’ sequence and the reconstructed 3D point cloud from three viewpoints.

Figure 5: Two images of the ’Plush Dog’ sequence and the reconstructed 3D point cloud from three viewpoints.

Figure 6: Two images of the ’Flacon’ sequence and the reconstructed 3D point cloud from three viewpoints.

Figure 7: Two images from the ’Poster’ sequence.

4 COMPARISON OF

WELL-KNOWN FEATURE

TRACKERS

Thought this paper does not concentrate on the com-

parison of feature trackers, we run the most popu-

lar trackers implemented in the OpenCV library

Each tracker consists of separated methods in order

to generate, describe, and ﬁnally track good features.

However, the generation and description is given by

the same algorithms in our examples. The tracking

(matching) is different, we selected the most accurate

tracker for the generators based on our tests.

The applied feature generators are as follows:

1. Scale Invariant Feature Transform (SIFT) (Lowe,

1999)

2. Speeded Up Robust Features (SURF) (Bay et al.,

2008)

3. KAZE (Alcantarilla et al., 2012)

http://opencv.org

4. Accelerate KAZE (AKAZE) (Alcantarilla et al.,

2013)

5. Binary Robust Invariant Scalable Keypoints

(BRISK) (Leutenegger et al., 2011)

6. ORB (Oriented FAST and Rotated BRIEF)

(Rublee et al., 2011)

Several matchers have been tested for the selected

feature detectors/descriptors. OpenCV supports a

brute-force based matchers as well as the Flann (Fast

Approximate Nearest Neighbor) matcher (Muja and

Lowe, 2009). In the case of the brute-force based

matchers, all descriptors on the ﬁrst image are com-

pared with all descriptors on the second image and

the best match, when the distance of the descriptors

is the lowest, is chosen. In Fig 12, ’BF L1’ means

that the brute-force matcher is used with the L

norm,

while ’BF H1’ means that the brute-force matcher is

used with the Hamming distance. L

norm is used for

algorithms ’BF L2’ and ’BF H2’.

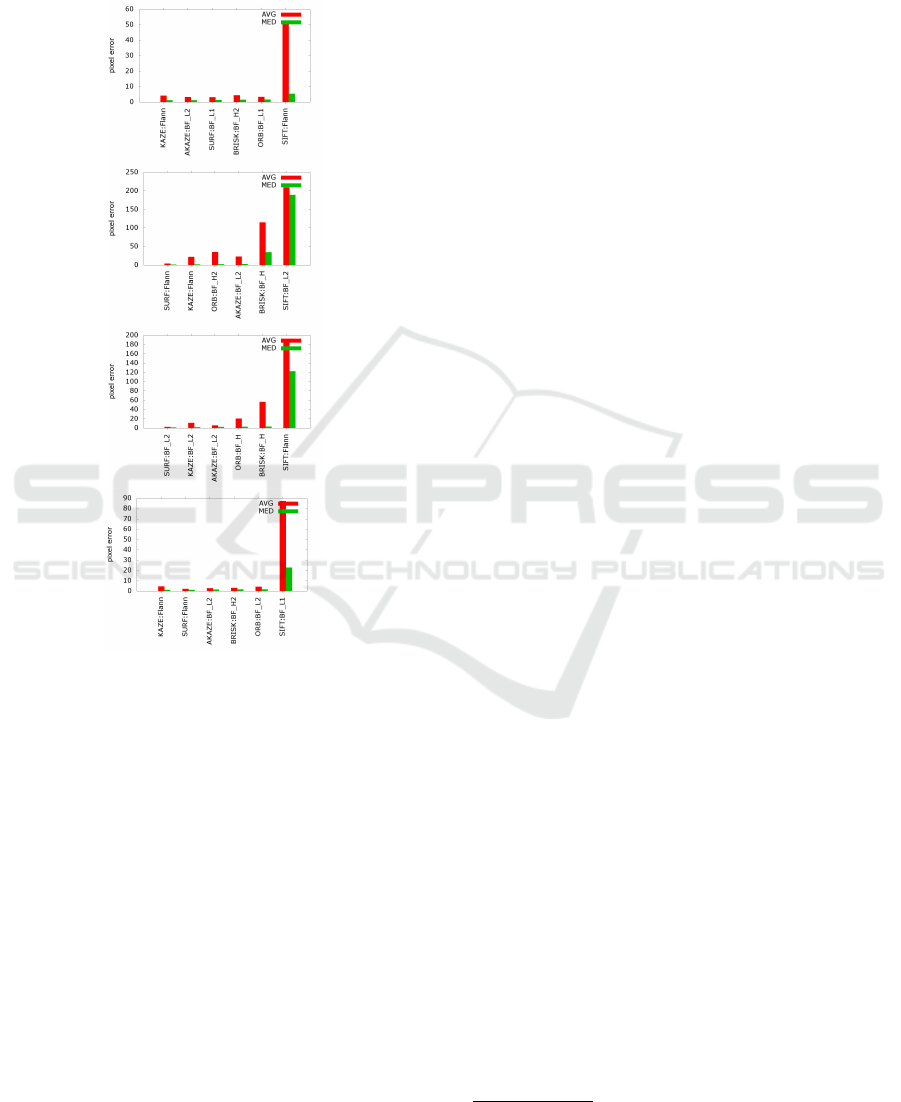
The rival trackers are compared on every test se-

quence. The error of the feature tracking is deﬁned

as the difference between the tracked and GT coor-

dinates. The averages are calculated for each frame,

and this mean values is the error for the examined fea-

ture. Then the error of all feature errors are computed

as well. The median of the feature errors is also cal-

culated. These mean and median values of the rival

trackers are visualized in the plots of Fig. 12.

The detailed description of the feature detectors

and the evaluation of the test results are out of the

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

508

Figure 8: The visualized ground truth tracking data drawn on images of the ’Flacon’ sequence. Top row: features generated

by a grid within valid image region. Bottom row: features generated by SIFT method.

Figure 9: The visualized ground truth tracking data drawn on images of the ’Dino’ sequence. Top row: features generated by

a grid within valid image region. Bottom row: features generated by SIFT method.

Figure 10: The visualized ground truth tracking data drawn on images of the ’Plush Dog’ sequence. Top row: features

generated by a grid within valid image region. Bottom row: features generated by SIFT method.

Figure 11: The visualized ground truth tracking data drawn on images of the ’Poster’ sequence. Top row: features generated

by a grid within valid image region. Bottom row: features generated by SIFT method.

A Turntable-based Approach for Ground Truth Tracking Data Generation

509

scope of this paper. We know that more informa-

tion are required to compare the methods, this short

description only wants to demonstrate that quantita-

tive comparison is possible by our equipment. A deep

comparison will be published very soon.

Figure 12: Tracking error for test sequences. Avg: mean,

Med: median. From top to bottom: Results for ’Flacon’,

’Dino’, Plush Dog’, and ’Poster’ testing objects.

5 LIMITATIONS & FUTURE

WORK

The main goal of the approach proposed here is to

be able to generate ground truth tracking data of

real-world rotating objects. Therefore, the turntable-

based equipment is unable to simulate moving cam-

eras. However, other databases (e.g. the famous Mid-

dlebury one) can do that, thus our approach should

be uniﬁed with existing datasets. Nevertheless, our

equipment contains two moving arms for both the

camera and projector, therefore novel viewpoints can

be added to the system. It is possible if the arms are

very accurately calibrated. This is a possible feature

work of our GT generation project.

Another disadvantage of the current system is that

part of the objects can be self-occluded due to the ob-

ject rotation. This cannot be detected by the hard-

ware, therefore surface reconstruction is required to

detect if the part of the scanned 3D object is occluded

by another part. To avoid this problem, we plan to de-

velop a continuous surface reconstruction method for

free-form spatial objects. If their quality is reliable,

it will help to detect the self-occlusion of the moving

objects.

6 CONCLUSIONS

We have proposed a novel GT tracking data genera-

tor here that can automatically produce very accurate

tracking data of rotating real-world spatial objects.

The main novelty of our approach is that it consists

of a turntable, and we showed how this turntable can

be accurately calibrated. Finally, the validation of our

equipment was shown. It was justiﬁed that the pro-

posed structured-light 3D scanner can produce accu-

rate tracking data as well as realistic 3D point clouds.

The GT tracking data are public, they are available at

our web page

REFERENCES

Alcantarilla, P. F., Bartoli, A., and Davison, A. J. (2012).

Kaze features. In ECCV (6), pages 214–227.

Alcantarilla, P. F., Nuevo, J., and Bartoli, A. (2013). Fast

explicit diffusion for accelerated features in nonlin-

ear scale spaces. In British Machine Vision Conf.

(BMVC).

Anwar, H., Din, I., and Park, K. (2012). Projector calibra-

tion for 3d scanning using virtual target images. Inter-

national Journal of Precision Engineering and Manu-

facturing, 13(1):125–131.

Audet, S.and Okutomi, M. (2009). A user-friendly method

to geometrically calibrate projector-camera systems.

In Computer Vision and Pattern Recognition Work-

shops, pages 47 – 54.

Baker, S., Scharstein, D., Lewis, J., Roth, S., Black, M.,

and Szeliski, R. (2011). A database and evaluation

methodology for optical ﬂow. International Journal

of Computer Vision, 92(1):1–31.

Bay, H., Ess, A., Tuytelaars, T., and Van Gool, L. (2008).

Speeded-up robust features (surf). Computer Vision

and Image Understanding, 110(3):346–359.

orck,

A. (1996). Numerical Methods for Least Squares

Problems. Siam.

Bradley, C., Vickers, G., and Tlusty, J. (1991). Automated

rapid prototyping utilizing laser scanning and free-

http://web.eee.sztaki.hu

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

510

form machining. CIRP Annals – Manufacturing Tech-

nology, 41(1):437–440.

Fischler, M. and Bolles, R. (1981). RANdom SAmpling

Consensus: a paradigm for model ﬁtting with appli-

cation to image analysis and automated cartography.

Commun. Assoc. Comp. Mach., 24:358–367.

”Fitzgibbon, A. W., Cross, G., and Zisserman, A. (”1998”).

”automatic 3D model construction for turn-table se-

quences”. In ”3D Structure from Multiple Images of

Large-Scale Environments, LNCS 1506”, pages ”155–

170”.

Gauglitz, S., H

ollerer, T., and Turk, M. (2011). Evaluation

of interest point detectors and feature descriptors for

visual tracking. International Journal of Computer

Vision, 94(3):335–360.

Hartley, R. I. and Sturm, P. (1997). Triangulation. Computer

Vision and Image Understanding: CVIU, 68(2):146–

157.

Hartley, R. I. and Zisserman, A. (2003). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press.

Jamil Drar

eni, S

ebastien Roy, P. S. (2009). Geometric

video projector auto-calibration. In Proceedings of the

IEEE International Workshop on Projector-Camera

Systems, pages 39–46.

Kazo, C. and Hajder, L. (2012). High-quality structured-

light scanning of 3D objects using turntable. In IEEE

3rd International Conference on Cognitive Infocom-

munications (CogInfoCom) , pages 553–557.

Lepetit, V., F.Moreno-Noguer, and P.Fua (2009). Epnp: An

accurate o(n) solution to the pnp problem. Interna-

tional Journal Computer Vision, 81(2):155–166.

Leutenegger, S., Chli, M., and Siegwart, R. Y. (2011).

Brisk: Binary robust invariant scalable keypoints. In

Proceedings of the 2011 International Conference on

Computer Vision, pages 2548–2555.

Liao, J. and Cai, L. (2008). A calibration method for un-

coupling projector and camera of a structured light

system. In IEEE/ASME International Conference on

Advanced Intelligent Mechatronics, pages 770 – 774.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In Proceedings of the International

Conference on Computer Vision, ICCV ’99, pages

1150–1157.

Martynov, I., Kamarainen, J.-K., and Lensu, L. (2011). Pro-

jector calibration by ”inverse camera calibration”. In

SCIA, volume 6688 of Lecture Notes in Computer Sci-

ence, pages 536–544.

Moreno, D. and Taubin, G. (2012). Simple, accurate, and

robust projector-camera calibration. In 2012 Second

International Conference on 3D Imaging, Modeling,

Processing, Visualization & Transmission, Zurich,

Switzerland, October 13-15, 2012, pages 464–471.

Muja, M. and Lowe, D. G. (2009). Fast approximate near-

est neighbors with automatic algorithm conﬁguration.

In In VISAPP International Conference on Computer

Vision Theory and Applications, pages 331–340.

Nayar, S. K., Krishnan, G., Grossberg, M. D., and Raskar,

R. (2006). Fast separation of direct and global com-

ponents of a scene using high frequency illumination.

ACM Trans. Graph., 25(3):935–944.

Pal, C. J., Weinman, J. J., Tran, L. C., and Scharstein, D.

(2012). On learning conditional random ﬁelds for

stereo - exploring model structures and approximate

inference. International Journal of Computer Vision,

99(3):319–337.

Park, S.-Y. and Park, G. G. (2010). Active calibration of

camera-projector systems based on planar homogra-

phy. In ICPR, pages 320–323.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). Orb: An efﬁcient alternative to sift or surf.

In Proceedings of the 2011 International Conference

on Computer Vision, ICCV ’11, pages 2564–2571.

Sadlo, F., Weyrich, T., Peikert, R., and Gross, M. H.

(2005). A practical structured light acquisition sys-

tem for point-based geometry and texture. In Sympo-

sium on Point Based Graphics, Stony Brook, NY, USA,

2005. Proceedings, pages 89–98.

Scharstein, D., Hirschm

uller, H., Kitajima, Y., Krathwohl,

G., Nesic, N., Wang, X., and Westling, P. (2014).

High-resolution stereo datasets with subpixel-accurate

ground truth. In Pattern Recognition - 36th German

Conference, GCPR 2014, M

unster, Germany, Septem-

ber 2-5, 2014, Proceedings, pages 31–42.

Scharstein, D. and Szeliski, R. (2002). A Taxonomy and

Evaluation of Dense Two-Frame Stereo Correspon-

dence Algorithms. International Journal of Computer

Vision, 47:7–42.

Scharstein, D. and Szeliski, R. (2003). High-accuracy

stereo depth maps using structured light. In CVPR

(1), pages 195–202.

Seitz, S. M., Curless, B., Diebel, J., Scharstein, D., and

Szeliski, R. (2006). A comparison and evaluation of

multi-view stereo reconstruction algorithms. In 2006

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition (CVPR 2006), 17-22

June 2006, New York, NY, USA, pages 519–528.

Sturm, J., Engelhard, N., Endres, F., Burgard, W., and Cre-

mers, D. (”2012”). ”a benchmark for the evaluation

of rgb-d slam systems”. In ”Proc. of the International

Conference on Intelligent Robot Systems (IROS)”.

Xu, Y. and Aliaga, D. G. (2007). Robust pixel classiﬁcation

for 3d modeling with structured light. In Proceedings

of the Graphics Interface 2007 Conference, May 28-

30, 2007, Montreal, Canada, pages 233–240.

Yamauchi, K., Saito, H., and Sato, Y. (2008). Calibration

of a structured light system by observing planar ob-

ject from unknown viewpoints. In 19th International

Conference on Pattern Recognition, pages 1–4.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22(11):1330–1334.

A Turntable-based Approach for Ground Truth Tracking Data Generation

511