Virtual Correction of Eyesight using Visual Illusions

Midori Aoki, Fumihiko Sakaue and Jun Sato

Department of Computer Science and Engineering, Nagoya Institute of Technology,

Gokiso, Showa, Nagoya 466-8555, Japan

Keywords:

Eyesight Correction, Visual Illusion, Lateral Inhibition, High Resolution, Deconvolution.

Abstract:

Degradation of eyesight is a serious problem, and the number of weak-sighted people is increasing rapidly in

recent years because of the spread of tablets and smart phones. The weak-sighted people often wear glasses and

contact lenses for recovering their eyesight. However, these rectiﬁcation devises are painful for weak-sighted

people. Thus, in this paper, we propose a novel method for displaying visual information for weak-sighted

people to see rectiﬁed images on displays. In particular, we show that visual illusions in human vision system

can be used efﬁciently for correcting the eyesight. By using our method, weak-sighted people can see clear

images on the display without wearing glasses and contact lenses. The efﬁciency of the proposed method is

tested by using synthetic signals and real images.

1 INTRODUCTION

In recent years, many people suffer from eyesight

problems. Young people often have nearsightedness

because of reading textbooks, tablets etc., and old

people have farsightedness because of aging. Once

we have eyesight problems, we usually wear eye

glasses or contact lenses. However, these glasses and

contact lenses are painful, and they also cause stress

to weak-sighted people.

Thus, we in this paper propose a method for cor-

recting the eyesight of weak-sighted people virtually

by showing modiﬁed images on displays. The near-

sightedness and farsightedness cause depth blurs on

the retina, and these depth blurs can be described by

the convolution of a point spread function (PSF) with

the original image.

For correcting the weak-sightedness, Alonso and

Barreto (Alonso and Barreto, 2003) proposed a

method for displaying deconvolution images with the

PSF of weak-sightedness. However, the dynamic

range of the deconvolution images becomes much

larger than that of the standard displays, and thus we

need to reduce the contrast of the deconvolution im-

ages, or cut out the over range signals which causes

errors in eyesight correction. For showing clear

images without reducing image contrast, Huang et

al. (Huang et al., 2012; Wetzstein et al., 2012; Huang

et al., 2014) proposed eyesight correction based on

light ﬁeld displays. The light ﬁeld displays can con-

trol the light ﬁeld emitted from the display system,

and thus they enable us to concentrate lights on the

retina in the eyeball, even if the eyeball has weak-

sightedness. Although the light ﬁeld displays can

correct weak-sightedness, they require micro lens ar-

rays in front of the display or multi-layer structure of

display planes. Thus their structures are very com-

plex, and precise calibrations of optical system are re-

quired. The light ﬁeld displays also require very high

resolution 2D displaying systems in general, since

they control 4D light ﬁelds.

In this paper, we propose a method for showing

clear images to weak-sighted people using standard

displays. For this objective, we consider visual illu-

sions in human visual systems. It is known that the

human visual system observes various types of illu-

sion, such as shape distortion, color distortion and

intensity distortion. In this paper, we in particular

consider visual illusion on perceived intensity. It is

known that the intensity illusion occurs based on the

so called lateral inhibition (Ratliff, 1965) in visual

neurons. The lateral inhibition can be considered as

a natural signal ﬁlter equipped in the human visual

systems. We in this paper use the lateral inhibition

of human visual systems to visualize clear images to

weak-sighted people.

Aoki, M., Sakaue, F. and Sato, J.

Virtual Correction of Eyesight using Visual Illusions.

DOI: 10.5220/0005719801250130

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 127-132

ISBN: 978-989-758-175-5

 2016 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

127

Figure 1: Chevreul illusion caused by the lateral inhibition.

These ﬁve intensities are constant in each area. However, at

the boundary of two different intensities, the bright intensity

is observed more brightly, and the dark intensity is observed

more darkly. As a result, we perceive the change in intensity

in a constant intensity area.

2 VISUAL ILLUSION AND

LATERAL INHIBITION

We ﬁrst consider visual illusion on perceived inten-

sity. There are many types of intensity illusions, but it

is known that most of the intensity illusions are based

on a simple property of human visual systems, that is

lateral inhibition. The lateral inhibition is an activity

in human visual systems, in which an excited neuron

suppresses the excitement of neighboring neurons in

visual systems. Because of the lateral inhibition, a

small difference in the input signal is emphasized in

the output signal. As a result, we perceive the over-

shoot and undershoot of intensity at the discontinuity

of original image intensity. These overshoot and un-

dershoot in perceived intensity cause various visual

illusions, such as Mach band illusion (Ratliff, 1965)

and Chevreul illusion (Chevreul, 1890). Fig. 1 shows

the example of Chevreul illusion, in which we per-

ceive the change in intensity in a constant intensity

area, which is caused by the overshootand undershoot

of perceived intensity at the boundary of two different

intensities.

The lateral inhibition can be modeled by the dif-

ference of Gaussian (DOG) or the Laplacian of Gaus-

sian (LOG) (Marr and Hildreth, 1980). In this paper

we model the lateral inhibition by using the Laplacian

of Gaussian ∇

G(x, y) as follows:

∇

G(x, y) =

G(x, y) +

G(x, y) (1)

Since the output signal S

(x, y) is the sum of the orig-

inal input signal S

(x, y) with the lateral inhibition, it

can be described by the following convolution:

(x, y) = L(x, y) ∗ S

(x, y) (2)

where, L(x, y) is a function which causes lateral in-

hibition, and can be described by using the Laplacian

of Gaussian and the Dirac delta function δ(x, y) as fol-

(a) original signal

(b) observed signal

Figure 2: Visual illusion caused by the lateral inhibition.

(a) shows the original input image signal, and (b) shows the

observed signal with the lateral inhibition.

lows:

L(x, y) = δ(x, y) − α∇

G(x, y) (3)

α denotes the magnitude of lateral inhibition in hu-

man visual systems, and its value must be chosen em-

pirically.

Fig. 2 shows the distortion of perceived intensity

caused by the lateral inhibition modeled by Eq. (2).

Fig. 2 (a) shows the original input signal and (b)

shows the output signal derived from Eq. (2). As

shown in this ﬁgure, the difference of intensity in the

original signal has been emphasized in the output sig-

nal. The important point is that the human visual sys-

tem can perceive higher intensity than the maximum

intensity of display system, and can also perceiveneg-

ative intensity, i.e. intensity lower than the zero level

of display system. This means the human visual sys-

tem can perceive wider dynamic range images than

those shown on the display. In the following part of

this paper, we use this property of human visual sys-

tems for correcting weak-sight in human vision efﬁ-

ciently.

3 PRE-FILTERING FOR

WEAK-SIGHTED PEOPLE

If we have nearsightedness or farsightedness, the ob-

served images have depth blur. This depth blur can

be described by the convolution of the original input

image S

(x, y) with a point spread function P(x, y) as

follows:

(x, y) = P(x, y) ∗ S

(x, y) (4)

Thus, if we know the point spread function P(x, y) of

a weak-sighted person, the clear non-blurring image

can be observed by the weak-sighted person by show-

ing the deconvolution image generated by the follow-

ing equation:

′

(x, y) = P(x, y)

−1

∗ S

(x, y) (5)

By substituting S

′

in Eq. (5) into S

in Eq. (4), we

ﬁnd that the observed image S

(x, y) will be identical

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

128

with the original image S

(x, y) as follows:

(x, y) = P(x, y) ∗ S

′

(x, y)

= P(x, y) ∗ P(x,y)

−1

(x, y)

= S

(x, y) (6)

This method is proposed by Alonso and Bar-

reto (Alonso and Barreto, 2003).

However, the intensity of the new input image S

′

derived from the deconvolution overﬂows the range

of display in general, and its intensity sometimes be-

comes higher than the maximum intensity of the dis-

play, and sometimes becomes minus. Since the mi-

nus intensity and out of range intensity cannot be

shown by the display, we have to modify the dy-

namic range of the deconvolution image S

′

, so that

its range is within the dynamic range of the display.

However, this modiﬁcation drastically degrades the

dynamic range of the observed image. For avoiding

this problem, Huand et al. (Huang et al., 2012) pro-

posed a multi-layer display system, which consists of

multiple display planes. Although is can control the

light ﬁeld and correcting weak-sightedness avoiding

the dynamic range problem, the device structure of

the multi-layer display is quite complex, and it is very

difﬁcult of construct as it is pointed out by the same

authors.

4 PRE-FILTERING BASED ON

VISUAL ILLUSION

For solving the dynamic range problem by using

the standard displaying system, we next propose a

method for generating display images based on visual

illusions in intensity.

In our method, we do not modify the dynamic

range of the input image S

. In stead of modifying

the dynamic range of S

, we simply cut out the out of

range intensity in the deconvolution image S

′

as fol-

lows:

′′

(x, y) = C[S

′

(x, y)]

= C[P(x, y)

−1

∗ S

(x, y)] (7)

where, C[I] is a cut out function which takes the fol-

lowing values according to the intensity I:

C[I] =







0 (I < 0)

255 (I > 255)

I (otherwise)

(8)

However, S

′′

is no longer identical with S

′

, and thus

the observed image S

of S

′′

is not identical with the

(a) sinusoidal signal (b) step signal

Figure 3: The original image signals used in our experi-

ments. (a) is a sinusoidal signal and (b) is a step signal.

original image S

as follows:

(x, y) = P(x, y) ∗ S

′′

(x, y)

= P(x, y) ∗C[P(x, y)

−1

(x, y)]

6= S

(x, y) (9)

Thus, what we need to do is to ﬁnd a display image

′′

(x, y), which minimizes the following observation

error E:

E =

∑

||S

(x, y) − P(x, y) ∗ S

′′

(x, y)||

(10)

As we have seen in section 2, the human visual

system can perceive higher dynamic range images

than those shown by the display system. Thus, by

using this property, we may be able to derive better

display images for human observers. For counting the

lateral inhibition L(x, y) in human vision system, we

consider the following observation error E

′

instead of

E in Eq.(10):

′

∑

||L(x, y) ∗ S

(x, y)

−L(x, y) ∗ P(x, y) ∗ S

′′

(x, y)||

(11)

However, S

′′

(x, y) does not have enough freedom to

minimize E

′

effectively. Thus, we consider a high res-

olution image S

′′

′

, y

′

) as the display image, and de-

rive the high resolution display image S

′′

′

, y

′

) which

minimizes the following observation error E

′′

∑

||L(x, y) ∗ S

(x, y)

−D[L(x

′

, y

′

) ∗ P(x

′

, y

′

) ∗ S

′′

′

, y

′

)]||

(12)

where, D[·] denotes the down sampling from high

resolution to the original image resolution, and

L(x

′

, y

′

) and P(x

′

, y

′

) represent lateral inhibition and

PSF in high resolution. Assuming the lateral inhibi-

tion and the PSF of the observer are known, the opti-

mum display image S

′′

′

, y

′

) can be derived from the

objective image S

(x, y) by minimizing E

′′

5 EXPERIMENTS

We next show the efﬁciency of the proposed method

by using synthetic image signals and real images.

Virtual Correction of Eyesight using Visual Illusions

129

(a) normal sight

(b) normal sight

(d) weak sighted

Figure 4: The images observed by a normal sight observer

and a weak-sighted observer. (a) and (b) show the observa-

tion of the normal sight observer, and (c) and (d) show the

observation of the weak-sighted observer respectively.

5.1 Synthetic Image Experiments

We ﬁrst show results from synthetic image signals.

Fig. 3 (a) and (b) show two different original image

signals. (a) is a sinusoidal signal and (b) is a step

signal. In this experiment, we assume that the lateral

inhibition of human observer is modeled by Eq.(3),

where the standard deviation of the Gaussian function

is 1.0 pixel and α = 3.0. The PSF of the weak-sighted

observer is a Gaussian function with the standard de-

viation of 2.5 pixels. Then, Fig. 4 (a) and (b) show

the observation of a normal sight observer, and (c)

and (d) show the observation of the weak-sighted ob-

server. As shown in (c) and (d), the observations of

the weak-sighted observer are blurred. Also, the ob-

served intensity range of the weak-sighted observer is

smaller than that of the normal sight observer.

We derived display images for weak-sighted ob-

server by using four different methods, that is (1)

existing method, (2) lateral inhibition method, (3)

high resolution method, and (4) lateral inhibition with

high resolution method. The existing method derives

display images based on Eq.(7). The lateral inhibi-

tion method derives display images which minimize

Eq.(10). The high resolution method derives display

images based on Eq.(11). The lateral inhibition with

high resolution method derives display images which

minimize Eq.(12). The number of image pixels in the

high resolution display is twice of that in the normal

resolution display in this experiment. i

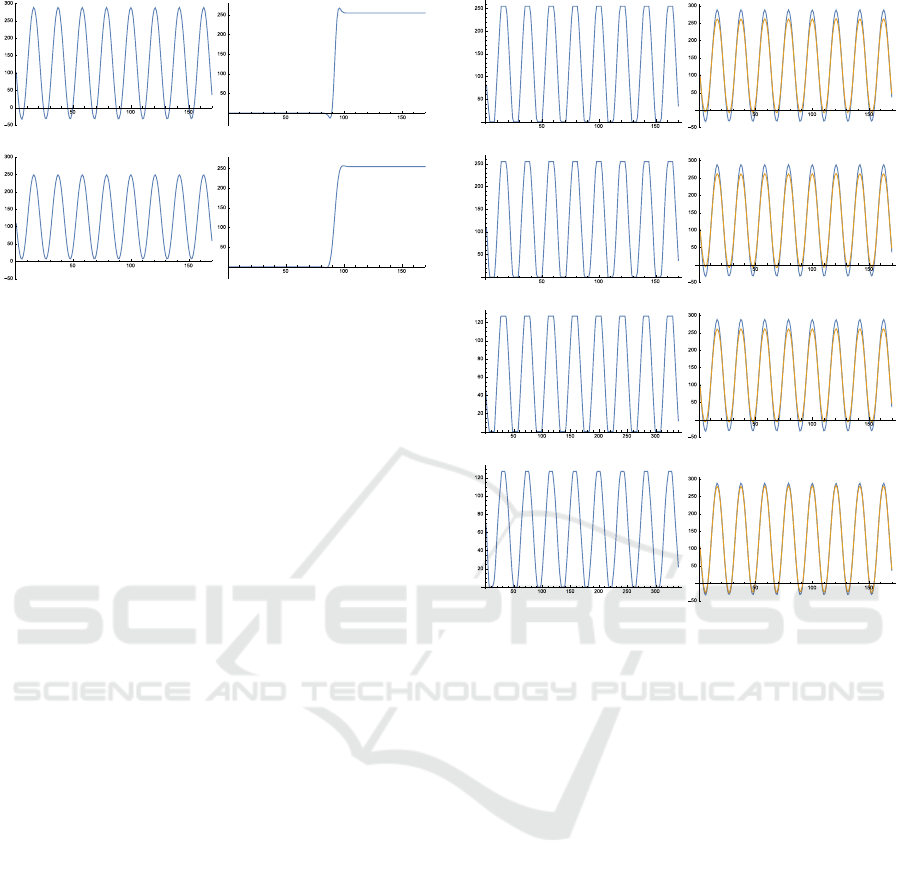
The left column of Fig. 5 shows display images

generated by using these four methods, and the right

column of Fig. 5 shows images observed by a weak-

sighted observer. The red lines show observed images

and the blue lines show their ground truth. The RMS

errors of observed images are also shown in the right

(1) existing method

RMSE = 16.13

(2) lateral inhibition

RMSE = 16.21

(3) high resolution

RMSE = 16.53

(4) lateral inhibition with high

resolution

RMSE = 4.46

Figure 5: The display images and observed images. The

left column shows display images generated from (1) exist-

ing method, (2) lateral inhibition method, (3) high resolu-

tion method, and (4) lateral inhibition with high resolution

method. The red lines in the right column show these im-

ages observed by a weak-sighted observer and the blue lines

show the ground truth of observed images.

column. Fig. 6 shows the results from the step signal.

As shown in these images, the simple lateral inhi-

bition and the simple high resolution method do not

provide us better results. However, the proposed lat-

eral inhibition with high resolution method provides

us much better results than the existing methods and

other methods. Note, the proposed method enables

us to observe negative intensities and over range in-

tensities accurately as shown in Fig. 5 (d) and Fig. 6

(d). These results show the efﬁciency of the combi-

nation of lateral inhibition and high resolution in the

proposed method.

5.2 Real Image Experiments

We next show results from real image experiments.

Fig. 7 (a) and (b) show original images used in our

experiments. The lateral inhibition and the PSF of a

weak-sighted observer is the same as those used in

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

130

(1) existing method

RMSE = 4.33

(2) lateral inhibition

RMSE = 4.65

(3) high resolution

RMSE = 4.46

(4) lateral inhibition with high

resolution

RMSE = 1.73

Figure 6: The display images and observed images. The

left column shows display images generated from (1) exist-

ing method, (2) lateral inhibition method, (3) high resolu-

tion method, and (4) lateral inhibition with high resolution

method. The red lines in the right column show these im-

ages observed by a weak-sighted observer and the blue lines

show the ground truth of observed images.

(a) (b)

Figure 7: The images used in our real image experiments.

the synthetic image experiments. Fig. 4 (a) and (b)

show the observation of a normal sight observer, and

observer.

We derived display images for weak-sighted ob-

server by using the existing method and the proposed

method which combines the lateral inhibition with

(a) display image (b) observed image

Figure 8: (a) and (b) show the display image and the ob-

served image of a weak sighted observer in the existing

method. (c) and (d) show those in the proposed method.

high resolution displaying. Fig. 8(a) shows the dis-

play image derived from the existing method, and

(b) shows the image observed by a weak-sighted ob-

server. Fig. 8(c) shows the display image derived

from the proposed method, and (d) shows the image

observed by a weak-sighted observer. Fig. 9 shows

the results from another image. Note, the resolu-

tion of the observed images in the proposed method

is same as that in the existing method. As shown

in Fig. 8 (b) and (d) and Fig. 9 (b) and (d) , the

proposed method provides us better observation for

weak-sighted observer. This is because the proposed

method uses the lateral inhibition in human observers

efﬁciently.

Fig. 10 shows the comparison of the frequency

characteristics of observed images in the existing

method and the proposed method, i.e. lateral inhi-

bition with high resolution. Fig. 10 (a) is the fre-

quency characteristic of the ground truth observation

of Fig. 7 (a). Fig. 10 (b) is that of the existing method,

and (c) is that of the proposed method. As shown

in these images, both the existing method and the

proposed method lose high frequency components.

However, the proposed method can preserve more

high frequency components than the existing method.

Since the high frequency components correspond to

the sharpness of images, these results conﬁrm that the

weak-sighted people can observe better images.

Virtual Correction of Eyesight using Visual Illusions

131

(a) display image (b) observed image

Figure 9: (a) and (b) show the display image and the ob-

served image of a weak sighted observer in the existing

method. (c) and (d) show those in the proposed method.

(a) ground truth

(b) existing method (c) proposed method

Figure 10: The frequency characteristics of observed im-

ages. (a) is the ground truth, (b) is the observation in the

existing method, and (c) is the observation in the proposed

method.

6 CONCLUSION

In this paper, we proposed a method for displaying vi-

sual information for weak-sighted people to see clear

images on the display. For this objective, we used the

lateral inhibition which causes visual illusions in hu-

man visual systems. The lateral inhibition enhances

input signals and thus the human visual systems can

observe wider dynamic range than that in the display

device. By using this property, we generated the op-

timum display images for weak-sighted observed to

see original clear images without wearing glasses and

contact lenses. We showed that the lateral inhibition

works efﬁciently by combining it with high resolution

displaying. The efﬁciency of the proposed method is

tested by using synthetic images and real images.

REFERENCES

Alonso, M. and Barreto, A. (2003). Pre-compensation for

high-order aberrations of the human eye using on-

screen image deconvolution. In Proc. Annual Interna-

tional Conference of the IEEE EMBS, pages 556–559.

Chevreul, M. (1890). The Principles of Harmony and Con-

trast of Colors. George Bell and Sons.

Huang, F., Lanman, D., Barsky, B., and Raskar, R. (2012).

Correcting for optical aberrations using multilayer

displays. In Proc. ACM SIGGRAPH Asia.

Huang, F., Wetzstein, G., Barsky, B., and Raskar, R.

(2014). Eyeglass-free display: Towards correcting vi-

sual aberrations with computational light ﬁeld display.

In Proc. ACM SIGGRAPH.

Marr, D. and Hildreth, E. (1980). Theory of edge detection.

Proceedings of Royal Society of London, B(27):187–

217.

Ratliff, F. (1965). Mach Bands: Quantitative Studies on

Neural Networks in the Retina. Holden Day.

Wetzstein, G., Lanman, D., Hirsch, M., and Raskar, R.

(2012). Tensor displays: Compressive light ﬁeld syn-

thesis using multilayer displays with directional back-

lighting. In Proc. ACM SIGGRAPH.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

132