How Effective Are Aggregation Methods on Binary Features?

Giuseppe Amato, Fabrizio Falchi and Lucia Vadicamo

ISTI, CNR, via G. Moruzzi 1, 56124, Pisa, Italy

Keywords:

Image Retrieval, Image Representation, Binary Local Features, ORB, Bag of Word, VLAD, Fisher Vector.

Abstract:

During the last decade, various local features have been proposed and used to support Content Based Image

Retrieval and object recognition tasks. Local features allow to effectively match local structures between

images, but the cost of extraction and pairwise comparison of the local descriptors becomes a bottleneck

when mobile devices and/or large database are used. Two major directions have been followed to improve

efﬁciency of local features based approaches. On one hand, the cost of extracting, representing and matching

local visual descriptors has been reduced by deﬁning binary local features. On the other hand, methods for

quantizing or aggregating local features have been proposed to scale up image matching on very large scale. In

this paper, we performed an extensive comparison of the state-of-the-art aggregation methods applied to ORB

binary descriptors. Our results show that the use of aggregation methods on binary local features is generally

effective even if, as expected, there is a loss of performance compared to the same approaches applied to non-

binary features. However, aggregations of binary feature represent a worthwhile option when one need to use

devices with very low CPU and memory resources, as mobile and wearable devices.

1 INTRODUCTION

During the last few years, local descriptors, as for in-

stance SIFT (Lowe, 2004), SURF (Bay et al., 2006),

BRISK (Leutenegger et al., 2011), ORB (Rublee

et al., 2011), to cite some, have been widely used to

support effective CBIR and object recognition tasks.

Executing image retrieval and object recognition

tasks, relying on local features, is generally resource

demanding. Each digital image, both queries and im-

ages in the digital archives, are typically described by

thousands of local descriptors. In order to decide that

two images match, since they contain the same or sim-

ilar objects, local descriptors in the two images need

to be pairwise compared, in order to identify match-

ing patterns. This poses various problems when local

descriptors are used on devices with low resources, as

for instance smartphones, or when response time must

be very fast even in presence of huge digital archives.

On one hand, the cost for extracting local descriptors,

storing all descriptors of all images, and performing

pairwise matching between two images must be re-

duced to allow their interactive use on devices with

limited resources. On the other hand, compact repre-

sentation of local descriptors and ad hoc index struc-

tures for similarity matching (Zezula et al., 2006) are

needed to allow image retrieval to scale up with very

large digital picture archives. These two issues, have

been addressed by following two different directions.

To reduce the cost of extracting, representing, and

matching local visual descriptors, researchers have in-

vestigated the use of binary local descriptors, as of

instance BRISK (Leutenegger et al., 2011) or ORB

(Rublee et al., 2011). Binary features are built from

a set of pairwise intensity comparisons. Thus, each

bit of the descriptors is the result of exactly one com-

parison. Binary descriptors are much faster to be ex-

tracted, are obviously more compact than non-binary

ones, and can also be matched faster by using the

Hamming distance (Hamming, 1950) rather than the

Euclidian distance. However, note that even if binary

local descriptors are compact, each image is still asso-

ciated with thousand local descriptors, making it dif-

ﬁcult to scale up to very large digital archives.

Reduction of the cost of image matching on a very

large scale has been addressed by deﬁning methods

for quantizing and/or aggregating local features.

Quantization methods, as for instance the bag of

words approach (BoW) (Sivic and Zisserman, 2003),

deﬁne a ﬁnite vocabulary of local descriptors, that is

a ﬁnite set of local descriptors to be used as represen-

tative. Every possible local descriptors is thus repre-

sented by its closest representative, that is the closest

element of the vocabulary. In this way images are

566

Amato, G., Falchi, F. and Vadicamo, L.

How Effective Are Aggregation Methods on Binary Features?.

DOI: 10.5220/0005719905660573

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 566-573

ISBN: 978-989-758-175-5

described by a set (a bag) of identiﬁers of representa-

tives, rather than a set of vectors.

Aggregation methods, as for instance Fisher Vec-

tors (FV) (Perronnin and Dance, 2007) or Vectors

of Locally Aggregated Descriptors (VLAD) (J

egou

et al., 2010b), analyze the local descriptors contained

in an image to create statistical summaries that still

preserve the effectiveness power of local descriptors

and allow treating them as global descriptors. In both

cases index structures for approximate or similarity

matching (Zezula et al., 2006) can be used to guaran-

tee scalability on very large datasets.

Recently, some approaches that attempt to inte-

grate the binary local descriptors with the quantiza-

tion and aggregation methods were proposed in litera-

ture. In these proposals, aggregation and quantization

methods were directly applied on top of binary local

descriptors. The objective is to leverage on the advan-

tages of both approaches, by reducing, or eliminating

the disadvantages.

In this paper we perform an extensive compar-

isons and analysis of the aggregation and quantization

methods applied to binary local descriptors. To the

best of our knowledge, there is not such a complete

analysis of these methods in the literature.

The results of our experiments show that the use

of aggregation and quantization methods with binary

local descriptors is generally effective even if, as ex-

pected, performance is slightly worse than the appli-

cation of the aggregation and quantization methods

directly to the non-binary features.

This paper is organized as follows. Section 2 sur-

veys the works related to local features and aggrega-

tion methods. Section 3 outlines how existing aggre-

gation methods can be used with binary local features.

Experimental results are discussed in the fourth sec-

tion and conclusions are drawn in the ﬁnal section.

2 RELATED WORK

One of the most popular aggregation method is the

Bag-of-Word (BoW), initially proposed in (Sivic and

Zisserman, 2003; Csurka et al., 2004) for match-

ing object in videos. BoW uses a visual vocabu-

lary to quantize the local descriptors extracted from

images and represents each image as a histogram

of occurrences of visual words. From the very be-

ginning words reductions techniques have been used

and images have been ranked using the standard

term frequency-inverse document frequency (tf-idf)

weighting. In order to improve the efﬁciency of BoW,

several approaches for the reduction of visual words

have been investigated (Thomee et al., 2010; Amato

et al., 2013). Search results obtained using BoW in

CBIR has also been improved by exploiting additional

geometrical information and applying re-ranking ap-

proaches (Philbin et al., 2007; Zhao et al., 2013; To-

lias and J

egou, 2013). To overcome the loss in in-

formation about the original descriptors, due to the

quantization process, more accurate representation of

the original descriptors and alternative encoding tech-

niques have been used, as for example Hamming

Embedding (J

egou et al., 2008) and soft/multiple-

assignment (Philbin et al., 2008; Van Gemert et al.,

2010; J

egou et al., 2010a).

Recently, other aggregation schemes, such as the

Fisher Vector (FV) (Perronnin and Dance, 2007;

Jaakkola and Haussler, 1998) and the Vector of Lo-

cally Aggregated Descriptors (VLAD) (J

egou et al.,

2010b), have attracted much attention because of their

effectiveness in both image classiﬁcation and large-

scale image search. Both FV and VLAD use some

statistics about the distribution of the local descriptors

in order to transform an incoming set of descriptors

into a ﬁxed-size vector representation.

The basic idea of FV is to characterize how a

sample of descriptors deviates from an average dis-

tribution that is modeled by a parametric generative

model. A Gaussian Mixture Model (GMM), esti-

mated on a training set, is typically used as generative

model and might be understood as a “probabilistic vi-

sual vocabulary”. While BoW counts the occurrences

of visual words and so takes in account just 0-order

statistics, the FV offers a more complete representa-

tion by encoding higher order statistics (ﬁrst, and op-

tionally second order) related to the distribution of the

descriptors. FV results also in a more efﬁcient rep-

resentation, since smaller visual vocabularies are re-

quired in order to achieve a given performance. How-

ever, the vector representation obtained using BoW

is typically quite sparse while that obtained using FV

is almost dense. This leads to some storage and in-

put/output issues that have been addressed by using

techniques of dimensionality reduction, as Principal

Component Analysis (PCA) (Bishop, 2006), compres-

sion with product quantization (J

egou et al., 2011)

and binary codes (Perronnin et al., 2010a).

The VLAD approach, similarly to BoW, uses a vi-

sual vocabulary to quantize the local descriptors of

an image. The visual vocabulary is learned using a

clustering algorithm, as k-means. Compared to BOW,

VLAD exploits more aspects of the distribution of

the descriptors assigned to a visual word. In fact, it

encodes the accumulated difference between the vi-

sual words and the associated descriptors, rather than

just the number of descriptors assigned to each vi-

sual word. As common post-processing step VLAD

How Effective Are Aggregation Methods on Binary Features?

567

is power and `

normalized. Furthermore, PCA di-

mensionality reduction and product quantization have

been applied and several enhancements to the basic

VLAD have been proposed (Arandjelovic and Zisser-

man, 2013; Chen et al., 2011; Delhumeau et al., 2013;

Zhao et al., 2013)

Aggregation methods have been deﬁned and used

almost exclusively in conjunction with non-binary lo-

cal features, as SIFT (Lowe, 2004) and SURF (Bay

et al., 2006). The cost of extraction and the memory

consumption of these local features become an issue

in the concurrent effort to use visual search on mobile

devices and to scale to even larger datasets. To con-

trast this, binary local descriptors, as BRIEF (Calon-

der et al., 2010), ORB (Rublee et al., 2011), BRISK

(Leutenegger et al., 2011) and FREAK (Alahi et al.,

2012) have been introduced. These features have a

compact binary representation that is computed di-

rectly from pixel-intensity comparisons. This make

them an attractive solution to reduce the computa-

tional effort for the detection and the comparison of

local features.

Few works have addressed the problem of modi-

fying the state-of-the-art aggregation methods to work

with the emerging binary local features. In (Galvez-

Lopez and Tardos, 2011; Zhang et al., 2013; Grana

et al., 2013; Lee et al., 2015), the use of ORB descrip-

tors has been integrated in the BoW model by using

various clustering algorithms. In (Galvez-Lopez and

Tardos, 2011) the visual vocabulary is calculated by

binarizing the centroids obtained using the standard k-

means. In (Zhang et al., 2013; Grana et al., 2013; Lee

et al., 2015) the k-means clustering has been mod-

iﬁed to ﬁt the binary features by replacing the Eu-

clidean distance with the Hamming distance, and by

replacing the mean operation with the median oper-

ation. In (Van Opdenbosch et al., 2014) the VLAD

image signature is tested with binary descriptors: k-

means is used for learning the visual vocabulary and

the VLAD vectors are computed in conjunction with

an intra-normalization and a ﬁnal binarization step.

In this work we present how the state-of-the-art

aggregation methods can be used with binary features

and we perform a complete comparison of their per-

formances on the benchmark INRIA Holidays (J

egou

et al., 2008) dataset.

3 AGGREGATION METHODS

In this section, we describe the most popular quantiza-

tion and aggregation methods, namely BoW, VLAD

and Fisher Vector, that aim to produce a single vector

representation of an image starting from a set of local

descriptors. We also review how these methods can

been adapted to work with the emerging binary local

features.

3.1 Bag of Word

The traditional Bag of Words (BoW) model, used

for text retrieval (Salton and McGill, 1986), has

been initially applied to images in (Sivic and Zisser-

man, 2003) for matching objects throughout a movie

database. Thereafter, BoW has been widely used for

classiﬁcation and CBIR tasks (Csurka et al., 2004;

egou et al., 2010a; J

egou et al., 2010b).

As for text documents, BoW uses a “visual vo-

cabulary” to represent each image as a vector of word

frequencies. The visual vocabulary is built by clus-

tering the local descriptors of a dataset, e.g. by using

k-means. The cluster centers, named centroids, act as

visual words of the vocabulary and they are used to

quantize the local descriptors extracted from images.

Speciﬁcally, each local descriptor of an image is as-

signed to its closest centroids and the image is rep-

resented by a histogram of occurrences of the visual

words.

The retrieval phase is performed using text re-

trieval techniques, where visual words are used in

place of text word, and considering a query image

as disjunctive term-query. Typically, the cosine sim-

ilarity measure in conjunction with a term weighting

scheme, e.g. tf-idf, is adopted for evaluating the sim-

ilarity between any two images.

The BoW scheme has been extended to work with

binary features by following two main directions. On

one hand, a naive approach is to treat binary vectors as

a particular case of ﬂoating-point vectors, so that tra-

ditional BoW (k-means + quantization) can be used.

On the other hand BoW can be adapted to cope with

binary features by considering cluster algorithms (e.g.

k-medoids and k-majority) able to deal with binary

strings and Hamming distance.

The k-medoids (Kaufman and Rousseeuw, 1987)

algorithm is suitable for binary data since each cluster

center is chosen as one of the input data points (in-

stead of the mean of the cluster elements). However,

it requires a computational effort to calculate a full

distance matrix between the elements of each cluster.

An alternative is to use the k-majority (Grana

et al., 2013) that exploits the Hamming distance and

a voting scheme to compute the centroids of a set of

binary vectors. Initially the centroids are randomly

selected and each vector of the collection is associ-

ated with its nearest centroid (computed by using the

Hamming distance). Subsequently, for each cluster,

a new centroid is computed by assigning 1 to its i-th

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

568

component if the majority of the binary vectors in the

cluster have 1 in their i-th component. The algorithm

iterates until no centroids are changed during the pre-

vious iteration. After that, the BoW aggregation can

be performed in the usual manner, by using the Ham-

ming distance rather than the Euclidean.

Also in (Zhang et al., 2013; Lee et al., 2015), the

BoW model and the k-means clustering have been

modiﬁed to ﬁt the binary features by replacing the Eu-

clidean distance with the Hamming distance, and by

replacing the mean operation with the median opera-

tion. However, the resulting representation is equiva-

lent to the BoW based on k-majority.

3.2 Vector of Locally Aggregated

Descriptors

The Vector of Locally Aggregation Descriptors

(VLAD) was initially proposed in (J

egou et al.,

2010b). As for the BoW, a visual vocabulary

{µ

,... ,µ

} is ﬁrst learned using a clustering algo-

rithm (e.g. k-means). Each local descriptor x

of a

given image is then associated to its nearest centroid

NN(x

) in the vocabulary. For each cluster, the resid-

ual vectors (i.e. the difference between the centroid

and the associated descriptors) are accumulated:

∑

:NN(x

)=µ

− µ

. (1)

Finally the sum of the residual are concatenated into

a single vector, referred to as VLAD: V = [v

.. .v

All the residuals have the same size D which is equal

to the size of the used local features. Thus the di-

mensionality of the whole vector V is ﬁxed too and

it is equal to DK. Power-law and `

normalization

are usually applied and Euclidean distance has been

proved to be effective for comparing two VLADs.

Since VLAD descriptors have high dimensionality,

PCA can been used to obtain a more compact rep-

resentation (J

egou et al., 2010b).

VLAD can be applied to binary local descrip-

tors by treating binary vectors as particular case of

ﬂoating-point vectors. In this way, the k-means al-

gorithm can be used to build the visual vocabulary

and the difference between the centroids and the de-

scriptors can be accumulated as usual. This ap-

proach has also been used in (Van Opdenbosch et al.,

2014), where a variation to the VLAD image signa-

ture, called BVLAD, has been deﬁned as the bina-

rization (by thresholding) of a VLAD obtained using

power-law, intra-normalization, `

normalization and

multiple PCA.

Similarly to BoW, various binary-cluster algo-

rithms (e.g. k-medoids and k-majority) and the Ham-

ming distance can be used to build the visual vocab-

ulary and associate each binary descriptor to its near-

est visual word. However, the use of binary centroids

may provide less discriminant information during the

computation of the residual vectors.

3.3 Fisher Vector

The Fisher Kernel is a powerful framework initially

used in (Jaakkola and Haussler, 1998) for classifying

DNA splice site sequences and to detect homologies

between protein sequences. In (Perronnin and Dance,

2007), the Fisher Kernel has been proposed, in the

context of image classiﬁcation, as efﬁcient tool to ag-

gregate image local descriptors into a ﬁxed-size vec-

tor representation.

The goal of the Fisher Kernel method is to derive

a function that measures the similarity between two

sets of data X and Y , as the sets of local descriptors

extracted from two images. To this scope a probabil-

ity distribution p(·|λ) with some parameters λ ∈ R

is ﬁrst estimated on a training set and is used as gen-

erative model over the space of all the possible data

observations. Then each sample X of observations, is

represented by a vector, named Fisher Vector (FV),

that indicates the direction in which the parameter λ

of the probability distribution p(·|λ) should be modi-

ﬁed to better ﬁt the data in X. In this way, two samples

are considered similar if the directions given by their

respective FV are similar. The Fisher Vector G

sample set X is deﬁned as the gradient of the sam-

ple’s log-likelihood with respect to the parameters λ,

scaled by the inverse square root of the Fisher Infor-

mation Matrix (F

), i.e.

= L

∇

log p(X |λ), (2)

where L

∈ R

m×m

is a matrix such that

−1

= L

(3)

and

= E

x∼p(·|λ)

∇

log p(x|λ) (∇

log p(x|λ))

. (4)

The FV is a ﬁxed size vector whose dimensionality

only depends on the number m of the parameter λ.

The FV is further divided by |X| in order to avoid the

dependence on the sample size (S

anchez et al., 2013).

The similarity between two set X and Y is mea-

sured by using the dot-product of their relative FV

or, equivalently, the dissimilarity is evaluated by us-

ing the Euclidean distance whenever the FVs are `

normalized (Perronnin et al., 2010b).

In the context of image retrieval and classiﬁcation

the FV are usually `

-normalized since, as proved in

(Perronnin et al., 2010b; S

anchez et al., 2013), this is

How Effective Are Aggregation Methods on Binary Features?

569

a way to cancel-out the fact that distinct images con-

tain different amounts of image-speciﬁc information

(e.g. the same object at different scales). Moreover,

a power-law normalization step is generally applied

to improve the performance of FV, as highlighted in

anchez et al., 2013).

To the best of our knowledge the Fisher Vector

has mainly been applied to non-binary local features,

such as SIFT (Lowe, 2004), using a Gaussian Mixture

Model (GMM) to represent the average distribution

p(·|λ). In our experiments, we tested the baseline FV

based on GMM by using the naive approach of treat-

ing binary features as ﬂoating-point vectors.

4 EXPERIMENTS

In the following we evaluate and compare the differ-

ent methods described in Section 3 for aggregating bi-

nary local features. We ﬁrst introduce the dataset used

in the evaluations and we describe our experimental

setup. We then report results and their analysis.

4.1 Dataset

Experiments were conducted using the INRIA Holi-

days dataset (J

egou et al., 2008), that is publicly avail-

able and often used in the context of image retrieval

egou et al., 2010b; Zhao et al., 2013; Arandjelovic

and Zisserman, 2013; Perronnin et al., 2010a; J

egou

et al., 2012).

The INRIA Holidays is a collection of 1 491 im-

ages, 500 of them being used as query. The images

are of high resolution and encompass a large variety

of scene type (natural, man-made, water, ﬁre effects,

etc). Each query represents a distinct scene or ob-

ject and a list of positive results is provided with the

dataset.

As in many other works we used an independent

dataset, namely Flickr60k (J

egou et al., 2008), for all

the learning stages (clustering, PCA evaluation, etc).

The Flickr60k dataset is composed of 67 714 images

extracted randomly from Flickr. Compared to Inria

Holidays, Flickr60k includes also low-resolution im-

ages and more photos of humans.

4.2 Experimental Setup

In the experiments we used ORB (Rublee et al., 2011)

binary feature, extracted with OpenCV (Open Source

Computer Vision Library)

. For INRIA Holidays we

http://lear.inrialpes.fr/ jegou/data.php

http://opencv.org/

detected up to 2 000 ORBs per image, while for the

training dataset we used up to 1000 ORBs per image.

Several aggregation methods were tested, i.e.

BoW, VLAD and FV, each of them parametrized by

an integer K. It corresponds to the number of visual

words (centroids) used in BoW and VLAD, and to

the number of mixture components of GMM used for

the FV computation. We used K = 20 000 for BoW

and K = 64 for VLAD and FV. All the learning stages

were performed using in order of 10

descriptors ran-

domly selected from all the ORBs extracted from the

training set.

Both k -medoids and k-majority algorithms were

tested to build the visual vocabularies used for BoW

and VLAD aggregations. We also tested the naive

approach of treating binary vectors as ﬂoating-point

vectors and learning the visual vocabularies via k-

means.

The binary vectors were treated as ﬂoating-point

vectors also for the GMM and FV computation. For

the FV representation, we had only used the com-

ponents associated with the gaussian mean vectors,

since, similarly to the non-binary case, we observed

that the components related to the mixture weights

do not improve the results. The GMM parameters

(mixture weights, mean vectors, diagonal covariance

matrices) were learned by optimizing a maximum-

likelihood criterion with the Expectation Maximiza-

tion (EM) algorithm (Bishop, 2006). As stopping cri-

terion for the estimation of the GMM we used the con-

vergence in `

-norm of the mean parameters. As sug-

gested in (Bishop, 2006), the GMM parameters used

in EM algorithm were initialized with: (a) 1/K for the

mixing coefﬁcients; (b) centroids precomputed using

k-means, for the mean vectors; (c) mean variance of

the clusters found using k-means, for the diagonal el-

ements of the covariance matrices.

As a common post-processing step (Perronnin

et al., 2010b; J

egou et al., 2012), the FV and VLAD

vectors were power-law normalized and subsequently

-normalized. The power-law normalization is de-

ﬁned as x → |x|

sign(x). In our experiments we used

α = 0.5. We also applied PCA to reduce the dimen-

sionality of VLAD and FV. The projection matrices

were estimated on the training dataset.

The similarity between BoW representations is

evaluated using the cosine similarity in conjunction

with tf-idf weighting scheme. VLAD and FV image

signatures are compared using the Euclidean distance.

For completeness, we also evaluate the retrieval

performance of the brute-force matching strategy as

alternative to the aggregation approaches. To com-

pute matches between the images we adopt the dis-

tance ratio criterion (Lowe, 2004; Heinly et al., 2012),

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

570

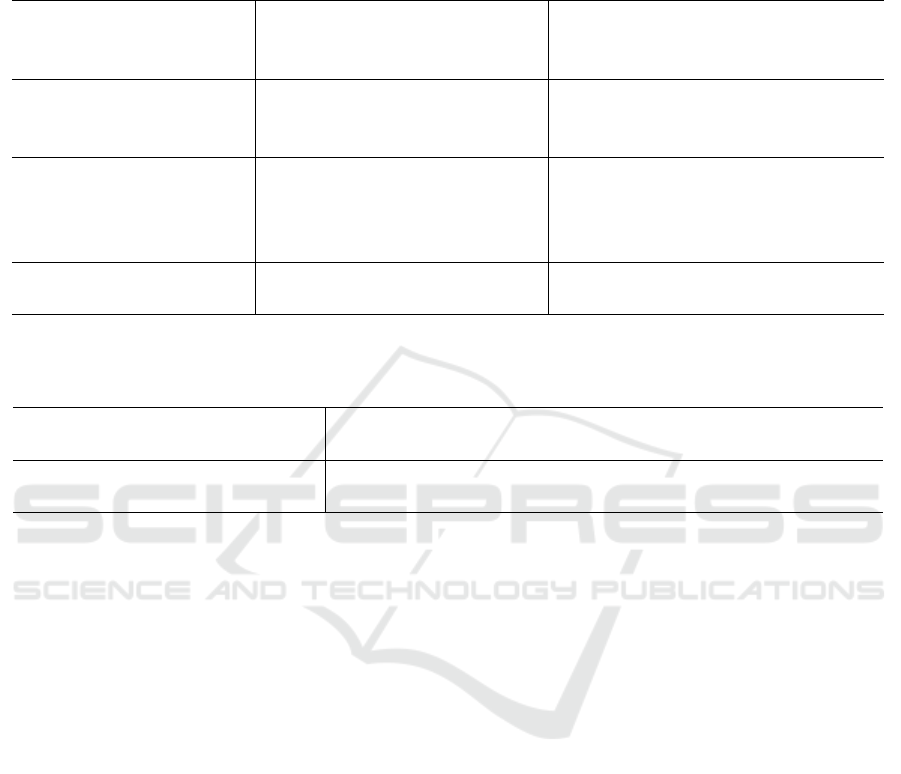
Table 1: Performance evaluation on INRIA Holiday dataset of various aggregation methods applied on ORB binary features

and comparison with the state-of-the-art counterpart methods applied on SIFT features (both full-size SIFTs and PCA-reduced

to 64 components). K indicates the number of centroids used in BoW and VLAD and the number of mixture components of

GMM used in FV; Dimensionality is the number of components of each vector representation (expressed in function of the

used local feature). The results related to SIFT and SIFTPCA are reported from (J

egou et al., 2010b) and (J

egou et al., 2012).

Method

Learning

method

K Dimensionality mAP

ORB SIFT SIFTPCA64 ORB

SIFT from

egou et al., 2010b)

SIFTPCA64 from

egou et al., 2012)

BoW k-means 20 000 20 000 20 000 20 000 40.2 40.4 43.7

BoW k-majority 20 000 20 000 - - 38.2 - -

BoW k-medoids 20 000 20 000 - - 34.8 - -

VLAD k-means 64 16 384 8 192 4 096 40.9 52.6 55.6

PCA

−−→ 128 128 128 40.7 51.0 55.7

VLAD k-majority 64 16 384 - - 29.5 - -

VLAD k-medoids 64 16 384 - - 30.7 - -

FV GMM 64 16 384 8 192 4 096 35.1 49.5 59.5

PCA

−−→ 128 128 128 37.8 49.2 56.5

Table 2: Retrieval performances after PCA reduction of VLAD and FV aggregations of ORB binary features. K indicates

the number of centroids used in VLAD and the number of Gaussian mixture components used in FV; D is the number of

components of each vector representation and D

is the dimensionality after PCA reduction.

Method

Learning

method

K D

mAP

=D →D

=1024 →D

=512 →D

=256 →D

=128 →D

=64 →D

=32

VLAD k-means 64 16 384 40.9 45.7 43.7 43.3 40.7 39.9 36.9

FV GMM 64 16 384 35.1 38.9 38.1 37.1 37.8 36.6 35.1

i.e. for each local feature of a query a candidate match

is found by identifying its nearest neighbor in the

database and the match is discarded if the ratio of the

distances between the two closest neighbors is above

a threshold of 0.8. In this case the similarity of two

images is deﬁned as the percentage of the features de-

tected on the query that are identiﬁed as match.

The retrieval performance of each tested method

was measured by the mean average precision (mAP),

with the query removed from the ranking list.

4.3 Results

In Table 1, we summarize the retrieval results ob-

tained using BoW, VLAD and FV on ORB binary

features and we compare their performance with the

counterpart aggregations techniques applied on SIFT

(both full-size SIFT and PCA-reduced to 64 compo-

nents). As expected, aggregation methods exhibit bet-

ter performance in combination with SIFT then with

ORB. However, binary features have been proposed

and used to improve efﬁciency, even though they are

always outperformed by the SIFT descriptor in terms

of effectiveness (Heinly et al., 2012).

The purpose of this paper is to explore the effec-

tiveness of aggregation methods, when binary local

features have to be used. Thus, we are interested in

identifying which aggregation method is more suit-

able for binary features.

Both for VLAD and BoW, the naive approach of

using k-means to cluster also binary vectors, works

better than using speciﬁc binary-clustering algorithm,

such as k-medoid and k-majority.

Speciﬁcally, we obtained a mAP of 40.9% for

VLAD and 40.2% for BoW wen using a visual vo-

cabulary learned via k-mean, respectively with K =

64 and K = 20 000 visual words. The performance

degradation observed when using binary-clustering

algorithms is limited in the case of BoW: in fact

we get a mAP of 38.2%/34.8% when k-majority/k-

medoids are used for the learning stages.

For BoW approach, k-means and k-majority per-

forms almost equally better than k-medoids. How-

ever, k-majority is preferable since the cost of the

quantization process is signiﬁcantly reduced by using

the Hamming distance, rather than Euclidean one.

The less effective performance are those of FV

(mAP of 35.1%) and VLAD in combination with vo-

cabularies learned by k-medoids (mAP of 30.7%) and

k-majority (mAP of 29.5%). For the computation of

VLAD, the use of k-majority/k-medoids results less

effective than k-means clustering, since the use of

How Effective Are Aggregation Methods on Binary Features?

571

binary centroids gives less discriminant information

during the computation of the residual vectors.

The reduced accuracy obtained using FV may re-

ﬂect the fact that a Gaussian Mixture Model is not

entirely adequate to represent the probability distri-

bution of binary vectors.

In Table 2 we investigate the impact of PCA di-

mensionality reduction for VLAD and FV. PCA re-

sults effective since it can provide a very compact

image signature (even smaller than one single local

feature) with just a slightly loss in accuracy. Dimen-

sion reduction does not necessarily reduce the accu-

racy. Conversely, limited reduction tend to improve

the retrieval performance for both VLAD and FV rep-

resentations. Moreover, the VLAD reduced to 1024

components achieves the best retrieval performance

(that is 45.7%) among all the aggregation methods

tested on binary features.

It is generally interesting to note that full-size

VLAD and PCA-reduced VLAD, computed using k-

means, perform better than BoW methods relying on

SIFT and SIFTPCA, which are typically considered

as a reference for comparisons.

It is also worth noting that the state-of-the-art FV

and VLAD get considerable beneﬁt from the PCA re-

duction (before the aggregation phase) of SIFT local

descriptors. This suggest that techniques, as VLAD

with k-means and FV, that treat binary vectors as

ﬂoating-point vectors, may also beneﬁt from the use

of PCA before the aggregation phase.

Actually, in the context of image retrieval, the

most common way of using binary features is the

brute-force matching strategy. In our experiments,

the mAP achieved on INRIA Holiday using the brute-

force matching of ORB descriptors was of 41.3%.

Thus our results shows that choosing to aggregate bi-

nary features is generally effective and aggregations

outperforms also brute-force matching both in efﬁ-

ciency and effectiveness.

5 CONCLUSIONS

This paper has performed an extensive comparisons

of techniques that mix together aggregation methods

and binary local features. Combining the two ap-

proaches allows, at the same time, executing image

retrieval on a very large scale and to reduce the cost

for feature extraction and representation.

Experiments show that performance is just

slightly degraded with respect to the use of aggre-

gation on non-binary vectors. However, with these

methods we can get both advantages of aggregation

methods and binary local features.

ACKNOWLEDGEMENTS

This work was partially supported by EAGLE, Euro-

peana network of Ancient Greek and Latin Epigra-

phy, co-founded by the European Commision, CIP-

ICT-PSP.2012.2.1 - Europeana and creativity, Grant

Agreement n. 325122.

REFERENCES

Alahi, A., Ortiz, R., and Vandergheynst, P. (2012). FREAK:

Fast Retina Keypoint. In Computer Vision and Pat-

tern Recognition (CVPR), 2012 IEEE Conference on,

pages 510–517.

Amato, G., Falchi, F., and Gennaro, C. (2013). On reduc-

ing the number of visual words in the bag-of-features

representation. In VISAPP 2013 - Proceedings of the

International Conference on Computer Vision Theory

and Applications, volume 1, pages 657–662.

Arandjelovic, R. and Zisserman, A. (2013). All about

VLAD. In Computer Vision and Pattern Recogni-

tion (CVPR), 2013 IEEE Conference on, pages 1578–

1585.

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). SURF:

Speeded Up Robust Features. In Computer Vision -

ECCV 2006, volume 3951 of Lecture Notes in Com-

puter Science, pages 404–417. Springer Berlin Hei-

delberg.

Bishop, C. M. (2006). Pattern Recognition and Ma-

chine Learning. Information Science and Statistics.

Springer.

Calonder, M., Lepetit, V., Strecha, C., and Fua, P. (2010).

BRIEF: Binary Robust Independent Elementary Fea-

tures. In Computer Vision - ECCV 2010, volume 6314

of Lecture Notes in Computer Science, pages 778–

792. Springer Berlin Heidelberg.

Chen, D., Tsai, S., Chandrasekhar, V., Takacs, G., Chen, H.,

Vedantham, R., Grzeszczuk, R., and Girod, B. (2011).

Residual enhanced visual vectors for on-device im-

age matching. In Signals, Systems and Computers

(ASILOMAR), 2011 Conference Record of the Forty

Fifth Asilomar Conference on, pages 850–854.

Csurka, G., Dance, C., Fan, L., Willamowski, J., and Bray,

C. (2004). Visual categorization with bags of key-

points. Workshop on statistical learning in computer

vision, ECCV, 1(1-22):1–2.

Delhumeau, J., Gosselin, P.-H., J

egou, H., and P

erez, P.

(2013). Revisiting the VLAD image representation.

In Proceedings of the 21st ACM International Confer-

ence on Multimedia, MM 2013, pages 653–656.

Galvez-Lopez, D. and Tardos, J. (2011). Real-time loop

detection with bags of binary words. In Intelligent

Robots and Systems (IROS), 2011 IEEE/RSJ Interna-

tional Conference on, pages 51–58.

Grana, C., Borghesani, D., Manfredi, M., and Cucchiara,

R. (2013). A fast approach for integrating ORB de-

scriptors in the bag of words model. In IS&T/SPIE

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

572

Electronic Imaging, volume 8667. International Soci-

ety for Optics and Photonics.

Hamming, R. W. (1950). Error detecting and error cor-

recting codes. The Bell System Technical Journal,

29(2):147–160.

Heinly, J., Dunn, E., and Frahm, J.-M. (2012). Compara-

tive evaluation of binary features. In Computer Vision

- ECCV 2012, Lecture Notes in Computer Science,

pages 759–773. Springer Berlin Heidelberg.

Jaakkola, T. and Haussler, D. (1998). Exploiting generative

models in discriminative classiﬁers. In In Advances

in Neural Information Processing Systems 11, pages

487–493. MIT Press.

egou, H., Douze, M., and Schmid, C. (2008). Ham-

ming embedding and weak geometric consistency for

large scale image search. In European Conference on

Computer Vision, volume I of LNCS, pages 304–317.

Springer.

egou, H., Douze, M., and Schmid, C. (2010a). Improving

bag-of-features for large scale image search. Interna-

tional Journal of Computer Vision, 87(3):316–336.

egou, H., Douze, M., and Schmid, C. (2011). Prod-

uct quantization for nearest neighbor search. Pat-

tern Analysis and Machine Intelligence, IEEE Trans-

actions on, 33(1):117–128.

egou, H., Douze, M., Schmid, C., and P

erez, P. (2010b).

Aggregating local descriptors into a compact image

representation. In IEEE Conference on Computer Vi-

sion & Pattern Recognition.

egou, H., Perronnin, F., Douze, M., S

anchez, J., P

erez,

P., and Schmid, C. (2012). Aggregating local im-

age descriptors into compact codes. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

34(9):1704–1716.

Kaufman, L. and Rousseeuw, P. (1987). Clustering by

means of medoids. In An introduction to L1-norm

based statistical data analysis, volume 5 of Compu-

tational Statistics & Data Analysis.

Lee, S., Choi, S., and Yang, H. (2015). Bag-of-binary-

features for fast image representation. Electronics Let-

ters, 51(7):555–557.

Leutenegger, S., Chli, M., and Siegwart, R. (2011). BRISK:

Binary Robust invariant scalable keypoints. In Com-

puter Vision (ICCV), 2011 IEEE International Con-

ference on, pages 2548–2555.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Perronnin, F. and Dance, C. (2007). Fisher kernels on vi-

sual vocabularies for image categorization. In Com-

puter Vision and Pattern Recognition, 2007. CVPR

’07. IEEE Conference on, pages 1–8.

Perronnin, F., Liu, Y., S

anchez, J., and Poirier, H. (2010a).

Large-scale image retrieval with compressed ﬁsher

vectors. In Computer Vision and Pattern Recogni-

tion (CVPR), 2010 IEEE Conference on, pages 3384–

3391.

Perronnin, F., S

anchez, J., and Mensink, T. (2010b). Im-

proving the ﬁsher kernel for large-scale image classi-

ﬁcation. In Computer Vision - ECCV 2010, volume

6314 of Lecture Notes in Computer Science, pages

143–156. Springer Berlin Heidelberg.

Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman, A.

(2007). Object retrieval with large vocabularies and

fast spatial matching. In Computer Vision and Pat-

tern Recognition (CVPR), 2007 IEEE Conference on,

pages 1–8.

Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman,

A. (2008). Lost in quantization: Improving partic-

ular object retrieval in large scale image databases.

In Computer Vision and Pattern Recognition, 2008.

CVPR 2008. IEEE Conference on, pages 1–8.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). ORB: An efﬁcient alternative to SIFT or

SURF. In Computer Vision (ICCV), 2011 IEEE In-

ternational Conference on, pages 2564–2571.

Salton, G. and McGill, M. J. (1986). Introduction to Mod-

ern Information Retrieval. McGraw-Hill, Inc., New

York, NY, USA.

anchez, J., Perronnin, F., Mensink, T., and Verbeek, J.

(2013). Image classiﬁcation with the ﬁsher vector:

Theory and practice. International Journal of Com-

puter Vision, 105(3):222–245.

Sivic, J. and Zisserman, A. (2003). Video google: A text re-

trieval approach to object matching in videos. In Pro-

ceedings of the Ninth IEEE International Conference

on Computer Vision, volume 2 of ICCV ’03, pages

1470–1477. IEEE Computer Society.

Thomee, B., Bakker, E. M., and Lew, M. S. (2010). TOP-

SURF: A visual words toolkit. In Proceedings of

the International Conference on Multimedia, MM ’10,

pages 1473–1476. ACM.

Tolias, G. and J

egou, H. (2013). Local visual query expan-

sion: Exploiting an image collection to reﬁne local

descriptors. Research Report RR-8325.

Van Gemert, J., Veenman, C., Smeulders, A., and Geuse-

broek, J.-M. (2010). Visual word ambiguity. Pat-

tern Analysis and Machine Intelligence, IEEE Trans-

actions on, 32(7):1271–1283.

Van Opdenbosch, D., Schroth, G., Huitl, R., Hilsenbeck,

S., Garcea, A., and Steinbach, E. (2014). Camera-

based indoor positioning using scalable streaming of

compressed binary image signatures. In IEEE Inter-

national Conference on Image Processing.

Zezula, P., Amato, G., Dohnal, V., and Batko, M. (2006).

Similarity Search: The Metric Space Approach, vol-

ume 32 of Advances in Database Systems. Springer.

Zhang, Y., Zhu, C., Bres, S., and Chen, L. (2013). Encod-

ing local binary descriptors by bag-of-features with

hamming distance for visual object categorization. In

Advances in Information Retrieval, volume 7814 of

Lecture Notes in Computer Science, pages 630–641.

Springer Berlin Heidelberg.

Zhao, W.-L., J

egou, H., and Gravier, G. (2013). Oriented

pooling for dense and non-dense rotation-invariant

features. In BMVC - 24th British Machine Vision Con-

ference.

How Effective Are Aggregation Methods on Binary Features?

573