
Generating Straight Outlines of 2D Point Sets and Holes
using Dominant Directions or Orthogonal Projections
Melanie Pohl and Dirk Feldmann
Fraunhofer IOSB, Department Scene Analysis, Ettlingen, Germany
Keywords:
Point Set, Outline, Boundary, Hull, Concave, Building, Footprint, Dominant Direction, Preference Angles.
Abstract:
Representing the shape of finite point sets in 2D by simple polygons becomes a challenge if the resulting
outline needs to be non-convex and straight with only few, distinct edges and angles. Such outlines are usually
sought in order to border point sets that originate from man-made objects, e.g., for the purpose of building
reconstruction from LIDAR data. Algorithms for computing hulls of point sets obtained from such structures
usually yield polygons having too many edges and angles and may thus not capture the actual shape very well.
Furthermore, many existing approaches cannot handle empty domains within the boundaries of a point set
(holes).
In this paper, we present methods that create straight, non-convex outlines of finite 2D point sets and of
possibly contained holes. The resulting polygons feature fewer vertices and angles than hulls and can thus
faithfully represent objects of angular shapes.
1 INTRODUCTION
The problem of finding simple, planar polygons that
outline a finite point set in 2D Euclidean space arises
in many practical applications. In order to automati-
cally create polygonal 3D models (meshes) of build-
ings or even entire cities, for instance, it is com-
mon practice to employ point data acquired by LI-
DAR devices or from aerial photographs by means
of photogrammetric methods. These points are usu-
ally based in a plane section in 2D Euclidean space.
The task of creating meshes from such finite point
sets comprises the detection of their outlines (also
called footprints) (Vosselman, 1999). The most no-
table solutions to this kind of problem are probably
convex hulls. In the case of constructing 3D models
of buildings, convex hulls may be inappropriate, be-
cause the outlines of many buildings or building com-
plexes are not convex. A better approach would be
the usage of methods for finding non-convex (con-
cave) hulls. But since man-made objects like build-
ings tend to have lots of long, straight edges, which
furthermore enclose few angles of discrete measures
(e.g., ±
π
2
), true hulls rarely reflect the desired out-
lines very well as shown in Figure 1: The outline
of the building obtained by the Concave Hull Algo-
rihtm (Moreira and Santos, 2007) is clearly prefer-
able over the convex hull, but it has too many ver-
tices and is not as straight as the underlying build-
ings’ exterior boundaries really are. For the task of
building reconstruction, having nicely straight out-
lines with only few vertices is desirable, because it
simplifies the process of 3D model generation and
the results are more realistic. Straightening outlines
obtained from concave hulls using methods like the
popular Ramer-Douglas-Peucker Algorithm (Ramer,
1972; Douglas and Peucker, 1973) is not a general
solution due to unintentional removal of certain cor-
ners as shown in Figure 1(b). Please note that we do
not deal with buildings having strongly curved bound-
aries, even though these can be found in many archi-
tectural landmarks.
Furthermore, input data obtained by measure-
ments are always noisy and the distribution of points
is likely to be non-uniform. Since hulls must include
every point of the set they enclose, unwanted outliers
will further diminish the desired quality of the result-
ing outlines.
The boundaries of finite point sets located in
a plane section in 2D Euclidean space may also
feature larger domains where no points are present
at all (called holes). In the process of building
reconstruction from LIDAR data, for instance, such
empty domains frequently result from buildings
or building complexes having inner courtyards or
atria. In order to give faithful representations of
Pohl, M. and Feldmann, D.
Generating Straight Outlines of 2D Point Sets and Holes using Dominant Directions or Orthogonal Projections.
DOI: 10.5220/0005720300570069
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 59-71
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
59

(a) convex hull. (b) concave hull (k = 100). (c) our method (orthogonal
projection).
Figure 1: Using the convex hull or the Concave Hull Algorithm to generate outlines of 2D point sets obtained from man-made
structures, like buildings, leads to shapes that do not necessarily reflect the actual object very well. Straightening the resulting
outlines using Ramer-Douglas-Peucker Algorithm (blue line in (b)) only little improves the result. Our method based on
orthogonal projection creates outlines that represent such objects more accurately. In Figure 1(b), k denotes the number of
neighbors considered (see Section 2.1).
the underlying objects, these holes also need to be
bounded by simple polygons.
We present two methods for finding simple out-
line polygons of 2D point sets which feature fewer
vertices and angles than hulls in order to faithfully
represent shapes of structures that are typically man-
made or originate from technical processes. These
structures may contain holes and are characterized by
straight edges and may be non-convex. Frequently,
they are moreover (near-)rectangular and have only
few angles and corners. Our methods are based on
the Concave Hull algorithm presented in (Moreira and
Santos, 2007). Although our application aims at gen-
erating outlines for the task of building reconstruc-
tion, and we therefore demonstrate and evaluate our
method in the context of that application, the proceed-
ings presented in this work are general and versatile.
2 RELATED WORK
Finding outlines of 2D point sets representing struc-
tures that have straight edges and enclose only few an-
gles in order to obtain “good” representations of the
underlying objects is an inherently ambiguous prob-
lem and strongly depends on the application. As
pointed out in (Galton and Duckham, 2006), there is
no single correct outline or footprint of a set of points.
Computing outlines by means of convex hulls, for in-
stance, is probably reasonable if the underlying ob-
jects are (almost) convex themselves. Convex hulls
are well-studied and many algorithms are known for
its computation (de Berg et al., 2008), but in case of
non-convex objects, convex hulls naturally yield un-
satisfactory outlines. Therefore, we do not further en-
ter on methods for their generation.
α-shapes (Edelsbrunner et al., 1983) are a gen-
eralization of convex hulls and allow for computing
non-convex (concave) outlines of 2D point sets. The
α-shape of a finite point set S ⊂ R
2
is the boundary
of the α-hull of S. The latter can be obtained by com-
puting the Delaunay triangulation of S and removing
those k-simplexes, 0 ≤ k ≤ 2, whose open circum-
scribed circles have radii ≥
1
α
or that contain any other
p ∈ S. Using α = 0, the α-shape of S is defined to be
its convex hull.
Another approach based on Delaunay triangula-
tion are characteristic shapes (χ-shapes) as presented
in (Duckham et al., 2008). The algorithm repeat-
edly removes the longest exterior edge whose length
is greater than some value L from the initial Delaunay
triangulation of S , provided that the remaining exte-
rior edges form a simple polygon. It is also possible to
parametrize χ-shapes by a normalized length parame-
ter λ =
l−l
min
l
max
−l
min
, where l denotes the length of an edge
and l
min
and l
max
are the minimal and maximal edge
length from the Delaunay triangulation, respectively.
The resulting outlines produced by α- and
χ-shapes depend on the choice of the respective
parameters α and l (or λ). Their choice involves
a-priori knowledge about the shape of the underlying
point set, or appropriate values must be found using
heuristics or by trial and error.
The Concave Hull Algorithm in (Moreira and
Santos, 2007) is based on the idea of Jarvis’ March
aka. Gift Wrapping Algorithm (Jarvis, 1973) for com-
puting convex hulls: Instead of considering all ele-
ments from the set of remaining points S , the Con-
cave Hull Algorithm only considers the 3 ≤ k ≤
|
S
|
nearest neighbors of the point that has been added
to the hull last. Using greater values for k results in
larger neighborhoods being considered, and the con-
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
60

cave hull becomes “more convex” as k increases. If
k =
|
S
|
, the algorithm computes the convex hull, be-
cause the set of points considered becomes the same
as with Jarvis’ March. Since our method is based on
the Concave Hull algorithm, it is briefly summarized
in Section 2.1.
The strength of Concave Hull is its simplicity
and that there is no need to compute any (Delaunay)
triangulation of which most information about con-
nectivity is not needed at all.
In (Asaeedi et al., 2013), the Alpha-Concave Hull
is presented, which is a simple polygon whose interior
angles are < π+α. If the parameter α = π, the Alpha-
Concave Hull is the minimal polygon of S ; in case of
α = 0, it is the convex hull.
In the field of photogrammetry, methods for gen-
erating rectangular outlines of buildings based on line
fitting of contour points, like the one presented in
(Vosselman, 1999), seem to be popular. The draw-
back of these methods is their limitation to the cre-
ation of only rectangular outlines. But even in the
application of detecting building outlines, there are
often boundaries that are not rectangular, at least in
some corners, like in cities that grew over centuries or
that were not planed from scratch.
There are also approaches based on statistical
estimates of the most appropriate outline for a given
set of points (Wang et al., 2006).
Furthermore, among the methods presented so far,
only α-shapes can create outlines of holes in 2D
(see Section 1), but the resulting outlines are overly
jagged. Representing holes, however, is essential
to obtain faithful representations of atria or build-
ing complexes enclosing inner courtyards. The so-
lutions presented in (Bendels et al., 2006), (Wang and
Oliveira, 2007) and (Wu and Chen, 2014) address the
detection (and also filling) of holes in point clouds
that represent surfaces in 3D, so that these methods
are difficult to apply to our problem.
2.1 Concave Hull Algorithm
To generate outlines, also called boundaries in the re-
mainder of this work, we adopt the Concave Hull Al-
gorithm in (Moreira and Santos, 2007) which is sum-
marized below, because it is the foundation of our ap-
proach. For a more detailed description, we refer to
the original article.
Let S be a finite set of points in 2D Euclidean
space where p
i
6= p
j
∀p
i
, p
j
∈ S ∧ i 6= j. Let further-
more p
0
∈ S be the point having minimal y-coordinate
and C
n
= (v
0
,v
1
,. . ., v
n
) the list of vertices of the out-
line computed so far.
Given k ∈ N, 3 ≤ k <
|
S
|
, start with n = 0, n ∈ N,
S
−1
= S, C
0
= (v
0
= p
0
), p = p
0
and e = −x, where
−x denotes the negative x-axis. Remove p from the
current set of points to obtain S
n
= S
n−1
\p and com-
pute the set K
n
(p) ⊂ S
n
of p’s k nearest neighbors.
The points q
i
∈ K
n
(p), 0 ≤ i < k are sorted accord-
ing to the clockwise angle ϕ
i
enclosed between the
directed edge e
i
= (q
i
− p) and edge e such that j = 0
be the index of the point p
j
= q
i
where ϕ
i
is largest,
j = 1 the one where ϕ
i
is second largest, etc.
Now let e
j
= (p
j
− p) denote the directed edge
from the last vertex of the outline polygon to the
point p
j
∈ K
n
(p), j = 0,1, . .. k. Starting at j = 0,
check if e
j
does not intersect any of the existing edges
v
n−2
v
n−3
,v
n−3
v
n−4
,. . ., v
1
v
0
of the polygon. If e
j
in-
tersects an existing edge of the hull, retry using e
j+1
,
if j < k. In case no e
j
remains, the outline computed
so far is discarded, k is increased and the algorithm is
restarted using n = 0 again. Otherwise, if no intersec-
tion of e
j
with an existing edge is found, set p
j
0
= p
j
to be the best match in K
n
(p), add p
j
0
to the list of
vertices, i.e., C
n+1
= C
n
∪ p
j
0
, and set e ← (v
n
− p
j
0
)
as the backwards directed edge formed by the last two
vertices of the hull. The process is then restarted set-
ting n ← n + 1 and p ← p
j
0
until p = p
0
again or all
points in S haven been processed. In order to ensure
that p = p
0
a second time and that the algorithm ter-
minates, p
0
must be added to S
n
again after the third
iteration. When p = p
0
the second time, it is neces-
sary to check if all remaining points in S
n
are actually
inside the resulting polygon C
n
so that it is actually a
hull in the proper sense. Otherwise, the outline is also
discarded, k is increased and the algorithm is restarted
using n = 0.
3 COMPUTING OUTER
BOUNDARIES
In this section we present two different approaches for
computing simple polygons that outline a given finite
point set S ⊂ R
2
. The outline’s edges only enclose
angles of a few, distinct values, and we call them an-
gular outlines in the following.
The first method relies on the concave hull and de-
termination of dominant edge directions. Our second
method modifies the Concave Hull Algorithm to di-
rectly compute an angular outline.
The advantage of the first method, presented in
Section 3.1, is that the hull can be straightened by
two predefined main angles. This idea follows the ap-
proach, that buildings are mostly oriented along two
Generating Straight Outlines of 2D Point Sets and Holes using Dominant Directions or Orthogonal Projections
61

directions to guarantee parallel walls. Furthermore, if
we also take the idea of perpendicularity into account,
we can force the straightened edges to form right an-
gles. Therefore, data that are very noisy or contain
holes can be bordered along the main directions or
perpendicular to it.
The second approach in Section 3.2 is preferable
if the underlying structure is not well approximated
by strictly rectangular outlines or if the edges of the
shape enclose more than two distinct angles. How-
ever, for this method to work, the initial orientation
of the underlying shape within a Cartesian coordinate
system must be provided.
3.1 Angular Outlines from Dominant
Directions
Let C
m
be the list of vertices of a concave hull of S and
E = (e
0
,..., e
m
) the list of edges with e
i
= v
i
v
i+1
, i =
0,1, . .. , (m − 1) and e
m
= v
m
v
0
. Since we do not
consider the orientation of an edge, each difference
vector e
i
is set to e
i
← sgn (e
i,y
) · e
i
. For each edge
e
i
, we compute the angle α
i
∈ [0,π] that is enclosed
with the positive x−axis. If α
i
= π, we set α
i
← 0.
The length of an edge e
i
is denoted by l
i
. We an-
alyze the directions and lengths of each edge of the
concave hull polygon and compute a length-weighted
angle histogram H(α
i
). Angle α
i
is assigned to the
respective bin of width w according to
−
w
2
+ (2n − 1) ·
w
2
≤ α
i
< (2n − 1) ·
w
2
+
w
2
,
n ∈ {1,2, ..., m}.
The value of the n-th bin is computed as
∑
i
l
i
.
From this histogram, we compute the two domi-
nant angles β and γ of the concave hull using one of
the following two options:
1. Approximate the histogram H(α
i
) by a bimodal
distribution. Then β and γ correspond to the an-
gles of the two maximums of the approximation.
2. β corresponds to the angle of the maximum value
in H and γ is offset by ±
π
2
:
β = argmax
0≤α
i
<π
(H (α
i
)), γ =
(
β +
π
2
, β <
π
2
β −
π
2
, β ≥
π
2
.
The advantage of option 1 (“peaks” option) is that the
edges of the boundary obtained from straightening of
the concave hull can enclose an arbitrary but fixed an-
gle that equals
|
β − γ
|
. Option 2 (“90
◦
” option) en-
sures that these edges always enclose right angles.
From β and γ we compute the corresponding dom-
inant directions
d
ϕ
=
cos(ϕ)
sin(ϕ)
, ϕ ∈
{
β,γ
}
and assign labels ρ
ϕ
to all edges of the concave hull
according to the dominant angle they belong to:
ρ
ϕ
= argmin
ϕ
{](e
i
,d
ϕ
)}, ϕ ∈ {β, γ}.
To simplify the straightening procedure it is advis-
able to shift the start point in the sequence of vertices
of the concave hull and the entries of the label vec-
tor to ensure a tuple of successive vertices having the
same label is not split by the start or end vertex. Af-
terwards, we collect every tuple of successive vertices
T
ρ
ϕ
= (t
1
,t
2
,...) from the concave hull that belong to
the same label ρ
ϕ
and compute the line ` through the
center of gravity along the corresponding main direc-
tion d
ϕ
:
` :~x =
1
|T
ρ
ϕ
|
∑
t
i
∈T
ρ
ϕ
t
i
+ µ d
ϕ
.
To limit these lines, we have to distinguish two
cases: If the foregoing (or subsequent) tuple belongs
to none of the dominant angles/directions we project
the first (or accordingly the last vertex) onto that line.
If the foregoing (or subsequent) tuple belongs to the
other dominant angle/direction, the end points are
specified by the intersection point of the line corre-
sponding to the foregoing (or subsequent) tuple and
the current tuple’s line.
3.2 Angular Outlines from Orthogonal
Projection
Our second approach to computing angular bound-
aries modifies the Concave Hull Algorithm in Sec-
tion 2.1 by projecting the edges of the hull onto or-
thogonal line segments and adjusting them. First, we
explain the process of projection onto orthogonal line
segments. This yields a strictly rectangular outline,
which is only a “good” representation if the underly-
ing shape is (almost) rectangular, too. The proceeding
is then extended by three modifications that improve
the shape of the outline in situations where strictly
rectangular outlines may be perceived as unsatisfac-
tory representations.
3.2.1 Orthogonal Projection
In this section, we use the same symbols from the
description of the Concave Hull Algorithm in Sec-
tion 2.1. In addition, let δ
i
= i ·
π
2
,i = 0,1, . .. , 4.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
62

When the Concave Hull has determined a candidate
p
j
0
among the sorted k nearest neighbors K
n
(p) of the
current point p ∈ S
n
that satisfies the requirements for
being a new vertex of the outline polygon, we modify
the algorithm to additionally compute
δ
0
= argmin
δ
i
δ
i
− ϕ
j
0
where ϕ
j
is the angle associated with p
j
such that δ
0
is
the angle that deviates least from ϕ
j
0
. If δ
0
happens to
be 0 or 2π, we discard p
j
0
and proceed with the next
candidate in K
n
(p), if there is any left. Otherwise, p
j
0
is discarded from the set of remaining points, just like
with the Concave Hull.
Using δ
0
, we compute the corresponding direction
d and an orthogonal vector u pointing to the “right-
hand side” of the ray R from p in direction d, away
from where the majority of points of S is located:
d =
cos(θ)
sin(θ)
, u =
sin(θ)
−cos (θ)
where θ = θ
n
+ (π − δ
0
) and θ
n
is the angle enclosed
by the last edge e of the outline computed so far and
the x-axis. Please notice that we have to use π − δ
0
instead of δ
0
to compute θ, because we chose clock-
wise angles in [0,2π] with the Concave Hull Algo-
rithm. The outer boundary is thus oriented counter-
clockwise. The vector e
j
0
= (p
j
0
− p), which corre-
sponds to edge p
j
0
p, is then projected onto d and u
to obtain the lengths l
d
= d · e
j
0
and l
u
= u · e
j
0
, re-
spectively. Next, the new vertex q to be added to the
current outline C
n
= (v
0
,v
1
,. . ., v
n
) is computed as
q = p +
|
l
d
|
· d + w
where
w =
(
max(l
u
,0) · u, δ
0
= π
l
u
· u, otherwise
(1)
Thus, if an edge is continued (i.e., δ
0
= π), w is either
zero or points towards the right-hand side. Otherwise,
if the new edge introduces a turn, it may also point to
the left-hand side of R. The outline polygon is then
updated by considering the following two cases:
1. If C
n
contains ≥ 2 vertices and the edge is about
to be continued, we replace the last vertex by q
and add w to the second last vertex:
v
n
← q, v
n−1
← (v
n−1
+ w) (2)
2. Otherwise, if δ
0
=
π
2
or δ
0
=
3π
2
and the outline is
about to make a left or right turn, respectively, or
if it contains only one vertex so far, we append q
to C
n
and add w to v
n
:
v
n+1
= q, v
n
← (v
n
+ w) (3)
In the next iteration n + 1, we proceed with q instead
of p
j
0
, after having removed p
j
0
from the point set
S
n+1
. As with the Concave Hull algorithm, we check
for self-intersections of the resulting polygon. In pos-
itive cases, we also discard the polygon and start the
algorithm from the beginning using k + 1. Likewise,
we terminate if p
j
0
= p
0
again, but since C
n
is obvi-
ously not a hull, it does not necessarily include all
points in S . Therefore, we omit the final check of
whether all points in S are located strictly inside C
n
.
Figure 2 illustrates the proceeding described above.
0
π
–
2
3
–π
2
π
p
φ
j'
p
j'
q
p
j'
p
q
d
n
p
p
j'
e
j'
0
π
–
2
3
–π
2
π
p
φ
j'
p
j'
q
p
j'
p
q
d
n
p
p
j'
e
j'
Figure 2: Creating angular outline by means of orthogonal
projection is based on the Concave Hull Algorithm, but in-
stead of adding p
j
0
to the list vertices, its projection q onto
d is added.
Due to the choice of w in Equation 1, we ensure
that edges are dragged only to the “outside” of the
shape and that more points (including p
j
0
) are located
“inside” the resulting outline, if an edge is continued.
In case of left or right turns, an edge may also be-
come dragged towards the “inside” (l
u
< 0) in order
to enclose the point set S more tightly. However, this
may cause some points of S to be found again among
the k nearest neighbors K
n+1
(p) in the next iteration.
Depending on the choice of k, this can lead to self-
intersections and the rejection of the current k. The
results of this proceeding are satisfactory in case of
shapes that are (almost) rectangular everywhere. In
cases where a shape’s corners deviate too much from
±
π
2
, e.g., in case of point sets derived from ancient or
architecturally unusual buildings, the outlines are less
appealing (see Figure 3).
3.2.2 Improvements for Non-Rectangular
Shapes
To make the outline match non-regular shapes more
accurately, e.g., if one or more corners deviate too
much from ±
π
2
, we introduce some modifications to
the proceeding described in Section 3.2.1. First, we
can simply omit the addition of w to the predecessor
of the last vertex in Equation 2 when an edge is con-
tinued. As a result, the continued edge is not neces-
sarily perpendicular to the previous one anymore, but
the outline captures a shape more accurately at cor-
ners where two edges join at angles ϕ >
π
2
. Corners
Generating Straight Outlines of 2D Point Sets and Holes using Dominant Directions or Orthogonal Projections
63
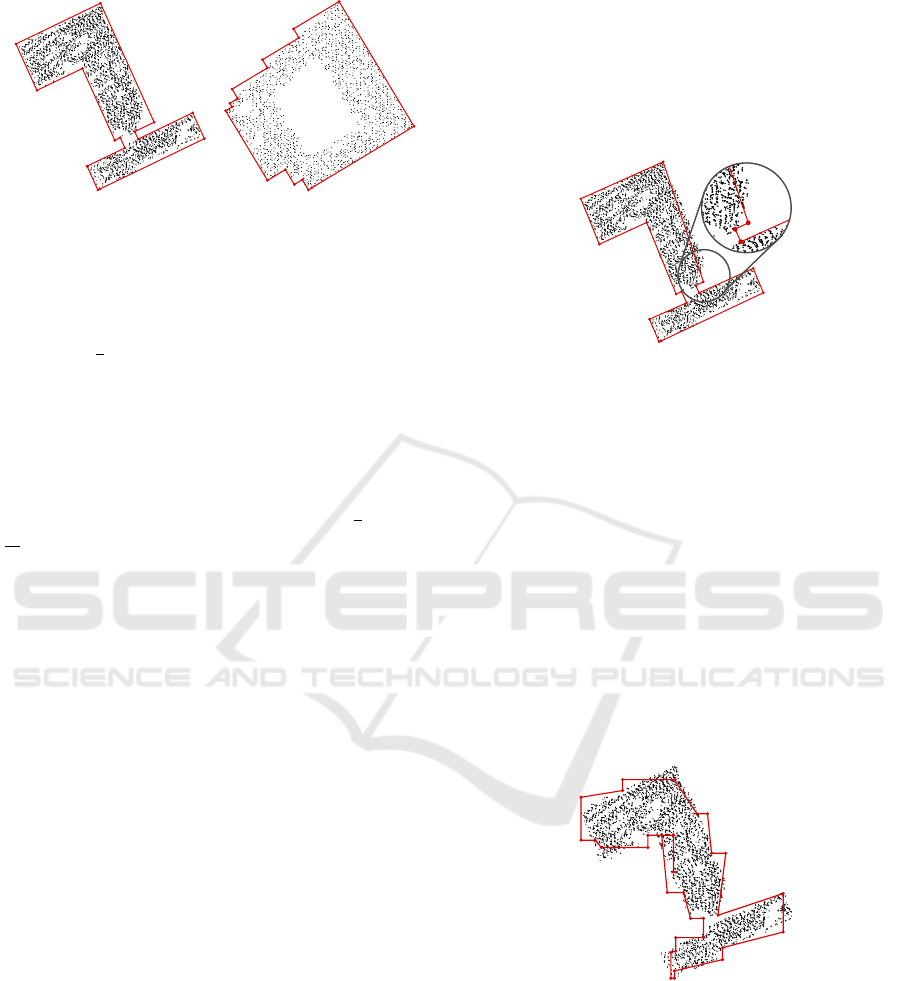
(a) (b)
Figure 3: Pure orthogonal projection and dragging contin-
ued edges only to the outside yields appealing results if the
underlying shape is almost rectangular itself (a), but causes
the appearance of unwanted steps if corners are present that
are not rectangular (b).
where ϕ <
π
2
remain approximated by steps, because
the line segment of a continued edge is only allowed
to being dragged outside due to Equation 1. Thus, we
modify Equation 1 to obtain Equation 4:
w =
(
max(l
u
,0) · u, if δ
0
= π ∧ outside = true
l
u
· u, otherwise.
(4)
The predicate outside is set to false if δ
0
=
π
2
or δ
0
=
3π
2
. It is set to true if δ
0
= π and if l
u
> 0 for any point
along the continued edge. In this way, a continued
edge may also become dragged towards the inside and
enclose S more tightly, as long as there is no need to
drag the edge outside again, i.e., l
u
< 0 over the whole
distance the edge is continued.
Dragging the last vertex of a continued edge to-
wards the inside can cause more points of K
n
(p) to
lie on the right-hand side of the edge, because p
j
0
is
not necessarily the first point in the descending or-
der of enclosed, clockwise angles. Those points may
be found in the next iteration in K
n+1
(p) again, and
they may introduce unwanted turns and corners in the
outline, or disturb the algorithm by self-intersections.
Therefore, we not only remove p
j
0
from S
n
to obtain
S
n+1
, but also every other point p
i
∈ K
n
(p) whose
associated edge (p
i
− p) encloses a clockwise angle
with the outline’s last edge e = (p − v
n−1
) that is
larger than the one enclosed between e and (q − p).
A further adjustment that affects concavities of a
shape is the enforcement of creating steps in the out-
line by modifying Equation 2 to obtain Equation 5:
v
n
← q
v
n−1
←
(
v
n−1
+ w, second last trun was right
v
n−1
, otherwise.
(5)
In other words, we add w to the second last vertex of
a continued edge, if the second last turn of the out-
line we encountered was a right turn, and the edge
is thus part of a concavity. In such concave regions,
the algorithm then behaves like the version in Sec-
tion 3.2.1, and problems as shown in Figure 4 are pre-
vented. The benefit of this modification, however, de-
pends on the application and the underlying point set,
and to some degree on the user’s judgment or personal
preferences.
Figure 4: Due to dragging only the last vertex of outlines,
edges may be moved into concavities and can unintention-
ally cut off too many points.
3.2.3 The Choice of Initial Direction
In the proceeding described in Section 3.2.1, the ini-
tial direction given by θ
0
is yet unspecified, but it in-
fluences the resulting outline as shown in Figure 5.
Using θ
0
= 0 is only reasonable if the lowest edge of
shape is (near) parallel to the x-axis. But since the ori-
entation of the shape we are trying to approximate by
angular outlines may be unknown in advance, we ei-
ther have to let the user specify θ
0
or obtain it from
analysis of the point set’s orientation by statistical
means, e.g., via principal component analysis (PCA)
or the methods employed in Section 3.1.
Figure 5: The shape represented by the point is actuall tilted
by ≈ 25
◦
against the x-axis. Not accounting for this initial
orientation yields unpleasant results.
Starting at point p
0
having lowest y-coordinate, we
might also run our algorithm using θ
0
= 0. The first
time we encounter δ
0
6= π, we can set θ to the angle
enclosed between the first edge and the x-axis. In this
way, θ
0
not only depends on p
0
, but also on the choice
of the size of the neighborhood k, which can be un-
satisfactory as outliers in the neighborhood of p
0
may
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
64

yield an inappropriate outline. However, if the point
set is sufficiently clean and dense in the area of the
outline’s first edge, this method works quite well. It
can also be used to give the user a hint of the initial
orientation of the shape.
3.3 Obtaining Simple Polygons
Due to the straightening process of the concave hull
(Section 3.1) or the dragging of edges (Section 3.2.1),
the outlines created by our methods may be self-
intersecting. To obtain simple polygons, these self-
intersections need to be detected, and the line seg-
ments between the points of intersection are cut off.
4 OUTLINES OF HOLES
The outlines of point sets in plane sections in 2D Eu-
clidean space may comprise larger areas where no
points are present. In the application of building
reconstruction from LIDAR data, for instance, this
happens if building complexes contain atria or inner
courtyards, because the data may only yield informa-
tion about distinctly elevated structures, like roofs.
We call such empty areas holes within the point set
and define them more formally as in Definition 1.
Definition 1. Let S ⊂ R
2
be a finite point set and
Ω(S ) ⊂ R
2
be the domain inside a simple polygon
that tightly encloses all elements of S (e.g., one of
its hulls or the minimal axis-aligned bounding box).
We call a connected region E ⊂ Ω(S) of finite area
a hole (in or of S ) of size r, if E is large enough to
fully overlap a circle of radius r > 0 at some location
c such that ∀p ∈ S :
k
p − c
k
≥ r.
r is called the size of hole E.
Our definition of hole depends on the choice of
polygon to border Ω(S): it is possible to choose dif-
ferent boundaries for S that have different numbers of
holes, or holes of different sizes. In this work, how-
ever, we are only interested in holes that do not border
on the enclosing polygons of point sets.
In order to obtain faithful outlines of the objects
represented by 2D points, we extend our methods by
creating inner boundaries. Since we are only inter-
ested in holes that are “large enough”, we choose a
minimum hole diameter d
min
that shall be detected.
The choice of d
min
depends on the application and the
average sampling density of the point set. In the ap-
plication of building reconstruction, for instance, d
min
might be related to the sizes of humans or vehicles,
if the holes originate from courtyards, because such
structures usually serve a purpose and thus need to be
accessible.
In contrast to outer boundaries, inner boundaries
shall be oriented clockwise. This is mainly due to
technical aspects and conventions, for it allows us to
easily determine whether a point is located inside or
outside the inner or outer boundary. Besides, we need
to take into account that there might be more than one
hole in a given point set.
4.1 Detecting Holes
The basic idea of detecting holes is to find points on
their border and to create their outlines by applying
modified versions of the methods presented in Sec-
tion 3. In order to find points on the border of holes,
we employ the following heuristic (see also Figure 6):
1. Let h be the extent of point set S along the y-axis;
choose a minimum hole diameter d
min
. Let fur-
thermore P be a simple, closed outline polygon of
S, e.g., a (concave) hull or any other outline ob-
tained by our methods.
2. Split S along y-axis into m strips of width w =
d
min
2
in such a way that m =
l
2h
d
min
m
∈ N.
3. Obtain disjoint point sets Y
j
for each of the 0 <
j ≤ m strips where ∀a, b ∈ [0, m − 1], a 6= b, Y
a
∩
Y
a+1
=
/
0 ∧
m−1
S
j=0
Y
j
= S.
4. For each set Y
j
, sort the points in Y
j
in ascending
order of x-coordinates.
5. For each two neighboring points p
i
, p
i+1
in Y
j
,
compute the distance d =
|
p
i+1,x
− p
i,x
|
.
6. If d ≥ 2 · w and m = (p
i,x
+ w, p
i,y
) is located in-
side P, add the directed line segment p
i
p
i+1
to the
list of candidates Q.
w
m
d
min
Figure 6: To find locations on the border of a hole from
where to start the generation of inner boundaries, the point
set is cut into strips perpendicular to the y-axis (left). Neigh-
boring points whose projections onto the x-axis have dis-
tances ≥ d
min
are candidates (red), if m (red circle) is inside
the point set’s boundary (green).
This approach will find the points on the borders
of all holes at once, but we cannot tell the hole a can-
didate belongs to. To solve this problem, we compute
Generating Straight Outlines of 2D Point Sets and Holes using Dominant Directions or Orthogonal Projections
65

an outline of the hole for the left vertex of first line
segment s
0
= a
0
b
0
in Q as described in Section 4.2
and remove it from Q. For each of the remaining line
segments s
j
= a
j
b
j
∈ Q, j > 0, we check if the mid-
point m
j
of s
j
is located inside any previously com-
puted outline of a hole, and discard s
j
if m
j
is in-
side. Furthermore, we check if any edge of a new hole
boundary intersects an edge of a previously computed
hole outline. If two outlines intersect, we can discard
one of them based on a reasonable criterion, e.g., the
size of its area or its number of vertices. Another op-
tion would be to merge the two outlines in order to
obtain a common outline, but we did not implement
this approach due to its complexity.
Alternatively, we may suspend the search for
further candidates after the first one. After generating
the hole boundary, we can fill the hole with phantom
data points based on a point density estimation. The
next candidate is then detected by restarting the
search procedure from the beginning.
With the approach described above, we cannot
yet guarantee that the resulting outline borders a hole
overlapping a circle of radius ≥ w and is therefore
consistent with Definition 1: Due to “cutting” the
point set perpendicular the y-axis into strips of width
w =
d
min
2
, the hole has at least a radius of half the size
of
w
2
. Cutting the point set into strips of width d
min
might cause holes around this size to be missed, be-
cause the strips are projected onto the x-axis and gaps
might be concealed from projections of points on the
top or bottom of the hole. This is a sampling problem
and the strip width w should thus be smaller than
d
min
2
in a practical implementation.
Verifying the size of the hole found by the heuris-
tic above turns out to be difficult, since we would need
to find the center of an empty circle with radius d
min
within the hole, but there are potentially infinite many
locations. By placing a circle of radius d
min
at the
centroid of the hole’s outline polygon, for example,
the hole can be accepted if the circle is empty, but it
cannot be safely reject, if the circle is not empty. In
practical applications that do not rely on the exact size
of a hole, it may still be sufficient to find holes that are
known overlap circles with radii the range of
w
2
and w.
4.2 Bordering Holes
Creating the outlines of holes is done using slightly
modified version of the procedures described in Sec-
tion 3 and the Concave Hull algorithm in Section 2.1.
The modifications basically account for changing the
orientation of the resulting polygon to clockwise, and
the different starting location.
Our modification to the Concave Hull algorithm
to obtain a clockwise oriented polygon for outlining
holes is as follows: Among all k neighbors K
n
of the
current point p = v
n
, we search for the point q
i
with
the smallest counter-clockwise angle ϕ
i
= ](ξ
n
, e
i
=
pq
i
) where ξ
n
is the previous edge directed back-
wards, i.e., ξ
n
= v
n−1
v
n
instead of v
n
v
n−1
. Initially,
we use the positive x−axis for ξ
0
.
By choosing p
0
as the first vertex a
j
of the line
segments s
j
∈ Q obtained by the heuristic given in
Section 4.1, we start at a point that is part of the left
border of the hole. The point may furthermore be lo-
cated on a sharp crease (like a v-shaped corner) such
that the smallest ϕ
i
may be associated with a point
at the opposite border of that crease. Thus, the out-
line generation might fail right away, if k was too
large. Replacing ξ
n
by an edge that is rotated counter-
clockwise by
π
2
to point inside the hole yields better
results, but if the neighborhood gets even larger, the
algorithm can still fail for the same reason.
Due to its position on the left border of the hole,
the point p
0
= a
j
may not necessarily be found in a k
nearest neighborhood a second time. Therefore, we
also have to extend the condition for terminating the
hole’s concave hull computation: For each new line
segment added to the hull, we additionally check if it
intersects the line segment s
j
= a
j
b
j
∈ Q . Starting
from point a
j
, the edges of the outline to be created
will enter the “upper” part of the hole. They can only
enter the “lower” part by crossing s
j
on the right
border at b
j
or close to it. Once a line segment enters
the “upper” part from the hole’s “lower” part again,
s
j
is crossed a second time, and we terminate the hull
computation, because the polygon has encircled the
hole.
Using our method to generate the outline of a hole
by means of dominant directions as presented in Sec-
tion 3.1, we first create a clockwise oriented concave
hull as described above, and apply the same proceed-
ing to straighten the concave hull of a hole afterwards.
Our method described in Section 3.2 merely needs to
be adjusted in the same way as the Concave Hull Al-
gorithm in order to create outlines of holes.
5 RESULTS AND DISCUSSION
We demonstrate the usability of our methods by
means of four different data sets D
1
– D
4
: the point
sets already depicted in Figures 3(a) (D
1
), 1 (D
2
) and
3(b) (D
3
), originate from airborne laser scans. The
point set depicted in Figure 12(a) (D
4
) is a synthetic
data set featuring a star-shaped hole. Data sets D
1
–
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
66
D
3
represent non-convex building complexes, but D
1
is moreover near-rectangular in contrast to D
2
and D
3
.
For the purpose of generating figures, we reduced the
number of points depicted, but to create outlines, we
always employed the original, denser point sets.
5.1 Results
The outline of D
1
generated by means of domi-
nant directions (see Section 3.1) is shown in Fig-
ure 7(a). With this data set, both options for determin-
ing the dominant directions (“peaks” and “90
◦
”) lead
to the same rectangular outline that is significantly
“straighter” than the concave hull for k = 60, but
satisfactorily represents the underlying shape. The
straightening process causes changes in areas as high-
lighted in Figure 7(b). These changes are small but
help to approximate the building’s true outline and
compensate for noise and mistaken measurements.
(a) outline dominant direc-
tions
(b) differences of over-
lapped areas
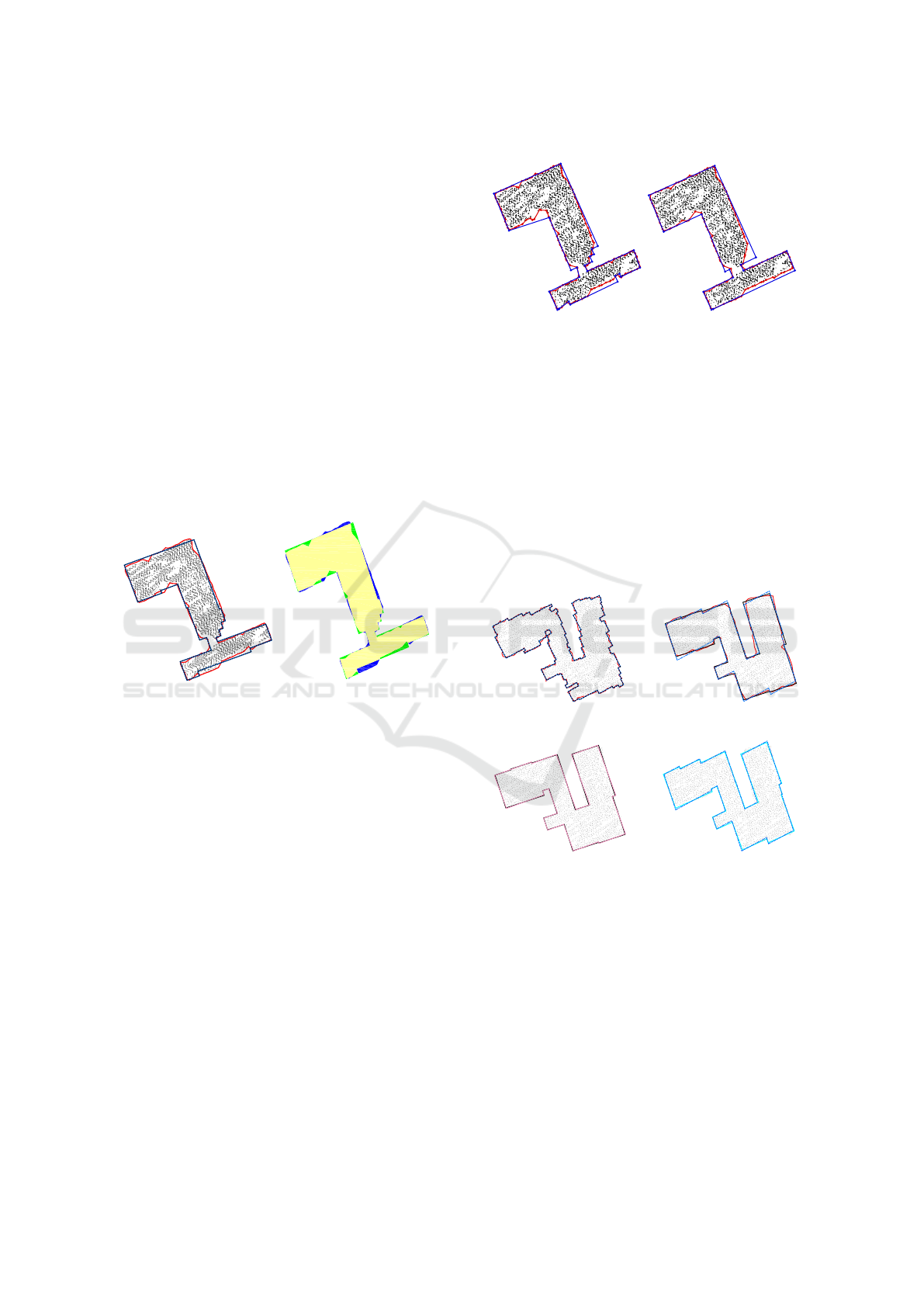
Figure 7: The concave hulls (red) of D
1
using k = 60 com-
pared to outlines generated by means of our method using
dominant directions. Left: the two options “90
◦
angles”
(black dotted) and “peaks” (blue) lead to same outline with
substantially fewer vertices than the concave hull. Right:
areas overlapped by the concave hull (yellow + blue) and
the straightened outline (yellow + green).
Like with the original Concave Hull algorithm,
we can influence the shape of the resulting outlines
by altering k. Using larger k yields boundaries that
look “more convex” than the ones created using
smaller k. This is illustrated in Figure 8 by means
of outlines of D
1
obtained by using orthogonal
projection (Section 3.2).
Boundaries of D
2
using dominant directions are
given in Figure 9. With this data set, the first main
direction is almost independent of k, but increasing
k also increases the uncertainty in the determination
of the second main direction. Since the later is also
influenced by the point distribution and data noise,
at larger k, the resulting outline looks a somewhat
(a) k = 60 (b) k = 100
Figure 8: Outlines of D
1
generated by using our method
based on orthogonal projection (blue) compared to the con-
cave hull (red) at different values of k.
skewed against the point set’s shape. In this case, the
outline created by using our “90
◦
” option encloses the
points more accurately. The remaining deviations re-
sult from the fact that the shape of D
2
is not truly rect-
angular. Figure 1(c) depicts an outline of this data set
generated by means of orthogonal projection. Since
the edges of that outline do not necessarily join or-
thogonally due to the dragging operations performed,
it captures the point set’s shape very well.
(a) k=20 (b) k=100
(c) k=100, straighten-
ing: 90
◦
; bin width
10
◦
(black) : 1
◦
(pink)
(d) k = 100, straight-
ening: main angles;
bin width 10
◦
(blue) :
1
◦
(cyan)
Figure 9: Straightened building outlines from the concave
hull (red) for k = 20 (a) and k = 100 (b) neighbors. Larger
k lead to smoother outlines but increase the uncertainty for
computing the main direction. Changing the bin sizes leads
to a tilt of the boundary.
D
3
is a real-world example of a point set acquired
from a non-rectangular, non-convex building that has
an atrium. Outlines of the outer and inner boundaries
created by means of our methods are shown in Fig-
ure 10. Figures 10(a) and 10(b) show the concave
hull and outlines of holes of minimum diameter d
min
Generating Straight Outlines of 2D Point Sets and Holes using Dominant Directions or Orthogonal Projections
67

of 100 units and 30 units, respectively. These bound-
aries were created by means of our dominant direc-
tions method, and the holes were found using our
heuristic in Section 4.1. Using a smaller hole size,
we are able to find and outline the additional hole in
the upper right corner, whereas a larger hole size only
allows for handling the atrium. However, the inner
and outer boundaries produced by the straightening
procedure do not faithfully represent the shape of the
underlying building: The lower part of the polygon
is approximated quite well when the concave hull is
straightened by using the “90
◦
” option, whereas the
upper edge is matched unsatisfactorily. Using the
“peaks” option, we have the opposite situation, and
the upper edge is matched quite well, although the
first main direction is equal with both options. Since
our approach based on dominant directions only al-
lows to straighten along two dominant directions, it
cannot match both edges at once.
(a) d
min
= 100 (b) d
min
= 30
Figure 10: Concave hull (red) and straightened outlines ob-
tained from dominant directions and ensuring 90
◦
angles
(black dashed) and with respect to histogram peak angles
(blue).
Our method based on orthogonal projection suc-
ceeds to accurately capture the building’s shape, in-
cluding the upper edge that is tilted by ≈ 12
◦
towards
the lower edge (see Figure 11).
To put our methods for detecting and outlining
holes to the test, we created the synthetic data set de-
picted in Figure 12. The star-shaped hole was man-
ually cropped and is especially challenging, because
it is very sensitive to the choice of k: The edges of
the spires are v-shaped and using large values of k
causes them to become cut off. Using smaller val-
ues of k increases the accuracy, but also increases the
uncertainty for determining the dominant directions
when straightening the outline (see Figures 12(b) and
12(c)). Since we only consider two dominant direc-
tions with this approach, the outline of the star almost
completely loses its initial shape. By means of or-
thogonal projection, we get a more faithful outline of
Figure 11: Inner and outer boundaries obtained by orthog-
onal projection (blue) compared to the concave hull (red) at
k = 20 of our test data set D
3
. The minimum hole diameter
is d
min
= 50 units.
(a) straightened bound-
aries
(b) straightened lower
left hole boundary
(c) straightened upper
right hole boundary
Figure 12: Outlines created from our approach based on
dominant directions of data set D
4
compared to the con-
cave hull (red) at k = 20 and k = 40 for the inner and outer
boundaries, respectively. With the star-shaped hole and the
outer boundary, the two dominant directions obtained from
the peaks of the angle histogram (blue) are the same as the
ones obtained by the “90
◦
angle” option (dashed black). In
case of the other hole, the two options yield different domi-
nant directions.
the star-shaped hole, which not perfect, though (see
Figure 13).
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
68

Figure 13: Outline of the star-shaped hole in data set D
4
cre-
ated by orthogonal projection (blue) using k = 10 in com-
parison to the concave hull (red).
5.2 Discussion
The two methods presented in this work for gener-
ating straight outlines have different advantages over
each other. Straightening concave hulls by means
of dominant directions can accurately capture certain
shapes of objects represented by point sets without
prior knowledge about the orientation of their edges.
However, it relies on the prior computation of concave
hulls and is likely to yield unsatisfactory results if the
shape’s edges run in more than two distinct directions
(cf. Figures 10 and 12(c)). Determining the domi-
nant direction is furthermore subject to the width of
bins used for the histogram of angles in the concave
hull. This influence becomes apparent in Figures 9(c)
and 9(d) where the bin widths are 10
◦
and 1
◦
, respec-
tively. Depending on the quality of the concave hull
(i.e., mainly on the choice of k) and the point distri-
bution, changing the bin width can tilt the generated
outline in an undesirable way. Especially by deter-
mining the second dominant direction from the his-
togram peaks, the choice of bin width may cause a
shift in the position of the peaks corresponding to the
dominant directions. For example, by enlarging the
bin width by 5
◦
, the bin associated with the second
maximum may coincide with a neighboring bin. In
this way, the second direction is tilted by about the
same amount. Of course, the first direction can suf-
fer from the same problem, if the point set is of rather
square or circular shape instead of an elongated one.
Our approach based on orthogonal projection and
the dragging of edges can create faithful outlines of
shapes whose edges run in more than two distinct
directions, but it requires hints about the initial ori-
entation of the shape and possibly contained holes.
These hints may be obtained automatically (see Sec-
tion 3.2.3) in some situations, but otherwise they have
to be provided by the user. With this method, it is not
necessary to compute concave hulls or other interme-
diate polygons in advance, though.
The choice of the size k of the neighborhood
considered is crucial for both our methods, but it
is also subject to the distribution of the underlying
points. While the Concave Hull Algorithm starts
at the smallest k = 3 and increases the value if the
outline has self-intersections or does not include all
points of the set, this proceeding is not guaranteed
to succeed with our methods, because our angular
outlines may deliberately exclude points. In our
experiments, we found that using k of about 5 – 10%
of the number of points in the set is a reasonable
initial choice, if the point distribution (excluding
holes to be detected) is approximately uniform.
The decision which outline matches the underly-
Generating Straight Outlines of 2D Point Sets and Holes using Dominant Directions or Orthogonal Projections
69

ing object “best” is up to the user who can incorporate
background information about the underlying object.
In case of the underlying building represented by D
1
(see Figures 7 and 8), for instance, we could not de-
cide whether the object is a single building complex
or if there are two separate buildings, possibly linked
by a corridor, if we solely rely on the information pro-
vided by the point set.
6 CONCLUSION AND FUTURE
WORK
In this article, we presented two methods based on
the Concave Hull Algorithm to create straight, angu-
lar and non-convex outlines of 2D point sets and pos-
sibly contained holes. The outlines of point sets rep-
resenting man-made structure, like buildings, created
by means of our methods are “better” than concave
hulls or boundaries obtained from α-shapes to the ef-
fect that our methods capture straight edges more ac-
curately and feature only few, distinct angles.
The employment of straightening concave hulls
by means of dominant directions to generate outlines
is preferable if the orientation of the underlying shape
is unknown or cannot be provided, or if the shape is
known to have edges running in only two distinct di-
rections, e.g., in case of rectangular buildings. Ad-
ditional directions could be obtained by introducing
an angle of tolerance ϕ
max
. If ](e
i
,d
ϕ
) > ϕ
max
∀ϕ ∈
{
β,γ
}
, the corresponding label vector entry is set to
zero (see Section 3.1). These edges would not be af-
fected by the straightening procedure, which is help-
ful if the building contains a narrowing or constric-
tions of angles other than the determined dominant
ones.
If information about the orientation of the shape
is available, our approach based on orthogonal pro-
jection can produce more faithful boundary polygons,
especially if the underlying shape features edges run-
ning in more than two distinct directions. More-
over, this approach forgoes the computation of con-
cave hulls or any other intermediate polygon.
The most challenging task is the reliable detection
of holes. We encountered this problem by means of
a heuristic that is subject to sampling problems and
may have several theoretical limitations. Although we
did not encounter major problems due to a rather spe-
cific, practical application, we would like to improve
on these potential issues. For example, holes might
be located close to the outer boundary of the associ-
ated point set, and they might thus share boundaries
with the exterior outline. This could cause our current
algorithms for bordering holes to fail, because the out-
line might “leave” the hole and intersect the exterior
boundary.
Moreover, we only considered “isolated” point
sets so far. In the application of building reconstruc-
tion, for example, this requires prior segmentation of
the source data. We would like to forgo this step
and determine spacings or gaps between distinct clus-
ters of points in larger point sets to segment these
while creating the corresponding outlines. This may
be accomplished by a combination of modifying and
constraining the neighborhoods employed by our ap-
proaches or the Concave Hull Algorithm, and adjust-
ments of our heuristic for hole detection to this prob-
lem, but remains future work to do.
REFERENCES
Asaeedi, S., Didehvar, F., and Mohades, A. (2013).
Alpha Convex Hull, a Generalization of Convex
Hull. The Computing Research Repository (CoRR),
abs/1309.7829.
Bendels, G. H., Schnabel, R., and Klein, R. (2006). De-
tecting Holes in Point Set Surfaces. Proceedings of
The 14th International Conference in Central Europe
on Computer Graphics, Visualization and Computer
Vision, 14.
de Berg, M., Cheong, O., van Krevald, M., and Overmars,
M. (2008). Computation Geometry. Springer, 3rd edi-
tion.
Douglas, D. and Peucker, T. (1973). Algorithms for the Re-
duction of the Number of Points Required to Repre-
sent a Digitized Line or Its Caricature. The Canadian
Cartographer, 10(2):112 –– 122.
Duckham, M., Kulik, L., Worboys, M., and Galton, A.
(2008). Efficient Generation of Simple Polygons for
Characterizing the Shape of a Set of Points in the
Plane. Pattern Recognition, 41(10):3224–3236.
Edelsbrunner, H., Kirkpatrick, D., and Seidel, R. (1983).
On the Shape of a Set of Points in the Plane. IEEE
Transactions on Information Theory, 29(4):551 – 559.
Galton, A. and Duckham, M. (2006). What is the Region
Occupied by a Set of Points? In Proceedings of the 4th
International Conference on Geographic Information
Science, GIScience’06, pages 81–98, Berlin, Heidel-
berg. Springer-Verlag.
Jarvis, R. A. (1973). On the Identification of the Convex
Hull of a Finite Set of Points in the Plane. Information
Processing Letters, 2(1):18 – 21.
Moreira, A. and Santos, M. Y. (2007). Concave hull: A
k-nearest Neighbours Approach for the Computation
of the Region Occupied by a Set of Points. Proceed-
ings of the 2nd International Conference on Computer
Graphics Theory and Applications (GRAPP), pages
61 – 68.
Ramer, U. (1972). An Iterative Procedure for the Polygonal
Approximation of Plane Curves. Computer Graphics
and Image Processing, 1(3):244 – 256.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
70

Vosselman, G. (1999). Building Reconstruction Using Pla-
nar Faces In Very High Density Height Data. In Inter-
national Archives of Photogrammetry, Remote Sens-
ing and Spatial Information Sciences, pages 87–92.
Wang, J. and Oliveira, M. M. (2007). Filling Holes on
Locally Smooth Surfaces Reconstructed from Point
Clouds. Image and Vision Computing, 25(1):103 –
113.
Wang, O., Lodha, S. K., and Helmbold, D. P. (2006). A
Bayesian Approach to Building Footprint Extraction
from Aerial LIDAR Data. In Proceedings of the Third
International Symposium on 3D Data Processing, Vi-
sualization, and Transmission (3DPVT’06), 3DPVT
’06, pages 192–199, Washington, DC, USA. IEEE
Computer Society.
Wu, X. and Chen, W. (2014). A Scattered Point Set
Hole-filling Method Based on Boundary Extension
and Convergence. In 11th World Congress on Intel-
ligent Control and Automation, pages 5329 – 5334.
IEEE.
Generating Straight Outlines of 2D Point Sets and Holes using Dominant Directions or Orthogonal Projections
71
