
HBD: Hexagon-Based Binary Descriptors
Yuan Liu and J. Paul Siebert
School of Computing Science, University of Glasgow, Glasgow, U.K.
Keywords:
Binary Descriptor, Hexagonal Structure, Hierarchical Grouping, Local Feature Matching, Pose Estimate.
Abstract:
In this paper, two new rotationally invariant hexagon-based binary descriptors (HBD), i.e., HexIDB and
HexLDB, are proposed in order to obtain better feature discriminability while encoding less redundant in-
formation. Our new descriptors are generated based on a hexagonal grouping structure that improves upon the
HexBinary descriptor we reported previously. The third level descriptors of HexIDB and HexLDB have 270
bits and 99 bits respectively fewer than that of SHexBinary, due to sampling ∼61% fewer fields. Using learned
parameters, HBD demonstrates better performance when matching the majority of the images in Mikolajczyk
and Scmidt’s standard benchmark dataset, as compared to existing benchmark descriptors. Moreover, HBD
also achieves promising level of performance when applied to pose estimation using the ALOI dataset, achiev-
ing ∼ 0.5 pixels mean pose error, only slightly inferior to fixed-scale SIFT, but around 1.5 pixels better than
standard SIFT.
1 INTRODUCTION
Local feature descriptors are deemed to be one of the
most significant research topics in computer vision,
since they are required to facilitate computer vision
tasks. Approaches to formulating local feature de-
scriptors have been intensively researched and can be
divided into two categories: floating-point descrip-
tors and binary descriptors. Floating-point descrip-
tors usually represent the distribution of local gra-
dient information, and the most widely-reported of
these is SIFT (Lowe, 2004). Variants of SIFT, have
been reported, which aims to improve overall com-
putational efficiency for descriptors, such as PCA-
SIFT (Ke and Sukthankar, 2004) and SURF (Bay
et al., 2006). However, new algorithms are needed to
generate highly efficient feature descriptors in terms
of computational and storage requirements because
of the increasing demands of real-time applications.
BRIEF (Calonder et al., 2010) is such a descrip-
tor having been designed to improve computational
efficiency by generating binary bit-strings that en-
code local pixel intensity comparisons. The perfor-
mance attained by BRIEF when matching local fea-
tures has resulted in binary descriptors being inves-
tigated intensely. BRISK (Leutenegger et al., 2011)
and FREAK (Alahi et al., 2012) are two examples of
the binary descriptors also computed by comparing
pixel intensity values for different sampling structure
configurations.
HexBinary (Liu et al., 2014) is a hierarchical bi-
nary descriptor that is based on the hexagonal group-
ing structure that was first employed by the HexHoG
(Liu and Siebert, 2014) descriptor. The HexBinary
descriptor employs a hierarchical grouping mecha-
nism which includes combining vectors representing
overlapping image regions to improve the feature’s
discriminability. However, this approach can result in
repeated overlapping of the same local image area to
produce excessive redundancy, thereby degrading the
descriptor’s performance. Therefore, the main con-
tribution in this paper is a new hexagonal grouping
structure that results in less redundant information, re-
duced computation and better feature distinctiveness
due to it sampling ∼61% fewer fields for the third
level descriptor. This new grouping structure has lead
us to formulate two new Hexagon-based Binary De-
scriptors (HBD): Hexagon-based Intensity Difference
Binary (HexIDB) and Hexagon-Based Local Differ-
ence Binary (HexLDB). In addition, the parameters
used to compute HBD are learned by training on a
well-known image dataset proposed by (Mikolajczyk
and Schmid, 2005). Descriptor variants of the HBD
that we have formulated outperform the variants of
the FREAK and SIFT descriptors we have used in
our local feature matching performance comparisons.
Moreover, HBD has been evaluated for use in pose
estimation using the ALOI (Geusebroek et al., 2005)
image dataset and exhibits competitive performance
when compared to fixed-scale SIFT (US-SIFT), and
Liu, Y. and Sieber t, J.
HBD: Hexagon-Based Binary Descriptors.
DOI: 10.5220/0005720401750182
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 175-182
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
175

much better performance than the standard SIFT in
terms of mean pose error.
2 RELATED WORK
In general, real-time applications necessitate descrip-
tors which are inexpensive in terms of computation
and storage requirements. BRIEF (Calonder et al.,
2010) is such a robust binary string descriptor, which
achieves a substantially improved efficiency in terms
of computation, matching and storage compared to
SURF and U-SURF (Bay et al., 2006). The BRIEF
descriptor encodes pairwise intensity comparisons,
each sampled over Gaussian weighted image regions;
as only the sign of the comparison is stored as a
binary bit, such a feature can be represented as a
binary string. The similarity between such binary-
string descriptors can be efficiently computed using
the Hamming distance, rather than L
2
norm distance.
ORB(Rublee et al., 2011) is a scale and rotation in-
variant version of BRIEF. In BRISK (Leutenegger
et al., 2011), its support region is sampled in a ro-
tationally symmetric manner, similar to that of the
DAISY (Tola et al., 2010) descriptor. Based on the
feature detection approach of BRISK, FREAK (Alahi
et al., 2012) approximates a retinal sampling pattern
whereby the sampling Gaussian kernel size increases
exponentially as a function of distance from the fea-
ture’s centre. This complex configuration has been
reported to generate highly discriminative features.
In contrast to the binary descriptors introduced
above, Local Difference Binary (LDB) (Yang and
Cheng, 2012) descriptors compute the binary bit not
only from intensity comparisons, but also from gra-
dient comparisons. The average intensity and gra-
dient in the x and y directions are compared be-
tween each of two grids to generate a 3 bit vector.
HexBinary (Liu et al., 2014) is a hierarchical descrip-
tor generated recursively from a hexagonal group-
ing structure. The binary bit is computed by com-
paring the pixel pairs sampled in a hexagonal struc-
ture. HexBinary is different to other lightweight de-
scriptors in that it achieves rotation invariance without
rotating the local sampling patch, but through util-
ising the inherent rotational symmetry of hexagonal
sampling. HexBinary’s hierarchy is constructed by
grouping new hexagons within in a hexagonal struc-
ture. This produces multiple or ”overlapping” encod-
ings of the same image region, and has been adopted
since this approach been reported to improve feature
discrimination performance (Dalal and Triggs, 2005).
However, repeated overlapping of the same image
area can produce excessive redundancy. In this paper,
we introduce a new hexagonal grouping structure that
has been designed to reduce the overlap frequency of
each sampling area. In addition, our new descriptor
encodes both the intensity and gradient comparison
information to generate the binary bits of a binary-
string feature representation. We employ the same
approach to compare Gaussian weighted image re-
gions as utilised within the second-order HexBinary
descriptor SHexBinary. Two new HBD are introduced
here: HexIDB and HexLDB, and their matching per-
formance is validated for pose estimation where the
descriptor’s parameters have been learned.
3 APPROACH
In this section, we give the details of how we construct
the hexagonal grouping structure to generate new hi-
erarchical binary descriptors: HexIDB and HexLDB.
Since the structure is based on that of the HexBinary
descriptor, we now briefly describe the HexBinary
structure below.
3.1 Sampling Structure
The sampling structure used to compute the second
level HexBinary descriptor is illustrated in Figure 1
(a). The red ? indicates the feature point position,
and the descriptor for this feature point is computed
from the neighbouring region in the hexagonal struc-
ture. The validation of the HexBinary descriptor has
demonstrated that this hierarchy, up to the third level,
is a good trade off between descriptor matching ef-
fectiveness and efficiency. Therefore, in this paper,
the hierarchy is also only considered up to the third
level.
The sampling structure used to construct three lev-
els of HexBinary descriptors is summarised as fol-
lows: a hexagon of defined size is constructed cen-
tred on the feature point p, so in total 7 points are
sampled at: the 6 vertexes and the central location of
the descriptor (p). For the first level HexBinary de-
scriptor termed as HexBinary1 of p, the binary bits
are computed from the 7 sampling points in this sin-
gle hexagon; For the second level descriptor HexBi-
nary2, the 7 sampling positions of the hexagon are
treated as 7 feature points. The HexBinary1 descrip-
tors comprising 7 feature points are similarly com-
puted, and are then concatenated together to form
the second level descriptor p; Similarly, the third
level descriptor HexBinary3 of p is generated by con-
catenating the HexBinary2 descriptors of the 7 fea-
ture points likewise computed, as described above.
Therefore, as the grouping level of the descriptor
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
176

(a) (b)
Figure 1: (a) is the second level structure of generating
HexBinary. (b) is the new proposed structure of the third
level hexagonal descriptor. The red star point represents
the key-point position where to sample the local descrip-
tor. The arrow illustrates the dominant orientation of the
local region around the key-point. The first level hexago-
nal grouping structure comprises the basic hexagon centred
at the red ?, and the sampling positions for comparison are
taken from the hexagon centre and the vertexes. The sec-
ond level hexagonal structure now covers more image area
around the key-point since six more hexagon centres are
sampled as shown in blue +, according to the difference
between (a) and (b) structure boundaries. For the third level
descriptor, another 12 more hexagon centres as shown in
yellow 4 in (b) are computed together with the previous 7
hexagon centres around the key-point, while in (a), 7 second
level structure will be constructed centred on the red ? and
blue +. All the black points indicate the sampling positions
according to the corresponding hexagonal centre positions.
increases, the information around the 7 sampling
positions will be repeatedly overlapped. Although
overlapped-sampling can improve the stability of a
local descriptor, repeated overlapping will eventu-
ally result in excessively redundant information be-
ing accumulated, which decreases the discriminabil-
ity of the feature descriptor. To address the issue of
redundant information when generating higher level
descriptors, the new proposed hexagonal structure is
constructed as in Figure 1 (b). The details of how to
compute a three level hierarchy are now presented in
the following steps:
1. Localise the key-point position, and compute the
dominant orientation of the local area around this
key-point.
2. According to the dominant orientation and the
given edge length of the hexagon, the sampling
positions of the basic hexagon vertexes are de-
fined. Then the first level hexagonal descriptor
could be computed according to the binary de-
scriptor generation method described in the fol-
lowing subsection, which is used by SHexBinary.
3. Sample another 6 positions to be the new hexagon
centres as the blue + shown in Figure 1 (b).
These new hexagon centres are not the same 6
vertexes comprising the basic hexagon generated
in first level, which is the main difference from
the HexBinary structure in Figure 1 (a). Each new
hexagon shares an edge with the basic hexagon
centred at the key-point.
4. The second level hexagonal descriptor is gener-
ated by concatenating the 7 first level hexago-
nal descriptors extracted centred on the 7 basic
hexagons.
5. Sample 12 more positions to be the new hexagon
centres as the yellow 4 in Figure 1 (b). This is a
similar process to that of step 3, which also differs
from the HexBinary structure.
6. Concatenate these first level descriptors extracted
centred on the 19 basic hexagons to generate the
third level hierarchical descriptor.
Throughout the above steps, the higher level de-
scriptors are generated by extending the feature area
without repeatedly overlapping the central area, while
in the HexBinary hierarchical structure, the overlap
frequency of the central area is increased as the group-
ing level of the hierarchy increases. For instance, the
blue + areas in Figure 1 (a) will be repeatedly over-
lapped by 7 times for constructing the second level
descriptor and 49 times for the third level descriptor,
while the same positions in Figure 1 (b) will be only
overlapped 3 times for all the higher level descriptors
over the first level. The pseudocode to generate the
new hierarchical HBD is presented in Algorithm 1.
Algorithm 1: Hierarchical HBD Descriptor Generation.
p
0
(x,y): Feature Point
θ
0
: Local Dominant Orientation Centred at p
0
L : Defined Edge Length of the Basic Hexagon
V
i
(x,y)(i ← 1,2...6): Vertex Positions of the Basic Hexagon
ts ← pi/3
for i ← 1 : 6 do
tv ← (i − 1)ts + θ
0
V
i
(x) ← L × cos(tv)
V
i
(y) ← L × sin(tv)
end for
Compute the First Level Descriptor HBD1
0
for Feature point p
0
for i ← 1 : 6 do
tv ← (i − 1)ts + θ
0
+ pi/6
p
i
(x) ← 2L × cos(pi/6) × cos(tv)
p
i
(y) ← 2L × cos(pi/6) × sin(tv)
end for
Compute the First Level Descriptor HBD1
i
for p
i
(i ← 1, 2...6)
Generate the Second Level Descriptor HBD2
0
for Feature point p
0
HBD2
0
← HBD1
0
HBD1
1
,...,HBD1
6
for i ← 7 : 12 do
tv ← (i − 7)ts + θ
0
p
i
(x) ← 3L × cos(tv)
p
i
(y) ← 3L × sin(tv)
end for
for i ← 13 : 18 do
tv ← (i − 12)ts + θ
0
+ pi/6
p
i
(x) ← 4L × cos(pi/6) × cos(tv)
p
i
(y) ← 4L × cos(pi/6) × sin(tv)
end for
Compute the First Level Descriptor HBD1
i
for p
i
(i ← 7, 8...18)
Generate the Third Level Descriptor HBD3
0
for Feature point p
0
HBD3
0
← HBD1
0
HBD1
1
,...,HBD1
18
HBD: Hexagon-Based Binary Descriptors
177

5"
1"
2"
3"
4"
6"
0"
Figure 2: The first level structure. The arrow indicates the
local dominant orientation.
3.2 Descriptor Construction
To afford the descriptor with rotation invariance, the
local dominant orientation is computed as introduced
in (Liu et al., 2014). The first level structure is de-
fined according to the dominant orientation as shown
in Figure 2. The image is first filtered by a Gaussian
kernel of standard deviation σ, and the smoothed in-
tensity values sampled at the hexagon centre and ver-
texes are denoted by: I
i
(i=0,1,...6). The first level de-
scriptor is then computed by comparing the intensity
differences. The binary bit τ of the descriptor is cor-
responding to :
τ (D; i, j) =
1 if D
i
< D
j
0 otherwise.
(1)
where(D
i
,D
j
) is a spatially adjacent pair of inten-
sity difference, e.g., (D
i
= I
1
− I
0
,D
j
= I
0
− I
4
;D
i
=
I
1
− I
6
,D
j
= I
2
− I
1
). The 9 pairs of (D
i
,D
j
) in the
hexagon are then selected to generate a 9 bit binary
string as the first level descriptor. When construct-
ing the next higher level descriptor, each newly con-
structed hexagon in the structure will generate a first
level descriptor, and these are concatenated together
to form the higher level descriptor. This new hexago-
nally structured hierarchical descriptor is termed Hex-
IDB (Hexagon-based Intensity Difference Binary).
Similarly, another new descriptor HexLDB
(Hexagon-based Local Difference Binary) is pro-
posed by not only encoding intensity differences, but
also by encoding gradient differences. This is similar
to but slightly different to the LDB descriptor. LDB
generates a 3 bit vector by comparing the differences
of the local average intensity, gradients in x and y di-
rections between the pair of grids, respectively. Here
the gradient information is also considered but with-
out being divided into x and y directions. A gradient
map is computed, then the comparison pair (D
i
,D
j
)
in Function 1 could be the gradient difference pair,
e.g., (D
i
= G
1
− G
0
,D
j
= G
0
− G
4
). G
i
(i=0,1,...6)
represents the gradient value of the sampling posi-
tion. Therefore, for each pair comparison, a 2-bit vec-
tor is generated, and in each level of the Hierarchy,
HexLDB will have double length of the vector than
HexIDB. The descriptor lengths and the number of
sampling fields of SHexBinary and the new proposed
HBD are illustrated in Table 1.
Table 1: The descriptor length (L) and the number of sam-
pling fields (N).
L|N Level1 Level2 Level3
HexIDB 9|7 63|49 171|133
HexLDB 18 |7 126|49 342|133
SHexBinary 9|7 63|49 441|343
4 PARAMETER LEARNING
Good feature descriptors always rely on the good
collaboration amongst their critical parameters. For
HBD, which we refer to as HexIDB and HexLDB
in this paper, the essential parameters are: the edge
length of the basic hexagon and the standard devia-
tion, σ, and support size of the Gaussian sampling
kernel. These parameters are learned through local
feature matching experiments. We determine the de-
scriptor’s matching performance for a specific param-
eter configuration by measuring the RecognitionRate
for nearest neighbour (NN) matching, as introduced
in (Calonder et al., 2010): RecognitionRate is com-
puted as follows:
Firstly, N key-points are detected in the reference
image, and N corresponding Key-points are inferred
in the test image according to the ground-truth geo-
metric relation between the two images; Secondly, we
compute the 2N key-point descriptors by the method
under consideration, and for each descriptor in the ref-
erence image, find its NN in the test image. There-
after, the RecognitionRate is given by C
n
/N, where
C
n
is the number of correct matches.
Any local feature detector could be employed to
indicate where to extract the HBD. FAST (Rosten
et al., 2010) is an efficient and widely used detector
which is employed in this paper. The HexBinary de-
scriptor reported in (Liu et al., 2014) is parameterised
with a hexagon edge length of 3 pixels, and the sup-
port size of the Gaussian sampling kernel is 9×9 pix-
els with σ = 2 pixels. We apply the same range of
numeric values here for HBD to learn the best param-
eters for the image dataset being matched. When one
of the parameters is under test, all the remaining pa-
rameters must be fixed. For instance, when learning
the σ of the Gaussian sampling kernel, the edge length
is set to 3, and the Gaussian kernel support size is set
to 9 × 9.
4.1 Dataset
The experiment is performed on the well-known and
publicly available image dataset by (Mikolajczyk and
Schmid, 2005) as shown in Figure 3. The images
contained in this dataset include typical image distur-
bances occurring in real-world scenarios, such as:
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
178

Graffi%&
Wall&
Bikes&
Trees&
Light&
Jpg&
Figure 3: Image sequences: each sequence has 6 images,
and only the first and the last images are illustrated here.
From the second to the sixth image, the difficulty in match-
ing to the first image increases progressively.
• viewpoint changes: Graffiti and Wall;
• image blur: Bikes and Trees;
• compression artefacts: Jpg
• illumination changes: Light
For each sequence, the test is designed to match the
first image to the remaining 5 images to get 5 pairs of
matching cases sorted in order of ascending difficulty.
Therefore, pair 1|6 is much harder to match than pair
1|2 for each sequence.
4.2 Learning Parameters
The Gaussian standard deviation Sigma is tested in
the range of [0.2,4.2] pixels. Only the performance of
the third level descriptor is presented here because the
third level descriptor always performs better than the
lower level descriptors. The RecognitionRate perfor-
mance according to different values of σ has been in-
vestigated and it was discovered that for each match-
ing pair, the RecognitionRate gradually improves as
σ increases, but it declines as the difficulty of match-
ing increases, due to the increasing dissimilarity be-
tween compared pairs of images. For both of these de-
scriptors, their performance becomes relatively con-
stant when σ reaches between [3, 4.2] pixels, for all
of the matching pairs. Therefore, a σ of 3.4 pixels was
chosen as a good compromise value to reduce sensi-
tivity to noise while retaining a distinctive structure
to achieve stable descriptors. Based on the above σ
value, an appropriately sized Gaussian kernel support
size has been selected comprising 17 × 17 pixels (we
evaluated different kernel support sizes in the range
13 × 13 to 23 × 23).
Having fixed the σ value of the Gaussian sampling
kernel and its associated support size, the experiments
for learning the hexagon edge length were then con-
ducted and we discovered: there is no significant dif-
ference in performance when the edge length varies
between 3 to 8 pixels for most images. In the cases
of the two blurred images, Bikes and Trees, the larger
edge length performs better than smaller edge length,
particularly when the image pair is harder to match
using more deeply blurred sequences. This may be
because the deeply blurred images loose more high
frequency information which makes the local point
indistinct within a small area. For all the later ex-
periments, an edge length of 3 pixels is employed to
construct the hexagonal structure for our local binary
descriptors.
Based on the above learned parameters , the
matching performance for 3 different grouping lev-
els of HexIDB and HexLDB are given in Figure 4. It
is clearly evident that higher grouping levels always
outperform the lower grouping levels because of their
extended area of image coverage, thereby including
more diagnostic image information. For the Graffiti,
Wall, Light and Jpg sequences, HexLDB performs
better than HexIDB. However, the two sequences with
blurring issues: Bikes and Trees, give different re-
sults. As the descriptor level increases, HexLDB
gradually loses its advantage of including gradient
comparison information and when the matching pair
comprises more dissimilar image pairs, such as Bikes
1|6, the gradient comparison information appears to
disadvantage the HexLDB descriptor. This indicates
that the gradient information in the image is be-
ing greatly reduced when the image is significantly
blurred, which results in gradient signals with a poor
SNR.
4.3 Performance Evaluation
In order to evaluate the new descriptors with the
learned parameters, the local feature True Positive
matching rate for the third level grouping of the
HBD (including SHexBinary3 (Liu et al., 2014), Hex-
IDB3, HexLDB3 ) is compared to the performance
obtained using state-of-the-art descriptors, FREAK
(Alahi et al., 2012) and SIFT (Lowe, 2004). HBDs are
claimed to have rotation invariance by directly con-
structing the sampling structure according to the local
dominant orientation. There is no need to pre-rotate
the local patch to align with the local dominant ori-
entation, which is the conventional standard way to
achieve rotation invariance. In order to have a fair
comparison, no scale and no orientation is considered
in this test. Both FREAK, SIFT and HBD have been
HBD: Hexagon-Based Binary Descriptors
179
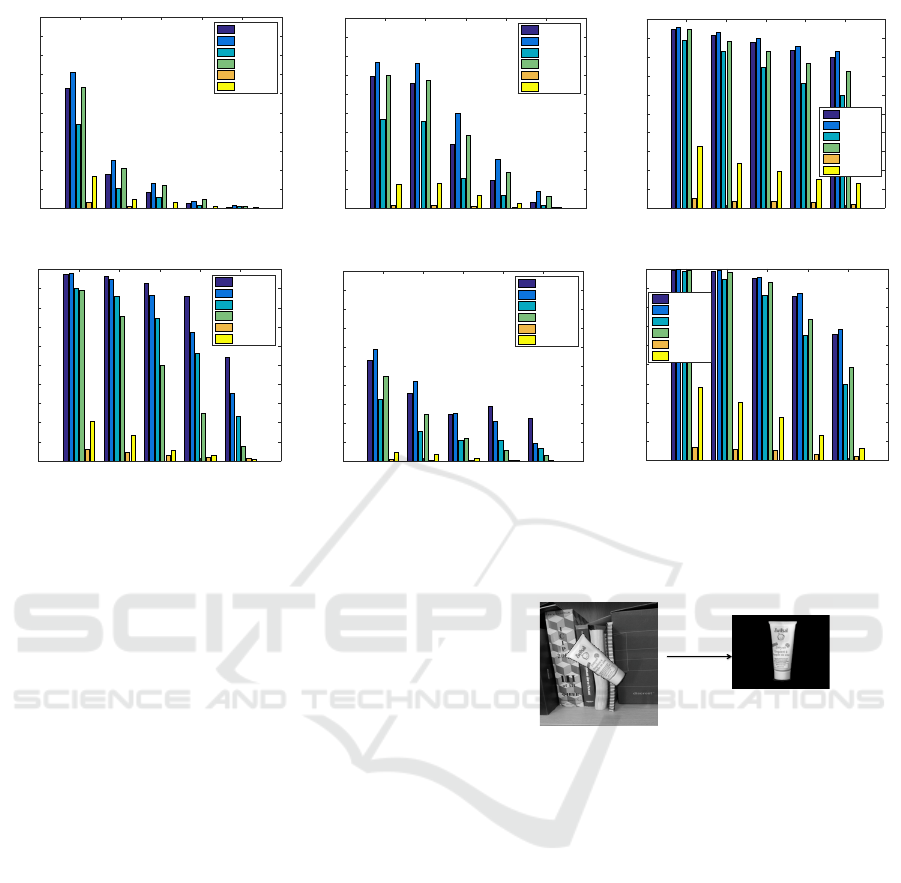
Graffiti1|2 Graffiti1|3 Graffiti1|4 Graffiti1|5 Graffiti1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Performance with sigma=3.4, kernel size=17x17, edge lenth=3
HexIDB3
HexLDB3
HexIDB2
HexLDB2
HexIDB1
HexLDB1
(a)
wall1|2 wall1|3 wall1|4 wall1|5 wall1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Performance with sigma=3.4, kernel size=17x17, edge lenth=3
HexIDB3
HexLDB3
HexIDB2
HexLDB2
HexIDB1
HexLDB1
(b)
Light1|2 Light1|3 Light1|4 Light1|5 Light1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Performance with sigma=3.4, kernel size=17x17, edge lenth=3
HexIDB3
HexLDB3
HexIDB2
HexLDB2
HexIDB1
HexLDB1
(c)
Bikes1|2 Bikes1|3 Bikes1|4 Bikes1|5 Bikes1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Performance with sigma=3.4, kernel size=17x17, edge lenth=3
HexIDB3
HexLDB3
HexIDB2
HexLDB2
HexIDB1
HexLDB1
(d)
Trees1|2 Trees1|3 Trees1|4 Trees1|5 Trees1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Performance with sigma=3.4, kernel size=17x17, edge lenth=3
HexIDB3
HexLDB3
HexIDB2
HexLDB2
HexIDB1
HexLDB1
(e)
Jpg1|2 Jpg1|3 Jpg1|4 Jpg1|5 Jpg1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Performance with sigma=3.4, kernel size=17x17, edge lenth=3
HexIDB3
HexLDB3
HexIDB2
HexLDB2
HexIDB1
HexLDB1
(f)
Figure 4: RecognitionRate (True Positive descriptor matching rate) performance obtained for Gaussian sigma=3.4, kernel
size=17 × 17, hexagon edge length=3. For each image pair, the matching performance obtained for each of the 3 grouping
levels used in the HexIDB and HexLDB descriptors is illustrated.
coupled to the FAST detector for single scale exper-
iments and termed as U-descriptor, which indicates
that they do not normalise the descriptor orientation.
Since SIFT is a multi-scale detected feature, for clar-
ity, SIFT without rotation and scale invariant property
is termed as USO-SIFT.
Figure 6 illustrates the matching performance of
each image pair with different descriptors. It is ob-
served that on all the image sequence pairs except
Graffiti, U-HBD and USO-SIFT both perform better
than U-FREAK. U-HexLDB3 always outperforms U-
HexIDB3 on image sequences of Graffiti and Wall.
They achieve quite similar results on Light and Jpg
image pairs, and also the first three image pairs of
Bikes and Trees sequence. For the harder-to-match
pairs of Bikes and Trees, U-HexLDB3 loses its ad-
vantage of utilising gradient comparison information.
U-SHexBinary3 is inferior to U-HexLDB3 and U-
HexIDB3 for almost all the image pairs, which con-
firms the improvement of distinctiveness for the new
proposed hierarchical hexagon structure. USO-SIFT
achieves similar performance to U-HexLDB3 and U-
HexIDB3 for most matching pairs comprising Light,
Bikes, and Jpg sequences. For the remainder of the
sequences, its performance is always inferior to that
of U-HexLDB3.
!
!
Figure 5: Pose estimate: each test image is only matched to
the corresponding reference image for detection and pose
estimate.
5 POSE ESTIMATION
We have also evaluated the new descriptors for pose
estimation and employed the same pose estimation
system and the same test dataset from Amsterdam Li-
brary of Object Images (ALOI) (Geusebroek et al.,
2005), as we presented in (Liu et al., 2014). Because
we are focusing on pose estimation, rather than ob-
ject detection, each test image contains the object of
interest set within a cluttered background and this is
directly matched to the corresponding reference im-
age, where the target object in set against a pure black
background, as shown in Figure 5. Therefore, one-to-
one image matching is implemented to detect the ob-
ject via the Generalised Hough Transform (GHT) and
we obtain a pose estimate by means of the RANSAC
algorithm.
We evaluate the pose estimation performance of
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
180

Graffiti1|2 Graffiti1|3 Graffiti1|4 Graffiti1|5 Graffiti1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
U-FREAK
U-HexLDB3
U-HexIDB3
U-SHexBinary3
USO-SIFT
(a)
Wall1|2 Wall1|3 Wall1|4 Wall1|5 Wall1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
U-FREAK
U-HexLDB3
U-HexIDB3
U-SHexBinary3
USO-SIFT
(b)
Light1|2 Light1|3 Light1|4 Light1|5 Light1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
U-FREAK
U-HexLDB3
U-HexIDB3
U-SHexBinary3
USO-SIFT
(c)
Bikes1|2 Bikes1|3 Bikes1|4 Bikes1|5 Bikes1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
U-FREAK
U-HexLDB3
U-HexIDB3
U-SHexBinary3
USO-SIFT
(d)
Trees1|2 Trees1|3 Trees1|4 Trees1|5 Trees1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
U-FREAK
U-HexLDB3
U-HexIDB3
U-SHexBinary3
USO-SIFT
(e)
Jpg1|2 Jpg1|3 Jpg1|4 Jpg1|5 Jpg1|6
Recognition Rate
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
U-FREAK
U-HexLDB3
U-HexIDB3
U-SHexBinary3
USO-SIFT
(f)
Figure 6: RecognitionRate performance with different descriptors.
our system by computing the mean and standard de-
viation of the pose errors of all the detected objects.
The precise location of the edge contours of the refer-
ence object in the test image can be obtained accord-
ing to the recorded ground-truth information, which
specifies the rotation and translation used to embed
the reference object pixels into a background image.
Similarly, according to the recovered pose estimation
using the system, the estimated object edge positions
could be labelled by projecting the reference edge po-
sitions into the test image. The Euclidean distance
between the estimated position and the ground-truth
position of each reference edge point is computed to
yield a pose estimate error for each matched edge lo-
cation.
Four different features are tested: standard SIFT
(SIFT), SIFT without scale invariance (US-SIFT),
HexIDB3 and HexLDB3. Except SIFT, which em-
ploys its own feature detector to afford scale invariant
matching, all the other features we examined are sam-
pled at locations defined by key-points detected by the
FAST detector at a single scale. Each reference im-
age has 5 different corresponding test images with dif-
ferent backgrounds, but without scale changes. 5000
synthetic images are tested and matched to their cor-
responding 1000 reference images. Our object detec-
tion and the pose estimation results are given in Table
2 and Table.3.
In Table 2, The number of detected images having
the corresponding pose error is accumulated in differ-
ent error ranges for each descriptor. Most of the de-
Table 2: Numeric distribution of images detected within a
given pose error range (pixels) and the corresponding error
ranges.
Error Range 0-0.5 0.5-1 1-1.5 1.5-2 2-3 3-4 4-5 5-Inf
SIFT 270 355 350 359 1348 108 44 146
US − SIFT 2787 387 165 179 69 40 22 132
HexIDB3 2401 471 176 92 88 51 38 1036
HexLDB3 2570 465 175 84 113 50 33 607
Table 3: Number of images successfully detected with a
pose error of less than 5 pixels, and their corresponding pose
error Mean (Mean) and standard deviation (SDV) in pixels.
Descriptor SIFT US-SIFT HexIDB3 HexLDB3
Number 2834 3549 3317 3490
Mean 1.9241 0.4209 0.5295 0.5207
SDV 0.9560 0.6541 0.7489 0.7375
tected images have a pose error of less than 5 pixels
for all the descriptors examined. Since there is always
a one-to-one image match, to better compare the per-
formance of different descriptors, each detected im-
age having pose error bigger than 5 pixels is defined
as a failed detection. The Number of successfully de-
tected images in Table 3 only accounts the images
with pose error smaller than 5 pixels, based on which,
the Mean and SDV of the pose error through the im-
ages are computed for each descriptor, respectively.
It is clearly shown in the results tables that, US-
SIFT achieves the best performance in terms of the
mean pose error. It has the biggest number of images
having pose error less than half pixel, while SIFT has
the least number of images successfully detected with
the mean pose error close to 2 pixels. The test im-
ages do not have scale changes from the reference im-
HBD: Hexagon-Based Binary Descriptors
181

ages, which might be the reason for SIFT exhibiting
inferior results to all of the other descriptors. Due to
multi-scale detection being applied in this case, the
associated Hough parameter space needs one more
dimension to be able to detect objects, compared to
the hough space generated for the other single scale
descriptors, which leads to lower pose estimate ac-
curacy. HexLDB3 works a little better than HexIDB3
due to the extra comparison information from the gra-
dient map. In summary, except SIFT, all of the other
descriptors gave close results in terms of pose estima-
tion, exhibiting an error of approximately half a pixel.
6 CONCLUSION
In this paper, we present two new HBD: HexIDB
and HexLDB descriptors. The new sampling struc-
ture of HBD reduces redundant information being en-
coded by decreasing the frequency of the same image
area being sampled, and produces shorter feature de-
scriptors for the third level of the feature hierarchy,
as compared to HexBinary descriptors. Moreover, a
gradient map is also employed to generate the binary
bits in the same way as the intensity map is encoded.
However, it is not a wise choice to use the gradient
map when the gradient information representing im-
age features has a low SNR. The HBD outperforms
SHexBinary and achieves very promising results com-
pared to fixed-scale U-FREAK and USO-SIFT de-
scriptors (no orientation normalisation). HBD is also
compared to the standard SIFT and a fixed-scale ex-
tracted descriptor US-SIFT within an object pose esti-
mation application. Although the parameters used in
this application are not learned from the training data,
HBD still produces much better performance than the
standard SIFT and shows competitive performance
compared to US-SIFT. In future work, we would like
to investigate dimensionality reduction methods for
HBD to decrease feature storage requirements and
improve its discriminability. We would also like to in-
vestigate the relationship between such hand-crafted
descriptors and those derived through learning tech-
niques, such as Deep Convolutional Neural Networks.
REFERENCES
Alahi, A., Ortiz, R., and Vandergheynst, P. (2012). Freak:
Fast retina keypoint. In Computer Vision and Pat-
tern Recognition (CVPR), 2012 IEEE Conference on,
pages 510–517. IEEE.
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. In Computer Vision–
ECCV 2006, pages 404–417. Springer.
Calonder, M., Lepetit, V., Strecha, C., and Fua, P. (2010).
Brief: binary robust independent elementary features.
In Computer Vision–ECCV 2010, pages 778–792.
Springer.
Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-
dients for human detection. In Computer Vision and
Pattern Recognition, 2005. CVPR 2005. IEEE Com-
puter Society Conference on, volume 1, pages 886–
893. IEEE.
Geusebroek, J.-M., Burghouts, G. J., and Smeulders, A. W.
(2005). The amsterdam library of object images. In-
ternational Journal of Computer Vision, 61(1):103–
112.
Ke, Y. and Sukthankar, R. (2004). Pca-sift: A more
distinctive representation for local image descriptors.
In Computer Vision and Pattern Recognition, 2004.
CVPR 2004. Proceedings of the 2004 IEEE Computer
Society Conference on, volume 2, pages II–506. IEEE.
Leutenegger, S., Chli, M., and Siegwart, R. Y. (2011).
Brisk: Binary robust invariant scalable keypoints. In
Computer Vision (ICCV), 2011 IEEE International
Conference on, pages 2548–2555. IEEE.
Liu, Y., Aragon-Camarasa, G., and Siebert, J. P. (2014).
Object edge contour localisation based on hexbinary
feature matching. In 2014 IEEE International Con-
ference on Robotics and Biomimetics (ROBIO), pages
99–106.
Liu, Y. and Siebert, J. P. (2014). Contour localization based
on matching dense hexhog descriptors. In Interna-
tional Conference on Computer Vision Theory and
Applications (VISAPP 2014), pages 656–666.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International journal of computer
vision, 60(2):91–110.
Mikolajczyk, K. and Schmid, C. (2005). A perfor-
mance evaluation of local descriptors. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
27(10):1615–1630.
Rosten, E., Porter, R., and Drummond, T. (2010). Faster and
better: A machine learning approach to corner detec-
tion. Pattern Analysis and Machine Intelligence, IEEE
Transactions on, 32(1):105–119.
Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.
(2011). Orb: an efficient alternative to sift or surf.
In Computer Vision (ICCV), 2011 IEEE International
Conference on, pages 2564–2571. IEEE.
Tola, E., Lepetit, V., and Fua, P. (2010). Daisy: An efficient
dense descriptor applied to wide-baseline stereo. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 32(5):815–830.
Yang, X. and Cheng, K.-T. (2012). Ldb: An ultra-fast fea-
ture for scalable augmented reality on mobile devices.
In Mixed and Augmented Reality (ISMAR), 2012 IEEE
International Symposium on, pages 49–57. IEEE.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
182
