Analyzing the Stability of Convolutional Neural Networks

against Image Degradation

Hamed Habibi Aghdam, Elnaz Jahani Heravi and Domenec Puig

Computer Engineering and Mathematics Department, Rovira i Virgili University, Tarragona, Spain

Keywords:

Convolutional Neural Network, Deep Learning, Object Recognition.

Abstract:

Understanding the underlying process of Convolutional Neural Networks (ConvNets) is usually done through

visualization techniques. However, these techniques do not provide accurate information about the stability of

ConvNets. In this paper, our aim is to analyze the stability of ConvNets through different techniques. First,

we propose a new method for ﬁnding the minimum noisy image which is located in the minimum distance

from the decision boundary but it is misclassiﬁed by its ConvNet. Second, we exploratorly and quanitatively

analyze the stability of the ConvNets trained on the CIFAR10, the MNIST and the GTSRB datasets. We

observe that the ConvNets might make mistakes by adding a Gaussian noise with σ = 1 (barely perceivable by

human eyes) to the clean image. This suggests that the inter-class margin of the feature space obtained from a

ConvNet is slim. Our second founding is that augmenting the clean dataset with many noisy images does not

increase the inter-class margin. Consequently, a ConvNet trained on a dataset augmented with noisy images

might incorrectly classify the images degraded with a low magnitude noise. The third founding reveals that

even though an ensemble improves the stability, its performance is considerably reduced by a noisy dataset.

1 INTRODUCTION

The common pipeline in recognizing objects is to ex-

tract some features for each object and train a model

to classify the objects using the extracted features.

Conventionally, features are extracted using hand-

crafted methods such as HOG, SIFT, BoW, Gabor,

LBP and Fisher Vectors. These methods transform

an image into another space where classes of objects

are separable. In large-scale object recognition tasks,

objects are likely to be non-linearly separable using

these feature extraction methods. As the result, a non-

linear model such as SVM, Random Forest or Gaus-

sian Process is required to learn the non-linear deci-

sion boundaries in this space.

One problem with the hand-crafted features is

their limited representation power. This causes that

some classes of objects overlap with other classes

which adversely affect the classiﬁcation performance.

Two common approaches for partially alleviating this

problem are to develop a new feature extraction al-

gorithm and to combine various methods. The prob-

lems with these approaches are that devising a new

hand-crafted feature extraction method is not trivial

and combining different methods might not separate

the overlapping classes.

Another solution is to automatically learn a func-

tion to transform the image into a feature space in

which classes are linearly separable. A Convolu-

tional Neural Network (ConvNet) is a highly non-

linear function which learns to extract these kinds of

features. Krizhevsky et al. (Krizhevsky et al., 2012)

developed a ConvNet to classify 1000 classes inside

the ImageNet dataset that was more accurate than the

methods based on hand-crafted features. More re-

cently, He et al. (He et al., ) designed a ConvNet

which surpassed the human performance on classiﬁ-

cation of objects in the ImageNet dataset. Similarly,

Jin et al. (Jin et al., 2014), Ciresan et al. (Cirean et al.,

2012), Aghdam et al.(Aghdam et al., 2015) and Ser-

manet and Le Cunn (Sermanet and Lecun, 2011) uti-

lized ConvNets with different architectures to classify

43 trafﬁc signs and obtained considerably higher clas-

siﬁcation accuracy compared with hand-crafted fea-

tures. In fact, the ﬁrst three ConvNets beat the human

performance in recognizing trafﬁc signs.

ConvNets are multi-layer feed forwards networks

consisting mainly of convolution, activation, pool-

ing, dropout, fully-connected and loss layers that are

trained using the Stochastic Gradient Descent (SGD)

method. In contrast to hand-crafted features, it is hard

to explain behaviour of a ConvNet under different cir-

370

Aghdam, H., Heravi, E. and Puig, D.

Analyzing the Stability of Convolutional Neural Networks against Image Degradation.

DOI: 10.5220/0005720703700382

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 370-382

ISBN: 978-989-758-175-5

cumstances without plugging data and analyzing the

output of each layer.

From optimization perspective, Glorot and Ben-

gio (Glorot and Bengio, 2010) investigated the prob-

lem of SGD and its sensitivity to the initialization.

They showed that logistic sigmoid activation can

derive the top layers to saturation. Sutskever et

al. (Sutskever et al., 2013) investigated the impor-

tance of initialization and momentum and showed that

a ConvNet can fail with a poor initialization or inap-

propriate tuning of momentum.

Yosinski et al. (Yosinski et al., 2014) studied the

degree of which a ConvNet is able to transfer its

knowledge to a new problem. They mentioned that

the bottom layers of a ConvNet are more generalized

and they become more class speciﬁc in the top lay-

ers. Goodfellow et al. (Goodfellow et al., 2013) em-

pirically analyzed the forgetting problem of the SGD

when they are ﬁrst utilized to train on one task and

then used to train on a second task. They found that

including a dropout layer in the network helps the

SGD method to remember the ﬁrst task while it is

running on the second task. Besides, other aspects

of ConvNets such as the size of the receptive ﬁeld

(Coates and Ng, 2011) and ﬁnding a shallow archi-

tecture corresponding to a deep architecture (Ba and

Caurana, 2013) are examined.

Notwithstanding, one of the important aspects of

ConvNets which is not adequately studied is their sta-

bility against image degradation. To be more spe-

ciﬁc, noise is a very common degradation that usually

occurs during image acquisition specially in insufﬁ-

ciently illuminated environment. For instance, a traf-

ﬁc sign recognition system must be able to recognize

signs during day, at night and under different weather

conditions.

Contribution: In this paper, we aim to inspect

the behaviour of ConvNets when they are plugged

with noisy images. To this end, we ﬁrst propose a

new method for ﬁnding the minimum additive noise

which causes the clean image to be incorrectly classi-

ﬁed with a minimum score margin between the ac-

tual class and predicted incorrect class (Section 3).

We apply our method on different ConvNets trained

on various datasets and show that although the mini-

mum noise is hardly perceivable for human eyes, but

it easily tricks a ConvNet (Section 4). Then, we em-

pirically study the behavior of these ConvNets under

various levels of noise and illustrate that ConvNets

are not stable against noise. Next, we inspect what

happens if we augment our dataset using many noisy

versions of each image with various levels of noise

and noise conﬁgurations. Finally, we study the sta-

bility of ensemble of ConvNets and conclude that an

ensemble of ConvNets is more stable but it is as prone

as a single ConvNet to low level noise.

2 RELATED WORK

In contrast to hand-crafted features that their internal

process is easily explained, ConvNets are still a mys-

tery for machine learning experts. There is a large

body of work on understanding the internal process

of ConvNets through visualization of hidden units.

Zeiler and Fergus (Zeiler and Fergus, 2013) visualize

the hidden units using Deconvolutional Networks. To

be more speciﬁc, they reconstruct the images which

have highly activated each unit. By this way, we can

assess how each unit see the world and which parts

of objects activate each neuron more. Simonyan et

al. (Simonyan et al., 2013) ﬁnd a L

-regularized im-

age for each class by maximizing the class speciﬁc

score. They also compute a class saliency map for the

input image.

Girshick et al. (Girshick et al., 2014) keep record

of activations for a speciﬁc unit by entering many im-

ages to ConvNet and calculating their activations on

the unit. Then, the images are sorted according to

their activation on this particular unit and illustrated.

Taking into account the fact that each unit in top lay-

ers has a corresponding receptive ﬁeld on the image,

it is possible to see which parts are important for each

unit.

Mahendran and Vedaldi (Mahendran and Vedaldi,

2014) invert the d-dimensional representation of an

image computed by function Θ : R

H×W×C

−→ R

This approach tells us that to which extend it is possi-

ble to reconstruct the image using the representation

function Θ. By applying this method on each layer

of the network we can understand which information

is preserved by each layer. Similarly, Dosovitskiy

and Brox (Dosovitskiy and Brox, 2015) reconstructed

the image by minimizing the squared Euclidean be-

tween the downsampled image and reconstructed im-

age. Recently, Nguyen et al. (Nguyen et al., 2015)

developed an evolutionary algorithm for generating

images that do not look like to any of objects in the

database but are classiﬁed with high score by Con-

vNet into one of object classes.

Even though the visualization approaches help us

to better understand the internal process of ConvNets,

they do not provide a tool for assessing the stability

of the network against noise. To address this prob-

lem, Szegedy et al. (Szegedy et al., 2013) proposed

a method for ﬁnding the L

regularized noise which

minimizes the score of a speciﬁc class. To our knowl-

edge, this is the only published work which has stud-

Analyzing the Stability of Convolutional Neural Networks against Image Degradation

371

ied the stability of ConvNets. As we will discuss

shortly, their objective function has a problem which

might not generate the optimal results. Furthermore,

they have not thoroughly studied different aspects re-

lated to the performance of ConvNets that we dis-

cussed in the last part of Section 1.

3 ANALYZING STABILITY

A ConvNet is a non-linear vector function that

transforms a D-dimensional input vector into a M-

dimensional vector in the layer before the classiﬁca-

tion layer. Ideally, small changes in the input should

produce small changes in the output. In other words,

if the classiﬁcation score of the input image X ∈

M×N

computed by ConvNet for class c is s

(X ) = z,

then, the score of image X

noisy

= X + r obtained by

adding a small degradation r ∈ R

M×N

to X must also

be s

(X ) = z ± ε. Note that c is the class with the

highest score when X is plugged into ConvNet.

However, f is strongly degraded as krk increases.

Therefore, at a certain point, the degraded image

noisy

is no longer recognizable. We are interested

in ﬁnding r with minimum krk that causes the X

noisy

and the X are classiﬁed differently. Szegedy et

al. (Szegedy et al., 2013) investigated this problem

and they proposed to minimize the following objec-

tive function with respect to r:

minimize λ|r| + loss(X + r, c)

s.t X + r ∈ [0, 1]

M×N

(1)

where c is the actual class label, λ is the regularizing

weight and loss(X + r, c) returns the loss of the de-

graded image X + r given the actual class of image

X . It is worth mentioning that loss is a vector that

shows the classiﬁcation score of the input image for

each class.

Denoting the loss vector by L ∈ [0, 1]

where K is

the total number of the classes, L[k] returns the score

of the predicted class where k = argmaxL . The im-

age is classiﬁed correctly if k = c. If max(L ) = 0.9,

the ConvNet is 90% conﬁdent that the input image

belongs to class k. However, there might be another

image where max(L ) = 0.3. This means that the im-

age belongs to class k with probability 0.3.

Conversely, assume two images that are misclas-

siﬁed by ConvNet. In the ﬁrst image, L [k] = 0.9 and

L [c] = 0.1 meaning that the network believes the in-

put image belongs to class k with probability 0.9 but

it belongs to class c with probability 0.1. In the sec-

ond image, the beliefs of ConvNet are L[k] = 0.51

and L[c] = 0.49. Even tough in both cases the images

are misclassiﬁed, however, the degrees of misclassiﬁ-

cation are different.

One problem with the objective function (1) is that

it tends to ﬁnd r such that loss(X + r, c) approaches

to zero. In other words, it tries to ﬁnd r such that

L [c] = ε and L [k] = 1 − ε. Assume a r such that

loss(X + r, c) = 0.3 and L[k] = 0.7. In other words,

the input image X is misclassiﬁed using the current

degradation r. Yet, the goal of the objective function

(1) is to settle in a point where loss(X + r, c) = ε. As

the result, it might change r which results in a greater

krk. Consequently, the degradation found by mini-

mizing the objective function (1) might not be opti-

mal. To address this problem, we propose the follow-

ing objective function to ﬁnd the degradation r:

∗

= argmin

ψ(loss(X + r), c) + λkrk

(2)

ψ(L , c) =



β × L [c] argmax L = c

L [k] − L [c] otherwise

(3)

where λ is the regularizing weight, β is a multiplier

to penalize those values of r that do not properly de-

grade the image so it is not misclassiﬁed by ConvNet.

The above objective function ﬁnds the value r such

that degrading the input image X using r causes the

image to be classiﬁed incorrectly and the difference

between the highest score in L and the true label of X

is minimum. This guarantees that X + r will be out-

side the decision boundary of actual class l but it will

be as close as possible to the decision boundary.

Our proposed objective function has an important

property. It ﬁnds the degradation r that causes the im-

age to be misclassiﬁed with a slim margin compared

with the actual class. In other words, the degraded im-

age lies very close to the decision boundary in the fea-

ture space computed by the layer just before the clas-

siﬁcation layer. This quantitatively shows the margin

between two classes.

Minimizing (2) using gradient descent method is

not trivial. For this reason, we minimize the objec-

tive function (2) using evolutionary algorithms. To

this end, we use real-value encoding scheme for rep-

resenting the population. The size of each chromo-

some in the population is equal to the number of the

elements in r. Each chromosome represents a solu-

tion for r. We use tournament method with tour size

5 for selecting the offspring. Then, a new offspring is

generated using arithmetic, intermediate or uniform

crossover operators. Finally, the offspring is mutated

by adding a small number in range [−10, 10] on some

of the genes in the population. Finally, we use elitism

to always keep the best solution in the population.

The algorithm is terminated when the maximum num-

ber of iterations reach or the solution is not improved

in the last 50 iterations.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

372

Figure 1: Minimum additive noise, found by optimizing (2), which causes test images in the CIFAR10 (left) and the MNIST

(right) datasets are misclassiﬁed. C

(c, k, w) shows a convolution layer with k ﬁlters of size w × w applied on the input with c

channels. P(m, n) indicates a MAX pooling layer with kernel size m ×m and stride n. Finally, FC(x) depicts a fully connected

layer with x neurons. In the case of CIFAR10, the feature maps are padded with border size 2 before applying the convolution

ﬁlters (best viewed in color and electronically).

We applied the above optimization proce-

dure on the ConvNets trained using the CI-

FAR10 (Krizhevsky, 2009), the MNIST (LeCun et al.,

1998) and the GTSRB (Stallkamp et al., 2012)

datasets. Figure 1 and Figure 2 illustrate the archi-

tecture of the utilized ConvNets and additive noise r

obtained for a few samples from these datasets.

Inspecting all the images in these ﬁgures, we real-

ize that the ConvNets can easily make mistakes even

for the noises which are not perceivable by human

eyes. In addition, taking into account the fact that

our proposed objective function results noisy images

which are very close to the decision boundary of each

class, we observe that the margin between the classes

are very slim since adding a noise with a high signal-

to-noise ratio (i.e. low-power noise) can alter the clas-

siﬁcation score drastically.

Furthermore, these results suggests that the func-

tion presenting by a ConvNet is highly non-linear

where small changes in the input may cause a signif-

icant change in the output. In other words, the mag-

nitude of gradient of the ConvNets in the last feature

extract layer are large. When the output changes dra-

matically, it might fall into a wrong class in the fea-

ture space. Hence, the image is incorrectly classiﬁed.

Note that because of our proposed objective function,

the difference between the wrongly predicted class

and the true class is positive but it is very close to

zero.

To further investigate the stability of ConvNets

against noise, we carry out several experiments in the

next Section to analyze different aspects of ConvNets.

4 EXPERIMENTS

We trained the ConvNets shown in Figure 1 and Fig-

ure 2 on the clean datasets. In the case of the GT-

SRB dataset, we augmented the dataset following the

same procedure in (Aghdam et al., 2015). Beside

the single ConvNet, we also created an ensemble of

ConvNets for the GTSRB dataset. The classiﬁca-

tion performance of the CIFAR10 and the MNIST

Analyzing the Stability of Convolutional Neural Networks against Image Degradation

373

Figure 2: Minimum additive noise, found by optimizing (2), which causes the test images in the GTSRB dataset are misclas-

siﬁed. The network architecture is taken from (Aghdam et al., 2015) (best viewed in color and electronically).

ConvNets on the clean test set is shown in Table 1.

In addition, the performance of the ConvNet trained

on GTSRB dataset is available in (Aghdam et al.,

2015). Tolerance against Noise: Having the Con-

vNets trained, we assess their stability under degra-

dation by additive noise. To this end, we degrade

each sample in the test set using the Gaussian noise

with σ ∈ {1, 2, 4, 8, 10, 14, 18, 20, 25, 30, 35, 40} and

for each value of sigma, we generate 150 noisy im-

ages. By this way, 1800 degraded images are gen-

erated for each clean sample in the test set. Then,

the ConvNets are evaluated using the noisy test sets.

We performed this procedure on the CIFAR10, the

MNIST and the GTSRB datasets. Figure 3, Figure

4 and Figure 5 to Figure 7 show the results.

Each chart illustrates per class scatter plot of the

peak signal-to-noise ratio (PSNR), calculated using

the noisy images and the clean images, against the

classiﬁcation score of each sample. A high PSNR

value corresponds to a small value of σ in the Gaus-

sian noise. As the result, all images with PSNR ≈ 50

are degraded using a Gaussian noise with σ = 1 and

those with PSNR ≈ 15 are degraded using a Gaussian

noise with σ = 40. The red points are related to the

misclassiﬁed samples and the gray points depict the

correctly classiﬁed samples.

We observe that there are many noisy images

which are misclassiﬁed by the ConvNets trained on

the CIFAR10 dataset regardless of the their PSNR.

Note that, the Gaussian noise with σ = 1 is not easily

perceivable for a human eye. However, we see that

this low magnitude noise might change the classiﬁca-

tion result. This is due to the fact that, the CIFAR10

dataset contains complex objects stored in very small

images. A small change in the image, may alter the

geometry and appearance of the object. Although

small changes might not be perceivable by human

eyes, they numerically change the appearance and

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

374

Table 1: Class speciﬁc precision and recall computed on the original CIFAR10 (left) and the MNIST (right) datasets.

CIFAR10

cls precision recall cls precision recall

1 0.81 0.82 6 0.63 0.77

2 0.89 0.89 7 0.87 0.83

3 0.71 0.73 8 0.80 0.86

4 0.64 0.58 9 0.90 0.88

5 0.79 0.75 10 0.91 0.80

accuracy (top-1): 78.95%

MNIST

cls precision recall cls precision recall

1 0.99 0.99 6 0.99 0.99

2 1.00 0.99 7 0.99 0.99

3 0.99 0.99 8 0.99 0.98

4 0.98 1.00 9 0.99 0.99

5 0.99 0.99 10 0.99 0.99

accuracy (top-1): 98.98%

Figure 3: Evaluating the ConvNet trained on the CIFAR10 dataset by creating a noisy test set (see the text). Red and

Gray points illustrate misclassiﬁed and correctly classiﬁed samples, respectively. High resolution images are available at

deim.urv.cat/ rivi/cnn-noise-tolerance/.

shape pattern. For this reason, the ConvNet makes

mistakes with little degradations in the input image.

Inspecting the results obtained from the ConvNet

trained on the MNIST dataset shows that despite the

simplicity of the objects in this dataset, the MNIST

ConvNet is also vulnerable to noise and it makes mis-

takes even with a low magnitude degradation. In ad-

dition, the scatter plots illustrate that the ConvNet

makes mistakes regardless of the object classes. This

is due to the fact that images in the MNIST dataset

do not have any texture and they can be considered

as binary images. Consequently, the network learns

edges and edgelets to recognize the digits. However,

when the image is degraded using a Guassian noise, it

changes the edge patterns dramatically. As the result,

the degraded image is misclassiﬁed.

The ConvNet trained on the GTSRB dataset uti-

lizes 48 × 48 images. In addition, the appearance and

perspective of the objects in this dataset do not vary

signiﬁcantly. Hence, the ConvNet learns parts and

patterns with higher abstraction level compared with

the two other ConvNets. For this reason, small degra-

dation of the image does not signiﬁcantly alter the

representation vector computed by the ConvNet and it

is classiﬁed correctly in most of the cases. However,

we observe that the ConvNet makes more mistakes

starting from σ = 8(PSNR ' 30).

Result: The above results reveal that ConvNets

are not noise-tolerant and their classiﬁcation score

might negatively alter with a small change in the in-

put. This is due to the fact that a ConvNet is a highly

non-linear function. Therefore, a slight change in the

input causes a great change in the output. From an-

other perspective, these results show that the margin

between two classes are very small in which a small

variation in the input moves the sample to another

class.

Beside the exploratory analysis, we conducted a

quantitative analysis as well. To be more speciﬁc,

we evaluated the performance of the ConvNets on the

noisy datasets in terms of precision and recall. Table

2 and Table 3 show the results. Comparing the results

with Table 1 and (Aghdam et al., 2015) we see a dras-

tic performance reduction in all three ConvNets. This

is more obvious in the case of the MNIST dataset for

the same reason we mentioned earlier.

Effect of Ensemble: It is shown that ensemble of

ConvNets can increase the classiﬁcation performance

(Aghdam et al., 2015; Jin et al., 2014; Cirean et al.,

2012). To see if the ensemble makes the classiﬁcation

more robust against noise, we created an ensemble for

each of the datasets. Each ensemble contains 5 Con-

vNets initialized and trained separately. We evaluated

the ensembles using the same noisy test sets. Table 4

and Table 5 show the results.

Result: We observe that the ensembles of the CI-

FAR10 and the GTSRB ConvNets produce more ac-

curate results compared with the corresponding single

Analyzing the Stability of Convolutional Neural Networks against Image Degradation

375

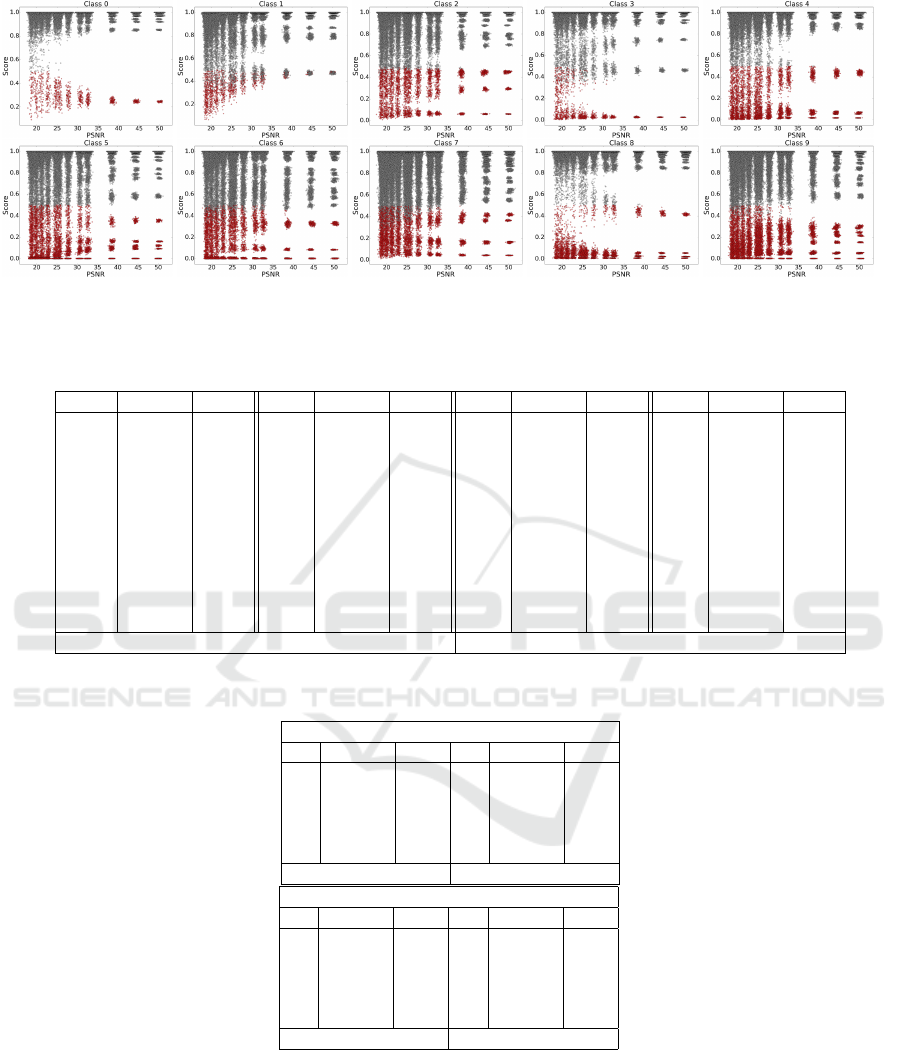
Figure 4: Evaluating the ConvNet trained on the MNIST dataset by creating a noisy test set (see the text). Red and

Gray points illustrate misclassiﬁed and correctly classiﬁed samples, respectively. High resolution images are available at

deim.urv.cat/ rivi/cnn-noise-tolerance/.

Table 2: Class speciﬁc precision and recall computed on the noisy version of the GTSRB dataset (refer to the text).

Class precision recall class precision recall class precision recall class precision recall

0 0.9198 0.9997 11 0.9626 0.9470 22 0.9988 0.9758 33 0.9865 0.9977

1 0.8993 0.9874 12 0.9565 0.9654 23 0.8392 0.8911 34 0.9866 0.9973

2 0.8808 0.9525 13 0.9811 0.9902 24 0.9178 0.9098 35 0.9933 0.9382

3 0.8524 0.8744 14 0.9721 0.9969 25 0.9288 0.9700 36 0.9849 0.9928

4 0.9707 0.8651 15 0.9898 0.9578 26 0.9105 0.9592 37 0.9507 0.9875

5 0.8387 0.9015 16 0.9993 0.9319 27 0.9470 0.9891 38 0.9651 0.9792

6 0.9324 0.7122 17 0.9911 0.9911 28 0.9777 0.9915 39 0.9724 0.9100

7 0.9377 0.8698 18 0.9682 0.8998 29 0.8453 0.9966 40 0.9061 0.9629

8 0.8324 0.9039 19 0.6640 0.7462 30 0.8102 0.7670 41 0.9508 0.9268

9 0.9606 0.9453 20 0.8314 0.9997 31 0.9666 0.8699 42 0.9082 0.9126

10 0.9864 0.8797 21 0.8995 0.9997 32 0.9773 0.8472

accuracy (top-1): 93.23%

Table 3: Class speciﬁc precision and recall computed on the noisy versions of the CIFAR10 (left) and the MNIST (right)

datasets (refer to the text).

CIFAR10

cls precision recall cls precision recall

1 0.86 0.54 6 0.68 0.49

2 0.89 0.72 7 0.37 0.92

3 0.69 0.48 8 0.82 0.71

4 0.60 0.39 9 0.78 0.80

5 0.59 0.66 10 0.75 0.76

accuracy (top-1): 64.36%

MNIST

cls precision recall cls precision recall

1 0.98 0.99 6 0.98 0.97

2 0.99 0.99 7 0.99 0.98

3 0.98 0.98 8 0.99 0.98

4 0.96 0.99 9 0.98 0.98

5 0.99 0.98 10 0.98 0.97

accuracy (top-1): 98.51%

ConvNets when they are applied on the noisy test sets.

However, the fact remains that the performance of the

ensemble is signiﬁcantly lower than the performance

of the ConvNets on the clean datasets. This founding

shows that an ensemble is not able to tackle the insta-

bility problem of the ConvNets against noisy images.

This is shown in the scatter plots beside Table 4 in

which images are still incorrectly classiﬁed using the

ensemble by adding a Gaussian noise with σ = 1.

Augmenting Noisy Images: It is a common prac-

tice to create a jittery dataset by applying simple

transformations such as cropping, contrast adjustment

and blurring on the original training dataset in order

to train a more accurate ConvNet. In this section, our

goal is to ﬁnd out if augmenting the training dataset

with many noisy images improve the stability of the

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

376

Figure 5: Evaluating the ConvNet trained on the GTSRB dataset (class 0 to class 14) by creating a noisy test set (see the

text). Red and Gray points illustrate misclassiﬁed and correctly classiﬁed samples, respectively. High resolution images are

available at deim.urv.cat/ rivi/cnn-noise-tolerance/.

Analyzing the Stability of Convolutional Neural Networks against Image Degradation

377

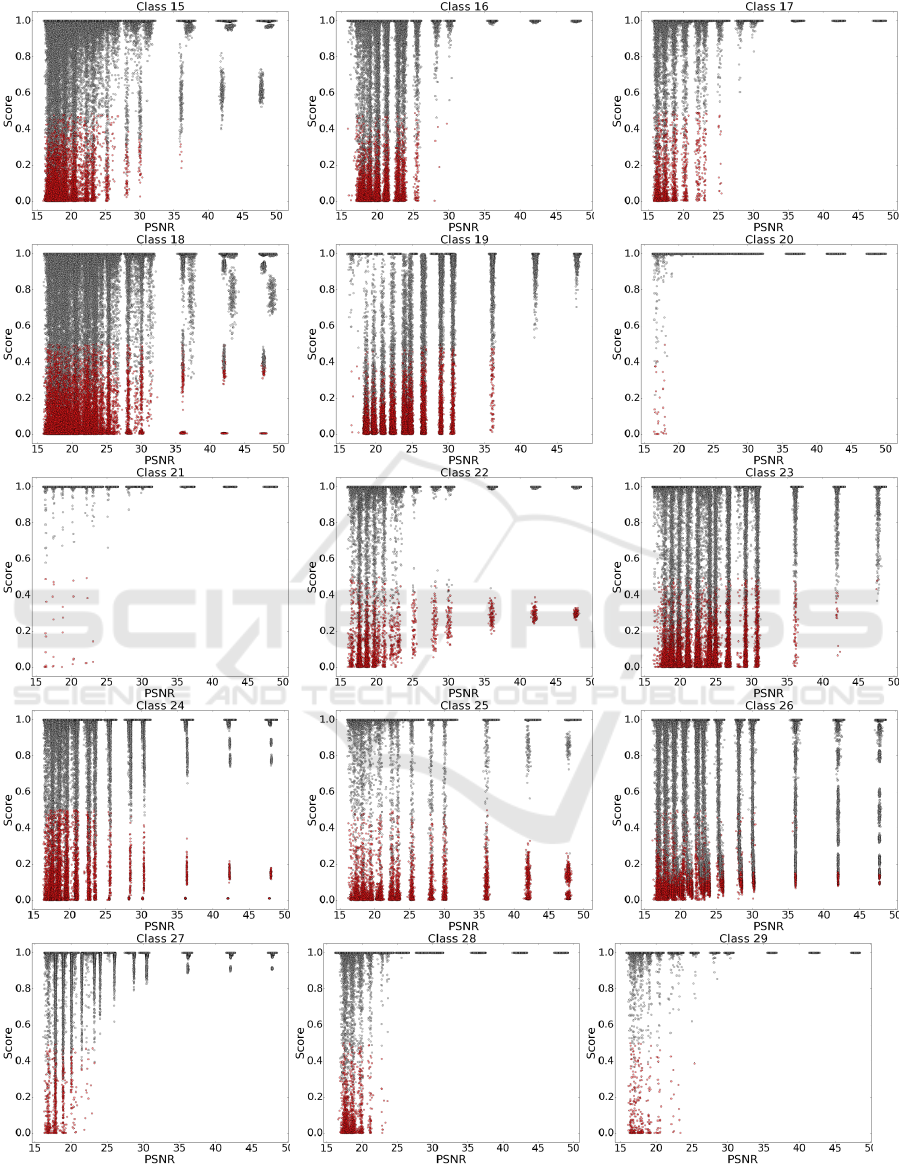
Figure 6: Evaluating the ConvNet trained on the GTSRB dataset (class 15 to class 29) by creating a noisy test set (see the

text). Red and Gray points illustrate misclassiﬁed and correctly classiﬁed samples, respectively. High resolution images are

available at deim.urv.cat/ rivi/cnn-noise-tolerance/.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

378

Figure 7: Evaluating the ConvNet trained on the GTSRB dataset (class 30 to class 42) by creating a noisy test set (see the

text). Red and Gray points illustrate misclassiﬁed and correctly classiﬁed samples, respectively. High resolution images are

available at deim.urv.cat/ rivi/cnn-noise-tolerance/.

Analyzing the Stability of Convolutional Neural Networks against Image Degradation

379

Table 4: Class speciﬁc precision and recall computed using the ensemble of 5 ConvNets on the noisy version of the GTSRB

dataset.

Class precision recall class precision recall class precision recall

0 0.9547 0.9970 15 0.9894 0.9762 30 0.8775 0.8524

1 0.9126 0.9917 16 0.9994 0.9585 31 0.9789 0.9101

2 0.8848 0.9667 17 0.9929 0.9947 32 0.9939 0.8542

3 0.9093 0.8982 18 0.9859 0.9030 33 0.9971 0.9982

4 0.9859 0.8896 19 0.8710 0.7784 34 0.9955 0.9995

5 0.8469 0.9429 20 0.9061 0.9996 35 0.9926 0.9678

6 0.9401 0.7909 21 0.9398 0.9993 36 0.9820 0.9984

7 0.9612 0.8853 22 0.9994 0.9788 37 0.9743 0.9956

8 0.8872 0.9279 23 0.9372 0.8838 38 0.9883 0.9832

9 0.9875 0.9653 24 0.9383 0.9024 39 0.9753 0.9266

10 0.9855 0.9311 25 0.9548 0.9872 40 0.8843 0.9732

11 0.9513 0.9786 26 0.9131 0.9877 41 0.9832 0.9909

12 0.9378 0.9791 27 0.9605 0.9953 42 0.9328 0.9631

13 0.9876 0.9919 28 0.9726 0.9912

14 0.9699 0.9991 29 0.8925 0.9985

accuracy (top-1): 95.15%

Table 5: Class speciﬁc precision and recall computed using two separate ensembles of 5 ConvNets on the noisy version of the

CIFAR10 (left) and MNIST (right) datasets.

CIFAR10

cls precision recall cls precision recall

1 0.88 0.57 6 0.74 0.52

2 0.91 0.78 7 0.39 0.94

3 0.73 0.53 8 0.88 0.72

4 0.67 0.42 9 0.82 0.81

5 0.70 0.63 10 0.65 0.86

accuracy (top-1): 67.88%

MNIST

cls precision recall cls precision recall

1 0.98 0.99 6 0.98 0.98

2 0.98 1.00 7 0.99 0.98

3 0.99 0.99 8 1.00 0.98

4 0.97 0.99 9 0.99 0.98

5 0.99 0.99 10 0.99 0.97

accuracy (top-1): 98.69%

Table 6: Class speciﬁc precision and recall computed using the ConvNet train on a training dataset augmented with noisy

images on the noisy version of the GTSRB dataset.

Class precision recall Class precision recall Class precision recall

0 0.9970 0.9906 15 0.9812 0.9750 30 0.9496 0.9448

1 0.9503 0.9728 16 0.9951 0.9728 31 0.9486 0.9466

2 0.9281 0.9586 17 0.9911 0.9884 32 0.9859 0.9393

3 0.9170 0.9004 18 0.9325 0.9723 33 0.9931 0.9733

4 0.9205 0.9242 19 0.9386 0.9417 34 0.9905 0.9833

5 0.8263 0.8987 20 0.9624 0.9451 35 0.9820 0.9815

6 0.9506 0.9386 21 0.9872 0.9805 36 0.9851 0.9786

7 0.9173 0.8734 22 0.9982 0.9962 37 0.9948 0.9825

8 0.8823 0.8834 23 0.9840 0.9485 38 0.9575 0.9761

9 0.9648 0.9558 24 0.9877 0.9663 39 0.9491 0.9753

10 0.9336 0.9596 25 0.9687 0.9710 40 0.9917 0.9613

11 0.9519 0.9678 26 0.9556 0.9631 41 0.9834 0.9684

12 0.9019 0.9960 27 0.9965 0.9831 42 0.9845 0.9400

13 0.9451 0.9852 28 0.9935 0.9695

14 0.9933 0.9956 29 0.9976 0.9913

accuracy (top-1): 96.08%

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

380

network. To this end, we generated 15 noisy im-

ages for each image in the training set with different

signal-to-noise ratios. Then, the ConvNets are trained

using the new noisy training sets. Finally, we evaluate

the ConvNets using the noisy test sets. Table 6 illus-

trates the result. Because of space limitation we could

not include the results from the CIFAR10 and the

MNIST datasets. However, the complete results are

available at deim.urv.cat/ rivi/cnn-noise-tolerance/.

Result: While augmenting the training set with

noisy images improves the performance, however, we

observe that the ConvNets are still sensitive to noise.

For instance, the scatter plots beside Table 6 shows

that even after training with noisy training set, it is

still possible to generate a Gaussian noise with σ = 1

in order to incorrectly classify the images.

5 CONCLUSIONS

In this paper we studied the degree of which Con-

vNets are tolerant against noise. For this purpose,

we ﬁrst proposed a method for ﬁnding the minimum

noisy image close to the decision boundary that is

misclassiﬁed by the ConvNet. We applied our method

on the ConvNets trained on the CIFAR10, the MNIST

and the GTSRB datasets and showed that it is possi-

ble to generate low magnitude noises which are hardly

perceivable by human eyes but they alter the classiﬁ-

cation score of the ConvNets. Then, we carried out

several experiments to study different aspects of sta-

bility. First, we randomly generated many noisy im-

ages with various signal-to-noise ratios and classiﬁed

them using the three ConvNets. We found out that the

three ConvNets makes mistakes even with very low

magnitude noisy images. This can be explained by the

fact that the inter-class margin of the feature vectors

computed by ConvNets might be very small. Another

possibility is that because ConvNets are highly non-

linear functions, a small change in the input causes a

signiﬁcant change in the output. For these two rea-

sons, images may fall into wrong classes when they

are degraded by a low magnitude noise. Second, we

examined the effect of ensemble of ConvNets and

found that although ensembles improve the classiﬁca-

tion accuracy but they are still very vulnerable to low

magnitude noises. Third, we investigated the effect

of augmenting the training datasets with many noisy

images on the stability. Results reveal that even Con-

vNets trained on noisy datasets are not stable against

noise and they easily make mistakes by low magni-

tude noises.

ACKNOWLEDGEMENTS

The authors are grateful for the support granted by

Generalitat de Catalunya’s Ag

ecia de Gesti

o d’Ajuts

Universitaris i de Recerca (AGAUR) through FI-DGR

2015 fellowship.

REFERENCES

Aghdam, H. H., Heravi, E. J., and Puig, D. (2015). Rec-

ognizing Trafﬁc Signs using a Practical Deep Neu-

ral Network. In Second Iberian Robotics Conference,

Lisbon. Springer.

Ba, L. and Caurana, R. (2013). Do Deep Nets Really Need

to be Deep ? arXiv preprint arXiv:1312.6184, pages

1–6.

Cirean, D., Meier, U., Masci, J., and Schmidhuber, J.

(2012). Multi-column deep neural network for traf-

ﬁc sign classiﬁcation. Neural Networks, 32:333–338.

Coates, A. and Ng, A. (2011). Selecting Receptive Fields

in Deep Networks. Nips, (i):1–9.

Dosovitskiy, A. and Brox, T. (2015). Inverting Convolu-

tional Networks with Convolutional Networks. pages

1–15.

Girshick, R., Donahue, J., Darrell, T., Berkeley, U. C., and

Malik, J. (2014). Rich feature hierarchies for accurate

object detection and semantic segmentation. Cvpr’14,

pages 2–9.

Glorot, X. and Bengio, Y. (2010). Understanding the

difﬁculty of training deep feedforward neural net-

works. Proceedings of the 13th International Con-

ference on Artiﬁcial Intelligence and Statistics (AIS-

TATS), 9:249–256.

Goodfellow, I., Mirza, M., Da, X., Courville, A., and

Bengio, Y. (2013). An Empirical Investigation of

Catastrophic Forgeting in Gradient-Based Neural Net-

works. arXiv preprint arXiv: . . . .

He, K., Zhang, X., Ren, S., and Sun, J. Delving Deep into

Rectiﬁers: Surpassing Human-Level Performance on

ImageNet Classiﬁcation.

Jin, J., Fu, K., and Zhang, C. (2014). Trafﬁc Sign Recog-

nition With Hinge Loss Trained Convolutional Neural

Networks. IEEE Transactions on Intelligent Trans-

portation Systems, 15(5):1991–2000.

Krizhevsky, A. (2009). Learning Multiple Layers of Fea-

tures from Tiny Images. pages 1–60.

Krizhevsky, a., Sutskever, I., and Hinton, G. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. Advances in neural information processing

systems, pages 1097–1105.

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2323.

Mahendran, A. and Vedaldi, A. (2014). Understanding

Deep Image Representations by Inverting Them.

Nguyen, a., Yosinski, J., and Clune, J. (2015). Deep Neural

Networks are Easily Fooled: High Conﬁdence Predic-

tions for Unrecognizable Images. Cvpr 2015.

Analyzing the Stability of Convolutional Neural Networks against Image Degradation

381

Sermanet, P. and Lecun, Y. (2011). Trafﬁc sign recognition

with multi-scale convolutional networks. Proceedings

of the International Joint Conference on Neural Net-

works, pages 2809–2813.

Simonyan, K., Vedaldi, A., and Zisserman, A. (2013).

Deep Inside Convolutional Networks: Visualising Im-

age Classiﬁcation Models and Saliency Maps. arXiv

preprint arXiv:1312.6034, pages 1–8.

Stallkamp, J., Schlipsing, M., Salmen, J., and Igel, C.

(2012). Man vs. computer: Benchmarking machine

learning algorithms for trafﬁc sign recognition. Neu-

ral Networks, 32:323–332.

Sutskever, I., Martens, J., Dahl, G., and Hinton, G. (2013).

On the importance of initialization and momentum in

deep learning. Jmlr W&Cp, 28(2010):1139–1147.

Szegedy, C., Zaremba, W., and Sutskever, I. (2013). In-

triguing properties of neural networks. arXiv preprint

arXiv: . . . , pages 1–10.

Yosinski, J., Clune, J., Bengio, Y., and Lipson, H. (2014).

How transferable are features in deep neural networks

? Nips’14, 27.

Zeiler, M. D. and Fergus, R. (2013). Visualizing and Un-

derstanding Convolutional Networks. arXiv preprint

arXiv:1311.2901.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

382