Facial Asymmetry Assessment from 3D Shape Sequences: The Clinical

Case of Facial Paralysis

Paul Audain Desrosiers

, Yasmine Bennis

, Boulbaba Ben Amor

, Mohamed Daoudi

and Pierre Guerreschi

Telecom Lille, CRIStAL (UMR CNRS 9189), Villeneuve d’Ascq, France

Service de Chirurgie Plastique Reconstructrice et Esth

etique, Universit

e Lille 2 Droit et Sant

e, Lille, France

Keywords:

4D Faces, Dense Scalar Fields, Face Asymmetry, Facial Paralysis, Dynamic Faces.

Abstract:

This paper addresses the problem of quantifying the facial asymmetry from dynamic 3D data. We investigate

here the role of 4D (i.e. 3D+time) data to reveal the amount of both static and dynamic asymmetry, in a clinical

use-case of facial paralysis. The ﬁnal goal is to provide tools and solutions to clinicians for facial paralysis

assessment and monitoring, which can provide qualitative and quantitative evaluations. To this end, the ap-

proach proposed here consider 3D facial sequences and adopt a recently-developed Riemannian approach for

facial deformation analysis. After a preprocessing step, each frame of a given 3D sequence is approximated

by an indexed collection of elastic radial curves. Riemannian shape analysis of obtained curves and their sym-

metrical counterparts, both elements of the same shape space, give rise to a feature vector, called Dense Scalar

Fields (DSFs). The use of these DSFs reveals the amount of bilateral asymmetry of the face, when conveying

expressions. That is, given a 3D frame, it is ﬁrst reﬂected with respect to the YZ-plane, then compared to the

obtained reﬂection using the DSFs. To exemplify the use of the proposed approach, a new dataset have been

collected (of patients) before and after injecting Botulinum Toxin (BT) in related facial muscles. Experimen-

tal results obtained on this dataset show that the proposed approach allows clinicians to evaluate the facial

asymmetry before and after the medical treatment.

1 INTRODUCTION

Human face is the most important non-verbal chan-

nel which allows to human beings to communicate

with their peers. Its dysfunction may causes discom-

fort among patients affected by facial paralysis. It oc-

curs in the case of partial or complete loss of func-

tioning of certain facial muscles. They are caused

by a lesion of the facial nerve for different reasons

– acute idiopathic facial paralysis (no cause) called a

Bell’s palsy, trauma, infection, chronic illness, tumor,

etc. One common medical treatment, widely used

since 1989 in surgery and aesthetic medicine (Clark

and Berris, 1989) (Filipo et al., 2012), is to inject

in the muscles of the face low doses of Botulinum

Toxin (BT) to handle compensatory over-activity of

the healthy muscles. The objective is to reduce the

degree of asymmetry in the facial dynamics (i.e the

facial temporal evolution) when talking or perform-

ing facial expressions. In general, the results of the

medical treatments are evaluated subjectively by the

clinicians after few weeks of each BT injection, so

no automated system exists to assist them conducting

their assessment. That is, the clinician ask the patient

to convey a speciﬁc facial expression or to read a text

and record him/her using a camera. The observation

of the video (recorded before the BT injection) and

the current dynamic allows the clinician to evaluate

the results and thus monitoring remaining treatments

(BT, surgery, etc.). To our knowledge, no automated

tools exist nowadays to allow clinicians quantitative

evaluation of the BT injection, in terms of facial dy-

namics.

1.1 Prior Work

Analyzing 3D facial sequences is still at the begin-

ning. The recent advances of 3D/4D sensors based

on two main technologies – stereo-photogrammetry

and structured-light – opened the doors to develop

approaches for analyzing static (3D) and dynamic

(4D) shapes. In particular, targeting the face recogni-

Desrosiers, P., Bennis, Y., Amor, B., Daoudi, M. and Guerreschi, P.

Facial Asymmetry Assessment from 3D Shape Sequences: The Clinical Case of Facial Paralysis.

DOI: 10.5220/0005721200300038

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 30-38

ISBN: 978-989-758-175-5

tion or expression classiﬁcation problems, few groups

have recently collected new datasets (Sun and Yin,

2008)(Zhang et al., 2014)(Cosker et al., 2011)(Ma-

tuszewski et al., 2012) and have developed ﬁrst tech-

niques (Sun et al., 2010)(Sandbach et al., 2012)(Ben

Amor et al., 2014) for expression recognition from 3D

sequences. These approaches have demonstrated the

role of 3D dynamic faces analysis to reveal deforma-

tions hidden in 2D videos. In fact, 2D images resulted

of the projection of the observed scene into a plane

(X-Y) which results in loosing the depth component

(Z). Using these 3D acquisition sensors allows to re-

cover the Z-coordinates and thus the use of a the com-

plete shape of the 3D face. Current literature is rich

of approaches for shape analysis of 3D and 4D faces.

However, only few studies have addressed the funda-

mental question of – How to quantify the amount of

bilateral facial asymmetry from the temporal evolu-

tion of 3D faces?

Earlier shape analysis studies are based on the de-

tection and tracking of 2D and 3D facial landmarks in

facial sequences. For instance, Al-Anezi et al. (Al-

Anezi et al., 2013) have proposed a new method for

automatic tracking of facial landmarks in 4D videos.

A set of 23 anthropometrics landmarks with no per-

manent ink are marked on the faces of 32 subjects

aged 18 to 35 years. The subjects are asked to per-

form a facial animation like maximal smile, lip purse,

cheek puff. They have concluded that an accurate

tracking solution facilitate the analysis of the dynamic

motion. Shujaat et al. (Shujaat et al., 2014) have pur-

sued the study conducted in (Al-Anezi et al., 2013)

and have developed a new method to quantify dy-

namic 3D facial animations, in order to character-

ize the dynamics of 3D lips movement in head, and

neck oncology patients before and after lower lip split

mandibulotomy. A dataset of 7 subjects aged 42-80

years old is collected. Moreover, a set of nine facials

soft tissue landmarks are manually annotated on the

ﬁrst frame of each 3D sequence by an operator, and

then tracked automatically. Six landmarks are used to

analyze the lip motions, assessing of the magnitude,

and the three others to track the effect of the head mo-

tion, and to align all the frames into a common ref-

erence frame. They measured the feasibility of the

change in the magnitude, speed, and motion simi-

larity of facial animation. The results show that the

magnitude and the speed difference decreased after

the surgical operation for the smile and the lip purse,

while motion similarity shows a high score in the case

of lip purse animation. Recently, Wei et al. (Quan

et al., 2012) proposed a novel approach to analyze

the asymmetry of the face on 3D dynamic scan. A

data set which comes from the Hi4D-ADSIP database

is used, and allow them to make a comparison be-

tween stroke patients and healthy individuals. At ﬁrst

sight, in each frame, the nose tip is determined, and

a sphere of radius r = 130 mm is centered at the nose

tip for segment of the 3D face. Then, with their pro-

posed method, they extracted the symmetry plan of

the 3D face. Thus, the asymmetry plan can be ex-

tracted directly from the symmetry plan by using the

original data and the mirrored data obtained by reﬂec-

tion across the symmetry plan. After matching the

original 3D face and its mirror with the help of ICP,

they calculated the Euclidean distance between each

point of the 3D original face and its mirror. From this,

they measured the higher asymmetry level of the 3D

face which based on the bigger value of the average

closest distance. They have concluded that, the pro-

posed method is able to measure the asymmetry of

the face, facial dysfunction, and the method is also

able to detect minor change in asymmetry which not

been observed by the clinician during examination.

1.2 Methodology and Paper

Organization

The main goal of this work is to propose a com-

prehensive and automated pipeline for efﬁcient facial

asymmetry evaluation. Using a 3D sensor, several 3D

video acquisitions are recorded before and after clin-

ician’s intervention. A preprocessing step is then ap-

plied to each frame of the 3D videos including – holes

ﬁlling, smoothing, pose normalization, and nose tip

detection. On preprocessed 3D faces a mirror opera-

tion with respect to the YZ-plane is applied to produce

new meshes (i.e the left half the original face corre-

sponds to the right half of the mirrored face). Shape

analysis of the obtained faces (original mesh and its

mirror) allows alignment and accurate dense registra-

tion, leaded jointly. In particular, using the initial ve-

locity vector along the geodesic path connecting their

shapes (Ben Amor et al., 2014), one can quantify the

amount of deformations between them. As a result,

at each instant of the 3D video, a Dense Scalar Field

which reﬂects the facial asymmetry is computed. Fi-

nally, the extension of the previous step to the tempo-

ral domain allows quantifying the evolution of facial

asymmetry across the video. An experimental illus-

tration of the above-mentioned idea is reported where

a new dataset of the patient’s face before and after BT

injection is recorded.

The rest of the paper is organized as follows. In

section 2, we describe the clinical data used in this

study which consists of 3D facial sequences of pa-

tients recorded before and after the clinician’s inter-

vention. The Riemannian shape analysis approach

Facial Asymmetry Assessment from 3D Shape Sequences: The Clinical Case of Facial Paralysis

and its capability to quantify the amount of facial

asymmetry is presented in section 3. An experimental

illustration involving the clinical dataset is discussed

in section 4. In section 5 are drawn some concluding

remarks and future investigation.

2 DATASET DESCRIPTION AND

PREPROCESSING

Due to the novelty of the topic, we have conducted

with clinicians the acquisition of patients suffering

from facial paralysis. The patients are asked to per-

form some speciﬁc facial expressions in front of the

3D camera. These expressions have been dictated by

the clinicians.

2.1 4D Data Acquisition

In total ﬁve patients with facial paralysis have been

invited for two acquisition sessions, one time before

the BT injection and a second time after two weeks

of the injection. The participants have been asked to

convey three different expressions (1) normal smile,

(2) forced smile, and (3) raising-up the eyebrows. The

average duration of the recorded 3D videos is 4-6 sec-

onds with a total of 60 to 100 3D frames. In our ac-

quisition process, we have used the ARTEC MHT 3D

scanner

. This single-view 3D scanner allows cap-

turing 3D videos of 15 fps (frame per second), each

frame consists of about 5500 vertices, and the 3D res-

olution is 0.5 mm. To allow an optimal acquisition,

the participants are asked to sit in front of the camera

at a distance of about 80 cm to continuously focus on

a ﬁxed point. In addition, we have recorded following

the same settings, 3D sequences of a healthy face (as

a control sample). Figure 1 illustrates a sequence of

3D facial surfaces obtained using the 3D sensor of a

patient’s face asked to exhibit a forced smile.

2.2 Pre-processing of 3D Frames

As mentioned before, the 3D sequences presents im-

perfections such as missing data (i.e holes in the

mesh), noise (i.e. spikes) and contain undesirable

parts (neck, clothes, hair, etc.). We applied the fol-

lowing pipeline in order to extract the informative part

of the face,

– Clean up the meshes by removing identical ver-

tices,

– Fill small holes on the mesh by interpolation,

http://www.artec3d.com/fr/hardware/artec-mht/

Figure 1: An example of 3D sequence of a patient’s face ex-

hibiting a forced (maximum) smile. The sequence follows

the evolution model neutral-onset-apex-offset-neutral.

– Detect the nose tip of each face on each frame,

– Crop the face, the nose tip is used to deﬁne a

sphere with a constant radius which serves to crop

the face region,

– Smooth the meshes using a Laplacian ﬁlter to re-

duce the noise,

– Apply a mirror operator on the 3D faces with re-

spect to the YZ-plan,

– Apply the ICP (Iterative Closest Point) algorithm

between the original 3D frame and the mirrored

3D frame for pose normalization.

An efﬁcient implementation of this pipeline is de-

signed using ﬁlters of the VTK

library. This pre-

processing pipeline is applied to each 3D frame of the

3D video, separately. As a result, we obtain a 3D

animations of the 3D faces and their mirrored. The

next step is to extract radial curves and to quantify the

amount of asymmetry by comparing each 3D shapes

to their reﬂections.

The problem is turned to a comparison of 3D

(static) facial shapes, i.e. at each instant t, we pre-

processed the 3D face with its mirrored. To achieve

such comparison, one needs for an accurate registra-

tion algorithm which can handle the non-rigid defor-

mations (bending, stretching/compression) of the fa-

cial surfaces. The registration of vertices across 3D

faces is an important ingredient when studying their

shapes (we assume here an invariance to rigid motions

– translation, scaling and rotation). Speciﬁcally, in

comparing shapes of faces, it is important that similar

http://www.vtk.org

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

biological parts are registered to each other, in partic-

ular the left and right halves of the face, when study-

ing the face asymmetry. Several methods have been

proposed in the literature as discussed above such as

the Non-rigid ICP algorithm (Cheng et al., 2015), the

Free Form Deformation (FFD) algorithm (Sandbach

et al., 2012) and the Thin-plate Spline (TPS) algo-

rithm (Fang et al., 2012). Most of these solutions try

to ﬁnd an optimal registration between two 3D faces,

however, their cost functions which minimize the dis-

tance between 3D meshes is not a proper metric; it is

not even symmetric. That is, the optimal registration

of a 3D face F

to another 3D face F

may not be

the same as the registration of F

to F

. This makes

difﬁcult to interpret the results (i.e. quantifying the di-

vergence between the compared 3D faces). The Rie-

mannian framework used in (Ben Amor et al., 2014)

for 4D facial expression analysis grounding on elastic

radial curves (i.e. an elastic metric is used (Srivastava

et al., 2011)) provides a nice physical interpretation

of measuring the facial deformations between curves

using a combination of stretching and bending. These

elastic deformations are captured by the Dense Scalar

Field (DSFs) features. Hence, the main motivation of

using a Riemannian approach is to perform registra-

tion that matches corresponding anatomical features,

and obtain deformation ﬁelds that are physically inter-

pretable. In the next section, we recall essential mate-

rials to compute the Dense Scalar Fields (DSFs) and

illustrates their used to quantify the amount of facial

asymmetry. Finally, we will make their extensions to

study dynamic 3D faces.

3 BILATERAL FACIAL

ASYMMETRY

Given a 3D facial sequence, our aim is to measure the

amount of bilateral symmetry at each time and extend

it to the temporal dimension. We will start by the ﬁrst

case (i.e. static 3D face), the most common way to

quantify the asymmetry is to ﬁrst detect the plane of

symmetry of the face (called also the mirror plane),

then apply registration algorithms as the well-know

Iterative Closest Point as proposed in (Quan et al.,

2012). Here, the most problematic step is to detect ac-

curately the mirror plane before comparing the shape

divergence between the two halves of the facial sur-

face. Quan et al. (Quan et al., 2012) consider the 3D

vertices of the face as a cloud of points in R

, they ap-

ply a Principal Component Analysis (PCA) to extract

its dominant direction, which corresponds to the mir-

ror plane. When this approach achieved good results

on ”normal” faces, it is problematic to use on faces

with paralysis. That is, in the latter, the plane location

may be far from the the nose tip, for example. A sec-

ond problem of this approach, is the use of the ICP al-

gorithm, which consider in its cost function only rigid

transformations (translation, scaling and rotation) and

a very basic optimization criteria based on the point-

to-point (or point-to-plane) distance. This makes dif-

ﬁcult to achieve any physical interpretation of the re-

sults. In the case of facial paralysis, the registration

algorithm may register different anatomical parts on

the two halves of the 3D face.

According to the above-mentioned issues, we pro-

pose in this paper a different approach to measure

the bilateral facial asymmetry, when ﬁrst avoiding the

mirror plane detection, and use a Riemannian shape

analysis framework developed recently (Ben Amor

et al., 2014) to achieve accurate registration. The ba-

sic idea is to approximate the facial surface by an in-

dexed (ordered) collection of radial curves, then con-

sider pairwise curves comparison, using a Rieman-

nian elastic metric which account for the stretching

and shrinking of the face. Before reaching this step,

we avoid the step of mirror plane detection by apply-

ing a simple mirroring to the original face according

to the YZ-plane, then align the two surfaces using the

ICP algorithm, and ﬁnally use the Riemannian ap-

proach to quantify the optimal deformation between

the 3D face and the mirrored face. To this end, we ex-

ploit the notion of geodesic (shortest path between the

facial surfaces) on the shape space that we will note

[0,2π]

, and we will detail later.

Let ﬁrst note the facial curves emanating from the

nose tip and tracking directions dictated by an angle

α ∈ [0, 2π[. The obtained collection of curves pro-

vides, Figure 2, not only a nice approximation of the

face, but also impose on it a parametrization. That

is, considering the nose tip as an origin, each point

on the face is identiﬁed, in a unique way, by α the

index of the curve and k, the index of the point on

the curve. Based on this radial curves representation,

the problem of face-to-face registration is turned to

a pairwise-curves registration. Elastic shape analysis

of open and closed curves is a well-explored prob-

lem. An emerging solution using Riemannian geom-

etry have demonstrated convincing results, when the

problems of alignment and registration are leaded in

the same and unique step. Recently, Ben Amor et

al. (Ben Amor et al., 2014) have extended the geo-

metric framework of curves proposed by (Srivastava

et al., 2011) to facial surfaces. Using the SRVF repre-

sentation q

(t) of the facial curves β

(t), where α is

the curve index on the face, to form the shape space

[0,2π]

. As the shape space is a quotient space an

Hyper-sphere of the Hilbert space L

([0, 1], R

), the

Facial Asymmetry Assessment from 3D Shape Sequences: The Clinical Case of Facial Paralysis

geodesic path between two facial shapes is given by

the minor arc of the great circle of the Hyper-sphere.

Figure 2: Three views of the same collection of curves ex-

tracted to approximate a 3D facial shape. The point in red

represent the detected nose tip (origin of the radial curves).

To capture and model the deformations between

the 3D face and its mirror during different facial ex-

pressions, we pursued with the work of Ben Amor et

al. (Ben Amor et al., 2014) which have proposed to

represent the facial surface through a set of parame-

terized radial curves that originate from the tip of the

nose. Approximating the facial surface by an ordered

set of radial curves, which locally captures its shape

can be seen as a parameterization of the facial surface.

The mathematical setup for the shape theory offered

here comes from Hilbert space analysis.

A facial surface is represented by a collection of

radial curves and a Riemannian framework is used

to study shapes of these curves. We start by repre-

senting facial curves as absolutely continuous maps

from β : [0, 1] → R

and our goal is to analyze shapes

represented by these maps. The problem in study-

ing shapes using these maps directly is that they

change with re-parameterizations of curves. If γ is

a re-parameterization function (typically a diffeomor-

phism from [0, 1] to itself), then under the standard

norm, the quantity kβ

− β

k 6= kβ

◦ γ − β

◦ γk,

which is problematic. The solution comes from

choosing a Riemannian metric under which this in-

equality becomes equality and the ensuing analysis

simpliﬁes. As described in (Srivastava et al., 2011),

we represent the facial curves using a new function q,

called the square-root velocity function (SRVF) (see

Eq. (1)). The advantage of using SRVF representa-

tion is that under this representation the elastic metric

becomes the standard L

metric and an identical re-

parameterization of curves preserves the L

norm of

between their SRVFs. The mapping from a curve β to

q is a bijection (up to a translation) and the space of

all SRVFs is the Hilbert space of all square-integrable

maps of the type q : [0, 1] → R

. This space under

the natural L

inner product is actually a vector space

and geodesics between points in this space are straight

lines.

With the proposed representation, a 3D facial sur-

face is approximated by an indexed collection of ra-

dial curves β

, where the index α denotes the angle

formed by the curve with respect to a reference radial

curve. In particular, the reference radial curve (i.e.,

the curve with α = 0) is chosen as oriented along the

vertical axis, while the other radial curves are sepa-

rated each other by a ﬁxed angle and are ordered in a

clockwise manner.

Considering a generic radial curve β of the face,

it can be parameterized as β: I → R

, with I = [0, 1],

and mathematically represented through the square-

root velocity function (SRVF) (Joshi et al., 2007; Sri-

vastava et al., 2011), denoted by q(t), according to:

q(t) =

β(t)

β(t)k

, t ∈ [0, 1]. (1)

This speciﬁc representation has the advantage of cap-

turing the shape of the curve and makes the calcu-

lus simpler. Let us deﬁne the space of the SRVFs as

C = {q : I → R

, kqk = 1} ⊂ L

(I, R

), with k · k

indicating the L

norm. With the L

metric on its tan-

gent space, C becomes a Riemannian manifold. Ba-

sically, with this parametrization each radial curve is

represented on the manifold C by its SRVF. Accord-

ing to this, given the SRVFs q

and q

of two radial

curves, the shortest path ψ

∗

on the manifold C be-

tween q

and q

(called geodesic path) is a critical

point of the following energy function:

E(ψ) =

ψ(τ)||

dτ , (2)

R where ψ denotes a path on the manifold C between

and q

, τ is the parameter for traveling along the

path ψ,

ψ ∈ T

(C ) is the tangent vector ﬁeld on the

curve ψ ∈ C , and ||.|| denotes the L

norm on the tan-

gent space.

Since elements of C have a unit L

norm, C is

a hypersphere in the Hilbert space L

(I, R

). As

a consequence, the geodesic path between any two

points q

, q

∈ C is simply given by the minor arc of

the great circle connecting them on this hypersphere,

∗

: [0, 1] → C . This is given by:

∗

(τ) =

sin(θ)

(sin((1 − τ)θ)q

+ sin(θτ)q

) , (3)

where θ = d

, q

) = cos

−1

(

, q

). We point out

that sin(θ) = 0, if the distance between the two curves

is zero, in other words q

= q

. In this case, for each

τ, ψ

∗

(τ) = q

= q

The tangent vector ﬁeld on this geodesic is then

written as

dψ

∗

dτ

: [0, 1] → T

(C ), and is obtained by the

following equation:

dψ

∗

dτ

−θ

sin(θ)

(cos((1 − τ)θ)q

− cos(θτ)q

) . (4)

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

Knowing that on geodesic path, the covariant deriva-

tive of its tangent vector ﬁeld is equal to 0,

dψ

∗

dτ

parallel along the geodesic ψ

∗

and one can represent

it with

dψ

∗

dτ

τ=0

without any loss of information. Ac-

cordingly, Eq. (4) becomes:

dψ

∗

dτ

τ=0

sin(θ)

− cos(θ)q

) (θ 6= 0). (5)

Based on the above representation, we deﬁne a Dense

Scalar Field capable to capture deformations between

two corresponding radial curves β

and β

of two 3D

faces approximated by a collection of radial curves.

Let q and q

the SRVFs of the curves β and its re-

ﬂection β

, respectively. ψ

∗

is the optimal path (the

geodesic) connecting q and q

and the angle θ is the

length of the geodesic which represents the geodesic

distance between q and q

. By integrating θ over all

α ∈ [0, 2π] gives rise to a scalar value which measures

the divergence between the face and its reﬂection. We

will use this measure later on in section 4 in our quan-

titative analysis. To quantify densely the divergence

between faces across a 3D video, Ben Amor et al.

(Ben Amor et al., 2014) proposed the Dense Scalar

Fields. Roughly speaking, it consists to compute the

initial velocity vector

dψ

∗

dτ

τ=0

along the geodesic ψ

∗

as the geodesic is by deﬁnition a constant speed curve

on the shape manifold in Eq. (5).

As describe above, the Dense Scalar Field (be-

tween a curve and its reﬂection) denotes the magni-

tude of

dψ

∗

dτ

τ=0

at each point of the curves.

Figure 3: An example of computing the Dense Scalar Fields

(DSFs) on a patient’s face with paralysis. From left to right

(a) original 3D face, (2) 3D face after reﬂection, and (3) the

DSFs shown as a color map mapped on the original 3D face.

Figure 3 illustrates this idea, on the left the origi-

nal static 3D face, in the middle its reﬂection and on

the right the result of DSFs computation given as a

color map of 64 colors ranging from blue to red. In

this ﬁgure, cold colors represent the most symmet-

ric parts of the 3D face and warm colors highlight

the most asymmetric parts. Colors in between reﬂect

a scale of the amount of bilateral asymmetry of the

face. Compared to the 3D landmarks-based approach

adopted in (Shujaat et al., 2014), our approach pro-

vides dense measurements of the bilateral asymme-

try on the face. This could be of high importance for

clinicians to evaluate locally the bilateral asymmetry

of the face. This is because the BT injection is done

locally in some speciﬁc muscles.

The main motivation behind computing the shape

deviation between an arbitrary 3D facial shape and its

mirrored shape is to avoid the difﬁcult task of mirror

plane detection. In fact, our approach allows to quan-

tify accurately the bilateral (left-right) face asymme-

try by (1) a ﬁne alignment of the two shapes using

the ICP algorithm, then (2) compute the shape devia-

tion using elastic radial curves (i.e. computing DSFs).

Thus, the quantifying the bilateral asymmetry is inde-

pendent of any plane of symmetry. In particular, this

is suitable when working with paralyzed faces when

conveying expressions for whom the detection of a

plane of symmetry is not an easy task.

4 EXPERIMENTS AND

DISCUSSIONS

In this section we illustrate experimentally the use of

DSFs to quantify the bilateral symmetry of the face.

To this end, we used some samples taken from the

new dataset described in section 2. To conduct these

experiments, given a 3D sequence of the face, each

frame is ﬁrst reﬂected then aligned to the original

face. As a ﬁnal step, the DSFs are calculated between

the original and the reﬂected (aligned) shapes. We

present in the following four main experiments which

involve (1) Neural states pre- and post-operative of a

patient’s face; (2) Smiling faces (natural) in pre- and

post-operative; (3) Forced smiling in pre- and post-

operative; and (4) Eyebrows raised in pre- and post-

operative. In the following, we report also quantita-

tive and qualitative results on a control subject’s face

(i.e. normal or healthy subject’s face). In these ex-

periments, the facial surfaces are approximated with

a total of 100 radial curves, each consists of 50 points,

in total each DSF vector contains 5000 scalar points.

1. Neutral State – in this experiment, we simply

restrict our study to a static neutral face. Thus, a sin-

gle 3D surface is considered for the patient’s face be-

fore and after the BT injection. Figure 4 illustrates the

DSFs computed to capture densely the degree of bi-

lateral symmetry on the 3D face. It is quite clear from

this ﬁgure that only minors changes are shown when

comparing the pre- and the post-operative asymmetry

results. In contrast, a difference exists when compar-

ing with the asymmetry of a control healthy face. We

can note also that the face is not perfectly symmetric

(see third row of Figure 4, and the acquisition pro-

cess may cause some aberrant depth calculations, in

particular in the eyes regions.

Facial Asymmetry Assessment from 3D Shape Sequences: The Clinical Case of Facial Paralysis

Figure 4: From left to right, the original shape, its reﬂec-

tion, and the bilateral asymmetry mapped into the reﬂection

shape. From top to bottom, DSFs on (a) pre-operative, (b)

post-operative , and (c) healthy subject’s faces.

From this ﬁrst experiment, its is important that the

patient convey a facial expression to allow in-depth

analysis of the results.

2. Smiling – in this experiment, the patient is

asked to perform a natural smile. In Figure 5 we re-

port the degree of asymmetry for the apex (maximum

expression) of the smile. Compared to the previous

experiment (Figure 4) the DSFs reveal the difference,

in terms of asymmetry, between the pre-operative and

the post-operative result. Looking to the ﬁrst two

rows of Figure 5, one can note an improvement of

facial symmetry after the BT injection on the same

patient. This can be seen in the surface of the blue

areas in the two DSFs. It is clear that the amount of

asymmetry is reduced along the Zygomaticus muscle.

We recall that the post-operative 3D acquisitions hap-

pened 2 weeks after the BT injection.

The bilateral asymmetry is evaluated at each

frame of the 3D video, we can note here report the

DSFs color map along the 3D video, however, we re-

port in Figure 6, the geodesic distance (global devi-

ation value) between the facial shape and its reﬂec-

tion. From this graph, we note a decrease of the facial

asymmetry when the expression happened in the tem-

poral segment between the frames 28 and 60.

This graph showed clearly the importance of con-

sidering the temporal evolution of the facial 3D shape

in stead of the static one. When comparing the post-

operative results with the healthy face (curves in red

and green) in Figure 6, one can note the efﬁciency of

Figure 5: Natural smiling experiment (a) pre-operative, (b)

post-operative and (c) healthy subject.

Figure 6: Degree of asymmetry across the video for the nat-

ural smiling experiment.

the BT injection to symmetrizing the facial shape and

its temporal evolution. However, what happen if the

expression is more prominent than a natural smile?

3. Forced Smiling – in response of the previous

question, the patients are asked to convey a forced

(maximum) smile. Then the same pipeline is applied

as previously.

From Figure 7, one can establish the same con-

clusions than in the previous experiment. That is the

degree of asymmetry of static and dynamic faces de-

creases after the BT injection. It can be seen from

this graph in Figure 8 that during the time-interval

between frames 14 to the end, when the expression

happened the amount of bilateral asymmetry before

the injection is higher (red curve) than after. The blue

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

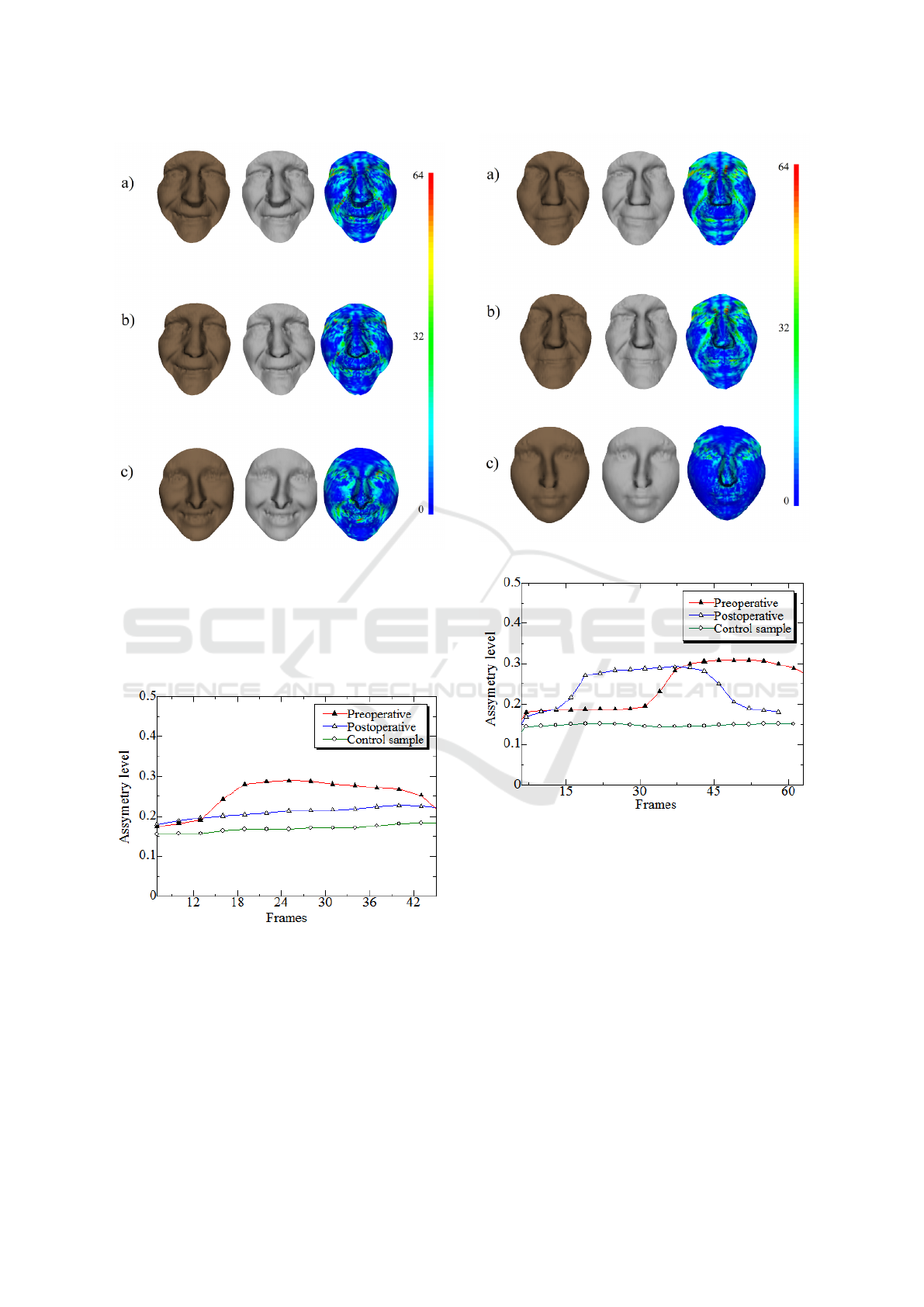
Figure 7: Forced (maximum) smiling experiment.

curve (after the BT injection) is always higher than the

green one (healthy subject). This could be explained

by the fact that healthy face taken is our experiments

is younger than the patient’s face.

Figure 8: Forced smiling in the experiment.

4. Raising-up the Eyebrows – in this experiment,

the patients are asked to raised up his eyebrows. From

ﬁgure 9, one can note again that the amounts of the

asymmetry before and after the BT injection are com-

parable. This is mainly due to the fact that the BT in-

jection is concentrated only on the zygomaticus mus-

cles and the muscles related to the eyebrows move-

ments (i.e. the corrugator muscle) do not received any

treatments. This result is also conﬁrmed with the con-

Figure 9: Raising-up the eyebrows experiment.

Figure 10: Asymmetry along time for the raising-up the

eyebrows experiment.

trol sample, the amount of asymmetry is huge in the

patient’s face compared to the normal face.

The graph reported in Figure 10 conﬁrm this ob-

servation. We note here a shift in the time interval

which corresponds to different starting and ending

time of the expression performed before and after re-

ceiving the treatments.

In the table 1, we present the amount of the asym-

metry level measured in each 3D video sequence.

We can observe that, in the the pre-operative (pre-

op) case, the asymmetry level is higher than the post-

operative (post-op) case, and the control sample (cs)

has the lower asymmetry level during all facial ex-

pressions.

Facial Asymmetry Assessment from 3D Shape Sequences: The Clinical Case of Facial Paralysis

Table 1: Maximum asymmetry level in each 3D video.

Facial Expression pre-op post-op cs

Smiling 0.218 0.173 0.159

Force smiling 0.288 0.227 0.182

Raise up the eyebrows 0.308 0.291 0.146

5 CONCLUSIONS

In this paper we have proposed a new technique to

quantify facial asymmetry from 4D facial data. The

main ingredient of this approach is the accommoda-

tion of the recently-developed Dense Scalar Fields

(Ben Amor et al., 2014) to compare a given face with

its reﬂection and achieve a vertex-to-vertex registra-

tion in order to accurately measure the amount of

asymmetry in the face. A new dataset of ﬁve pa-

tients has been collected in clinical conditions. We

have demonstrated using the collected 3D dynamic

sequences the usefulness of the proposed methodol-

ogy. In particular, the comparison of the facial asym-

metry by using DSF features before and after the BT’s

injection reveals shows that the proposed approach is

a promising solution. This work provides a quanti-

tative tools to the clinicians in order to evaluate the

treatment.

REFERENCES

Al-Anezi, T., Khambay, B., Peng, M., O’Leary, E., Ju, X.,

and Ayoub, A. (2013). A new method for automatic

tracking of facial landmarks in 3d motion captured im-

ages (4d). International Journal of Oral and Maxillo-

facial Surgery, 42(1):9 – 18.

Ben Amor, B., Drira, H., Berretti, S., Daoudi, M., and Sri-

vastava, A. (2014). 4-d facial expression recognition

by learning geometric deformations. IEEE T. Cyber-

netics, 44(12):2443–2457.

Cheng, S., Marras, I., Zafeiriou, S., and Pantic, M. (2015).

Active nonrigid ICP algorithm. In 11th IEEE Interna-

tional Conference and Workshops on Automatic Face

and Gesture Recognition, FG 2015, Ljubljana, Slove-

nia, May 4-8, 2015, pages 1–8.

Clark, R. and Berris, C. (1989). Botulinum toxin: a treat-

ment for facial asymmetry caused by facial nerve

paralysis. Plast Reconstr Surg, 84(2):353—5.

Cosker, D., Krumhuber, E., and Hilton, A. (2011). A facs

valid 3D dynamic action unit database with applica-

tions to 3D dynamic morphable facial modeling. In

Int. Conf. on Computer Vision (ICCV), pages 2296–

2303.

Fang, T., Zhao, X., Ocegueda, O., Shah, S. K., and Kaka-

diaris, I. A. (2012). 3d/4d facial expression analysis:

An advanced annotated face model approach. Image

and Vision Computing, 30(10):738–749.

Filipo, R., Spahiu, I., Covelli, E., Nicastri, M., and Bertoli,

G. (2012). Botulinum toxin in the treatment of fa-

cial synkinesis and hyperkinesis. The Laryngoscope,

122(2):266–70.

Joshi, S., Klassen, E., Srivastava, A., and Jermyn, I. (2007).

A novel representation for Riemannian analysis of

elastic curves in R

. In Proc. IEEE Conf. on Com-

puter Vision and Pattern Recognition, pages 1063–

6919, Minneapolis, MN.

Matuszewski, B., Quan, W., Shark, L.-k., McLoughlin, A.,

Lightbody, C., Emsley, H., and Watkins, C. (2012).

Hi4d-adsip 3D dynamic facial articulation database.

Image and Vision Computing, 30(10).

Quan, W., Matuszewski, B. J., and Shark, L. (2012). Fa-

cial asymmetry analysis based on 3-d dynamic scans.

In Proceedings of the IEEE International Conference

on Systems, Man, and Cybernetics, SMC 2012, Seoul,

Korea (South), October 14-17, 2012, pages 2676–

2681.

Sandbach, G., Zafeiriou, S., Pantic, M., and Rueckert, D.

(2012). Recognition of 3D facial expression dynam-

ics. Image and Vision Computing, 30(10):762–773.

Shujaat, S., Khambay, B., Ju, X., Devine, J., McMahon,

J., Wales, C., and Ayoub, A. (2014). The clinical ap-

plication of three-dimensional motion capture (4d): a

novel approach to quantify the dynamics of facial an-

imations. International Journal of Oral and Maxillo-

facial Surgery, 43(7):907 – 916.

Srivastava, A., Klassen, E., Joshi, S. H., and Jermyn, I. H.

(2011). Shape analysis of elastic curves in euclidean

spaces. IEEE Trans. Pattern Anal. Mach. Intell.,

33(7):1415–1428.

Sun, Y., Chen, X., Rosato, M. J., and Yin, L. (2010).

Tracking vertex ﬂow and model adaptation for three-

dimensional spatiotemporal face analysis. IEEE

Transactions on Systems, Man, and Cybernetics, Part

A, 40(3):461–474.

Sun, Y. and Yin, L. (2008). Facial expression recognition

based on 3d dynamic range model sequences. In Pro-

ceedings of the 10th European Conference on Com-

puter Vision: Part II, ECCV ’08, pages 58–71.

Zhang, X., Yin, L., Cohn, J. F., Canavan, S., Reale, M.,

Horowitz, A., Liu, P., and Girard, J. M. (2014). Bp4d-

spontaneous: a high-resolution spontaneous 3D dy-

namic facial expression database. Image and Vision

Computing, 32(10):692 – 706.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications