Inﬁnite 3D Modelling Volumes

E. Funk and A. B

orner

Department of Information Processing for Optical Systems, Institute of Optical Sensor Systems,

German Aerospace Center, Berlin, Germany

Keywords:

Large Scale automated 3D Modelling, Mobile Robotics, Efﬁcient Data Structures, 3D Database.

Abstract:

Modern research in mobile robotics proposes to combine localization and perception in order to recognize

previously visited locations and thus to improve localization as well as the object recognition processes recur-

sively. A crucial issue is to perform updates of the scene geometry when novel observations become available.

The reason is that a practical application often requires a system to model large 3D environments at high res-

olution which exceeds the storage of the local memory. The underlying work presents an optimized volume

data structure for inﬁnite 3D environments which facilitates i) successive world model updates without the

need to recompute the full dataset, ii) very fast in-memory data access scheme enabling the integration of high

resolution 3D sensors in real-time, iii) efﬁcient level-of-detail for visualization and coarse geometry updates.

The technique is ﬁnally demonstrated on real world application scenarios which underpin the feasibility of the

research outcomes.

1 INTRODUCTION

Research on autonomous vehicles has become emi-

nent in recent years. A signiﬁcant driving force is the

vision of autonomous transport. Cars or pillars, which

can operate autonomously 24 hours a day are highly

attractive for logistics and public or private transport

(Andreasson et al., 2015). This vision has lead to in-

tensive research that is also emphasized by the Euro-

pean Commission (EUC, 2015).

Another fruitful area of research is the automa-

tion of production sets, where robots optimized for

a single-task are carefully separated from people

(Bekris et al., 2015). The future of automation lies

in ﬂexible factory ﬂoors and quick burst manufactur-

ing processes, which can provide complex, short-life-

cycle products without investing into reconﬁguration

of the production set.

Both research disciplines have a particular aspect

in common: When it comes to simultaneous appli-

cation of multiple robots, lifelong world modelling

or accurate localization using optical 3D sensors be-

comes a critical task. Moreover, both research disci-

plines heavily rely on 3D sensors such as stereo cam-

eras or laser scanners. These are the low-level inter-

faces between the algorithmic data analysis and the

physical world. The goal is to integrate each 3D mea-

surement from the environment, whether a recognized

object, its state or its geometrical 3D shape, into a

global and consistent database. Such a database aims

at supporting all other mobile platforms in navigation

and scene understanding. Only when a mobile robot

can localize itself with respect to walls or other static

obstacles, it is able to move and to approach targeted

locations.

Common 3D sensors such as laser scanners, stereo

or time of ﬂight cameras provide samples in R

of the

environment. The set of all given samples is usually

referred to as a point cloud, since no structural infor-

mation is provided by the sensors. The goal in per-

ception robotics is further to process the point clouds

to meaningful information, such as 3D maps, obsta-

cles and its positions, or any other objects of inter-

est. In fact, autonomous vehicles are able to avoid ob-

stacles, to navigate or to pick up load only when the

3D samples have successfully been processed to an

application speciﬁc model. The information process-

ing challenge is aggravated by the circumstance that

the sensors deliver large 3D point datasets. A stereo

camera, working at VGA resolution (640×480) at 10

frames per second delivers 3 million 3D points per

second. Therefore, in order to integrate all measure-

ments over multiple days or even years, a highly efﬁ-

cient 3D database is required. Only then it is possible

to deploy a long-term operating robot capable of sur-

face extraction, or object recognition.

Today, intensive research is undertaken by the

robotics community focusing on the 3D perception.

248

Funk, E. and Börner, A.

Inﬁnite 3D Modelling Volumes.

DOI: 10.5220/0005722002460253

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 248-255

ISBN: 978-989-758-175-5

Issues such as strong noise, huge data sets and re-

stricted computation resources make the task partic-

ularly challenging. Furthermore, 3D modelling via

stereo cameras is remarkably difﬁcult since varia-

tions in light or object surface properties lead to non-

gaussian errors and hamper the modelling processes.

Stereo cameras for autonomous vehicles are, how-

ever, favourable since no interference between other

sensors and no a priori infrastructure in the applica-

tion domain is required. Improvements in this do-

main are expected to enable autonomous vehicles to

operate in factories and in public environments with

a strong impact on the production efﬁciency, trafﬁc

safety, logistics and public transportation.

When processing 3D points from range sensor in

general, it is an accepted practice to group the 3D

samples into small cubic volumes, voxels. This en-

ables redundant data to be removed and the memory

layout to be structured efﬁciently since the voxel res-

olution is deﬁned by the user a priori.

The underlying work presents a voxel-based

database approach which makes it possible to create

and to store 3D models and maps of unlimited size

and to access voxels efﬁciently by a given 3D coor-

dinate (x,y,z). In contrast to standard approaches,

where the modeling volume is bounded, the presented

technique enables the extension of the volume dy-

namically. This is of particular interest for all 3D

robotics applications, where the size of the environ-

ment the robot needs to operate upon is now known a

priori.

Section 2 introduces details from the state of the

art research on 3D modelling via voxels, aligned to

the proposed approach. Section 3 states the research

objectives investigated in this work. In Section 4 the

proposed methodology is presented, which clariﬁes

the novel data structure (Sec. 4.1) and its implication

on the voxel query speed using 3D coordinates (Sec.

4.2). Section 5 introduces the 3D modelling frame-

work. A standard approach is discussed critically with

respect to its limitations and an improved technique is

proposed. Section 6 demonstrates the application of

the voxel database and the 3D fusion technique from

range (RGBD-D) camera images. Finally, concluding

remarks and aspects for further research are given in

Section 7.

2 LITERATURE OVERVIEW

Random access of a 3D point by a given coordinate

(x,y,z) is a difﬁcult task, since the search complex-

ity usually depends on the number of samples in the

database. Grouping the data to cubic cells on a regu-

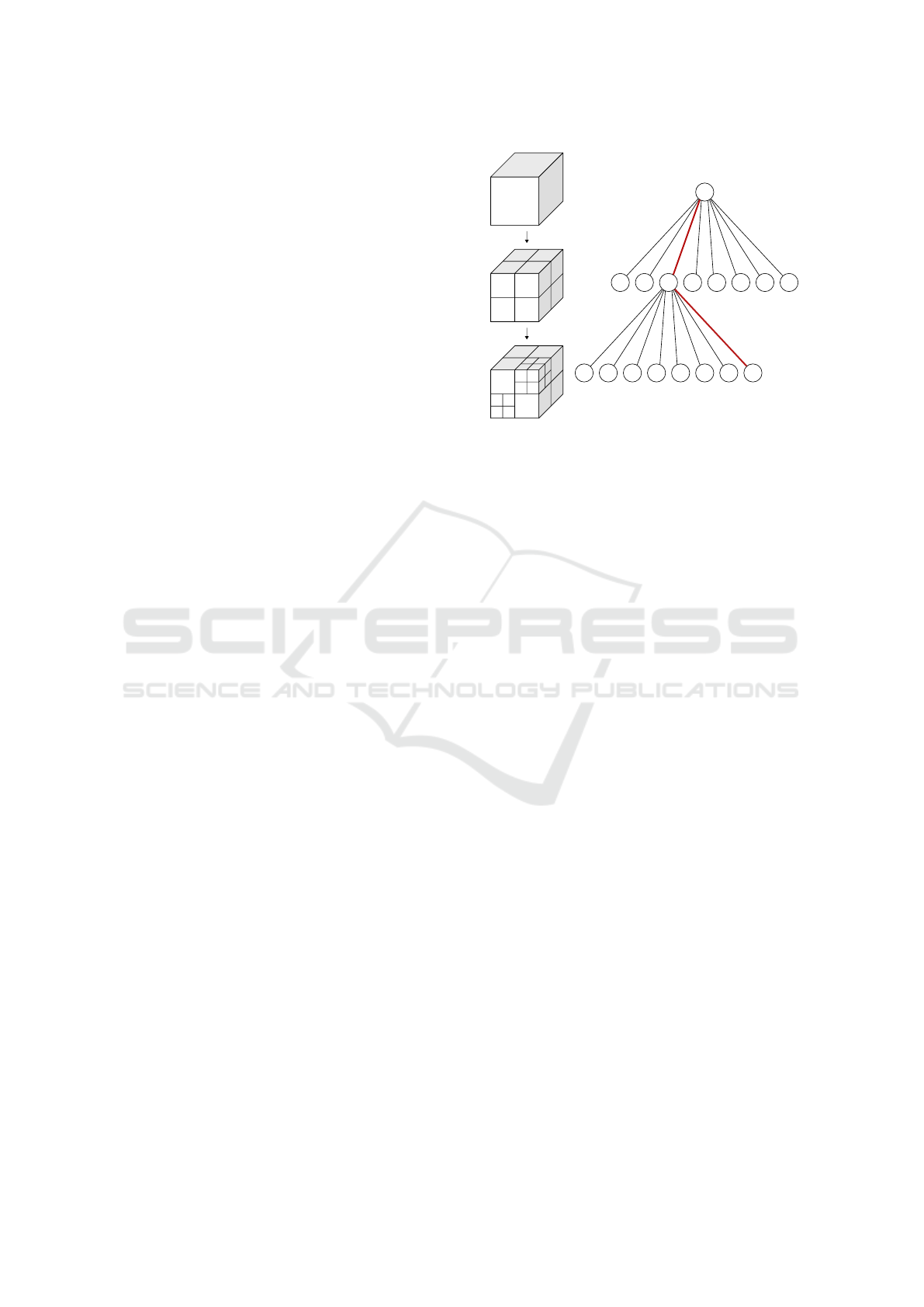
Search in 3D for: (x,y,z)

(x,y,z)

start

Figure 1: Illustrated octree structure and the data ac-

cess path (red), when searching for a voxel at coordinates

(x,y,z).

lar grid and storing them in a 3D array enables very

fast access and has been the state of the art technique

for many years. The reason is, when the resolution

r of a volume is known, e.g. r = 1cm, then the ac-

cess to the corresponding voxel coordinate x = 13m

is performed by computing its index i in the stor-

age array i = x/r = 1300. The drawback of this ap-

proach is that the memory requirements grow with

the cube of the space size. Representing a dense vol-

ume 100 × 100 × 100 m

at 1cm resolution, would re-

quire 3.7 TB of memory when using 32 bit data in-

side each cell. A common approach to this issue is

to structure the occupied cells with a hierarchical oc-

tree, where each node (cube) contains eight cubes of

smaller sizes ((Frisken et al., 2000), (Hornung et al.,

2013)). When searching a voxel given a coordinate

(x,y,z), the tree is traversed starting from the largest

top node, as shown in Figure 1. This means, that the

number of hierarchy levels increases the number of

path checks and thus directly affects the access speed

of a voxel. Each time an arbitrary voxel is addressed,

either when iterating or performing random access, it

is necessary to traverse the full height of the octree.

In short, the search technique in octrees suffers from

the access complexity O(d) with d being the octree-

depth.

Teschner (Teschner et al., 2003) proposed to apply

a hash-map to achieve constant time access O(1) to

sparse voxels. In principal, a coordinate (x,y,z) is en-

coded to a hash index which is used for direct data ac-

cess. Another beneﬁt of hash based databases, is that

the amount of data can be theoretically inﬁnite. This

further allows to store data at nearly arbitrary reso-

lution enabling huge models to be managed which is

only limited by the capacity of the physical memory.

Inﬁnite 3D Modelling Volumes

249

However, generating unique hash values is a difﬁcult

if not an impossible task. The goal is to avoid gener-

ating a hash value representing different coordinates

(Teschner et al., 2003).

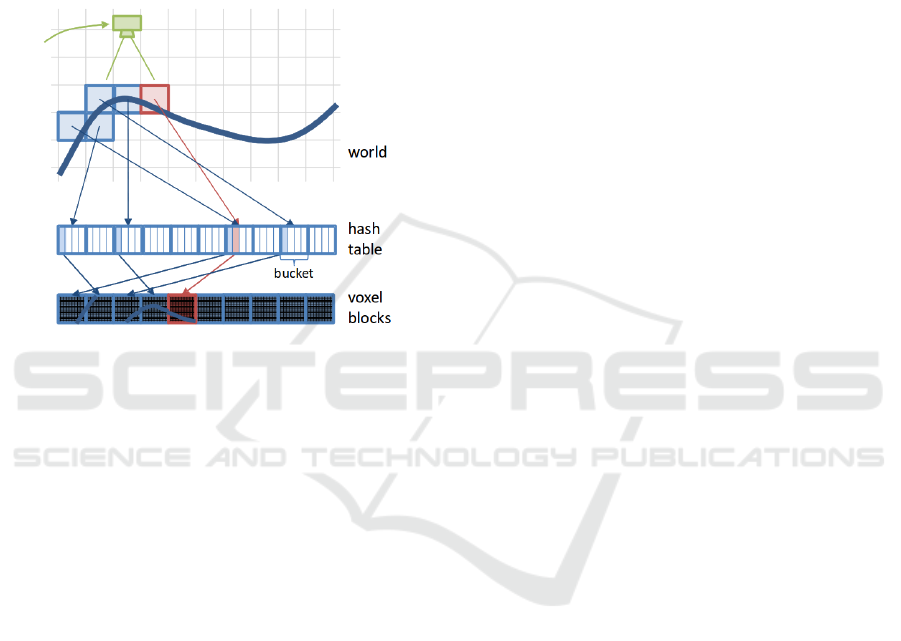
Niessner (Nießner et al., 2013) approached the

collision issue by storing also the coordinate of a

voxel and by grouping voxels with same hash values

to buckets (See Figure 2). When a voxel is found by a

hash value, which does not correspond to the searched

coordinate, the next element in the bucket is accessed.

Figure 2: Niessner (Nießner et al., 2013) applied a hash

table for voxels. Voxel coordinates leading to the same hash

key are grouped to buckets.

However, direct voxel hashing does not allow to

apply level of detail (LOD) visualization or multi

scale 3D modelling which is favourable when low

and high resolution processing is required. In fact,

LOD data structure enables to perform coarse render-

ing depending on the distance to the virtual camera

and coarse 3D modelling depending on the expected

error of a measurement (Floater and Hormann, 2005).

Practically speaking, when it is known that the covari-

ance of a 3D sample covers several meters, it is not

necessary to perform high resolution modelling on a

1cm grid.

The efﬁciency of the hash maps and the LOD ca-

pability of octrees motivated the development of a hy-

brid hashed octree, which is discussed next. We com-

bine the hashing technique from Teschner (Teschner

et al., 2003), approach the collision issue similarly to

Niessner but reference entire octrees by a hash index

instead of small voxels.

3 RESEARCH OBJECTIVES

The ﬁrst research objective is the development of

voxel database to enable storage of geometrical mod-

els or 3D maps of unlimited size. The hash search

collision issues need to be addressed in order to guar-

antee correct voxel access given a coordinate query.

The second objective is the integration of multiple

levels of detail. Since direct voxel hashing does not

enable to query larger spatial groups of voxels, the

objective is to use the hashing technology for entire

octrees covering larger volumes. This would combine

efﬁcient data access known from hash tables and the

favourable LOD data access scheme known from oc-

trees.

The third research objective is the development

of a 3D modelling technique applied upon the pro-

posed voxel database. Motivated by the application

in autonomous vehicles, successive 3D measurements

need to be used for successive model updates. That

means that each new point cloud from a camera frame

is expected to update an existing geometrical model.

Thus, a recursive technique is required for this task to

be accomplished in real-time. A crucial aspect is the

suppression of noise and outliers from the input data.

Section 4 presents the developed octree hashing

technique, and the hash table applied for storage and

search of hash indices. In Section 5 the proposed

voxel database is applied for successive 3D mod-

elling. In contrast to the work from (Nießner et al.,

2013), the proposed work incorporates an adaptive

noise suppression technique enabling low cost and

low power range sensors such as stereo cameras to

be applied.

4 METHODOLOGY

The hashing technique, inspired by (Teschner et al.,

2003) is extended to octrees. The fundamental part

of the technique is the storage and search of arbi-

trary data elements indices via a hash map (Google

inc., 2015). Finally, the performance of the developed

hashed octree framework is compared to a standard

octree approach and the sparse octree technique from

(Hornung et al., 2013).

4.1 Hash Indexing

We propose to combine octrees with a hash table (Fig-

ure 3) leading to sparse voxel representation. The

hash table is used to access the top level root nodes

which further contain an octree in itself. Since the

internal octrees are constructed with low depth (e.g.

d = 2), this signiﬁcantly decreases the access time

compared to standard octrees. To access the voxel at

central index coordinates (x, y,z), we begin by com-

puting the rootKey

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

250

int r o o t K e y [ 3 ]= { x & ˜ ((1 < < d ) - 1 ) ,

y &˜(( 1 < < d ) -1) ,

z &˜(( 1 < < d ) -1)} ;

where d is the depth of the internal octree, & and

˜ denote, respectively, bit-wise AND and NOT opera-

tions. At compile time, this reduces to just three hard-

ware AND instructions. The shift by d makes sure

that the coordinates (x,y,z) are represented by coarser

values. For instance, applying an internal octree of

depth d = 3 with 2

= 8 subdivision nodes in each

dimension the space is divided in coordinate ranges

{[0,7],[8,15],· · ·}. This process is illustrated in Fig-

ure 4. For example, the operation (1<<3)-1 results in

ﬁrst three bits set to one. Negating the same, leads to

ﬁve one-bits and three zero bits, as shown in the illus-

tration of ˜((1<<3)-1). Similar to (Teschner et al.,

2003), the rootKey is further processed to a hash us-

ing large prime numbers.

un si gn e d i n t ro o t Ha sh = ((1 << N ) - 1)&

( r oo tK ey [0] * 73 85 6 09 3 ˆ

ro ot Ke y [ 1] * 1 9 34 9 66 3 ˆ

ro ot Ke y [ 2] * 83 49 2 79 1 );

Here, N is the constant bit-length of the hash, the

three constants are large prime numbers, ˆ is the bi-

nary XOR operator and << is the bit-wise left shift op-

erator. Since the hash is imperfect, collisions occur so

that multiple different coordinates are mapped by the

same hash. The size of the hash map N inﬂuences the

collision probability. In our experiments N was set to

32 bit leading to 70cpm (collisions per million of dis-

tinct coordinates). A drawback of the hash is that it is

not well suited for negative coordinates. Thus, when

negative values in (x,y,z) are processed to a hash, the

number of collisions increases by up to 50%. Such

high rates require countermeasures which are under-

taken by additional octree place holders (green cells

in Figure 3). Each octree reference stores also its co-

ordinate. When an octree is searched by coordinate

given by the user, the resulting octree is validated. If

the validation fails, next cell in the reference list is

checked. Finally, an octree root node enclosing the

searched coordinate is traversed to give the targeted

voxel. The linear search within a hash block slightly

reduces the performance since the hash keys are small

and ﬁt into the Level-1 cache of the CPU.

Hash Table

Level 1

Level 2 - Voxels

#HashEntries

Empty

Allocated

Figure 3: Multiple octrees are stored independently refer-

enced by a hash.

(1<< 3)-1

1 1 1

0 0 0 0

~((1<< 3)-1)

1 0 0 01 1 1 1

0 1 0 10 1 0 1

x&~((1<< 3)-1)

0 0 0 00 1 0 1

Figure 4: Illustration of the key generation steps.

4.2 Hashed-Octree Performance

We have compared the performance of the proposed

hashed-octree with a standard octree implementation

and the recent work from (Hornung et al., 2013). The

second column in Table 1 shows the achieved random

access times for each approach. The third column

contains the best achievable resolution applying the

corresponding technique. For example, using an

octree with depth d = 16, the maximum number

of voxels is 32768

which corresponds to (327m)

when each voxel represents a box volume of 1cm

While octrees are usually limited, the hashed octree

approach is not. In theory, geometrical models of

inﬁnite size can be represented by the proposed

technique. However, direct storage of the voxels in

the computer memory is not practical and streaming

out of core techniques (Baert et al., 2013) need to be

considered.

Table 1: Octree access time comparison.

Method Access time

Max.

resolution

Octree

(d = 16)

6.43 µs

32768

(327m)

@1cm

Octree

(Hornung

et al., 2013)

(d = 16)

2.55 µs

32768

(327m)

@1cm

Hashed-

Octree

(d = 2)

0.45 µs ∞

5 APPLICATION TO 3D

MODELLING

The ﬁnal goal of the presented research work is the

application of the developed hashed octree techniques

for successive 3D modelling. When a new measure-

ment, a 3D point cloud, becomes available from the

range sensor, the goal is to update the existing 3D

model as fast as possible. Several years ago Curless

and Levoy (Curless and Levoy, 1996) proposed a vol-

umetric update approach, applying the Nadaraya Wat-

Inﬁnite 3D Modelling Volumes

251

son regression technique (Nadaraya, 1964) for suc-

cessive volume updates from streaming range mea-

surements. In contrast to standard surface modelling

techniques with polygons, the surface is represented

by a zero level set. In principle, each voxel contains a

positive or a negative scalar value indicating its loca-

tion inside or outside of an object. Figure 5 outlines

this concept. When a surface is observed by a range

camera, the volumetric model divides the full space

into interior and exterior areas. The goal is further to

assign correct values to the voxels around the surface

in order to approximate the shape as accurate as pos-

sible.

During the reconstruction process each pixel in

the camera image is processed to a 3D point p ∈ R

The ray between the camera centre and the 3D point

is traversed updating the implicit value of each voxel

lying on the ray. In order to increase the computation

speed and to reduce the memory overhead, only vox-

els within a small distance away from p are updated.

Figure 6a shows the updated neighbouring voxels in

red and the sample p as a dark red circle. As men-

tioned before, it is assumed that voxels inside an ob-

ject receive a negative and outside-voxels a positive

scalar value. The distribution of the positive and neg-

ative values is described by a signed distance function

(SDF) in Figure 6b. The goal is ﬁnally to incorporate

the SDF into the voxel model updating existing val-

ues.

As illustrated in Figure 6b), each voxel receives a

Inside

Outside

Figure 5: Implicit shape representation by the zero level set

of voxels.

Support

Camera

sample

SDF and Weight

Inside

Outside

SDF

Weight

r - Distance to sample p

0.0

a) b)

Figure 6: a) Range of inﬂuenced voxels from a 3D sample

p. b) The signed distance function applied and its weight

over the distance away from the sample p.

Camera

Rays to

samples

Plane/Obstacle

Positive

Negative

Reconstructed

plane

a) b)

3D Sample

sample

cone

Camera

c) d)

e) f)

Figure 7: a) Camera faces a wall in a synthetic setup, b) re-

sulting voxel values, c) point cloud from a camera observing

a road, d) the proposed cone fusion concept, e) mesh recon-

struction of the road segment with the standard Curless &

Levoy technique, f) mesh reconstruction with the proposed

cone fusion technique.

weight decreasing with the distance r away from the

sample p. This represents the certainty of the SDF

value f

around p. Given the SDF function values f

and its weight w

, the existing voxels along the ray and

around the sample p are updated following eq. (1).

The new state (k + 1) of the i-th voxel is computed

from its previous weight w

and its previous implicit

value f

also incorporating the novel measurements

and f

k+1

· w

+ f

(r) · w

(r)

+ w

k+1

= w

+ w

(r)

(1)

Where r is representing the distance away from p.

The weights follow the Gaussian distribution

(r) = w

sample

= e

−λr

(2)

where λ is set to λ =

−r

max

ln(0.1)

which gives a weight of

0.1 at the boundaries of the SDF support. Figure 7a

shows a simple synthetic scene, where a range cam-

era faces a wall. A ray is traversed through each cam-

era pixel and its intersection point with the plane is

integrated into the 3D model as a sample. After the

fusion operation (1) is applied, the voxels in front of

the plane receive positive and voxels behind the wall

receive negative values. This is shown in Figure 7b.

Because of the simplicity of this technique, it is being

applied in several 3D modelling frameworks (Nießner

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

252

et al., 2013; Chajdas et al., 2014; Izadi et al., 2011).

However, this technique does not consider the sam-

ple sparsity and scale of the measurement errors. In

cases when a wall is far away from the camera, its

sample distribution is very sparse. In such a case, two

neighbouring pixels in a range camera represent sam-

ples which are far away from each other (see point

cloud in Figure 7c). This leads to holes in a volume

grid and in the reconstructed surface, which are not

recovered by the algorithm (Figure 7e). Thus, con-

sistent 3D modelling of surfaces is not possible when

the standard technique is applied.

In order to prevent this, the technique from Cur-

less and Levoy is extended to cones. The width of the

cone is small close to the camera and large when the

distance is increased (Figure 7d). Furthermore, the

weights w

are extended to

f ull

= w

sample

· w

cone

= e

−λ

(3)

with r

as the distance of the i-th voxel orthogonal

to the ray. Similar to (2) λ

is set to give 0.1 at the

boundary of the cone, which is however not a critical

parameter.

This extension is the main difference of the pre-

sented 3D modelling approach compared to the state

of the art methods. Figures 7e-f show the effect of

cone fusion on 3D samples acquired from a road

surface. While the application of the standard fu-

sion technique is likely to produce holes caused by

sparse samples and noise, the presented approach still

achieves consistent surfaces.

Note, that the recursive nature of the update pro-

cess has a linear time complexity and is not affected

by the size of the 3D model. Moreover, the voxel up-

dates (1) inferred by each sample can be performed in

parallel which further increases the computation efﬁ-

ciency of the technique.

Section 6 discusses the application of the tech-

nique on realistic datasets from a multi view high

resolution UAV-set-up and a mobile stereo system

mounted on a vehicle.

6 EXPERIMENTS

The cone based 3D fusion technique with hashed oc-

trees is demonstrated on two different applications.

In the ﬁrst application a UAV with a high resolution

camera ﬂew around a chapel. The images have been

processed by a multi view software similar to (Wu,

2011). In principle, each image is compared with all

other images and similar point features (SIFT (Lowe,

2004)) are matched. After estimating the trajectory

with a bundle block adjustment (Moulon et al., 2013)

technique, the images have been processed by a multi

view stereo matching algorithm from (Hirschmuller

and Scharstein, 2009). Finally, the obtained depth

images for each camera frame are integrated into a

global 3D model via the proposed 3D fusion tech-

nique. Figure 8 shows one of the acquired camera

images (a) and the resulting 3D model (b). The full

model consists of 167 millions of voxels, which has

been acquired from 450 image frames. The resolu-

tion of the scene was set to 0.1m. Note, that the holes

are caused by occlusions and areas which have not

been observed by the UAV camera during the ﬂight.

These often relates to the ground under the trees, or

the ground in the backyard of the chapel occluded by

the walls.

The second application uses a stereo camera sys-

tem in combination with an inertial measurement unit

(IMU). This enables to obtain the six degrees of free-

dom (6dof) pose of the camera in real time. This set-

up is of particular interest for a wide range of indoor

applications such as inspection, autonomous transport

or logistics. More details about the hardware and

software of the real time localization system can be

found in (Baumbach and Zuev, 2014). Again, the

stereo images are processed to dense disparity images

(Hirschmuller and Scharstein, 2009). The trajectory

provided by the IMU+stereo system and the dispar-

ity images are directly used for 3D fusion. Figure 9

shows a point cloud (a) and the resulting 3D model

(b) when the cone based 3D fusion using the hashed

octree is applied.

The presented results clearly show that the devel-

oped technique is capable of handling large data sets

and to process them to simpliﬁed 3D models in linear

time depending on the number of 3D samples. It has

been observed that the multi view 3D reconstruction

point clouds suffer from less noise and errors than

the real time stereo depth images. The reason is that

when multiple images from a single object are avai-

lable, each pixel in each depth image contains multi-

ple depth hypotheses. This enables the optimization

of the depth consistency and to increase the overall

3D reconstruction quality dramatically. As for the

stereo data, the standard 3D fusion technique (Cur-

less and Levoy, 1996) lead to a high number of holes

and artefacts in the ﬁnal model. Only the cone fusion

approach achieved smooth and consistent surfaces.

When the standard 3D fusion technique from

(Curless and Levoy, 1996) is applied, the algorithm

achieves a runtime performance of 500ms for a single

VGA (640 × 480) depth image on a standard desk-

top PC with 16 cores. After extending the algorithm

Inﬁnite 3D Modelling Volumes

253

a) b)

Figure 8: a) Obtained 3D model from UAV at 1cm resolu-

tion, c) enlarged view on the chapel tower.

to the cone fusion approach, the support width of the

SDF depends on the distance between the camera and

centre and p. This increases the runtime by about

20%. The worst case run time (in seconds) for a sin-

gle frame via cone fusion can be estimated a priori

via

f rame

res

· p

sup

· r

sup

·t

(4)

with n

res

as the resolution of the image (e.g. 640 ×

480 = 307200 = n

res

), p

sup

is the width of the support

around a sample (see w

sample

Fig. 7d), and r

sup

as the

maximal width of the cone in voxels (Fig. 7d). The

value t

= 0.45 · 10

−6

represents the time required to

access a single voxel in the database as shown in Table

Compared to the recently proposed GPU driven

3D fusion technique from Niessner (Nießner et al.,

2013), the runtime performance is signiﬁcantly lower.

Niessner reported processing times around 15ms,

which is possible when the data is cached in the in-

ternal GPU memory. In contrast to this, our method

focuses on multi-threading and distributed computing

which enables to obtain 3D models even when low

power and low cost sensors are set-up on vehicles and

the raw data is sent to a cloud computer. This strategy

enables to develop a server-client architecture where

the autonomous vehicles communicate with a central

server and update the local environment map from a

single consistent source.

a) b)

Figure 9: a) Point cloud from stereo, b) modelled surface of

the road.

7 CONCLUSION AND OUTLOOK

A highly efﬁcient data structure for voxel based 3D

geometry has been presented. The approach enables

to model arbitrary geometries and to modify them dy-

namically, for instance when new 3D measurements

become available from a mobile robot. The technique

is fundamental to all long time operating robotic sys-

tems which are expected to interact with an unknown

environment.

An advanced 3D modelling technique has been

presented and applied on the 3D voxel database. The

application enables very large environments to be

modelled and to create high resolution maps.

Future research will focus on the integration of

loop-closing localization algorithms. Another aspect

of future developments will cover the extension of the

presented framework to a cloud computing architec-

ture. Low level communication with sensors, con-

sistent global mapping and client based visualization

will be targeted. The mid term goal of the project is an

ubiquitous framework focusing on 3D object detec-

tion, 3D mapping and visualization of huge 3D scene.

REFERENCES

Andreasson, H., Bouguerra, A., Cirillo, M., Dimitrov, D.,

Driankov, D., Karlsson, L., Lilienthal, A., Pecora, F.,

Saarinen, J., Sherikov, A., and Stoyanov, T. (2015).

Autonomous transport vehicles: Where we are and

what is missing. Robotics Automation Magazine,

IEEE, 22(1):64–75.

Baert, J., Lagae, A., and Dutr

e, P. (2013). Out-of-core con-

struction of sparse voxel octrees. In Proceedings of

the 5th High-Performance Graphics Conference, HPG

’13, pages 27–32, New York, NY, USA. ACM.

Baumbach, D. G. D. and Zuev, S. (2014). Stereo-Vision-

Aided Inertial Navigation for Unknown Indoor and

Outdoor Environments. In Proceedings of the Interna-

tional Conference on Indoor Positioning and Indoor

Navigation (IPIN), 2014 . IEEE.

Bekris, K., Shome, R., Krontiris, A., and Dobson, A.

(2015). Cloud automation: Precomputing roadmaps

for ﬂexible manipulation. Robotics Automation Mag-

azine, IEEE, 22(2):41–50.

Chajdas, M. G., Reitinger, M., and Westermann, R. (2014).

Scalable rendering for very large meshes. WSCG

2014, International Conference on Computer Graph-

ics.

Curless, B. and Levoy, M. (1996). A volumetric method for

building complex models from range images. In Pro-

ceedings of the 23rd Annual Conference on Computer

Graphics and Interactive Techniques, SIGGRAPH

’96, pages 303–312, New York, NY, USA. ACM.

EUC (2015). FP7-Transport, Research supported by the

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

254

European Commission. http://bit.ly/1btLACw. Ac-

cessed: 2015-09-22.

Floater, M. S. and Hormann, K. (2005). Surface parame-

terization: a tutorial and survey. In Dodgson, N. A.,

Floater, M. S., and Sabin, M. A., editors, Advances

in Multiresolution for Geometric Modelling, Mathe-

matics and Visualization, pages 157–186. Springer,

Berlin, Heidelberg.

Frisken, S. F., Perry, R. N., Rockwood, A. P., and Jones,

T. R. (2000). Adaptively sampled distance ﬁelds: A

general representation of shape for computer graph-

ics. In Proceedings of the 27th Annual COnference

on Computer Graphics and Interactive Tehniques,

pages 249–254. ACM PRess/Addison-Wesley Pub-

lishing Co.

Google inc. (2015). Google sparse hash, ver1.5.

http://goog-sparsehash.sourceforge.net/. Accessed:

2014-09-26.

Hirschmuller, H. and Scharstein, D. (2009). Evaluation of

stereo matching costs on images with radiometric dif-

ferences. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 31(9):1582–1599.

Hornung, A., Wurm, K. M., Bennewitz, M., Stachiss, C.,

and Burgard, W. (2013). OctoMap: An efﬁcient prob-

abilistic 3D mapping framework based on octrees. Au-

tonomous Robots.

Izadi, S., Kim, D., Hilliges, O., Molyneaux, D., Newcombe,

R., Kohli, P., Shotton, J., Hodges, S., Freeman, D.,

Davison, A., and Fitzgibbon, A. (2011). Kinectfu-

sion: Real-time 3d reconstruction and interaction us-

ing a moving depth camera. In ACM Symposium on

User Interface Software and Technology. ACM.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. Int. J. Comput. Vision, 60(2):91–

110.

Moulon, P., Monasse, P., and Marlet, R. (2013). Global fu-

sion of relative motions for robust, accurate and scal-

able structure from motion. In The IEEE International

Conference on Computer Vision (ICCV).

Nadaraya, E. A. (1964). On estimating regression. Theory

of Probability & Its Applications, 9(1):141–142.

Nießner, M., Zollh

ofer, M., Izadi, S., and Stamminger,

M. (2013). Real-time 3d reconstruction at scale us-

ing voxel hashing. ACM Transactions on Graphics

(TOG).

Teschner, M., Heidelberger, B., Mueller, M., Pomeranets,

D., and Gross, M. (2003). Optimized spatial hashing

for collision detection of deformable objects. Pro-

ceedings of Vision, Modeling, Visualization (VMV

2003), pages 47–54.

Wu, C. (2011). Visualsfm: A visual structure from motion

system. http://ccwu.me/vsfm/. Accessed: 2015-08-

30.

Inﬁnite 3D Modelling Volumes

255