Parameter Estimation for HOSVD-based Approximation of Temporally

Coherent Mesh Sequences

Michał Romaszewski and Przemysław Głomb

Institute of Theoretical and Applied Informatics, Polish Academy of Sciences, Bałtycka 5, 44-100, Gliwice, Poland

Keywords:

3D Animation, Compression, TCMS, HOSVD, Decomposition, Approximation.

Abstract:

This paper is focused on the problem of parameter selection for approximation of animated 3D meshes (Tem-

porally Coherent Mesh Sequences, TCMS) using Higher Order Singular Value Decomposition (HOSVD). The

main application of this approximation is data compression. Traditionally, the approximation was done using

matrix decomposition, but recently proposed tensor methods (e.g. HOSVD) promise to be more effective.

However, the parameter selection for tensor-based methods is more complex and difﬁcult than for matrix de-

composition. We focus on the key parameter, the value of N-rank, which has major impact on data reduction

rate and approximation error. We present the effect of N-rank choice on approximation performance in the

form of rate-distortion curve. We show how to quickly create this curve by estimating the reconstruction error

resulting from the N-rank approximation of TCMS data. We also inspect the reliability of created estima-

tor. Application of proposed method improves performance of practical application of HOSVD for TCMS

approximation.

1 INTRODUCTION

Three-dimensional meshes are one of the most com-

mon representations of a virtual surface with applica-

tions in computer simulations, entertainment, medical

imaging and digital heritage documentation. Com-

plexity of processing, visualization and storage of

modelled objects resulted in the rapid development

of methods for mesh compression, as summarised in

(Maglo et al., 2015).

Particularly interesting group of methods is re-

lated to compression of temporally coherent mesh se-

quences (TCMS), also called dynamic animations or

animated meshes, well deﬁned in (Arcila et al., 2013).

TCMS is a sequence of meshes ordered in time, with

a constant number of vertices, connectivity and topol-

ogy. One particularly successful approach to TCMS

compression employs Principal Component Analysis

(PCA). The general idea was presented in (Alexa and

Muller, 2000). The animation was converted to a ma-

trix by stacking meshes frame-by-frame. Authors rep-

resented each frame of the animation as a linear com-

bination of principal components, obtained through

decomposition of the animation matrix. Such repre-

sentation allows to transmit only a limited number of

ﬁrst principal components and efﬁciently reconstruct

the original sequence with limited distortion. Further

works reﬁned this idea, e.g. the COBRA algorithm

described in (V

sa and Skala, 2009) reaches compres-

sion ratio between 0.5 and 5 bit per frame per ver-

tex (bpfv) for a KG error (a measure commonly used

to compare TCMS compression algorithms and de-

scribed in (Karni and Gotsman, 2004)) of 0.05%.

As an alternative to matrix approximation, TCMS

data can be expressed in the form of a mode-3 ten-

sor T and tensor decomposition may be employed.

One particularly suitable method is the Higher Order

Singular Value Decomposition (HOSVD), described

in detail in (Kolda and Bader, 2009). Its recent ap-

plication to data compression was presented e.g. in

(Ballester-Ripoll and Pajarola, 2015).

HOSVD transforms the mode-3 TCMS tensor T

into the Tucker operator (TO). The TO consist of the

core tensor C and three orthogonal factor matrices.

The key property of this representation is the approxi-

mation. The energy of the core tensor is concentrated

in the frontal-upper-left corner so large magnitudes

correspond to its low indices. The TO can be trun-

cated by zeroing the low-index elements, forming a

truncated Tucker operator (TTO). Original data can

be reconstructed from the TTO with the reconstruc-

tion error expressed in the form of tensor Frobenius

norm as ||T −T

||.

When applied to TCMS data, HOSVD may al-

140

Romaszewski, M. and Głomb, P.

Parameter Estimation for HOSVD-based Approximation of Temporally Coherent Mesh Sequences.

DOI: 10.5220/0005723501380145

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 140-147

ISBN: 978-989-758-175-5

low to reach higher data reduction ratio with lower

distortion than PCA, as presented in (Romaszewski

et al., 2013), where authors compare HOSVD and

PCA applied to lossy reconstruction of TCMS se-

quences. They present the performance of these meth-

ods in terms of data size and reconstruction error for

a set of well-known, representative sequences.

The main challenge, hovewer, when applying

HOSVD for TCMS compression lies in ﬁnding the

N-rank value to minimize the TTO size with an ac-

ceptable reconstruction error. Usually (e.g. in (Ro-

maszewski et al., 2013)) this is done by searching

through the parameter space. Since the reconstruc-

tion of T from TTO is computationally expensive, the

questions arise: how to estimate the reconstruction er-

ror associated with the speciﬁc N-rank, how to ﬁnd its

optimal value and how reliable is such estimation for

TCMS data?

This paper concentrates on the problem of N-

rank estimation for approximating TCMS data with

HOSVD. The distortion resulting from approximation

is expressed in the form of KG error, commonly used

to compare TCMS compression methods. We show

how to use the estimator to graphically represent the

effect of HOSVD reconstruction in the form of a rate-

distortion curve. We also discuss the estimation relia-

bility using a set of well-known TCMS samples.

The article is organised as follows. The introduc-

tion and related work are presented in Section 1. Def-

initions and methodology are presented in Section 2.

Results are presented in Section 3, while conclusions

can be found in Section 4.

2 METHODOLOGY

Our goal is to estimate the error associated with the N-

rank approximation of the TCMS tensor T using the

HOSVD algorithm. We use this estimation to form

the rate-distortion curve based on N-rank TTO trun-

cation.

2.1 Input Data

Our input data is the temporally coherent mesh se-

quence (TCMS), described in detail in (Arcila et al.,

2013). Such sequence consists of meshes with con-

stant connectivity and varying positions of vertices

in time. We consider only the vertex position data,

since it has the most signiﬁcant impact on animation

volume. Animation vertices can be represented as a

sequence of F matrices M

∈ R

K×J

. The rows of

are positions of mesh vertices v

∈ R

, 0 ≤ i < K.

These matrices can form a tensor T = t

i, j,k

∈ R

K,J,F

by stacking M

as frontal slices T

::k

, using the nota-

tion from (Kolda and Bader, 2009). In our experi-

ments vertex features are the standard euclidean coor-

dinates only, therefore J = 3.

2.2 Higher Order Singular Value

Decomposition

Higher Order Singular Value Decomposition is a gen-

eralisation of SVD from matrices to tensors. Based

on description provided in (Romaszewski et al., 2013)

and following the conventions presented in (Kolda

and Bader, 2009), HOSVD can be explained in the

following way:

A tensor

T = {t

,...,i

}

−1,I

−1,...,I

−1

,...,i

∈ R

,...,I

(1)

has N modes. Each of the indices corresponds to one

of the modes i.e. i

to mode l.

By multiplication of tensor T by matrix U =

}

−1,D

,d=0

∈ R

in mode l we deﬁne tensor T

∈

,...,I

l−1

,D,I

l+1

,...,I

, such that:

= (T ×

...i

l−1

d i

l+1

...i

−1

∑

...i

(2)

By unfolding tensor T in mode l we deﬁne matrix

(l)

such that

(l)

)

i, j

= t

...i

l−1

j i

l+1

...i

, (3)

where i = 1 +

∑

k=1

l6=l

− 1)J

and J

∏

k−1

m=1

m6=l

Given tensor T , deﬁned as in Eq. (1), a new sub-

tensor T

=α

can be created according to the equation

with the following elements:

=α

= {t

...i

l−1

l+1

...i

}

−1,I

−1,...,α,...,I

−1

=0,i

=0,...,i

=α,...,i

(4)

where

=α

∈ R

,...,1,...,I

. (5)

The scalar product hA,Bi of tensors A, B ∈

,...,I

is deﬁned as

hA, Bi =

−1

∑

−1

∑

. . .

−1

∑

,...,i

. (6)

We say that if scalar product of tensors equals zero,

then they are orthogonal.

The Frobenius norm of tensor T is given by

||T || =

hT , T i.

Given tensor T , in order to ﬁnd its HOSVD,

in the form of the so called Tucker operator

JC ;U

(1)

, . . . , U

(N)

K, such that C ∈ R

,...,I

and U

(k)

∈

are orthogonal matrices, Algorithm 1 can be

used.

Parameter Estimation for HOSVD-based Approximation of Temporally Coherent Mesh Sequences

141

Tensor C is called the core tensor and has the fol-

lowing useful properties. Reconstruction: T = C ×

(1)

(2)

. . . ×

(N)

, where U

(i)

are orthogo-

nal matrices. Orthogonality: hC

=α

, C

=β

i = 0 for all

possible values of l, α and β, such that α 6= β. Or-

der of sub-tensor norms: ||C

|| ≤ ||C

|| ≤ . . . ≤

||C

|| for all n.

Input: Data Tensor T

Output: Tucker operator JC; U

(1)

, . . . , U

(N)

for k ∈ {1, . . . , N} do

(k)

left singular vectors of T

(k)

in unfolding k;

end

C = T ×

(1)T

. . . ×

(N)T

;

return JC; U

(1)

, . . . , U

(N)

Algorithm 1: HOSVD algorithm uset to ﬁnd the

Tucker operator from the tensor T .

Therefore, informally, one can say that larger

magnitudes of a core tensor are denoted by low values

of indices. To explain the HOSVD approximation we

will deﬁne the tensor

T =

C ×

(1)

(2)

. . . ×

(N)

, (7)

where

C = {c

,...,i

}

−1,R

−1,...,R

−1

,...,i

∈ R

,...,R

(8)

is a truncated tensor in such a way that in each mode l

indices span from 0 to R

−1 ≤ I

−1 and

(l)

∈ R

matrices whose columns are orthonormal and rows

form orthonormal basis in respective vector spaces.

Given (R

)

l=1

we say that

T approximates T in the

sense of their euclidean distance ||

T − T ||.

2.3 Estimation of Reconstruction Error

One way of ﬁnding the optimal (given the error

threshold) N-rank value for the data tensor T , is to

perform multiple reconstructions of T from TTO. Un-

fortunately, such search is time consuming. It could

be, however, avoided with a reliable estimator of the

N-rank reconstruction error. Our task is therefore to

deﬁne the reconstruction error metric, to ﬁnd an esti-

mator, and to assess its reliability.

2.3.1 The Metric for Reconstruction Error

We argue that the most useful error metrics for the

TCMS reconstruction estimator would be the distor-

tion measure used to compare TCMS compression al-

gorithms, namely the KG error. The KG error was

deﬁned in (Karni and Gotsman, 2004) to express the

distortion of TCMS compression based on PCA. Its

beneﬁt is that it allows to compare the distortion in-

troduced by HOSVD-based approximation with the

ﬁnal results of state-of-art TCMS compression algo-

rithms. It should be noted, however, that KG error

does not correlate well with perceptual distortion of

animations and its shortcomings were noted e.g. in

sa and Skala, 2009). Since the KG error was origi-

nally deﬁned using matrix operations, we will express

it using the tensor notation in the following way:

Given tensor T = t

i, j,k

∈ R

K,J,F

we deﬁne the

average trajectory tensor E(T ) = e

i, j,k

∈ R

K,J,F

which each mode-3 (tube) ﬁber is substituted by an

average mode-3 ﬁber of T , so e

i jk

= avg

1<k

≤F

i jk

This allows us to express the KG error as

(T ,

T ) = 100

||T −

T ||

||T −E(T )||

. (9)

2.3.2 The Estimation of the N-rank

Reconstruction Error

An estimator for the upper bound of HOSVD recon-

struction error may be found in (De Lathauwer et al.,

2000). It is expressed in the form of the following

property.

Let the HOSVD of T be given and let ranks of T

in unfolding T

(n)

be equal to R

(1 ≤ n ≤ N). Deﬁne

a tensor

T by discarding the smallest singular values

(n)

, σ

(n)

, . . . , σ

(n)

for given values of I

(1 ≤ n ≤

N) in unfolding T

(n)

, i.e., set the rest of them to zero.

Then we have

||T −

T ||

≤ E(I

+ 1, .., I

+ 1). (10)

where

E(I

, .., I

) =

∑

(1)

+. . . +

∑

(N)

. (11)

The nature of this estimation allows us to con-

clude two useful properties of HOSVD reconstruc-

tion. Firstly, the upper bound of reconstruction error

is no higher than the sum of errors resulting from each

(n)

unfolding truncation. This means that we can

treat the truncation of each mode separately for the

purpose of reconstruction parameter selection. Sec-

ondly, the error is proportional to the sum of squared

singular values discarded from T

(n)

decomposition.

Therefore the value of error will rapidly decrease for

small number of ﬁrst components.

Based on equations (9) and (10), we can estimate

the upper bound of the KG error for the N-rank recon-

struction of T as:

(est)

(T ,

T ) = 100

E(I

+ 1, .., I

+ 1)

||T −E(T )||

. (12)

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

142

where e

(T ,

T ) ≤ e

(est)

(T ,

T ).

If we further assume that the estimation of error

with Eq. (10) is saturated for TCMS data, i.e. it’s

close to the actual reconstruction error, we can use

this estimation to ﬁnd the optimal N-rank.

In order to test this estimation reliability we will

deﬁne the relative estimator error as

ψ(T ,

T ) =

(T ,

T ) − e

(est)

(T ,

T )|

(T ,

T )

. (13)

2.3.3 The Choice of Reconstruction Parameters

Input: The rate array R and the corresponding

distortion array D.

Output: Sequence of distortions d

and

corresponding reduction rates r

d = vec(D);

r = vec(R);

i = argsort d in ascending order;

sort d, r with i;

= [];

for i ∈ {1, . . . , length(d)} do

if is empty r

or r

[i] < r

[i − 1] then

append d[i] to d

;

append r[i] to r

;

end

return (d

, r

)

Algorithm 2: The algorithm to create the rate-

distortion curve by computing the sequence of re-

construction errors d

and corresponding reduction

rates r

The choice of the N-rank value that minimizes the

TTO size while also minimizing the reconstruction er-

ror is not obvious. Desired values depend on the spe-

ciﬁc application of the algorithm. Their mutual rela-

tion may be presented graphically in the form of the

rate-distortion curve in the following way:

The TCMS tensor T = t

i, j,k

∈ R

K,J,F

can be ap-

proximated by the N-rank tensor

T with the error

(T ,

T ). The e

(T ,

T ) value can be estimated

from the Eq. (12). The N-rank is a reconstruction pa-

rameter denoted rank

(T ) = (R

, R

). The num-

ber of possible N-ranks of T is R

× R

. How-

ever, the second mode of the TCMS tensor is short

since J = 3 and the mode-2 truncation introduces

huge distortion into the approximation. Therefore,

we only consider the truncation of mode-1 and mode-

3 components. We denote the N-rank reconstructed

tensor

such that rank

(

) = (i, 3, k).

The number of ﬂoats required to store the

equals S(

) = i × K + 9 + k × F + i × 3 × k. The

data reduction rate resulting from using

can be ex-

pressed as

Θ(

) =

)

K × J × F

. (14)

We will deﬁne a rate array as R = {a

} where

= Θ(

) and a corresponding distortion array D =

} such that b

= e

(T ,

i j

). This allows us to

deﬁne a sequence of all pairs RD = ([a

, b

]) where

∈ R, b

∈ D, and the [a

, b

] pairs are ordered

such that ∀

m−1

< a

and ∀

, b

m−1

> b

. To obtain

this sequence we use the simple algorithm presented

as Alg. (2). The graphical representation of this se-

quence is the rate-distortion curve of T .

2.4 Principal Component Analysis

As a reference for approximation of TCMS data with

HOSVD, we use the Principal Component Analy-

sis described e.g. in (Jolliffe, 2005). We follow

the methodology described in (Romaszewski et al.,

2013). In order to apply the PCA, tensor T = t

i, j,k

∈

K,J,F

is unfolded according to Eq. (3). We consider

a mode-3 (frame) unfolding wchich forms the matrix

X ∈ R

F,J×K

3 EXPERIMENT RESULTS

The goal of our experiments is to assess the reliability

of error estimation for N-rank HOSVD reconstruction

of TCMS.

3.1 Implementation Setup

We apply the HOSVD algorithm presented as Alg.

(1) to samples of TCMS data. Than, for all pos-

sible N-rank values we reconstruct

and compute

(T ,

) using the Eq. (9). We also estimate N-

rank reconstruction error using the Eq. (12). We

compute the estimator error as ψ(T ,

) using the

Eq. (13). We present the relation between the re-

construction and estimation errors in the form of a

rate-distortion curve. Results are presented using four

standard TCMS sequences. The chicken is an arti-

ﬁcial animation of a running cartoon character, pub-

lished by Jed Lengyel

. Crane, samba and march are

motion capture sequences published by Daniel Vla-

sic

http://jedwork.com/jed

http://people.csail.mit.edu/drdaniel/mesh animation

Parameter Estimation for HOSVD-based Approximation of Temporally Coherent Mesh Sequences

143

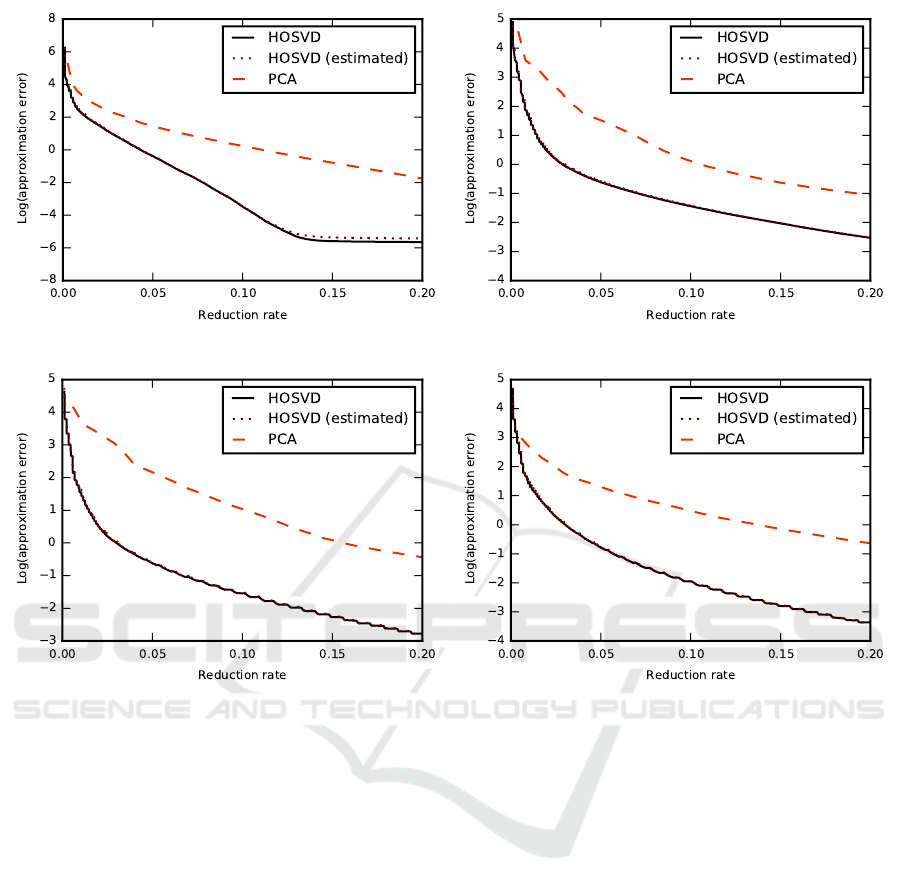
(a) (b)

Figure 1: Rate-distortion curves for animations: chicken (a), march (b), crane (c), samba (d). The horisontal axis represents

the reduction rate Θ(

) and the vertical axis is the logarithm of reconstruction error e

(T ,

T ). Plots present actual and

estimated error values for HOSVD. Error values for PCA are provided for reference. The difference between the estimated

and actual values of approximation error for HOSVD are very small.

3.2 Results

The reconstruction error introduced by HOSVD ap-

proximation of TCMS data is presented in Fig. 3.

Each pixel in panels (a), (c) and (e) represents the N-

rank reconstruction while axes show the number of

mode-1 and mode-3 components. The error is mono-

tonic and it drops sharply from the highest value in the

lower-left corner (reconstruction from only one com-

ponent in both modes) to the low error value in the

upper-right corner. The perceptual distortion of re-

constructed animation becomes very small for ∼ 50

mode-1 and mode-3 components which corresponds

to values lying above and on the right from the isoline

zero.

Panels (b), (d) and (f) in Fig. 3 represent the corre-

sponding values of the estimation error ψ(T ,

). We

can imminently see that ψ(T ,

) values are small.

That means that the error estimation obtained using

Eq. (12) is close to its actual value. However, it is

apparent that the estimation is more accurate for large

error values in the upper-left and lower-right corners,

separated with the isoline (−8). At the same time

an obvious strategy for optimal N-rank choice are the

values close to the diagonal line connecting the lower-

left and upper-right corners of the array. These param-

eters results in low reconstruction error but are also

less accurately estimated. Nevertheless, for parame-

ters representing the perceptually acceptable TCMS

approximation, the estimation is accurate enough that

there is no difference in the parameter choice based

on estimated or accurate error values.

The rate-distortion curves for actual and estimated

values of HOSVD approximation error are presented

in Fig. 1. PCA approximation error is provided for

reference. The perceptual distortion of the animation

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

144

(a) (b)

Figure 2: Estimation error for animations: chicken (a), march (b), crane (c), samba (d). The horisontal axis represents the

reduction rate Θ(

) and the vertical axis is the logarithm of estimation error ψ(T ,

). Each error bar represents the median,

lower and upper quantile as well as error range in one of ten non-overlaping windows of equal length. Values on the horizontal

axis are in the middle of a corresponding window.

becomes acceptable for reduction rate ∼ 5% original

data size, and almost indistinguishable when the re-

duction rate is ∼ 10% of the original size.

Fig. 2 is the visualization of estimation error for

our animations. Each error bar represents the median,

lower and upper quantile and error range in the ten

non-overlaping horizontal windows. As we can see

the estimation is more precise for high reduction rate,

but with signiﬁcant variance. This is more visible

for artiﬁcial chicken sequence than for motion-capture

animations. This effect results mostly from the im-

proper estimation for very low N-rank values located

in the lower-left corner of the parameter array. On the

other hand, for lower reduction rate the estimator is

less precise but with a low variance.

4 CONCLUSIONS

We have shown how to estimate the N-rank HOSVD

reconstruction error for TCMS data. We argue that for

representative sequences the estimator is saturated.

That means that the estimated distortion is very close

to its actual value and can aid in selection of approx-

imation parameters. Expressing the distortion result-

ing from approximation of T in the form of KG error

is useful during the creation of HOSVD-based TCMS

compression algorithms.

ACKNOWLEDGEMENTS

This work has been partially supported by the

project ‘Representation of dynamic 3D scenes

Parameter Estimation for HOSVD-based Approximation of Temporally Coherent Mesh Sequences

145

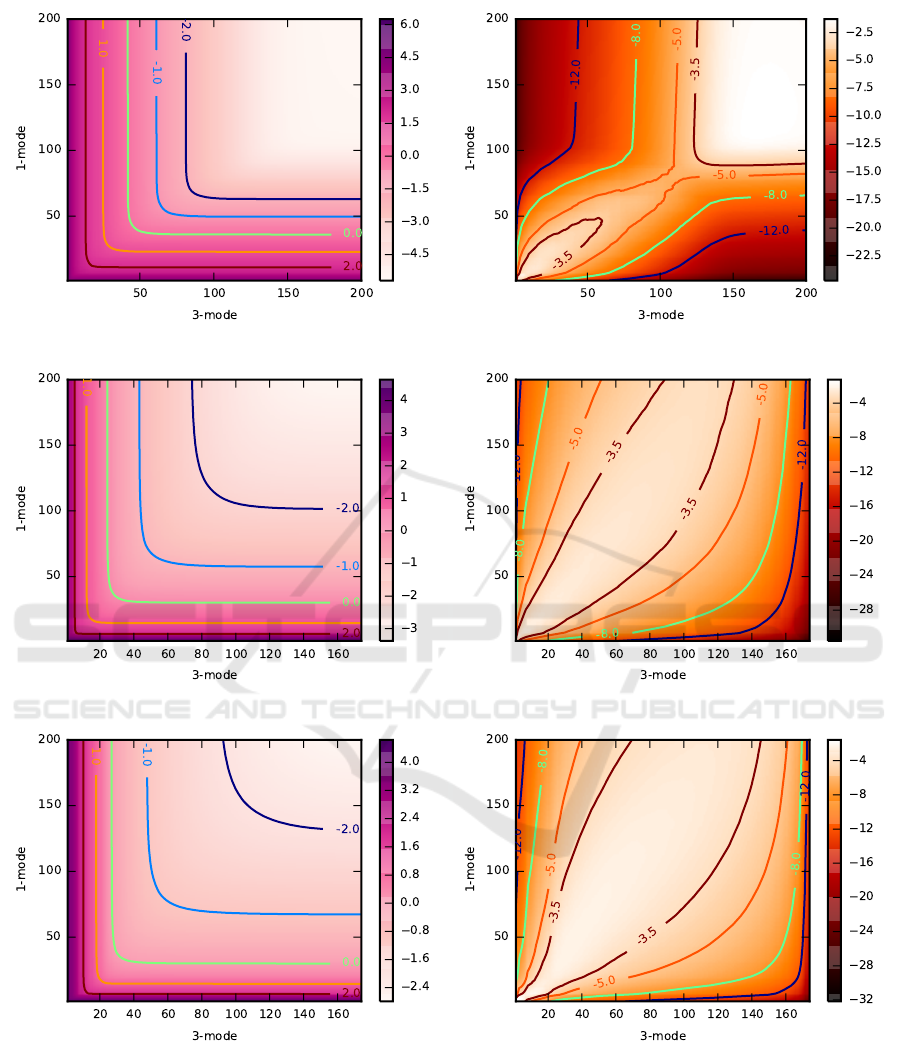
(a) (b)

(e) (f)

Figure 3: Reconstruction and estimation errors for three animations: chicken (the upper row), crane (the middle row), samba

(the lower row). Pixels in arrays (a),(c) and (e) represent the logarithm of e

(T ,

) as a function of the number of mode-1

and mode-3 components used for reconstruction. Arrays (b),(d) and (f) present the corresponding estimation errors ψ(T ,

)

deﬁned by Eq. (13).

using the Atomic Shapes Network model’ ﬁ-

nanced by National Science Centre, decision DEC-

2011/03/D/ST6/03753. We would like to thank our

reviewers for their insightful comments. We would

also like to thank P. Gawron for fruitful discussions.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

146

REFERENCES

Alexa, M. and Muller, W. (2000). Representing animations

by principal components. In Computer Graphics Fo-

rum, volume 19, pages 411–418. Citeseer.

Arcila, R., Cagniart, C., H

etroy, F., Boyer, E., and Dupont,

F. (2013). Segmentation of temporal mesh sequences

into rigidly moving components. Graphical Models,

75(1):10–22.

Ballester-Ripoll, R. and Pajarola, R. (2015). Lossy volume

compression using tucker truncation and thresholding.

The Visual Computer, pages 1–14.

De Lathauwer, L., De Moor, B., and Vandewalle, J.

(2000). A multilinear singular value decomposition.

SIAM journal on Matrix Analysis and Applications,

21(4):1253–1278.

Jolliffe, I. (2005). Principal component analysis. Wiley

Online Library.

Karni, Z. and Gotsman, C. (2004). Compression of soft-

body animation sequences. Computers & Graphics,

28(1):25–34.

Kolda, T. G. and Bader, B. W. (2009). Tensor Decomposi-

tions and Applications. SIAM Review, 51(3):455–500.

Maglo, A., Lavou

e, G., Dupont, F., and Hudelot, C. (2015).

3d mesh compression: Survey, comparisons, and

emerging trends. ACM Computing Surveys (CSUR),

47(3):44.

Romaszewski, M., Gawron, P., and Opozda, S. (2013). Di-

mensionality reduction of dynamic mesh animations

using ho-svd. Journal of Artiﬁcial Intelligence and

Soft Computing Research, 3(4):277–289.

sa, L. and Skala, V. (2009). Cobra: Compression of the

basis for pca represented animations. In Computer

Graphics Forum, volume 28, pages 1529–1540. Wi-

ley Online Library.

Parameter Estimation for HOSVD-based Approximation of Temporally Coherent Mesh Sequences

147