Enhanced Depth Estimation using a Combination of Structured Light

Sensing and Stereo Reconstruction

Andreas Wittmann

, Anas Al-Nuaimi

, Eckehard Steinbach

and Georg Schroth

Chair of Media Technology, Technische Universitt Mnchen, Arcisstrae 21, Munich, Germany

NavVis GmbH, Blutenburgstrae 18, Munich, Germany

Keywords:

Stereo Vision, Google Project Tango, Structured Light, 3D Scanning.

Abstract:

We present a novel approach for depth sensing that combines structured light scanning and stereo reconstruc-

tion. High-resolution disparity maps are derived in an iterative upsampling process that jointly optimizes

measurements from graph cuts-based stereo reconstruction and structured light sensing using an accelerated

α-expansion algorithm. Different from previously proposed fusion approaches, the disparity estimation is

initialized using the low-resolution structured light prior. This results in a dense disparity map that can be

computed very efﬁciently and which serves as an improved prior for subsequent iterations at higher resolu-

tions. The advantages of the proposed fusion approach over the sole use of stereo are threefold. First, for

pixels that exhibit prior knowledge from structured lighting, a reduction of the disparity search range to the

uncertainty interval of the prior allows for a signiﬁcant reduction of ambiguities. Second, the resulting limited

search range greatly reduces the runtime of the algorithm. Third, the structured light prior enables a dynamic

tuning of the smoothness constraint to allow for a better depth estimation for inclined surfaces.

1 INTRODUCTION

In recent years research and applications in 3D vi-

sion have been experiencing strong growth driven by

the increasing availability of low-cost hardware that

can sense the environment in 3D. Critical to these ad-

vancements was the release of the Microsoft Kinect

in 2010 which is the ﬁrst consumer device that can

reliably sense its immediate vicinity in 3D and in

real time using the structured light (SL) sensing tech-

nique.

Other recent trends, including the proliferation of

smart portable devices, which are equipped with pow-

erful processors and a plethora of sensors, have called

upon the deployment of 3D sensors to enable new

applications including Augmented Reality. Indeed,

Google launched the ﬁrst smartphone with an active

3D sensor, similar to that of the Kinect, named Project

Tango device (Piszczor and Yang, 2014). Other

companies, such as Occipital (Occipital, 2015), of-

fer smartphone attachable 3D sensors which use the

same sensing principle.

The deployment of such 3D sensors in portable

devices is signiﬁcant but their impact may be lim-

ited by the characteristic limitations inherent to the

used sensing technique. Most notably, SL-based 3D

sensing has a relatively limited range of a few meters.

Critically, 3D sensing fails on glossy surfaces, edges,

ﬁne structures and elements that are illuminated by

bright light owing to the infrared-based depth percep-

tion. The latter also severely degrades the usability

outdoors.

Unlike depth from SL, 3D reconstruction from

stereo can provide 3D data for larger distances, ﬁne

structures as well as outdoor scenes. Contrary to

SL techniques, it beneﬁts from bright illumination

and sharp object boundaries. However, local stereo

matching requires well-textured surfaces, something

SL-based 3D scanning does not depend on. Also,

global stereo reconstruction algorithms are often slow

and depend on the structure of the underlying scene,

which forbids its sole use for applications that require

a consistent performance.

The complimentary nature of depth from stereo

and depth from SL, as further demonstrated by a real

example in Section 3, motivated us to develop a joint

depth estimation algorithm that uses image and 3D

data acquired on a smartphone prototype to generate

enhanced depth images. It builds upon the strengths

of both sensing techniques while compensating for

their shortcomings. For this purpose, we utilized the

Google Project Tango device, henceforth also termed

“smartphone”.

512

Wittmann, A., Al-Nuaimi, A., Steinbach, E. and Schroth, G.

Enhanced Depth Estimation using a Combination of Structured Light Sensing and Stereo Reconstruction.

DOI: 10.5220/0005724605100521

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 512-523

ISBN: 978-989-758-175-5

To achieve our goal we combine a graph cuts-

based state-of-the-art stereo algorithm (Kolmogorov

et al., 2014) with the depth maps captured by the SL

sensor of the smartphone. To that end we redesigned a

global energy function typically used in stereo imag-

ing to incorporate the SL sensor data while consid-

ering its error characteristics as explained in Sec-

tion 4.1. Beyond solving for depth values using a

joint energy function, the algorithm utilizes the smart-

phones’s active range measurements to limit the dis-

parity label space for the stereo algorithm, resulting in

a substantially faster convergence (see Section 5). In

Section 4.2 we explain how this technique, which ex-

ploits depth priors from the smartphone, is applied in

an iterative process involving sequential upsampling

and stereo reconstruction to produce higher resolution

depth maps. The results in Section 5 demonstrate the

gains achievable with our proposed fusion scheme.

Prior to the detailed explanations of the contributions,

we give background information in 3D sensing and

survey related work on stereo-range data fusion in

Section 2. Also, the Project Tango device is brieﬂy

presented in the same section.

2 RELATED WORK &

BACKGROUND

3D sensors can be broadly categorized into passive

and active sensors. The former rely on the ambient

lighting of the environment while the latter project

(visible or invisible) patterns or beams of light to

sense the environemt. Passive and active 3D sensors

are introduced in Section 2.1 and Section 2.2, respec-

tively. In Section 2.4 the Project Tango device, which

we simultaneously use for active and passive 3D sens-

ing, is brieﬂy introduced. In Section 2.3 we survey re-

lated work on enhanced depth estimation with active

and passive 3D sensors.

2.1 Passive 3D Sensing

Standard passive 3D sensing involves capturing the

scene from multiple perspectives and using visual cor-

respondences to infer the 3D shape. There exists

a variety of approaches including multi-view stereo

(MVS) and structure-from-motion (SfM), that take

two or more images to reconstruct a 3D scene. A spe-

cial case is two-view stereo that only considers a pair

of images to derive the depth in a scene.

The aforementioned approaches either utilize sev-

eral cameras, or as in case of SfM, a single mov-

ing camera. Seitz et al. (Seitz et al., 2006) com-

pare different multi-view approaches which are typ-

ically slow and are generally applied in ofﬂine pro-

cessing. However, real-time capable SfM algorithms

such as Dense Tracking and Mapping (DTAM) (New-

combe et al., 2011) and Large-Scale Direct Monocu-

lar SLAM (LSD-SLAM) (Engel et al., 2014), which

both employ GPU computing to signiﬁcantly speed

up processing, exist. Nevertheless, SfM-based multi-

view methods suffer from drift and an inherent scale

ambiguity that does not allow us to restore the true

scale of a scene. Multi-view stereo reconstruction

typically allows for a true scale representation of a

scene by utilizing a setup that involves multiple cam-

eras with rigid transformations among the individual

camera frames. Obviously, reconstruction via MVS

requires extensive efforts and is therefore not suited

for consumer use. The accuracy for multi-view ap-

proaches is not clearly related to the number of input

images. Furthermore, SfM reconstruction approaches

are only suitable for static scenes.

For two-view stereo matching approaches,

Scharstein and Szeliski (Scharstein and Szeliski,

2002) present a large number of techniques includ-

ing a performance assessment. Their datasets are

considered standard for performance evaluations in

stereo vision and their online database lists the latest

algorithms in this domain (Scharstein and Szeliski,

2015).

Advanced stereo reconstruction (henceforth al-

ways referring to two-view stereo except otherwise

noted) algorithms consider a global energy formu-

lation and ﬁnd the set of disparities that minimizes

the energy function. The minimization is usually

performed with inference algorithms such as belief-

propagation (Felzenszwalb and Huttenlocher, 2006)

or graph cuts (Boykov et al., 2001). Tappen and Free-

man (Tappen and Freeman, 2003) compare the two

approaches. They conclude that belief-propagation is

in general faster than graph cuts but the results are less

smooth. Although Tappen and Freeman (Tappen and

Freeman, 2003) found graph cuts and belief propaga-

tion to perform similar on their dataset, we observed a

signiﬁcantly better performance of graph cuts for our

real world datasets, which is why we decided to uti-

lize the state-of-the-art graph cuts stereo algorithm by

Kolmogorov and Zabih (Kolmogorov et al., 2014) in

our work.

2.2 Active 3D Sensing

Two major types of active 3D sensors exist: Time-of-

Flight (ToF) and Structured Light (SL).

ToF sensors emit infrared-light (IR) and capture

its reﬂection. The distance assigned to a pixel is

inferred from the time delay between emission and

Enhanced Depth Estimation using a Combination of Structured Light Sensing and Stereo Reconstruction

513

reception of the IR-signal. ToF sensors run in real

time and provide good results even on textureless sur-

faces. Yet, the sensors suffer from limited resolu-

tion as well as various error sources such as noise,

multi path, ”ﬂying pixels” and are susceptible to back-

ground illumination (Foix et al., 2011). Due to size

and power limitations it is difﬁcult to deploy ToF on

smartphones.

SL sensors work by projecting a light pattern onto

the scene and then capturing it with a camera. The

distortion is used to infer the 3D geometry as it is

a function of the 3D shape (Scharstein and Szeliski,

2003a). The light pattern acts as texture and hence

texture-less scenes can also be sensed. The Mi-

crosoft Kinect performs SL sensing on a dedicated

chip achieving real-time 3D imaging. Since the pro-

jected pattern is made up of IR light, it does not work

in the presence of sunlight. The projected pattern is

relatively weak due to power limitations thus limiting

the sensing range to < 10m. Since SL sensing essen-

tially performs stereo vision, the sensing accuracy is

a function of the IR camera resolution and the depth

of the scene. In our paper we show how to properly

account for the decreasing accuracy with increasing

depth in the fusion algorithm (Section 4.1.1).

2.3 Enhanced Depth Estimation

through Fusion

In (Wei-Chen Chiu and Fritz, 2011), a promising ap-

proach that utilizes cross modal stereo reconstruction,

known as IR-image RGB registration, is proposed to

ﬁnd correspondences between the IR and RGB im-

ages of the Kinect. By combining the RGB channels

with appropriate weightings, the image response of

the IR-sensor is resembled, which allows for depth

estimation for reﬂective and transparent objects via

stereo reconstruction. Fusing the stereo reconstruc-

tion results with the structured light measurements

extends the abilities of the Kinect without the need

for additional hardware. The stereo reconstruction

approach proposed in our work does not require an

optimization as it is proposed by Wei-Chen et al. By

utilizing the same camera for both stereo images we

avoid a degradation of stereo resulting from the use of

two different cameras.

(Li et al., 2011), (Scharstein and Szeliski, 2003b)

and (Choi et al., 2012) achieve a highly accurate fu-

sion of structured light scans and stereo reconstruc-

tion by recording a projected pattern with a set of

stereo RGB cameras. The structured light sensor used

in our work provides reliable depth measurements out

of the box. Moreover, it records RGB and depth im-

ages from SL with the same sensor chip and therefore

achieves a highly precise alignment as well.

(Gandhi et al., 2012) generate a high-resolution

depth map by using ToF measurements as a low-

resolution prior that they project into the high-

resolution stereo image pair as an initial set of corre-

spondences. Utilizing a Bayesian model allows prop-

agating the depth prior to generate high-resolution

depth images.

In (Somanath et al., 2013), high-resolution stereo

images are fused with the depth measurements from

the Microsoft Kinect. The authors use a graph cuts-

based stereo approach for the fusion. Therefore, the

inﬂuence of the individual sensors is considered with

a conﬁdence map, which is determined by the stereo

images as well as the Kinect measurements. For

the fusion, Somanath et al. project the SL measure-

ments into the high-resolution stereo images, which

results in a reduced conﬁdence of the Kinect data. In-

stead, our setup allows capturing the RGB as well

as the depth images from SL with a single camera

and avoids the resulting alignment errors in the fu-

sion. Therefore, our conﬁdence consideration is not

affected by alignment and projection issues and is

solely based on the error characteristics of the smart-

phones’s SL sensor.

The aforementioned stereo-range superresolution

approaches (Li et al., 2011), (Gandhi et al., 2012) and

(Somanath et al., 2013) perform a fusion of passive

stereo vision and active depth measurements by pro-

jecting a low resolution prior into the stereo images

to perform a fusion at high-resolution. In contrast,

we propose an iterative fusion approach that is ini-

tialized at the low-resolution of the SL depth images.

This approach results in a tremendous acceleration of

the correspondence computation, since both, the num-

ber of pixels that have to be assigned a disparity and

the considered label space, are much smaller at low-

resolution. Iteratively launching the algorithm with

the disparities found in the stereo-SL depth fusion al-

lows us to retrieve a superresolution depth image in

much shorter time than the previously mentioned ap-

proaches.

2.4 Google Project Tango

Figure 1 depicts the Google Project Tango device that

we use in our experiments to perform a fusion of

SL and stereo depth maps. The Project Tango de-

vice uses essentially the same sensing technique as

the Kinect. In fact, it is equipped with a Primesense

chip for hardware-based disparity computation (Gold-

berg et al., 2014), just as is the Kinect. Contrary to

the Kinect, however, the Project Tango device uses

the same camera (Identiﬁed as “4MP” in Figure 1)

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

514

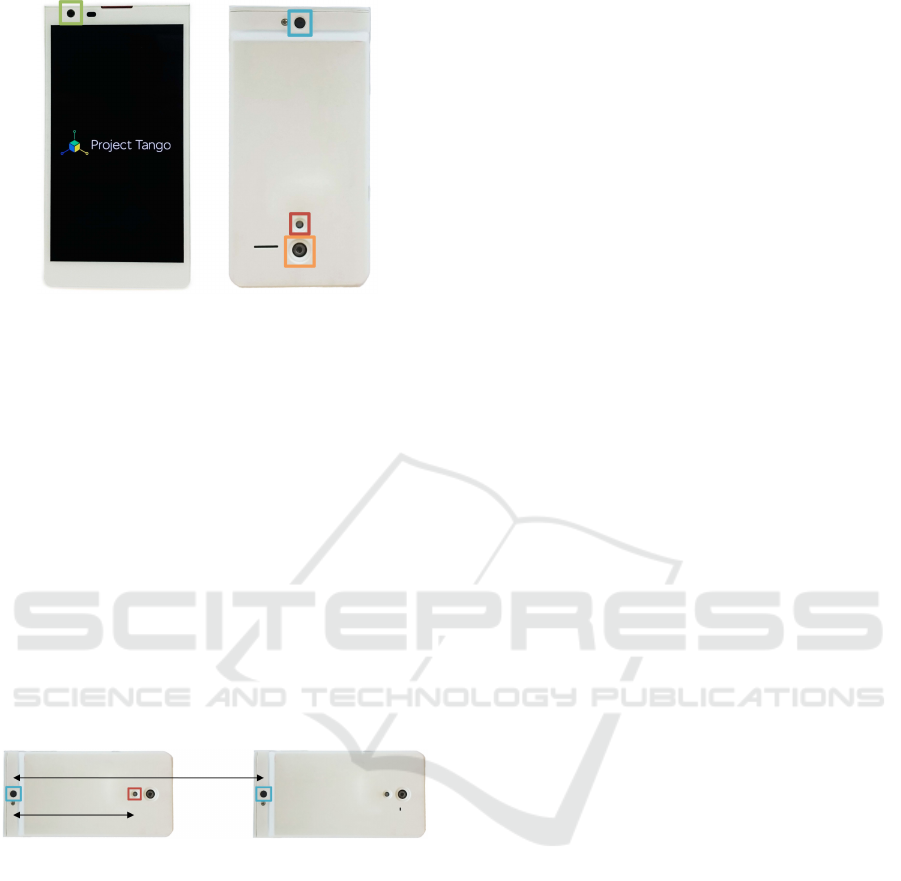
4 MP

IR projector

170

◦

ﬁsheye-camera

Figure 1: Front and back view. The image sensors are high-

lighted. According to (Goldberg et al., 2014), the 4MP cam-

era is used to capture RGB images as well as the IR pattern,

projected by the IR projector, for depth estimation.

to capture RGB images as well as the projected IR

pattern for depth estimation. This is important since

both, the RGB and the corresponding SL depth im-

ages are readily aligned.

In our experimental setup, we achieve a horizon-

tal shift of b

stereo

between the stereo image pairs, as

shown in Figure 2, by moving the Project Tango de-

vice on a slider. Strictly speaking, this is SfM (see

Section 2.1). However, due to the controlled move-

ment, we are simulating a stereo camera pair.

The stereo depth image is computed w.r.t. the ini-

tial position and is fused with the SL depth image cap-

tured at the same position.

stereo

= 30cm

Figure 2: Recording depth images with the Project Tango

device: The smartphone is moved by b

stereo

to capture a

stereo image pair. Simultaneously, the internal SL chip

computes a depth image using the projected IR pattern

which has an effective baseline of b

, which we determined

in a calibration process.

3 PROBLEM FORMULATION

Here we illustrate the problem of depth estimation us-

ing solely SL sensing or only stereo reconstruction

more formally and demonstrate their complementary

properties to motivate our proposed solution for depth

map fusion using stereo and SL vision. For that, we

use the setup introduced in Section 2.4.

Figure 3 reveals the strengths and weaknesses of

the Project Tango device’s SL depth sensing abili-

ties. The ﬁgure shows an RGB image along with a

heatmap that encodes depth values up to a distance

of 10 meters. It can be seen that the sensor performs

well on nearby and smooth elements, but fails on illu-

minated or glossy surfaces. We note that although the

shown depth map has been generated with the Project

Tango device, it is exemplary for common SL 3D sen-

sors.

Similar to Figure 3, Figure 4 shows the depth map

for the same scene, however this time computed us-

ing standard stereo vision. In this case, the depth es-

timation provides good results for elements that are

affected by the projector image, as well as the glossy

poster in the scene. As expected, it fails on textureless

elements such as the wall or the nearby chair.

The complementary properties of the two depth

maps that correspond to Figures 3 and 4 are shown

in Figure 5. From a naive fusion, where the depth

estimate for a pixel is adopted from SL whenever

available and ﬁlled with a value from the depth map

from stereo otherwise, it can be seen that a depth map

with a substantially reduced amount of “holes” is pro-

duced. The ﬁgure clearly shows that a substantial

amount of depth data is contributed by either depth

map, hinting only the combination of both can lead

to signiﬁcant improvement of the depth maps. Hence,

the goal of this paper is to develop a fusion approach

for joint stereo & structured light depth map esti-

mation. The complementary character of both tech-

niques inspired us to think of a more sophisticated fu-

sion than a simple naive fusion, since not only lots of

information gained from stereo vision is wasted, but

also geometric priors, typically incorporated in stereo

reconstruction through regularization, are enabled.

4 PROPOSED FUSION SCHEME

In this section we propose a fusion scheme that ex-

ploits the complementary properties of stereo recon-

struction and structured light sensing beyond the sim-

ple fusion approach presented in Section 3. To that

end, a global energy formulation that models the data

cost as well as the cost for the spatial conﬁguration

of the disparities, as is typically the case in state-of-

the-art stereo vision, is considered. The data term of

the energy function is extended to incorporate prior

knowledge derived from the SL data as explained in

Section 4.1.1. This prior knowledge is also incorpo-

rated in the smoothness term, as explained in Section

4.1.2, to compensate for the shortcomings of typically

employed smoothness constraints in state-of-the-art

stereo reconstruction. The resulting fusion scheme

is applied in an iterative process involving sequen-

Enhanced Depth Estimation using a Combination of Structured Light Sensing and Stereo Reconstruction

515

0 2 4

8 10

Figure 3: Sample scene captured by Tango’s SL sensor. Depth values are color coded. 0 depth (dark blue) represents missing

depth data. Key regions are highlighted (

-

), where

 does not include any depth information due to the projector

image that is confusing the IR-pattern;

 is punctured with multiple holes indicating the maximum range of the SL projector

has been reached (exceeded). Also the depth values are strongly varying despite the planar shape which is due to the high

depth uncertainty at large distances;

 highlights a glossy poster which makes the IR-pattern unusable for the IR-camera;

 exhibits missing depth values next to the edge of the chair due to IR projection pattern occlusion;

 displays the partly

reconstruction of the backs of two chairs illuminated by the projector image;

,

 show the well estimated depth values for

the backs of the two nearby chairs.

0 2 4

8 10

Figure 4: Depth map from stereo using block-matching. Key regions are highlighted by boxes (

-

), where

 shows a

richly textured area that allows a good reconstruction;

 is poorly reconstructed as a result of missing texture in this area;

 depicts a glossy poster that is well reconstructed;

 provides rich texture for a good reconstruction ;

 only allows a

fragmented reconstruction resulting from missing texture of the scene;

 performs better than

 despite having the same

shape owing to the poster.

tial upsampling and joint reconstruction to produce

higher resolution depth maps as explained in Sec-

tion 4.2.

Before diving into the details we want to note that

we interchangeably use the terms disparity and depth

since they are related directly to one another. As will

be apparent, however, all mathematical formulas and

the actual implementation are based on disparities and

disparity maps.

4.1 Joint Optimization using Stereo and

Strucured Light

We propose a fusion of structured light and stereo

depth maps based on the built-in sensors of the smart-

phone shown in Figure 2. The energy formulation

used to ﬁnd the optimal set of disparities is inspired

by (Kolmogorov et al., 2014). The disparity f

∈

, L

, . . . , L

}, for every pixel p ∈ P, is found such

that the resulting conﬁguration of the disparities f

minimizes the energy

E( f ) = E

data

( f ) + E

smoothness

( f ) + E

( f ), (1)

where E

data

( f ) represents the data cost that also

incorporates the structured light measurements.

smoothness

( f ) considers the spatial conﬁguration of

the disparities and E

( f ) aggregates the occlusion

and the uniqueness term which are explained in (Kol-

mogorov et al., 2014).

We note here that whenever using the word “orig-

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

516

 Fused depth map

 Color coding of

depth source

Figure 5: Naive fusion of depth maps from stereo and struc-

tured light.

 shows the depth map obtainable with a naive

fusion scheme adopting the SL value whenever available for

a pixel and using the stereo value otherwise.

 Red implies

a depth value from stereo reconstruction was used as op-

posed to blue which encodes values from SL. Black means

no depth value sensed using either technique. Both sensing

techniques are seen to contribute signiﬁcantly towards the

ﬁnal outcome.

inal” we refer to Kolmogorov and Zabih’s algorithm

in its original form and as implemented by them.

4.1.1 Data Cost

We propose to extend the data term introduced in

Equation (1) which typically accounts for the stereo

matching cost C

with an additional term to account

for the structured light measurements as follows:

( f ) =

∑

(p) +C

(p), (2)

where C

describes the cost contributed by the struc-

tured light sensor. We propose to model C

accord-

ing to

(p) = w





1 − e

( f

− f

)





= w

(p).

(3)

The weighting factor w

controls the inﬂuence of the

cost term and c

is the maximal penalty that can

be assigned. C

(p) represents an inverse Gaussian

function and is motivated by the assumption of a nor-

mally distributed structured light disparity measure-

ment error. This cost term ensures that whenever a

prior measurement f

is available and the considered

disparity f

deviates from it, a penatly is contributed.

More speciﬁcally, the cost added by C

(p) depends

on the assigned disparity f

as well as the disparity

measured by the SL sensor f

, weighted using the

Gaussian function. We deﬁne the weighting factor w

according to

(

ρ f

∈ [ f

− 3σ

, f

+ 3σ

]

0 else,

(4)

where ρ can be chosen from the interval (0, 1] accord-

ing to the weight to be assigned for the prior. We

are inspired for this particular design by the work of

(Khoshelham and Elberink, 2012) in which they in-

vestigated the Kinect’s sensing accuracy. Assuming

a normally distributed disparity measurement of con-

stant variance, they derived the depth measurement

error. They concluded and experimentally veriﬁed

that the depth measurement uncertainty has a standard

deviation that quadratically increases with the sensed

distance. Since the Project Tango device’s SL sen-

sor essentially works the same way, we use the same

uncertainty model assuming the error in the dispar-

ity domain is distributed in a Gaussian fashion with a

constant variance σ

For the standard data term C

(p) in stereo match-

ing, we use the Birchfeld-Tomasi pixel dissimilarity

measure (Birchﬁeld and Tomasi, 1998) as follows:

(p) = w

min



T (I

(p), I

(q))

, c



, (5)

T (•, •) computes the data cost according to the com-

monly used Birchfeld-Tomasi dissimilarity measure

for the pixel at position p in the left image I

and the

pixel at position q in the right image I

. c

trims the

cost and the weighting factor is set to be w

= 1 −w

We obtained the best results for considering the struc-

tured light related term with a larger weighting than

the Birchfeld-Tomasi term, resulting from the higher

reliability of structured lighting. We empirically de-

termined the best fusion results for w

∈ [0.6; 0.8],

depending on the underlying scene.

This particular energy formulation allows for a

signiﬁcant acceleration of the computation of the dis-

parities. Figure 6 illustrates how the speed-up is

achieved. In the ﬁgure, the grid represents the pixel

positions for which the disparities have to be esti-

mated, which have to be evaluated for the whole la-

bel space [L

min

max

], if no prior information from

the structured light depth map is available. Whenever

prior information is available from the SL data, indi-

cated by the red dots, the label search can be limited

to the uncertainty interval of the structured light mea-

surements. We explicitly limit the label space for f

to a range of f

± 3σ

, since there is a 99% chance

that the true disparity

is within that interval assum-

ing normally distributed SL disparity measurements.

This reduces the complexity in case of large search in-

tervals and high-resolution stereo images signiﬁcantly

as shown in the results (see Section 5).

4.1.2 Smoothness Cost

The smoothness term is based on the assumption

that neighboring pixels with similar intensity values

should be assigned the same disparity. If this assump-

tion is violated, a large penalty is added to the cost

function in Equation (1). In case of a strong contrast

Enhanced Depth Estimation using a Combination of Structured Light Sensing and Stereo Reconstruction

517

(p) ± 3 σ

max

min

Figure 6: Disparity label search space with and without

prior knowledge on the disparities.

among neighboring pixels, the penalty for changing

neighboring disparities is smaller and equal dispari-

ties among neighboring pixels do not contribute any

cost. In (Kolmogorov et al., 2014), the authors set the

threshold for similar pixels according to

max(|I

) − I

∞

, |I

) − I

∞

) < 8, (6)

where p

, p

are neighboring pixels in the left and

, q

in the right image. The smoothness term in (1)

can therefore be expanded to

( f ) =

∑

∼a

· 1( f (a

) 6= f (a

)), (7)

where a

∼ a

indicates that pixels p

and p

are

adjacent and share the same disparity f

= f

. In

that case, both assignments should be either active

or inactive, hence 1 ( f (a

) 6= f (a

)), otherwise the

smoothness term contributes a penalty V

. The

terms active and inactive refer to whether a disparity

is necessarily assigned to a pixel or a pixel is other-

wise labeled as occluded and accordingly not active.

In (Kolmogorov et al., 2014) the smoothness cost is

deﬁned as follows











3λ if max(|I

) − I

∞

) − I

∞

) < 8

λ if max(|I

) − I

∞

) − I

∞

) ≥ 8

, (8)

where λ is a constant that models the inﬂuence of the

smoothness term. However, in case of slanted sur-

faces (here we refer to surfaces that are not parallel to

the imaging plane and hence appear slanted) that ex-

hibit a homogeneous coloring, such as the wall on the

right hand-side of Figure 7

, the assumption that

neighboring pixels with similar intensity should be

assigned equal disparities is no longer valid and re-

sults in a clustering of the assigned disparity values as

 Scene with slanted wall

 Gradient map from SL

 Original smoothness

constraint (8)

 Modiﬁed smoothness

constraint (9)

Figure 7: Beneﬁts of the modiﬁed smoothness constraint

compared to the original one used in (Kolmogorov et al.,

2014). The modiﬁed constraint exploits prior depth knowl-

edge from structured lighting to compute a disparity gradi-

ent map which is used to downweight the smoothness con-

straint for slanted surfaces disallowing the enforcement of a

uniform disparity on surfaces of homogeneous pixel inten-

sity however with a varying depth. Notice, the ﬂoor is still

largely assigned a single disparity value as no SL measure-

ments are available on this image region and accordingly a

gradient map for this region cannot be computed.

shown in 7

. To overcome this deﬁciency, we again

exploit the prior information available from the SL

sensor. We introduce an additional term that is based

on the gradient map of the structured light sensor data

(which is shown for the same example in Figure 7

)

such that the smoothness penalty becomes aware of

the existence of slanted surfaces and is adapted ac-

cordingly. More speciﬁcally, the smoothness penalty

is extended by

= 0.1 λ if











O,l

≤ OD

) ≤ c

O,u

O,l

≤ OD

) ≤ c

O,u

(9)

where OD

is the gradient map of the SL sensor

measurement. The constant c

O,l

(respectively c

O,u

)

serves as a lower (upper) threshold for the gradient

values. The thresholds are introduced to assign a low

smoothness penalty for slanted surfaces for which the

gradient values are supposed to vary within an inter-

val [c

O,l

O,u

]. The gradient constraint in Equation

(9) is dominant and overrules Equation (8). The ad-

ditional constraint was found to signiﬁcantly improve

the performance of the algorithm for slanted surfaces

as shown in Figure 7

.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

518

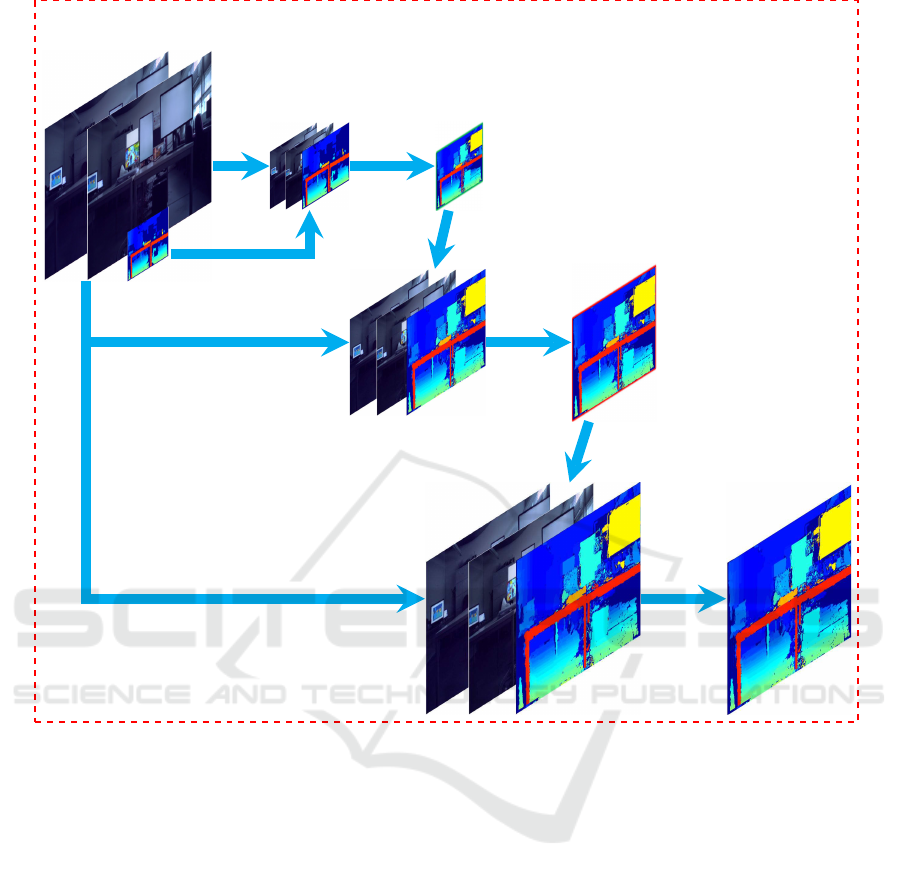
Downsample RGB

4 ↓

Joint

Optimization

Joint

Optimization

Joint

Optimization

Upsample 2 ↑

Downsample RGB

2 ↓

RGB Full Resolution

320 × 180

1280 × 720

Iterative Upsampling

Stage

320 × 180

Iterative Upsampling

Stage

640 × 360

Iterative Upsampling

Stage

1280 × 640

Figure 8: Iterative fusion: Starting with down-sampled stereo images, a ﬁrst iteration of fusion is very efﬁciently achieved

resulting in a dense depth map, which, after upsampling, serves as an enhanced prior for a second iteration of fusion at a

higher resolution. The process can be continued until achieving the desired resolution. In all stages, a joint optimization of

the prior and the RGB-images is performed by utilizing a global energy formulation.

4.2 Depth Map Superresolution

Since the structured light measurements and the

stereo images recorded with the Google Project Tango

device do not have the same resolution, we designed

an iterative algorithm that increases the resolution of

the disparity map from the low-resolution of the struc-

tured light sensor to the high-resolution of the stereo

images. As opposed to other approaches that project

a low resolution depth prior into the high resolution

stereo images to initiate a fusion, we propose an it-

erative approach that initializes the fusion at low-

resolution to obtain a dense disparity map, which is

then upsampled and used to reinitialize the algorithm

in a second iteration. Again, a nearest neighbor up-

sampling is applied to the disparity map found in the

second stage and the algorithm is initialized a third

time and converges at the resolution of the stereo im-

ages. The underlying rationale behind starting the fu-

sion at the lower resolution of the SL depth maps is

related to Equations (3) and (4). In essence, an up-

sampling of the SL depth image by a factor s to adapt

its resolution to the stereo image pair also implies ex-

tending the disparity search range by the same factor.

Accordingly, we do the converse by ﬁrst downsam-

pling the stereo image pair. Hence, we obtain a great

reduction of the disparity search intervals for pixels

with and without a disparity prior, leading to a very

fast computation of the ﬁrst fused depth map at the

same resolution of the SL depth map. The results

in Figure 12 show that this ﬁrst fused depth map is

computed at a fraction of that with the full stereo im-

age pair resolution. This ﬁrst fused depth map in turn

makes up a reliable prior for the second fusion stage

Enhanced Depth Estimation using a Combination of Structured Light Sensing and Stereo Reconstruction

519

 Unprocessed image

 Histogram equalization

+ bilateral ﬁltering

 Unprocessed image

 Bilateral ﬁltering with

background subtraction

Figure 9: Effect of histogram equalization + bilateral ﬁlter-

ing (

 →

) and bilateral ﬁltering with background sub-

traction (

 →

) on sample images.

at the doubled resolution and in turn signiﬁcantly re-

duces the disparity search space for the pixels. For the

ﬁrst iteration, the disparity search range for a pixel p

that exhibits prior knowledge is set to f

± 3σ as

explained in Section 4.1.1. However, if the disparity

map resulting from the ﬁrst iteration of the algorithm

can be assumed to exhibit the true disparities, upsam-

pling it by a factor of 2

would result in an uncer-

tainty of ±2

n−1

pixels. Therefore, unlike in the ﬁrst

iteration, the initialization of the proposed fusion al-

gorithm with the disparity map obtained from the pre-

vious stage upsampled by a factor of 2, only requires

a search interval of f

± 1 pixels for a pixel p that

exhibits prior knowledge in the 2

and 3

stage. An

initialization of the algorithm with a dense prior there-

fore ensures a tremendous acceleration of the dispar-

ity computation for the 2

and 3

iteration of the

iterative fusion. Figure 8 shows the 3 stages of the

proposed algorithm.

5 RESULTS

This section presents results that we obtained using

the fusion approach explained in Section 4. Before

running the algorithm, the stereo images are prepro-

cessed to adjust their brightness and remove noise.

Depending on the image scene, we found a pipeline

of histogram equalization (Liling et al., 2012) and bi-

lateral ﬁltering (Ansar et al., 2004) (see Figure 9

,

), or bilateral ﬁltering with background subtraction

(Ansar et al., 2004) (see Figure 9

,

) to improve

the performance of the algorithm.

 Depth from

structured light

 Depth from

original graph cuts stereo

 Our approach

stage

 Our approach

stage

Figure 10: From the depth map obtained using SL sens-

ing

 many regions have no depth values due to bright

illumination or their surface properties.

 shows a depth

map computed using state-of-the-art stereo reconstruction

via graph cuts. Of particular note is that several objects in

the scene are assigned a wrong disparity (e.g. the backs

of a chair, table top) which can be related to ambiguities

in the cost computation. Also, the slanted wall on the left-

hand side of the disparity map contains a large number of

missing assignments and exhibits a strong clustering of dis-

parities.

 and

 show the result achieved with the fusion

algorithm proposed in this work. Both disparity maps con-

tain a signiﬁcantly higher number of disparity assignments

than

 and

. At a ﬁrst glance, both images look alike, but

 has a higher spatial resolution (pixels) and depth resolu-

tion than

. The latter can be observed from the magniﬁed

parts in

 and

, where only two disparities are assigned

for the enlarged part of

, while for the enlarged part in

,

a range of disparity assignments results in a ﬁner discretiza-

tion of the depth space (a seperate colormap is used for this

enlargement).

5.1 Datasets

To the best of our knowledge there exists no bench-

mark dataset for joint stereo-SL depth estimation. Ac-

cordingly, we show the results obtained on three sam-

ple scenes captured with the Project Tango device.

Through detailed analysis we highlight how individ-

ual blocks contribute towards providing a ﬁnal esti-

mation that is better than that obtainable with either

stereo or SL reconstruction alone.

Lecture Hall: We generated depth images of

the scene shown in Figure 9

, with SL sensing and

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

520

 Uncertainty

stage

 Uncertainty

structured light

 Uncertainty

stage

0 100 200 300

Figure 11: Uncertainty/resolution in the depth computation

for the ﬁrst stage of the fusion algorithm

, the structured

light sensor

 and the third stage of the iterative fusion

 in mm. For

, the uncertainty/resolution is computed

using the focal length and the baseline b

assuming a stan-

dard deviation in disparity measurement σ

-pixel dis-

parities, a value adopted from a well-known fact about the

Kinect’s Primesense chip. The uncertainty/resolution plot

shows that the 3

-stage of the iterative fusion approach has

a higher depth resolution than

 and

.

stereo reconstruction as well as using our proposed

fusion algorithm. The resulting depth maps are de-

picted in Figure 10. The regions of the depth maps

covering surfaces illuminated by the strong light from

the projector reveal how beneﬁcial the proposed fu-

sion of SL sensing and stereo reconstruction is. The

noise in the stereo depth map (Figure 10

) observed

on the back of the close chair no longer appears in the

fused depth map, as the adapted data term (Section

4.1.1) reduces the ambiguity in disparity assignments.

Furthermore, our approach reduces the clustering of

disparities, also observable in

, by utilizing a gradi-

ent map based on the SL measurements as explained

in Section 4.1.2.

Figure 11 shows the depth resolution of our ap-

proach vs. the depth resolution of the structured light

sensor of the Project Tango device. It can be seen that

the ﬁnal stage of the suggested algorithm achieves

a better depth resolution than the SL measurements.

Figure 12: Computation time required by the original graph

cuts stereo reconstruction algorithm vs. computation time

of the iterative fusion approach for the dataset ”lecture hall”

in seconds. From left to right: original graph cuts stereo re-

construction, iterative fusion approach 1

stage, - 2

stage

and - 3

stage.

 RGB image

 Depth from

structured light sensing

 Depth from

original graph cuts stereo

 Depth using

proposed approach

Figure 13: The structured light sensor

 could not cap-

ture the depth measurements for the monitors shown in

, since the infrared pattern cannot be retrieved in that

case. The original graph cuts stereo reconstruction algo-

rithm

 shows many wrong disparity assignments, result-

ing from occlusion and ambiguities. The corresponding

disparity map also contains many fragments and is rather

noisy. The iterative fusion approach

 instead, provides

a dense disparity map that outperforms the individual mea-

surements by far and even reconstructs the slanted wall and

ﬂoor, which is challenging for the original graph cuts stereo

reconstruction algorithm.

Beyond the enhanced depth image quality, the pro-

posed iterative fusion algorithm allows us to tremen-

dously reduce the computational complexity of the

disparity search, as illustrated in Figure 12. It shows

the processing times of the original graph cuts stereo

reconstruction algorithm vs. the three stages of the it-

erative upsampling approach. It can be seen that the

computation time of the depth image is reduced by

almost 90%.

Student Lab: Figure 13 depicts the evaluation

of the dataset ”student lab”, which shows a common

ofﬁce environment. In this case, reconstruction using

structured light scanning fails for the monitors, which

disturbs the IR-pattern. However, the global stereo re-

construction approach successfully reconstructs most

of the monitors. The ﬁgure clearly shows how the

proposed iterative fusion approach compensates for

the shortcomings of both modalities and also allows

a strong reduction of the required computation time

from 1464s to 83.7s. In other words, the calculation

time is reduced by 94.3%.

Stairs: Figure 14 shows the evaluation of the

dataset ”stairs”. The scene exhibits a large number of

Enhanced Depth Estimation using a Combination of Structured Light Sensing and Stereo Reconstruction

521

 RGB image

 Depth from

structured light

 Depth from

original graph cuts stereo

 Depth using

proposed approach

Figure 14: The structured light sensor

 is signiﬁcantly

disturbed by the sunlight that can be observed through the

large glass windows. The original graph cuts stereo recon-

struction algorithm

 fails to reconstruct the ﬂoor as well

as to resolve the large number of depth levels associated

with the steps. The slanted wall is represented by a few dis-

parity clusters and does not allow to recognize the geometry

of the scene. The iterative fusion approach

 instead, per-

forms a good reconstruction of the slanted wall exploiting

the SL measurements and also resolves the ﬁne depth levels

of the steps in the scene to a large extent. Stereo reconstruc-

tion also beneﬁts the fusion by partly reconstructing the wall

in the background.

discrete depth levels at the steps of the stairs, as well

as a continuously increasing depth along the slanted

wall on the right hand side of

. The iterative fusion

approach allows resolving the ﬁne depth levels of the

stairs and also outperforms the standard graph cuts

stereo reconstruction of the slanted wall in the scene.

The computation time of the graph cuts stereo algo-

rithm was measured with 560s, while all three stages

of the iterative fusion approach only require 48.7s,

which corresponds to a reduction 91.3%.

6 CONCLUSION

In this paper, we presented a novel approach to gener-

ate high-resolution depth maps from a fusion of a low-

resolution structured light prior with state-of-the-art

stereo reconstruction in an iterative process. Unlike

other approaches that perform a fusion of active and

passive methods in 3D imaging, we do not upsam-

ple a low-resolution prior to match the high-resolution

of the stereo images, but instead perform a fusion at

low-resolution and use the resulting disparity map as

a prior to iteratively reinitialize the algorithm until it

converges. This strategy has two major advantages.

Limiting the disparity search to the uncertainty inter-

val of the prior greatly reduces ambiguities and also

allows for a signiﬁcant reduction of the runtime of the

algorithm. Initializing the fusion at low-resolution

ampliﬁes the effect, as not only the disparity search

range for low-resolution images is smaller, but also

the number of pixels that have to be assigned a dispar-

ity. High-resolution disparity maps are then inferred

in an iterative upsampling process that ensures a con-

sistent computational complexity, also for sparse pri-

ors. For the fusion approach discussed in this paper,

we found the following points to have potential for

further improvement in future work.

• Without a prior, surfaces with continuously

changing disparities are challenging for the algo-

rithm. This problem could be reduced with an ad-

ditional constraint based on the stereo images.

• A GPU-implementation of the algorithm could

help to signiﬁcantly accelerate the computation.

• Initializing the algorithm at even lower resolution

can further decrease the runtime.

REFERENCES

Ansar, A. I., Huertas, A., Matthies, L. H., and Goldberg, S.

(2004). Enhancement of stereo at range discontinu-

ities. In Defense and Security, pages 24–35. Interna-

tional Society for Optics and Photonics.

Birchﬁeld, S. and Tomasi, C. (1998). Depth discontinuities

by pixel-to-pixel stereo. In Computer Vision, 1998.

Sixth International Conference on, pages 1073–1080.

Boykov, Y., Veksler, O., and Zabih, R. (2001). Fast ap-

proximate energy minimization via graph cuts. Pat-

tern Analysis and Machine Intelligence, IEEE Trans-

actions on, 23(11):1222–1239.

Choi, S., Ham, B., Oh, C., gon Choo, H., Kim, J., and

Sohn, K. (2012). Hybrid approach for accurate depth

acquisition with structured light and stereo camera.

In Broadband Multimedia Systems and Broadcast-

ing (BMSB), 2012 IEEE International Symposium on,

pages 1–4.

Engel, J., Sch

ops, T., and Cremers, D. (2014). Lsd-slam:

Large-scale direct monocular slam. In Computer

Vision–ECCV 2014, pages 834–849. Springer.

Felzenszwalb, P. F. and Huttenlocher, D. P. (2006). Efﬁcient

belief propagation for early vision. International jour-

nal of computer vision, 70(1):41–54.

Foix, S., Alenya, G., and Torras, C. (2011). Lock-in time-

of-ﬂight (tof) cameras: A survey. 11(9):1917–1926.

Gandhi, V., Cech, J., and Horaud, R. (2012). High-

resolution depth maps based on tof-stereo fusion. In

Robotics and Automation (ICRA), 2012 IEEE Interna-

tional Conference on, pages 4742–4749.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

522

Goldberg, A. O., S., L., M., D., T., t., J., S., J., D.,

and T., G. (2014). Google tango teardown.

www.iﬁxit.com/Teardown/Project+Tango+Teardown/23835.

Khoshelham, K. and Elberink, S. O. (2012). Accuracy and

resolution of kinect depth data for indoor mapping ap-

plications. Sensors, 12(2):1437–1454.

Kolmogorov, V., Monasse, P., and Tan, P. (2014). Kol-

mogorov and Zabihs Graph Cuts Stereo Matching Al-

gorithm. Image Processing On Line, 4:220–251.

Li, Q., Biswas, M., Pickering, M. R., and Frater, M. R.

(2011). Accurate depth estimation using structured

light and passive stereo disparity estimation. In Im-

age Processing (ICIP), 2011 18th IEEE International

Conference on, pages 969–972.

Liling, Z., Yuhui, Z., Quansen, S., and Deshen, X. (2012).

Suppression for luminance difference of stereo image-

pair based on improved histogram equalization. Pro-

ceedings of the computer science and technology, 6:2.

Newcombe, R. A., Lovegrove, S. J., and Davison, A. J.

(2011). Dtam: Dense tracking and mapping in real-

time. In Computer Vision (ICCV), 2011 IEEE Inter-

national Conference on, pages 2320–2327. IEEE.

Occipital (2015). Occipital depth sensors.

http://occipital.com/.

Piszczor, M. and Yang, C. (2014). Project tango.

https://sites.google.com/a/google.com/project-tango-

sdk/home.

Scharstein, D. and Szeliski, R. (2002). A taxonomy and

evaluation of dense two-frame stereo correspondence

algorithms. International journal of computer vision,

47(1-3):7–42.

Scharstein, D. and Szeliski, R. (2003a). High-accuracy

stereo depth maps using structured light. In Com-

puter Vision and Pattern Recognition, 2003. Proceed-

ings. 2003 IEEE Computer Society Conference on,

volume 1, pages I–195.

Scharstein, D. and Szeliski, R. (2003b). High-accuracy

stereo depth maps using structured light. In Com-

puter Vision and Pattern Recognition, 2003. Proceed-

ings. 2003 IEEE Computer Society Conference on,

volume 1.

Scharstein, D. and Szeliski, R. (2015). A

taxonomy and evaluation of dense two-

frame stereo correspondence algorithms.

http://www.vision.middlebury.edu/stereo/.

Seitz, S. M., Curless, B., Diebel, J., Scharstein, D., and

Szeliski, R. (2006). A comparison and evaluation of

multi-view stereo reconstruction algorithms. In Com-

puter vision and pattern recognition, 2006 IEEE Com-

puter Society Conference on, volume 1, pages 519–

528. IEEE.

Somanath, G., Cohen, S., Price, B., and Kambhamettu, C.

(2013). Stereo+kinect for high resolution stereo cor-

respondences. In 3D Vision - 3DV 2013, 2013 Inter-

national Conference on, pages 9–16.

Tappen, M. F. and Freeman, W. T. (2003). Comparison

of graph cuts with belief propagation for stereo, us-

ing identical mrf parameters. In Computer Vision,

2003. Proceedings. Ninth IEEE International Confer-

ence on, pages 900–906. IEEE.

Wei-Chen Chiu, U. B. and Fritz, M. (2011). Improving

the kinect by cross-modal stereo. In Proceedings of

the British Machine Vision Conference, pages 116.1–

116.10.

Enhanced Depth Estimation using a Combination of Structured Light Sensing and Stereo Reconstruction

523